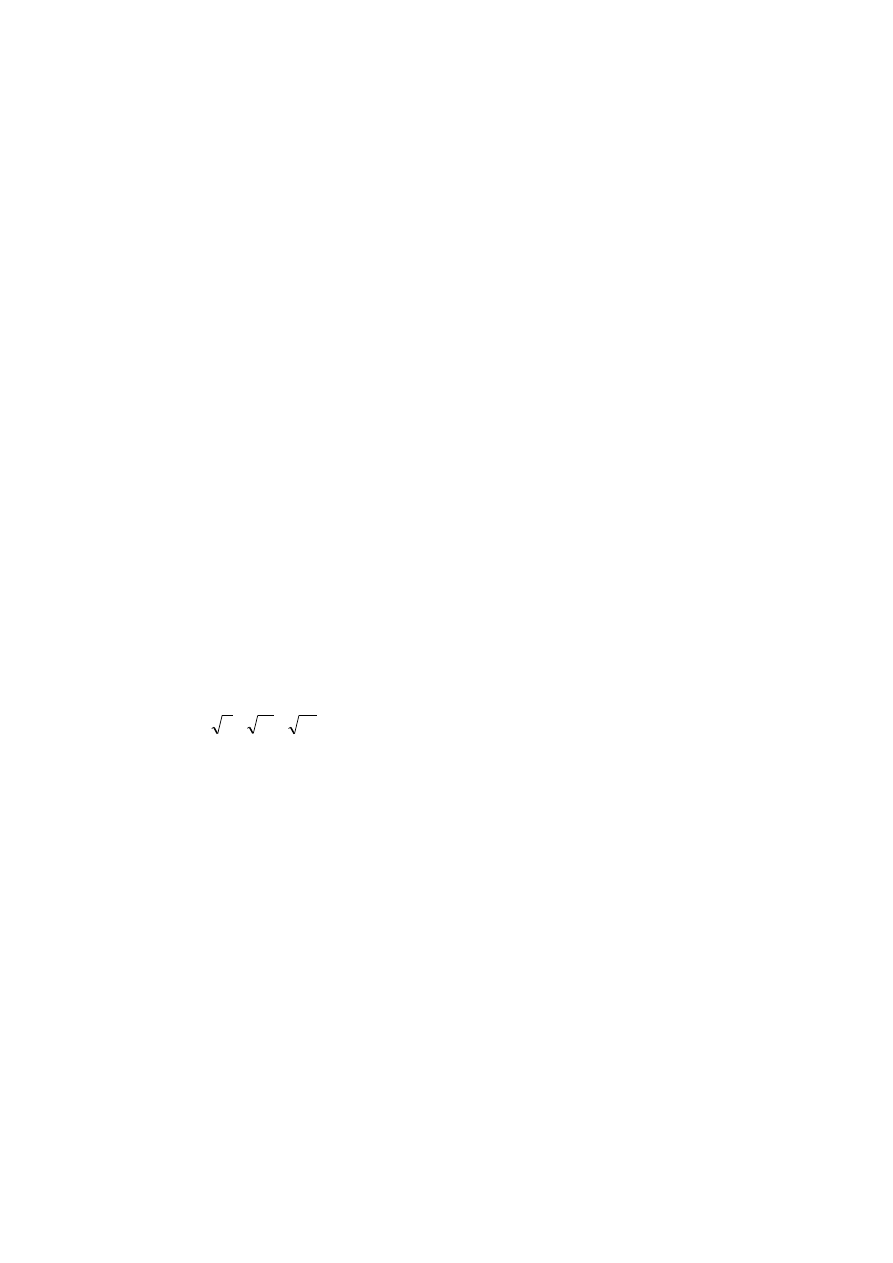
UKSW ALGEBRA LINIOWA
Matematyka, Informatyka i ekonometria Kazimierz Jezuita
ZADANIA DOMOWE - Seria 1
1. Relacja rekurencyjna, konwencja sumacyjna, suma ciągu geometrycznego.
Znaleźć wzór na ogólny wyraz ciągu opisanego relacją rekurencyjną:
3
1
x
,
n
n
n
x
x
2
1
,
sprowadzając problem do obliczania sumy
n
k
k
n
a
x
0
,
?
k
a
.
2. Konwencja sumacyjna, zmiana wskaźnika sumacyjnego, przemienność sumowania .
Obliczyć sumę
n
k
n
k
S
0
)
2
1
(
w następujący sposób. Dokonując zamiany wskaźnika
sumacyjnego
k
n
l
k
otrzymujemy nową postać sumy
n
l
n
S
0
)
(
. Dodając oba
wyrażenia na sumę obliczamy
n
S
2
( wskaźniki sumacyjne oznaczamy przy tym tą samą literą
j
).
3. Konwencja sumacyjna, dwumian Newtona, symbol Newtona.
Przedstawić wyrażenie
10
1
x
x
w postaci sumy. Obliczyć współczynniki liczbowe przy
5
x
i
0
x
.
4. Konwencja sumacyjna, symbol Newtona, zasada indukcji 1, suma ciągu arytmetycznego.
Wykazać metodą indukcji, że
3
1
)
(
0
n
k
k
n
n
k
.
5. Relacja rekurencyjna, zasada indukcji 2 .
Wykazać metodą indukcji, że ogólny wyraz ciągu określonego rekurencyjnie:
6
1
a
,
18
2
a
,
18
8
2
1
2
n
n
n
a
a
a
ma postać
2
4
n
n
a
.
6. Dowód nie wprost, ciąg arytmetyczny, liczby wymierne i niewymierne.
Czy liczby rzeczywiste a,b,c mogą być wyrazami (niekoniecznie kolejnymi) ciągu
arytmetycznego, jeśli
c
b
a
;
a
i
b
są wymierne, natomiast
c
niewymierne?
7. Dowód nie wprost, ciąg geometryczny, rozkład liczby naturalnej na czynniki pierwsze.
Czy liczby
17
,
11
,
7
mogą być wyrazami (niekoniecznie kolejnymi) ciągu
geometrycznego?
8. Iloczyn kartezjański, relacje.
Zbadać właściwości następujących relacji
R
w zbiorze
2
,
1
,
0
A
:
A
A
R
n
m
)
,
(
jeśli
a)
m
mn
, b)
A
n
m
, c)
1
,
max n
m
, d)
2
2
2
n
m
, e)
n
m
9. Relacja, częściowy porządek.
Niech
4
,
3
,
2
,
1
B
. Wykazać, że relacja w zbiorze
B
B
określona następująco:
)
,
(
~
)
,
(
l
k
n
m
jeśli
k
m
i
l
n
, jest relacją porządku? Podać przykład najdłuższego,
uporządkowanego ciągu elementów zbioru
B
B
.
10. Relacja równoważności, klasy równoważności.
Wykazać, że relacja w
R
R
taka, że
2
2
1
1
,
~
,
y
x
y
x
jeśli
1
2
2
1
y
x
y
x
jest relacją
równoważności. Opisać klasy równoważności.
11. Relacja, wykres funkcji.
Czy relacja
Z
N
R
,
2
2
:
)
,
(
y
x
y
x
R
może być wykresem funkcji
Z
N
f
:
?
12. Funkcja, injekcja, surjekcja, obraz zbioru, przeciwobraz zbioru.
Czy funkcja
Z
Z
Z
f
:
,
1
)
,
(
n
m
n
m
f
jest: a) injekcją? b) surjekcją?
Znaleźć
})
1
{
(
A
f
oraz
})
0
({
1
f
i
})
3
({
1
f
.