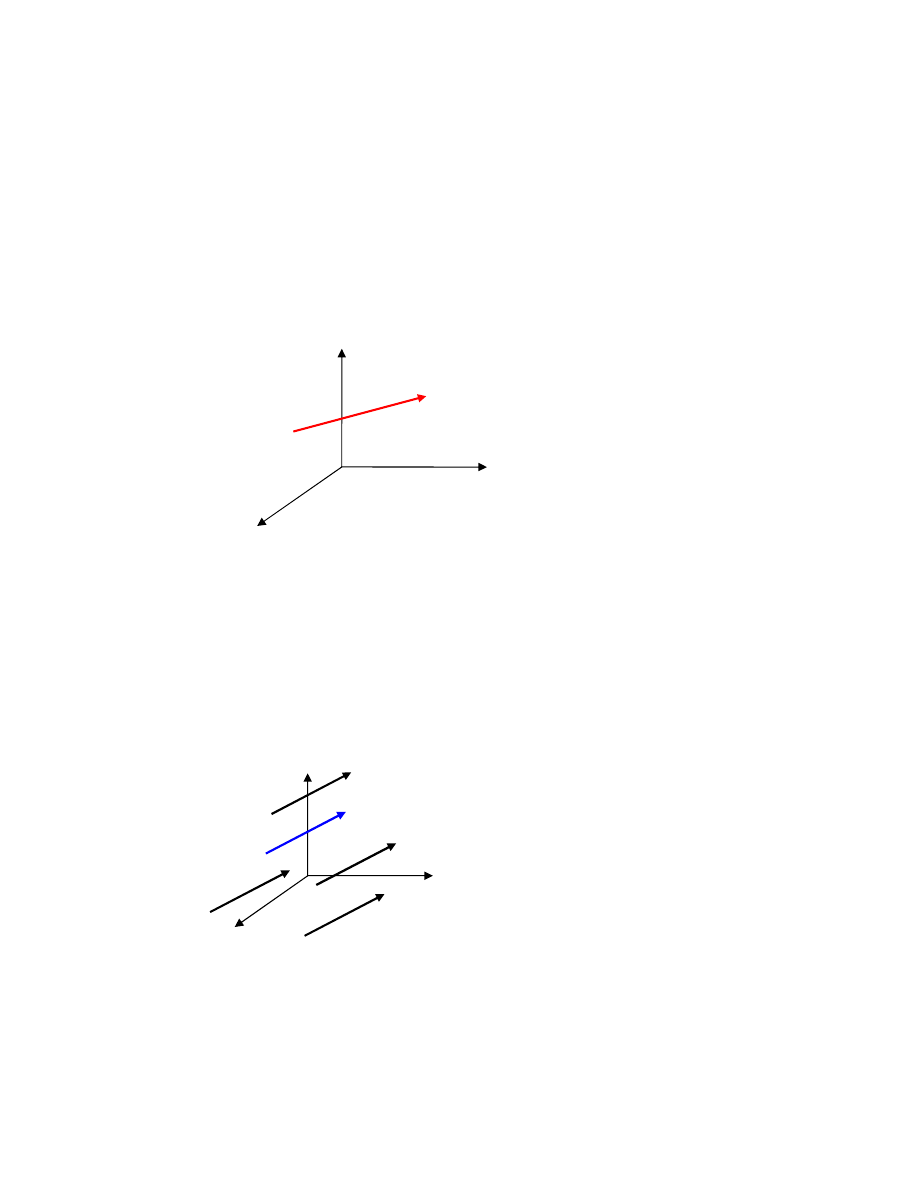
1. Definicja wektora w ukùadzie wspóùrzêdnych
Niech
A
A
A
z
,
y
,
x
A
,
B
B
B
z
,
y
,
x
B
b
êd¹ punktami w prostok¹tnym ukùadzie
wsp
óùrzêdnych
.
Wektorem zaczepionym
AB
u
nazywamy uporz
¹dkowan¹ pa
r
ê punktów
B
,
A
.
Tr
ójkê liczb
z
y
x
u
,
u
,
u
gdzie
A
B
x
x
x
u
,
A
B
y
y
y
u
,
A
B
z
z
z
u
nazywamy
wspóùrzêdnymi wektora
u
.
Wektor w uk
ùadzie
OXYZ
Wektorem swobodnym wyznaczonym przez wektor zaczepiony
u
nazywamy
zbi
ór wszys
tkich wektor
ów posiadaj¹cych te
same wsp
óùrzêdne
co wektor
u .
Wektor
u
nazywamy
reprezentantem wektora swobodnego.
Cz
êsto uto¿samiamy
u
i odpowiedni wektor swobodny. Piszemy
z
y
x
u
,
u
,
u
u
.
wektory swobodne
Wektory zapisujemy ma
ùymi literami
np.
u
,
v
,
a
lub du
¿ymi jeœli mamy ustalony
pocz
¹tek i koniec wektora np.
AB
- to wektor o pocz
¹tku w punkcie A
i ko
ñcu w
punkcie
B
;
BA
- to wektor o pocz
¹tku w punkcie B
i ko
ñcu w punkcie
A
.
wektor
zaczepiony
wsp
óùrzêdne
wektora
wektor swobodny
reprezentant
wektora
swobodnego
X
Y
Z
u
X
Y
Z
)
z
,
y
,
x
(
A
A
A
A
)
z
,
y
,
x
(
B
B
B
B
id3698312 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com
..........................................................................................
PRZYK£AD
Dane s
¹ punkty
3
1
2
,
,
A
,
5
2
3
,
,
B
.
Wyznaczy
ã wspóùrzêdne wektorów
AB
,
BA
.
Rozwi
¹zanie
Obliczamy kolejne wsp
óùrzêdne wektora
AB
u
odejmuj
¹c od wspóùrzêdnych
ko
ñca wektora (punkt B
) odpowiednie wsp
óùrzêdne pocz¹tku wektora (punkt A)
:
5
2
3
A
B
x
x
x
u
3
1
2
A
B
y
y
y
u
2
3
5
A
B
z
z
z
u
Ostatecznie
2
3
5
,
,
AB
.
Analogicznie obliczamy kolejne wsp
óùrzêdne wektora
BA
v
5
3
2
B
A
x
x
x
v
3
2
1
B
A
y
y
y
v
2
5
3
B
A
z
z
z
v
Ostatecznie
2
3
5
,
,
BA
.
............................................................................................
Wektor
0
0
0
0
,
,
nazywamy
wektorem zerowym.
Wektor
z
y
x
u
,
u
,
u
u
nazywamy
wektorem przeciwnym
do wektora
z
y
x
u
,
u
,
u
u
.
Wektor
AB
jest wektorami przeciwnym do wektora
BA
i na odwr
ót.
...........................................................................................
PRZYK£AD
Wektor przeciwny do wektora
0
4
2
,
,
, to wektor
0
4
2 ,
,
.
...........................................................................................
Wektory
z
y
x
u
,
u
,
u
u
i
z
y
x
v
,
v
,
v
v
s¹ równe
wtedy i tylko wtedy je
œli ich
sk
ùadowe s¹
r
ówne, czyli
v
u
x
x
,
v
u
y
y
,
v
u
z
z
.
Dùugoœã wektora
z
y
x
u
,
u
,
u
u
okre
œlona jest wzorem
2
2
2
z
y
x
u
u
u
u
.
wektor zerowy
wektor przeciwny
r
ównoœã
wektor
ów
d
ùugoœã
UWAGA.
0
0
u
u
.
............................................................................................
PRZYK£AD
Wyznaczy
ã dùugoœã wektor
1
3
2
,
,
v
.
Rozwi
¹zanie
Zgodnie
ze
wzorem
na
d
ùugoœã
mamy
14
1
3
2
2
2
2
v
.
............................................................................................
Wektor jednostkowy
(wersor) to wektor o d
ùugoœci jeden.
Aby otrzyma
ã wektor jednostkowy równolegùy do danego wektora
z
y
x
u
,
u
,
u
u
nale
¿y wspóùrzêdne
tego wektora podzieli
ã przez jego dùugoœã, tzn.
u
u
,
u
u
,
u
u
z
y
x
.
Przyk
ùadowymi wektorami jednostkowymi s¹ werso
ry osi OX , OY , OZ , kt
óre
oznaczamy odpowiednio
i
,
j
,
k
, gdzie
0
0
1 ,
,
i
,
0
1
0 ,
,
j
,
1
0
0 ,
,
k
.
............................................................................................
PRZYK£AD
Znale
êã wektor jednostkowy równolegùy do wektora
2
1
2
,
,
v
.
Rozwi
¹zanie
Zgodnie ze wzorem na d
ùugoœã mamy
3
9
2
1
2
2
2
2
v
.
wektora
wektor
jednostkowy
X
Y
Z
i
j
k
Szukany wektor to
3
2
3
1
3
2
,
,
w
lub
3
2
3
1
3
2
,
,
w
.
............................................................................................
Niech
A
A
A
z
,
y
,
x
A
,
B
B
B
z
,
y
,
x
B
.
Wsp
óùrzêdne punktu
S
S
S
z
,
y
,
x
S
b
êd¹cego œrodkiem
odcinka
AB
mo
¿emy
wyliczy
ã ze wzoru
2
2
2
B
A
S
B
A
S
B
A
S
z
z
z
y
y
y
x
x
x
.
............................................................................................
PRZYK£AD
Znale
êã œrodek
odcinka
AB
je
œli
2
6
5
,
,
A
,
4
8
3 ,
,
B
.
Rozwi
¹zanie
Wyznaczamy kolejne wsp
óùrzêdne œrodka
1
2
3
5
2
B
A
S
x
x
x
2
2
8
6
2
B
A
S
y
y
y
3
2
4
2
2
B
A
S
z
z
z
Ostatecznie
3
2
1 ,
,
S
.
..........................................................................................
K
¹ty, jakie two
rzy wektor
u
z osiami uk
ùadu wspóùrzêdnych okreœlaj¹ nastêpuj¹ce
wzory
œrodek odcinka
X
Y
Z
u
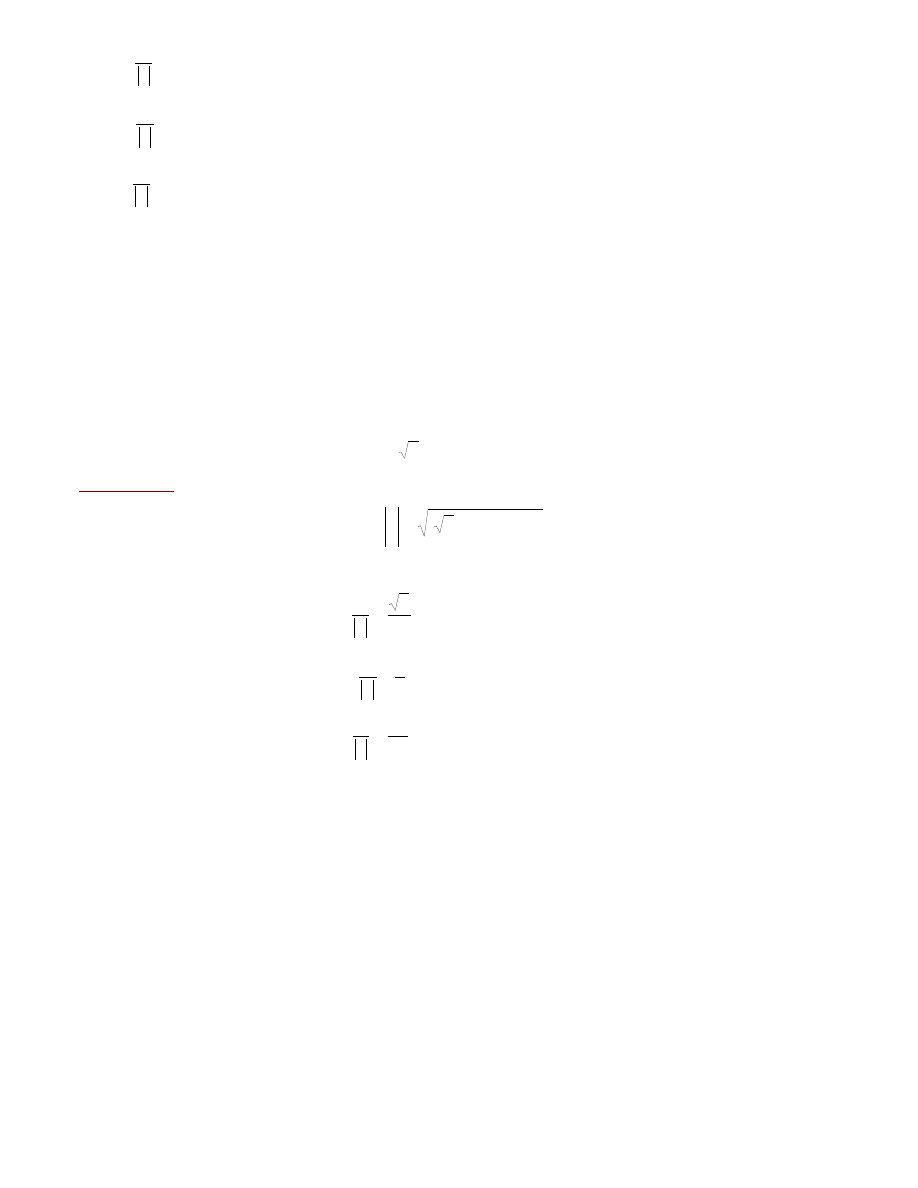
u
u
cos
x
-
k
¹t miêdzy wektorem a osi¹ OX,
u
u
cos
y
-
k
¹t miêdzy wektorem a osi¹ OY,
u
u
cos
z
-
k
¹t miêdzy wektorem a osi¹ OZ,
Poniewa
¿ cosinusy te opisuj¹
kierunek wektora w przestrzeni nazywamy je
cosinusami kierunkowymi
.
Cosinusy te spe
ùniaj¹ warunek
1
2
2
2
cos
cos
cos
.
..........................................................................................
PRZYK£AD
Obliczy
ã cosinus kierunkowe wektora
1
1
2
,
,
u
.
Rozwi
¹zanie
Najpierw wyznaczamy d
ùugoœã wektora
2
1
1
2
2
2
2
u
. Mo
¿emy teraz
wyliczy
ã cosinusy kierunkowe
o
x
u
u
cos
45
2
2
o
y
u
u
cos
60
2
1
o
z
u
u
cos
120
2
1
..........................................................................................
cosinusy
kierunkowe