 | Pobierz cały dokument Dok cw nr 12 RPiS id 139083 Nieznany .pdf Rozmiar 248,4 KB |
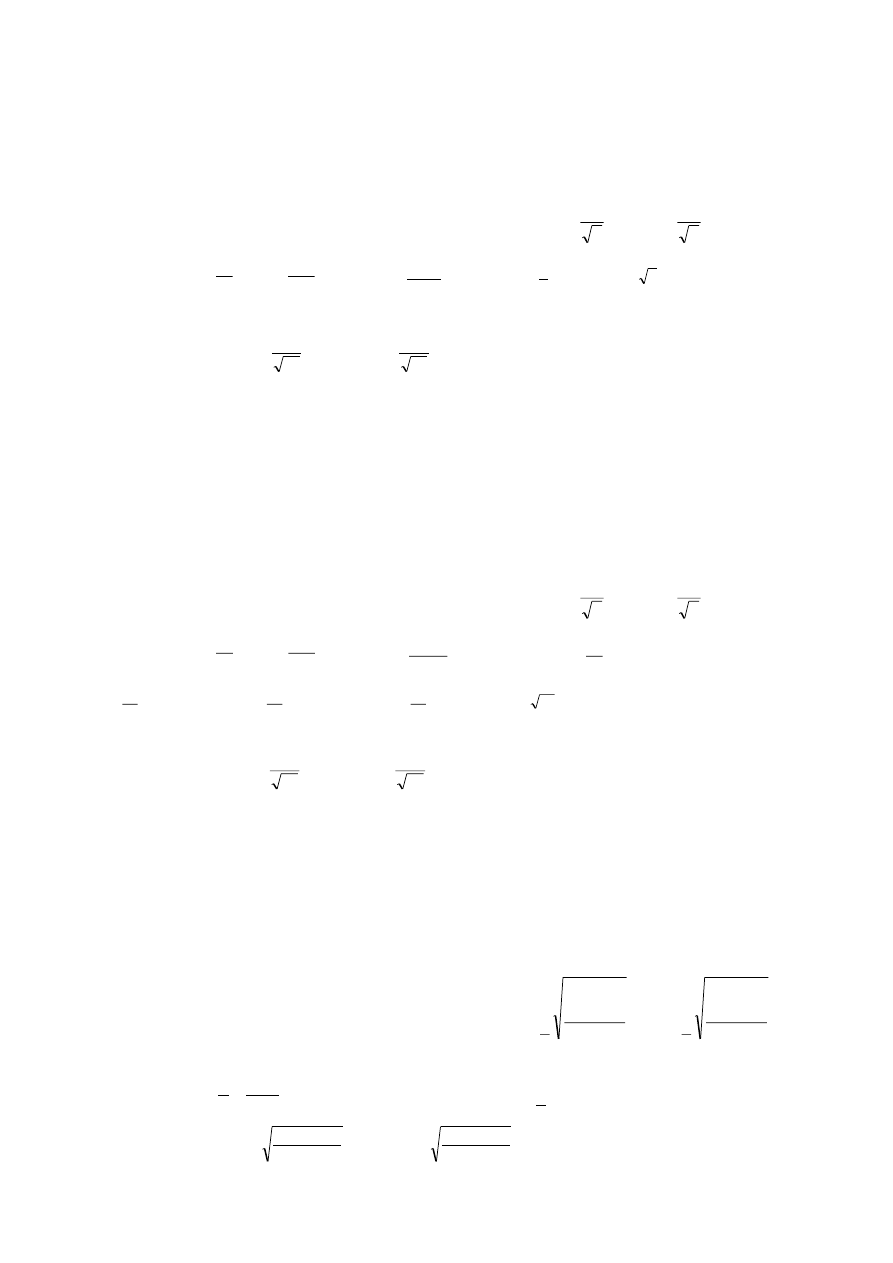
Dokończenie rozwiązań zadań z zestawu do ćwiczeń nr 11, 12 (dokończenie ćwiczeń nr 12)
Zad. 4 (ćw. 11, 12).
Populacja: pola (ogół pól pewnego regionu),
Cecha X : plon zboża,
Założenie:
,
~
m
N
X
, gdzie
m
,
– nieznane,
Cel: oszacować przedziałowo parametr
m
– nieznaną średnią plonu zboża dla ogółu pól regionu,
Technika statystyczna: wyznaczenie 95%-owej realizacji przedziału ufności dla
m
.
Wzór na realizację przedziału ufności dla średniej
m
:
n
s
t
x
n
s
t
x
m
n
n
1
;
_
1
;
_
,
;
Obliczenia:
20
10
200
10
1
10
1
_
i
i
x
x
,
2
4
4
36
9
1
1
10
1
10
1
2
_
2
s
x
x
s
i
i
,
2622
,
2
05
,
0
95
,
0
1
9
;
05
,
0
1
;
t
t
n
.
Stąd:
43
,
1
20
;
43
,
1
20
10
2
2622
,
2
20
;
10
2
2622
,
2
20
m
, czyli
1,43
2
;
57
,
18
m
.
Odp. Średni plon zboża dla ogółu pól pewnego regionu jest jakąś liczbą z przedziału
1,43
2
;
57
,
18
.
Zaufanie do tego wniosku wynosi
%
95
.
Zad. 5 (ćw. 11, 12).
Populacja: pracownicy (ogół pracowników pewnego zakładu pracy),
Cecha X : czas dojazdu do pracy,
Założenie:
,
~
m
N
X
, gdzie
m
,
– nieznane,
Cel: oszacować przedziałowo parametr
m
– nieznany średni czas dojazdu do pracy w populacji ogółu
pracowników zakładu,
Technika statystyczna: wyznaczenie 95%-owej realizacji przedziału ufności dla
m
.
Wzór na realizację przedziału ufności dla średniej
m
:
n
s
t
x
n
s
t
x
m
n
n
1
;
_
1
;
_
,
;
Obliczenia:
25
17
425
17
1
17
1
_
i
i
x
x
,
2
2
_
17
1
2
2
25
17
10881
16
1
17
1
17
1
x
x
s
i
i
=
4
16
16
256
16
1
625
10
881
10
16
1
625
17
881
10
16
1
s
,
1199
,
2
05
,
0
95
,
0
1
16
;
05
,
0
1
;
t
t
n
.
Stąd:
06
,
2
25
;
06
,
2
25
17
4
1199
,
2
25
;
17
4
1199
,
2
25
m
, czyli
7,06
2
;
94
,
22
m
.
Odp. Średni czas dojazdu do pracy w populacji ogółu pracowników zakładu jest jakąś liczbą
z przedziału
7,06
2
;
94
,
22
. Zaufanie do tego wniosku wynosi
%
95
.
Zad. 6 (ćw. 11, 12).
Populacja: pojazdy ,
Cecha X : brak ubezpieczenia „OC” ( = 1, gdy pojazd nie ma wykupionego „OC”/ = 0, w p.p.),
Założenie:
p
D
X ~
, gdzie p – frakcja samochodów bez wykupionego „OC” – jest nieznana,
Cel: oszacować przedziałowo parametr p – nieznaną frakcję (odsetek) samochodów bez „OC”,
Technika statystyczna: wyznaczenie 95%-owej realizacji przybliżonego przedziału ufności dla p .
Wzór na realizację przedziału ufności, gdy
n
duże:
n
p
p
u
p
n
p
p
u
p
p
1
,
1
2
1
2
1
;
Obliczenia:
08
,
0
1000
80
n
k
p
,
96
,
1
05
,
0
95
,
0
1
975
,
0
2
1
u
u
.
Stąd:
1000
92
,
0
08
,
0
96
,
1
08
,
0
;
1000
92
,
0
08
,
0
96
,
1
08
,
0
p
, czyli
%
,7
9
%;
3
,
6
097
,
0
;
063
,
0
p
Odp. Odsetek pojazdów bez wykupionego ubezpieczenia „OC” jest jakąś liczbą z przedziału
%
,7
9
%;
3
,
6
. Zaufanie do tego wniosku wynosi
%
95
.
| Pobierz cały dokument Dok cw nr 12 RPiS id 139083 Nieznany .pdf Rozmiar 248,4 KB |