Kryteria zbieżności szeregów

1

Kryteria zbieżności szeregów

Kryteria zbieżności szeregów to grupa twierdzeń pozwalających ustalić, czy dany szereg jest zbieżny, czy nie.

Jeżeli szereg spełnia warunki podane w kryterium, to przesądza to o jego zbieżności lub rozbieżności. Większość

kryteriów dostarcza jedynie warunki konieczne na zbieżności lub rozbieżności szeregu (wyjątkiem jest warunek

Cauchy'ego dla szeregów). Oznacza to, że w pewnych sytuacjach kryteria nie dostarczają informacji pozwalającej na

ocenę zbieżności szeregów. Zaletą kryteriów zbieżności jest względna łatwość ich sprawdzenia i szerokie

zastosowanie praktyczne. Korzystając z kryteriów zbieżności, zwykle wyliczamy pomocnicze wielkości związane z

szeregiem i na tej podstawie wydajemy osąd.

Niech 

będzie szeregiem liczbowym, tzn. o wyrazach rzeczywistych lub zespolonych.

Warunek konieczny zbieżności

Podstawowym kryterium zbieżności szeregu jest warunek konieczny zbieżności. Pozwala on stwierdzić kiedy dany

szereg nie jest zbieżny. Badanie problemu zbieżności szeregu powinno się zaczynać od sprawdzenia tego kryterium,

a jeśli warunek konieczny jest spełniony przejść do kolejnych kryteriów.

Warunek konieczny zbieżności szeregu: Jeśli wyraz ogólny 

szeregu 

nie zbiega do 0, symbolicznie

, to szereg ten jest rozbieżny.

Przykład. Szereg 

jest rozbieżny, gdyż 

.

Jeśli 

, to warunek konieczny nie rozstrzyga, czy szereg jest zbieżny czy nie i trzeba użyć innego

kryterium. Na przykład szereg harmoniczny 

jest rozbieżny mimo, że 

.

Przykład. Aby wyznaczyć granicę 

rozważmy szereg 

. Korzystając z kryterium d'Alemberta

nietrudno pokazać, że szereg ten jest zbieżny. Zatem na mocy warunku koniecznego zbieżności szeregu

otrzymujemy, że 

.

Warunek Cauchy'ego zbieżności

Dla szeregów liczbowych zachodzi następujący warunek zbieżności, pochodzący od Cauchy'ego:

Szereg liczbowy 

jest zbieżny wtedy i tylko wtedy, gdy: 

Jest to

równoważne temu, że ciąg sum częściowych 

szeregu 

jest ciągiem Cauchy'ego.

Kryteria zbieżności szeregów

2

Zbieżność bezwzględna

Szereg 

nazywamy zbieżnym bezwzględnie, jeżeli zbieżny jest szereg 

. Jeżeli dany szereg jest

zbieżny bezwzględnie, to jest on zbieżny również w zwykłym sensie.

Dowód. Załóżmy, że 

jest zbieżny. Spełnia on warunek Cauchy'ego, tzn. dla każdej liczby 

istnieje

liczba 

taka, że

dla dowolnych 

. Ponieważ 

, więc szereg 

także spełnia

warunek Cauchy'ego, czyli jest zbieżny.
Powyższe rozróżnienie jest istotne, może się bowiem zdarzyć, że dany szereg jest zbieżny, lecz nie jest zbieżny

bezwzględnie – mówimy wtedy, że szereg jest zbieżny warunkowo. Twierdzenie Riemanna mówi, że można tak

poprzestawiać wyrazy szeregu warunkowo zbieżnego liczb rzeczywistych, aby jako sumę nowego szeregu otrzymać

dowolną, z góry zadaną liczbę (zobacz: szereg).

Wszystkie poniższe twierdzenia rozstrzygają o zbieżności bezwzględnej szeregu 

. Zauważmy, że zbieżność

szeregu 

jest równoważna zbieżności szeregu 

, gdzie 

jest dowolną liczbą naturalną. Oznacza to,

że zbieżność szeregu nie zależy od skończonej liczby jego wyrazów. Ta obserwacja pozwala na nieznaczne

wzmocnienie poniższych kryteriów, przez dopisanie, że pewne warunki zachodzą dla dostatecznie dużych n, tzn

istnieje liczba 

taka, że pewien warunek zachodzi dla 

. W kryteriach d'Alemberta i Raabego

wystarczy założyć, że 

zachodzi dla dostatecznie dużych n. W kryterium porównawczy wystarczy założyć,

że 

zachodzi dla dostatecznie dużych n. W kryterium całkowym wystarczy założyć, że 

jest funkcją

monotonicznie malejącą dla 

, gdzie 

jest pewną stałą.

Kryterium d'Alemberta

Kryterium d'Alemberta: Załóżmy, że 

dla każdego 

. Jeżeli 

, to szereg

jest zbieżny; jeżeli istnieje liczba 

taka, że nierówność 

zachodzi dla wszystkich 

większych od 

, to szereg 

jest rozbieżny.

Kryterium nie przesądza o zbieżności lub rozbieżności szeregu w przypadku, gdy granica 

jest

równa 1. Warto zauważyć, że warunek 

(podobnie jak 

) implikuje, że istnieje

taka, że nierówność 

zachodzi dla wszystkich 

, a zatem implikuje rozbieżność szeregu

.

W przypadku, gdy szereg 

ma wyrazy dodatnie kryterium d'Alemberta można zapisać w następującej

uproszczonej i łatwiejszej do zapamiętania formie:

Kryteria zbieżności szeregów

3

szereg 

jest zbieżny

szereg 

jest rozbieżny

kryterium nie rozstrzyga

Dowód: Załóżmy, że 

. Oznacza to, że istnieją liczby 

oraz 

takie, że dla

każdego 

mamy 

. Zatem 

dla każdego 

. Stąd otrzymujemy

dla każdego 

. Szereg

jest zbieżny, gdyż jest szeregiem geometrycznym o ilorazie 

. Jest on zbieżną majorantą szeregu

.

Na mocy kryterium porównawczego szereg 

jest zbieżny, co implikuje zbieżność szeregu 

.

Załóżmy teraz, że istnieje liczba 

taka, że nierówność 

zachodzi dla wszystkich  większych od 

. Oznacza to, że 

dla 

, czyli

To oznacza, że ciąg 

nie zbiega do zera. Zatem szereg 

nie jest zbieżny, bo nie spełnia warunku

koniecznego zbieżności szeregów.

Przykład 1. Kryterium d'Alemberta jest szczególnie pomocne, gdy wyraz ogólny 

szeregu 

zawiera

symbol silni. Rozważmy następujący przykład 

.

Wyraz ogólny tego szeregu jest postaci 

. Mamy

.

Zatem korzystając z faktu, że 

otrzymujemy 

, co dowodzi

zbieżności rozważanego szeregu.

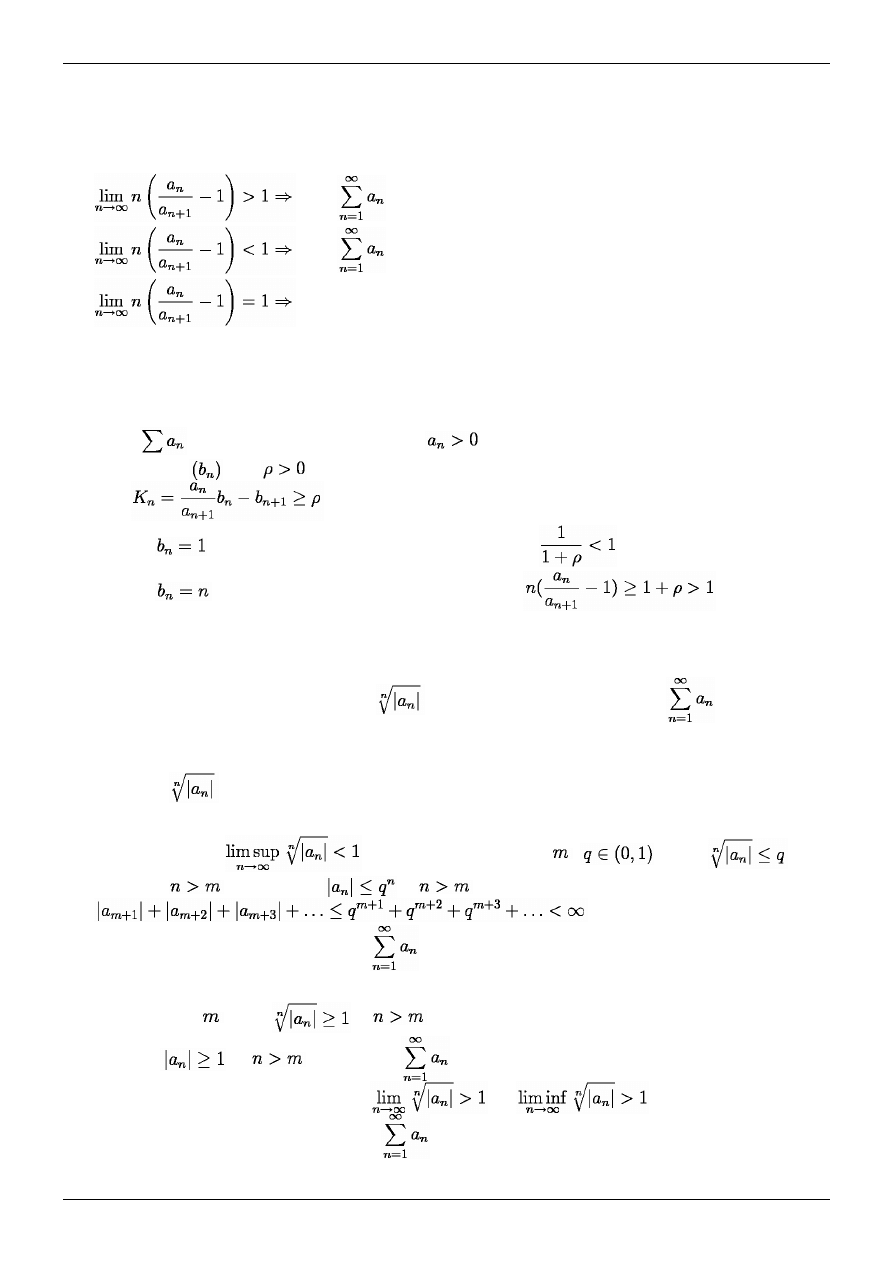
Przykład 2. Kryterium d'Alemberta nie pozwala rozstrzygnąć czy szereg 

jest zbieżny, gdy

. Aby to zilustrować rozważmy dwa szeregi 

i 

, gdzie 

i 

.

Wówczas 

. Jednak 

jest rozbieżny jako szereg harmoniczny, a 

jest

zbieżny, jako szereg harmoniczny rzędu 2.

Kryteria zbieżności szeregów

4

Kryterium Raabego

Jeżeli kryterium d'Alemberta nie rozstrzyga czy dany szereg jest zbieżny lub rozbieżny, warto skorzystać z

kryterium Raabego:

szereg 

jest zbieżny

szereg 

jest rozbieżny

kryterium nie rozstrzyga

Należy zwrócić uwagę na fakt, że, aby szereg był zbieżny, granica z kryterium Raabego musi być większa od 1 –

inaczej niż w przypadku kryterium d'Alemberta i Cauchy'ego.

Kryterium Kummera

Szereg 

dla którego dla dostatecznie dużych n 

jest zbieżny wtedy i tylko wtedy, gdy istnieją ciąg

liczb dodatnich 

i stała 

takie, że dla dostatecznie dużych n zachodzi:

Dla ciągu 

wynika stąd pierwsza część kryterium d'Alemberta.(bo 

)

Dla ciągu 

wynika stąd pierwsza część kryterium Raabego.(bo 

)

Kryterium Cauchy'ego

Kryterium Cauchy'ego (nazywane także kryterium pierwiastkowym Cauchy'ego dla odróżnienia od kryterium

całkowego Cauchy'ego): Jeżeli granica ciągu 

istnieje i jest mniejsza od 1, to szereg 

jest zbieżny;

jeżeli granica ta jest większa od 1, szereg jest rozbieżny.

Jak w przypadku poprzedniego kryterium, jest to wersja uproszczona. Wersja subtelniejsza mówi, że jeśli granica

górna ciągu 

jest mniejsza od 1, to szereg jest zbieżny; jeżeli granica dolna jest większa od 1, to szereg jest

rozbieżny.

Dowód. Załóżmy, że 

. To oznacza, że istnieją liczby 

i 

takie, że 

dla każdego 

. To oznacza, że 

dla 

, czyli

,

co dowodzi zbieżności bezwzględnej szeregu 

.

Załóżmy teraz, że

(1) istnieje liczba 

taka, że 

dla 

.

Wówczas 

dla 

, więc szereg 

jest rozbieżny, bo nie spełnia warunku koniecznego

zbieżności szeregów. Zauważmy, że warunki 

oraz 

implikują warunek (1) i

w konsekwencji implikują rozbieżność szeregu 

.

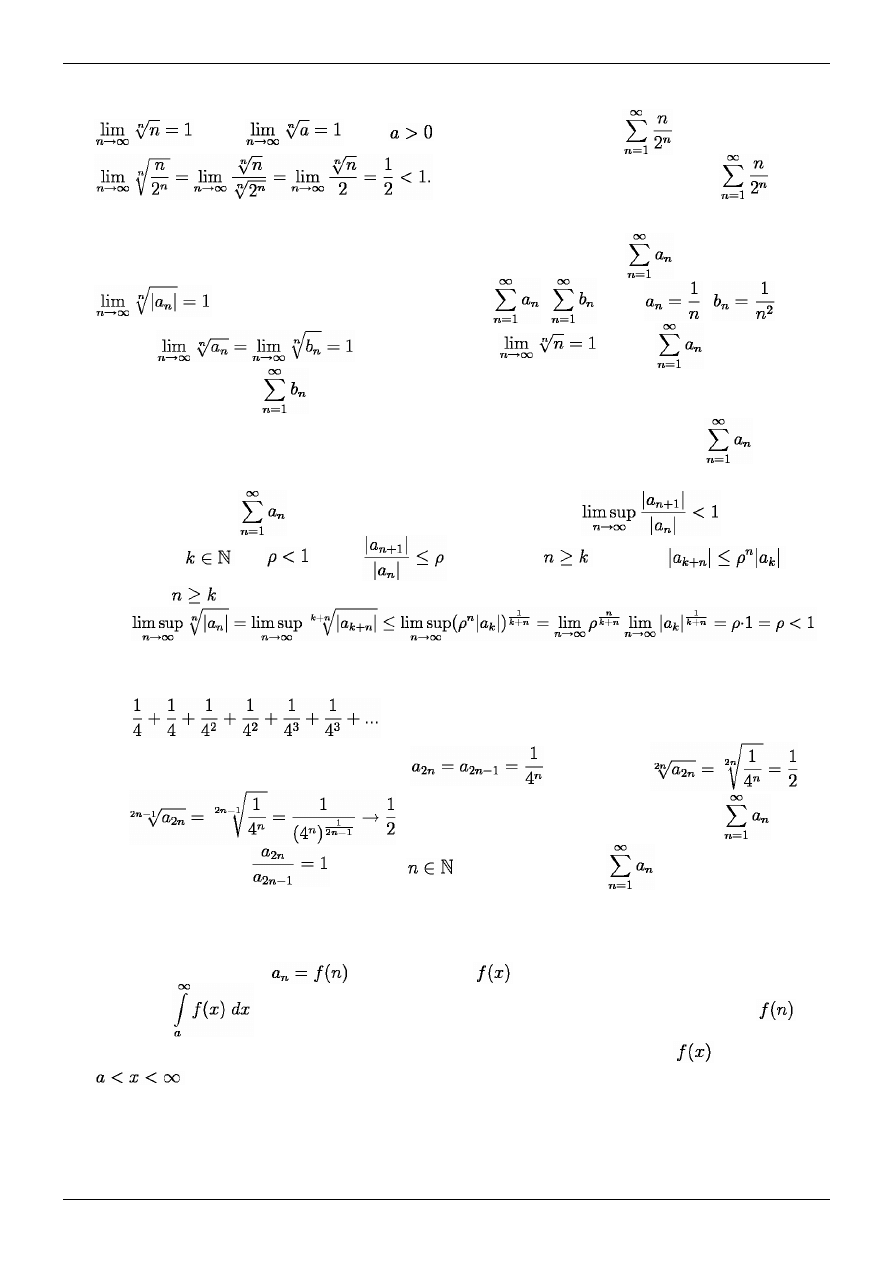
Kryteria zbieżności szeregów

5

Przykład 1. W zastosowaniach kryterium Cauchy'ego przydatna jest znajomość następujących granic:

oraz 

dla 

. Rozważmy szereg 

. Wówczas

Zatem na mocy kryterium Cauchy'ego szereg 

jest

zbieżny.

Przykład 2. Kryterium Cauchy'ego nie pozwala rozstrzygnąć czy szereg 

jest zbieżny, gdy

. Aby to zilustrować rozważmy dwa szeregi 

i 

, gdzie 

i 

.

Wówczas 

(korzystamy z faktu, że 

). Jednak 

jest rozbieżny

jako szereg harmoniczny, a 

jest zbieżny, jako szereg harmoniczny rzędu 2.

Twierdzenie. Kryterium Cauchy'ego jest silniejsze niż kryterium d'Alemberta, tzn. jeśli szereg 

spełnia

warunek kryterium d'Alemberta, to spełnia też warunek Cauchy'ego, ale nie na odwrót.

Dowód. Załóżmy, że 

spełnia warunek kryterium d'Alemberta, tzn. 

. Wówczas

istnieją liczba 

oraz 

taka, że 

dla dowolnego 

. Wówczas 

dla każdego 

. Zatem

.

Twierdzenia tego nie da się odwrócić, co ilustruje następujący przykład.

Przykład 3. Rozważmy szereg

Wówczas ogólny wyraz tego szeregu jest postaci 

. Zauważmy, że 

oraz 

. Zatem na mocy kryterium Cauchy'ego szereg 

jest

zbieżny. Z drugiej strony 

dla każdego 

, co pokazuje, że szereg 

nie spełnia warunku z

kryterium d'Alemberta.

Kryterium całkowe

Szereg o wyrazie ogólnym 

jest zbieżny, jeżeli 

jest funkcją monotonicznie malejącą i całka

niewłaściwa 

jest zbieżna; natomiast jeżeli całka ta jest rozbieżna, to szereg o wyrazie ogólnym 

jest rozbieżny. Przy tym dolną granicę całkowania a należy tak obrać, żeby funkcja 

w przedziale

była oznaczona i nie miała punktów nieciągłości.

Kryteria zbieżności szeregów

6

Kryterium porównawcze

Niech 

i 

będą szeregami o wyrazach nieujemnych. Jeśli 

dla każdego 

, to

(i) jeśli 

jest zbieżny, to 

jest zbieżny;

(ii) jeśli 

jest rozbieżny, to 

jest rozbieżny.

Dowód: Na początek zauważmy, że implikacja (ii) wynika z (i) na mocy tautologii 

.

Pokażemy (i). W tym celu załóżmy, że 

jest zbieżny do pewnej liczby 

. Oznacza to, że

.

Skoro 

dla każdego 

, to 

dla każdego 

. Skoro ciąg 

jest zbieżny, to jest ograniczony. Zatem ograniczony jest też ciąg 

. Pokażemy, że ciąg 

jest monotoniczny. Niech 

. Wtedy 

. To pokazuje, że

jest niemalejący i ograniczony, a zatem zbieżny. To oznacza, że zbieżny jest szereg 

.

Implikacje (i) oraz (ii) te nie dają się odwrócić. Niech 

i 

dla każdego 

.

Wówczas 

oraz 

oraz 

. To pokazuje, że jeśli 

, to z

rozbieżności 

nie wynika rozbieżność 

, a ze zbieżności 

nie wynika zbieżność 

.

Warunek 

dla każdego 

można osłabić zakładając jedynie, że istnieje liczba 

taka, że dla

każdego 

mamy 

(mówimy wtedy, że nierówność 

zachodzi dla prawie wszystkich

).

Stosowanie tego kryterium wymaga pewnego zasobu szeregów, o których wiadomo, że są zbieżne. Często wygodnie

jest porównywać dany szereg z szeregiem harmonicznym lub geometrycznym.

Kryterium zagęszczania

Następujące proste kryterium również pochodzi od Cauchy'ego. Załóżmy, że szereg 

jest taki, że ciąg

jest malejący, a  jest liczbą naturalną większą od 1. Jeżeli zbieżny jest szereg 

, to zbieżny

jest szereg 

.

Kryteria zbieżności szeregów

7

Kryterium ilorazowe (nazywane też kryterium porównawczym w postaci granicznej)

Jeżeli mamy szeregi 

, 

i jeden z nich jest zbieżny, oraz 

, to drugi również jest

zbieżny. Podobnie gdy jeden z szeregów jest rozbieżny, a granica ta jest skończona i dodatnia, możemy

wnioskować, że drugi również jest rozbieżny.
Ponadto:

Jeżeli 

i 

jest zbieżny, to 

jest zbieżny.

Jeżeli 

i 

jest zbieżny, to 

jest zbieżny.

Szeregi o wyrazach dowolnych

Kryterium Leibniza

Jeżeli ciąg 

spełnia następujące dwa warunki:

1.

,

2. ciąg 

jest nierosnący,

to szereg 

jest zbieżny.

Dowód: Z założenia wynika, że 

. Rozważmy podciąg ciągu sum częściowych

postaci 

. Pokażemy, że ciąg ten jest niemalejący i ograniczony z góry, a zatem zbieżny.

Mamy

(ciąg jest niemalejący)

oraz

(ciąg

jest ograniczony).

Niech 

. Aby zakończyć dowód trzeba pokazać, że 

. Mamy

.

Kryterium Abela

Jeżeli szereg 

jest zbieżny, a ciąg 

jest monotoniczny i ograniczony, to szereg 

jest zbieżny.

Kryterium Dirichleta

Jeżeli ciąg sum częściowych 

szeregu 

jest ograniczony, a ciąg 

jest monotoniczny i

zbieżny do 0, to szereg 

jest zbieżny.

Źródła i autorzy artykułu

8

Źródła i autorzy artykułu

Kryteria zbieżności szeregów  Źródło: http://pl.wikipedia.org/w/index.php?oldid=33611121  Autorzy: 4C, Alef, B11Blanco, BartekChom, Beno, Blotowij, CiaPan, Googl, KNMPL, Katafrakt,
Kbsc, Konradek, Kuki, Majkelx, Markosek, Mik01aj, Milek80, Mitrandir77, Papageno, Pazabo, Pazdro, Petryk, Polimerek, Qblik, Robpal, Rosomak, Stepa, ToSter, Wiggles007, Wiktoryn,
WojciechSwiderski, Wojteks, Wolf359, Wzarebs, 42 anonimowych edycji

Licencja

Creative Commons Attribution-Share Alike 3.0 Unported
//creativecommons.org/licenses/by-sa/3.0/