„Teoria sygnałów”
Zdzisław Papir
•Warunki zbieżności Dirichleta
•Zachowanie szeregu Fouriera
w punktach nieciągłości
•Peter G. L. Dirichlet
•Zbieżność średniokwadratowa
•Twierdzenie Parsevala
•Moc ułamkowa
•Efekt Gibbsa
•Okna Fejera, Lanczosa...
•Podsumowanie
Zbieżność szeregu
Fouriera
„Teoria sygnałów” Zdzisław Papir
Szereg Fouriera
sygnału x(t)
,
2
,
1
,
0
1
o
o
o
n
dt
e
t
x
T
X
e
X
t
x
T
t
x
t
x
T
t
jn
n
n
t
jn
n
m
n
T
m
n
dt
e
e
e
e
n
e
T
t
m
j
t
jn
t
jm
t
jn
t
jn
,
,
0
,
2
,
1
,
0
,
o
o
o
o
o
o
Jeżeli sygnał x(t) w przedziale [0, T]:
klasa sygnałów A
A1)
posiada skończoną liczbę punktów nieciągłości I
rodzaju,
A2)
posiada skończoną liczbę ekstremów,
A3)
jest ograniczony
klasa sygnałów B
B1)
posiada skończoną liczbę punktów nieciągłości II
rodzaju,
B2)
poza punktami nieciągłości
B1)
spełnia warunki
A1A3
,
B3)
jest bezwzględnie całkowalny
to wykładniczy szereg Fouriera jest
zbieżny
(jednostajnie)
do sygnału x(t) we wszystkich
punktach jego
ciągłości.
„Teoria sygnałów”
Zdzisław Papir
Warunek zbieżności
Dirichleta (I)
T
dt
t
x
Warunki Dirichleta są warunkami wystarczającymi.
t
x
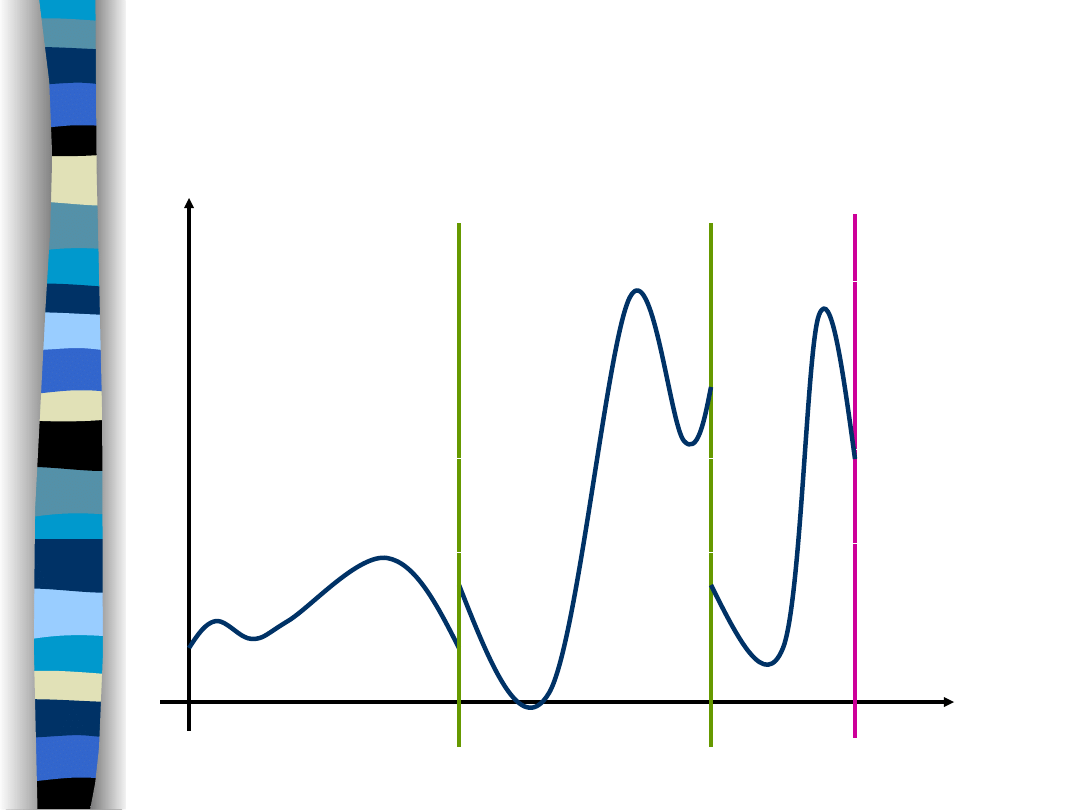
Warunek Dirichleta (I)
„Teoria sygnałów” Zdzisław Papir
czas
x(t)
0
T
sygnał klasy A
I
I
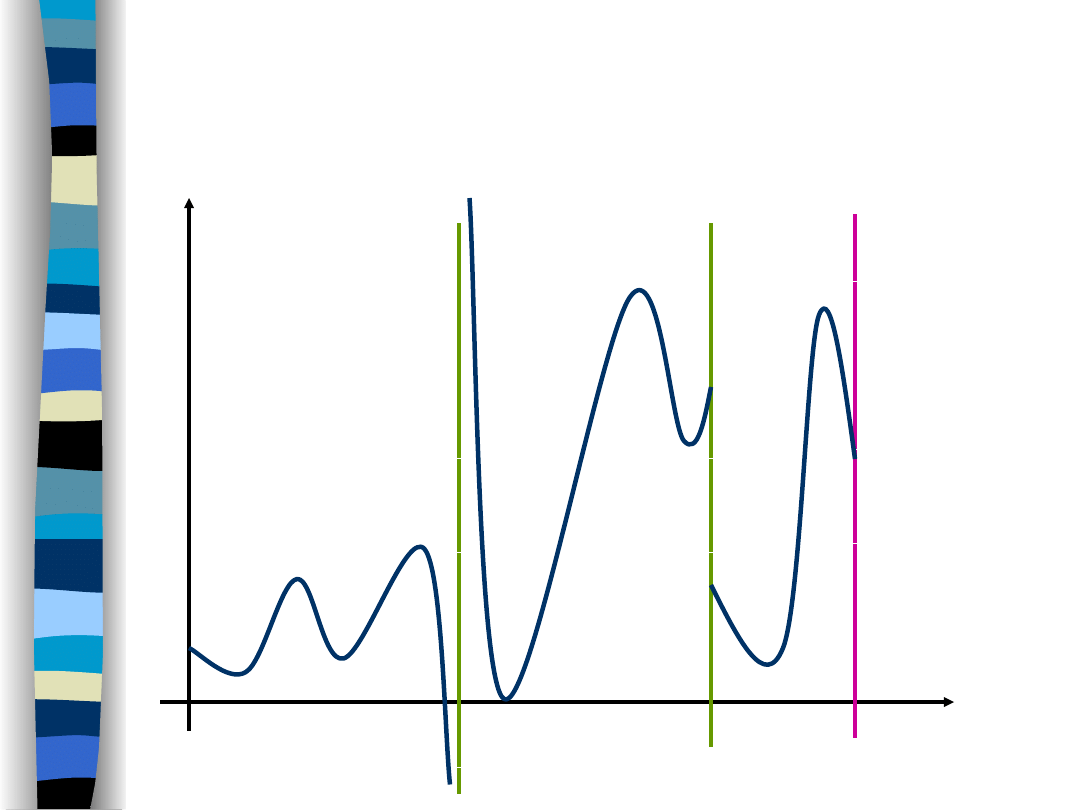
Warunek Dirichleta (I)
„Teoria sygnałów” Zdzisław Papir
czas
x(t)
0
T
sygnał klasy B
I
II
„Teoria sygnałów” Zdzisław Papir
Warunek Dirichleta (I)
t
x
t
x
t
x
t
x
2
1
lim
lim
2
1
o
o
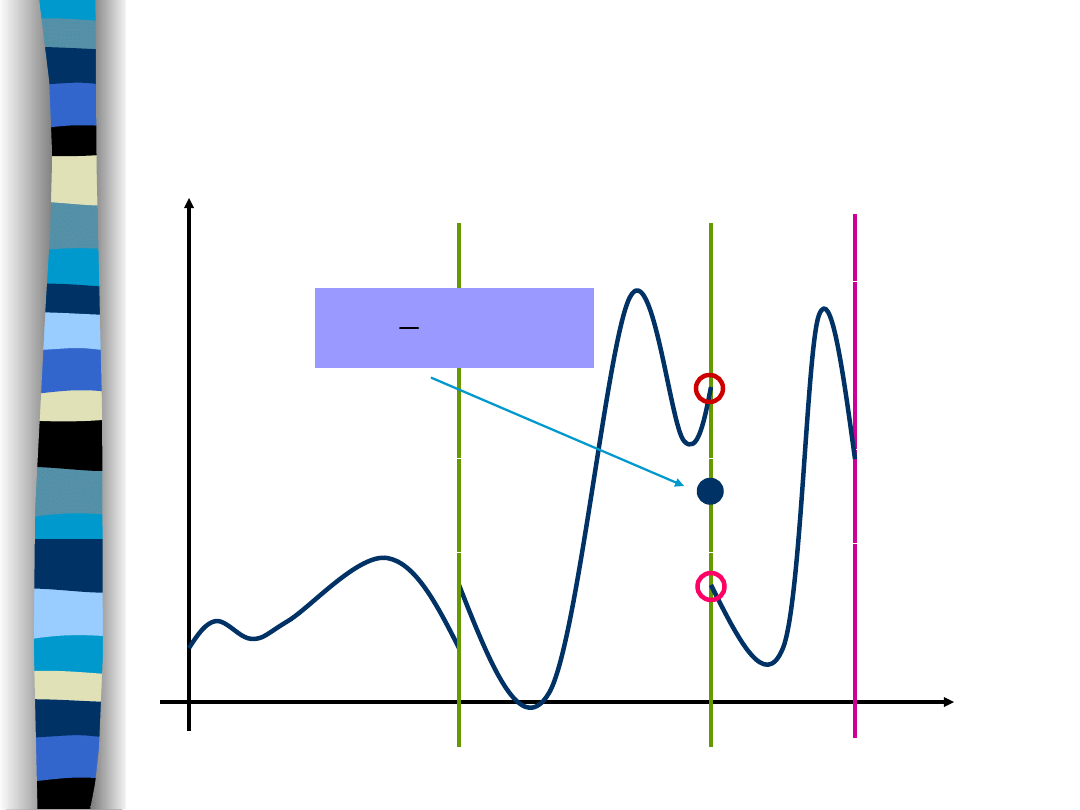
W punktach nieciągłości
I rodzaju
szereg Fouriera
przyjmuje wartość:
sugerujący, że w punktach nieciągłości sygnału
x(t) jego wartość powinna być równa
średniej
arytmetycznej granicy lewo- i prawostronnej
.
Umowa ta gwarantuje zbieżność szeregu Fouriera do
sygnału we
wszystkich
chwilach czasu (ale jednostajną
wyłącznie w punktach ciągłości).
„Teoria sygnałów”
Zdzisław Papir
Zachowanie szeregu
Fouriera w punkcie
nieciągłości
czas
x(t)
0
T
t
x(t-)
x(t+)
t
x
t
x
t
x
2
1
„Teoria sygnałów” Zdzisław Papir
Punkt nieciągłości
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
0
2
4
6
8
10
12
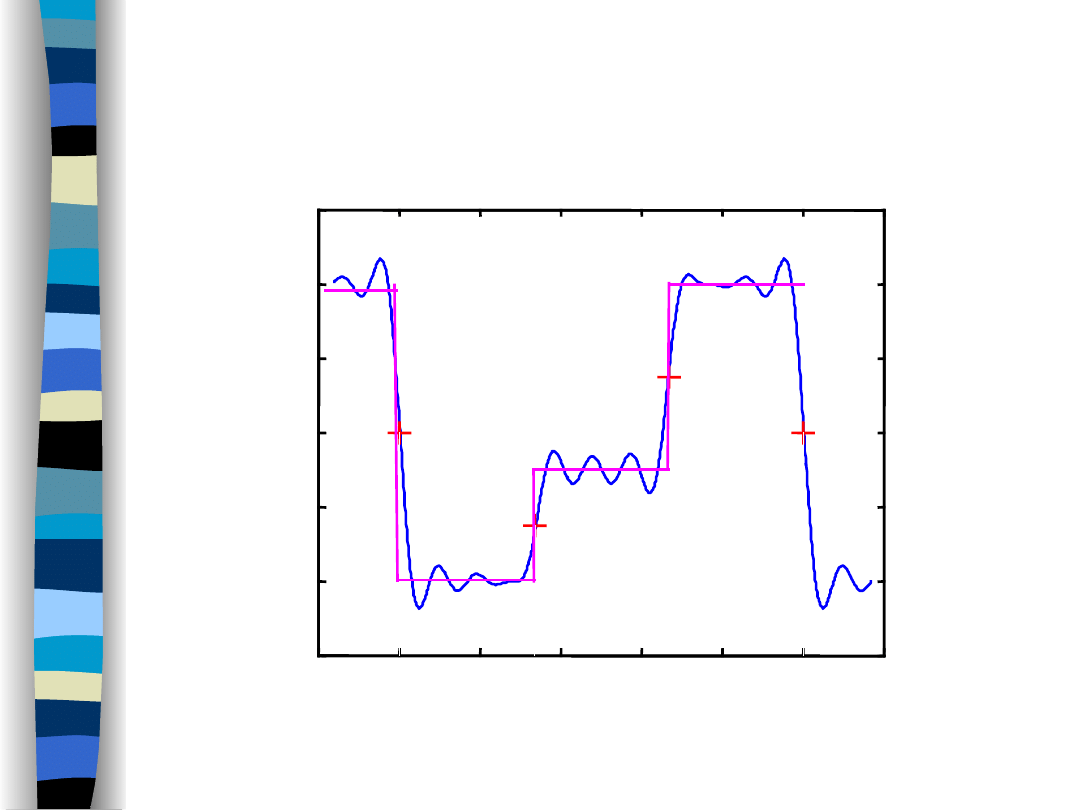
Zachowanie się szeregu Fouriera w pkt. nieciągłości
czas
(10 harmonicznych)
„Teoria sygnałów” Zdzisław Papir
Punkt nieciągłości
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
0
2
4
6
8
10
12
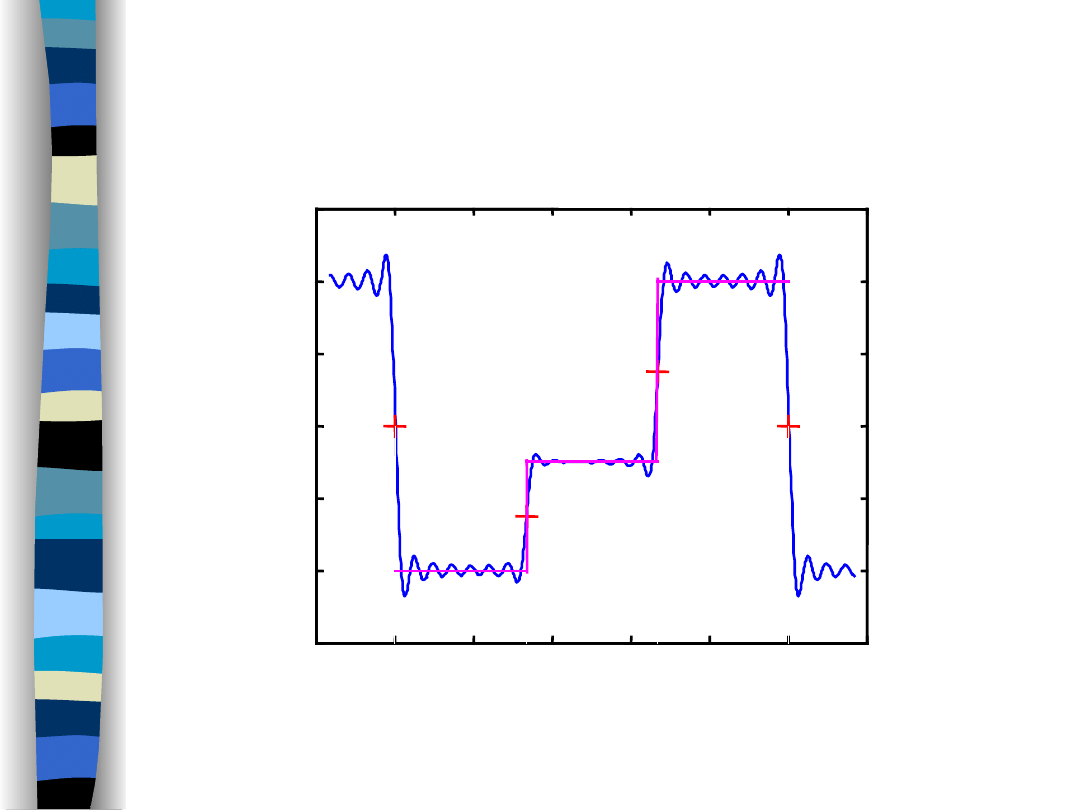
Zachowanie się szeregu Fouriera w pkt. nieciągłości
czas
(20 harmonicznych)
„Teoria sygnałów” Zdzisław Papir
Warunek zbieżności
Dirichleta - II
T
dt
t
x
1
0
1
1
2
1
o
0
n
i
i
i
n
i
i
t
x
t
x
T
t
t
t
t
t
t
E
OGRANICZON
WAHANIE
warunek II
Jeżeli sygnał x(t) w przedziale [0, T]:
klasa sygnałów A
A1)
ma wahanie ograniczone
klasa sygnałów B
B1)
posiada skończoną liczbę punktów nieciągłości II
rodzaju,
B2)
poza punktami nieciągłości
B1)
spełnia warunek
A1
,
B3)
jest bezwzględnie całkowalny
to wykładniczy szereg Fouriera jest zbieżny
(jednostajnie) do sygnału x(t) we wszystkich
punktach jego ciągłości.
warunek I
„Teoria sygnałów” Zdzisław Papir
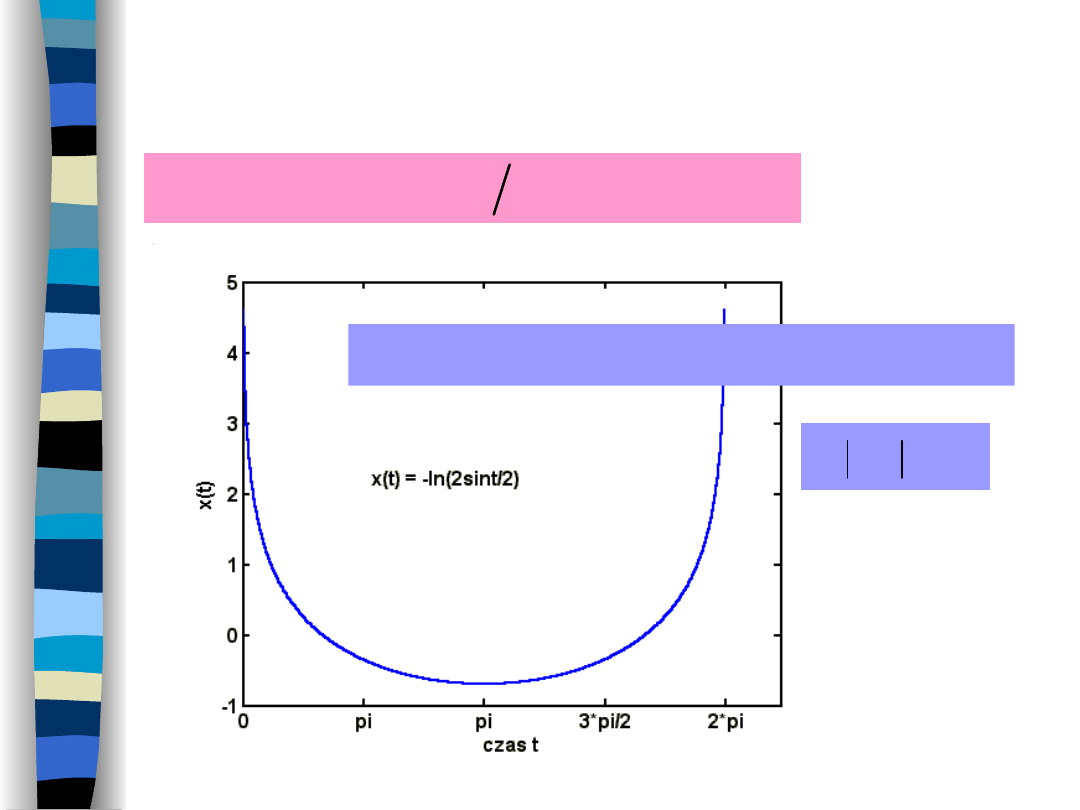
Warunek zbieżności Dirichleta -
II
2
0
,
2
sin
2
ln
t
t
t
x
Sygnał bezwzględnie całkowalny wg. G. M. Fichtenholz
„Rachunek różniczkowy i całkowy”, tom II, str. 507
2
o
dt
t
x
„Teoria sygnałów” Zdzisław Papir
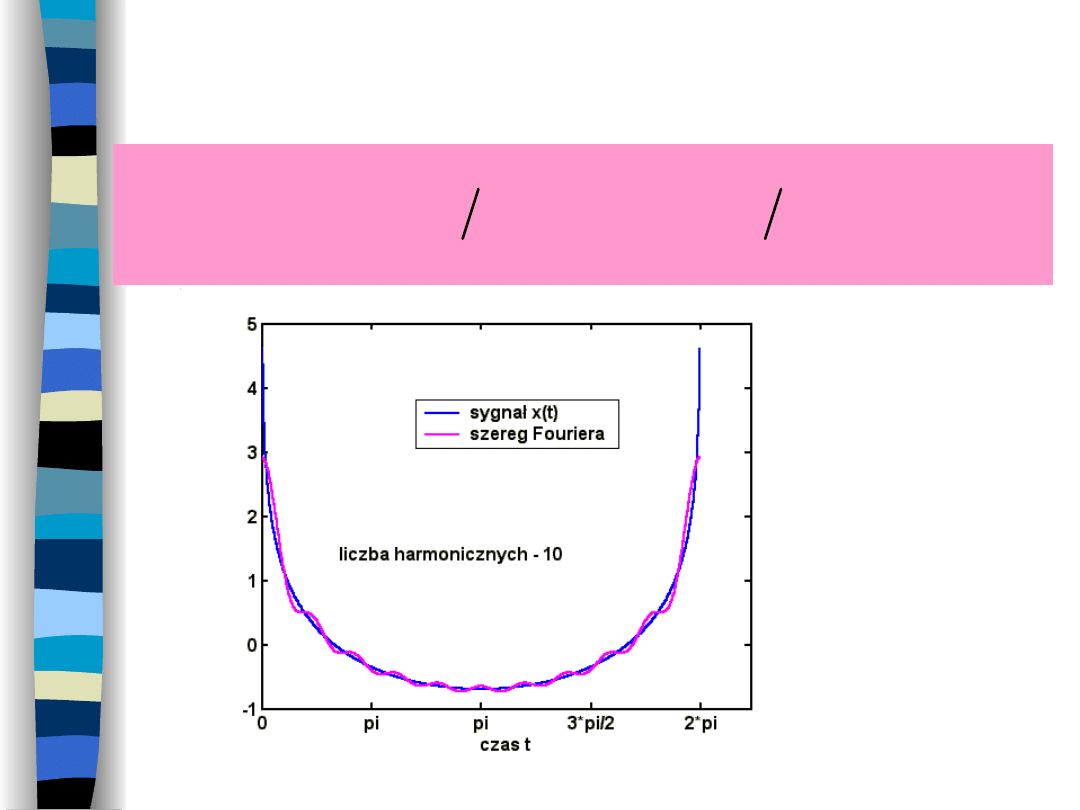
Warunek zbieżności Dirichleta -
II
2
0
,
cos
2
sin
2
ln
1
t
n
nt
t
t
x
n
„Teoria sygnałów” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
•
Matematyk niemiecki, I poł. XIX wieku
• Najważniejsze osiągnięcia:
• teoria liczb
- funkcje dzeta
• teoria mnogości
- zasada szufladkowa
• teoria szeregów
- zasada zbieżności
„Teoria sygnałów” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Funkcje dzeta Riemanna:
(przypadek funkcji Dirichleta)
1
Re
,
1
1
s
n
s
n
s
Tożsamość Eulera:
pierwszych
liczb
zbiór
,
1
Re
,
1
1
1
p
s
p
s
p
s
„Teoria sygnałów”
Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Hipoteza Riemanna:
(nieudowodniona do dzisiaj)
1
Re
0
,
0
1
1
s
n
s
n
s
jb
s
2
1
Wszystkie miejsca zerowe (a jest ich nieskończenie wiele)
funkcji dzeta Riemanna mają postać:
Dowód hipotezy Riemanna zmieniłby
oblicze teorii liczb; obliczenia numeryczne
wskazują, że przeszło 1,5 x 10
9
liczb spełnia
hipotezę Riemanna.
„Teoria sygnałów” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Twierdzenie o liczbach pierwszych:
(korzysta z funkcji dzeta Dirichleta)
x
x
x
x
x
x
x
x
x
x
x
dla
ln
1
ln
lim
2
,
pierwszych
liczb
liczba
-
Błąd oszacowania:
x = 10
10
4,5%
x = 10
14
3,0%
x = 10
18
2,5%
„Teoria sygnałów”
Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Zasada pudełkowa Dirichleta:
Jeżeli N przedmiotów umieścimy w K < N pudełkach,
to w którymś z pudełek znajdą się co najmniej 2 przedmioty.
N = 4
K = 3
Zastosowanie:
W Krakowie mieszkają 2 osoby mające tę samą liczbę
włosów na głowie (
N 800.000
)
Największa liczba włosów na głowie - K = 500 000
„Teoria sygnałów” Zdzisław Papir
Zbieżność
średniokwadratowa
aproksymacja
szeregiem Fouriera
k
k
n
t
jn
n
n
t
jn
n
e
X
t
x
e
X
t
x
o
o
a
szereg Fouriera
Średniokwadratowy błąd aproksymacji
0
1
o
2
a
2
T
dt
t
x
t
x
T
e
„Teoria sygnałów”
Zdzisław Papir
Zbieżność
średniokwadratowa
Szereg Fouriera stanowi
aproksymację średniokwadratową
sygnału. Warunkiem jej istnienia jest
skończona wartość całki
:
0
1
2
o
2
2
k
k
k
n
n
T
X
dt
t
x
T
e
T
dt
t
x
T
o
2
1
a więc
skończona energia (moc)
sygnału.
„Teoria sygnałów” Zdzisław Papir
Twierdzenie Parsevala
n
n
T
X
dt
t
x
T
2
o
2
1
Twierdzenie Parsevala pozwala wyznaczyć moc sygnału:
T
dt
t
x
T
P
o
2
1
w dziedzinie częstotliwości:
n
n
X
P
2
„Teoria sygnałów”
Zdzisław Papir
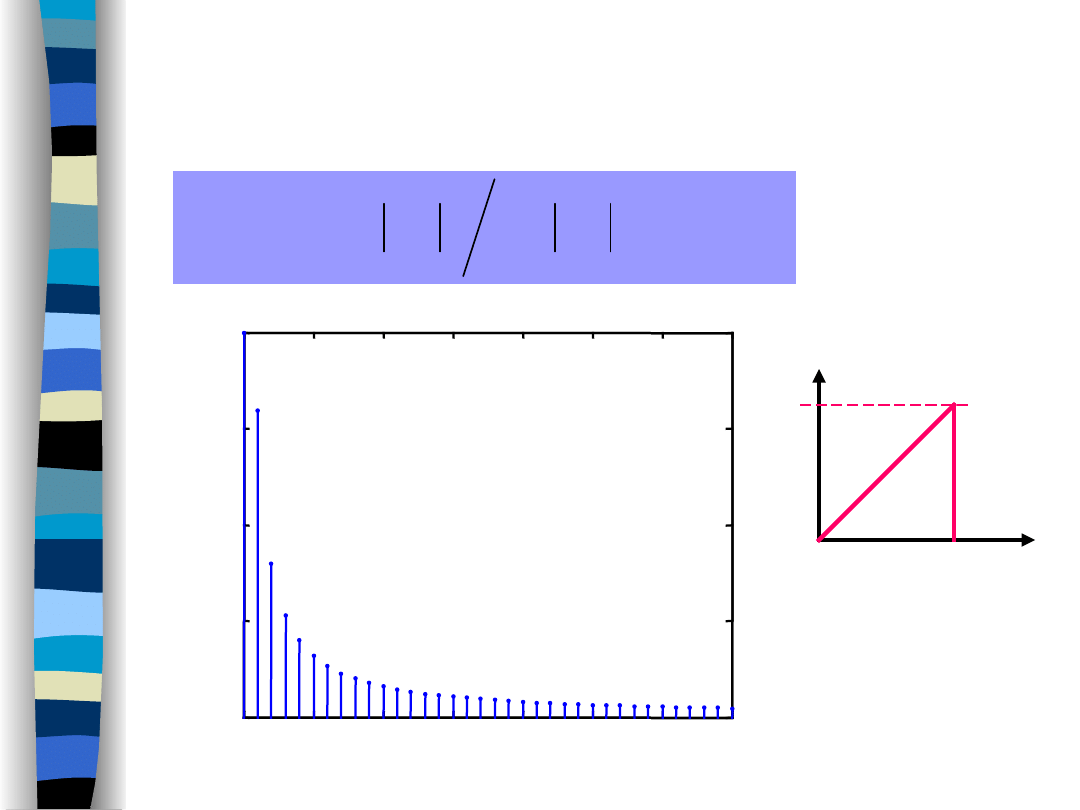
Moc ułamkowa
1
2
2
o
u
k
n
n
k
k
n
n
X
X
kf
P
0
5
10
15
20
25
30
35
0
0.05
0.1
0.15
0.2
kf
o
|X
k
|
Moc ułamkowa
T = 1
t
1
„Teoria sygnałów”
Zdzisław Papir
Moc ułamkowa
t
n
n
e
n
j
t
x
n
t
jn
n
n
o
1
2
o
sin
1
1
2
1
1
2
2
1
0
5
10
15
20
25
30
35
75
80
85
90
95
100
kf
0
P
(k
f
o
)
[%
]
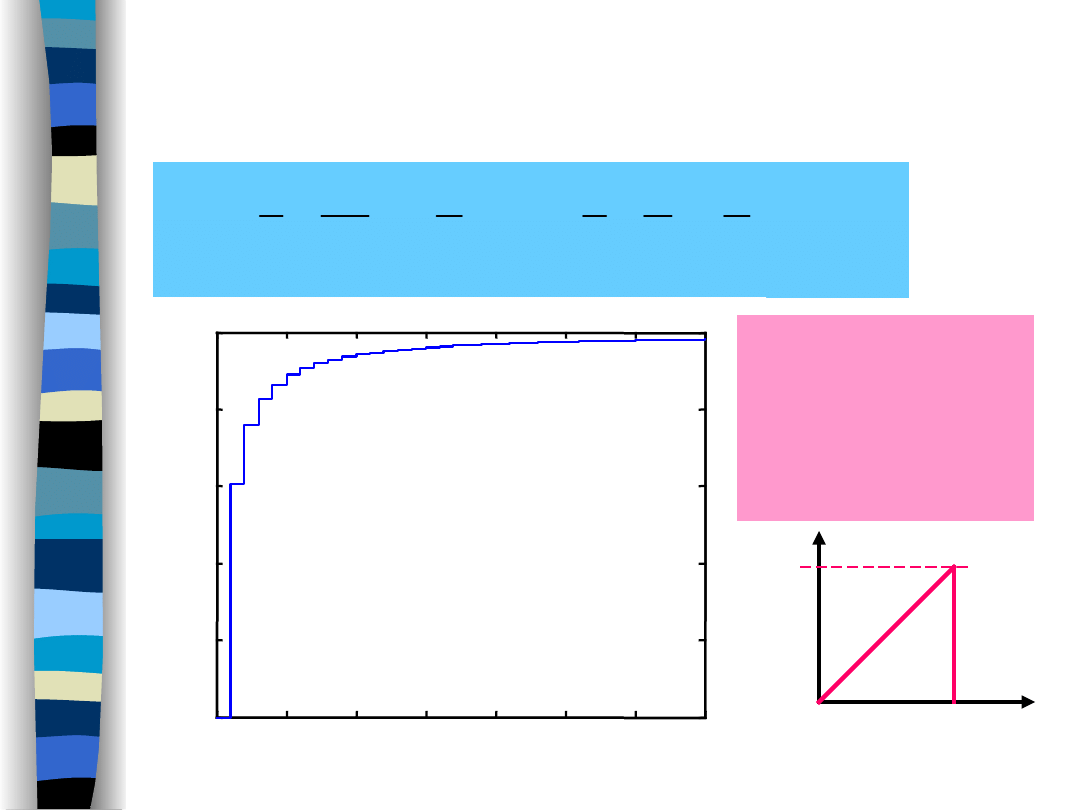
Sygnał piłokształtny
%
99
16
%
95
4
%
90
2
o
u
o
u
o
u
f
P
f
P
f
P
T = 1
t
1
„Teoria sygnałów” Zdzisław Papir
Moc ułamkowa
(sygnał piłokształtny -
90%)
0
0.5
1
1.5
0
0.2
0.4
0.6
0.8
1
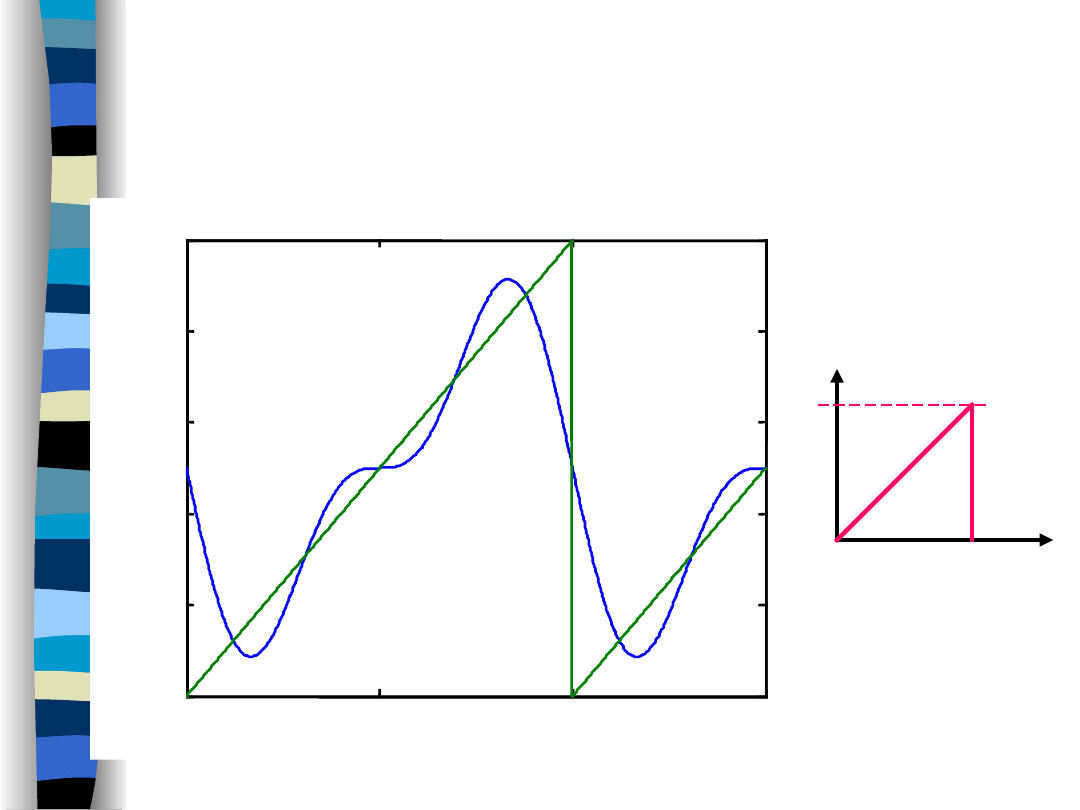
Aproksymacja sygnału piłokształtnego
2 harmoniczne
90% mocy sygnału
T = 1
t
1
„Teoria sygnałów” Zdzisław Papir
Moc ułamkowa
(sygnał piłokształtny -
95%)
0
0.5
1
1.5
0
0.2
0.4
0.6
0.8
1
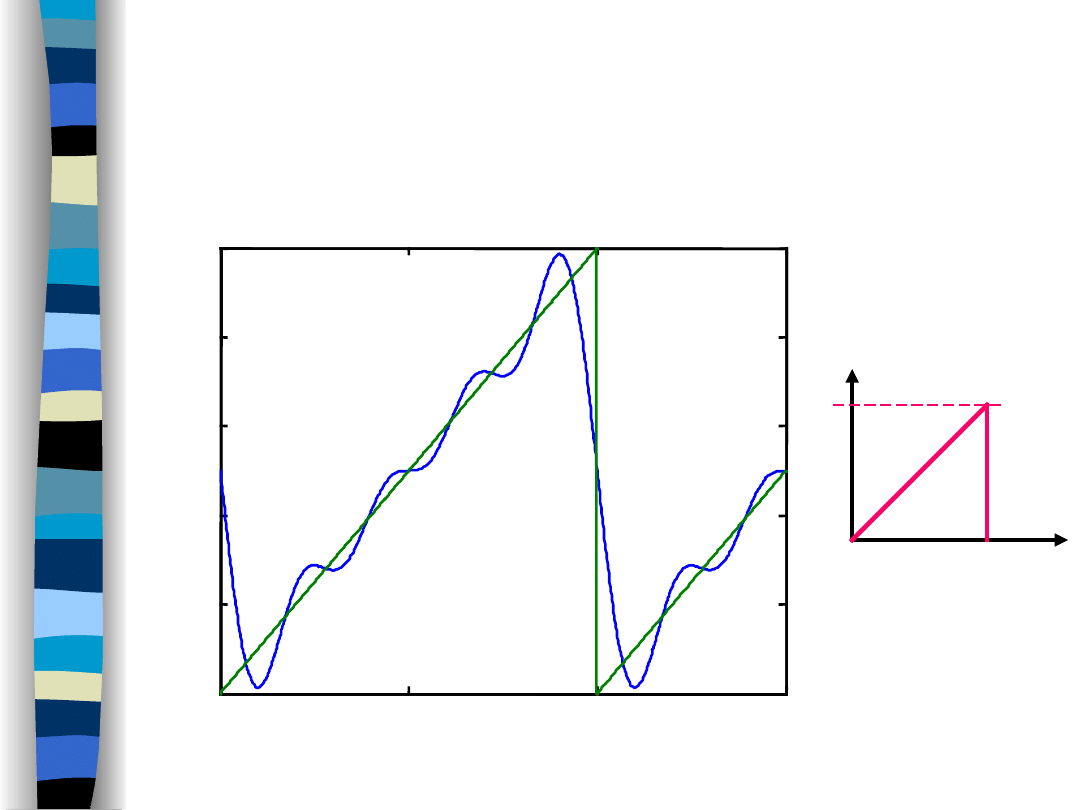
Aproksymacja sygnału piłokształtnego
4 harmoniczne
95% mocy sygnału
T = 1
t
1
„Teoria sygnałów” Zdzisław Papir
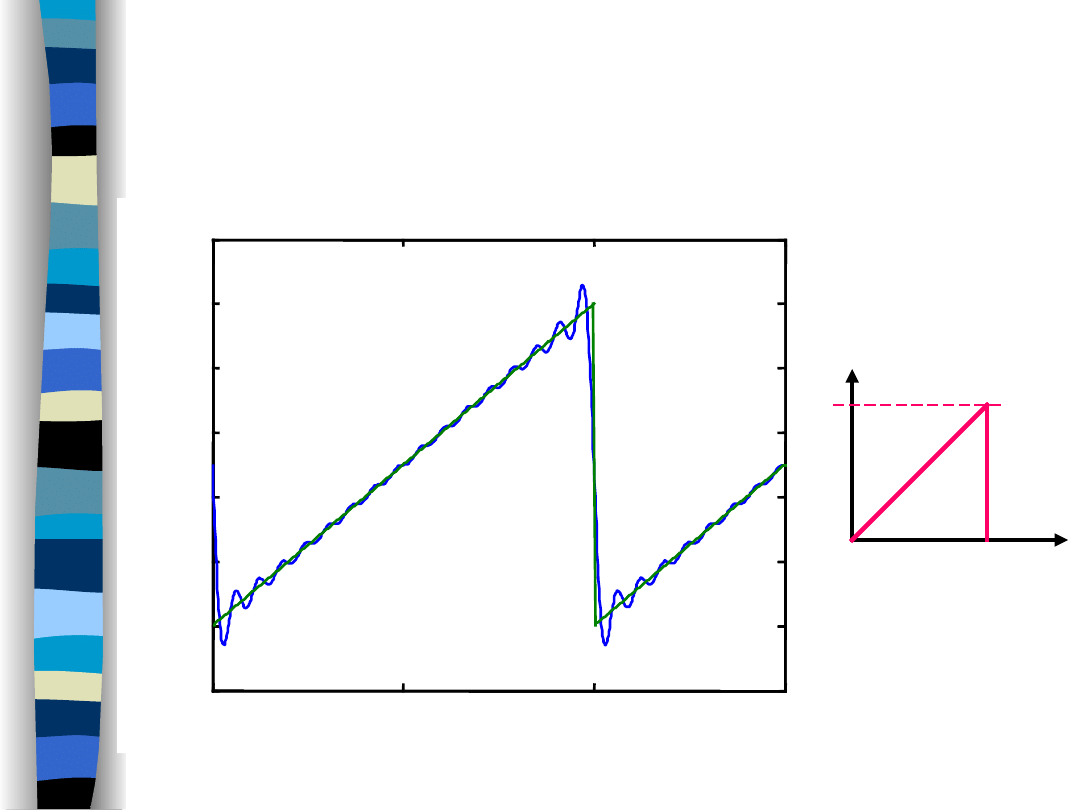
Moc ułamkowa
(sygnał piłokształtny -
99%)
0
0.5
1
1.5
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
Aproksymacja sygnału piłokształtnego
16 harmonicznych
99% mocy sygnału
T = 1
t
1
„Teoria sygnałów” Zdzisław Papir
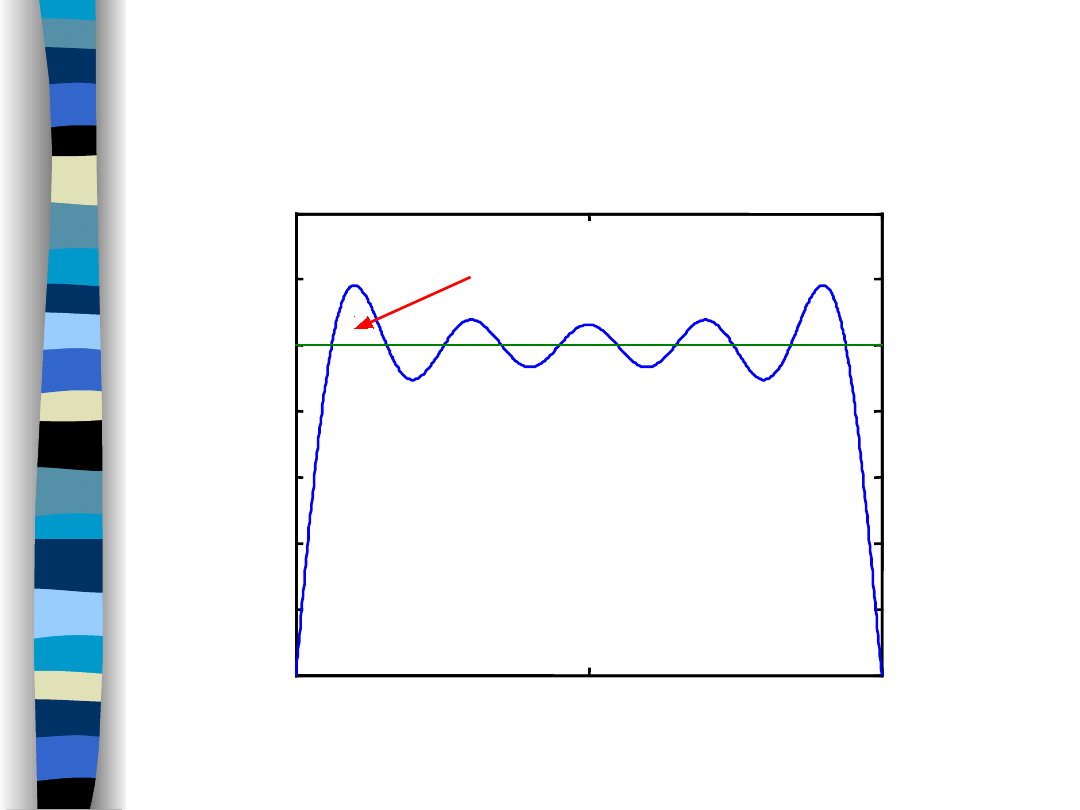
Efekt Gibbsa
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
efekt Gibbsa
Impuls prostokątny
11 harmonicznych
„Teoria sygnałów” Zdzisław Papir
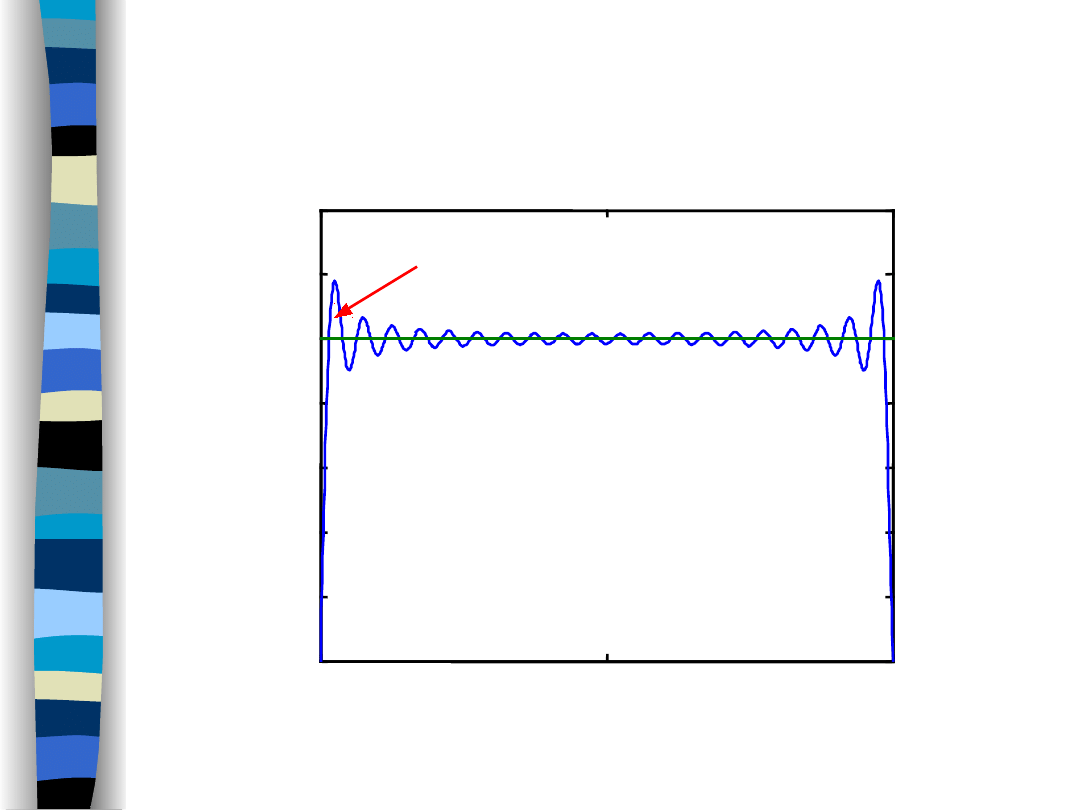
Efekt Gibbsa
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
efekt Gibbsa
Impuls prostokątny
39 harmonicznych
„Teoria sygnałów” Zdzisław Papir
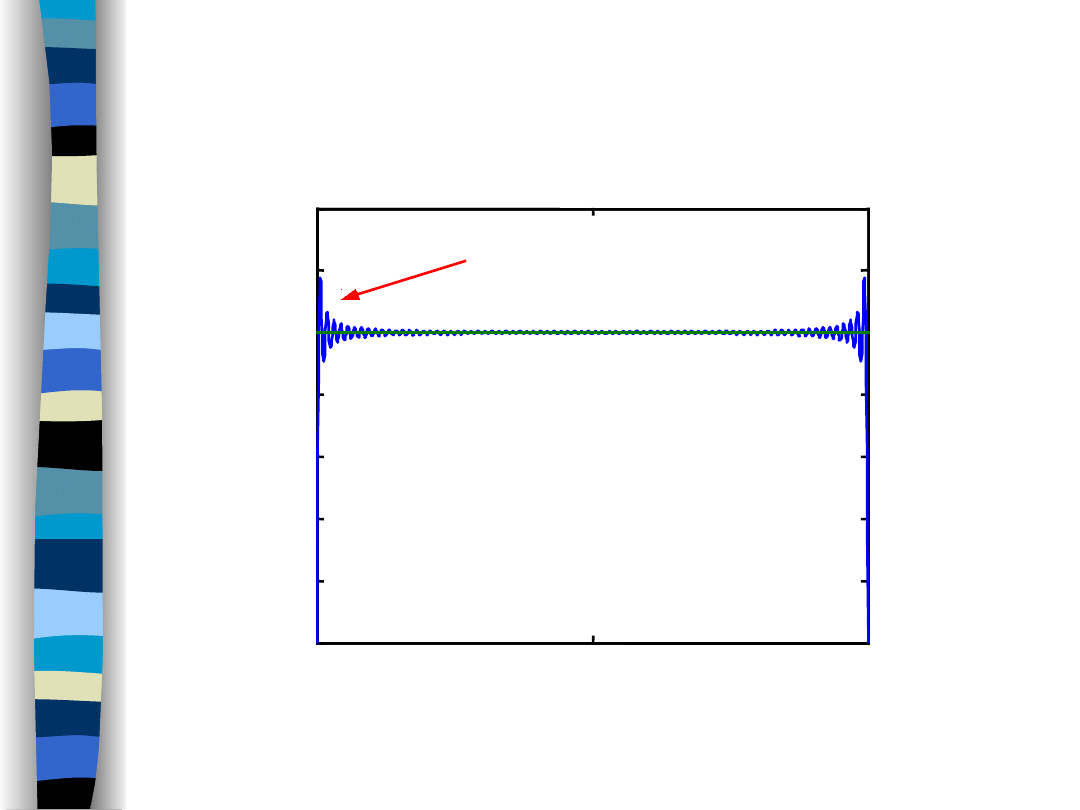
Efekt Gibbsa
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
efekt Gibbsa
Impuls prostokątny
79 harmonicznych
„Teoria sygnałów” Zdzisław Papir
Efekt Gibbsa
Efekt Gibbsa występuje w punktach
nieciągłości sygnału,
a objawia się jako nadmierne oscylacje
aproksymacji
skończonym szeregiem Fouriera; poziom
oscylacji jest
niezależny od długości aproksymacji.
„Teoria sygnałów” Zdzisław Papir
Okna Fejera,
Lanczosa...
k
k
n
t
jn
n
n
n
t
jn
n
e
X
w
t
s
e
X
t
x
o
o
Funkcja okna (ang. window)
k
n
w
n
,
0
jest dobierana w celu minimalizacji efektu Gibbsa.
W klasycznej aproksymacji jest stosowane
okno prostokątne o wagach
k
n
w
n
,
1
„Teoria sygnałów”
Zdzisław Papir
Okna Fejera,
Lanczosa...
Okno prostokątne Okno Fejera
k
n
w
n
,
1
k
n
k
n
w
n
,
/
1
Okno Lanczosa
Okno von Hanna, Hamminga, Kaisera...
x
x
x
Sa
k
n
k
n
Sa
w
n
/
sin
,
/
„Teoria sygnałów”
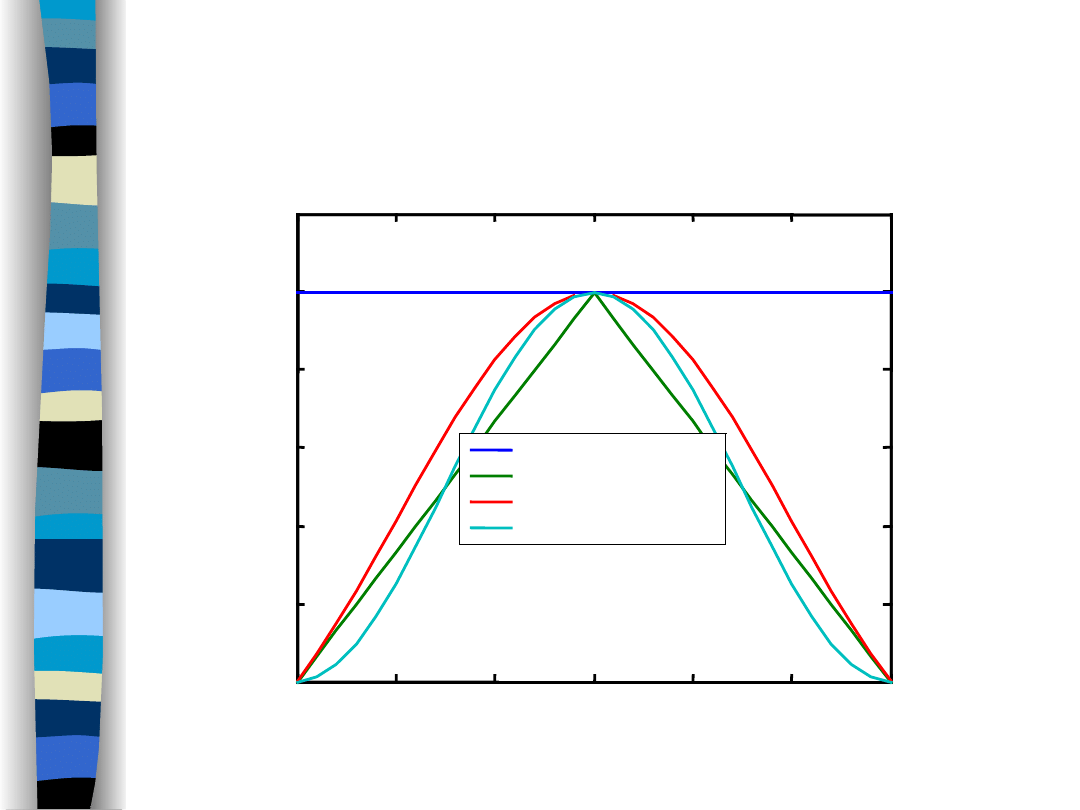
Zdzisław Papir
Okna Fejera,
Lanczosa...
-15
-10
-5
0
5
10
15
0
0.2
0.4
0.6
0.8
1
Okna aproksymacji szeregiem Fouriera
numery wyrazów szeregu Fouriera n
w
a
g
a
w
n
okno prostokątne
okno Fejera
okno Lanczosa
okno von Hanna
podwójna szerokość okna 2*k + 1
„Teoria sygnałów” Zdzisław Papir
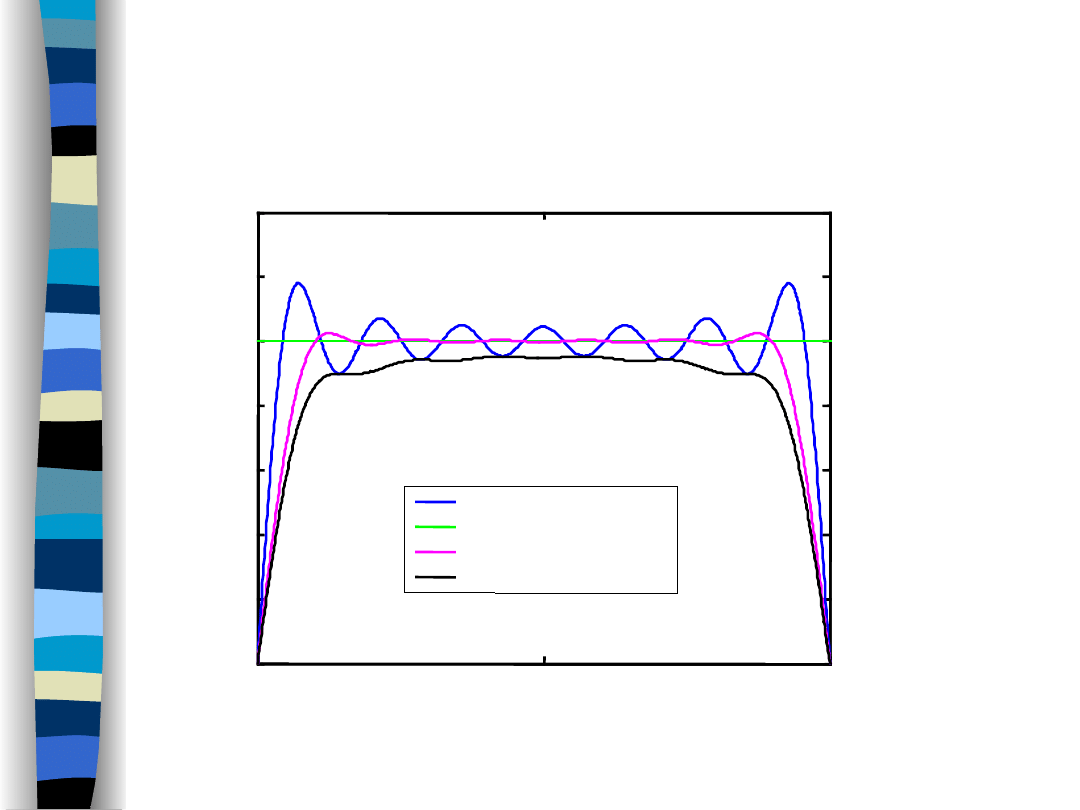
Okna Fejera,
Lanczosa...
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
okno prostokatne
impuls prostokątny
okno Fejera
okno Lanczosa
Impuls prostokątny
11 harmonicznych
Impuls prostokątny
7 harmonicznych
„Teoria sygnałów” Zdzisław Papir
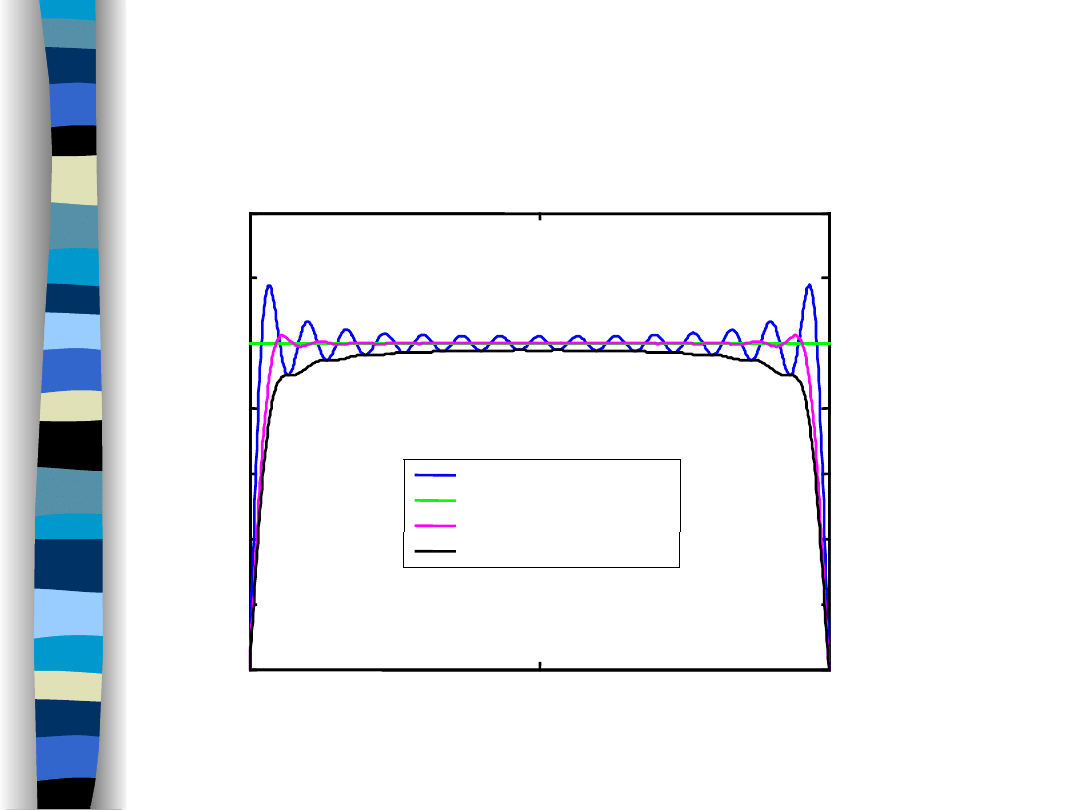
Okna Fejera,
Lanczosa...
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
okno prostokatne
impuls prostokątny
okno Fejera
okno Lanczosa
Impuls prostokątny
15 harmonicznych
„Teoria sygnałów” Zdzisław Papir
Okna, efekt Gibbsa,
błąd aproksymacji...
Okna Fejera, Lanczosa pozwalają w dużym stopniu zmniejszyć
efekt Gibbsa
(oscylacje w pobliżu punktu nieciągłości sygnału),
ale
kosztem wzrostu błędu średniokwadratowego.
Pamiętajmy, że przecież
szereg Fouriera (z oknem prostokątnym)
stanowi
najlepszą aproksymację sygnału,
zapewniającą
minimum błędu średniokwadratowego.
„Teoria sygnałów” Zdzisław Papir
Podsumowanie
•
Warunki Dirichleta zapewniają zbieżność szeregu Fouriera
do wartości sygnału; w punktach nieciągłości szereg Fouriera
generuje „średnią arytmetyczną” nieciągłości.
•
Praktycznym warunkiem zbieżności jest skończona wartość mocy
sygnału (zbieżność średniokwadratowa).
•
Ze zbieżności średniokwadratowej wynika twierdzenie Parsevala
pozwalające wyznaczyć moc sygnału poprzez moc poszczególnych
składowych harmonicznych.
•
Moc ułamkowa (konsekwencja tw. Parsevala) pozwala szacować
w praktyce użyteczną szerokość pasma sygnału.
•
W pobliżu punktów nieciągłości aproksymacja szeregiem Fouriera
wykazuje nadmierne i utrzymujące się fluktuacje (efekt Gibbsa).
•
Okna Fejera, Lanczosa i inne pozwalają redukować efekt Gibbsa,
ale kosztem dokładności aproksymacji.