Analiza obwodów

liniowych

pobudzanych

okresowymi

przebiegami

niesinusoidalnymi

 

• Zajmujemy się analizą obwodów liniowych w

stanie ustalonym przy wymuszeniach

okresowych, niesinusoidalnych

• Odpowiedzi takich obwodów są również

okresowymi funkcjami niesinusoidalnymi

• Obwody pobudzane wymuszeniami

sinusoidalnymi o jednakowej pulsacji są

szczególnym przypadkiem rozważanych

obwodów

• Okresowe przebiegi niesinusoidalne są

nazywane odkształconymi

Zgodnie z twierdzeniem Fouriera

funkcję okresową f(t) o okresie T można
przedstawić w postaci szeregu utworzonego ze
składowej stałej oraz funkcji sinusoidalnych o
częstotliwościach kf, jeżeli funkcja ta spełnia
warunki Dirichleta:
1)    w każdym przedziale o długości T funkcja
f(t) jest bezwględnie całkowana, czyli
 

 
2)    w każdym przedziale o długości T funkcja
f(t) ma co najwyżej skończoną liczbę maksimów i
minimów,
3)    funkcja f(t) może mieć w przedziale o
długości T co najwyżej skończoną liczbę
punktów nieciągłości, przy czym w każdym
punkcie nieciągłości istnieją granice –
lewostronna i prawostronna.

 







T

t

t

f

d





k

k

m

t

k

A

A

t

f

k

















0

1

0

sin

)

(

T







2

0

harmoniczna zerowa (wartość

stała ):

pierwsza ( podstawowa )

harmoniczna:

gdzie:

2

0

0

C

A 





1

0

1

sin





 t

A

m





sin

cos

cos

sin

sin

0

0

0

t

k

A

t

k

A

t

k

A

k

m

k

m

k

m

k

k

k



















k

sin 



k

m

k

A

C

k

m

k

k

A

B





cos





t

k

B

t

k

C

t

k

A

k

k

k

m

k

0

0

0

sin

cos

sin















 





















1

0

0

0

cos

sin

2

k

k

k

t

k

C

t

k

B

C

t

f

2

2

k

k

m

C

B

A

k





k

k

k

B

C

tg

arc





Funkcje przemienne:

Są to funkcje, których wartość średnia za okres

równa się zeru

 

0

d

0





t

t

f

T

 

T

C

t

t

f

T

2

d

0

0





0

0



C

t

T

0

f (t)

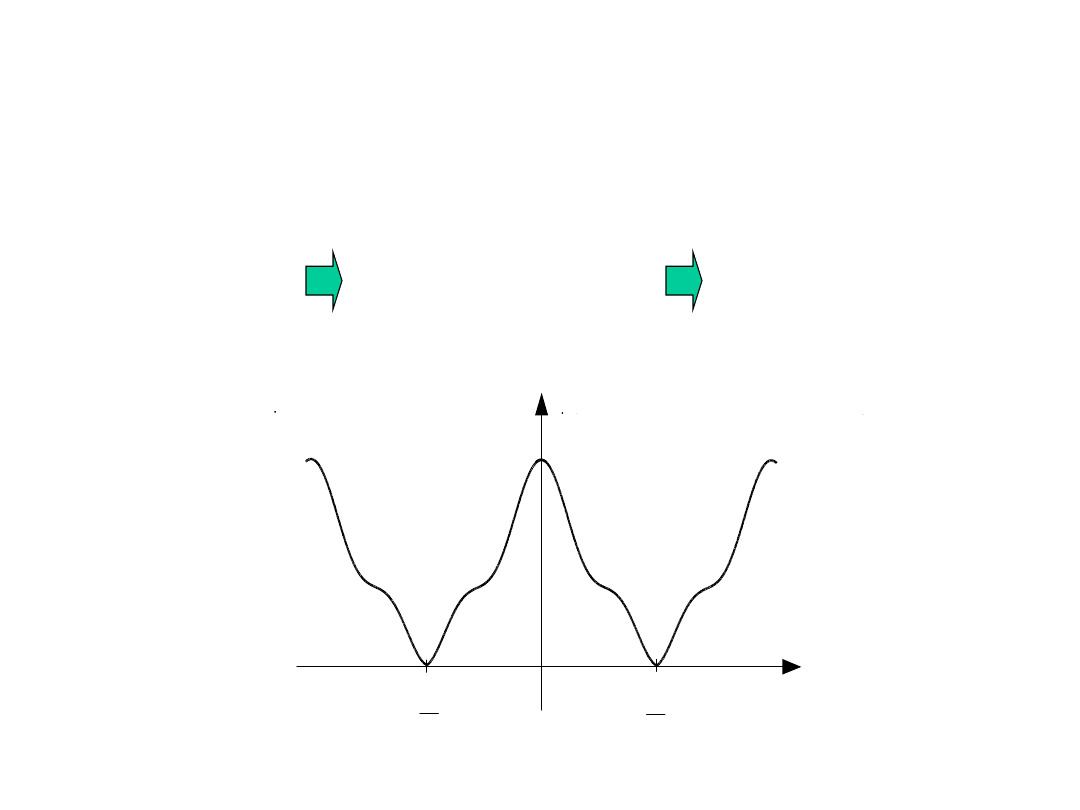
Funkcje parzyste:

Są to funkcje symetryczne względem osi

rzędnych

)

(

)

(

t

f

t

f





0

t

sinkω

B

k









2,

1,

0





k

B

k

2

T

2

T



0

f (t)

t

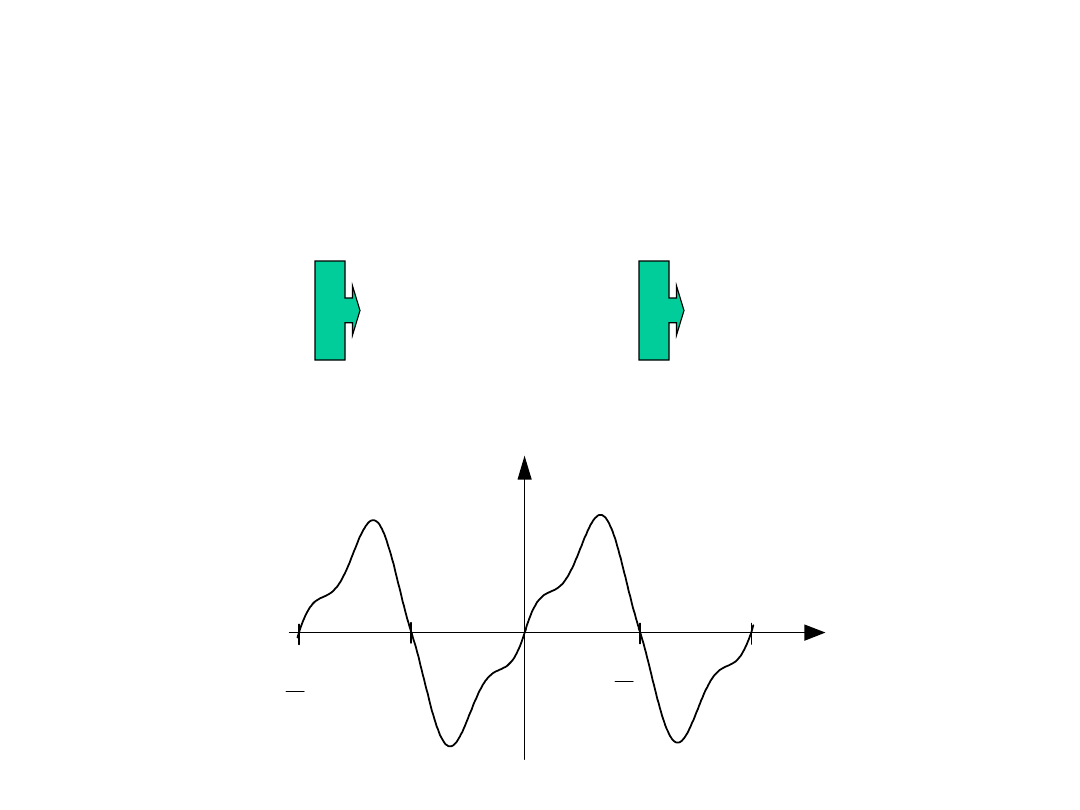
Funkcje nieparzyste:

Są to funkcje symetryczne względem początku układu

współrzędnych

)

(

)

(

t

f

t

f







0

ω

t

k

sin

C

k



0

/2

C

0









2,

1,

0





k

C

k

t

T

f (t)

2

T

0

-T

2

T



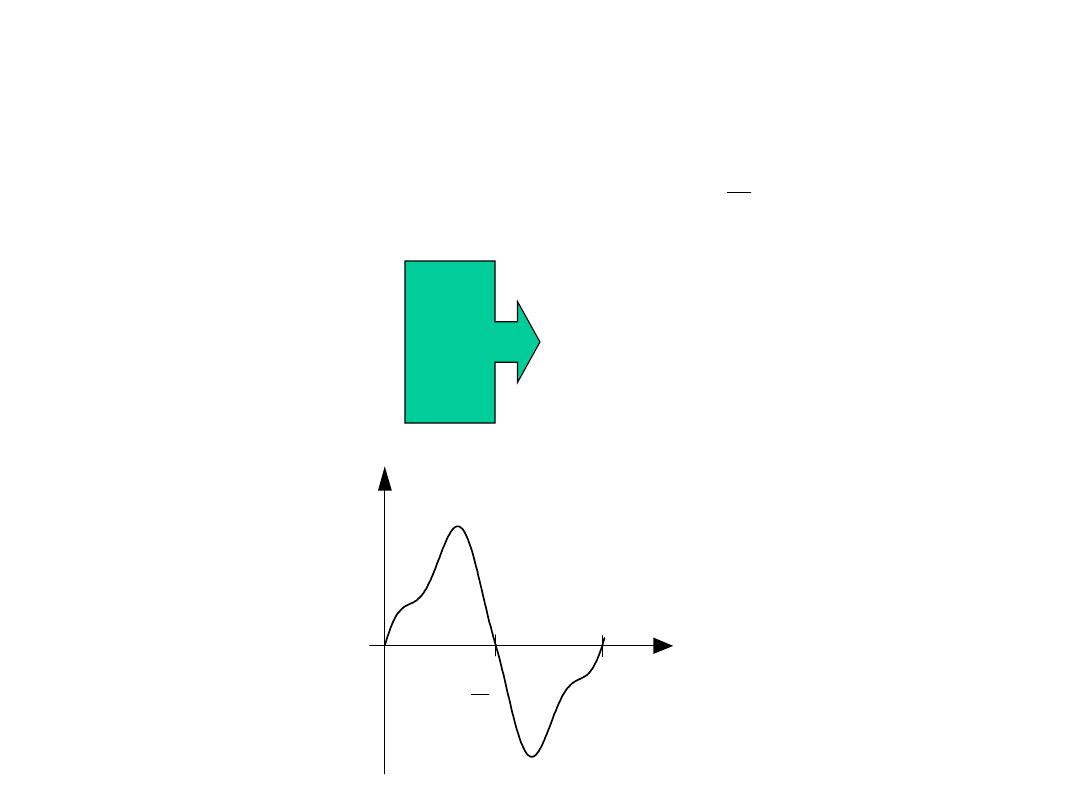
Funkcje antysymetryczne (o
odwrotnej zgodności półokresów):

Są to funkcje spełniające warunek:

)

(

2

t

f

T

t

f















 

0

/2

C

0



0

t

ω

k

sin2

B

2k



0

t

ω

k

2

cos

C

2k



0

0



C

0

2



k

B







2,

1,

0

2





k

C

k

t

T

f

(

t

)

2

T

0

Obliczanie współczynników szeregu

Fouriera

 

T

C

t

t

f

T

2

d

0

0









T

t

t

f

T

C

0

0

d

)

(

2

.

d

)

(

1

2

0

0

0







T

t

t

f

T

C

A

Zależności ułatwiające wyprowadzenie wzorów

na współczynniki C

k

oraz B

k

( k =1,2,... )















,

k

m

T

k

m

t

t

kω

t

mω

T

t

t

dla

2

≠

dla

0

∫

d

sin

sin

0

0

0

0



















,

dla

2

≠

dla

0

d

∫

cos

cos

0

0

0

0

k

m

T

k

m

t

t

k

t

m

T

t

t











T

t

t

t

t

k

t

m

0

0

0

d

cos

sin

0

0

Korzystając ze wzorów oznaczonych gwiazdami
oraz ze wzoru:

otrzymujemy:

 





















1

0

0

0

cos

sin

2

k

k

k

t

k

C

t

k

B

C

t

f

2

d

cos

d

cos

)

(

0

0

0

0

0

2

0

T

C

t

t

k

C

t

t

k

t

f

T

t

t

k

k

T

t

t

















 

t

t

k

t

f

T

C

T

t

t

k

d

cos

2

0

0

0









2

=

∫

d

ω

sin

=

d

∫

ω

sin

)

(

+

0

2

+

0

0

0

0

0

T

B

t

t

k

B

t

t

k

t

f

k

T

t

t

k

T

t

t

t

t

k

t

f

T

B

T

t

t

k

d

∫

ω

sin

)

(

2

=

+

0

0

0

Funkcje parzyste

zachodzi relacja:

uwzględniając ją we wzorze na C

k

oraz

przyjmując:

otrzymujemy:

k=1, 2, ...

Funkcje nieparzyste

zachodzi relacja:

uwzględniając ją we wzorze na B

k

oraz

przyjmując:

otrzymujemy:

)

(

)cos

(

)cos

(

0

0

t

k

t

f

t

k

t

f











t

t

k

t

f

T

C

T

k

d

cos

)

(

4

0

2

0







2

0

T

t





2

0

T

t





....

2,

1,

d

sin

)

(

4

0

2

0









k

t

t

k

t

f

T

B

T

k

)

(

)sin

(

sin

)

(

0

0

t

k

t

f

t

k

t

f











Funkcje antysymetryczne

zachodzą relacje:

oraz

gdzie k jest nieparzyste

Podstawiając we wzorze na C

k

: t

0

= 0

otrzymujemy:

k = 1, 3,
5, ...
Postępując analogicznie ze wzorem na B

k

otrzymujemy:

k = 1, 3,

5, ...











 













 





2

cos

2

)cos

(

0

0

T

t

k

T

t

f

t

k

t

f











 













 





2

sin

2

)sin

(

0

0

T

t

k

T

t

f

t

k

t

f

,

dt

t

k

t

f

T

C

T

k







0

0

cos

)

(

2

d

cos

)

(

4

0

2

0

t

t

k

t

f

T

C

T

k







t

t

k

t

f

T

B

T

k

d

sin

)

(

4

2

0

0







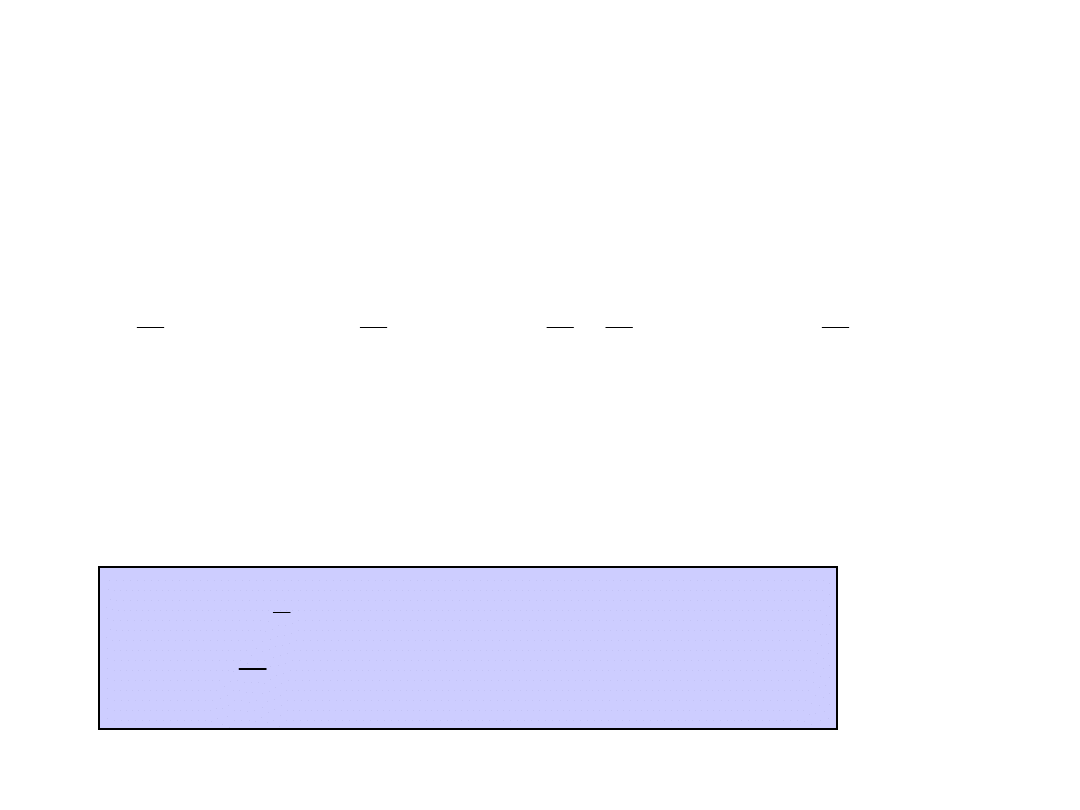
Funkcje parzyste i antysymetryczne

zachodzi relacja:

uwzględniając wyżej przedstawioną zależność
we wzorze na C

k

dla funkcji antysymetrycznych

otrzymujemy:

k = 1, 3,
5, ...





.

cos

)

(

)cos

(

2

cos

2

2

2

cos

2

0

0

0

0

0

t

k

t

f

k

t

k

t

f

t

k

T

k

t

T

T

f

t

T

k

t

T

f





































































 













 

t

t

k

t

f

T

C

T

k

d

cos

)

(

8

4

0

0







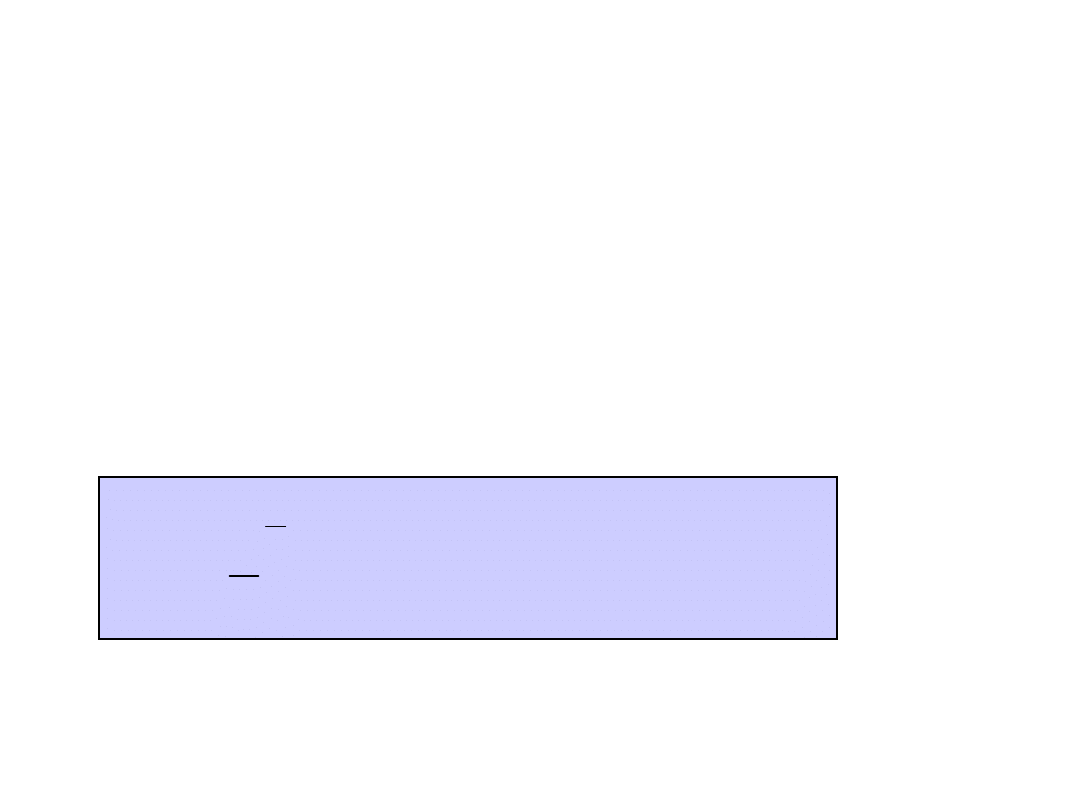
Funkcje nieparzyste i
antysymetryczne

Zachodzi relacja analogiczna jak dla funkcji
parzystych i antysymetrycznych. Uwzględniając
tę zależność we wzorze na B

k

dla funkcji

antysymetrycznych otrzymujemy:

k = 1, 3,
5, ...

t

t

k

t

f

T

B

T

k

d

∫

ω

sin

)

(

8

=

4

0

0

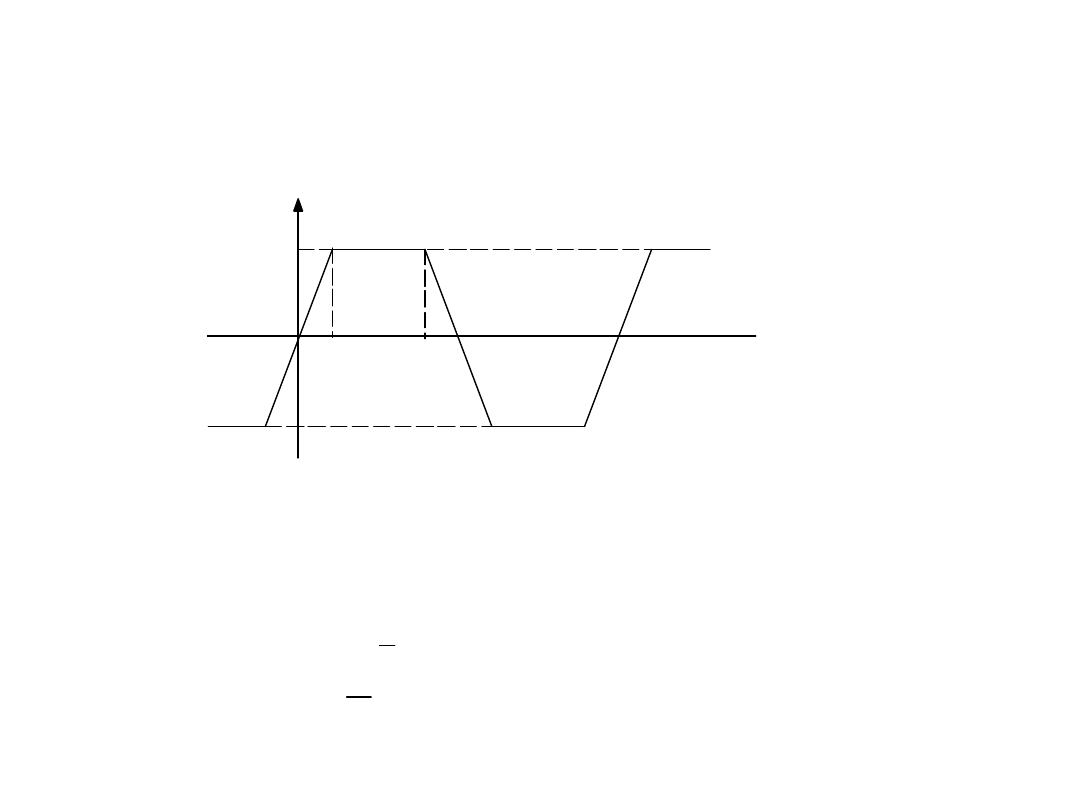
Przykład

Rozwinięcie w szereg Fouriera funkcji
trapezowej

Funkcja jest nieparzysta i
antysymetryczna, więc:

f (t)

A

0



__

T

2

(



- )

__

T

2

T

-A

0,

C

k



0

2



k

B







,

,

k

2

1









4

0

0

d

sin

)

(

8

T

k

t

t

k

t

f

T

B

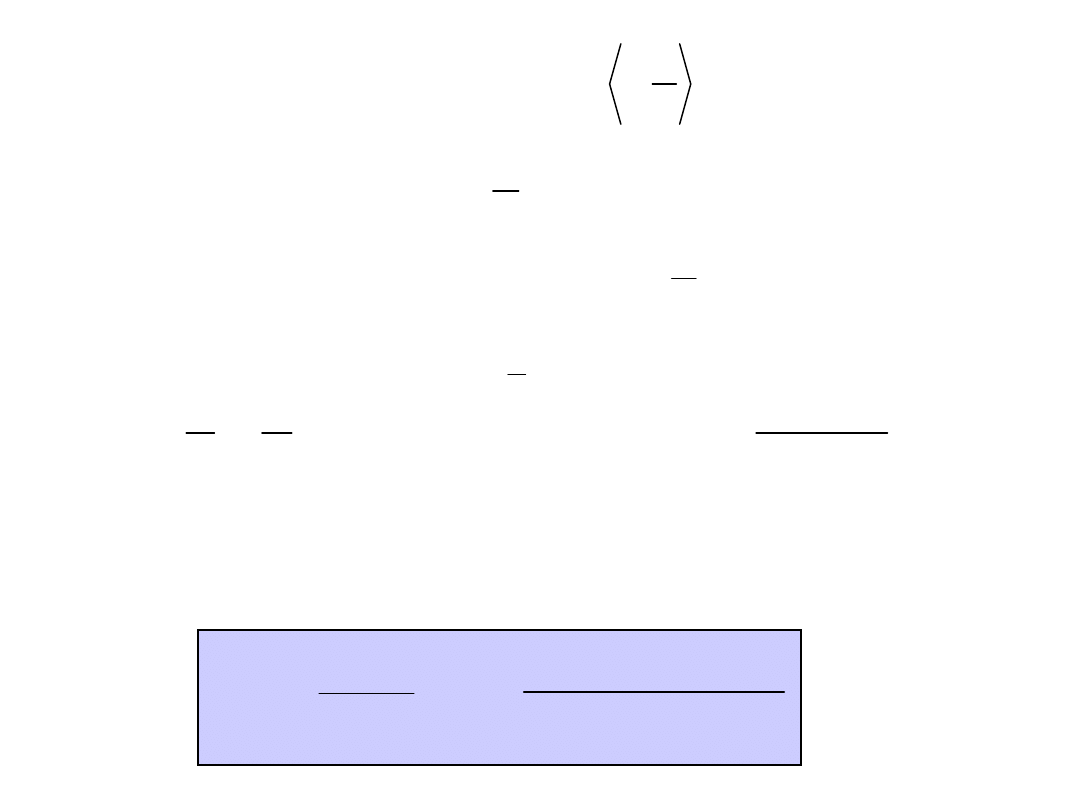
Równanie funkcji w przedziale jest
następujące:

Rozwinięcie funkcji w szereg Fouriera jest
następujące:

 

t

f

4

0

T

,





























4

0

)

(

T

t

A

t

t

A

t

f

















































0

2

0

0

4

0

0

sin

4

d

sin

d

sin

8

k

k

A

t

t

k

A

t

t

k

t

A

T

B

T

k







0

4

)

(

A

t

f











,...

,

k

k

t

k

k

3

1

2

0

0

sin

sin

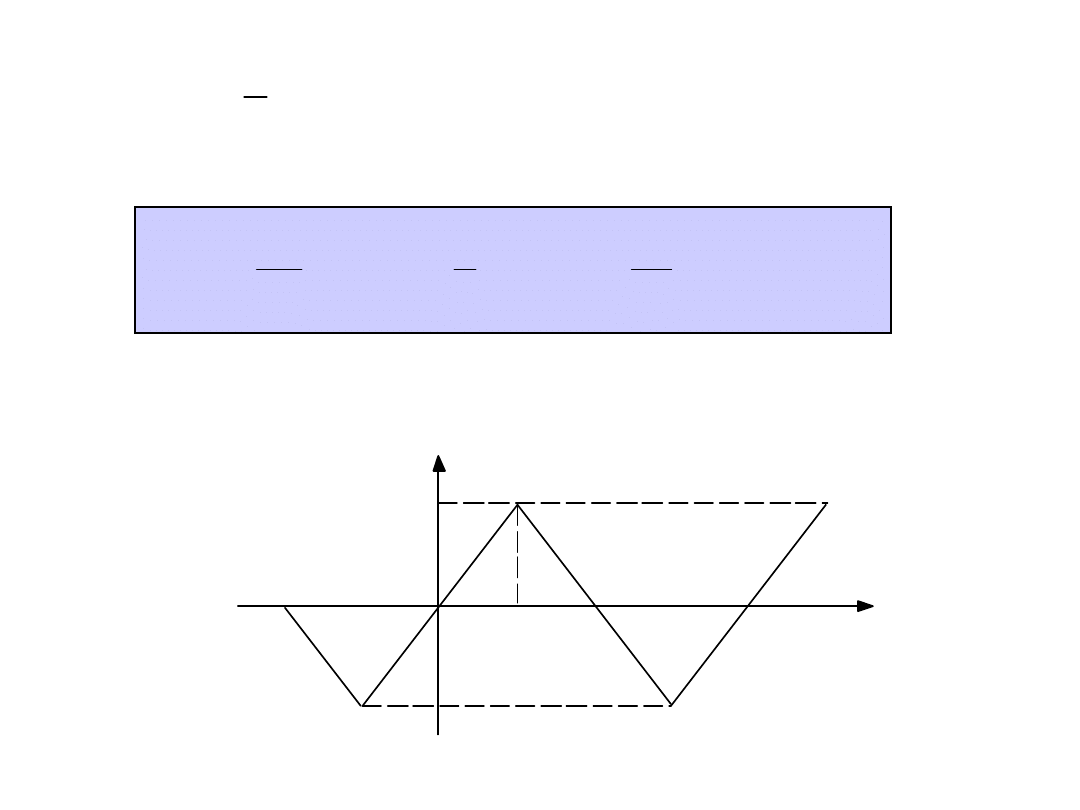
Jeżeli , to otrzymujemy krzywą trójkątną i
na podstawie wyznaczonego powyżej wzoru
znajdujemy:

4

T

































...

t

t

t

A

t

f

0

0

0

2

5

sin

25

1

3

sin

9

1

sin

8

)

(

f

(t)

A

0

_

_

T

4

_
_

T

2

T

t

-A

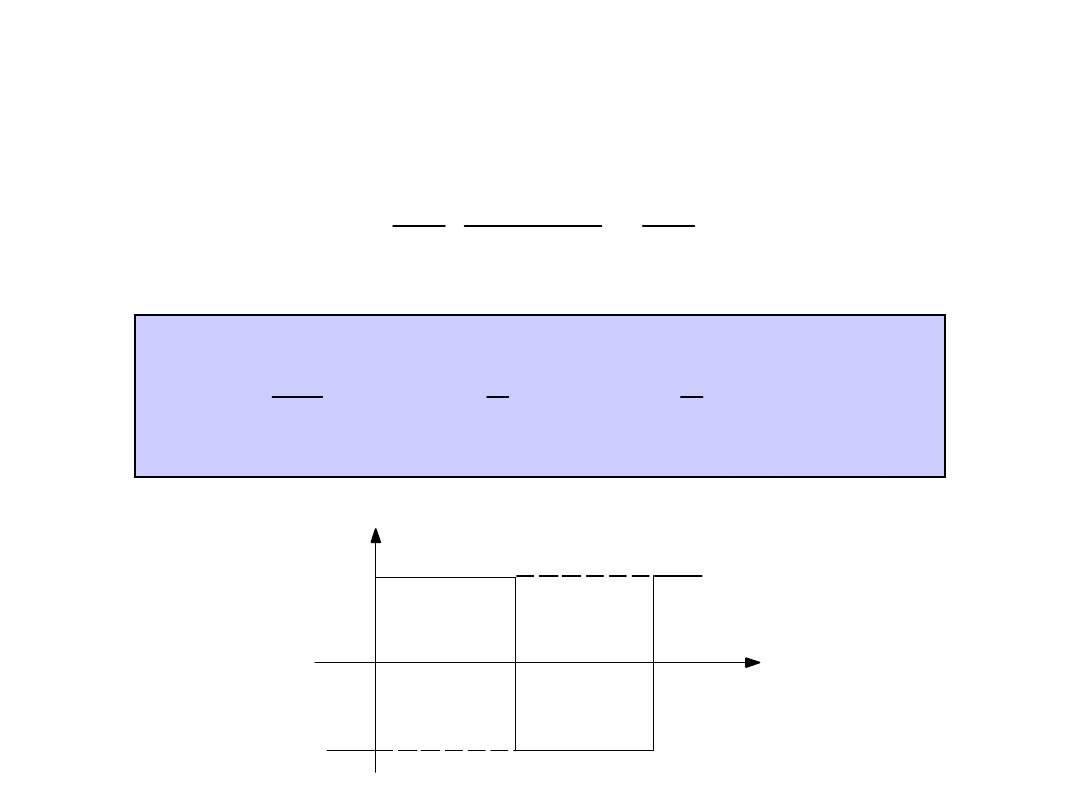
Jeżeli , to otrzymujemy krzywą
prostokątną i na podstawie wyznaczonego
powyżej wzoru znajdujemy:

0





k

A

k

k

k

A

B

k





















4

sin

4

lim

0

0

0





























...

t

t

t

A

t

f

0

0

0

5

sin

5

1

3

sin

3

1

sin

4

)

(

f (t)

0

-A

A

__

T

2

T

t

Wykładnicza postać szeregu

Fouriera

Weźmiemy pod uwagę szereg Fouriera funkcji

w postaci

Przyjmujemy oznaczenie:

 

t

f





















1

0

0

0

cos

sin

2

)

(

k

k

k

t

k

C

t

k

B

C

t

f









.

e

e

2

1

cos

,

e

e

j

2

1

sin

0

0

0

0

j

j

0

j

j

0

t

k

t

k

t

k

t

k

t

k

t

k























































1

j

j

0

0

0

e

2

j

e

2

j

2

)

(

k

t

k

k

k

t

k

k

k

B

C

B

C

C

t

f

0,1,2...

2

j







k

B

C

V

k

k

k

Badamy wyrażenie:

Wykres , określony dla dyskretnych wartości
, to widmo amplitudowe funkcji f(t). Ponieważ
, to widmo amplitudowe jest symetryczne względem
osi rzędnych. Wykres
, to widmo fazowe. Jest ono
symetryczne

względem

początku

układu

współrzędnych.

2

j

k

k

k

B

C

V











k

k

C

C 



k

k

B

B







*

k

k

k

k

V

B

C

V









2

j

t

k

k

k

t

k

k

k

V

V

V

t

f

0

0

j

1

j

1

0

e

e

)

(

























t

k

k

k

V

t

f

0

j

e

)

(













k

V

,...

,

,

k

2

1

0







k

k

V

V





k

k

V

V

arg

arg







t

)

t

(

f

T

V

T

t

t

t

k

k

d

e

1

0

0

0

j











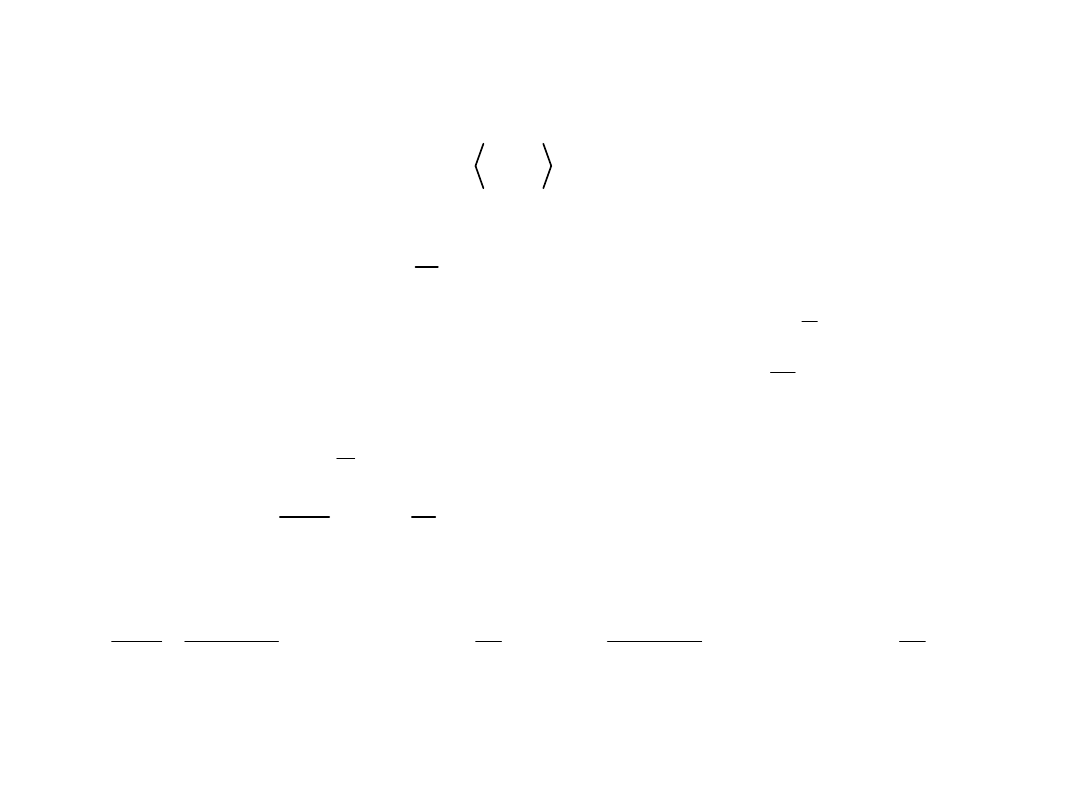
Przykład

Jako przykład rozpatrujemy wyprostowaną
sinusoidę
Jejrównanie w przedziale jest
następujące:

Funkcja jest parzysta, stąd: oraz:

,

0

,

2

1

sin

)

(

0

T

t

t

A

t

f









T

,

0

0



k

B

t

t

k

t

f

T

C

T

k

d

cos

)

(

4

2

0

0















.

1

2

1

2

cos

2

1

1

1

2

1

2

cos

2

1

1

2

d

cos

2

1

sin

4

0

0

2

0







































































k

k

k

k

A

t

t

k

t

T

A

C

T

k

2

k

k

C

V 





A

V

2

0

...

A

,

A

,

A

V



















35

2

V

15

2

V

3

2

3

2

1

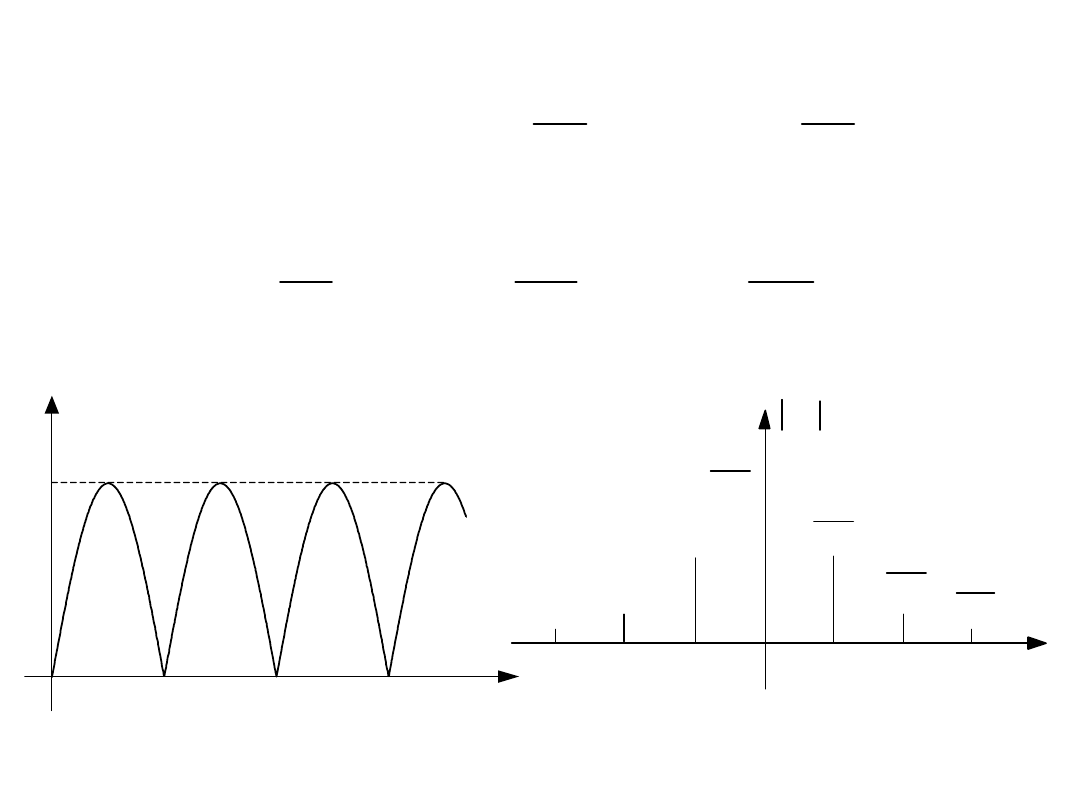
Stąd otrzymujemy:

f(t)

t

2T

3T

T

0

A

V

k

-3

-2

-1

0

1

2

3

k



2A



3

2A



15

2A

 

2A