„Teoria sygnałów” Zdzisław Papir

•Dekompozycja sygnału na składowe - idea

•Optymalna aproksymacja sygnału

•Sygnały ortogonalne

•Ortogonalność i sygnał wykładniczy

•Ortogonalny układ funkcji zespolonych

•Ortogonalny układ zespolonych sygnałów
wykładniczych

•Wykładniczy szereg Fouriera

•Trygonometryczny szereg Fouriera

•Charakterystyki częstotliwościowe

•Joseph Fourier

•Podsumowanie

Dekompozycja
sygnałów
Szereg Fouriera

Dekompozycja sygnału
na
składowe - idea

„Teoria sygnałów” Zdzisław Papir

ULS

st

e

 

 

st

e

s

H

t

y 

ULS

 





n

t

s

n

n

e

X

t

x

 

 

t

s

n

n

n

n

e

s

H

X

t

y





Dekompozycja dowolnego sygnału x(t)
na składowe
wykładnicze X

n

exp(s

n

t) pozwala

wyznaczyć odpowiedź ULS na dowolny
sygnał wejściowy.

Optymalna
aproksymacja
sygnału

„Teoria sygnałów” Zdzisław Papir

 

 

t

cx

t

x

a



2

1

t

t

t





   

 

t

cx

t

x

t

x

a

e





•Znamy sygnał x(t) oraz sygnał go
aproksymujący x

a

(t).

•

Poszukujemy amplitudy sygnału cx

a

(t)

tak, aby
zapewnić jak najlepszą aproksymację:

 

 













2

1

2

1

2

2

1

min

min

t

t

a

c

c

dt

t

cx

t

x

t

t

e

Rozwiązanie

 

 













2

1

2

1

2

2

1

min

min

t

t

a

c

c

dt

t

cx

t

x

t

t

e

 

   

 





   

 





0

2

2

0

2

2

1

1

2

2

1

1

2

2

1

2

2

2

2

1

2

























t

t

a

a

t

t

t

t

a

a

dc

d

t

t

dt

t

cx

t

x

t

x

dc

e

d

dt

t

x

c

t

x

t

cx

t

x

dc

e

d







2

1

2

1

)

(

)

(

)

(

2

t

t

a

t

t

a

dt

t

x

dt

t

x

t

x

c

„Teoria sygnałów” Zdzisław Papir

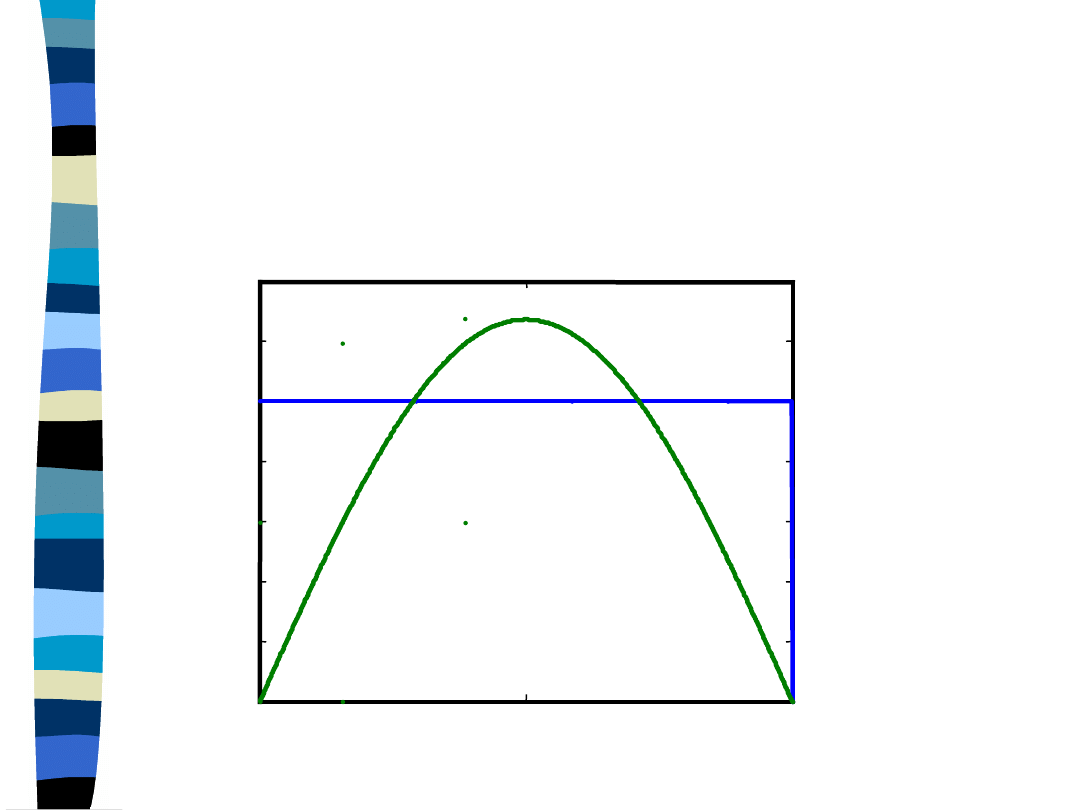
Aproksymacja impulsu
prostokątnego
1 harmoniczna

-0.5

0

0.5

0

0.2

0.4

0.6

0.8

1

1.2

1.4

czas t

y(t) = (4/pi) *
cos(pi*t)

„Teoria sygnałów” Zdzisław Papir

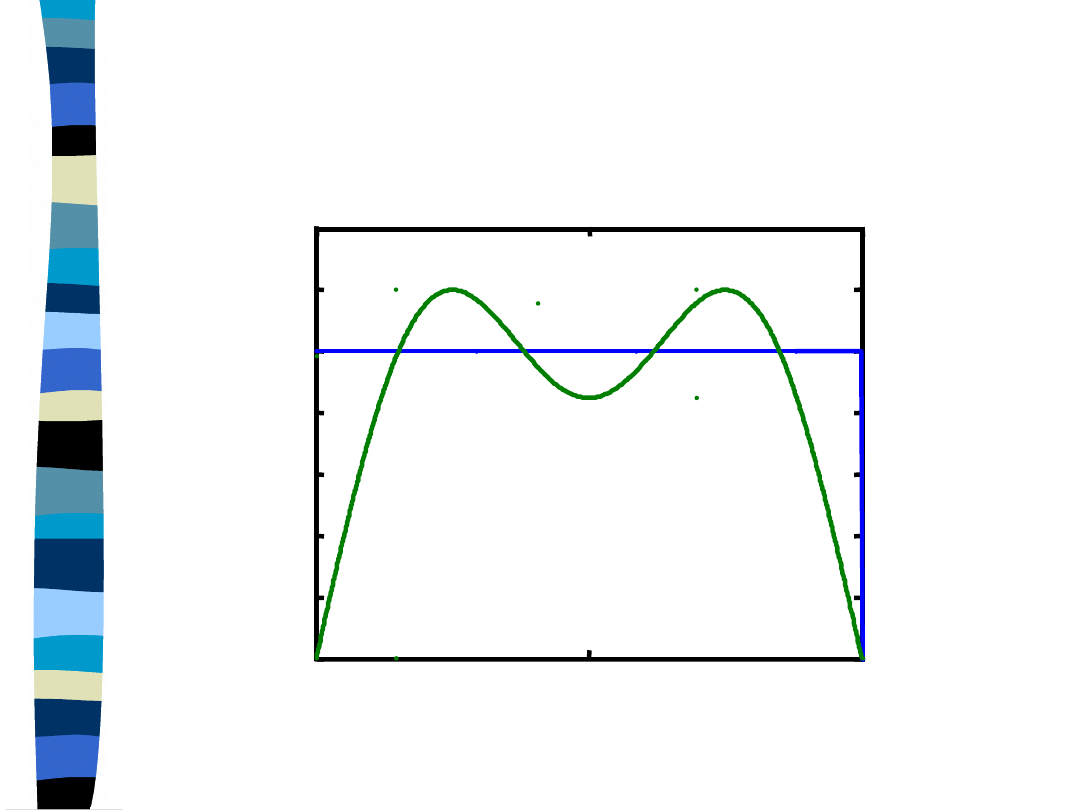
Aproksymacja impulsu
prostokątnego
1 + 3 harmoniczna

-0.5

0

0.5

0

0.2

0.4

0.6

0.8

1

1.2

1.4

czas t

y=(4/pi) * cos(pi*t) - (4/3pi) * cos(3*pi*t)

„Teoria sygnałów” Zdzisław Papir

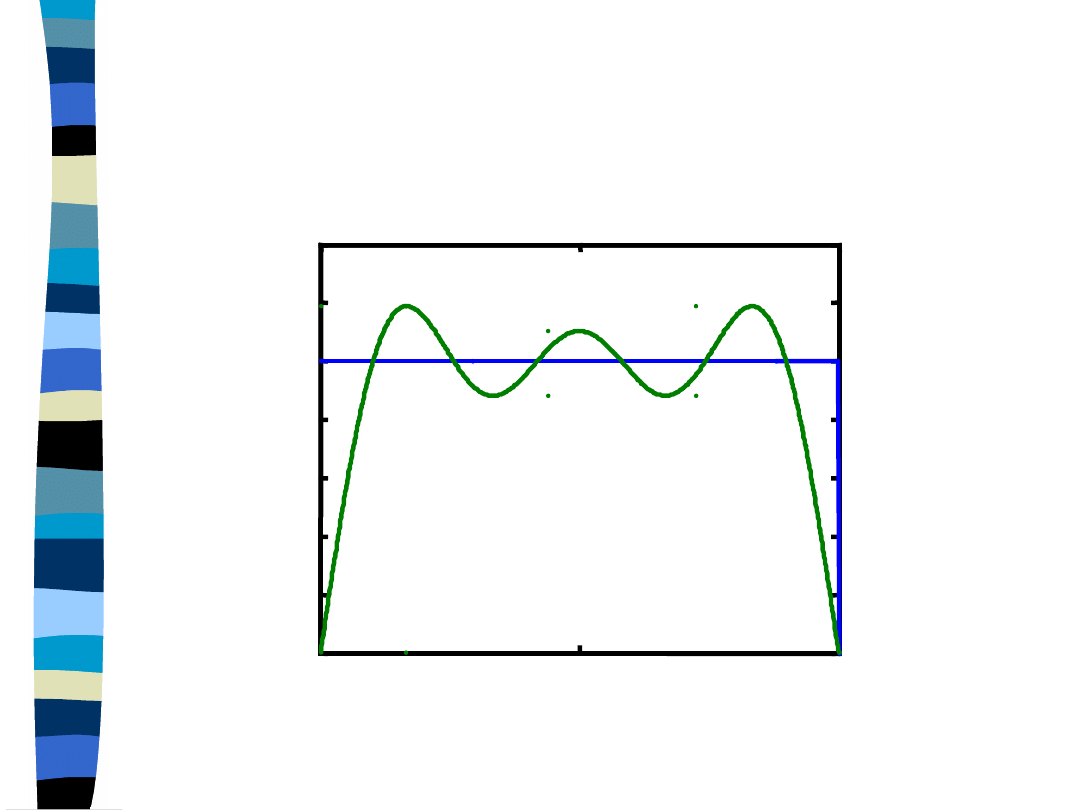
Aproksymacja impulsu
prostokątnego
1 + 3 + 5 harmoniczna

-0.5

0

0.5

0

0.2

0.4

0.6

0.8

1

1.2

1.4

czas t

y = (4/pi) * cos(pi*t) - (4/3pi) * cos(3*pi*t) +

+ (4/5pi) * cos(5*pi*t)

„Teoria sygnałów” Zdzisław Papir

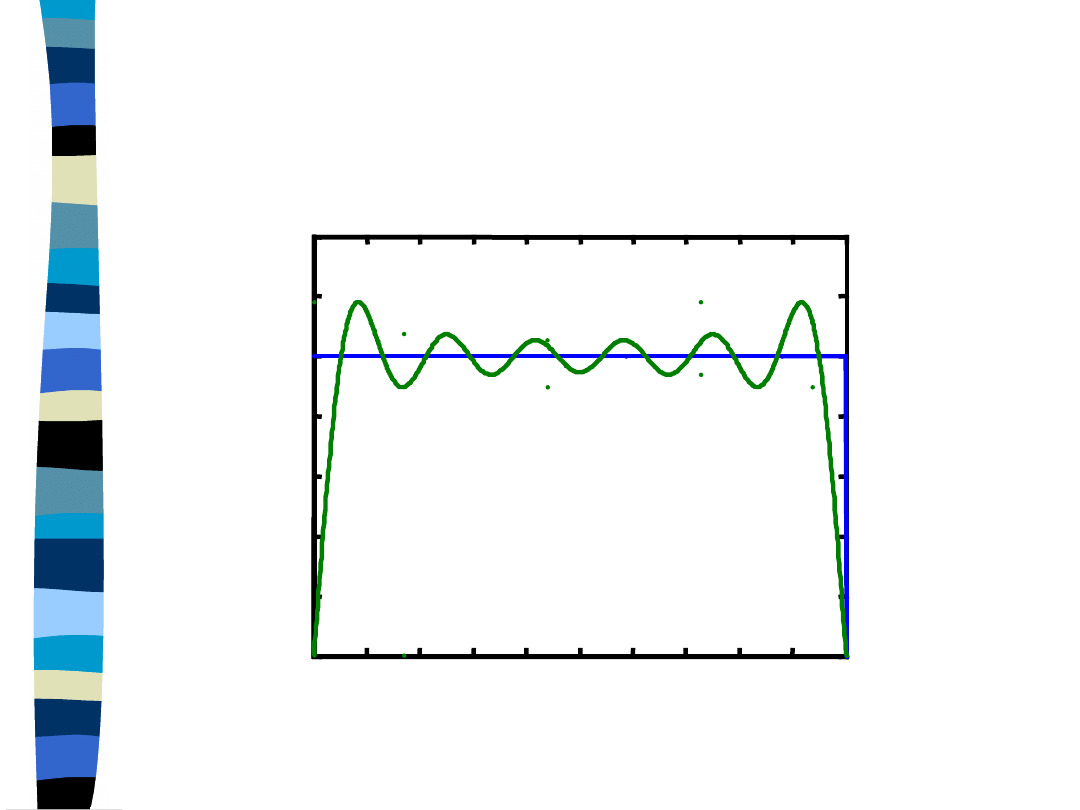
Aproksymacja impulsu
prostokątnego
1 + 3 + 5 + ... + 11 harmoniczna

-0.5 -0.4 -0.3 -0.2 -0.1

0

0.1

0.2

0.3

0.4

0.5

0

0.2

0.4

0.6

0.8

1

1.2

1.4

czas t

Aproksymacja za pomocą 11 harmonicznych

„Teoria sygnałów” Zdzisław Papir

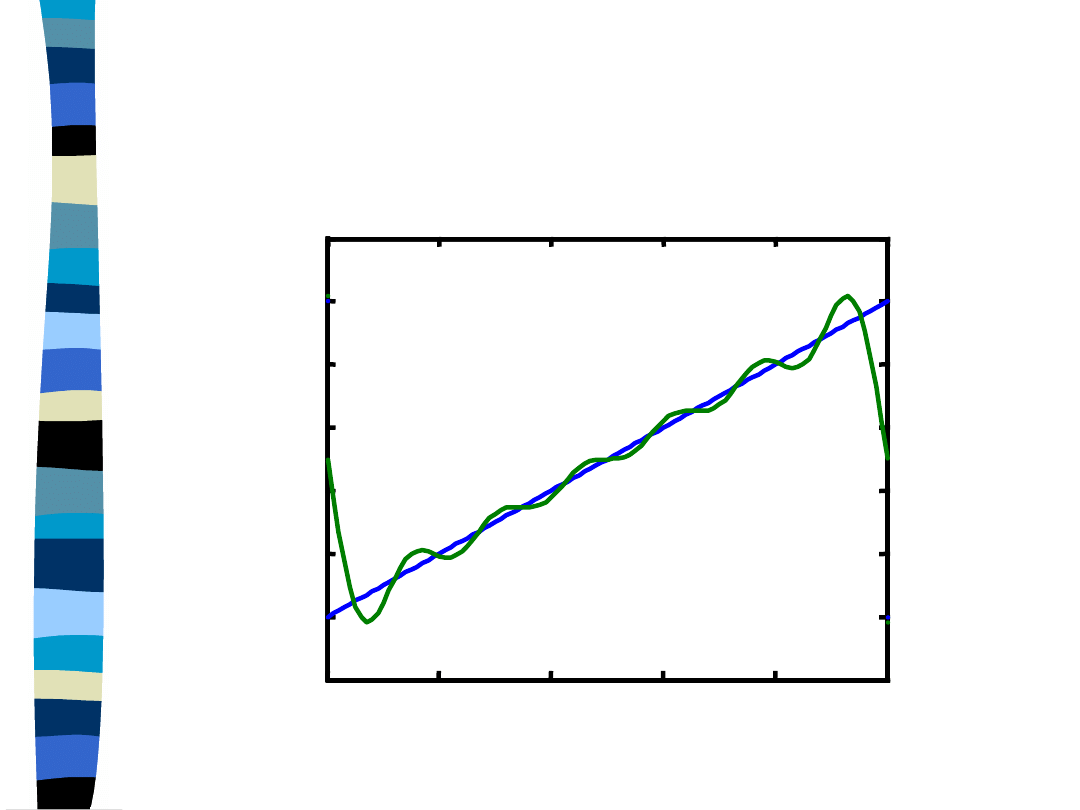
Aproksymacja impulsu
trójkątnego
1 + 2 + 3 + 4 + 5 + 6
harmoniczna

0

0.2

0.4

0.6

0.8

1

-0.2

0

0.2

0.4

0.6

0.8

1

1.2

czas t

„Teoria sygnałów” Zdzisław Papir

Sygnały ortogonalne





)

(

),.....,

(

),

(

2

1

t

g

t

g

t

g

K

 

 

)

(

0

)

(

,

2

1

t

g

t

g

dt

t

g

t

g

n

m

t

t

n

m

n

m













 

2

1

,

t

t

t

t

g

n

n









R

 







2

1

2

2

,

t

t

n

n

n

G

dt

t

g

„Teoria sygnałów” Zdzisław Papir

Sygnały ortogonalne

„Teoria sygnałów” Zdzisław Papir

)

(

.....

)

(

)

(

)

(

2

2

1

1

t

g

c

t

g

c

t

g

c

t

x

K

K















K

n

n

n

a

t

g

c

t

x

1

)

(

)

(

 

 













2

1

1

2

1

1

2

1

)

,....

(

2

)

,....

(

min

min

t

t

a

t

t

c

c

c

c

dt

t

x

t

x

e

K

K

Optymalna
aproksymacja

„Teoria sygnałów” Zdzisław Papir

 

 













2

1

1

2

1

1

2

1

)

,....

(

2

)

,....

(

min

min

t

t

a

t

t

c

c

c

c

dt

t

x

t

x

e

K

K

0

....

2

2

2

1

2









K

dc

e

d

dc

e

d

dc

e

d

K

n

G

dt

t

g

t

x

dt

t

g

dt

t

g

t

x

c

n

t

t

n

t

t

n

t

t

n

n



,

2

,

1

)

(

)

(

)

(

)

(

)

(

2

2

2

1

2

1

2

1













Błąd optymalnej
aproksymacji

„Teoria sygnałów” Zdzisław Papir

 

 





 

0

lim

0

1

0

1

2

,

1

2

2

,

2

1

2

2

2

1

1

2

2

2

1

2

1









































e

G

c

dt

t

x

t

t

e

dt

t

g

c

t

x

t

t

e

K

K

K

n

n

n

K

const

t

t

t

t

K

n

n

n

 

 

















 

 









1

n

n

n

t

g

c

t

x

W miarę wydłużania aproksymacji
ortogonalnej jej błąd maleje.
Nieskończona długość aproksymacji
ortogonalnej
umożliwia dokładną reprezentację
ortogonalną sygnału.

Ortogonalność i sygnał
wykładniczy

ULS

 





n

t

s

n

n

e

X

t

x

 

 

t

s

n

n

n

n

e

s

H

X

t

y





Czy można znaleźć ortogonalną
reprezentację wykładniczą?

• łatwość wyznaczania współczynników
reprezentacji;

• łatwość opisu przetwarzania sygnału w
ULS.





















1

2

0

0

1

2

2

,

2

0

,

,

,

,

0

2

1

2

1

2

1

2

1

t

t

n

t

t

dt

e

dt

e

j

s

j

s

s

s

dt

e

dt

e

e

e

e

n

n

m

t

t

t

j

t

t

t

s

s

n

n

m

m

n

m

t

t

t

s

s

t

s

t

t

t

s

t

s

t

s

n

m

n

m

n

m

n

m

n

m







































































R

„Teoria sygnałów” Zdzisław Papir

Ortogonalny układ funkcji
zespolonych

 

 





 

 





 

 























2

1

2

1

*

1

2

2

1

2

2

1

1

t

t

a

a

t

t

a

dt

t

x

t

x

t

x

t

x

t

t

dt

t

x

t

x

t

t

e

„Teoria sygnałów” Zdzisław Papir





)

(

),.....,

(

),

(

2

1

t

g

t

g

t

g

K

 

 

)

(

0

)

(

,

2

1

*

t

g

t

g

dt

t

g

t

g

n

m

t

t

n

m

n

m













 

2

1

,

t

t

t

t

g

n

n









C

K

n

G

dt

t

g

t

x

c

n

t

t

n

n



,

2

,

1

)

(

)

(

2

*

2

1







 

 







K

n

n

n

a

t

g

c

t

x

1

 

   











2

1

2

1

2

*

2

,

t

t

t

t

n

n

n

n

n

G

dt

t

g

t

g

dt

t

g

Ortogonalny układ zespolonych
sygnałów wykładniczych

„Teoria sygnałów” Zdzisław Papir













































m

n

T

m

n

dt

e

e

e

e

T

t

t

t

t

n

e

T

t

t

t

jm

t

jn

t

jm

t

jn

t

jn

,

,

0

2

,

,

2

,

1

,

0

,

0

0

o

o

o

o

o

*

0

0

0

0

















Ortogonalny układ zespolonych
sygnałów wykładniczych

„Teoria sygnałów” Zdzisław Papir















































T

t

t

T

t

t

T

t

t

t

m

n

j

T

t

t

t

jm

t

jn

tdt

m

n

j

tdt

m

n

dt

e

dt

e

e

m

n

0

0

0

0

0

0

0

0

0

0

0

0

sin

cos

:

0

0

)

(

*







































T

t

t

T

t

t

t

n

n

j

T

t

t

t

jn

t

jn

T

dt

dt

e

dt

e

e

m

n

0

0

0

0

0

0

0

0

0

)

(

*

:







Wykładniczy szereg
Fouriera

T

T

t

t

t

e

X

t

x

n

t

jn

n







2

,

)

(

0

0

0

0



























T

t

t

t

jn

n

dt

e

t

X

T

X

0

0

0

)

(

1



„Teoria sygnałów” Zdzisław Papir

Wykładniczy szereg Fouriera przedstawia sygnał
jako złożenie zespolonych drgań harmonicznych
o różnych amplitudach.

Trygonometryczny szereg
Fouriera

„Teoria sygnałów” Zdzisław Papir

Dla sygnałów rzeczywistych
jest spełniony związek:

*

n

n

X

X 



Postać wykładnicza
współczynnika szeregu Fouriera:

n

j

n

n

e

X

X





 





n

n

n

t

n

X

X

t

x

















0

1

0

cos

2

Trygonometryczny szereg Fouriera przedstawia sygnał
jako złożenie drgań harmonicznych o różnych amplitudach
i fazach początkowych.

Trygonometryczny szereg
Fouriera

„Teoria sygnałów” Zdzisław Papir

 





 





























1

0

0

0

0

1

0

sin

sin

2

cos

cos

2

cos

2

n

n

n

n

n

n

n

n

t

n

X

t

n

X

X

t

x

t

n

X

X

t

x













n

a

n

b

2

0

a

 

















1

0

0

0

sin

cos

2

n

n

n

t

b

t

n

a

a

t

x





 

 

 













T

T

n

n

T

tdt

t

x

T

b

tdt

t

x

T

a

dt

t

x

T

a

0

0

0

0

0

0

sin

2

cos

2

1





Okresowość szeregu Fouriera

„Teoria sygnałów” Zdzisław Papir









 

t

x

e

e

X

e

X

T

t

x

T

t

t

t

e

X

t

x

jn

n

t

jn

n

n

T

t

jn

n

n

t

jn

n



















































2

0

0

0

0

0

,

)

(

Wykładniczy szereg Fouriera jest
okresowy,
a więc generuje okresowe
przedłużenie sygnału x(t)
w przedziale rozwinięcia t

0

< t < t

0

+ T.

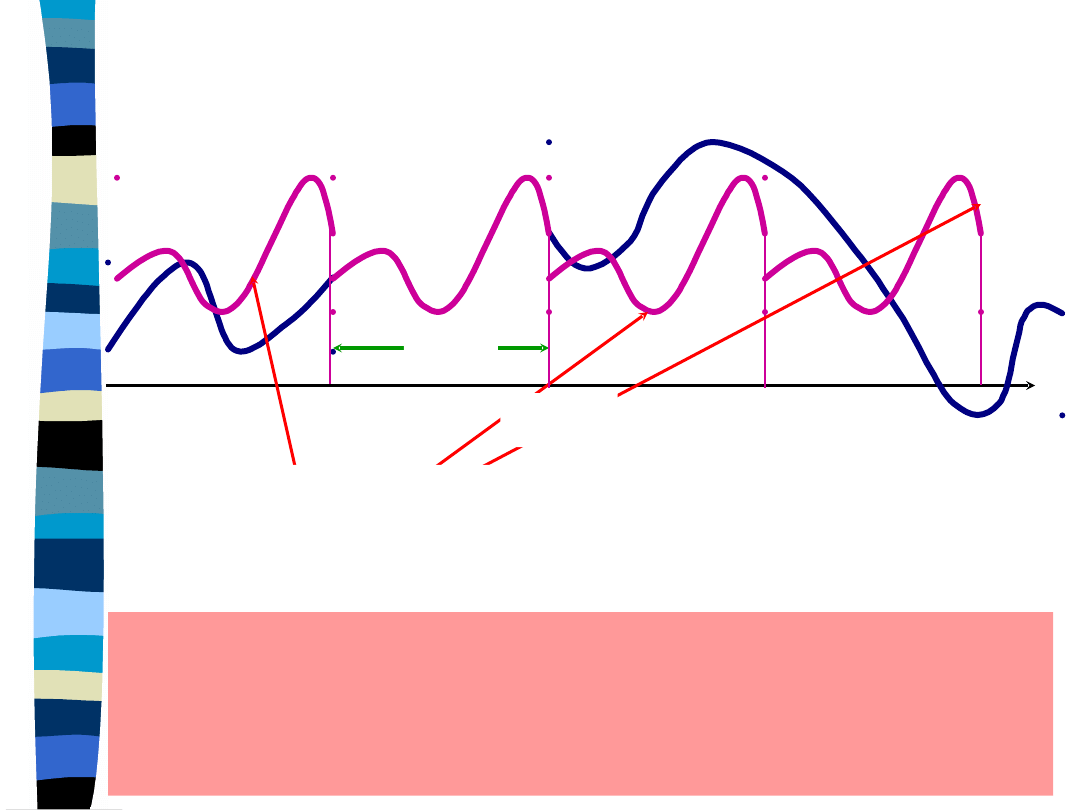
Okresowość szeregu Fouriera

„Teoria sygnałów” Zdzisław Papir

t

-T/2

x(t)

okresowe przedłużenie sygnału
przez szereg Fouriera

+T/2

Trygonometryczny szereg Fouriera „pokrywa
się” dokładnie z sygnałem, jeżeli jest on
okresowy, a długość przedziału rozwinięcia
jest równa okresowi.

Charakterystyki
częstotliwościowe





n

n

n

n

t

jn

n

t

n

j

X

e

X

t

x





























0

exp

)

(

0

Charakterystyka amplitudowo-częstotliwościowa (a-cz):





0



n

X

X

n

n



Charakterystyka fazowo-częstotliwościowa (f-cz):





0







n

n

n



„Teoria sygnałów” Zdzisław Papir

Charakterystyki
częstotliwościowe

„Teoria sygnałów” Zdzisław Papir

Dla sygnałów rzeczywistych
jest spełniony związek:

*

n

n

X

X 



Postać wykładnicza
współczynnika szeregu Fouriera:

n

j

n

n

e

X

X





Charakterystyka a-cz jest funkcją
parzystą:









0

0





n

X

n

X

n

n







Charakterystyka f-cz jest funkcją
nieparzystą:









0

0









n

n

n

n









Charakterystyki
częstotliwościowe

„Teoria sygnałów” Zdzisław Papir



2



2



T

t

 

 

 









































0

,

1

0

,

0

2

sgn

0

2

n

n

n

n

X

e

n

e

e

n

e

t

x

n

n

jnt

n

j

n

n

jnt

j











 

















0

,

2

0

,

2

n

n

n







2

8

6

4

Joseph Fourier

„Teoria sygnałów” Zdzisław Papir

Matematyk i fizyk francuski
1768 - 1830
1798 - wyprawa z Napoleonem
do Egiptu
1807 - posiedzenie
Francuskiej Akademii Nauk;
J. Fourier przedstawia
szereg trygonometryczny

Badanie szeregów Fouriera przyczyniło się
do wielu odkryć matematycznych - całek
Riemanna i Lebesgue’a, mocy zbioru,
rodzajów zbieżności szeregów funkcyjnych
oraz uogólnień definicji funkcji i
różniczkowalności.

Podsumowanie

•

Dekompozycja dowolnego sygnału x(t) na składowe

wykładnicze X

n

exp(s

n

t) pozwala wyznaczyć odpowiedź ULS

na dowolny sygnał wejściowy.

•

Minimalizacja błędu średniokwadratowego (w sensie całkowym)

pozwala wyznaczyć optymalną aproksymację sygnału.

• Aproksymacja sygnału polepsza się wraz ze wzrostem liczby
sygnałów aproksymujących.

•

Ortogonalność (w sensie całkowym) sygnałów aproksymujących

istotnie ułatwia wyznaczenie optymalnej aproksymacji.

• W miarę wydłużania aproksymacji ortogonalnej jej błąd maleje.
Nieskończona długość aproksymacji ortogonalnej umożliwia
dokładną reprezentację ortogonalną sygnału.

•

Ortogonalny układ sygnałów wykładniczych można skonstruować,

gdy dopuścimy urojone wartości wykładników.

•

Trygonometryczny szereg Fouriera przedstawia sygnał

jako złożenie drgań harmonicznych o różnych amplitudach
i fazach początkowych.

•

Wykładniczy szereg Fouriera przedstawia rozkład widmowy

wyłącznie sygnałów okresowych.

„Teoria sygnałów” Zdzisław Papir