1.Układ termodynamiczny-obiekt wyodrębniony do
rozważań z otaczającego środowiska. obiekty znajdujące się
na zewnątrz układu nazywamy otoczeniem. Granicę między
układem a otoczeniem nazywamy osłoną lub ścianką.
a)zamknięty-nie wymienia masy z otoczeniem, może
wymieniać energię
b)otwarty-może wymieniać masę i energię z otoczeniem
c)izolowany-całkowicie niezależny od wpływu otoczenia(nie
wymienia ani energii ani masy)
osłony:
a)nieprzepuszczalna-nie dopuszcza do wymiany masy między
układem a otoczeniem
b)pólprzepuszczalna-pozwala na przepływ niektórych
substancji i jednocześnie nie dopuszcza do wymiany innych
c)diatermiczna-pozwala na zmianę stanu układu zamkniętego
przez wymianę energii z otoczeniem na sposób ciepła
d)adiabatyczna-pozwala na zmianę układu zamkniętego
jedynie przez wykonanie na nim pracy
Parametry stanu:
-Objętość właściwa-

objętość

zajmowana w dowolnych

warunkach przez substancję o

masie

1

kg

, wyrażona w

metrach sześciennych

na

kilogram

. Jest odwrotnością

gęstości

.Objętość właściwa odnosi się zwykle do gazów i jest

jedną z

funkcji stanu

. Znając jej wartość i wartość dowolnego

innego

parametru stanu

, można wyznaczyć pozostałe funkcje i

parametry stanu.
-Gęstość-

masa

jednostki

objętości

, dla substancji

jednorodnych określana jako stosunek masy m do objętości V:

Gęstość jest cechą charakterystyczną substancji, a

w określonych

warunkach standardowych

stanowi jedną z

najważniejszych cech substancji – służy do obliczania masy i
ciężaru określonej objętości substancji.
-Ciężar właściwy-γ, stosunek

ciężaru

ciała do jego

objętości

:

W odróżnieniu od gęstości, ciężar właściwy zależy

też od

siły ciążenia

, czyli w warunkach nieważkości wynosi

zero, gdy gęstość pozostaje taka sama (podobnie jak masa).

γ

stanowi ciężar odniesiony do jednostki objętości płynu:

γ

= ρ

g. Jednostką ciężaru właściwego jest 1kg / (m

2

s

2

), co wynika

z poniższego zapisu:(kg/m

3

)(m/s

2

) = (N m)(g m

3

s

2

) = (N m

s

2

)/(m m

3

s

2

) = (N/m

2

)(1/m) = Pa/m

-Temperatura- jest miarą stanu cieplnego danego ciała.
Temperaturę można ściśle zdefiniować tylko dla stanów

równowagi termodynamicznej

, z termodynamicznego bowiem

punktu widzenia jest ona wielkością reprezentującą wspólną
własność dwóch układów pozostających w równowadze ze
sobą. Temperatura jest związana ze średnią

energią kinetyczną

ruchu i drgań wszystkich cząsteczek tworzących dany

układ

i

jest miarą tej energii.
-Ciśnienie-to

wielkość skalarna

określona jako wartość

siły

działającej prostopadle do powierzchni podzielona przez
powierzchnię na jaką ona działa, co przedstawia zależność:

W przypadku

gazów

w stanie ustalonym w

spoczynku, ciśnienie jakie gaz wywiera na ścianki naczynia
jest funkcją

objętości

,

masy

i

temperatury

i dlatego w

termodynamice

traktowane jest jako

funkcja stanu

.

-Strumień objętościowy-(objętościowe natężenie przepływu)
- iloczyn

prędkości

(v) czynnika przepływającego przez

przewód rurowy (rurę) i powierzchni przekroju S tego
przewodu.Q = vS
-------------------------------------------------------------
2. Gaz doskonały definiować można zarówno na poziomie
mikroskopowym (przez podanie właściwości elementów, z
których jest zbudowany), jak i na poziomie makroskopowym
(poprzez podanie jego właściwości jako całości). Równanie
stanu - równanie Clapeyrona
Pełna postać równania stanu gazu doskonałego jest
następująca:p V = n R T i nazywane jest ono równaniem
Clapeyrona. Przy czym p oznacza ciśnienie gazu, V -
objetość, T - temperaturę, n - liczbę moli gazu a R jest tzw.
stałą gazową równą R = 8, 314 J/mol·K. Nic nie przeszkodzi,
używając związku R = N

A

k zapisać równania następująco:p

V = N k T gdzie k = R / N

A

jest stałą Boltzmanna.Na uwagę

zasługuje fakt, że wymiarem prawej (i lewej) strony jest
wymiar energii.

4.roztwory gazów (udziały masowe, molowe objętościowe)
Wielkości zastępcze dla roztworów gazowych-Oblicza się w
ten sposób, że mnoży się wielkości indywidualne przez
udziały i sumuje się tak obliczone iloczyny.
a)udziały gramowe – jeżeli jednostka danej wielkości zawiera

w mianowniku kg np. R
b)udziały molowe (objętościowe) jeżeli jednostka danej
wielkości zawiera w mianowniku kmol np. M [kg/kmol]
c)objętościowe - jeżeli m3 lub mm3

Roztwór gazowy jest to

roztwór

w którym wszystkie

składniki są

gazami

. Roztwory gazowe mieszają się bez

ograniczeń ilościowych. Zjawisko to wynika z tego, że
odległości między

cząsteczkami

gazów są duże a

oddziaływania międzycząsteczkowe

bardzo słabe. Gazy w

temperaturze i ciśnieniu większym od ciśnienia i temperatury

punktu krytycznego

, mają wiele właściwości cieczy i mogą w

nich rozpuszczać się

ciecze

i

ciała stałe

.

5. Ciepło właściwe

Całkowite ciepło przejęte przez ciało o masie m podczas
podgrzewania od T

1

do T

2

jest równe ciepłu dostarczonemu z

zewnątrz i ciepłu tarcia (ciepło wewnątrz ciał) Q

c 1-2

=Q

1-2

+Q

f

przy czym

)

t

t

(

CI

m

Q

1

2

2

t

1

t

2

1

c

−

⋅

=

−

przekształcając wg.

)

t

t

(

m

Q

CI

CI

1

2

2

1

c

2

t

1

t

2

t

1

t

−

=

⇒

−

K

kg

J

⋅

)

dt

dQ

(

m

1

C

c

=

α

Średnie ciepło

właściwe

2

t

1

t

CI

jest to ilość ciepła jaką należy dostarczyć

jednej jednostce ilości substancji, aby zmienić temperaturę o
1K w całym rozpatrywanym okresie temp. Zależy od:rodzaju
ciała ,temperatury t

1

t

2

,warunków ogrzewania ciał. Stosunek

C

p

/C

v

=

χ

Jeżeli mam ciało o masie m i podgrzewam od t do

∆

t+t to nastąpi przyrost ciepła

∆

Q

c

)

t

(

m

Q

CI

c

t

t

t

∆

⋅

∆

=

∆

+

dt

dQ

t

m

Q

)

t

(

C

c

m

1

c

lim

0

t

⋅

=

∆

⋅

∆

=

→

∆

2

t

1

t

CI

-rośnie wraz ze wzrostem t i jest wysokością prostokąta

o szerokości (t

2

-t

1

). F pole figury nieregularnej równe polu

prostokąta o wysokości. Wielkości ciepła właściwego C i
szerokości t

2

-t

1

.

Pole figury F=(t

2

-t

1

)*c

_______________________________________________

6.

pierwsza zasada termodynamiki, pojęcie entalpii, praca

absolutna i techniczna

I zasada termodynamiki
W układzie odosobnionym tzn. osłoniętym osłoną adiabatyczną, ilość
energii wewnętrznej układ jest stała E

d

=

∆

E

u

+E

w

[J]

⇒

równ bilansu

energetycznego można traktować jako I zasadę termodynamiki dot.
Układu zamkniętego. Energia doprowadzona do układu wyodrębnionego
osłoną adiabatyczną pozostaje częściowo w układzie a część jest
wyprowadzona z układu. Interpretacja graficzna – wykr. Sankeya

Energia układu jest sumą E

p

, E

k

, E

w

, E

j

, E

ch

; E

u

=E

p

+E

k

+E

ch

+E

j

+E

w

;

E

w

-zależy od temp, stanu skupienia gazów rzeczywistych. Jeżeli układ

działa w sposób ustalony (jego energi nie zmienia się w czasie lub zmienia
się w sposób periodyczny i po skończonej liczbie cykli wraca do wart.

Początkowych) to bilans energetyczny przyjmuje postać

w

d

E

E





=

ponieważ

0

>

w

E

to do czynnego silnika

⇒

>

0

d

E

że jest rzeczą

niemożliwą skonstruowanie perpetum mobile pierwszego rodzaju
(silnika pracującego bez zasilania energią z zewnątrz).

0

,

0

,

>

=

>

=

L

E

E

E

E

w

d

w

d

idem

E

E

u

u

=

=

∆

,

0

pojęcie entalpii
To wielkość termodynamiczna określająca stan termodynamiczny układu i
równa jest sumie energii wewnętrznej U układu oraz iloczynowi jego
objętości i ciśnienia. Zmiana entalpii przy stałym ciśnieniu jest miarą ilości
ciepła wymienionego przez układ z otoczeniem. I – entalpia, U – energia
wewnętrzna, p – ciśnienie statyczne bezwzgl., V – objętość całkowita
ciała. I = U + p V (funkcja Gipsa). Entalpia jest funkcją tych samych
parametrów stanu co energia wewnętrzna. Entalpia dla gazów doskonałych
i półdoskonałych: i=u+pV=C

v

T+RT=T(R+C

v

)=C

p

T, C

p

-C

v

=R

Entalpia – sposób obliczania

a)

ciała stałe i ciecze i=u+pv, gdzie v - obj. właść., p - bezwzględne
ciśnienie statyczne, u – właściwa energia wewnętrzna

b)

gaz doskonały (funkcja tylko temp, nie zależy od ciśnienia i
objętości) i=c

p

T+u

o

, gdzie c

p

– ciepło wł. przy stałym ciśnieniu, T

– temp, u

o

– energia otoczenia

c)

gaz półdoskonały (funkcja tylko temp)

o

T

p

u

T

I

c

i

+

=

0

; gdzie

T

0

p

I

c

- średnie ciepło właściwe od 0 doT, T – temp

d)

para nasycona mokra i=i`+x(i``-i`), gdzie i – entalpia pary nasyc.
mokrej, i` - entalpia cieczy, i`` - ilość pary suchej nasyconej, x –
stopień wilgotności

e)

para przegrzana i=i``q

p

, gdzie q

p

– ciepło przegrzania pary

f)

para mokra nasycona i=q+r+pr, gdzie r – entalpia parowani

praca absolutna bezwzględna
Jest to praca wykonana przez czynnik termodynamiczny wtedy gdy
ciśnienie otoczenia jest równe zero. Pracę tę można obliczyć rozpatrując
układ cylinder – tłok

Przy

∞

małym dx czynnik wykonuje pracę dl=kdx, gdzie k – siła, dx

droga. Przy pracy bez tarcia siłę k równoważy ciśnienie działające na tłok.
Stąd: k=pA, gdzie p – ciśnienie, A- przekrój, dl=p A dx

⇒

dl=p dv

p – bezwzględne ciśnienie statyczne wewn. cylindra
dv – przyrost objętości w cylindrze

Praca bezwzględna

∫

=

−

2

1

2

1

pdv

dl

; interpr. graficzna (założenie – znam

zależność p od v)

L

1-2

– zależy od drogi przemiany a nie tylko od stanu początkowego i

końcowego
L

1-2

– dotyczy przemian zachodzących bez strat na rzecz tarcia (wtedy dl

<pdv)
Zastosowanie: w układach otwartych i zamkniętych, pseudoodwr. dl = p
dv - dl

t

= p dv - dQ

f

stąd dl < p dv

dl

t

– praca na rzecz tarcia, dQ

f

– ciepło na rzecz tarcia

praca techniczna
Pracę fizyczną rozpatrujemy wg idealnej maszyny przepływowej tzn.
-

nie występuje tarcie poruszających się względem siebie
powierzchni

-

zawory nie stawiają oporu

-

w wewnętrznym zwrotnym położeniu tłok dotyka cylindra

Praca techniczna element. dL

t

= -Vdp, L

t

>0 gdy dp<0

Praca

skończona

L

t

1-2

=

(

pdV − pdV −Vdp)=

¿

p

1

V

1

+

∫

1

2

pdV − p

2

V

2

=

∫

1

2

pdV −d ( pV )=

∫

1

2

¿

∫

−

2

1

Vdp

dL

t

>0 gdy dp<0; dL

t

<0 gdy dp>0

7.

przemiany termodynamiczne gazów doskonałych

Wyróżniamy następujące przemiany gazowe:
przemiana izotermiczna (prawo Boyle`a i Mariotte`a)

T =const

pV =const

p

1

V

1

=

p

2

V

2

pV =nRT

Praca bezwzględna

pdV =RT

∫

1

2

dV

V

=

RT ln

V

2

V

1

=

¿

p

1

V

1

ln

V

2

V

1

L

1−2

=

∫

1

2

¿

Praca techniczna

L

t

=

L

1−2

=

Q

1−2

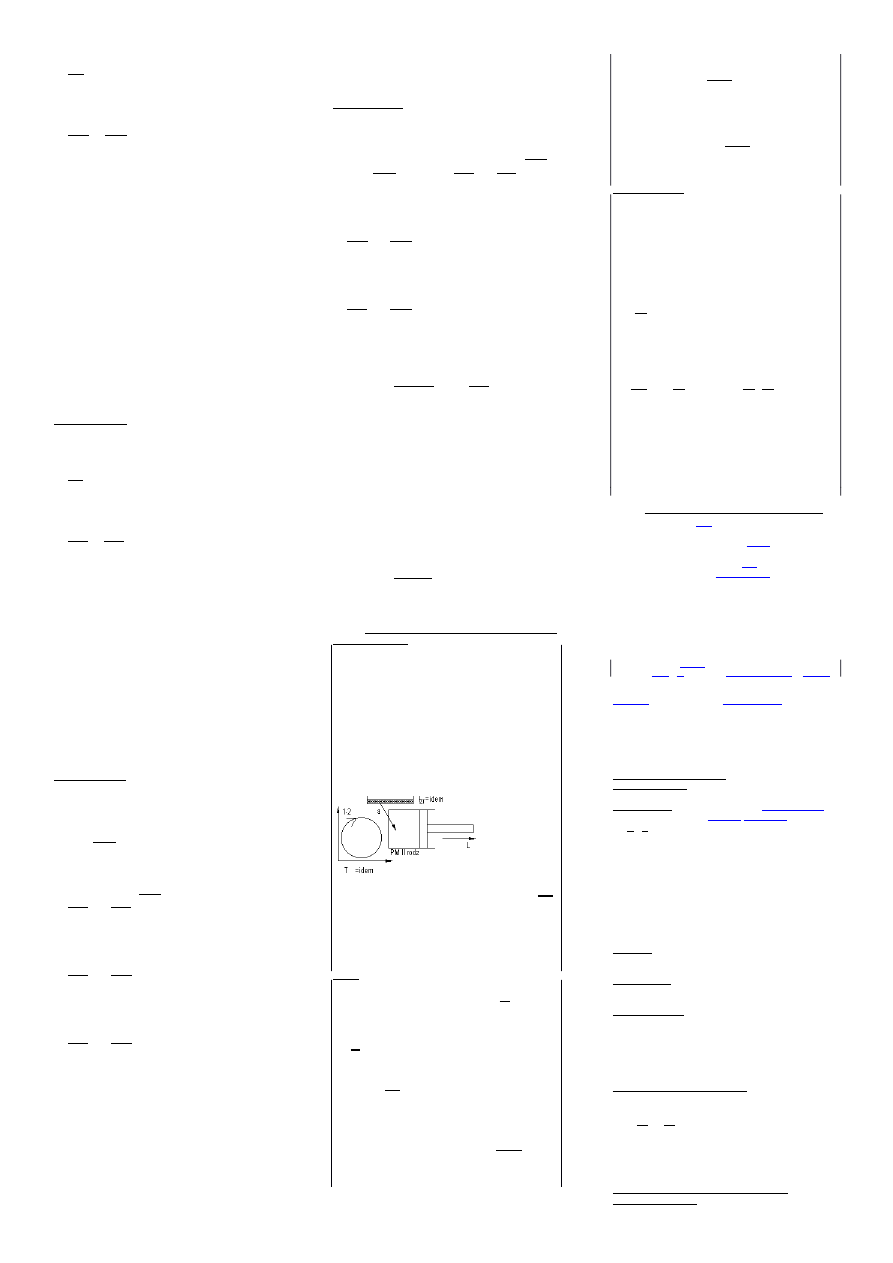
przemiana izobaryczna (prawo Gay-Lussaca)

p=const

dx – odległość
przesunięcia
tłoka

Jeżeli:
dv>0 to dl>0
dv<0 to dl<0

L

t

=L

n

+L

1-2

+L

w

= p

1

v

1

+L

1-2

-p

2

v

2

L

n

– praca napełniania

L

1-2

– praca przemiany zamknietej

L

w

– praca wytłaczania

zał. p

1

>p

2

a)

w.z.p. – przemiana
napełniania

b)

z.z.p. – ilość czynnika
= const

V

T

=

const

V

1

T

1

=

V

2

T

2

Praca bezwzględna

pdV =

¿

∆ Vp

L

1−2

=

∫

1

2

¿

Praca techniczna

L

t

=

p

(

V

1

−

V

2

)

+

p

(

V

2

−

V

1

)

=

0

Ciepło bezwzględne

C

p

dT =

¿

m ∙ ∆T ∙ C

p

Q

1−2

=

∫

1

2

¿

przemiana izochoryczna

V =const

p

T

=

const

p

1

T

1

=

p

2

T

2

Praca bezwzględna

L

1−2

=

0

Praca techniczna

Vdp=

¿

V

(

p

1

−

p

2

)

L

t

=

∫

1

2

¿

Ciepło bezwzględne

Q

1−2

=

∆U =m∙ ∆ T ∙ C

p

przemiana adiabatyczna

p V

k

=

const

k =

C

p

C

v

T

1

T

2

=

(

p

1

p

2

)

k −1

k

T

2

T

1

=

(

V

2

V

1

)

k−1

p

1

p

2

=

(

V

2

V

1

)

k

Praca bezwzględna

L

1−2 ad

=

Q

1−2

−

∆ U =m∙ C

v

(

T

1

−

T

2

)

Praca techniczna

L

t

=

H

d

−

H

w

=

m∙ C

p

(

T

1

−

T

2

)

Ciepło bezwzględne

Q

1−2

=

0

przemiana politropowa

p V

ϑ

=

const

ϑ =

C

p

C

v

T

1

T

2

=

(

p

1

p

2

)

ϑ −1

ϑ

T

2

T

1

=

(

V

2

V

1

)

ϑ−1

p

1

p

2

=

(

V

2

V

1

)

ϑ

Praca bezwzględna

L

1−2

=

p

1

V

1

k −1

(

1−

T

2

T

1

)

Praca techniczna

L

t

=

H

d

−

H

w

=

m∙ C

p

(

T

1

−

T

2

)

L

t

=

ν ∙ L

1−2

Ciepło bezwzględne

Q

1−2

=

m∙ c (T

2

−

T

1

)

c=c

v

∙

ϑ−k
ϑ −1

8.

II zasada termodynamiki, entropia, zasada wzrostu entropii

II zasada termodynamiki
sformułowanie
a)

Plancka. Jest rzeczą niemożliwą skonstr. takiego silnika (maszyny
działającej periodycznie), którego działanie polegało by na
podnoszeniu ciężarów i równoczesnym ochładzaniu jednego
źródła ciepła. Silnik taki nosi nazwę perpetum mobile II rodzaju.

b)

Clausjusa ciepło nie może przejść samorzutnie od ciała o temp
niższej do ciała o temp wyższej. Aby spowodować taki przepływ
ciepła musimy zastosować lewo bieżną maszynę cieplną i
wkładać do niej energię z zewnątrz, tzn. wywoływać zmiany w
innych ciałach.

•

Samorzutne przejście – zjawisko któremu nie towarzyszą żadne
zmiany w otoczeniu (otoczenie nie oddziałuje na układ)

c)

Schmidta – nie można całkowicie odwrócić przemiany, w której
występuje tarcie. Pracę w całości można zmienić na ciepło przez
tarcie, jednak z tego ciepła nie można w całości odzyskać pracy.

d)

Ostwalda – perpetum mobile II rodzaju jest niemożliwe –
DOWÓD

czyli cykl pracy silnika stąd

∆

S

PM II R

=0 bo entropia jest wielkością stanu a

stan w punkcie 1-2 jest sobie równy to

∆

=0;

π

=

∆

S

PM II R

+S

ŹR

=0 -

ŹR

T

Q

;

Q – ciepło tarcia

π

> 0 sprzeczne z prawem wzrostu entropii

e)

entropia układu zamkniętego i izolowanego nie może maleć
podczas dowolnej przemiany i wzrastać przy przemianach
nieodwracalnych.

Entropia
Jest to funkcja stanu termodynamicznego, której zmiana równa się

ilorazowi dostarczonego ciepłą i temperatury

T

dq

dS

=

; S – entropia

całkowita

T

d q

ds

=

; s – entropia właściwa w odniesieniu do 1kg czynnika; dla

źródła

∆

S = -

źr

źr

T

Q

źródło oddaje energię więc przyrost entropii jest

ujemny. Entropia mówi nam o kierunku przemian zachodzących w

przyrodzie.

∮

dS =

∮

dQ

T

=

0

S

2

−

S

1

=

∫

1

2

dQ

T

- nie zależy od stanów

pośrednich,

S (1)=

∫

0

1

dQ

T

zasada wzrostu entropii
- we wszystkich procesach odwracalnych suma entropii wszystkich ciał
biorących udział w zjawisku jest stała
- suma wszystkich przyrostów jest równa zero (proces odwracalny)
- w procesach nieodwracalnych suma wszystkich ciał biorących udział w
zjawisku jest różna
- suma wszystkich przyrostów jest różna od zera dla ciał w procesach
nieodwracalnych
Wyróżniamy dwa przypadki:
I przemiana odwracalna
a)

T

cz

= T

źr

; b) brak tarcia dQ

t

= 0

przyrost entropii układu odosobnionego

∆

s =

π

, natomiast elementarny

przyrost ozn. d

π

= ds.

u

+ds

ot

sdm

T

dQ

ds

cz

u

+

=

- przyrost entropii układu

zb

źr

ot

ds

ds

d s

+

=

- przyrost entropii otoczenia















−

=

π

⇒

−

−

+

=

π

źr

cz

źr

cz

T

1

T

1

d Q

d

sdm

T

dQ

sdm

dT

dQ

d

0

d

T

T

cz

źr

=

π

⇒

=

Wniosek: W układzie odosobnionym sumą

przyrostów entropii wszystkich ciał uczestniczących w zjawisku
odwracalnym jest = 0. Warunek ten jest spełniony nawet w najmniejszej
części zjawiska.
II przemiana nieodwracalna tzn. t

źr

≠

t

cz

9.

para nasycona i przegrzana obj. Właściwa, gęstośc pary

Para nasycona,

para

będąca w równowadze

termodynamicznej z fazą skondensowaną. Para
nasycona pozbawiona kropel

cieczy

nosi nazwę pary

nasyconej suchej.

Para przegrzana, para nienasycona,

para

w temperaturze

wyższej aniżeli temperatura

pary nasyconej

. Para przegrzana

nie jest w stanie równowagi termodynamicznej z fazą
skondensowaną.

Temperatura i ciśnienie pary przegrzanej są wzajemnie
niezależne. Podwyższanie temperatury pary przegrzanej
zwiększa sprawność energetyczną obiegu siłowni parowej.

Objętość właściwa –

objętość

zajmowana w dowolnych warunkach przez

substancję o

masie

1

kg

, wyrażona w

metrach sześciennych

na

kilogram

.

W termodynamice nie jest istotna wartość całkowitej entalpii, lecz jej
przyrost lub spadek w danym procesie. Przyrost entalpii występuje w

sprężarkach

, natomiast spadek — w

turbinach cieplnych

.

12.Elementy wymiany ciepla:
przewodzenie ciepła – przenoszenie ciepła w obrębie danego
ciała od jednych drobin do drugich lub przez dyfuzję
Prawo Fouriera- gęstość przewodzonego

strumienia ciepła

jest

wprost proporcjonalna do

gradientu

temperatury

.

(

)

2

1

T

T

A

s

t

Q

Q

−

=

=

•

λ

•

Q

- strumień ciepła [W]; T

1

,T

2

- temperatury [K];

Q - ilość przewodzonego ciepła [J]; t- czas[s];
λ- współczynnik przewodzenia ciepła [w/(m*K)]; s- droga
przewodzenia ciepła [m]; A- powierzchnia przewodząca
ciepło [m

2

]

konwekcja – (unoszenie ciepła) ciepło płynie z cząsteczkami
płynu od ściany przegrody do rdzenia strumienia lub
odwrotnie
promieniowanie – ciepło przenosi się od jednego ciała do
drugiego w postaci energii promienistej (za pośrednictwem fal
elektromagnetycznych)
Prawo NEWTONA- (równanie wnikania ciepła)

(

)

2

1

T

T

A

Q

−

=

•

α

T

1

-T

2

=ΔT – różnica temperatur,

α

- współczynnik wnikania

ciepła [W/(m

2

*K), A – powierzchnia ścianki lub

powierzchnia międzyfazowa [m

2

]

Prawo STEFANA-BALTZMANNA

- opisuje gęstość

strumienia ciepła wypromieniowanego przez ciało doskonale
czarne.





























−













=

4

2

4

1

100

100

T

T

C

q

C=5,67 [W/(m

2

*K

4

) – stała promieniowania ciała doskonale

czarnego; T

1

, T

2

– temperatury bezwzględne odpowiednio

powierzchni promieniującej i powierzchni otaczających
_______________________________________
13.Powietrze wilgotne

wilgotność powietrza - zawartość pary wodnej w powietrzu.

∫

=

gyzdF

N

ρ

η

wilgotność bezwzględna - masa pary

wodnej wyrażona w gramach zawarta w 1 m³ powietrza,

V

m

w

=

ρ

∫

∫

=

dF

y

g

ydF

g

2

sin

sin

α

ρ

α

η

ρ

wilgotność właściwa - masa

pary wodnej wyrażona w gramach przypadająca na 1 kg
powietrza (powietrza ważonego razem z parą wodną),

ps

pw

m

m

x

=

wilgotność względna - wyrażony w procentach stosunek
ciśnienia cząstkowego pary wodnej zawartej w powietrzu do
prężności pary wodnej nasyconej w tej samej temperaturze,

wn

w

m

m

=

φ

(w – pary wodnej; wn – pary wodnej nasyconej)

prężność pary wodnej - ciśnienie parcjalne (cząstkowe),
wywierane przez parę wodną w powietrzu.
entalpia pary wilgotnej- jest równa sumie entalpi pow.
suchego i pary wodnej.

(

)

r

x

t

c

x

c

i

pw

p

⋅

+

⋅

+

=

(

)

c

c

x

c

pw

p

=

⋅

+

________________________________________
14.

Lepkość

– jest to zdolność cieczy do stawiania oporu przy

wzajemnym przesuwaniu się jej cząstek. Jest to
hydrodynamiczna cecha cieczy rzeczywistej, co oznacza, że
ujawnia się dopiero w czasie jej ruchu. Przejawia się ona
powstawaniem sił stycznych przy wzajemnym przesuwaniu
się
jej warstw po sobie. Lepkość jest przyczyną występujących
podczas ruchu oporów, a tym samym strat energii
mechanicznej strumienia.
Hipoteza Newtona – tarcie wewnętrzne w ruchu laminarnym
Na granicy pomiędzy warstwami wody powstaje siła tarcia
(oporu) płynu T, która przeciwdziała
ruchowi górnej płyty i jest proporcjonalna do:
• gradientu prędkości dυ /dy w kierunku prostopadłym do
ruchu,
• powierzchni styku warstw A,
gdzie współczynnikiem proporcjonalności jest współczynnik
lepkości dynamicznej μ (zależny od fizycznych właściwości
cieczy, tzn. od jej rodzaju i temperatury).

dy

d

A

T

ν

µ

⋅

⋅

=

Dzieląc obie strony równania przez powierzchnię
A, otrzymamy wzór Newtona postaci:

dy

d

ν

µ

τ

⋅

=

gdzie τ jest naprężeniem stycznym (wielkością
oporu przypadającą na jednostkę powierzchni
płyty).

Moduł w powyższych wzorach pozwala uwzględnić
bezwzględną wartość naprężenia, którego znak
zależy od:
– obranego kierunku osi y,
– tego, czy rozpatrujemy oddziaływanie górnej warstwy
cieczy na dolną, czy odwrotnie.
Powyższe prawo jest słuszne dla:
• niewielkich prędkości i niewielkich rozmiarów szczeliny. Po
ich przekroczeniu ruch przestaje
być laminarny i występują zaburzenia, w wyniku których
naprężenia styczne wzrastają
ponad te, określone wzorem Newtona. Ruch ten nosi nazwę
turbulentnego;
• cieczy newtonowskich, spełniających równanie (I-2) (np.
czekolada, płynny beton nie
podlegają powyższej teorii Newtona).
________________________________________

15. Statyka płynów:
Równanie równowagi statycznej (wyprowadzenie)

z

p

k

y

p

j

x

p

i

gradp

∂

∂

+

∂

∂

+

∂

∂

=

Ze wzgl. na dowolność

obszaru całkowania V można
napisać:

0

=

−

gradp

F

m

ρ

w układzie współrzędnych
kartezjańskich równanie to
można wyrazić w postaci
trzech rów. skalarnych

X,Y,Z-siła składowa w
określonym kierunku-
składowa jednolita

dV=dxdydz jest w
równowadze, jeżeli rzuty sił na
osie układu są równe zeru,
zatem można napisać:

Wykorzystując fakt,że masa
elementu płynu wynosi:

pdxdydz

dV

dm

=

=

ρ

Po dodaniu stronami trzech
składowych można napisać:

dz

z

p

dy

y

p

dx

x

p

Zdz

Ydy

Xdx

∂

∂

+

∂

∂

+

∂

∂

=

+

+

)

(

ρ

Prawa strona jest różniczką
zupełną ciśnienia dp, wobec
czego można napisać:

(

)

Zdz

Ydy

Xdx

dp

+

+

=

ρ

Parcie hydrostatyczne (parcie,

napór

) – siła nacisku jaką płyn

wywiera na daną powierzchnię. Siła ta jest normalna do danej
powierzchni.

Parcie jest związane z ciśnieniem wzorem

→

→

=

S

pd

P

d

gdzie:

→

S

d

– wektor powierzchni nieskończenie małego fragmentu

ds powierzchni S,
p – ciśnienie hydrostatyczne panujące na poziomie, na którym
znajduje się powierzchnia ds.

Ponieważ rozpatrywane są nieskończenie małe elementy,
przyjmuje się, że ciśnienie jest stałe na poziomie każdej takiej
powierzchni ds.

Dla powierzchni płaskich i stałego ciśnienia w każdym
punkcie powierzchni, wzór na parcie upraszcza się do postaci:

pS

P

=

Płyn w stanie spoczynku wywiera napór hydrostatyczny
zarówno na dno jak i ścianę naczynia.

Parcie na ścianę poziomą można zapisać:

ghS

N

ρ

=

gdzie
N – parcie (napór) hydrostatyczne,
ρ – gęstość cieczy,
h – wysokość słupa cieczy;
S – powierzchnia ściany

Wzór na parcie dla ściany pionowej:

S

gh

N

0

ρ

=

gdzie
h

0

– głębokość środka ciężkości.

Środek naporu oznacza punkt, w którym wypadkowa siła
naporu przebija rozpatrywaną ścianę. Na powierzchni płaskiej
rozpatrujemy element powierzchniowy.

położony w odległości y od osi x. Odległość środka naporu

Σ

od osi x oznaczamy jako

η

. Z warunku równowagi momentów

względem osi x otrzymamy:
Ponieważ jednak

zdF

g

N

∫

=

ρ

oraz

α

sin

y

z

=

Otrzymamy wyrażenia:

x

J

dF

y

=

∫

2

s

M

ydF

=

∫

Stanowią odpowiednio
geometryczny moment
bezwładności i moment
statyczny figury płaskiej
względem osi x. Po
przekształceniach otrzymamy:

x

x

M

J

ydF

dF

y

=

∫

∫

=

2

η

Odległość środka naporu hydrostatycznego od krawędzi
przecięcia lustra cieczy i rozpatrywanej ściany jest równa
ilorazowi geometrycznego momentu bezwładności i momentu
statycznego względem tej krawędzi.
Jeżeli oznaczymy jako y

s

odległość środka geometrycznego od

osi x oraz uwzględniając, że:

∫

=

=

s

x

Fy

ydF

M

otrzymamy:

s

x

Fy

J

=

η

Na podstawie twierdzenia Steinera

F

y

J

J

s

ox

x

2

+

=

i ostatecznie:

F

y

J

y

F

y

F

y

J

s

ox

s

s

s

ox

+

=

+

=

2

η

Z zależności tej wynika
jednoznacznie, że środek
naporu hydrostatycznego leży
zawsze głębiej niż środek
geometryczny figury płaskiej,
jaką tworzy rozpatrywana
ściana

.

_________________________________________
16.Kinematyka płynów Rownanie ciaglosci :
Pochodna substancjonalna (dH/dt) ma ona określony sens
fizyczny, gdyż d/dt dotyczy zmiany tego samego
poruszającego się elementu płynu, czyli zmiany związanej z
jego „substancją”.Jest ona sumą pochodnej lokalnej ∂H/∂t i
pochodnej konwekcyjnej (v

⋅∇

)H. Pochodna ∂H/∂t oznacza

zmianę wielkości H w czasie. Pochodna (v

⋅∇

)H wyraża

zmianę wielkości H przy przesunięciu punktu o współrz. X,y,z
po torze co łączy się z polem prędkości w otoczeniu tego
punktu.

(

)

H

v

t

H

dt

dH

∇

⋅

+

∂

∂

=

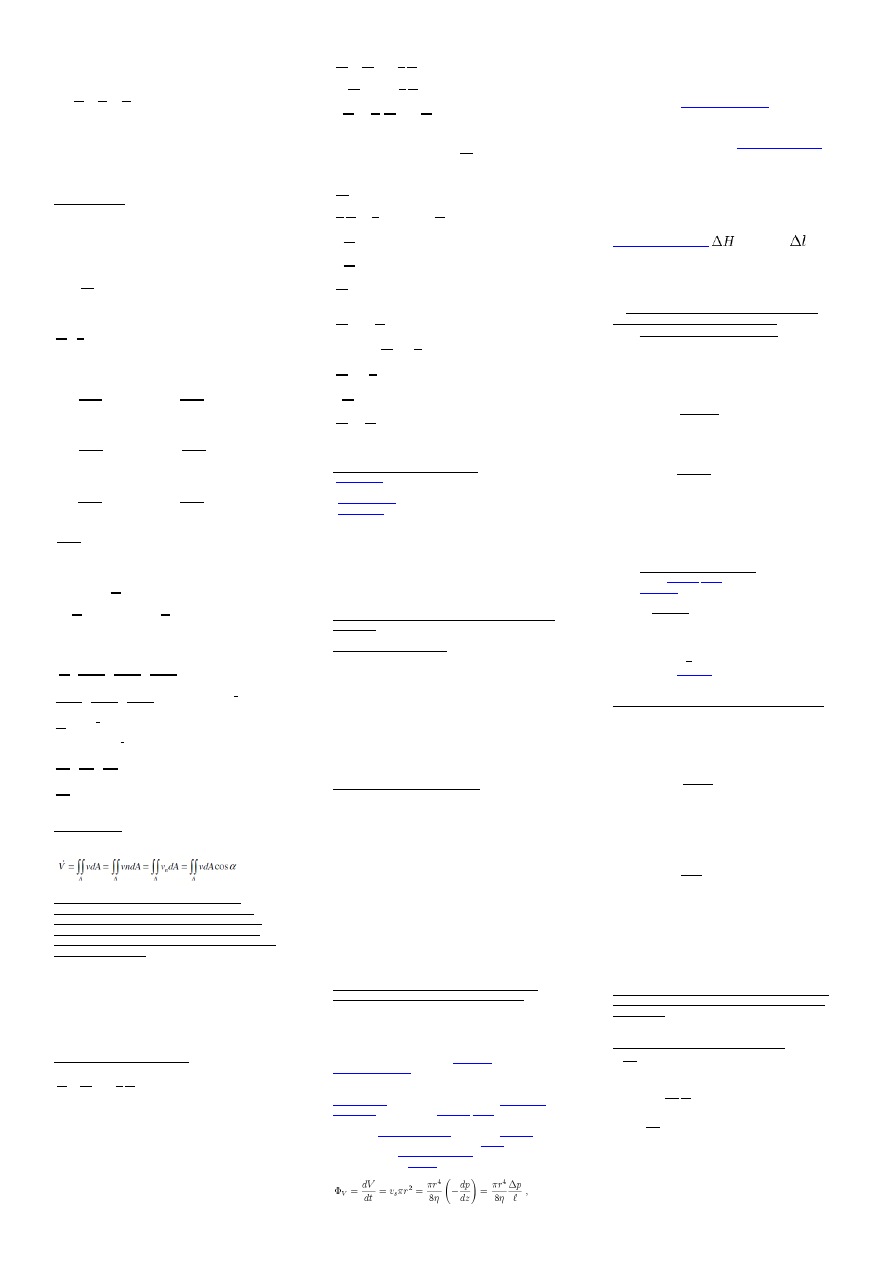
gdzie

∇

jest operatorem nabla:

z

k

y

j

x

i

∂

∂

+

∂

∂

+

∂

∂

=

∇

Wyrażenie

(

)

∇

⋅

v

jest iloczynem skalarnym dwóch

wektorów, tj. wektora prędkości i operatora nabla

∇

Równanie ciągłości:
strumienie masy przepływającej

(dopływ-odpływ) przez

powierzchni

e

A musz

a równać się akumulacji

masy:

dA

V

dt

m

n

A

ρ

∫

∫

=

•

masa zakumulowana w objętości V jest równa:

dt

t

V

m

∂

∂

=

ρ

łącząc te dwie wielkości, otrzymuje się:

0

1

=

∫

∫

+

∂

∂

vdA

V

t

A

ρ

ρ

dla prostopadłościanu przyrost masy jest równy:
dla osi x:

dxd yd zdt

x

V

d ydzdt

V

d ydzdt

dx

x

V

V

x

x

x

x

∂

∂

=

−

∂

∂

+

)

(

)

)

(

(

ρ

ρ

ρ

ρ

dla osi y:

dxdydzdt

y

V

dxdzdt

V

dxdzdt

dy

y

V

V

y

y

y

y

∂

∂

=

−

∂

∂

+

)

(

)

)

(

(

ρ

ρ

ρ

ρ

dla osi z:

dxd yd zdt

z

V

d xdydt

V

d xdydt

dz

z

V

V

z

z

z

z

∂

∂

=

−

∂

∂

+

)

(

)

)

(

(

ρ

ρ

ρ

ρ

R

d xdydzdt

z

V

z

−

∂

∂

)

(

ρ

A

dxdydzdt

t

dxdydz

dxdydz

dt

t

dxdydz

dt

t

dt

t

dxdydz

t

−

∂

∂

=

−

∂

∂

+

∂

∂

+

→



+

−

ρ

ρ

ρ

ρ

ρ

ρ

ρ

)

(

)

(

R+A=0

rowy

jednowymia

przeplyw

x

V

owy

trójwymiar

przeplyw

z

V

y

V

x

V

v

div

cons

v

div

t

v

div

a

divergencj

z

V

y

V

x

V

dxdydzdt

z

V

y

V

x

V

t

x

z

y

x

z

y

x

z

y

x

(

0

(

0

0

)

(

0

)

(

)

(

)

(

)

(

)

(

0

)

)

(

)

(

)

(

(

−

=

∂

∂

−

=

∂

∂

+

∂

∂

+

∂

∂

=

=

=

+

∂

∂

−

−

∂

∂

+

∂

∂

+

∂

∂

=

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

Strumień objętości

[m

3

/s]jest iloczynem skalarnym

prędkości v i

odpowiednio zorientowanego

wektora elementu powierzchni dA.

_________________________________________
17.dynamika płynów doskonałych: równanie

Bernoulliego (założenia, interpretacja

fizyczna

i

graficzna), przykłady zastosowania r.Bernoulliego

(pomiar prędkości rurką Pitota, Prandtla, zwężki,
ustalony i

nieustalony wypływ przez otwory

, przelew)

Równanie Bernoulliego

opisuje zachowanie gęstości

energii całkowitej na

linii prądu

. Obowiązuje w

podstawowej wersji dla

stacjonarnego przepływu

nieściśliwego

płynu idealnego

, a w wersji rozszerzonej dla

idealnego

płynu barotropowego

. Równanie Bernoulliego

wynika z

zasady zachowania energii

i według intencji jego

autora stanowić powinno jej zapis za pomocą parametrów
hydrodynamicznych.

Wyprowadzenie wzoru bernulliego
- przepływ jednowymiarowy, przepływ bezwirowy

→

∂

∂

−

=

∂

∂

+

∂

∂

s

p

F

s

V

V

t

v

m

ρ

1

równanie Eulera dla przepływu

jednowymiarowego
przepływ ustalony

)

2

(

)

2

(

1

/*

1

2

2

V

d

d s

V

s

ds

s

V

V

d s

s

p

ds

F

ds

s

V

V

d s

s

p

F

s

V

V

d

V

m

m

=

∂

∂

=

∂

∂

∂

∂

−

=

∂

∂

+

∂

∂

−

=

∂

∂

+

∂

∂

ρ

ρ

siły masowe są potencjalne

s

U

F

m

∂

∂

=

U-potencjał

const

g

g

z

g

V

g

const

p

gz

V

const

p

gz

V

Bern

równ

const

p

gz

V

const

równania

postac

const

dp

gz

V

z

g

U

ziemskiego

pola

potencjale

const

R

U

V

R

U

V

d

dR

dU

V

d

dp

R

dR

dp

ds

s

p

dU

ds

s

U

=

+

+

=

+

+

=

+

+

=

+

+

=

→

=

+

+

=

=

+

−

=

+

−

−

=

=

→

=

=

∂

∂

=

∂

∂

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

2

:

/

2

/*

2

.

.

2

1

2

*

2

0

)

2

(

)

2

(

1

1

2

2

2

2

2

2

2

2

Zastosowanie równania Bernoulliego:

-

rurka Pitota

pomiar :prędkości nurtu rzeki ; w

lotnictwie do pomiaru prędkości

statków powietrznych

.

-

Rurka Prandtla

- pomiar ciśnienia dynamicznego

-

zwężki tam

gdzie wymagane jest wytworzenie

podciśnienia

, np. w

wodnych pompkach

próżniowych. Jest

również stosowana do sterowania, np. w przepływowych

bojlerach gazowych

.

- ustalony i nieustalony wypływ przez otwory

???

- przelew do pomiaru strumienia objętości w przewodach
(kanałach) otwartych

18. przepływ laminarny i turbulentny, doświadczenie

Reynoldsa

Ruch laminarny i turbulentny
Ruch laminarny (warstwy się nie nakładają) tory cząstek

mało różnią się od siebie. Pozostające w ruchu medium
można traktować jako zbiór oddzielnych warstw,

poruszających się względem siebie z różną prędkością i
nie mieszających się ze sobą. Ruch taki występuje w

mediach o dużej lepkości (μ), np. lawa wulkaniczna.
Re<2300

Ruch turbulentny ( warstwy mieszają się ze sobą) ruch
cząstek płynu powoduje mieszanie się ze sobą rożnych

warstw, Ruch ten występuje w mediach o względnie malej
lepkości (μ), np. woda, powietrze. Re>50000

Opis doświadczenia Reynoldsa (1883)

Ćwiczenie polega na obserwacji zachowania się strugi
barwnika (fluoresceiny) przy różnych

średnich prędkościach przepływu wody w przewodzie i na
obliczeniu w każdym przypadku liczby

Reynoldsa. Urządzenie użyte w tym doświadczeniu
pozwala na regulację prędkości przepływu w

przewodzie oraz prędkości wypływu barwnej strugi. Przy
przepływie o charakterze laminarnym,

kiedy strugi cieczy są równoległe i nie następuje wymiana
elementów płynu pomiędzy sąsiednimi

warstwami, struga barwnika rysuje się ostro i wyraźnie,
biegnąc prawie równolegle do ścianki

przewodu. Powyżej pewnej prędkości przepływu w rurze
struga ta tuż za wylotem rurki podlega

intensywnemu rozproszeniu, a następnie bardzo prędko
zabarwia całą masę wody w przewodzie.

19.przepływ laminarny w przewodzie kołowym –
prawo Hagena-Pouiseuilla z wyprowadzeniem

Prawo Hagena-Poiseuille'a - prawo fizyczne opisujące
zależność między strumieniem objętości cieczy a jej
lepkością (która wynika z tarcia wewnętrznego),
gradientem ciśnień (który jest

bodźcem

termodynamicznym

powodującym przepływ płynu), a

także wielkościami opisującymi wielkość naczynia
(długość, promień przekroju poprzecznego).Przy

stacjonarnym

(tj. niezmiennym w czasie),

laminarnym

przepływie

nieściśliwego,

lepkiego

płynu

w cylin-

drycznym przewodzie (tj. w rurze o stałym, kołowym
przekroju),

strumień objętości

przepływu (

objętość

przepływającego płynu na jednostkę

czasu

) propor-

cjonalny jest do

gradientu ciśnienia

wzdłuż przewodu, a

zatem i do różnicy

ciśnień

na końcach przewodu:

gdzie poszczególne symbole oznaczają:

ΦV – strumień objętości przepływu,
V, dV/dt – objętość, pochodna objętości
względem czasu,
z –

współrzędna walcowa

, długość liczona

wzdłuż osi przewodu,
vs – średnia prędkość płynu w kierunku z,
r – promień wewnętrzny przewodu,
η – współczynnik

lepkości dynamicznej

płynu,
p – ciśnienie uśrednione w przekroju
przewodu,
-dp/dz – gradient ciśnienia wzdłuż osi z,
Δp – różnica ciśnień na końcach
przewodu,
l – długość przewodu.

Spadkiem hydraulicznym nazywamy stosunek spadku

wysokości hydraulicznej

do odległości

na jakiej

spadek ten nastąpił
Bardziej ściśle, spadek hydrauliczny jest to wzięta ze
znakiem ujemnym pochodna wysokości hydraulicznej
hwzględem odległości l, na której nastąpiła zmiana
parametru .
20.

S

traty ciśnienia w przewodzie: wskutek tarcia wzór

Darcy-Weisbacha, na oporach miejscowych

Straty ci

ś nienia podczas tarcia

Straty ciśnienia są wywołane tarciem
wewnętrznym płynu w obszarze warstwy
przyściennej.Straty te nazywane też są stratami
liniowymi.
Straty ciśnienia

p

str

i

=

λ

Lρ v

2

2D

z

str

i

=

λ

L v

2

2Dg

Wzór ten umożliwia obliczenie strat ciśnienia
wskutek tarcia, dotyczy przepływu laminarnego

i turbulentnego, ale współczynnik λ w obu
przypadkach przyjmuje inna wartość
Równanie Darcyego-Weisbacha- równanie opisujące
spadek

ciśnienia

płynu

na skutek oporów jego

przepływu

w przewodzie.

D

l

v

p

2

*

*

*

2

ρ

λ

=

∆

λ - współczynnik oporu - f(Re)
l- długość przewodu

[1]

D - średnica (ew.

zastępcza

) przewodu

v - prędkość płynu
ρ - gęstość płynu
Straty ci

ś nienia w wyniku oporów miejscowych

Opory miejscowe są spowodowane zmiana
wartości i kierunku prędkości. Zmiany te
zachodzą w różnych miejscach przewodu i są
spowodowane takimi przeszkodami, jak kolana,
przewężenia, rozszerzenia, rozgałęzienia.

p

str

m

=

ξ

ρ v

2

2

Przy przepływie cieczy stratę często wyraża sie w
metrach słupa danej cieczy, a mianowicie:

z

str

m

=

ξ

v

2

2g

Współczynniki strat miejscowych ξ są określone
na drodze doświadczalnej.
opracowanie na

21.uogólnione równanie Bernoulliego (ze stratami),
przykłady zastosowań do obliczania przepływów w

przewodach

uogólnione prawo Bernoulliego + ze stratami

ρ

ξ

ρ

λ

ρ

ρ

ρ

2

2

)

(

2

2

2

2

2

1

1

2

1

V

p

di

L

V

p

p

p

p

p

p

p

gh

p

gh

p

V

m

i

i

i

i

t

L

m

t

str

str

L

=

∑

=

∑

∑

+

∑

=

∑

∑

+

+

=

+

+

- współczynnik ξ możemy obliczyć dla nagłego
rozszerzenia przewodu

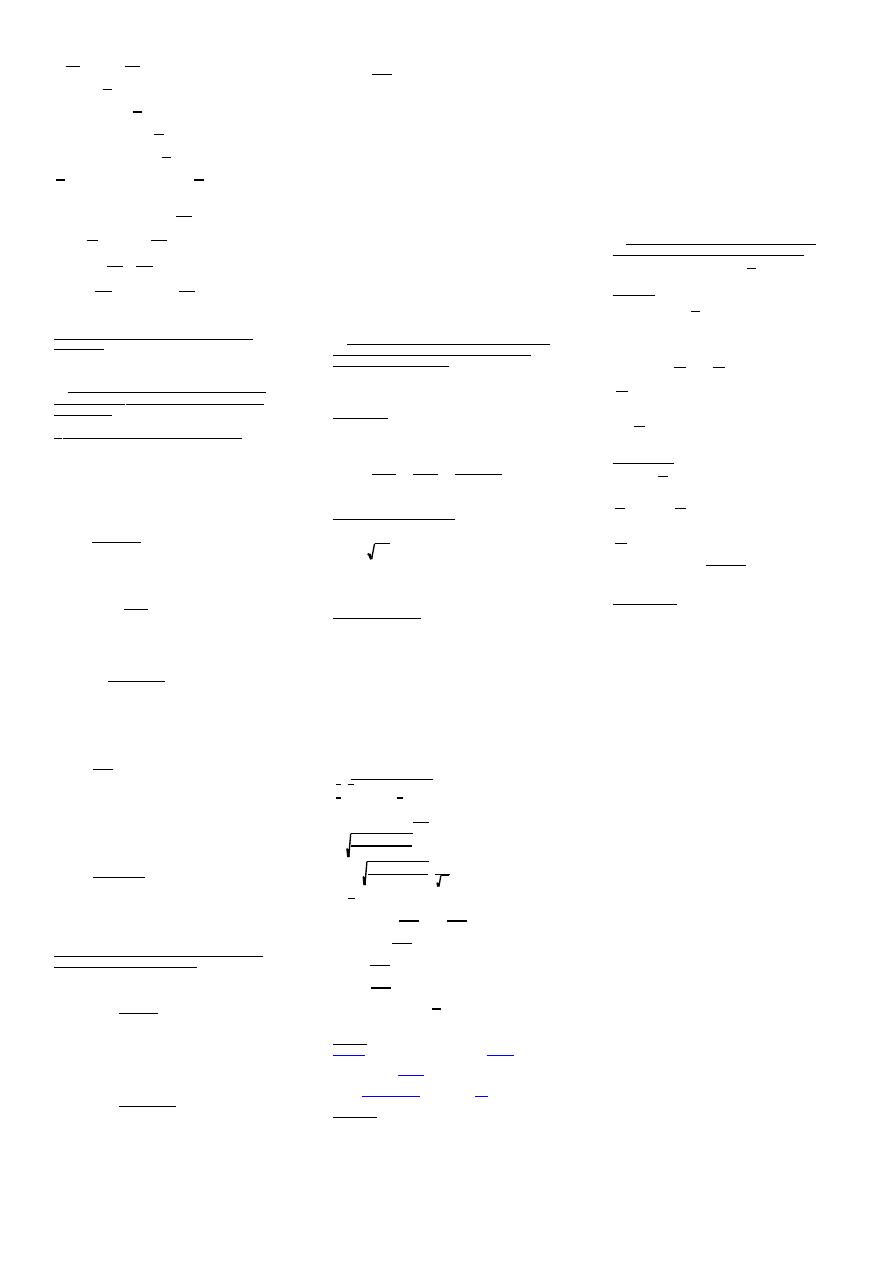
2

2

1

1

2

2

2

2

2

1

2

2

2

1

2

2

2

1

2

2

2

1

2

2

1

2

2

2

2

2

1

2

2

1

2

2

2

2

1

1

2

2

2

2

1

2

1

)

(

2

)

2

2

(

2

)

(

2

)

(

]

)

(

2

[

)

(

]

)

(

2

[

)

(

)

(

2

2

2

V

V

V

V

V

V

V

V

V

V

V

V

p

p

V

V

A

V

V

A

V

p

V

V

A

V

V

m

p

V

V

p

p

p

p

V

p

V

L

L

L

L

L

−

=

−

+

−

=

−

+

−

−

=

−

−

=

−

−

−

=

−

−

−

=

−

+

+

=

+

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

2

2

1

2

1

2

1

2

2

1

2

2

1

1

1

1

2

1

1

2

2

2

1

1

)

1

(

2

2

)

1

(

)

(

2

A

A

V

p

V

A

A

p

A

A

V

V

V

pL

A

A

V

V

A

V

A

V

L

L

−

=

=

−

=

−

=

=

⇒

−

ξ

ρ

ξ

ρ

ρ

Przykłady zastosowań do obliczania przepływów w
przewodach:

wypływ cieczy ze zbiornika, lewar hydrauliczny, inżektory

22.

W

yznaczanie współczynnika tarcia wewnętrznego

λ

,

wykres zależność

λ

od liczby

Reynoldsa i chropowatości

ścian przewodu

W

yznaczanie współczynnika tarcia wewnętrznego

λ

Współczynnik tarcia podczas przepływu laminarnego w
przewodzie o przekroju kołowym może być wyznaczony w
sposób analityczny z wzoru Hagena-Poiseuille’a. Po

uwzględnieniu

́

v

=

v

wzór ten przyjmuje

postać

v=

p

str

D

2

32μL

Podstawiając liczbę Reynoldsa

ℜ=

vD

v

otrzymuje się

p

str

=

64Lρ v

2

Re2D

Współczynnik tarcia λ podczas przepływu
laminarnego wynosi

λ=

64

ℜ

Współczynnik tarcia podczas przepływu
turbulentnego może być określony tylko
eksperymentalnie. Wzór Blasiusa :

λ=

0,3164

ℜ

1 /4

Ten wzór potęgowy dotyczy przepływów w przewodach
gładkich.
Współczynnik tarcia w warstwie przy

ś ciennej,

wpływ chropowato

ś ci przewodu

Straty ciśnienia wskutek tarcia obliczane są ze
wzoru Darcy-Weisbacha

p

str

=

λ

Lρ v

2

2D

gdzie

λ

- współczynnik tarcia wewnętrznego płynu

w przewodzie
prostoliniowym o średnicy D i długości L, inaczej:

p

str

=

λ

64Lρ v

2

Re2D



Współczynnik tarcia:

λ=

64

ℜ

Wpływ chropowatości na wartość współczynnika
_, a wiec i na opory tarcia jest złożony.
Grubość podwarstwy laminarnej decyduje o tym,
czy przewód może być uznany za
hydraulicznie gładki
a) lam k

<δ

(czyli chropowatość bezwzględna k

mniejsza od grubości podwarstwowej warstwy
laminarnej) – brak wpływu chropowatości na
współczynnik tarcia.
b) lam k

>δ

(zakres przejściowy) – wpływ

chropowatości zmienia sie wraz ze zmiana liczby
Reynoldsa
c) lam k

>>δ

(chropowatość bezwzględna dużo

większą niż grubość warstwy laminarnej) – w
pełni rozwinięty wpływ chropowatości –
współczynnik tarcia

λ

nie zależy od Re.

Chropowatość bezwzględna to średnia
wysokość nierównomierności ścian rury.

23.

P

rzepływ w kanałach otwartych (spadek hydrauliczny,

obliczanie strumienia objętości, optymalny przekrój)
Przepływ w kanałach otwartych Ciecz wypełnia tylko części
tego przekroju, niezależnie od tego czy jest to rurociąg, czy
odkryty kanał. Istotą kanału otwartego jest istnienie
swobodnej powierzchni cieczy, w skutek czego na ciecz jest
wywierane to samo ciśnienie ( najczęściej atmosferyczne).
Pojęcie spadku hydraulicznego wykorzystywane jest
najczęściej w hydrologii i hydrogeologii. Stosowane jest
głównie przy opisie ruchu wód w strefie przypowierzchniowej
płytkich gruntów

I =

h

str

L

=

Δ h

L

=

z

1

−

z

2

L

przepływy w kanałach otwartych

, równanie jednostronne,

prędkość, przekrój optymalny, wzór chezy’ego
- wzór chezy’ego

I

r

c

V

n

sr

=

- przekrój optymalny- max strumień objętości przepływający
kanałem o stałym nachyleniu i stałym przekroju
poprzecznym- kształt okrągły będzie najbardziej optymalny
Strumie

ń

obj

ę

to

ś ci

vdA=liint

vndA=liint

́

v=liint

¿

A

¿

❑

¿

A

¿

❑

¿

A

¿

❑

v

n

¿ ¿

dA=liint

¿

A

¿

❑

vdAcos α

jest iloczynem skalarnym predkosci v i
odpowiednio
zorientowanego wektora elementu powierzchni
Da

24.

O

pływ ciał – rotametr

2

2

2

2

1

2

2

1

2

2

2

1

2

2

,

,

2

,

,

2

min

.

.

.

2

.

2

2

)

(

2

,

2

)

(

),

(

4

1

*

)

(

2

)

(

2

0

2

)

(

0

v

DH

C

R

a

ko

dla

opor

zaw ietrzna

stro na

v

k

p

p

do wietrzna

stro na

v

k

p

p

v

k

k

p

p

v

k

p

v

k

p

cisnienie

z

f

Q

d

D

A

A

c

A

gV

vA

Q

A

c

gV

v

V

A

c

gV

gV

W

gV

G

R

W

G

A

x

pa

a

pa

a

pa

p

n

pa

p

pa

n

x

p

p

plywaka

p

x

p

plywaka

p

x

p

plywaka

plynu

plywaka

p

x

ρ

ρ

ρ

ρ

ρ

ρ

π

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

=

−

=

+

=

−

=

−

=

=

−

=

−

=

−

=

=

−

=

=

−

−

=

=

=

+

−

Rotametr, właśc. przepływomierz o zmiennym przekroju –

przyrząd

do pomiaru natężenia przepływu

płynów

. Ma postać

pionowej szklanej rury, rozszerzającej się ku górze. W rurze
umieszczony jest

pływak

. Płyn wprowadza się od dołu rury.

Ruch płynu powoduje unoszenie pływaka do położenia, w
którym

zrównoważą się

działające nań

siły

: ciężkości, wyporu

i tarcia.
Opływ ciała- zestawienia tematyczne

a)

podczas opływu przez wiatr budynków
powstaje określony rozkład prędkości, który
prowadzi do rozkładu ciśnień na
powierzchniach tych ciał, czyli do działania sił
aerodynamicznych na te powierzchnie,

b)

drobne ciała są poddawane działaniu oporu
płynu podczas takich procesów, jak
wentylacja,, sedymentacja, aeracja

c)

działanie wiatru na kominy fabryczne,
budynków, wzniesienia i zagłębienia terenu
wytwarza określony rozkład prędkości i stref
oderwań co ma decydujący wpływ na
rozprzestrzenianie się zanieczyszczeń w
atmosferze

25.

P

rzepływ w ośrodkach porowatych – prawo Darcy,

przykład obliczania dopływu wody do studni, rowu

Porowatość ośrodka w ogólności

V

V

p

=

ε

Porowatość

powierzchniowa

V

A

=

η

Przepływ w ośrodku porowatym (prawo Darcyego)

EGO

prawoDARCY

dx

dh

k

u

JI

wspFILTRAC

k

I

k

u

ny

hydraulicz

spadek

I

L

h

l

g

p

z

g

p

z

h

h

h

−

=

−

=

−

=

∆

+

−

+

=

−

=

*

:

/

)

(

)

(

1

1

2

2

1

1

ρ

ρ

Dopływ do rowu

Q

h

H

sk

L

depresji

krzywej

zasięa

h

H

L

sk

Q

H

h

L

x

depresji

krzywej

rów

h

h

x

sk

Q

dh

h

dx

sk

Q

LTRACJI

pręrędkość

u

dx

dh

hsk

hsu

Q

h

h

x

2

)

(

.

.

2

,

.

.

2

*

2

0

2

2

0

2

2

0

2

0

0

−

=

→

−

=

=

=

−

−

=

=

∫

=

∫

−

=

=

Dopływ do studni

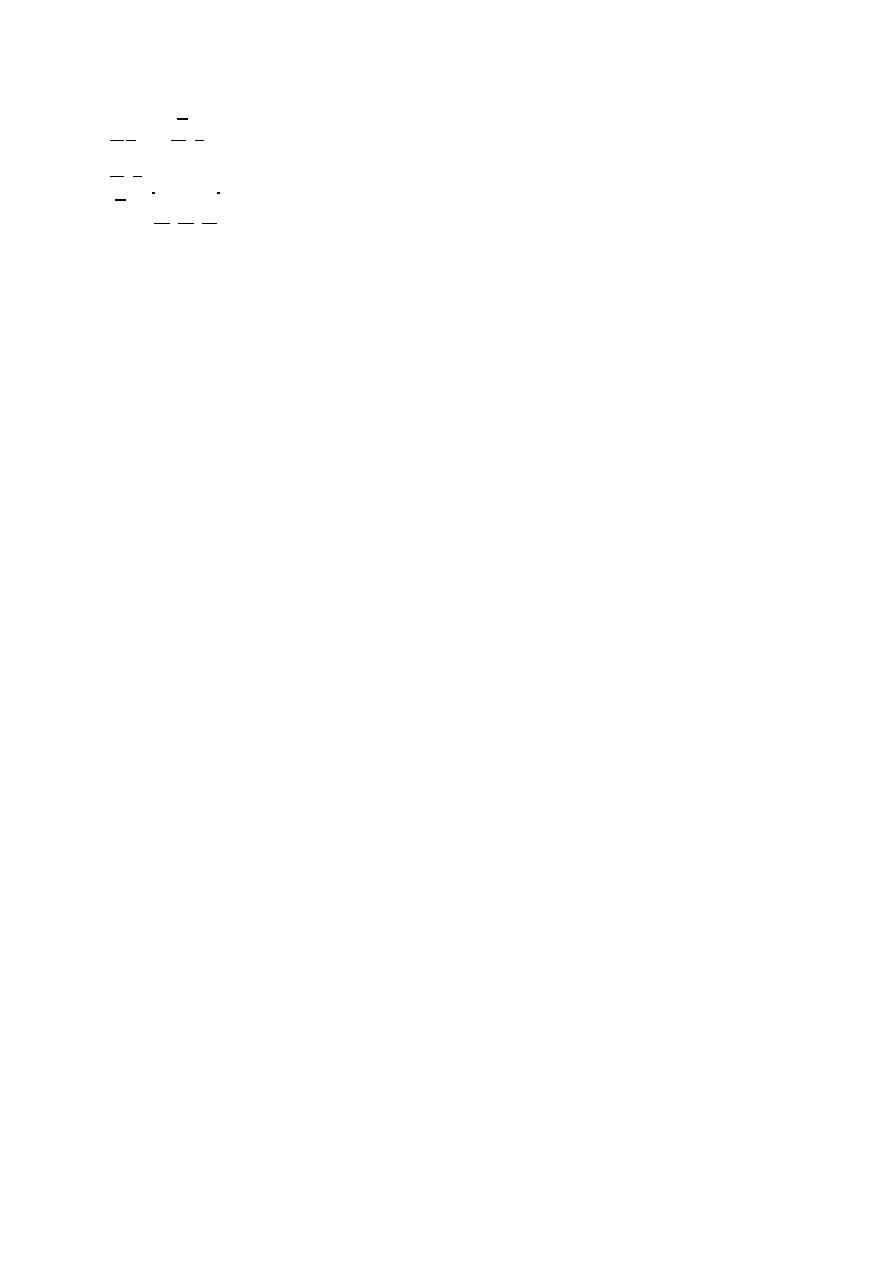
0

,

*

0

,

,

0

)

(

.

.

ln

2

2

,

ln

2

2

*

2

2

*

2

2

2

2

2

2

2

2

0

2

0

2

0

2

0

0

=

∂

∂

+

∂

∂

+

∂

∂

=

=

=

=

+

∂

∂

−

−

=

=

=

−

=

⇒

=

=

=

z

p

y

p

x

p

gra dp

k

v

v

div

co nst

v

d iv

t

g o

d epresyjn e

leja

za sięa

h

H

r

R

k

Q

H

h

R

r

h

h

r

r

k

Q

d

h

r

dv

k

Q

d v

d h

rh k

u

v

Q

o

ρ

ρ

ρ

ε

π

π

π

π

π