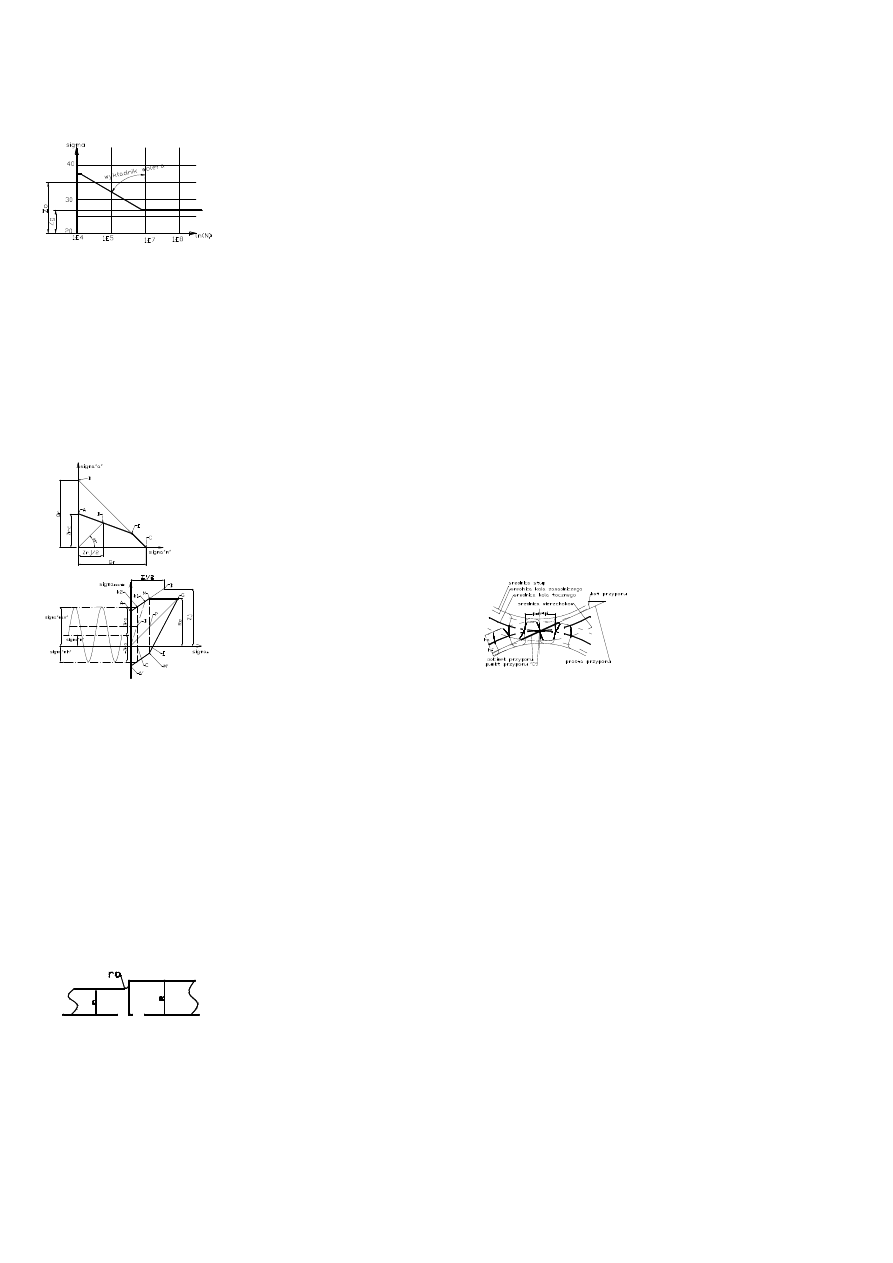
ZMĘCZENIÓWKA

Wykres Wöhlera

Zk- obszar wytrzymałości zmęczeniowej przy małej
ilości cykli
Zo- obszar wytrzymałości zm. przy ograniczonej
ilości cykli
Zz- obszar wytrzymałości zm. przy nieograniczonej
ilości cykli

Sposoby

obliczenia

współczynnika

w

poszczególnych obszarach:
1.N

c

<10

4

-obszar obciążeń statycznych

δ

=Re/

σ

max

2.10

4

<N

c

<10

7

– obszar wytrzymałości ograniczonej

δ

z

=Z

o

/

σ

max

(Z

o

-wyznaczone doświadczalnie lub

obliczone Z

o

=Z

g

(10

7

/N

c

)^

ς

)

3.N

c

>10

7

– obszar wytrzymałości nieograniczonej

δ

=Z

g

/

σ

max

Liczba całkowita cykli
N

c

=n(1/min)*60*h(ilość

godzin)*z(liczba

zmian)*D(dni)*l(lat)

σ

m

=(

σ

max

+

σ

min

)/2- naprężenie średnie

σ

a

=(

σ

max

-

σ

min

)/2- amplituda naprężeń

R=

σ

min

/

σ

max

–współczynnik asymetrii cyklu

Kappa=

σ

m

/

σ

a

- współczynnik stałości obciążenia

Wykres Haigha

Wykres Smitha

Aby narysować wykres potrzeba Re, Zo,Zj.
Jeżeli przy wzroście obciążenia stosunek amplitudy

σ

a

do naprężenia średniego

σ

m

będzie stały to

wartość wytrzymałości zmęczeniowej określa punkt
k1

σ

a

/

σ

m

=const, x

2

=z

1

/

σ

max

=E*k1/CD

Jeśli przy wzroście obciążeń naprężenie średnie
cyklu

pozostaje

stałe

to

wytrzymałość

zmęczeniowa odpowiadająca punktowi D określona
jest punktem k2, współczynnik bezpieczeństwa

σ

m

=const x2=Z2/

σ

z

=Ck2/CD

D-punkt pracy.


CZYNNIKI

WPŁYWAIĄCE

NA

WYTRZ.

ZMĘCZENIOWĄ
Pod pojęciem KARBU należy rozumieć wszelkie
nieciągłości poprzecznych przekrojów przedmiotu
lub zmiany krzywizn powierzchni ograniczających
przedmiot (rowki, otwory, gwinty)
Rozkład naprężeń w obszarze karbu zależy od
geometrii

karbu,

związanej

z

wymiarami

przedmiotu. Charakterystykę zmęczeniową karbu
ujmujemy w tzw. współczynniku kształtu

α

k

.

Wartość współczynnika

α

k

zależy od: stosunku

promienia krzywizny dna karbu

ρ

do promienia lub

połowy szerokości przekroju r w elementach
płaskich w płaszczyźnie karbu, oraz od stosunku
promienia połowy szerokości elementu R w
miejscu nie osłabionym karbem do promienia r.

β

k

- współczynnik działania karbu- stosunek

wytrzymałości próbek gładkich bez karbu do
wytrzymałości próbek gładkich z karbem.

β

k

-

zależy od współczynnika kształtu i współczynnika
wrażliwości materiału na działanie karbu.

β

k

=1+

η

k

(

α

k

+1) gdzie

η

k

- współczynnik

wrażliwości materiału na działanie karbu (jest
zależny od Rm,

ρ

o

) =1 dla materiałów doskonale

sprężystych „szkło” =0 dla materiałów
niewrażliwych na działanie karbu „żeliwo szare”.
Współczynnik

β

p

charakteryzuje

zmianę

wytrzymałości elementów po różnej obróbce
skrawaniem w porównaniu z próbką polerowaną.
Do obliczeń elementów z karbem o znanym

β

k

posługujemy się zależnością

β

=

β

k

+

β

p

-1 (w

przypadku karbów prostych

β

p

pomijamy, dla

żeliwa po usunięciu naskórku odlewniczego
przyjmujemy

β

p

=1)

β

pz

- dla powierzchni ulepszanych

β

=

β

k

*

β

pz

Współczynnik wielkości elementu

ε

=z

d

/z, z

d

-

wytrzymałość zmęczeniowa próbki o średnicy d, z-
wytrzymałość zmęczeniowa próbki o średnicy od 7
do 10mm (

γ

=1/

ε

).

δ

-rzeczywisty współczynnik bezpieczeństwa

δ

<1 nie występuje

δ

=1.3-1.4

–ścisłe

obliczenia

na

podstawie

dokładnych danych doświadczalnych

δ

=1.4-1.7 - dla zwykłej dokładności obliczeń, bez

doświadczalnego sprawdzenia obliczeń

δ

=1.7- 2 – dla zmniejszonej dokładności obliczeń,

przy możliwości określenia naprężeń i obciążeń

δ

=2-3 – przy orientacyjnym określaniu obciążeń i

naprężeń dla niepewnych lub specjalnie ciężkich
warunków pracy (odlewy)


OBLICZENIA

ZMĘCZENIOWE

PRZY

OBCIĄŻENIACH ZŁOŻONYCH
Przy

jednoczesnym

występowaniu

naprężeń

różnego rodzaju naprężenia te składamy przy
zastosowaniu odpowiedniej hipotezy wytężeniowej.
Naprężenia

zastępcze

dla

obciążeń

niesymetrycznych (wahadłowych) obliczamy tak
samo jak dla obciążeń stałych. Przy przewadze
naprężeń normalnych

σ

z

=(

σ

2

+(k

σ

*

τ

/k

τ

)

2

)^(1/2).

Przy

przewadze

naprężeń

stycznych

σ

z

=((k

τ

*

σ

/k

σ

)

2

+

τ

2

)^(1/2).

Rozwiązując

te

zależności

można

dowieść,

że

rzeczywisty

współczynnik

bezpieczeństwa

jest

równy

δ

z

=1/(1/

δ

σ

2

+1/

δ

τ

2

)

1/2

δ

σ

,

δ

τ

-składowe

rzeczywistego

współczynnika

bezpieczeństwa obliczane tak jakby działało tylko
zmienne naprężenie normalne lub styczne.

WAŁY I OSIE
Jeśli jest przenoszony moment skręcający to taką
część nazywamy wałem, jeśli nie to osią. Części
wałów osi na których są osadzone współpracujące
z nimi elementy nazywamy czopami.
ETAPY PROJEKTOWANIA WAŁÓW:
1.Projektowanie

wstępne

polegające

na

ukształtowaniu wału na podstawie uproszczonych
obliczeń wytrzymałościowych i zadanych dyspozycji
wymiarowych
2.Obliczenia sprawdzające- sztywności(kąta ugięcia
i strzałki), obliczenia dynamiczne (prędkości
krytycznej ii drgania rezonansowe), obliczenia
zmęczeniowe

(rzeczywisty

współczynnik

bezpieczeństwa)
3.Ostateczne kształtowanie wału.

MATERIAŁY NA WAŁY
1.St3-St5 wtedy gdy o kształcie wału decyduje
sztywność
2.35-45 gdy wał przenosi duże obciążenie w
szczególności

45

gdy

wskazanej

jest

powierzchniowe utwardzenie czopów
3.dla wałów uzębionych materiał taki jak dla kół
zębatych (stale CrNi do ulepszania cieplnego,
nawęglania i azotowania)

KSZTAŁTOWANIE WAŁU
Kształtowanie

powierzchni

swobodnych

przeprowadzamy po ukształtowaniu powierzchni
roboczych, czyli czopów-należy uwzględnić aby
d

1

/d

2

<=1,2 , natomiast czopy należy kształtować

według zaleceń normy.
Gładkość powierzchni
1.czopów końcowych :R

z

=2,5-0,32

µ

m

2.powieszchni swobodnych : wały wolno obrotowe
i średnio bieżne (R

z

=10-5

µ

m), wysokoobrotowe (

R

z

=2,5

µ

m)

Tolerancje – powierzchnie swobodne wykonujemy
w tolerancji warsztatowej IT14 (h14) przy dużych
obrotach IT12 do IT10

Uwzględnianie wpustu:
1.Jeżeli obciążenie jest w przybliżeniu statyczne
wystarczy, by moment bezwładności przekroju z
rowkiem

był

nie

mniejszy

od

momentu

bezwładności zarysu teoretycznego.
2.Gdy wał pracuje w zmiennym cyklu obciążenia
przy niewielkim udziale momentu skręcającego
moment bezwładności koła wpisanego winien być
nie mniejszy niż teoretyczny
3.Gdy

występuje

duży

udział

momentu

skręcającego

moment

bezwładności

koła

współśrodkowego z przekrojem poprzecznym
wału, stycznego zewnętrznie do dna rowka pod
wpust winien być nie mniejszy od teoretycznej

Sprawdzenia – ugięcie dopuszczalne (F

dop

=2-3*10

-4

rozstawu łożysk), dopuszczalny kąt skręcenia
(

ϕ

dop

=0,002-0,01rad/m)

ŁOŻYSKA TOCZNE
Dwie ostatnie cyfry oznaczają średnicę otworu
wewnętrznego

(00-10,01-12,02-15,03-17,04-

20,05-25,06-30,07-*5)

Cyfry

początkowe

oznaczają serię łożyska i niekiedy grupę
konstrukcyjną (62-kulkowe zwykłe, 72-kulkowe
skośne,303-stożkowe.293-baryłkowe wzdłużne)
Materiały- pierścień i części toczne wykonywane są
ze specjalnej stali chromowej ŁH 15 lub ŁH 15SG

Dobór łożysk :
1.ograniczenia wymiarowe łożysk
2.wielkości i kierunki obciążenia
3.prędkość obrotowa
4.możliwość ograniczenia błędu współosiowości
5.wymagana dokładność i cichobieżność
6.sztywność ułożyskowania

Nośność spoczynkowa n<10 1/min , jest to takie
obciążenie które wywołuje łączne odkształcenie
plastyczne równe 0,0001mm elementów tocznych

Trwałość – jest to czas pracy łożyska w milionach
obrotów lub godzin

L=(C/P)

ρ

c-nośność ruchowa, p- obciążenie (

ρ

=3-

łożysko kulkowe,

ρ

=10/3-łożysko wałeczkowe)

L

10

-trwałość umowna osiągana przez 90% łożysk

L=a1*a2*a3*L

10

Algorytm doboru łożysk tocznych :
1.ustalenie

schematu

konstrukcyjnego

łożyskowania
2.pokreślenie wartości i kierunków obciążeń i
prędkości obrotowej łożysk
3.dla obciążeń zmiennych obliczamy P

n

i n

n

.

4.ustalenie ograniczeń geometrycznych
5.wybór typu łożyska
6.przyjęcie wymaganej trwałości L
7.wyznaczenie stosunku C/P dla odpowiedniego L i
typu łożyska
8.obliczenia obciążenia zastępczego P=VxP

r

+

ψ

*P

a

9.obliczenia obciążenia efektywnego P

e

=f

d

*P

10.obliczenia nośności ruchowej C=P

e

(C/P)

11.obliczenie

efektywnej

nośności

ruchowej

C

e

=f

t

*C

12.obliczenie

zastępczego

obciążenia

spoczynkowego P

0

=max(P

01

,P

02

) P

01

=X

0

*P

r0

+Y

0

*P

0a

P

02

=P

r0

13. Obliczanie wymaganej nośności spoczynkowej
14.Dobór z katalogu jego nośności oraz wymiarów
geometrycznych
15.Sprawdzenie

trwałości

ściernej

łożyska-

weryfikacja

nośności

efektywnej

c

0

=s

0

*P

0

L

e

=a

1

*a

2

*a

3

*(C

e

/P

e

)

ρ

16.Dobór środka smarnego.
17. Przyjęcie prasowań w gnieździe i na czopie
oraz uszczelek (filc-mała prędkość obrotowa, oringi
i

simeringi-

średnia

prędkość

obrotowa,

uszczelnienia labiryntowe- duża prędkość) .

a

1

- uwzględnia wymaganą niezawodność łożyska

≠

0.9

a

2

- dokładność wykonania łożyska i gatunek stali

a

3

- zależy od wartości tarcia, rzeczywistym

współczynnikiem

grubości

elastohydrodynamicznego filmu olejowego

Obliczanie obciążeń zastępczych P=VxP

r

+Y*Pa

P

r

- obciążenie promieniowe

P

a

- obciążenie wzdłużne

V- współczynnik obrotów
X-współczynnik obciążenia poprzecznego
Y- współczynnik obciążenia wzdłużnego

Tolerancje (HB, kB) pasowania (HB/h7, H7/kB)

PRZEKŁADNIE ZĘBATE
Istotnym zespołem składniowym jest zazębiająca
się kara kół zębatych zazębiających się w ten
sposób że uzyskane jest

Zarys zęba miejsce geometryczne punkt styku z
drugim zębem

Koło

podziałowe

odpowiada

walcom

podziałowym dzieli ząb na dwie części powyżej
koła podziałowego- głowa zęba i to co poniżej-
stopa zęba

Wrąb- przestrzeń pomiędzy zębami jednego koła
Grubość zęba- jest mierzona na średnicy
podziałowej

Luz- różnica pomiędzy grubością zęba a
podziałką(/2 chyba)
Wysokość zęba-

Luz wierzchołkowy- odległość pomiędzy walcem
wierzchołkowym jednego koła a walcem den
wrębów drugiego koła c=0.25*m

Wskaźnik wysokości zęba y=h

a

/m (y=1 zęby

zwykłe, y>1 zęby wysokie, y<1 zęby niskie)

Znormalizowane: h

f

=1.25*m, h

a

=m

Linia przyporu jest linią wyznaczoną przez kolejne
punkty styku.
Odcinek przyporu jest to część lini przyporu
ograniczona punktami przecinania się kół na
których znajdują się końce czynnych zarysów zęba
(koła wierzchołków).
Ewolwenta jest to krzywa powstała przez
przetaczanie prostej po okręgu.
Punkt przyporu jest to punkt styku dwóch
współpracujących ewolwent.
Centralny punkt przyporu „C” wyznacza przecięcie
lini przyporu z linią łączącą środki kół.
Kąt przyporu jest to kąt pomiędzy prostą przyporu
a styczną do kół tocznych w punkcie „C”.
Liczba przyporu

ε

stosunek długości odcinak

przyporu do podziałki zasadniczej

ε

>1.

Zarys odniesienia jest to zarys zębów zębatki
nazywanej zębatką odniesienia. Powstaje ona jako
zarys styczny do dwóch zarysów ewolwentowych
współpracujących kół. Można ją interpretować jako
koła zębate o nieskończenie dużej średnicy,
zarysem takiego koła są odcinki proste jako
szczególny przypadek ewolwent.

Nacinanie kół zębatych – zębatka Maga(prosta),
zębatka Fellowsa.

Zalety zarysu ewlowentowego:
- mała wrażliwość na odchyłki odległości kół,
- kierunek siły międzyrębnej niemienia się podczas
pracy przekładni
- koła zębate o tych samych podziałkach i
nominalnych kątach zarysu mogą być kojarzone w
dowolne pary
- koła uzębione zewnętrznie mogą być kojarzone z
uzębieniem zewnętrznym, wewnętrznym czy też
zębatką.

- ewolwentowe koła zębate można wykonywać
wydajnymi

i

dok

ładnymi

metodami

obwiedniowymi
- za pomocą tego samego narzędzia można
wykonać koła o różnej ilości zębów.

KOREKCJE
Podcięcia zęba podczas obtaczania obwiedniowego
występuje wówczas gdy część narzędzia zębatki
wytwarza zarys który nie jest ewolwentą.
W praktyce podcięcie występuje wtedy gdy
występuje bardzo mało zębów.
Graniczna

liczba

zębów

Z

g

=y*2/sin

2

α

o

z

g

(

α

o

=20st)=17, a gdy dopuszczamy niewielkie

podcięcie zębów z

g

’=14

Korekcja uzębienia
Jest potrzebna w przypadku gdy na kole o liczbie
zębów z<z

g

chce się uniknąć podcięcia zęba u

podstawy. Polega ona na przesunięciu narzędzia
zębatkowego z położenia 0 w położenie1, w
którym nie występuje podcięci zęba lecz
zmniejszyła się grubość zęba u wierzchołka.
X=x*m –przesunięcie zarysu (x- współrzędna
przesunięcia ,”+”-wysuwanie ,”-„-wsuwanie).
x

g

=y*(z

g

-z)/z

g

Przy z=12 x

g

=1*(17-12)/17, X=x

g

*m

Korekcja zazębienia
1.PO – przesunięcie zarysu bez zmiany odległości
osi.(X-X) Polega na przesunięciu narzędzia
zębatkowego na jednym kole na zewnątrz o taką
samą wielkość, o jaką w drugim kole- ku wnętrzu.
Stosuje się z

1

+z

2

>=2z

g

(z

g’

)

Zastosowanie PO pozwala na usunięcie podcięcia
$&%$#^% kole ale jest także gdy podcięcie nie
grozi poprawności współpracy z większą liczbą
przyporu.
2.P- przesunięcie zarysu ze zmianą odległości osi
(X+X). Stosuje się gdy z

1

+z

2

<2z

g

, oraz gdy

względy

konstrukcyjne

wymagają

zmiany

odległości osi. Po zastosowaniu przesunięcia
zarysu x

1

,x

2

osie kół ulegają rozsunięciu i nowa

odległość osi będzie równa a

p

=a

0

+(x

1

+x

2

)*m-

odległość pozorna.
Aby skasować luz obwodowy zbliża się koła na
odległość a

r

=a

0

*cos

α

0

/cos

α

t

α

t

toczny kąt

przyporu

a

0

=z

1

+z

2

/2*m

inv

α

t

=2*(x

1

+x

2

)/(z

1

+z

2

)*tg

α

0

+inv

α

0

Dla zachowania luzu wierzchołkowego należy ściąć
głowy o k

m

=a

p

+a

m

Mamy do rozdysponowania x

1

+x

2

=const, w

praktyce x

2

=0 lub x

1

=0 lub x

1

=x

2

.

Uszkodzenia kół zębatych
-rysy hartownicze –pęknięcia
-uszkodzenia interferencyjne –występują przy
nadmiernym nacisku pomiędzy stopą a głową
-odpryski – są inicjowane przez rysy i pęknięcia w
utwardzonej warstwie
-wytarcia i wydarcia- są wynikiem obecności
twardych zanieczyszczeń pomiędzy zębami
-zatarcie i przegrzanie – powstaje przy zaniku
smaru i metalicznym styku zęba
-piting- ma postać piramidkowych ubytków na
powierzchniach bocznych jest inicjowany przez
pęknięcia w które wszedł olej
-zgniot i złamanie – uszkodzenie nieutwardzonych
zębów o zbyt małej granicy plastyczności

Obliczanie przekładni otwartych – na złamanie
zęba, zamkniętej na naciski powierzchniowe.