DEFEKT MASY, ENERGIA WIĄZANIA:

Doświadczenia Rutherforda w 1911 r. polegające na przepuszczaniu cząstek przez cienką folię ze
złota wykazały, że atom posiada jądro, które stanowi bardzo niewielką część średnicy atomu (rzędu

10

-10

– 10

-9

m) i w którym skupiona jest prawie cała masa atomu. Przestrzeń wewnątrzatomowa

pozostaje praktycznie pusta. Fakt, że prawie cała masa atomu jest zawarta w jądrze atomowym i

skoncentrowana w bardzo małej objętości (10

-14

- 10

-15

m) tłumaczy dlaczego gęstość materii jądrowej

jest bardzo duża (rzędu 10

15

kg/m

3

).

W skład jądra wchodzą nukleony, jednakże masa jądra atomu nie jest równa sumie mas protonów i
neutronów. Różnica masy jądra atomowego i mas nukleonów wchodzących w jego skład nosi

nazwę defektu masy. Im większy atom, tym większy jest defekt masy.

Δm = Z

.

m

p

+ (A-Z)

.

m

n

- m

j

Δm - defekt masy (deficyt masy, niedobór masy)
Z - liczba atomowa (= liczba protonów)
A - liczba masowa (= liczba nukleonów, czyli protonów i neutronów)
m

p

- masa protonu, m

p

= 1,007277u

m

n

- masa neutronu, m

n

= 1,008665u

m

j

- masa jądra, m

j

= m

a

-m

c.e

m

a

- masa atomu, [u], 1u = 1,660531

.

10

-27

kg

m

c.e

- masa elektronów, wchodzących w skład atomu (czasem jest pomijana ze względu na

stosunkowo małą wartość), masa jednego elektronu

m

e

= 0,00054859u = 9,1094

.

10

-31

kg.

Defekt masy charakterystyczny dla atomu helu tzn. różnica między masą atomową, a masą 2

protonów, 2 neutronów i 2 elektronów wynosi ok. 0,031 u.
Energia i masa są powiązane równaniem Einsteina E = mc

2

, gdzie E - energia, m - masa, c - prędkość

światła w próżni.
Defekt masy można przeliczyć na energię wiązania nukleonów w jądro (E

w.n

) według wzoru

E

w.n.

= Δm

.

c

2

lub zastosować przeliczniki:
1 u = 931,4812 MeV = 8,982

.

10

10

kJ/mol

Inaczej mówiąc, "brakująca" masa zostaje "zamieniona" na energię odpowiedzialną za utrzymywanie

jądra w całości. Wartość energii wiązania jest miarą trwałości jądra. Im większa jest energia wiązania
nukleonów, tym większe nakłady energii wymagane są do rozbicia atomu na części składowe, tym

bardziej trwałym jest jądro.

Przykłady obliczeń:
1. Obliczyć energię wiązania przypadającą na jeden nukleon dla

12

6

C, przyjmując, że masa jego jądra

wynosi 12,000000u.
Δm=Z

.

m

p

+ (A-Z)

.

m

n

- m

j

=6

.

(1,007277u) + 6

.

(1,008665u) - 12,000000u

Δm= 0,095652u
E

w.n.

=

0,095652u

.

931,4812MeV/u = 89,098040MeV

Dla jednego nukleonu: E

w.1n.

= 89,098040 MeV/12 = 7,424837MeV

2. Obliczyć energię wiązania nukleonów E

w.n.

w przypadku jednego mola jąder atomowych

9

4

Be.

Masa mola protonów wynosi 1,007g/mol, neutronów – 1,009g/mol.
Δm = Z

.

m

p

+ (A-Z)

.

m

n

– m

j

= 4

.

(1,007 g/mol) + 5

.

(1,009 g/mol) – 9,012g/mol

Δm =0,061g/mol
Pamiętamy, że kg

.

m

2

/s

2

= J, wtedy:

E

w.n.

= Δm

.

c

2

= 0,061

.

10

-3

kg/mol

.

(3

.

10

8

m/s)

2

= 5,49

.

10

12

J/mol

DUALISTYCZNY CHARAKTER PROMIENIOWANIA

ELEKTROMAGNETYCZNEGO:

U podstawy współczesnych poglądów dotyczących struktury i własności mikroukładów atomowych

leży koncepcja, wysuniętą w 1900 roku przez M.Plancka, zgodnie z którą materia emituje i pochłania
energię promienistą nie w sposób ciągły, lecz w porcjach nazywanych kwantami:

,

gdzie:
E – energia jednego kwantu promieniowania, [J];
h – stała Plancka, h = 6,6260693

.

10

-34

J

.

s;

- częstość promieniowania, [s

-1

].

,

gdzie:
c – prędkość światła w próżni, c = 299792458 m/s;

- długość fali światła, [m].

Przykłady obliczeń:

1. Obliczyć częstość drgań światła czerwonego o długości fali = 650 nm oraz energię E fali
świetlnej.

,

= (2,998

.

10

8

m/s) / 650

.

10

-9

m = 4,612

.

10

14

s

-1

E = (6,626

.

10

-34

J

.

s)

.

4,612

.

10

14

s

-1

= 3,056

.

10

-19

J

2. Oblicz energię 1 mola fotonów światła zielonego o długości fali = 490 nm

- jest to energia jednego fotonu.

1 mol zawiera N

a

= 6,022

.

10

23

fotonów, więc energia 1 mola fotonów będzie wynosiła:

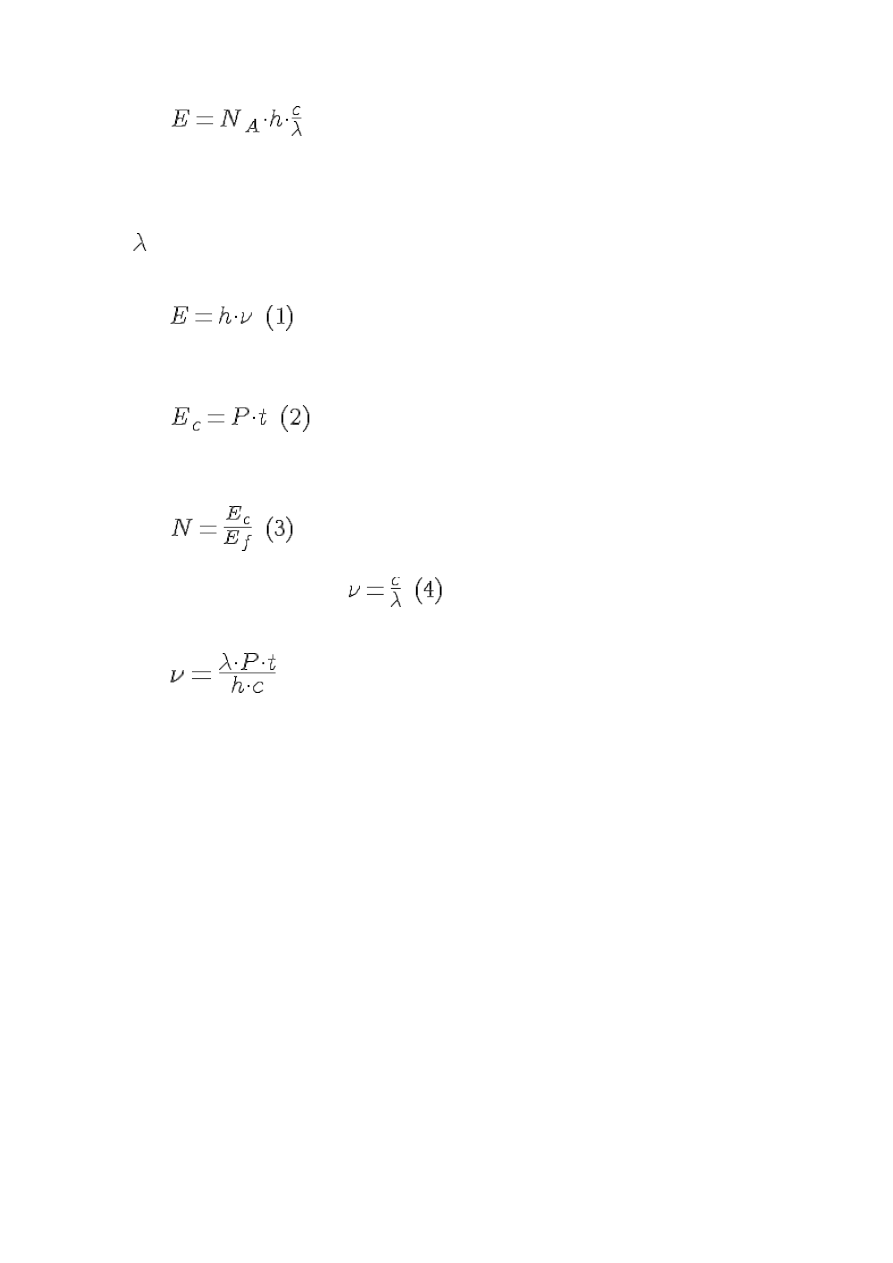
E

mol

= 6,022

.

10

23 .

(6,626

.

10

-34

J

.

s)

.

(2,998

.

10

8

m/s) / 490

.

10

-9

m

E

mol

= 244,1 kJ/mol

3. Ile fotonów N emituje w ciągu 1ms lampa o mocy 10 W, wysyłająca światło fioletowe o długości

fali = 0,40 µm, przy 100% wydajności świetlnej.
Energia jednego fotonu wynosi

Energia wszystkich fotonów jest równa całkowitej energii emitowanej przez lampę E

c

, którą

obliczamy według wzoru (2):

,

gdzie P – moc lampy, t – czas emisji światła. Znając energię wszystkich fotonów znajdzujemy ich ilość
N:

Pamiętamy, że częstotliwość drgań

, a W = J/s. Podstawiamy (1), (2) i (4) w (3), po

przekształceniach otrzymamy:

N = {(0,40

.

10

-6

m)

.

(10 J/s)

.

(1

.

10

-3

s)} / {(6,626

.

10

-34

J

.

s)

.

(2,998

.

10

8

m/s)}

N = 2,014

.

10

16

fotonów.

DUALISTYCZNY CHARAKTER CZĄSTEK MATERII:

Relacja de Broglie’a:

Dualizm korpuskularno-falowy jest cechą nie tylko cząstek światła (fotonów), lecz i wszystkich
sząstek materialnych o masie spoczynkowej różnej od zera. Tę hipotezę Lui de Broglie ogłosił w
1924 roku.

Z ruchem każdej cząstki materii związany jest pewny ruch falowy, przy czym wielkości
charakteryzujące ruch mechaniczny cząstki (pęd, energia) i towarzyszącą mu falę materii
(długość fali, częstość drgań) związane są równaniami:

,

De Broglie podał następujący wzór na długość fali materii:

,

gdzie:

- długość fali poruszającej się cząstki materii (długość fali de Brogli’a);

h – stała Plancka,

;

m – masa cząstki, [kg];

– prędkość, z którą porusza się cząstka, [m/s];

– pęd poruszającej się cząstki,

.

Zasada nieoznaczoności:

Z powodu dualistycznej natury mikrocząstek ich położenie i pęd nie mogą być ze względów
zasadniczych jednocześnie dokładnie zadane. Zwiększenie dokładności pomiaru położenia powoduje
zawsze zaburzenia zwiększające nieokreśloność pędu cząstki i na odwrót. Stwierdzenie to jest jednym
ze szczególnych przypadków zasady nieoznaczoności Heisenberga : Niemożliwe jest określenie
jednocześnie z dowolnie dużą precyzją zarówno pędu, jak i położenia cząstki.

Analiza rachunkowa wielu doświadczeń prowadzi do wniosku, że iloczyn nieokreśloności

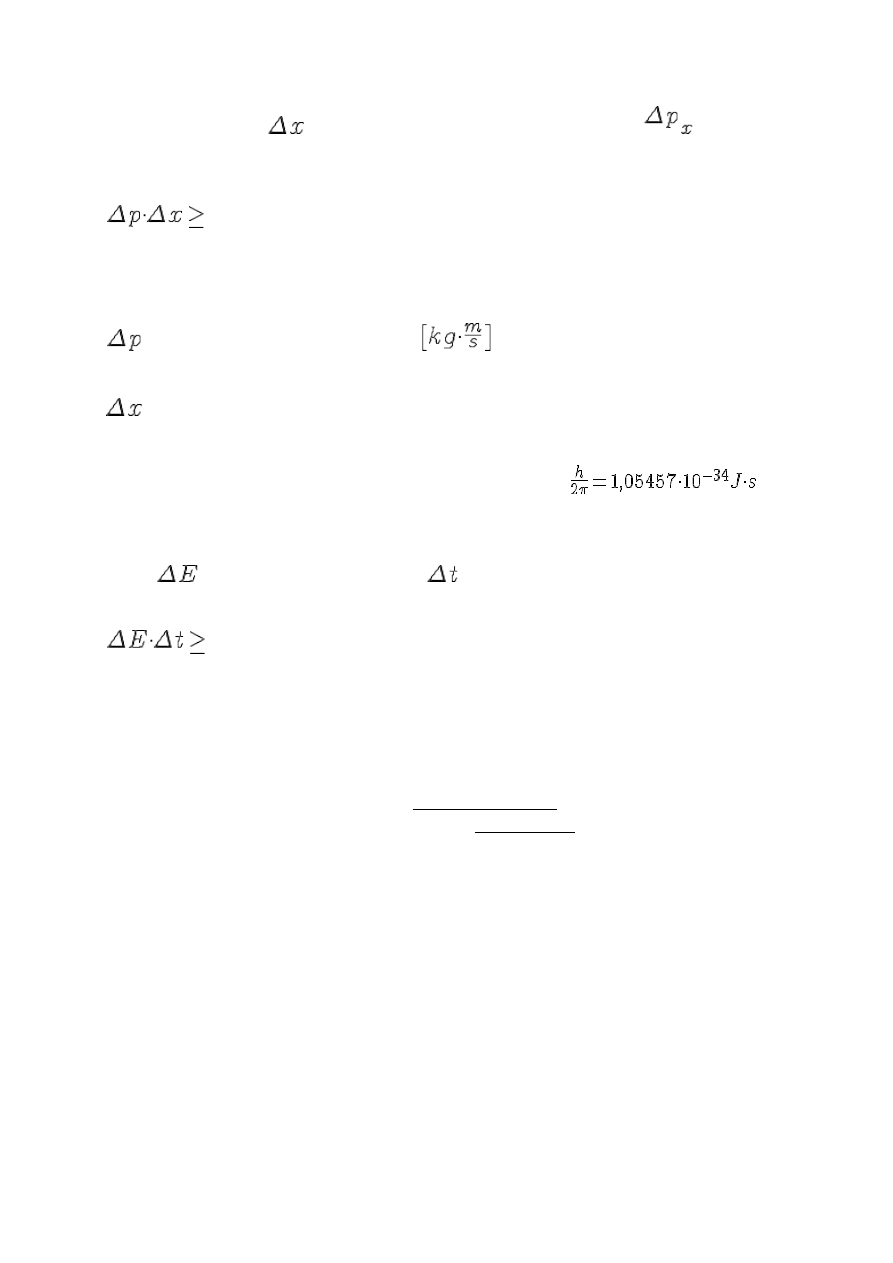
współrzędnej położenia

i odpowiadającej jej składowej pędu mikrocząstki

musi być co

najmniej rzędu elementarnego kwantu działania, czyli stałej Plancka. Wyraża to relacja:

ħ/2,

gdzie:

– nieoznaczoność pędu w kierunku osi x,

;

– nieoznaczoność położenia wzdłuż tej osi, [m];

h – modyfikacja stałej Plancka, stała Diraca (czytamy: h-kreślone), h=

.

Zasadę nieoznaczoności można też wyrazić przez iloczyn nieokreśloności wartości energii

układu

i czasu zajścia pewnego zjawiska

:

ħ/2

Sformułowana w ten sposób zasada nieoznaczoności wyznacza dolną granicę szerokości linii
widmowych.

Uwaga! Ze względu na małą wartość h zasada nieoznaczoności nie stanowi żadnego ograniczenia dla
jednoczesnego wyznaczenia położenia i pędu ciał makroskopowych z największą wymaganą
dokładnością. Jednakże w opisie stanu mechanicznego mikroukładów

(np. elektronów) rezygnujemy z

dokładnie zadanych wartości współrzędnych położenia cząstek, wprowadzając w mechanice
kwantowej zamiast tego pojęcie prawdopodobieństwa znalezienia cząstki w interesującym nas
elemencie objętości.

Przykłady obliczeń:

1. Obliczyć długość fali de Brogli’a dla protonu poruszającego się z prędkością 0,01% prędkości
światła.

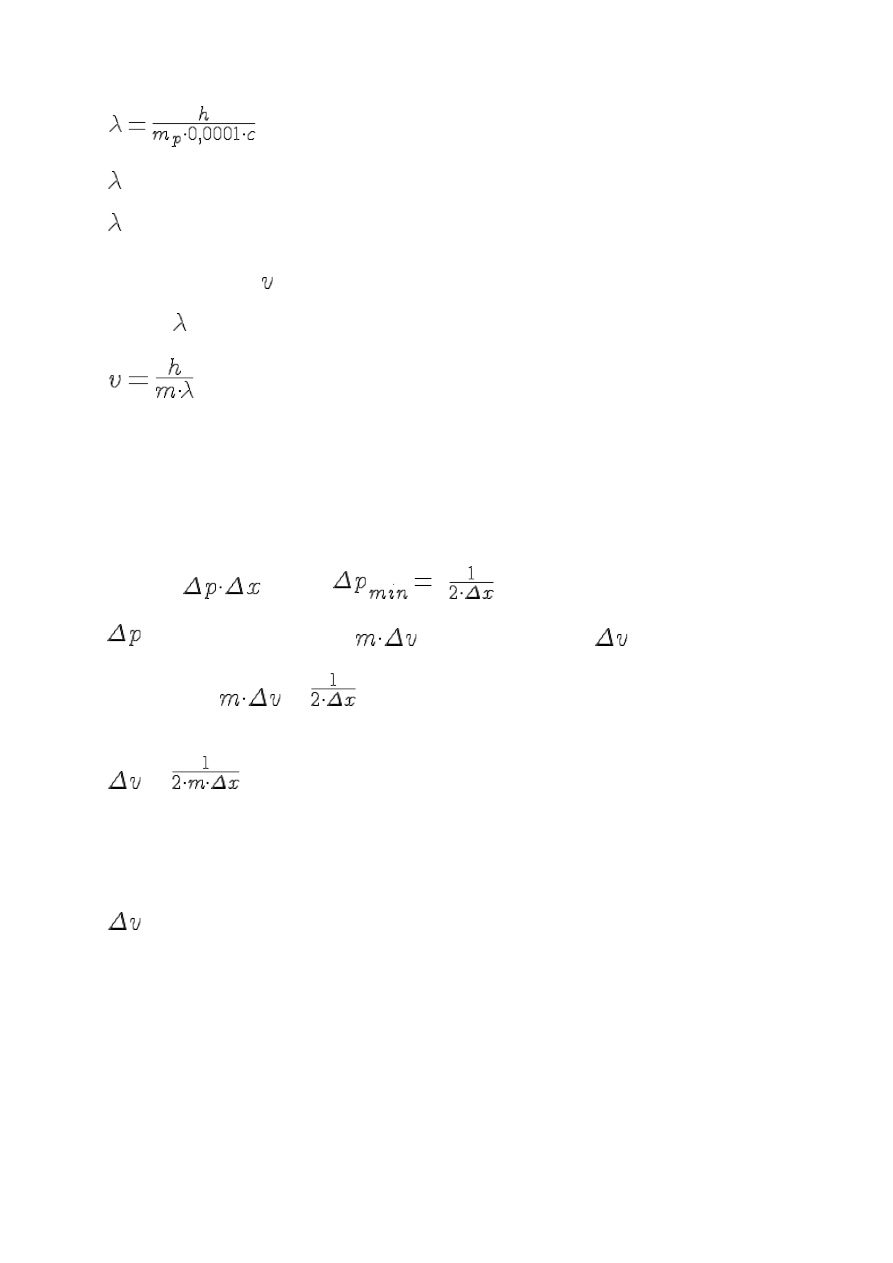
= 6,6262

.

10

-34

J

.

s/((1,6726

.

10

-27

kg)

.

(0,0001

.

2,9979

.

10

8

))

= 1,3215

.

10

-11

m

2. Jaka była prędkość cząsteczki azotu (w m/s), jeżeli wiadomo, że długość fali de Brogli’a

wynosiła = 45 µm?

v = 6,6262

.

10

-34

J

.

s/((14,0067

.

2

.

1,6605

.

10

-27

kg)

.

(45

.

10

-12

m))

v = 316,55 m/s

3. Jaka jest najmniejsza nieoznaczoność prędkości elektronu w jednowymiarowym obszarze o
długości rzędu 10 pm?

Ponieważ

≥ħ/2, to

ħ

.

możemy również zapisać jako

, gdzie m – masa cząstki,

– nieoznaczoność jej

prędkości, czyli

= ħ

. Wobec tego nieoznaczoność prędkości jest równa:

= ħ

.

Dla elektronu o masie 9,1094

.

10

-31

kg w jednowymiarowym obszarze najmniejsza nieoznaczoność

prędkości wynosi:

= 1,05457

.

10

-34

J

.

s/(2

.

9,1094

.

10

-31

kg

.

10

-11

m)

= 5,7884

.

10

6

m/s.

KONFIGURACJE ELEKTRONOWE:

Wraz ze wzrostem liczby atomowej pierwiastka wzrasta liczba elektronów. Poszczególne

powłoki elektronowe atomu wypełnia się elektronami, umieszczając je na różnych
orbitalach atomowych zgodnie z trzema regułami:

1. Zasada rozbudowy.

Konfiguracje elektronowe buduje sie od dołu, wykorzystując najpierw

orbitale o niższej energii.

Kolejność energetyczna orbitali jest następująca: 1s, 2s, 2p, 3s, 3p,

4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d

*)

2. Reguła Hunda.

W orbitalach zdegenerowanych zachowana jest maksymalna multipletowość

spinowa

, czyli sparowanie elektronów nie następuje, dopóki każdy zdegenerowany orbital

nie jest w połowie wypełniony.

3. Zakaz Pauliego.

Nie mogą istnieć dwa elektrony scharakteryzowane przez te same cztery

liczby kwantowe.

Gdy dwa elektrony zajmują ten sam orbital, muszą mieć różne spiny.

Ponieważ spinowa liczba kwantowa przybiera tylko jedną z dwóch wartości (-1/2, +1/2), na

orbitalu może znajdować się najwyżej dwa elektrony.

Jeżeli wyżej wymienione reguły są spełnione, odpowiadająca im konfiguracja elektronowa jest
konfiguracją stanu podstawowego pierwiastków. Możliwe są inne konfiguracje elektronowe, są to
jednak konfiguracje stanów wzbudzonych. Będziemy rozpatrywać konfiguracje elektronowe stanu
podstawowego pierwiastków. W przypadku cięższych pierwiastków (o większych liczbach
atomowych) mogą nastąpić odstępstwa od podanej kolejności wynikające z oddziaływania
elektronów między sobą.

Przykłady pytań:

1. Czy są możliwe następujące konfiguracje elektronowe atomów w stanie podstawowym:

a) 1s

2

2s

2

2p

6

3s

2

3p

8

4s

2

b) 1s

2

2s

2

2p

6

3s

2

3p

6

4s

1

3d

10

4p

6

c) [Kr] 4s

2

4p

6

5s

2

d) 1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

14

4p

6

5s

2

e) [Ne] 5s

2

4d

8

5p

6

6s

2

f) 1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

8

4p

6

5s

2

g) 1s

2

2s

2

2p

x

2

2p

y

1

2p

z

0

Odp.: Żadna z podanych konfiguracji elektronowych nie jest możliwa.Są naruszone zasady:

a) 1s

2

2s

2

2p

6

3s

2

3p

8

4s

2

- zakaz Pauliego;

b) 1s

2

2s

2

2p

6

3s

2

3p

6

4s

1

3d

10

4p

6

- zasada rozbudowy;

c) [Kr] 4s

2

4p

6

5s

2

- użyto nieodpowiedniego rdzenia konfiguracji elektronowej;

d) 1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

14

4p

6

5s

2

- zakaz Pauliego;

e) [Ne] 5s

2

4d

8

5p

6

6s

2

- użyto nieodpowiedniego rdzenia konfiguracji elektronowej;

f) 1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

8

4p

6

5s

2

- zasada rozbudowy;

g) 1s

2

2s

2

2p

x

2

2p

y

1

2p

z

0

- reguła Hunda.

2. Napisać konfigurację elektronową jonu jednododatniego pierwiastka o liczbie atomowej
Z=47.

Odp.: 1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

10

4p

6

5s

0

4d

10

lub [Kr] 4d

10

Uwaga 1: Należy pamiętać, że elektronami walencyjnymi są elektrony
najbardziej zewnętrznych powłok elektronowych (czyli znajdujących sie najdalej radialnie od
jądra). W rozpatrywanym przypadku odrywany jest elektron z 5sa nie z 4d.

Uwaga 2: Podczas pisania konfiguracji elektronowych jedyną informacją potrzebną (i
dostępną!) jest liczba atomowa pierwiastka. Posługiwanie się układem okresowym
pierwiastków jest zabronione.

Uwaga 3: Nie należy mylić kolejności wypełniania elektronami powłok elektronowych
a kolejności zapisu konfiguracji elektronowych. Ta ostatnia dopuszcza dwie formy: 1. zgodnie
z kolejnością wypełniania orbitali; 2. zgodnie z kolejnością radialną (pisanie powłokami). Np.
dla Z=30 zgodnie z pierwszą formą zapiszemy: 1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

10

, wg drugiego

sposobu zapisu będzie: 1s

2

2s

2

2p

6

3s

2

3p

6

3d

10

4s

2

. Pierwsza forma sprzyja prawidłowemu

napisaniu konfiguracji elektronowej atomu ( o ile sie zna kolejność wypełniania!), druga
pomaga podczas pisania konfiguracji elektronowej jonu bezbłędnie określić, z której powłoki
najpierw zostaną oderwane elektrony.

OKRESOWOŚĆ WŁAŚCIWOŚCI PIERWIASTKÓW:

Układ okresowy odkryto dzięki obserwacji systematycznych zmienności właściwości pierwiastków.

Jeżeli umieścimy obok siebie pierwiastki chemiczne szeregując je według rosnących liczb atomowych,
to dostrzeżemy, że co 8-my, co 18-ty lub co 32-gi pierwiastek wykazuje podobne cechy chemiczne.

Okresowość zmian charakteru chemicznego pierwiastków wraz ze wzrostem masy atomowej była
podstawą w skonstruowanej przez D.I. Mendelejewa tablicy nazwanej układem okresowym

pierwiastków. Dzisiaj wiemy, że o własnościach chemicznych i fizycznych pierwiastka decyduje ilość
elektronów w atomie a szczególnie ilość elektronów na powłokach zewnętrznych oraz ich kształt.

Takimi właściwościami są:



rozmiary atomów i jonów,



wartości energii jonizacyji,



powinowactwo elektronowe,



elektroujemność i elektrododatność,



własności elektryczne i magnetyczne,



okresowość cech chemicznych pierwiastków.

Zobaczymy na przykładzie energii jonizacji i promieni atomowych zależność tych właściwości od

konfiguracji elektronowych.

PROMIENIE ATOMOWE I JONOWE:

Promień atomowy - odległość najdalej położonych elektronów występujących w danym atomie od
jądra tego atomu, ustalana teoretycznie dla atomów uczestniczących w hipotetycznych wiązaniach

chemicznych.
Promienie atomowe, w odróżnieniu od rzeczywistych promieni walencyjnych ustalanych

eksperymentalnie, są określane na drodze teoretycznych obliczeń kwantowo-mechanicznych
(wartości ich mogą się różnić, mimo że ich definicja jest bardzo podobna).

W okresie promienie atomów zmniejszają się wraz ze wzrostem liczby atomowej. Jest to związane z

silniejszym przyciąganiem elektronów przez jądro, ładunek którego wzrasta. Największe promienie
atomów w poszczególnych okresach mają litowce (tab.1), najmniejsze - helowce .

Tabela 1. Promienie atomowe pierwiastków II i III okresów (w pikometrach).

3

Li

167

4

Be

112

5

B

87

6

C

67

7

N

56

8

O

48

9

F

42

11

Na

190

12

Mg

145

13

Al

118

14

Si

111

15

P

98

16

S

88

17

Cl

79

W obrębie grup promienie atomów wzrastają wraz ze wzrostem liczb atomowych

.

Jest to

spowodowane większą liczbą powłok elektronowych (tab.2), co ma większy wpływ, niż wzrastający
ładunek jądra.

Tabela 2. Promienie atomowe pierwiastków I i II grup (w pikometrach).

3

Li

167

4

Be

112

11

Na

190

12

Mg

145

19

K

243

20

Ca

194

37

Rb

265

38

Sr

219

55

Cs

298

56

Ba

253

Okresowym zmianom ulegają również rozmiary jonów pierwiastków.
Promień jonowy - to odległość najbardziej oddalonych elektronów od jądra atomu w przypadku
jonów utworzonych z jednego atomu, lub też od geometrycznego centrum jonów złożonych z

większej liczby atomów.
Promienie jonowe wyznacza się na podstawie rentgenostrukturalnych pomiarów kryształów

jonowych. Przyjmuje się tu podobną zasadę, jak w przypadku wyznaczania promieni walencyjnych
atomów, uśredniając długości wiązań jonowych, jakie tworzy dany jon z innymi jonami.
W przypadku jonów prostych, tj. utworzonych z pojedynczych atomów, ich promień jonowy jest
zazwyczaj większy lub mniejszy od promieni Van der Waalsa wyjściowych atomów. Promienie

anionów są większe od promieni tworzących ich atomów, zaś w przypadku kationów jest odwrotnie.

Czym większy ładunek ujemny posiada dany anion, tym jego promień jest większy, a czym większy
ładunek dodatni ma kation, tym jego promień jest mniejszy. Jest to związane z liczbą elektronów

( pod warunkiem, że ładunek jądra jest stały) - im więcej jest elektronów, tym większe są siły
odpychania pomiędzy nimi, tym większy jest promień jonu (atomu).
Promieni jonowe zależą również od ładunku jądra. Przy identycznej liczbie elektronów (jony
izoelektronowe) wraz ze wzrostem liczby atomowej promień jonowy maleje. Jest to wynikiem

przyciągania powłok elektronowych bliżej jądra przez większy dodatni ładunek. (tab.3)

Tablica 3. Promienie niektórych jonów izoelektronowych

Gaz szlachetny,
konfigurację

elektronową
którego

posiadają jony
izoelektronow

e

Jon

Promień,

pm

Jon

Promień,

pm

Jon

Promień,

pm

Jon

Promień,

pm

Ne

O

2-

140

F

-

119

Na

+

96

Mg

2+

65

Ar

S

2-

212

Cl

-

170

K

+

133

Ca

2+

99

Kr

Se

2-

202

Br

-

187

Rb

+

148

Sr

2+

113

Xe

Te

2-

222

I

-

212

Cs

+

169

Ba

2+

135

ENERGIA JONIZACJI:

Energia jonizacji (pierwsza) pierwiastka - jest to minimum energii potrzebnej do oderwania jednego

elektronu od atomu danego pierwiastka w stanie gazowym [2].

Proces ten opisuje równanie:

W odniesieniu do oderwania się odpowiednio 2, 3 i więcej elektronów od atomu wieloelektronowego

mówi się o drugiej, trzeciej itp. energii jonizacji. W miarę usuwania kolejnych elektronów atomu
energia jonizacji powstałego kationu rośnie, przy czym największa energia jonizacji związana jest z

oderwaniem elektronu z powłoki wewnętrznej (w tabeli 4 jest zaznaczona kolorem czerwonym).

Tabela.4

Kolejne energie jonizacji I

n

(kJ/mol) atomów pierwiastków trzeciego okresu

[1]

Pierwiastek

I

1

I

2

I

3

I

4

I

5

I

6

I

7

Na

495,8

4564

—

—

—

—

—

Mg

737,7

1451

7730

—

—

—

—

Al

577,6

1817 2744

11600

—

—

—

Si

786,5

1577 3228 4350

16100

—

—

P

1011,8

1904 2910 4950

6270

21200

—

S

999,6

2253 3380 4565

6950

8490

27000

Cl

1251,2

2296 3850 5160

6560

9360

11000

Ar

1520,6

2666 3946 5770

7230

8780

12000

Energia jonizacji (E.j.) zmienia się wraz ze zmianą liczby atomowej (l.a.). Wraz ze wzrostem tej

ostatniej w grupie E.j. maleje.
Wraz ze wzrostem liczby atomowej w okresie E.j. ma tendencje do wzrostu, jednak nie jest ten

wzrost liniowy (rys. 1). Jak widać z wykresu największe wartości energii jonizacji posiadają helowce
(mają wypełnioną powłokę elektronową), najniższe - litowce (po oderwaniu 1 elektronu uzyskują

konfigurację elektronową najbliższego helowca).Jak wynika z wykresu wartość energii jonizacji
związana jest z konfiguracją elektronową. Również wysokimi wartościami E.J. charakteryzują się

azotowce (w połowie wypełniona podpowłoka) oraz berylowce i cynkowce ( w całości wypełnione
podpowłoki).