Laboratorium układów elektronicznych
Ćwiczenie numer 4
Filtry aktywne
Zagadnienia do przygotowania
• Rodzaje, zastosowania i parametry filtrów aktywnych
• Transmitancje filtrów aktywnych II rzędu
• Transformacje częstotliwości
• Charakterystyki amplitudowe i fazowe filtrów
• Filtry Butterwortha, Bessela, Czebyszewa
• Filtry Sallena – Keya II rzędu
• Filtry z wielokrotnym sprzężenie zwrotnym
• Filtry realizowane metodą zmiennych stanu
• Filtry z przełączanymi pojemnościami
• Pomiar oscyloskopem przesunięcia fazowego
Literatura
[1]. Tietze U., Schenk Ch., Układy półprzewodnikowe,
Warszawa WNT 1997.
[2]. Kuta S., Elementy i układy elektroniczne, cz.I. AGH
UWND, Kraków 2000.
[3]. Nosal Z., Baranowski J., Układy elektroniczne cz.I. Układy
analogowe liniowe. WNT, Warszawa 1998.
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
2
[4]. Guziński A., Liniowe elektroniczne układy analogowe,
WNT , Warszawa 1993,
[5]. Białko M., Filtry aktywne RC, Warszawa WNT 1979.
[6]. Temes G., Mitra S., Teoria i projektowanie filtrów,
Warszawa WNT 1978.
[7]. Prałat A., Laboratorium układów elektronicznych cz. II,
Oficyna Wydawnicza Politechniki Wrocławskiej
Wrocław 2001.
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
3
1. Wprowadzenie
Filtr aktywny jest to najczęściej czwórnik służący do wyodrębnienia pożądanego
pasma częstotliwości z wielu sygnałów podawanych na wejście czwórnika. Wyjątek
stanowią filtry pasmowo zaporowe służące do wytłumienia niepożądanej częstotliwości
lub niepożądanego pasma. W układach elektronicznych spotyka się wiele użytecznych
rodzajów filtrów jak:
- filtry RLC,
- filtry ceramiczne,
- filtry krystaliczne,
- filtry mechaniczne,
- filtry mikrofalowe,
- filtry aktywne RC o stałych skupionych
- filtry aktywne RC o stałych rozłożonych,
- filtry N- gałęziowe,
- filtry cyfrowe.
Celem ćwiczenia jest zapoznanie studentów z filtrami aktywnymi RC o stałych
skupionych, ich strukturą topologiczną i pomiarami podstawowych parametrów.
1. Rodzaje filtrów aktywnych
Filtry dzielimy na filtry pierwszego rzędu, drugiego trzeciego i wyższych rzędów.
Rząd filtru określa liczba biegunów transmitancji napięciowej:
∏
∏
=
=
−
−
−
−
−
−
=
+
+
+
+
+
+
+
+
=
=
n
j
j
m
i
i
n
m
m
n
m
n
m
m
m
m
wu
we
p
s
z
s
b
a
b
s
b
s
b
s
b
a
s
a
s
a
s
a
U
U
s
H
1
1
0
1
1
1
0
1
1
1
)
(
)
(
.....
.....
)
(
4.1
gdzie :
a
i
bj - rzeczywiste współczynniki wielomianu
z
i
p
j
- zera i bieguny transmitancji H(s).
Ze względu na sposób realizacji filtry aktywne dzielimy na:
- filtry aktywne RC,
- filtry aktywne C przełączane,
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
4
- filtry aktywne C pracujące w czasie ciągłym.
Ze względu na przebieg charakterystyk częstotliwościowych mamy filtry:
- Butterwortha (o charakterystyce maksymalnie płaskiej),
- Czebyszewa (o charakterystyce równomiernie falistej),
- Bessela (o charakterystyce maksymalnie liniowej fazy),
- Cauera (o charakterystyce eliptycznej).
Charakterystyki filtrów mogą być filtrów mogą być opisane przez rozkład zer i
biegunów na płaszczyźnie zmiennej zespolonej, współczynniki a
i
b
j
lub przez dobroć i
pulsacje biegunów transmitancji H(s).
Ze względu na pasmo przenoszonych częstotliwości możemy mówić o filtrach:
dolnoprzepustowych , górnoprzepustowych, środkowoprzepustowych ,
środkowozaporowych oraz o filtrach wszechprzepustowych..
2. Filtry aktywne drugiego rzędu
Transmitancja filtrów wyższych rzędów może być rozłożona na iloczyn funkcji
wymiernych stopnia drugiego, gdy rząd filtru jest liczbą parzystą. Transmitancje filtrów
o rzędzie nieparzystym można przedstawić jako iloczyn wymiernych funkcji stopnia
drugiego i jednej funkcji stopnia pierwszego. Stąd wynika kaskadowa metoda realizacji
filtrów wyższych rzędów i szczególna rola filtrów aktywnych drugiego rzędu. Filtr rzędu
wyższego niż drugi możemy zbudować z połączonych kaskadowo sekcji filtrów drugiego
rzędu i ewentualnie i jednej sekcji filtru pierwszego rzędu. Sekcje filtru drugiego rzędu
powinny realizować transmitancję o postaci
0
1
2
0
1
2
0
1
2
2
)
(
)
(
b
s
b
s
s
N
b
s
b
s
a
s
a
s
a
s
H
k
k
+
+
=
+
+
+
+
=
4.2
Wzór (4.2) można zapisać jako:
)
)(
(
)
(
)
(
)
(
2
1
2
0
0
2
p
s
p
s
s
N
s
Q
s
s
N
s
H
k
k
k
−
−
=
+
+
=
ω
ω
4.3
Bieguny transmitancji p
1
i p
2
otrzymamy przyrównując mianownik do zera
2
0
0
2
,
1
4
1
2
2
Q
Q
Q
p
−
±
−
=
ω
ω
4.4
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
5
Dla Q > 0,5 otrzymujemy bieguny zespolone sprzężone
1
4
2
2
2
0
0
2
,
1
−
±
−
=
Q
Q
j
Q
p
ω
ω
4.5
Transmitancje filtrów drugiego rzędu przedstawiają poniższe wzory:
- filtr dolnoprzepustowy (4.6),
2
0
0
2
2
0
0
)
(
ω
ω
ω
+
+
=
s
Q
s
H
s
H
LP
4.6
filtr górnoprzepustowy (4.7),
2
0
0
2
2
0
)
(
ω
ω
+
+
=
s
Q
s
s
H
s
H
HP
4.7
filtr środkowoprzepustowy (4.8)
2
0
0
2
0
0
)
(
ω
ω
ω
+
+
=
s
Q
s
s
H
s
H
BP
4.8
jeżeli Q
z
> Q mamy filtr środkowozaporowy (4.9)
2
0
0
2
2
2
0
)
(
ω
ω
ω
ω
+
+
+
+
=
s
Q
s
s
Q
s
H
s
H
z
z
z
BP
4.9
jeżeli Q
z
= ∞ mamy filtr eliptyczny (4.10)
2
0
0
2
2
2
0
)
(
ω
ω
ω
+
+
+
=
s
Q
s
s
H
s
H
z
BP
4.10
filtr wszechprzepustowy (4.11)
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
6
2
0
0
2
2
0
0
2
0
)
(
ω
ω
ω
ω
+
+
+
−
=
s
Q
s
s
Q
s
H
s
H
AP
4.11
3.1 Filtry aktywne z wielokrotnym ujemnym sprzężeniem zwrotnym
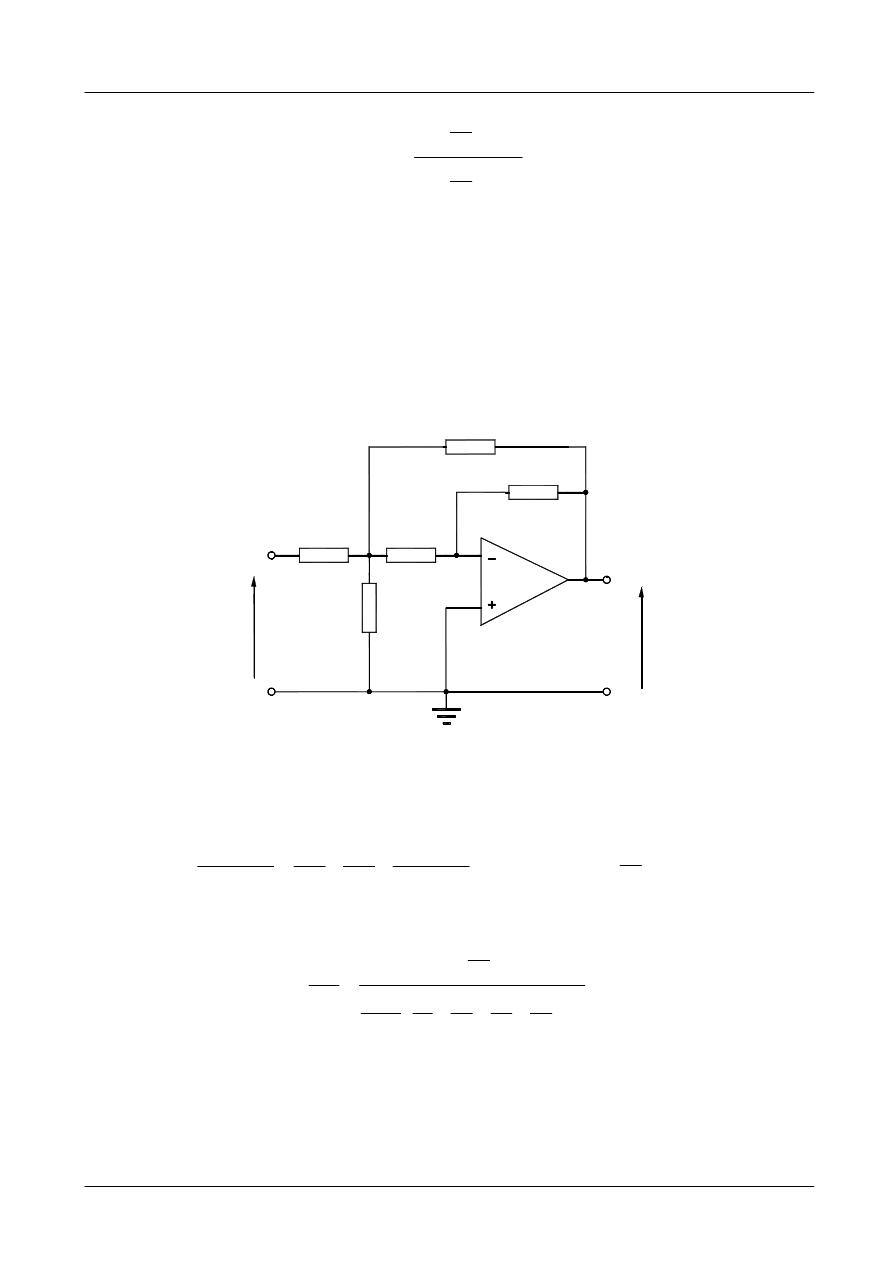
Rozważmy układ jak na rys. 1 ze wzmacniaczem operacyjnym idealnym.
Rys. 1. Struktura filtru z wielokrotnym sprzężeniem zwrotnym.
Transmitancję H(s) układu 1 można wyznaczyć eliminując U
Z4
z układu równań (4.12):
2
4
3
4
4
4
1
4
Z
U
U
Z
U
Z
U
Z
U
U
wy
Z
Z
Z
Z
we
−
+
+
=
−
i
3
5
4
Z
Z
U
U
Z
wy
−
=
4.12
1
1
1
1
1
)
(
4
3
2
1
5
3
2
1
2
+
+
+
+
−
=
=
Z
Z
Z
Z
Z
Z
Z
Z
Z
U
U
s
H
we
wy
4.13
Z
2
Z
5
Z
1
Z
3
U
we
Z
4
U
wy
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
7
Wstawiając we wzorze (4.13): Z
1
= R
1
, Z
2
= R
2,
Z
3
= R
3,
2
4
1
sC
Z =
,
1
5
1
sC
Z =
otrzymamy
transmitancję filtru dolnoprzepustowego z wielokrotnym ujemny sprzężeniem zwrotnym
(MBF – Multiple Feedback Topology):
2
1
3
2
2
3
2
2
2
1
2
2
1
3
2
1
2
1
1
1
1
1
C
C
R
R
s
C
R
C
R
C
R
s
C
C
R
R
R
R
H
LP
+
+
+
+
−
−
=
4.14
o pulsacji biegunów (4.15)
2
1
3
2
0
1
C
C
R
R
=
ω
4.15
i dobroci (4.16)
1
3
2
3
2
1
2
3
2
R
R
R
R
R
C
C
R
R
Q
+
+
=
4.16
Zauważmy, że ω
0
nie zależy od wartości rezystora R
1
, a wzmocnienie filtru dla prądu
stałego wynosi:
1
2
0
R
R
K
U
−
=
, zatem filtr odwraca fazę dla małych częstotliwości.
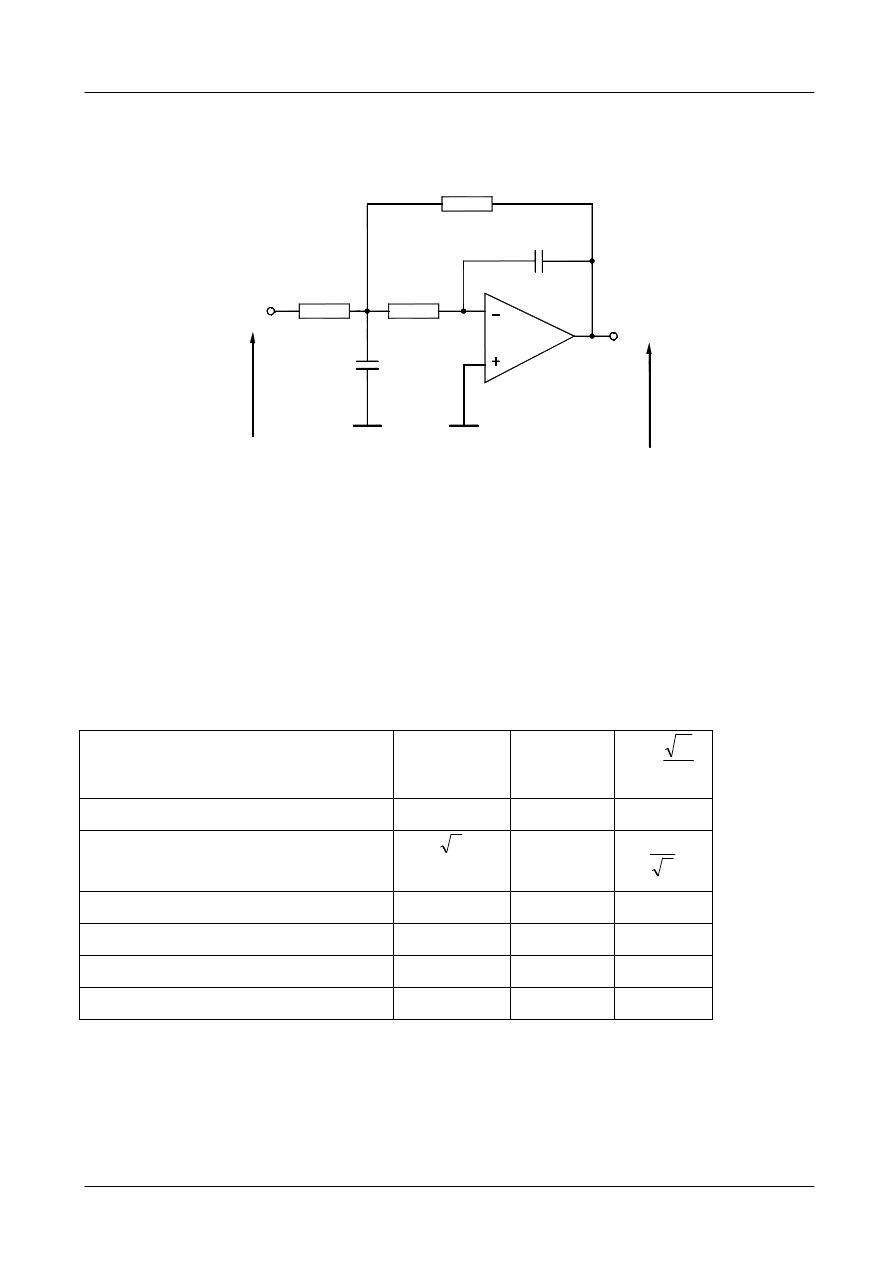
Schemat filtru dolnoprzepustowego odpowiadający transmitancji (4.14)
przedstawiono na rys. 2. Wzory projektowe dla filtru z rys.2 są następujące:
1
2
0
R
R
K
U
−
=
4.17
+
+
=
1
3
2
3
2
1
1
R
R
R
R
R
C
a
g
ω
4.18
3
2
2
1
2
1
R
R
C
C
b
g
ω
=
4.19
Projektowanie tego filtru polega na wyborze kondensatorów C
1
i C
2
z dostępnego
szeregu np. E12 czy E24 spełniających warunek
1
2
1
0
2
)
1
(
4
C
a
K
b
C
U
−
≥
, i obliczeniu
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
8
wartości rezystorów spełniających równania (4.17), (4.18), (4.19). Współczynniki a
1
, b
1
dla różnych typów filtrów rzędu drugiego zebrano w tablicy 1.
Rys. 2. Filtr dolnoprzepustowy z wielokrotnym ujemnym sprzężeniem zwrotnym.
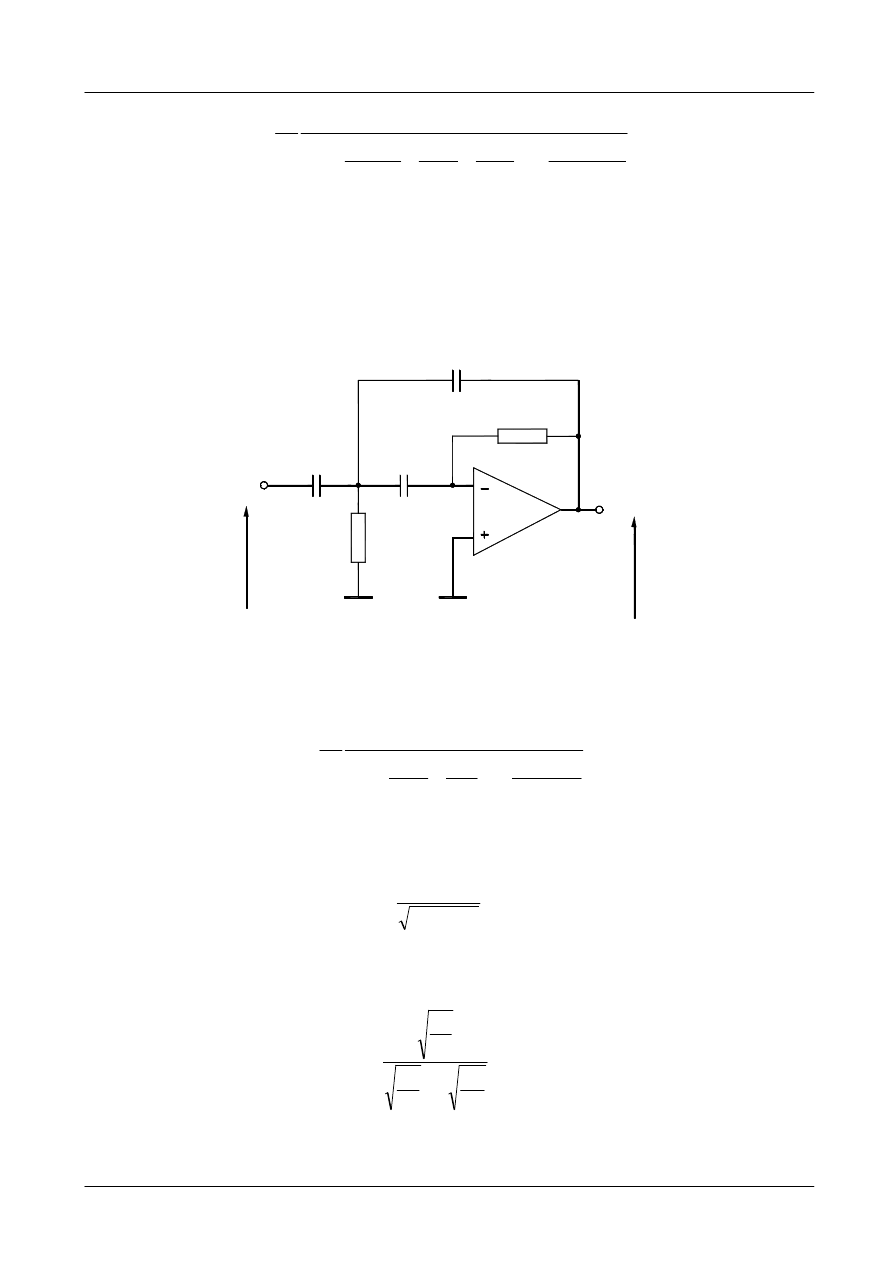
Filtr górnoprzepustowy możemy otrzymać z filtru dolnoprzepustoweg zamieniając
rezystory pojemnościami, a pojemności rezystorami. Schemat filtru górnoprzepustowego
odpowiadający transmitancji (4.12) przedstawiono na rys. 3.
TABELA 1
Współczynniki a
1
, b
1
dla różnych typów filtrów rzędu drugiego.
Typ filtru
a
1
b
1
1
1
a
b
Q =
Filtr o tłumienności krytycznej
1,2872
0,4142
0,5
Filtr Butterwortha
2
1
2
1
Filtr Bessela
1,3617
0,6180
0,577
Filtr Czebyszewa o falistości 1dB
1,3022
1,5515
0,96
Filtr Czebyszewa o falistości 2dB
1,1813
1,77251
1,127
Filtr Czebyszewa o falistości 3dB
1,065
1,9305
1,30
Transmitancja filtru z rys.3 obliczona ze wzoru (4.13) wynosi:
R
2
R
1
R
3
C
1
U
we
C
2
U
wy
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
9
3
2
3
2
3
1
2
1
1
2
1
3
2
2
2
1
1
1
1
C
C
R
R
s
C
R
C
R
C
C
R
C
s
s
C
C
H
HP
+
+
+
+
−
=
4.20
W praktyce najczęściej przyjmuje się w tym filtrze C
1
= C
3
= C. Mamy wówczas
transmitancję:
Rys. 3. Filtr górnoprzepustowy z wielokrotnym ujemnym sprzężeniem zwrotnym.
2
2
1
1
2
1
2
2
2
1
1
2
CC
R
R
s
C
R
C
R
s
s
C
C
H
HP
+
+
+
−
=
4.21
o pulsacji biegunów (4.22)
2
2
1
0
1
CC
R
R
=
ω
4.22
i dobroci (4.23)
2
2
2
1
2
C
C
C
C
R
R
Q
+
=
4.23
C
2
R
1
C
1
C
3
R
2
U
we
U
wy
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
10
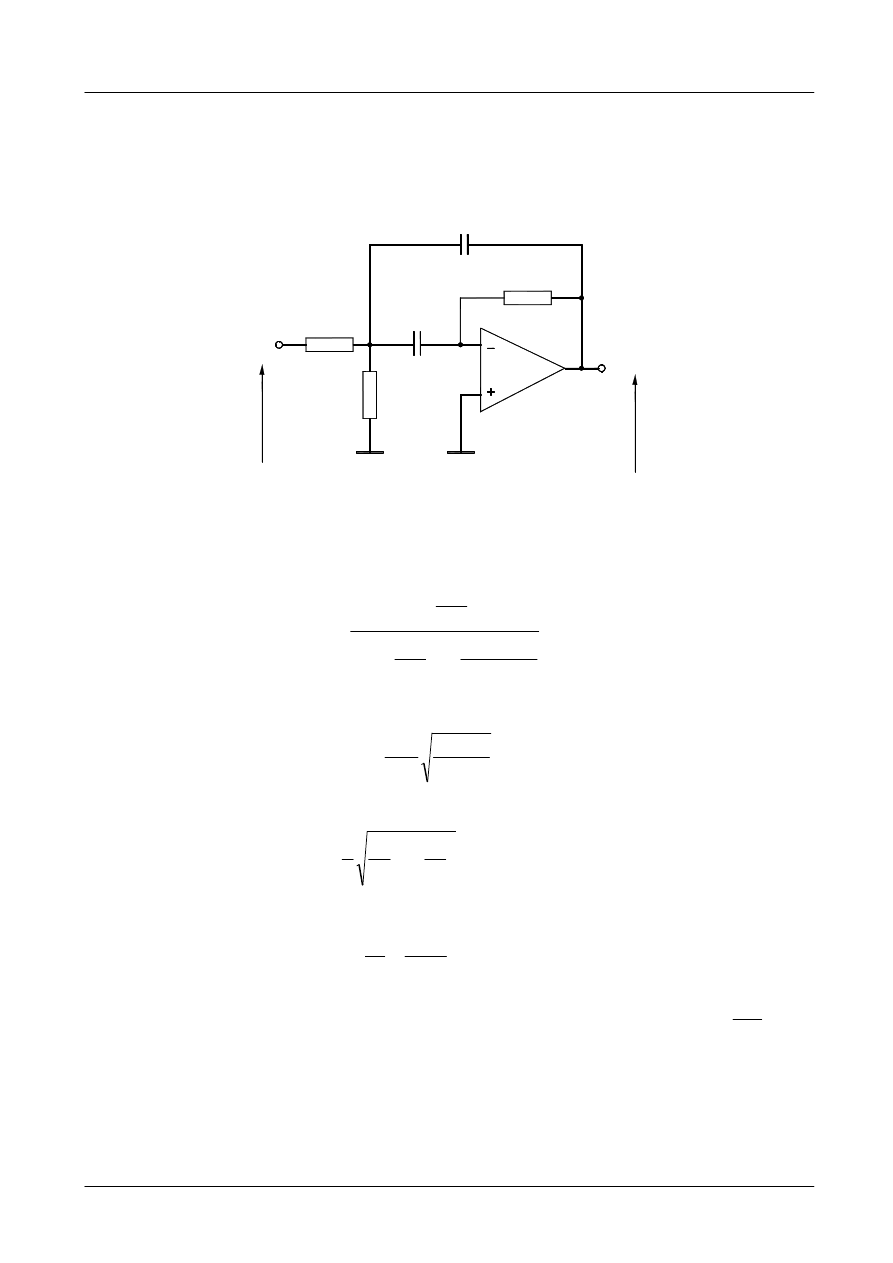
Schemat filtr pasmowoprzepustowego z wielokrotnym ujemnym sprzężeniem
zwrotnym pokazano na rysunku 4. Transmitancję tego filtru dla często spotykanego
rozwiązania, gdy C
1
= C
2
= C przedstawia wzór 4.24).
Rys. 4. Filtr pasmowoprzepustowy z wielokrotnym ujemnym sprzężeniem zwrotnym.
2
3
2
1
3
1
1
2
1
2
C
R
R
R
R
R
s
C
R
s
C
R
s
H
BP
+
+
+
−
=
4.24
a częstotliwość rezonansowa wyniesie:
3
2
1
3
1
2
1
R
R
R
R
R
C
f
r
+
=
π
4.25
dobroć zaś:
r
f
CR
R
R
R
R
Q
2
3
1
1
2
1
2
1
π
=
+
=
4.26
Szerokość pasma wyniesie:
2
1
CR
Q
f
f
r
π
=
=
∆
, nie zależy ona od wartości rezystorów R
1
i
R
3
. Wzmocnienie tego filtru dla częstotliwości rezonansowej wynosi:
1
2
max
2R
R
K
u
−
=
3.2 Filtry aktywne z dodatnim sprzężeniem zwrotnym
C
2
R
2
R1 C
1
R
3
U
we
U
wy
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
11
Do realizacji filtrów dolnoprzepustowych wykorzystuj się najczęściej strukturę
Sallena – Keya (rys. 5) ze wzmacniaczem operacyjnym nieodwracającym i dodatnim
sprzężeniem zwrotnym. Transmitancja układu z rysunku 5 wynosi:
]
)
1
(
[
)
(
)
(
4
2
1
4
2
1
3
4
3
1
Z
K
Z
Z
Z
Z
Z
Z
Z
Z
K
U
U
s
H
U
U
we
wy
−
+
+
+
+
=
=
4.27
Rys. 5. Topologia filtru Sallen – Keya drugiego rzędu.
Wstawiając we wzorze (4.27): Z
1
= R
1
, Z
2
= R
2,
1
3
1
sC
Z =
,
2
4
1
sC
Z =
otrzymamy
transmitancję filtru dolnoprzepustowego z dodatnim sprzężeniem zwrotnym
2
1
2
1
2
2
1
2
1
1
2
2
1
2
1
1
1
1
1
C
C
R
R
s
C
R
K
C
R
C
R
s
C
C
R
R
K
H
U
U
LP
+
−
+
+
+
=
4.28
2
1
2
1
0
1
C
C
R
R
=
ω
4.29
1
1
2
2
2
1
2
1
2
1
)
1
(
C
R
K
C
R
C
R
C
C
R
R
Q
U
−
+
+
=
4.30
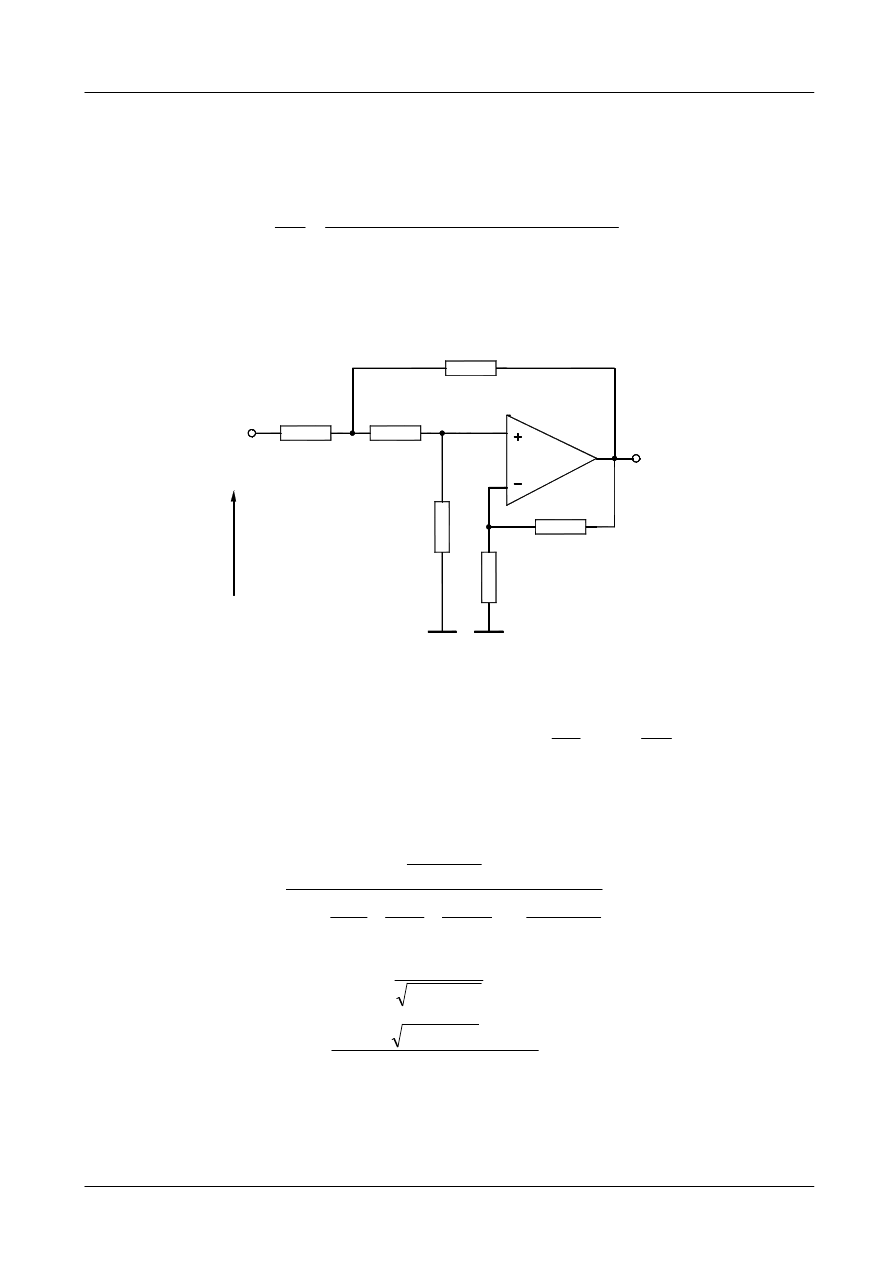
Schemat elektryczny tego filtru pokazano na rysunku 6.
Z
3
Z
1
Z
2
wy
U
we
Z
4
(K
U
– 1)R
R
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
12
Rys. 6. Filtr dolnoprzepustowy Sallen – Keya drugiego rzędu.
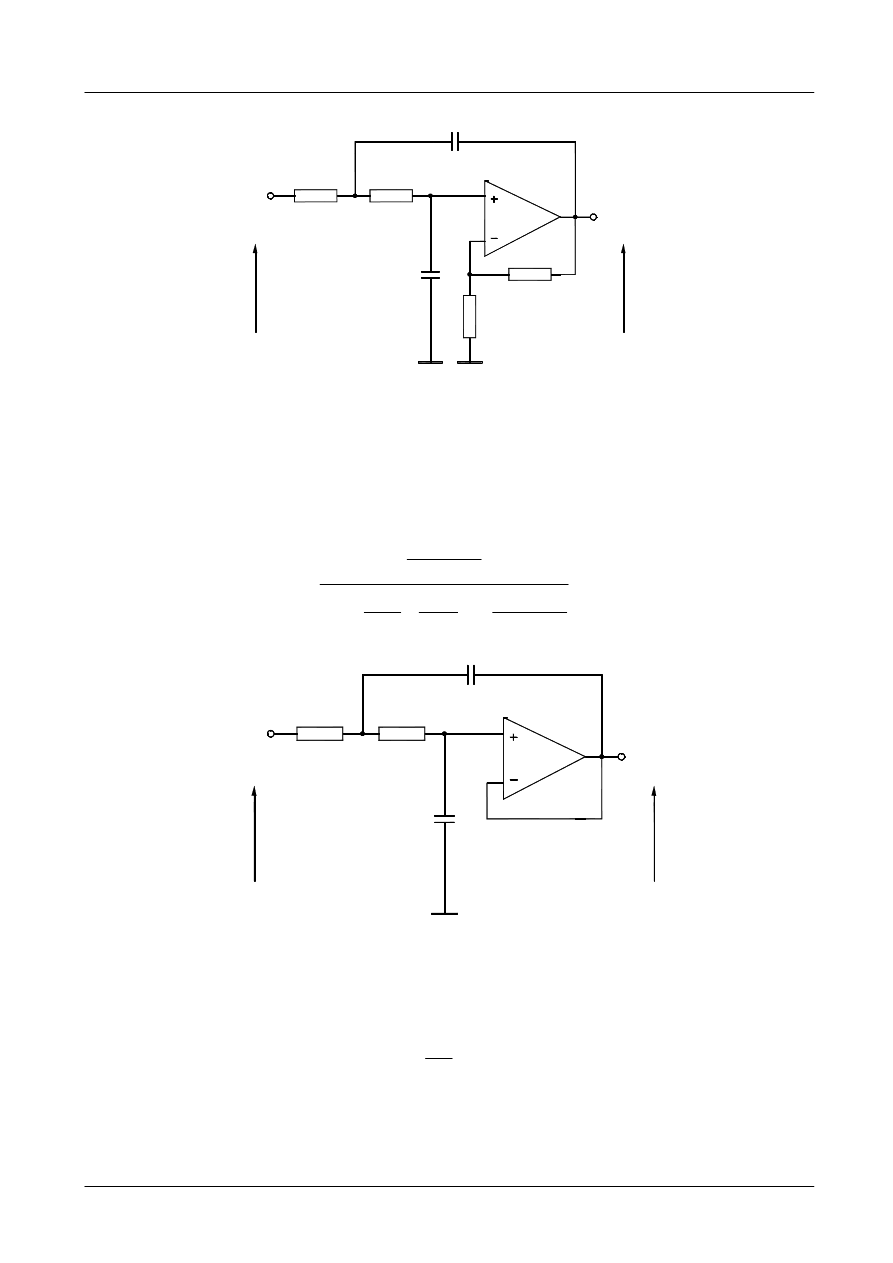
Filtr dolnoprzepustowy Sallen – Keya o wzmocnieniu jednostkowym pokazano na
rysunku 7. Tranmitancja tego filtru wynosi:
2
1
2
1
1
2
1
1
2
2
1
2
1
1
1
1
1
C
C
R
R
s
C
R
C
R
s
C
C
R
R
H
LP
+
+
+
=
4.31
Rys. 7. Filtr dolnoprzepustowy Sallen – Keya o wzmocnieniu jednostkowym.
RC
1
0
=
ω
4.32
C
1
R
1
R
2
U
we
C
2
U
wy
C
1
R
1
R
2
U
we
C
2
U
wy
(K
U
-1)R
R
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
13
2
1
1
2
1
2
R
R
C
C
R
R
Q
+
=
4.33
Ciekawym przypadkiem jest filtr dolnoprzepustowy Sallen – Keya o jednakowych
elementach R
1
= R
2
= R, C
1
= C
2
= C, mamy wówczas:
2
2
2
)
(
1
2
)
(
RC
s
RC
s
RC
K
H
U
LP
+
+
=
4.34
RC
1
0
=
ω
4.35
U
K
Q
−
=
3
1
4.36
Jak wynika ze wzoru (4.36) dobroć tego filtru nie zależy od wartości elementów
RC. Regulując wzmocnienie K
U
możemy zmieniać dobroć Q a tym samym typ filtru
dolnoprzepustowego. Wzmocnienie K
U
dla różnych typów filtrów o strukturze Sallen
– Keya zebrano w tabeli 2
TABELA 2
Wzmocnienie K
U
dla różnych typów filtrów rzędu drugiego.
Typ filtru
Q
K
U
Filtr o tłumienności krytycznej
0,5
1
Filtr Butterwortha
2
1
1,586
Filtr Bessela
0,577
1,205
Filtr Czebyszewa o falistości 1dB
0,96
1,958
Filtr Czebyszewa o falistości 2dB
1,127
2,113
Filtr Czebyszewa o falistości 3dB
1,30
2,230
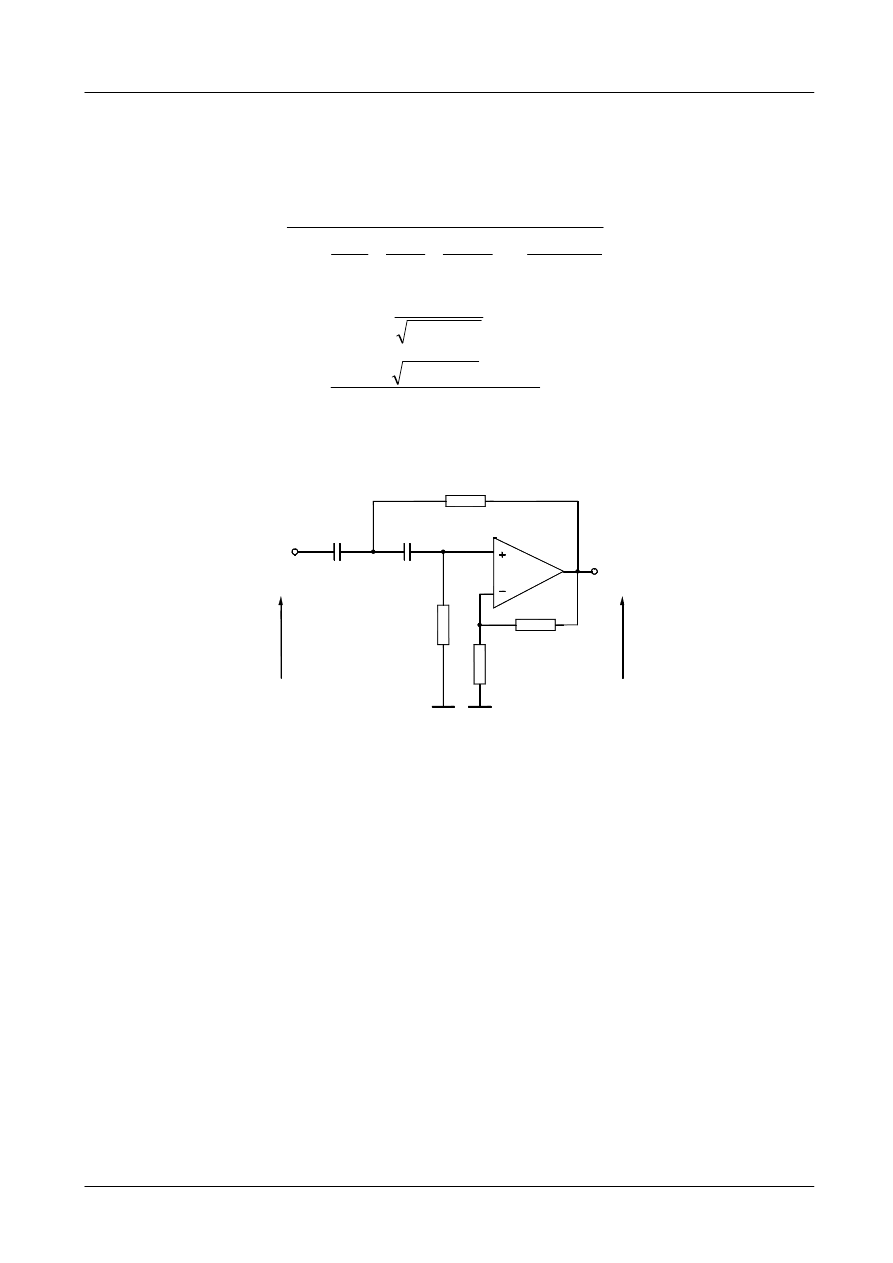
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
14
Filtr górnoprzepustowy o strukturze Sallen- Keya otrzymamy zamieniając
miejscami kondensatory z rezystorami w filtrze dolnoprzepustowym z rysunku 7.
Transmitancja tego filtru jest określona wzorem (4.37).
2
1
2
1
1
2
2
1
1
1
2
2
1
1
1
1
C
C
R
R
s
C
R
K
C
R
C
R
s
s
K
H
U
U
HP
+
−
+
+
+
=
4.37
2
1
2
1
0
1
C
C
R
R
=
ω
4.38
2
1
2
2
1
2
2
1
2
1
)
1
(
C
R
K
C
R
C
R
C
C
R
R
Q
U
−
+
+
=
4.39
Rys. 8. Filtr górnoprzepustowy Sallen – Keya drugiego rzędu.
W praktyce spotyka się najczęściej dwa rozwiązania tego filtru o wzmocnieniu
jednostkowym oraz jednakowych elementach R, C. Charakterystyka częstotliwościowa
filtru górnoprzepustowego jest lustrzanym odbiciem charakterystyki częstotliwościowej
filtru dolnoprzepustowego.
4. Filtry z przełączanymi pojemnościami
Filtry z pojemnościami przełączanymi (C –przełączane lub SC – ang. Switched
Capacitor) realizuje się najczęściej jako układy scalone w technologii CMOS. W
układach tych rezystory i indukcyjności symuluje się kondensatorami przełączanymi
kluczami analogowymi (tranzystory MOSFET).
R
2
C
1
C
2
U
we
R
1
U
wy
(K
U
-1)R
R
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
15
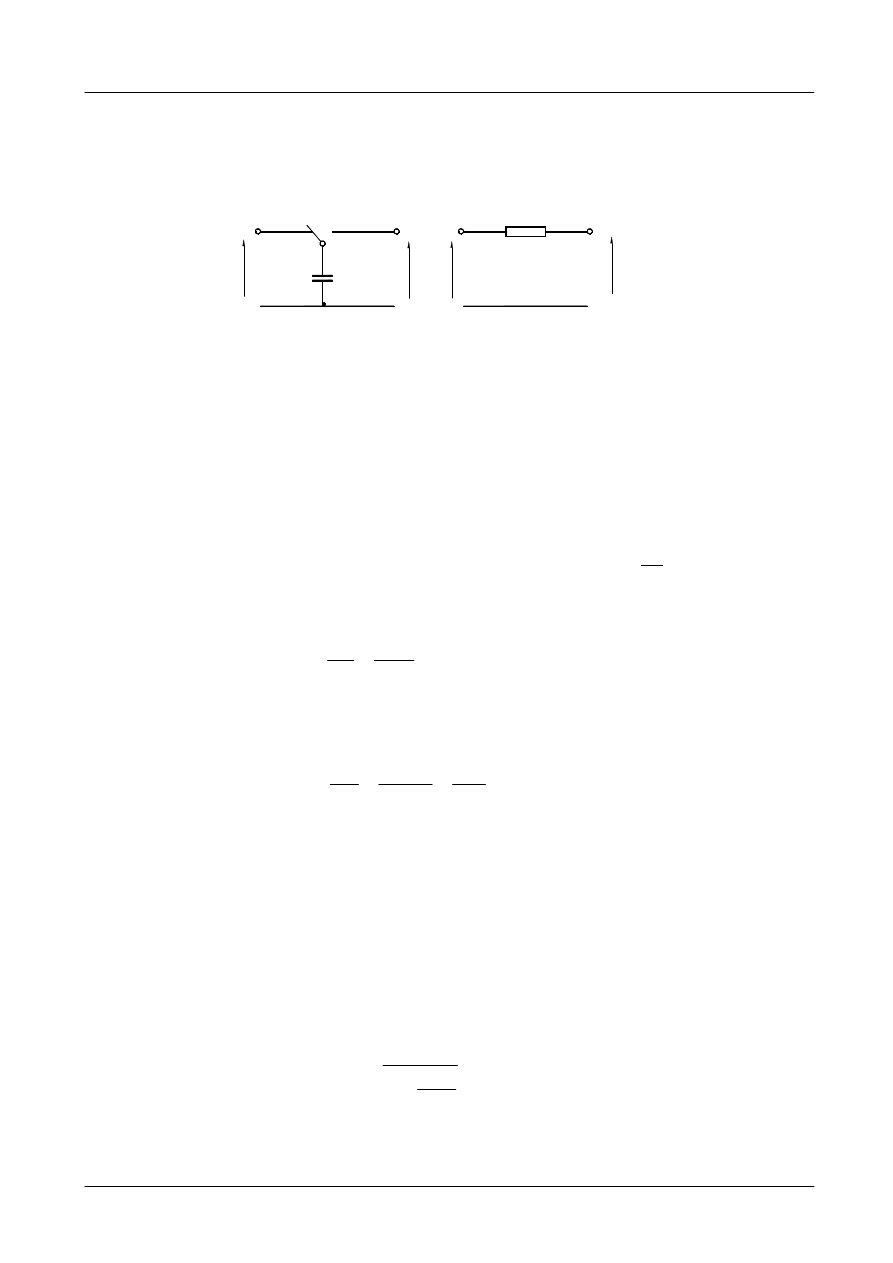
Na rys.1 pokazano strukturę SC z kluczem przełączanym do symulacji
rezystancji.
Rys.1 Układ SC symulujący rezystancję z kondensatorem równoległym.
Kondensator C jest przełączany między końcówkami 1 i 2 kluczem K z
częstotliwością f
p.
Gdy kondensator jest dołączony do końcówki 1 gromadzi ładunek
elektryczny Q
1
= CU
1
. Po dołączeniu kondensatora do końcówki 2 ładunek zgromadzony
w kondensatorze wyniesie Q
2
= CU
2,
przełączenie klucza powoduje przepływ ładunku ∆Q
= C(U
1
– U
2
) = C∆U. Ponieważ klucz jest przełączany z okresem
p
p
f
T
1
=
, prąd jaki
przepłynie od końcówki 1 do końcówki 2 wyniesie:
C
Uf
T
U
C
t
Q
I
p
p
∆
=
∆
=
∆
∆
=
4.1
Symulowana rezystancja odpowiadająca temu przepływowi ładunku elektrycznego
będzie równa :
C
f
C
Uf
U
I
U
R
p
p
1
=
∆
∆
=
∆
=
4.2
Jak wynika ze wzoru (4.2) wartość symulowanej rezystancji może być regulowana przez
zmianę częstotliwości f
p
generatora przełączającego klucz K. Przełączany klucz K można
zastąpić dwoma kluczami zwiernymi sterowanych na przemian: K1 zwarty K2 otwarty i
odwrotnie: K1 otwarty K2 zwarty. W układach SC klucze sterowane są sygnałami
zegarowymi które nie nakładają się na siebie, aby w trakcie przełączania nie
następowała utrata ładunku kondensatora.
Prosty filtr SC dolnoprzepustowy rzędu pierwszego pokazano na rys.2.
1
2
1
1
)
(
C
f
C
s
s
H
p
+
=
4.3
Częstotliwość górna tego filtru wynosi:
K R
1 2 1 2
U
1
C U
2
U
1
U
2
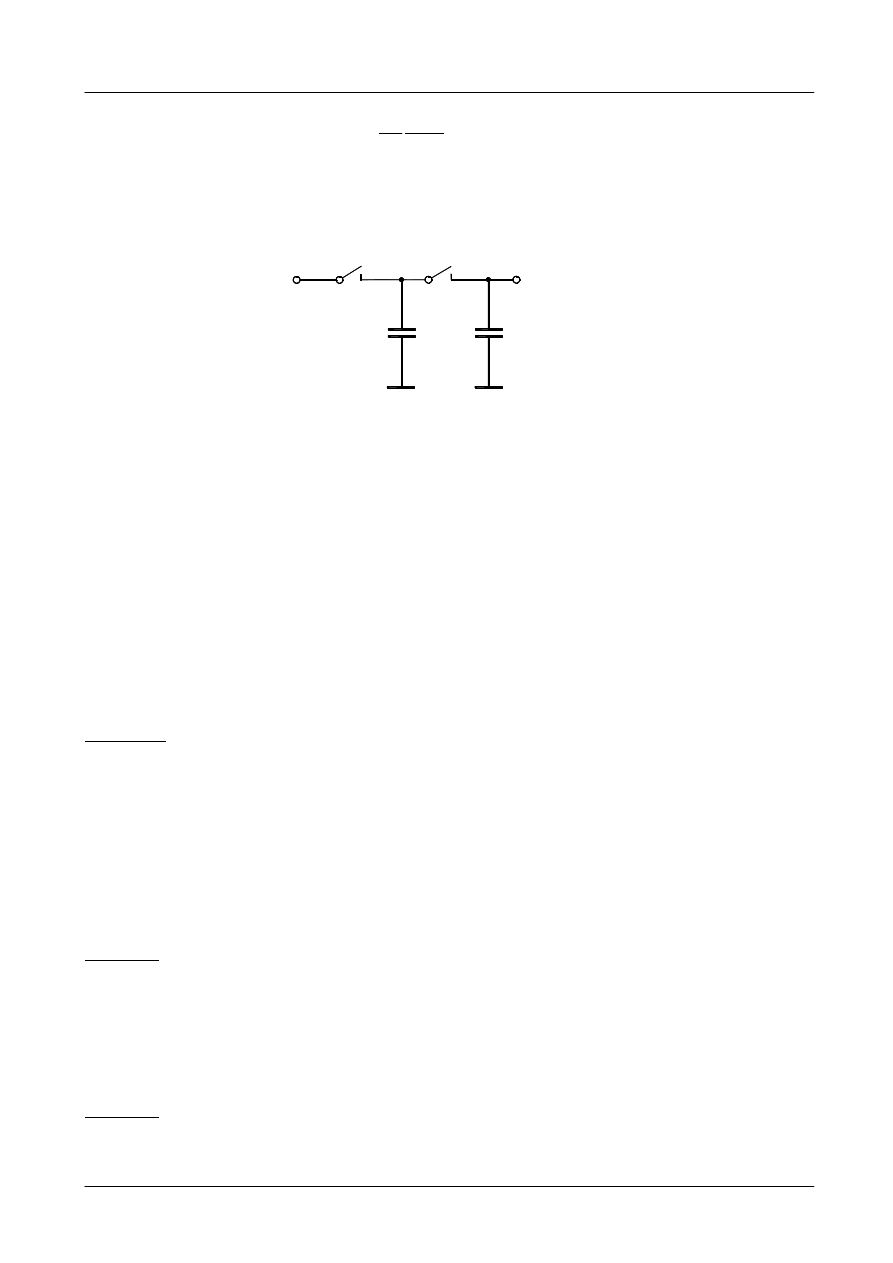
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
16
21
1
2
1
C
C
f
f
p
g
π
=
4.4
Jak wynika ze wzoru (4.4) częstotliwość górna tego filtru może być regulowana
elektronicznie przez zmianę częstotliwości f
p
generatora .
Rys.2 Filtr SC dolnoprzepustowy rzędu pierwszego.
Sygnał na wejściu filtrów SC nie powinien zawierać składowych o
częstotliwościach leżących powyżej 0,5f
P
. Sygnał na wyjściu filtru zawsze ma kształt
schodkowy zawiera więc składowe widma częstotliwościowego związanego
z częstotliwością przełączania kluczy.
5. Zadania projektowe
Projekt 1.
Zaprojektować filtr dolnoprzepustowy Butterwortha drugiego rzędu o wzmocnieniu
dla składowej stałej :
K
U0
= -1, -2 .-3, -4, -5 V/V - (wybór przez prowadzącego)
i częstotliwości górnej: f
g
= 1, 3, 5 7, 10 kHz . - (wybór przez prowadzącego),
wykorzystując filtr uniwersalny UAF42 firmy Burr-Brown
Projekt 2.
Zaprojektować filtr dolnoprzepustowy Bessela drugiego rzędu o wzmocnieniu dla
składowej stałej : K
U0
= -1 V/V
i częstotliwości górnej: f
g
= 1, 3, 5 7, 10 kHz . - (wybór przez prowadzącego),
wykorzystując filtr uniwersalny UAF42 firmy Burr-Brown
Projekt 3.
K1 K2
C
1
C
2
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
17
Zaprojektować filtr dolnoprzepustowy Czebyszewa o falistości 3 dB drugiego rzędu o
wzmocnieniu dla składowej stałej : K
U0
= -1 V/V
i częstotliwości górnej: f
g
= 1, 3, 5 7, 10 kHz . - (wybór przez prowadzącego),
wykorzystując filtr uniwersalny UAF42 firmy Burr-Brown
Projekt 4.
Zaprojektować filtr środkowoprzepustowy drugiego rzędu o wzmocnieniu dla
częstotliwości rezonansowej K
Umax
= 5 V/V i częstotliwości środkowej:
a) f
r
= 1 kHz i szerokości pasma ∆f = 100 Hz
b) f
r
= 1 kHz i szerokości pasma ∆f = 200 Hz
c) f
r
= 3 kHz i szerokości pasma ∆f = 400 Hz
d) f
r
= 3 kHz i szerokości pasma ∆f = 500 Hz
e) f
r
= 5 kHz i szerokości pasma ∆f = 1000 Hz (wybór przez prowadzącego),
wykorzystując filtr uniwersalny UAF42 firmy Burr-Brown.
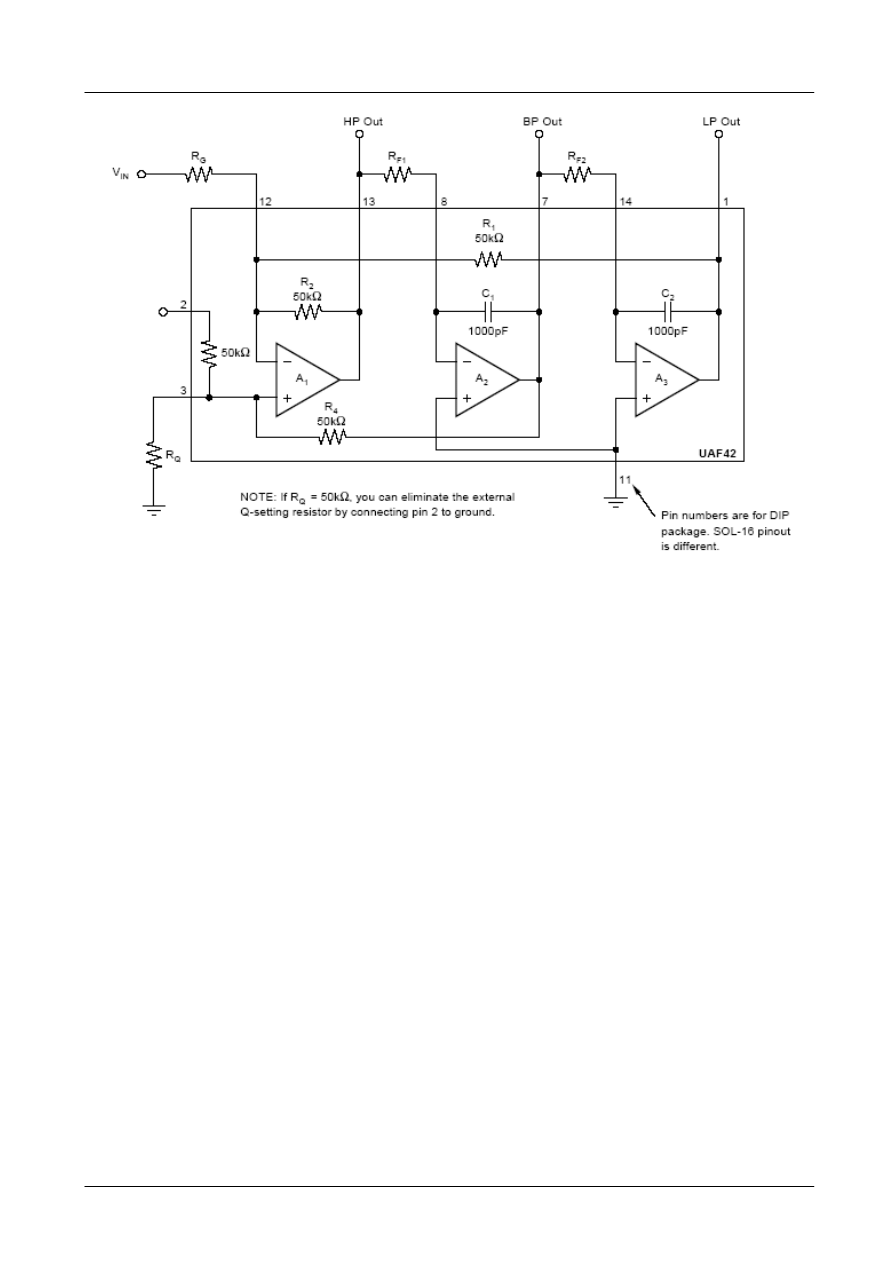
Schemat filtru UAF42 z zewnętrznymi rezystorami i wzory projektowe
zaczerpnięto z firmowej noty aplikacyjnej i przedstawiono poniżej.
2
1
2
1
1
2
2
C
C
R
R
R
R
F
F
n
⋅
⋅
⋅
⋅
=
ϖ
4.40
2
1
2
2
2
1
1
1
2
1
4
1
1
1
1
1
⋅
⋅
⋅
⋅
⋅
+
+
⋅
+
=
C
R
R
R
C
R
R
R
R
R
R
Q
F
F
G
Q
4.41
G
LP
R
R
A
1
=
4.42
G
LP
HP
R
R
A
R
R
A
2
1
2
=
=
4.43
+
+
⋅
⋅
+
=
G
G
Q
BP
R
R
R
R
R
R
A
1
1
1
1
1
2
1
4
4.44
2
/
1
2
2
2
1
1
1
2
1
=
=
C
R
R
C
R
R
A
R
R
QA
QA
F
F
BP
HP
LP
4.45
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
18
Rys. 9. Filtr uniwersalny UAF42 firmy Burr-Brown.
6. Przebieg ćwiczenia
Przed rozpoczęciem pomiarów zapoznać się z instrukcja obsługi oscyloskopu
cyfrowego i generatora. Zmontować zgodnie z projektem obliczone rezystory R
Q
, R
F1
,
R
F2
, R
G
w filtrze UAF42. Podłączyć generator i oscyloskop do badanego filtru , włączyć
napięcia zasilające makietę pomiarową z filtrami. Sygnał z generatora ustawić na około
500 mV V
pp
,
zmieniając częstotliwość generatora zmierzyć charakterystykę
amplitudową i fazową zaprojektowanego filtru .Sposób pomiaru przesunięcia fazowego
podano w dodatku A z ćwiczenia nr 2.
Zmierzyć odpowiedź filtru na sygnał fali prostokątnej o wypełnieniu 50% i
amplitudzie 1V i wyznaczyć czas narastania t
r
i czas opadania t
f
(rys.10). Częstotliwość
generatora ustawić kilkakrotnie razy mniejszą od częstotliwości górnej filtru a dla filtru
pasmowoprzepustowego ustawić częstotliwość środkową.
Zmierzyć i wykreślić charakterystykę Uwy = f(Uwe) filtru dla kilku częstotliwości
leżących w paśmie przepustowym.
Wykonać powyższe pomiary jednego z trzech filtrów dolnoprzepustowych
makiety pomiarowej.
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
19
Na podstawie pomiarów wykreślić charakterystyki amplitudowe i fazowe
badanych filtrów Wyznaczyć wzmocnienia i częstotliwości górne lub środkowe filtrów .
Dla filtru pasmowoprzepustowego wyznaczyć szerokość pasma i dobroć Q.
6.1 Pomiary filtru C- przełączane
1. Włączyć zasilanie makiety
±
18 V.
2. Na wejście f
p
podać sygnał prostokątny 0
÷
5V o wypełnieniu 0,5. Zakres
częstotliwości przełączających 1 kHz do 100 kHz.
3. Podłączyć kanał 1 oscyloskopu na wejście filtru (wyjście wzmacniacza
różnicowego), kanał 2 oscyloskopu do wyjścia filtru.
4. Podłączyć drugi generator sygnałowy do wzmacniacza różnicowego
wzmocnieniu 1. ( Sygnał z wyjścia tego wzmacniacza mierzony oscyloskopem
jest dla filtru C-przełączane sygnałem wejściowym).
5. Zmierzyć charakterystyki częstotliwościowe filtru dla kilku częstotliwości
przełączania
(Sygnał generatora ustawić na około 1 V
pp
).
6. Zmierzyć zależności: U
we
=f(U
wy
) dla kilku częstotliwości przełączających
i U
wy
= f(f
P
) dla U
we
= 1 V
pp
, f =100 Hz.
7. Dokonać pomiaru odpowiedzi filtru na sygnał fali prostokątnej o
wypełnieniu 0,5 i amplitudzie 1V, wyznaczyć czas narastania t
r
i czas
opadania t
f
, częstotliwość generatora ustawić kilkakrotnie razy mniejszą od
częstotliwości górnej filtru.
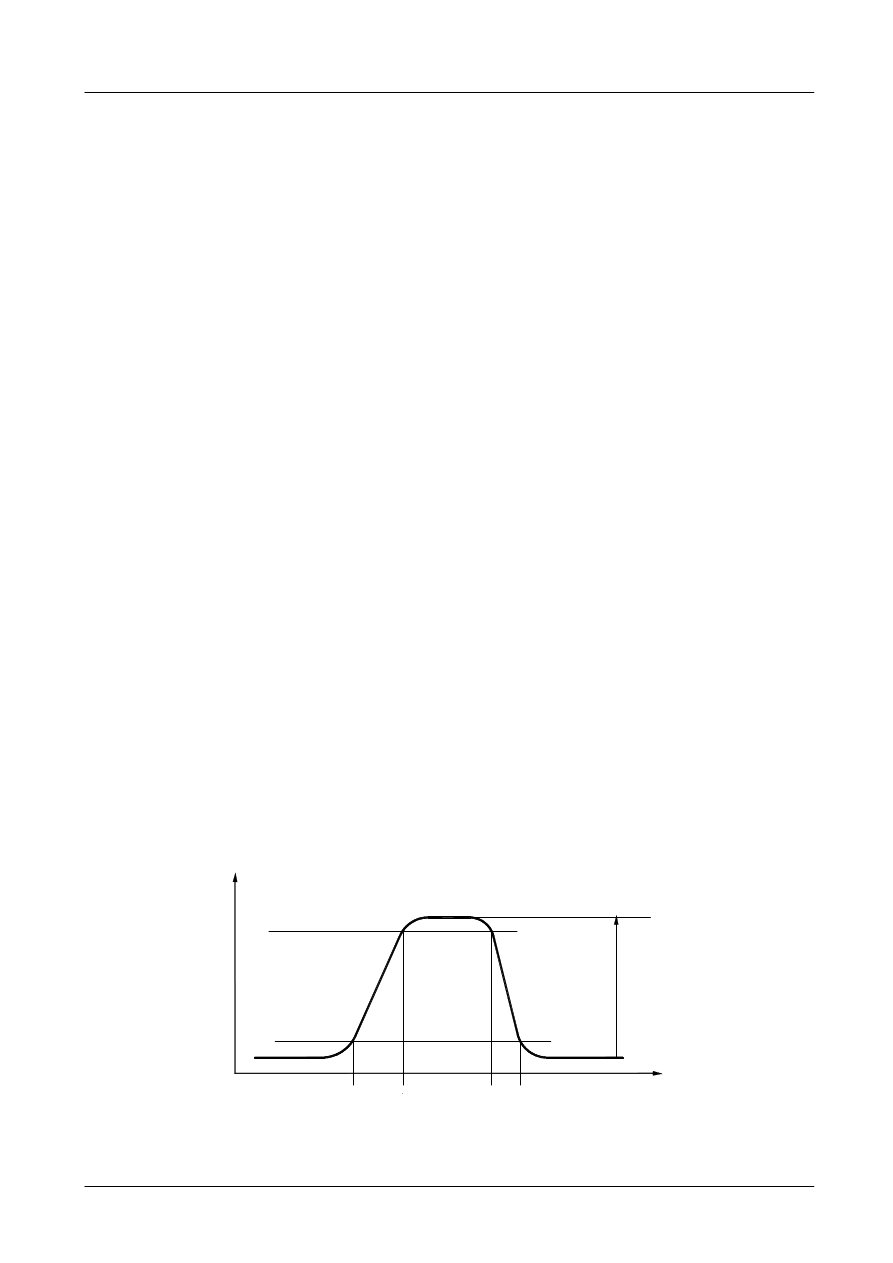
Sposób pomiaru oscyloskopem czasu narostu t
r
i czasu opadania impulsu t
f
pokazano na rysunku 10.
Rys. 10. Czas narostu t
r
i czas opadania t
f
impulsu.
U
90% U
m
U
m
10% U
m
t
r
t
f
t
Wydział Elektroniki Mikrosystemów i Fotoniki, Politechnika Wrocławska
Laboratorium układów elektronicznych
Ćwiczenie numer 4: Filtry aktywne
20