Elektrodynamika - wykład 9

1

Wnioski z równań Maxwella.

Najpierw pokażemy, ze poprzednio omawiane trudności znikają po wprowadzeniu prądu przesunięcia.

Ad.1

Biorąc dywergencję równania

∇ · (∇ × B) = 0 = µ

0

∇ · J + µ

0

ε

0

∂∇ · E

∂t

= µ

0

∇ · J + µ

0

∂ρ

∂t

= µ

0

(∇ · J +

∂ρ

∂t

) = 0

z uwagi na zasadę zachowania ładunku elektrycznego.

Ad.2

W przypadku kondensatora płaskiego wiemy, że:

E =

σ

ε

0

=

Q

Aε

0

oraz

∂E

∂t

=

1

Aε

0

∂Q

∂t

=

I(t)
Aε

0

skąd:

Z

Sj

(∇ × B) · dS =

Z

S

j

(µ

0

J + µ

0

ε

0

∂E

∂t

)dS =

(

µ

0

I

gdy j=1

µ

0

ε

0

dE

dt

A gdy j=2

ale µ

0

ε

0

dE

dt

A = µ

0

ε

0

I

Aε

0

A = µ

0

I i wszystko się nam już zgadza.

Możemy teraz odwrócić kierunek myślenia przyjmując równania Maxwella jako postulat i patrzeć jakie
wnioski z nich płyną.

(1) po pierwsze z naszych rachunków od razu wynika równanie ciągłości

∇ · J +

∂ρ

∂t

= 0

co oznacza, że równania Maxwella mają wbudowaną zasadę zachowania ładunku elektrycznego.

1

(2) obliczamy pełną moc wydatkowaną przy przemieszczaniu się ładunków elektrycznych w pewnym
(skończonym) obszarze:

dW

dt

=

Z

V

JEd

3

r =

1

µ

0

Z

V

(∇ × B)Ed

3

r − ε

0

Z

V

∂E

∂t

Ed

3

r.

Stosując odpowiednią tożsamość wektorową otrzymujemy:

dW

dt

= −

ε

0

2

∂

∂t

Z

V

E

2

d

3

r +

1

µ

0

Z

V

B(∇ × E)d

3

r −

1

µ

0

Z

V

∇ · (E × B)d

3

r.

Przechodząc w ostatniej całce do całki po brzegu obszru:

dW

dt

= −

ε

0

2

∂

∂t

Z

V

E

2

d

3

r −

1

2µ

0

∂

∂t

Z

V

B

2

d

3

r −

1

µ

0

Z

∂V

(E × B)dS.

Taka postać naszego równania sugeruje wprowadzenie pojęcia gęstości energii magnetycznej oraz elek-

trycznej:

u

magn

:=

1

2µ

0

B

2

(1)

oraz

u

el

:=

ε

0

2

E

2

(2)

i ostatecznie

d

dt

Z

V

(u

mech

+ u

magn

+ u

el

)d

3

r = −

1

µ

0

Z

∂V

(E × B)dS.

Lewa strona tego równania opisuje całkowitą zmianę energii z w wybranym obszarze. Zatem całka po

prawej stronie musi być równa wypływowi energii z tegoż obszaru przez jego brzeg. Wektor:

S :=

1

µ

0

E × B

(3)

nazywamy wektorem Poyntinga. Ma on nastepujący wymiar:

[S] =

J

m

2

s

.

Przykład

Obliczamy wektor Poyntinga na powierzchni drutu oporowego przez który płynie prąd. Chodzi o to by

2

stwierdzić ile energii przypływa albo wypływa z drutu w jednostce czasu? Następnie porównamy uzyskaną
wielkość z ciepłem Joula-Lenza.

..

(3) Najbardziej doniosłą konsekwencją równań Maxwella jest występowanie bardzo szczególnych rozwiązań
w postaci fal elektromagnetycznych. Najpierw zbadamy ich własności w próżni.

Obliczamy:

∂

2

B

∂t

2

=

∂

∂t

(∇ × E) = −∇ ×

∂E

∂t

= −∇ × (

1

µ

0

ε

0

∇ × B)

następnie korzystając ze wzoru na rotację rotacji:

∂

2

B

∂t

2

= −

1

µ

0

ε

0

[∇(∇ · B) − ∇

2

B]

ponieważ ∇ · B = 0 więc ostatecznie otrzymujemy poszukiwane równanie falowe:

∂

2

B

∂t

2

−

1

µ

0

ε

0

∇

2

B = 0.

(4)

Postępując zupełnie analogicznie z polem elektrycznym dostajemy równanie postaci:

∂

2

E

∂t

2

−

1

µ

0

ε

0

∇

2

E = 0

(5)

Teraz spóbujemy zastanowić się nad interpretacją fizyczną rozwiązań tych równań. Zaczniemy od anal-

izy takiego równania w jednym wymiarze, gdzie dla pewnej funkcji f będzie miało ono postać:

∂

2

f

∂t

2

− α

∂

2

f

∂x

2

= 0

gdzie α jest pewną stałą.
Twierdzimy, że ogólne rozwiązanie tego równania jest postaci

f (x; t) = A

1

(x − vt) + A

2

(x + vt),

gdzie A

j

∈ C

2

są dwiema dowolnymi funkcjami. Wówczas

∂

2

f

∂t

2

= (A

00

1

(x − vt) + A

00

2

(x + vt))v

2

3

oraz

∂

2

f

∂x

2

= A

00

1

(x − vt) + A

00

2

(x + vt)

i po wstawieniu do naszego równania otrzymujemy warunek

v

2

− α = 0.

t

t+

0

t

v

Na rys. powyżej: rozwiązanie A

1

(x − vt)

Stąd wniosek - na podstawie bliższej analizy odpowiedniego rysunku - że v mozna interpretować jako

prędkość rozchodzenia się zaburzenia oraz, że tę rolę w przypadku fale elektromagnetycznych spełnia
wielkość:

c

2

=

1

µ

0

ε

0

(6)

zwana prędkością światła w próżni.

Szczególnym przypadkiem rozwiązań równań falowych są tzw. fale płaskie, które określamy następująco:

E(r; t) = E

0

exp i(kr − ωt)

(7)

oraz

B(r; t) = B

0

exp i(kr − ωt)

(8)

Po wstawieniu tych wielkosci do równań falowych i obliczeniu drugich pochodnych otrzymamy następujący
zwiazek:

ω

2

=

k

2

µ

0

ε

0

= c

2

k

2

.

4

Wygodnie jest zapisywać pola w postaci zespolonej. Oczywiście zawsze będziemy rozumieć, że fizyczne

pola to części rzeczywiste z wprowadzonych wielkości.

2

Płaskie fale elektromagnetyczne

Na poprzednim wykładzie wyprowadzone zostało równanie falowe dla fali elektromagnetycznej:

(4 − ε

0

µ

0

∂

2

∂t

2

) ~

E = 0.

(9)

W dalszym ciągu interesuje nas szczególny rodzaj rozwiązania tego równania, mianowicie postaci:

~

E(~r, t) = ~

E

0

e

i(~k~r−ωt)

,

(10)

gdzie

ω

2

=

~k

2

ε

0

µ

0

.

(11)

To nasze zainteresowanie wynika głównie z faktu, że każde rozwiązanie równania (9) da się przedstawić

jako granicę superpozycji rozwiązań postaci (10). Falę, która wyraża się równaniem (10), nazywamy falą
płaską.

Wyprowadźmy najpierw zależność na prędkość fazową V

f

fali płaskiej w kierunku jej rozchodzenia się.

Przyjmijmy, że fala rozchodzi się w kierunku osi OX (~k = (k

x

, 0, 0), k

x

> 0). Z definicji jest to predkość

rozchodzenia się stałej fazy, czyli musimy mieć

~k~r − ωt = k

x

x − ωt = const

(12)

różniczkując obustronnie po czasie otrzymujemy

k

x

V

f

− ω = 0

(13)

czyli ponieważ fala rozchodzi się wzdłuż osi OX, to

V

f

=

ω

k

.

(14)

Porównując teraz powyższą zależność z zależnością (11) i wykorzystując fakt, że c =

1

√

µ

0

ε

0

otrzymujemy,

że V

f

= c.

W celu wyprowadzenia innych własności fali płaskiej rozważmy równania Maxwella dla próżni pozbaw-

ionej prądów i ładunków:

~

5 · ~

E = 0

~

5 × ~

E = −

∂ ~

B

∂t

~

5 · ~

B = 0

~

5 × ~

B = ε

0

µ

0

∂ ~

E

∂t

5

Wiemy, że występowanie fali elektromagnetycznej związane jest z drganiami pola ~

E i ~

B. Przyjmijmy

teraz, że w rozważanej przez nas przestrzeni występują tylko dwa drgania:

1. drganie pola ~

E

~

E(~r, t) = ~

E

0

e

i( ~

k

1

~r−ω

1

t)

(15)

2. drganie pola ~

B

~

B(~r, t) = ~

B

0

e

i( ~

k

2

~r−ω

2

t)

(16)

Oba te drgania spełniają równanie falowe, pozostaje nam tylko zobaczyć, jakie warunki nakłada

konieczność spełniania przez nie równań Maxwella.

Po pierwsze mamy

~

5 · ~

E = i ~

k

1

· ~

E, ~

5 × ~

E = −i ~

k

1

× ~

E,

(17)

zaś

~

5 · ~

B = i ~

k

2

· ~

B, ~

5 × ~

B = −i ~

k

2

× ~

B.

(18)

Z równań Maxwella wiemy, że

~

5 · ~

E = i ~

k

1

· ~

E = 0, ~

5 · ~

B = i ~

k

2

· ~

B = 0

(19)

czyli zarówno drgania pola ~

E jak i ~

B są prostopadłe do kierunku ich propagacji czyli fale elektro-

magnetyczne są poprzeczne.

Z drugiej pary równań Maxwella otrzymujemy, że

~

5 × ~

E = i ~

k

1

× ~

E = −

∂ ~

B

∂t

= iω

2

~

B, ~

5 × ~

B = i ~

k

2

× ~

B = ε

0

µ

0

∂ ~

E

∂t

= −iε

0

µ

0

ω

1

~

E

(20)

czyli

~

k

1

× ~

E = ω

2

~

B

(21)

~

k

2

× ~

B = −ε

0

µ

0

ω

1

~

E

(22)

Przyjrzyjmy się teraz równaniu (21), wstawmy do niego postacie drgań ~

E i ~

B. Otrzymamy wtedy

równość

i ~

k

1

× ~

E

0

e

i( ~

k

1

~r−ω

1

t)

= ω

2

~

B

0

e

i( ~

k

2

~r−ω

2

t)

.

(23)

Ponieważ po obu stronach mamy funkcje okresowe, to ich okresy muszą być równe czyli

~

k

1

~r − ω

1

t = ~

k

2

~r − ω

2

t

(24)

korzystając teraz z dowolności ~r i t dostajemy, że

~

k

1

= ~

k

2

= ~k, ω

1

= ω

2

= ω.

(25)

6

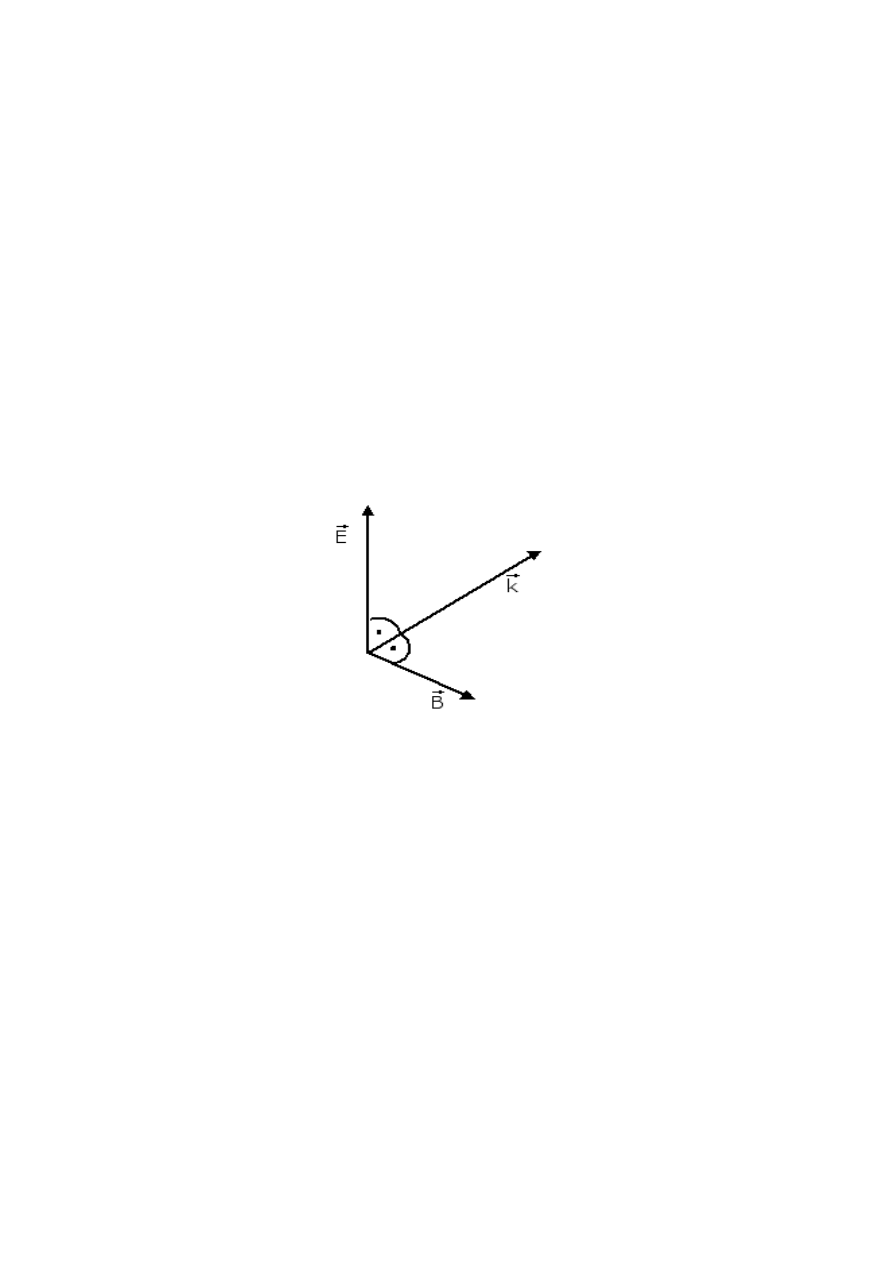
Czyli te drgania muszą mieć tę samą częstość i rozchodzić się w tym samym kierunku. A zatem ~

E i ~

B

leżą w płaszczyźnie prostopadłej do ~k.

Co więcej po wstawieniu wniosków (25) do równania (23) otrzymujemy

~k × ~

E

0

= ω ~

B

0

(26)

czyli wobec prostopadłości ~

E

0

, ~

B

0

do wektora ~k mamy

−k(E

0

)

y

= ω(B

0

)

x

, −k(E

0

)

x

= ω(B

0

)

y

(27)

czyli pola ~

E i ~

B są do siebie prostopadłe i ich amplitudy powiązane są zależnością

E

0

= cB

0

.

(28)

Czwarte równanie Maxwella nie wnosi żadnych dodatkowych ograniczeń.

7