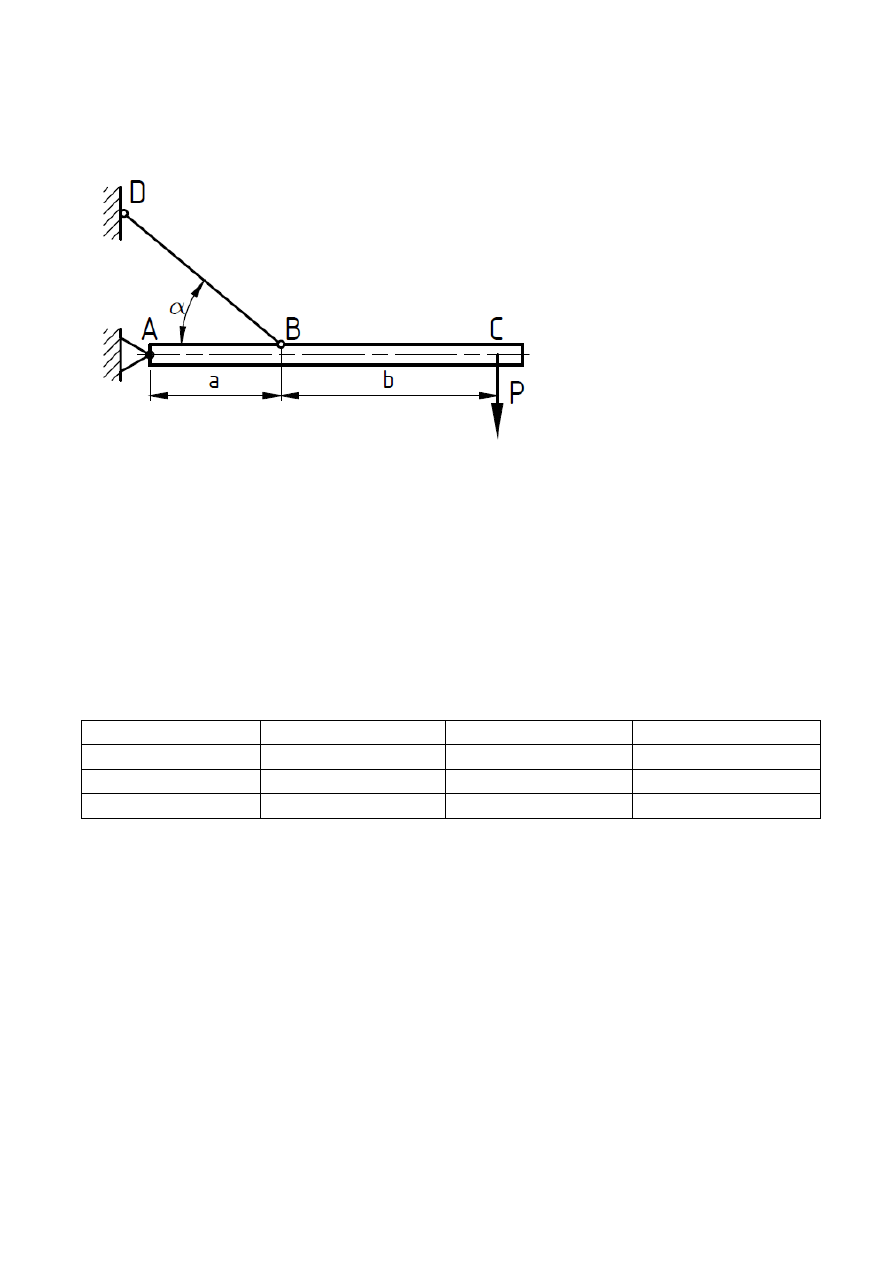
Zadanie nr 1

Dźwignia o długości L i ciężarze Q, zawieszona jest na cięgnie.

1. Dla danych P, Q, L, a, b, α wyznacz reakcje R

Ax

, R

Ay

, R

B

.

2. Sporządź wykres dla zbadania zależności siły napinającej R

B

cięgna od kąta α.

3. Oblicz średnice cięgna.
4. Zakładając, że k

r

(naprężenie dopuszczalne na rozciąganie dla cięgna) oraz b są zmiennymi

losowymi o rozkładzie normalnym wyznacz w Mathcadzie prawdopodobieństwo przekroczenia
naprężenia dopuszczalnego.
5. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.

Dane do zadania

k

r

, MPa

Rozrzut k

r

, %

Rozrzut b, %

A

84

±15

±10

B

90

±50

±12

C

70

±33

±33

Dane:
P = 2000 N,
a = 0.3 m,
b = 0.7 m,
α = 30

0

,

Q = 44 N,
L = a+b,

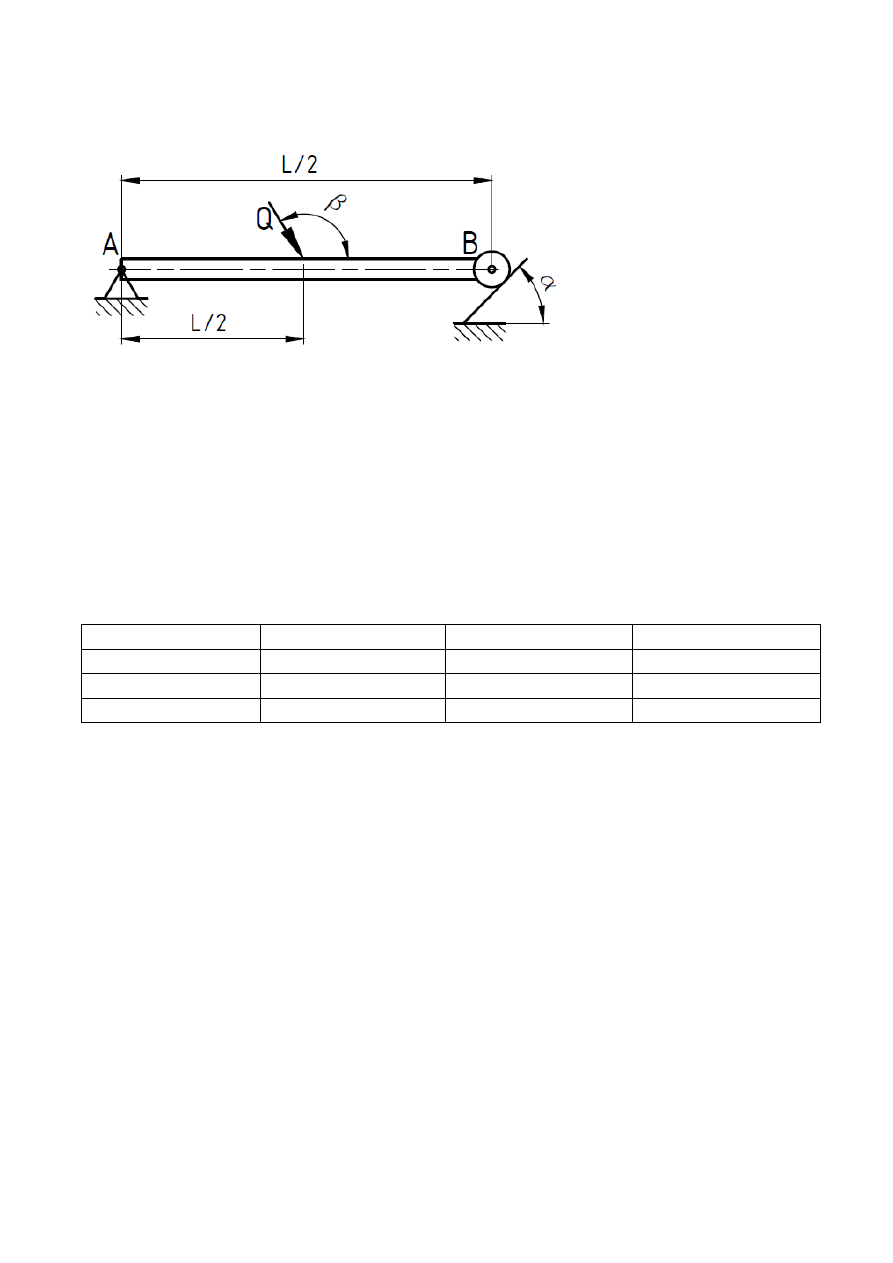
Zadanie nr 2

Dana jest belka.
1. Dla danych: Q, α, β, L - wyznacz reakcje.
2. Sporządź wykres dla zbadania zależności reakcji R

B

od β.

3. Oblicz przekrój poprzeczny belki przyjmując przekrój kołowy jeżeli naprężenie dopuszczalne na
zginanie wynosi k

g

[MPa].

4. Zakładając, że k

g

oraz Q są zmiennymi losowymi o rozkładzie normalnym wyznacz w Mathcadzie

prawdopodobieństwo przekroczenia naprężenia dopuszczalnego.
5. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.
Pomiń wpływ grawitacji i tarcia.

Dane do zadania

k

g

, MPa

Rozrzut k

g

, %

Rozrzut Q, %

A

120

±20

±10

B

154

±32

±32

C

100

±10

±50

Dane:
L = 4 m,
Q = 200 N,
α = 45

0

,

β = 120

0

,

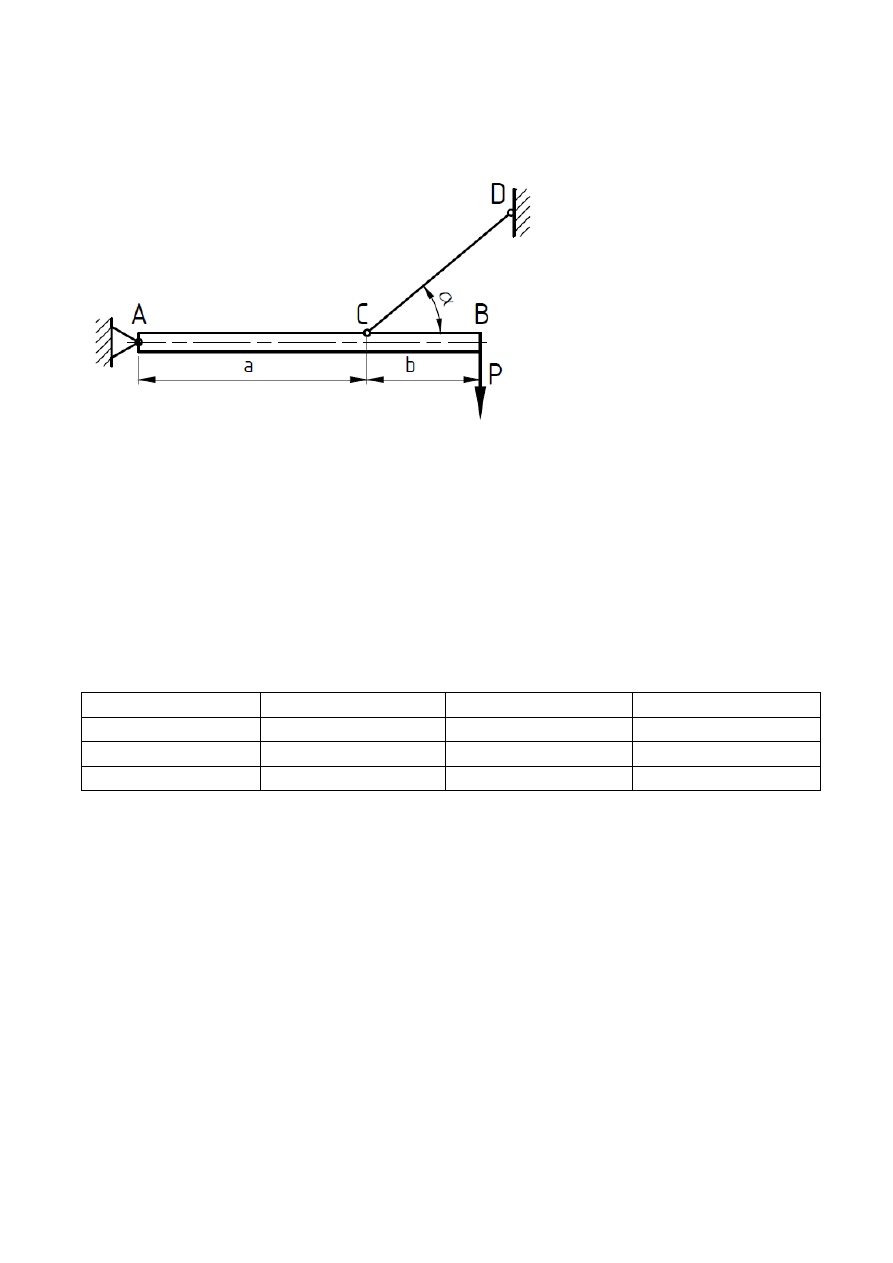
Zadanie nr 3

Dla przedstawionego układu na rysunku:
1. Dla danych: P, α, a, b wyznacz w Mathcadzie reakcje R

A

i S

CD

.

2. Sporządź wykres dla zbadania zależności: siły napinającej cięgno CD od α (punkt D przesuwa się
w prawo).
3. Oblicz jaki przekrój poprzeczny powinno mieć cięgno jeżeli naprężenie dopuszczalne na
rozciąganie wynosi k

r

[MPa].

4. Zakładając, że k

r

oraz P są zmiennymi losowymi o rozkładzie normalnym wyznacz w Mathcadzie

prawdopodobieństwo przekroczenia naprężenia dopuszczalnego.
5. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.

Dane do zadania

k

r

, MPa

Rozrzut k

r

, %

Rozrzut P, %

A

90

±16

±15

B

93

±40

±23

C

77

±43

±43

Dane:
a = 2 m,
b = 1 m,
α = 45

0

,

P = 1000 N,

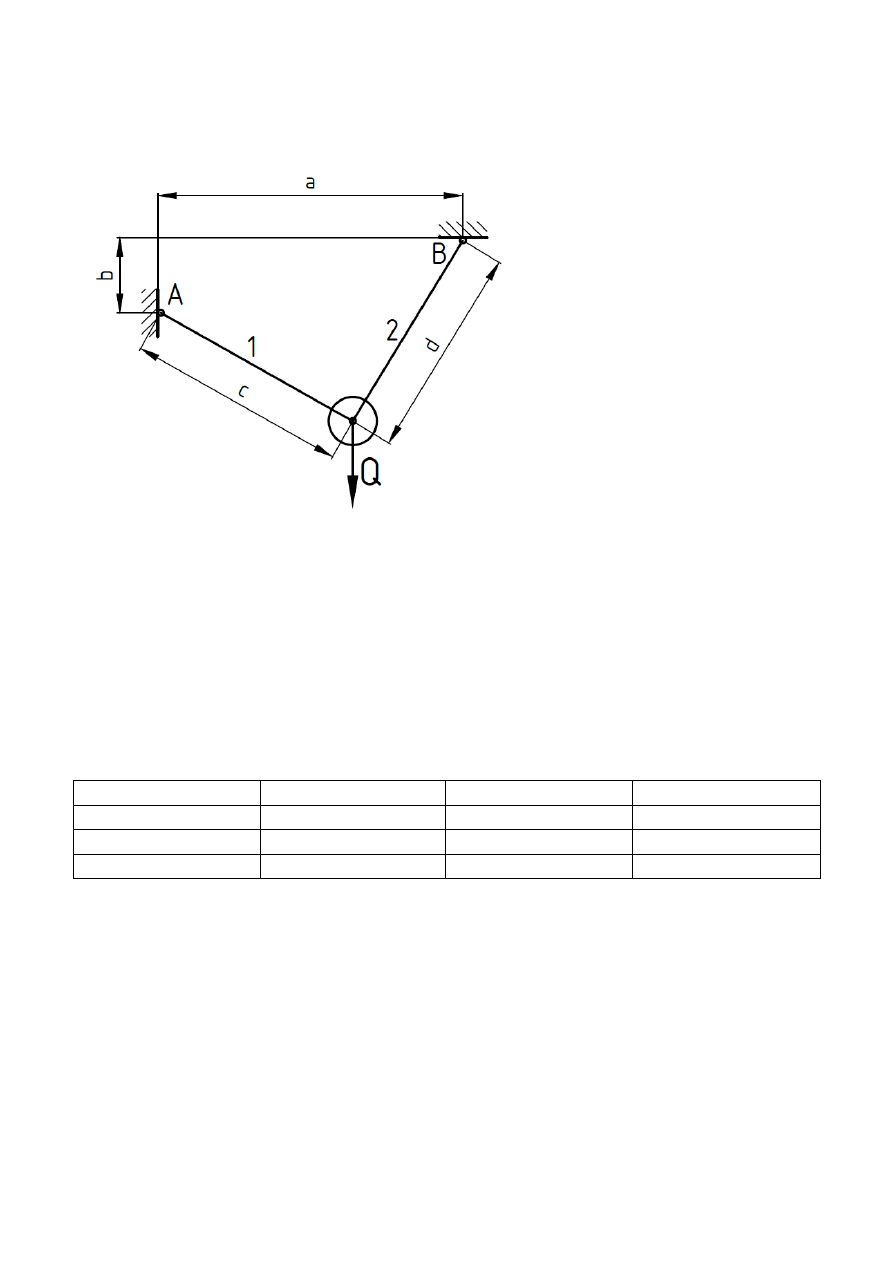
Zadanie nr 4

Dla przedstawionego układu na rysunku:
1. Dla danych: Q, a, b, c=2b, d=2b wyznacz w Mathcadzie reakcje w cięgnach 1 i 2.
2. Sporządź wykres dla zbadania zależności siły w wybranym cięgnie w zależności od "a".
3. Oblicz jaki przekrój poprzeczny powinno mieć bardziej obciążone cięgno jeżeli naprężenie
dopuszczalne na rozciąganie wynosi k

r

[MPa].

4. Zakładając, że k

r

oraz "a" są zmiennymi losowymi o rozkładzie normalnym wyznacz w

Mathcadzie prawdopodobieństwo przekroczenia naprężenia dopuszczalnego.
5. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.

Dane do zadania

k

r

, MPa

Rozrzut k

r

, %

Rozrzut a, %

A

134

±18

±18

B

76

±40

±32

C

88

±33

±32

Dane:
a = 0,4 m,
b = 0,35 m

Q = 500 N

Zadanie nr 5

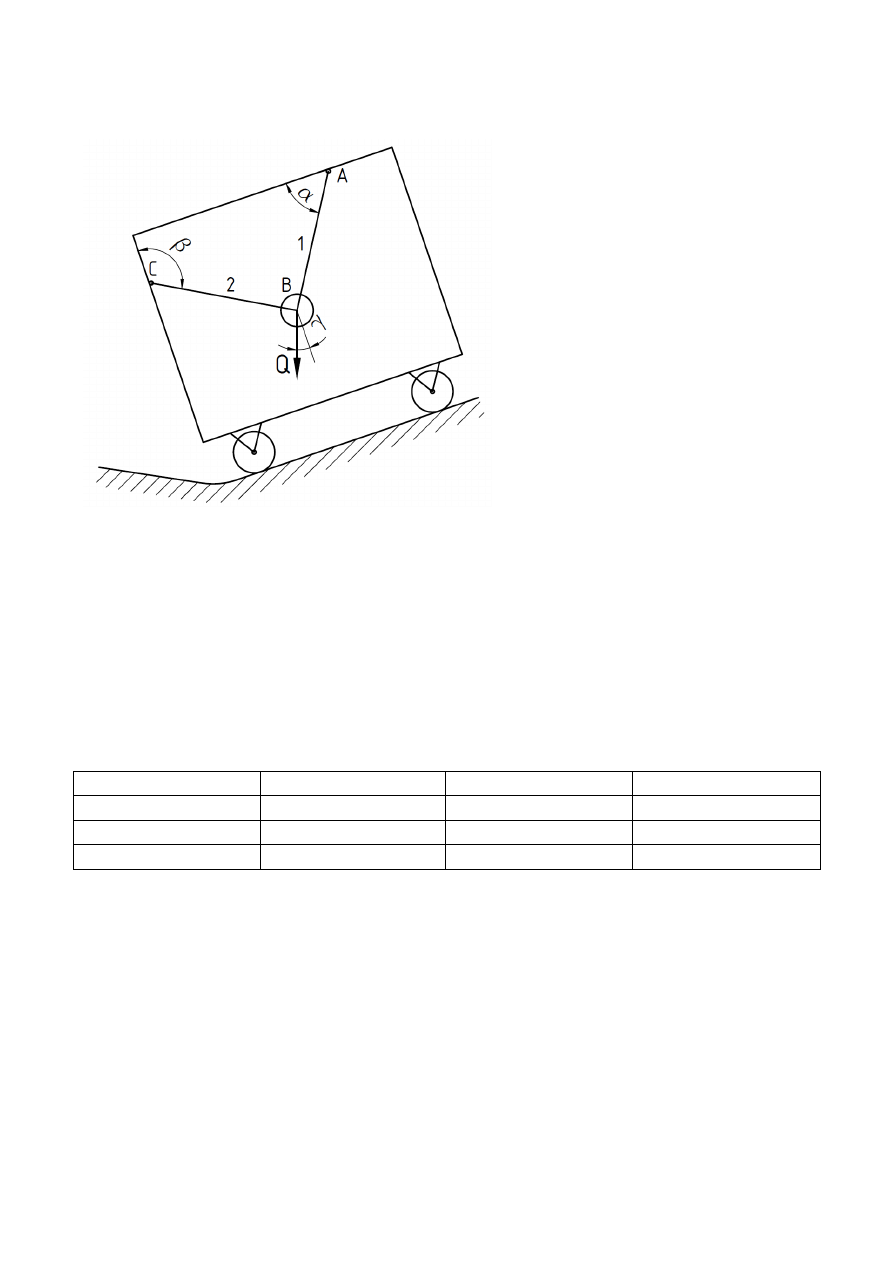
W pojeździe zawieszony jest ciężar Q:
1. Dla danych: Q, α, β oraz kąta γ nachylenia pojazdu wyznacz w Mathcadzie reakcje w cięgnach 1 i 2.
2. Sporządź wykres zależności siły napinającej cięgno 1 od zmian kąta nachylenia pojazdu γ.
3. Oblicz przekrój poprzeczny bardziej obciążonego cięgna jeżeli naprężenie dopuszczalne na
rozciąganie wynosi k

r

[MPa].

4. Uwzględniając losowy rozrzut k

r

oraz γ i zakładając, że można je opisać rozkładem normalnym

wyznacz w Mathcadzie prawdopodobieństwo przekroczenia naprężenia dopuszczalnego.
5. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.

Dane do zadania

k

r

, MPa

Rozrzut k

r

, %

Rozrzut γ, %

A

144

±15

±18

B

76

±20

±32

C

87

±23

±35

Dane:
α = 20

0

,

β = 110

0

,

γ = 5

0

Q = 500 N

Zadanie nr 6

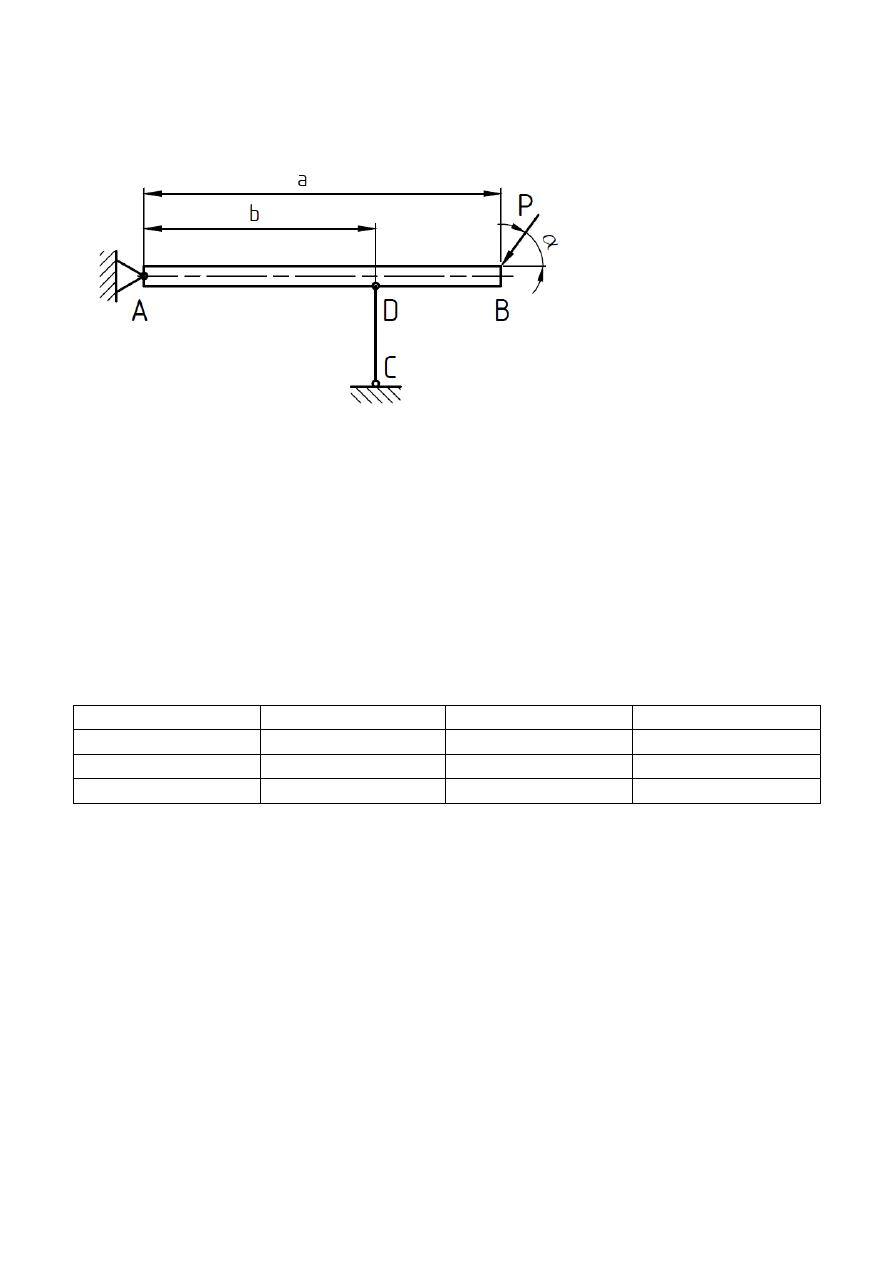
Dźwignia o wadze Q jest na końcu zamocowana przegubowo, natomiast w odległości b jest

podparta pionowym prętem zamocowanym na podporze przesuwnej.
1. Dla danych: P, α, a, b, Q wyznacz w Mathcadzie reakcje.
2. Sporządź wykres dla zbadania zależności reakcji R

A

od kąta α.

3. Oblicz jaki przekrój poprzeczny powinien mieć pręt CD aby nie uległ zniszczeniu w wyniku
ściskania.
4. Uwzględniając losowy rozrzut k

c

oraz α i zakładając dla nich rozkłady normalne wyznacz w

Mathcadzie prawdopodobieństwo przekroczenia naprężenia dopuszczalnego.
5. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.

Dane do zadania

k

c

, MPa

Rozrzut k

c

, %

Rozrzut α, %

A

170

±30

±18

B

180

±21

±32

C

210

±44

±44

Dane:
P = 100 N,
Q = 50 N,
a = 2 m,
b = 1 m,
α = 45

0

,

Zadanie nr 7

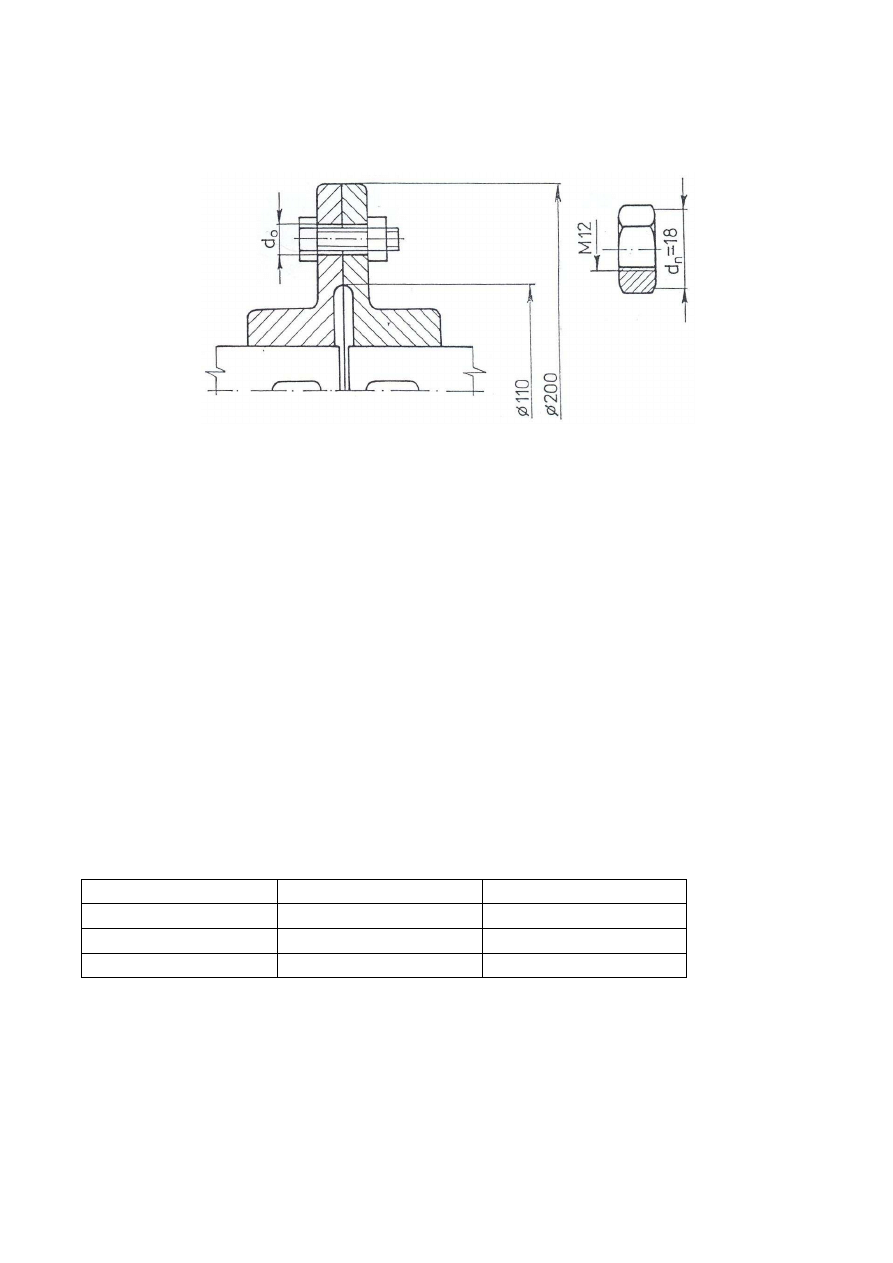
Dla przedstawionego sprzęgła:
1. Obliczyć maksymalny moment M

S

jaki może przenieść sprzęgło tarczowe skręcone sześcioma

luźnymi śrubami M12x1, oraz moment M

D

jakim należy dokręcić nakrętki. Śruby wykonano ze

stali, dla której k

r

=280 MPa.

2. Sporządź wykres dla zbadania zależności momentu dokręcania nakrętki od średniej średnicy
śruby. Przyjąć zakres zmienności średnicy średniej d

s

= 5÷14 mm.

3. Uwzględniając losowy rozrzut przenoszonego momentu M

S

oraz momentu dokręcania M

D

i

zakładając rozkłady normalne wyznacz w Mathcadzie prawdopodobieństwo utraty sprzężenia
ciernego.
4. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.

Dane:
µ = 0,15
d

r

= 10,773 mm, średnica rdzenia śruby,

d

s

= 11,351 mm, średnia średnica śruby,

d

o

= 13 mm,

d

n

= 18 mm, średnia tarcia nakrętki,

k

r

=280 MPa.

Dane do zadania

Rozrzut M

S

, %

Rozrzut M

D

, %

A

±15

±44

B

±25

±34

C

±41

±37

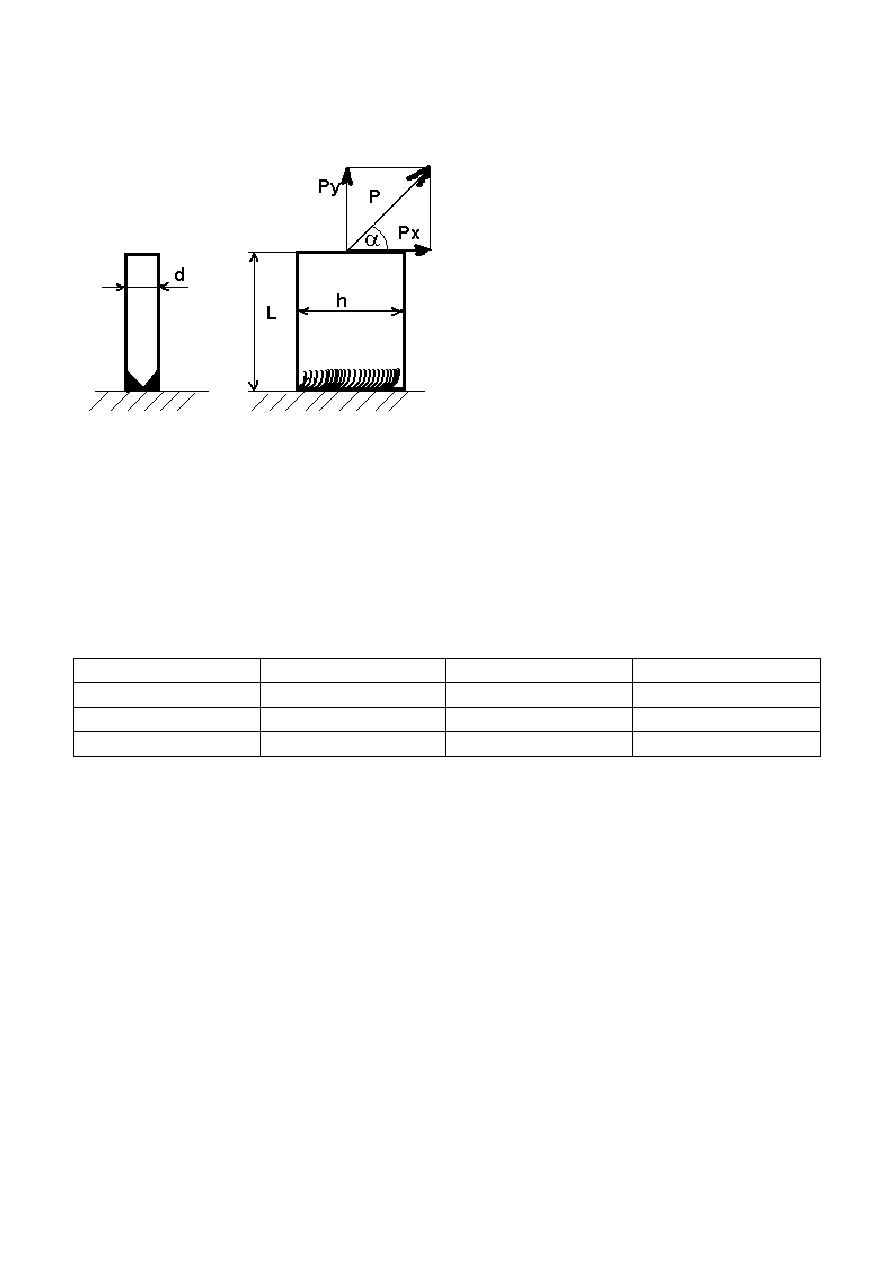
Zadanie nr 8

Dla przedstawionego wspornika przyspawanego spoiną czołową do podłoża:
1. Dla danych: P, α, d, h wyznacz maksymalne naprężenie zastępcze w spoinie.
2. Sporządź wykres dla zbadania zależności naprężenia zastępczego od h i od L.
3. Uwzględniając losowy rozrzut naprężenia dopuszczalnego k

g

' oraz α i zakładając dla nich

rozkłady normalne wyznacz w Mathcadzie prawdopodobieństwo przekroczenia naprężenia
dopuszczalnego.
4. Sporządź wykresy dystrybuant i gęstości prawdopodobieństwa.

Dane do zadania

k

g

', MPa

Rozrzut k

g

', %

Rozrzut α, %

A

170

±31

±14

B

180

±25

±22

C

210

±44

±34

Dane:
P = 3000 N,
d = 15 mm,
h = 40 mm,
L = 50 mm,
α = 20

0