
1
ZJAWISKA TRANSPORTU ORAZ ZASADA PRZEWODNICTWA
CIEPLNEGO
1.1. Zjawiska transportu.
Krystaliczne ciało stałe jest tradycyjnym obiektem bada mechaniki
kwantowej. Wykorzystuj c formalizm mechaniki kwantowej wytłumaczono
przyczyn istnienia ciał o ró nych wła ciwo ciach elektrycznych tj. dielektryków,
półprzewodników i metali, wyja niono obserwowan zale no ciepła wła ciwego
i przewodnictwa metali od temperatury, oraz natur magnetyzmu ciał stałych
i rozwini to zagadk nadprzewodnictwa. Zjawisko przewodnictwa cieplnego, obok
kilku innych termodynamicznych procesów nierównowagowych, zaliczamy do tzw.
zjawisk transportu.
Podstawowe termodynamiczne parametry stanu, tj. temperatura, ci nienie itp. s
ci le zdefiniowane jedynie w stanie równowagi termodynamicznej. W odniesieniu do
stanów nierównowagowych okre lenie funkcji termodynamicznych mo e sta si b d
niejednoznaczne, b d pozbawione sensu fizycznego. Istnieje jednak szeroka klasa
zjawisk nierównowagowych, których opis jest stosunkowo prosty, poniewa
nawi zuje do opisu stanów równowagi. Do takich zjawisk nale zjawiska
przenoszenia lub transportu, do których zaliczamy: przewodnictwo cieplne
i elektryczne, dyfuzj i lepko . W dalszej cz ci tej pracy uwag swoj skupi na
przewodnictwie cieplnym.
Przewodnictwo cieplne polega na przekazywaniu energii pomi dzy cz ciami ciała,
których temperatury s ró ne. Z tym zjawiskiem mamy do czynienia wówczas, gdy
wydzielon cz
ciała podgrzejemy. Po pewnym czasie dzi ki przekazywaniu energii,
temperatura całego ciała wyrówna si . Wielko ci przenoszon jest energia
wewn trzna ciała, a zjawisko zachodzi dzi ki temu, e w tym ciele wyst puje gradient
temperatury.
Wprawdzie mechanizmy przewodno ci cieplnej, elektrycznej, lepko ci i dyfuzji
s zupełnie od siebie ró ne, to maj wspólne, makroskopowe cechy, co da si wyrazi
ogólnym równaniem transportu:

2
gradA
j
β
−
=
gdzie j jest wektorem g sto ci strumienia odpowiedniej wielko ci (energii
wewn trznej, ładunku, masy, p du),
β
jest współczynnikiem proporcjonalno ci
(przewodno ci cieplnej, elektrycznej, dyfuzji, lepko ci), za A jest zale n od
współrz dnych przestrzennych, wielko ci skalarn , której gradient powoduje dane
zjawisko (temperatur , potencjałem, g sto ci , pr dko ci ). Dokładnie tak sam
posta ma prawo Fouriera, które opisuje nam przewodnictwo cieplne. Prawo to
zostanie szerzej omówione w rozdziale drugim. Wszystkie procesy, w których
parametry stanu z biegiem czasu zmieniaj si , nosz nazw niestacjonarnych.
1.2. Sposoby przekazywania ciepła.
Podstawy teoretyczne opisuj ce proces przekazywania ciepła wewn trz
pewnego obiektu lub mi dzy kilkoma podobiektami mog cymi oddziaływa na siebie
obejmuj jeden z obszernych rozdziałów termodynamiki. Podstawowym prawem
przekazywania ciepła jest druga zasada termodynamiki, która głosi, e samoczynne
przekazywanie ciepła jest mo liwe tylko w kierunku spadku temperatury,
za o intensywno ci przekazywania ilo ci ciepła decyduje głównie ró nica temperatur.
Przekazywanie ilo ci ciepła jest nauk opart na termodynamice obiektów nie
znajduj cych si w równowadze termicznej. Ilo ciowe uj cie wymienionej energii
musi podlega pierwszej zasadzie termodynamiki. Badania naukowe wykazały, e
przekazywanie ilo ci ciepła nie stanowi jednolitej cało ci pod wzgl dem metod
stosowanych w rozwi zaniu poszczególnych problemów. Dlatego wyodr bnia si trzy
podstawowe, ró ne pod wzgl dem fizycznym, sposoby realizacji przekazywania ilo ci
ciepła zwane: przewodzeniem ciepła, konwekcj oraz przekazywaniem ciepła przez
promieniowanie. Ka dy z tych sposobów przekazywania ciepła jest opisywany innymi
podstawami teoretycznymi.
1.2.1. Przewodnictwo cieplne.
Przewodzenie ciepła, jak wy ej było wspomniane, polega na bezpo rednim
przekazywaniu energii kinetycznej jednej cz stki innej cz stce, a wi c jest mo liwe
tylko wówczas gdy wyst puje bezpo redni kontakt mi dzy molekułami

3
(cz steczkami). Cz stki znajduj ce si w cieplejszych miejscach ciała s obdarzone
wi ksz energi ni pozostałe i cz
swej energii oddaj bezpo rednio cz stkom
s siednim, nale cym do chłodniejszej cz ci ciała. Proces ten trwa dopóty, dopóki nie
nast pi mo liwie równomierny rozkład pr dko ci w całym ciele, ewentualnie w całej
przestrzeni. Przewodzenie ciepła mo e odbywa si zarówno w substancjach stałych,
jak i w cieczach oraz gazach. Jednak e ciecze i gazy wykazuj mniejsz zdolno
przewodzenia ciepła (z wyj tkiem ciekłych metali).
Teoria zagadnie obejmuj cych przewodzenie ciepła sprowadza si do rozwi zania
równa ró niczkowych cz stkowych w zmiennych warunkach brzegowych.
Metale, które s najlepszymi przewodnikami elektryczno ci, s równocze nie
najlepszymi przewodnikami ciepła. Przyczyna tkwi w tym, e ciepło w metalach jest
przekazywane nie tylko przez drgaj ce atomy, lecz tak e przez wyst puj ce w nich
swobodne elektrony.
1.2.2. Konwekcja.
Cho gazy i ciecze le przewodz ciepło, dobrze jednak przekazuj ciepło przez
unoszenia, czyli konwekcje. Konwekcja polega na w drówce substancji wraz ze swym
ciepłem z jednego miejsca na inne. Wyró niamy dwa rodzaje konwekcji, mianowicie
konwekcj swobodn , która wyst puje wówczas gdy ruch o rodka (płynu lub gazu)
wywołany jest jedynie ró nic temperatur oraz konwekcj wymuszon – gdy ruch
o rodka wywołany jest za pomoc pompy lub wentylatora.
Dobrymi przykładami konwekcji s wiatry, centralne ogrzewanie oraz pr dy morskie,
np. Golfstrom, który unosi ciepło z Zatoki Meksyka skiej a do północno –
wschodnich wybrze y Europy i dalej do Morza Arktycznego. Je eli warunki, w jakich
znajdzie si gaz, uniemo liwiaj powstawanie pr dów, a zatem i unoszenie ciepła, to
gaz staje si dobrym izolatorem ciepła; przykładem mo e tu by warstwa powietrza
mi dzy podwójnymi oknami i podwójnymi drzwiami, wypełnione powietrzem puste
miejsca i pory w ubraniu, w wacie, w słomie itd. Najlepszym izolatorem cieplnym jest
pró nia, przestrze pozbawiona powietrza i innych gazów; wobec braku cz steczek
nie jest tu mo liwe ani przewodzenie, ani unoszenie ciepła. Najbardziej znane jest
zastosowanie izoluj cej wła ciwo ci pró ni w termosie. Jego cianki s podwójne,

4
a przestrze mi dzy nimi opró niona jest z powietrza. Aby utrudni przenoszenie
ciepła przez promieniowanie, cianki termosu s posrebrzane, wskutek czego odbijaj
promieniowanie cieplne.
1.2.3. Promieniowanie.
W pustej przestrzeni istnieje jednak trzecia mo liwo transportu ciepła – przez
promieniowanie. W taki wła nie sposób dociera ciepło ze Sło ca na Ziemi
przebywaj c 150 milionów kilometrów przez pozbawion substancji przestrze
kosmiczn .
Energia promienista zaabsorbowana przez o rodek materialny jest zamieniana na
ciepło, co powoduje, e w ten sposób mo emy ogrzewa dane ciało.
Ogrzewaj c ciało dostarcza si mu energi powoduj c wzmo enie drga atomów
i cz steczek, które przechodz w stan wzbudzony (w tym przypadku wzbudzony
termicznie, czyli za pomoc ciepła). Stany wzbudzone trwaj jednak bardzo krótko, na
ogół tylko ułamek sekundy. Po upływie tego czasu atomy i cz steczki na powierzchni
ciała przechodz z wy szego stanu energetycznego w stan ni szy i ró nica energii
zostaje wypromieniowana w postaci fotonu. Fotony w druj w przestrzeni po liniach
prostych z pr dko ci wiatła jako niewidzialne promieniowanie cieplne dopóty,
dopóki nie zostan pochłoni te przez inne cz stki i wyzyskane do wzbudzenia, a wi c
do ogrzania. Energia promieniowania ulega przemianie w energi drga atomów
i cz steczek.
Dodatkow cech charakterystyczn przekazywania ilo ci ciepła przez
promieniowanie jest to, e odbywa si ono mi dzy substancjami nie b d cymi
w kontakcie ze sob .
W warunkach rzeczywistych wy ej wymienione sposoby przekazywania ilo ci
ciepła bardzo rzadko wyst puj pojedynczo, a w wi kszo ci przypadków stanowi ich
ł czne przekazywanie ciepła.
Cz sto w praktyce in ynierskiej mo na pomin jeden ze sposobów przekazywania
ciepła. Je li w danym zjawisku wyst puje równocze nie promieniowanie
i przewodzenie, to mo na pomin ten sposób przekazywania ciepła, który ma
mniejsze oddziaływanie na całe zjawisko.

5
1.3. Mechanizmy przewodzenia ciepła.
1.3.1. Mechanizm przewodzenia ciepła w gazach.
Kinetyczna teoria gazów
Teoria kinetyczna gazów (nazywana te teori kinetyczno-molekularn albo
kinetyczno-cz steczkow ) jest efektem zastosowania zasad dynamiki i prostych
technik u redniania do układu cz steczek okre lonego w mikroskopowej definicji gazu
doskonałego. Jest pierwotn i okrojon wersja mechaniki statystycznej. Pozwala
ł czy kinematyczne wielko ci dotycz ce pojedynczych cz stek gazu
z termodynamicznymi parametrami takimi jak ci nienie czy temperatura. Rozwin li j
m.in. R. Boyle, D. Bernoulli, R. Clausius i C. Maxwell.
Gaz - zgodnie z przyj tym modelem - to zespół wielu cz steczek - punktów
materialnych poruszaj cych si chaotycznie. Cz steczki te zderzaj si ze sob oraz
ze ciankami naczynia i wła nie zderzenia ze ciankami s dla nas szczególnie
interesuj ce. Podczas tych zderze zmienia si wektor pr dko ci cz steczek. Zgodnie
z drug zasad dynamiki F = m (
∆v/
∆
t) do zmiany pr dko ci ciała potrzebna jest siła.
W tym przypadku jest to siła z jak cianka działa na cz steczk podczas zderzenia,
a skoro cianka działa na cz steczki gazu, to, zgodnie z trzecia zasad dynamiki,
cz steczki gazu oddziałuj pewn sił na cianki. Widzimy wi c, e na poziomie
mikroskopowym za ci nienie gazu wywierane na cianki naczynia odpowiedzialne jest
oddziaływanie cz steczek gazu ze ciankami podczas zderze .
Poni ej pokazane jest wyprowadzenie wzoru na ci nienie gazu wywierane na
cianki naczynia.
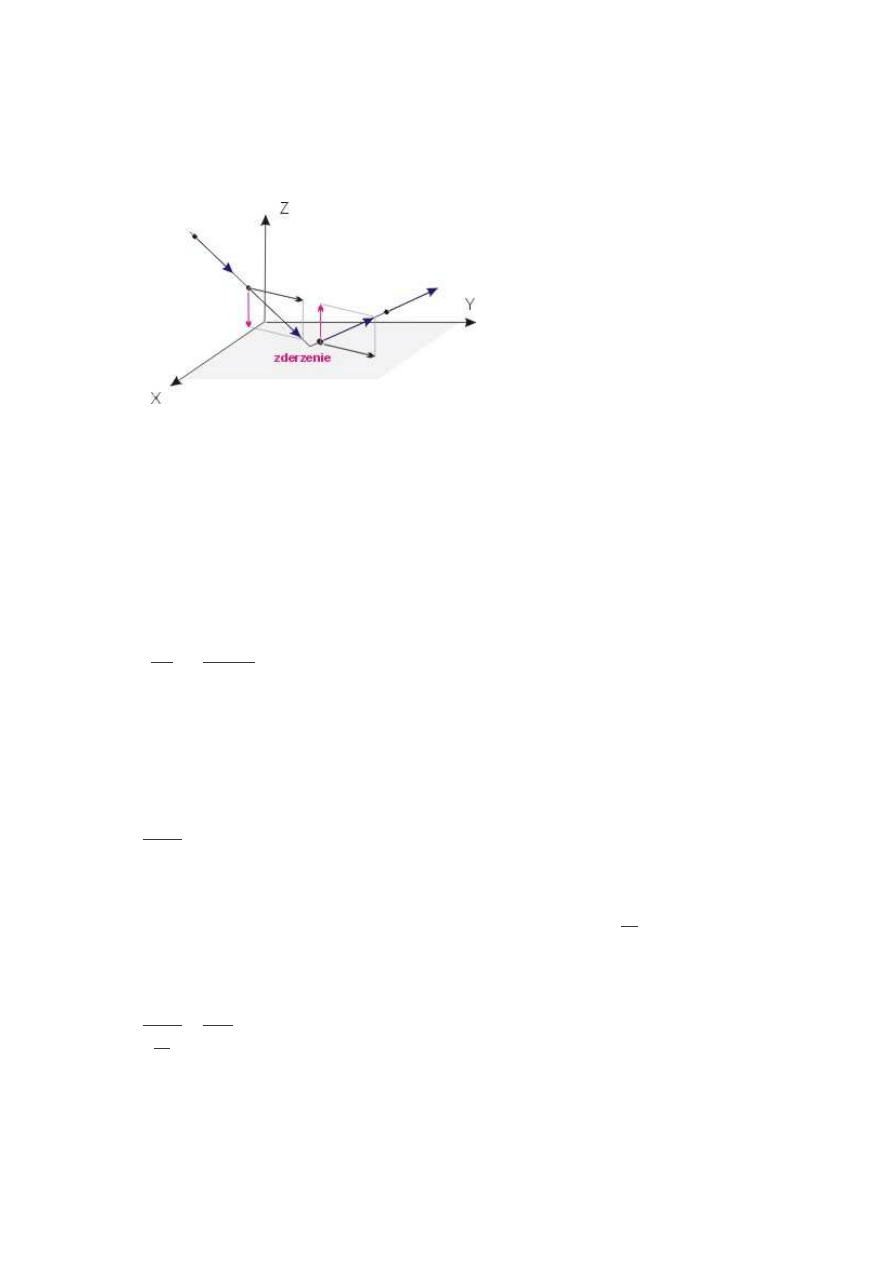
Rozwa my gaz - zespół cz steczek chaotycznie poruszaj cych si w pudle -
sze cianie o kraw dzi l. Podczas spr ystych zderze z wybran - powiedzmy "doln
poziom " - ciank zmienia si na przeciwn składowa pr dko ci prostopadła do
cianki, dwie pozostałe składowe - le ce w płaszczy nie cianki - nie ulegaj
zmianie.
Wektory p du i cz steczki przed i po zderzeniu mo emy zapisa :
(
)
z
y
x
przed
mv
mv
mv
p
,
,
=
6
(
)
z
y
x
przed
mv
mv
mv
p
−
=
,
,
co ilustruje poni szy rysunek.
Zmiana p du dana jest przez:
(
)
z
przed
po
mv
p
p
p
2
,
0
,
0
−
=
−
=
∆
a wi c ma tylko jedn składow i jej warto równa jest:
z
mv
p
2
−
=
∆
Druga zasada dynamiki daje natychmiast warto siły działaj cej na cz stk :
t
mv
t
p
F
z
∆
−
=
∆
∆
=
2
Znak minus oznacza tu, e siła działaj ca na cz steczk skierowana jest "od cianki".
Trzecia zasada dynamiki pozwala zauwa y , e siła z jak cz steczka działa na
ciank równa jest:
t
mv
F
z
∆
=
2
Czas mi dzy zderzeniami to czas potrzebny do przebycie przez cz steczk
drogi "tam i z powrotem" pomi dzy ciankami naczynia:
z
v
l
t
2
=
∆
, i takiej warto ci
czasu u yjemy obliczaj c redni warto siły.
l
mv
v
l
mv
F
z
z
z
2
2
2
=
=
Jest to wkład od jednej cz steczki. Sumuj c wkład od wszystkich cz steczek
otrzymamy:

7
(
)
...
2
2
2
1
+
+
=
z
z
v
v
l
m
F
W nawiasie sumujemy tu kwadraty z-owej składowej wszystkich cz steczek.
Praw stron podzielimy i pomno ymy przez liczb cz steczek N:
(
)
N
v
v
l
mN
F
z
z
...
2
2
2
1
+
+
=
Łatwo zauwa y , e drugi ułamek jest po prostu redni kwadratu z-owej
składowej pr dko ci w całym zespole:
(
) { }
2
2
2
2
1
...
z
z
z
v
N
v
v
=
+
+
Wzór na sił przybiera posta :
{ }
2
z
v
l
Nm
F
=
Ci nienie z kolei jest stosunkiem siły działaj cej na powierzchni (w naszym
przypadku ciank ) do pola tej powierzchni (u nas kwadratowa ciana sze cianu ma
pole S = l
2
)
{ }
{ } { }
2
2
3
2
z
z
z
v
V
v
M
l
v
Nm
S
F
p
ρ
=
=
=
=
Pozostaje uwolni si od wybranego do rozwa a kierunku z. Dla ka dej
cz steczki mamy v
2
= v
x
2
+ v
y
2
+ v
z
2
, co dla redniej w zespole daje:
{v
2
} = {v
x
2
} + {v
y
2
} + {v
z
2
}
Poniewa aden kierunek nie jest wyró niony i rednie pr dko ci we
wszystkich kierunkach s równe wi c {v
x
2
} = {v
y
2
} = {v
z
2
} . Mo emy napisa :
{v
2
} = {v
z
2
} + {v
z
2
} + {v
z
2
} = 3{v
z
2
}
czyli
{ } { }
2
2
3
1
v
v
z
=
Wzór na ci nienie da si wi c zapisa nast puj co:
{ }
2
3
1
v
p
ρ
=

8
gdzie v
2
oznacza redni w całym zespole warto kwadratu pr dko ci cz stki a
ρ
jest
g sto ci gazu.
Inn popularn posta tego wzoru otrzymujemy pami taj c, e
oraz M = Nm -
ilo cz steczek pomno ona przez mas cz steczki.
Daje to:
{ }
2
3
1
v
Nm
pV
=
Iloczyn masy cz steczki i kwadratu pr dko ci prowadzi do poj cia energii kinetycznej.
Wzór mo na wi c zapisa jako:
{ }
K
E
N
pV
3
2
=
Oczywi cie
{ }
2
2
1
mv
E
K
=
oznacza redni warto energii kinetycznej cz steczek
gazu.
Kinetyczna interpretacja temperatury gazu
Znajomo wyprowadzonego powy ej wzoru na ci nienie gazu pozwala na
podanie kinetycznej interpretacji temperatury. Ł cz c zale no
K
NE
pV
3
2
=
z równaniem Clapeyrona
NkT
pV
=
otrzymujemy:
K
NE
NkT
3
2
=
czyli
kT
E
K
2
3
=
Wida wi c, e temperatura jest niczym innym jak miar redniej energii
kinetycznej cz steczek gazu i e energia cz steczek gazu zale y wył cznie od
temperatury.
Jest to podstawowy wynik kinetycznej teorii gazu doskonałego. Pami taj c, e
2
2
1
mv
E
K
=
, mo emy z powy szego zwi zku otrzyma "termiczn " posta wzoru na
redni pr dko kwadratow :
V
M
=
ρ

9
m
kT
v
v
kw
r
3
2
,
=
=
Ten ciekawy rezultat wi e wprost pr dko cz steczek z temperatur i mas .
Dla gazu składaj cego si z cz steczek o ró nych masach, w danej temperaturze
wi ksze pr dko ci (oczywi cie bior c pod uwag warto ci rednie) b d miały
cz steczki o mniejszej masie. Tym wła nie tłumaczymy nieobecno wodoru
w ziemskiej atmosferze. Cz steczki wodoru, jako najmniej masywne, miały
najwi ksze pr dko ci, w szczególno ci cz sto wi ksze od drugiej pr dko ci
kosmicznej (pr dko ucieczki) co spowodowało ich odpływ w przestrze kosmiczn .
Ró nicowanie pr dko ci w zale no ci od masy jest te podstaw rozdzielania
izotopów. Cz steczki zawieraj ce l ejsze j dra szybciej dyfunduj . Wielokrotnie
powtarzany proces dyfuzji przez porowate przegrody prowadzi do wyselekcjonowania
cz stek ró ni cych si mas , tak na przykład prowadzi si proces wzbogacania uranu.
Przewodnictwo cieplne gazów.
Z kinetycznej teorii gazów, po przyj ciu pewnych uproszcze , mo na
wyprowadzi wzór na przewodnictwo cieplne gazów .
Strumie cz stek w kierunku x wynosi
{ }
x
v
n
2
1
. Gdzie n jest koncentracj cz stek;
w warunkach równowagi istnieje strumie cz stek równy co do warto ci, lecz
przeciwnie skierowany. Je li przez c
w
oznaczymy ciepło wła ciwe cz stki, to
wówczas przy przesuni ciu jej z obszaru o temperaturze T+
∆
T do temperatury T
energia cz stki wynosi b dzie c
w
∆
T. Ró nica temperatur
∆
T mi dzy kra cami drogi
swobodnej cz stki wynosi teraz:
τ
x
v
dx
dT
T
=
∆
gdzie
τ
jest rednim czasem mi dzy zderzeniami.
Wypadkowy strumie energii (b d cy wynikiem obu strumieni cz stek) wynosi
zatem:
{ }
dx
dT
c
v
n
dx
dT
c
v
n
q
w
w
x
τ
τ
2
2
3
1
=
>
<
=
gdzie:

10
c
w
- ciepło wła ciwe
Je eli v jest stałe, tak jak w przypadku fononów, to powy szym wzór mo emy napisa
w postaci:
dx
dT
Cvl
q
3
1
=
w którym rednia droga swobodna cz steczek wynosi l=v
τ
, a C=c
w
n. Porównuj c ten
wzór z wzorem na strumie energii cieplnej w stanie ustalonym, mo emy stwierdzi ,
e współczynnik przewodno ci cieplnej jest równy
Cvl
3
1
=
λ
.
1.3.2. Mechanizm przewodzenia ciepła w ciałach stałych.
Jednym z fundamentalnych rezultatów kwantowej fizyki ciała stałego jest
wniosek, e struktura energetyczna kryształu, przy niezbyt wysokich temperaturach,
jest podobna do struktury energetycznej gazu nie oddziałuj cych obiektów
kwantowych zwanych quasi-cz stkami. Znaczy to, e energia ciała stałego jest sum
energii poszczególnych kwazicz stek, odpowiadaj cych ruchom elementarnym
kryształu.
Atomy kryształu zajmuj w ró nych jego komórkach identyczne poło enia i maj
identyczne otoczenia. Atomy te mo na porówna do obwodów drgaj cych
nastrojonych na t sam cz sto i zdolnych do wzajemnego rezonansu. Dowolne
wzbudzenie jednego z atomów powoduje analogiczne wzbudzenie w atomach
s siednich, poniewa kryształ jest o rodkiem spr ystym. Tak wi c wzbudzenie nie
utrzymuje si w danym miejscu, lecz w postaci fali rozchodzi si po całym krysztale.
Zgodnie z prawami mechaniki kwantowej ruch zwi zany z tymi falami powstaje
i mo e by przekazywany wył cznie w postaci okre lonych porcji energii (kwantu)
fali spr ystej.
Mechanizm przewodnictwa cieplnego sieci krystalicznych ciał stałych, nie
zawieraj cych elektronów swobodnych, jako ciowo ró ni si od przewodnictwa
cieplnego metali. Przewodnictwo cieplne takich ciał stałych jest ci le zwi zane
z charakterem ruchu cieplnego cz stek tworz cych ich sieci krystaliczne. Istotny jest
fakt, e cz stki te zwi zane s ze sob siłami wzajemnego oddziaływania, zale nymi
od odległo ci mi dzy nimi. Dlatego drgania cieplne jednych cz stek s przekazywane

11
drugim. Na przykład, drgania spr yste cz stek A w sieci jednowymiarowej, któr
mo na schematycznie przedstawi w postaci szeregu cz stek poł czonych ze sob
spr ynami (rys.1.), b d przekazywane cz stkom s siednim B, C itd.
Rysunek 1 Schematyczne przedstawienie sieci jednowymiarowej.
Proces ten prowadzi do rozchodzenia si w krysztale tzw. fal spr ystych,
przenosz cych energi drga od jednych w złów do drugich. Analogiczne fale
spr yste, rozchodz ce si w gazach i cieczach, stanowi fizyczn natur d wi ku
(fale akustyczne). Pr dko rozchodzenia si fal spr ystych w ciele stałym jest
w przybli eniu równa kilku kilometrom na sekund . Wydawałoby si , e z tak
pr dko ci powinna rozchodzi si w takim ciele energia cieplnych drga cz stek.
Tymczasem pr dko przekazywania tej energii od cieplejszych do zimniejszych
obszarów ciała stałego jest proporcjonalna do gradientu temperatury i pozostaje
stosunkowo mała, nawet przy bardzo du ych gradientach temperatury. Tylko w bardzo
niskich temperaturach współczynnik przewodnictwa cieplnego osi ga znaczne
warto ci. Mo na by było podsumowa to nast puj cym stwierdzeniem : „Zaburzenie
nie mo e oczywi cie rozchodzi si pr dzej, ni poruszaj si przekazuj ce je no niki,
podobnie jak wiadomo nie mo e przyby wcze niej ni nios cy j goniec”
1
.
Oczywi cie to tylko w małej mierze tłumaczy, dlaczego energia cieplnych drga
cz stek rozchodzi si wolniej ni fale spr yste.
Aby dokładniej wytłumaczy dlaczego tak si dzieje, konieczne jest
uwzgl dnienie nieharmonicznego charakteru drga cz stek ciała stałego. Okazuje si ,
e drgania te powoduj osłabianie i rozpraszanie fal cieplnych w krysztale.
Rozpraszanie fal cieplnych zwi ksza si ze wzrostem amplitudy nieharmonicznych
drga cz stek sieci, tj. ro nie z podwy szeniem temperatury, przy czym
przewodnictwo cieplne ciała maleje. Rozpraszanie fal cieplnych mo na uwzgl dni ,
1
Katscher F.: Fizyka popularna, wyd. Wiedza Powszechna, Warszawa 1976r., str.34.

12
wprowadzaj c poj cie redniej długo ci drogi swobodnej fal spr ystych w krysztale.
Wówczas wszystko odbywa si tak, jakby fala została urwana po okre lonym
przebiegu i na jej miejsce powstała nowa, o innym kierunku rozchodzenia si przy tym
przenoszenie energii od cieplejszej do zimniejszej cz ci kryształu jest znacznie
utrudnione, gdy fale cieplne nie rozchodz si prostoliniowo. Analogiczne zjawisko
wyst puje w przypadku przewodnictwa cieplnego gazów. Je li długo drogi
swobodnej cz stki b dzie wielokrotnie mniejsza od rozmiarów liniowych naczynia,
którego przeciwne cianki utrzymywane s w ró nych temperaturach, wówczas
cz steczki, ulegaj c cz stym zderzeniom z drugimi cz steczkami, powoli dyfunduj
od cianki ciepłej do zimnej, poruszaj c si po zło onej zygzakowatej drodze.
Stan kryształu zmienia si wraz ze zmian temperatury. Rozpatrzmy sytuacj kiedy
ciało znajduje si w temperaturze zera bezwzgl dnego. Z punktu widzenia fizyki
klasycznej przy T=0 [K] ustaje wszelki ruch. Atomy i jony powinny zastyga w swych
poło eniach równowagi. Mechanika kwantowa obala ten wniosek jako niezgodny
z zasad Heisenberga. A wi c ruch trwa nawet w T=0 [K] i nosi on nazw drga
zerowych.
Podwy szenie
temperatury
oznacza
zwi kszenie
energii
chaotycznego,
nieuporz dkowanego ruchu atomów. W ciele stałym ruch dowolnej cz stki wywiera
wpływ na jej s siadów, a wi c w ciele stałym mo liwe s tylko kolektywne ruchy
cz stek (patrz rys. 1.).
Atomy mo na traktowa jako trójwymiarowe oscylatory harmoniczne. Energia takich
oscylatorów jest skwantowana i jak wykazano, dozwolone warto ci energii s opisane
wzorem:
ν
h
n
E
n
+
=
2
1
gdzie n=0, 1, 2,..., natomiast
ν
jest cz sto ci drga mechanicznych. Zmiany energii
towarzysz ce przej ciu ze stanu energetycznego opisanego liczb kwantow n
1
do
s siedniego stanu o wi kszej energii opisanego liczb kwantow n
2
, wynosz :
(
)
ν
ν
ν
ν
h
h
n
n
h
n
h
n
E
E
n
n
=
−
=
+
−
+
=
−
1
2
1
2
1
2
2
1
2
1

13
poniewa liczby całkowite n
1
oraz n
2
ró ni si o jeden. Wobec tego, gdy atom
pochłania energi ciepln , jego energia wzrasta co najmniej o h
ν;
natomiast
w przej ciu odwrotnym, atom emituje energi . Sytuacja jest całkiem podobna do
przej zwi zanych z absorpcj i emisj fotonów, a nazwa fonon słu y do opisu
kwantu energii cieplnej absorbowanej lub emitowanej przez atom.
Absorpcja fononów powoduje przesuni cia atomów, co prowadzi do wibracji sieci
i dlatego fonony mo na uwa a za niedoskonało ci kryształu, poniewa w idealnej
sieci wszystkie atomy powinny si znajdowa w stanie spoczynku.
Najprostsz form ruchu kolektywnego atomów w ciele stałym s ich drgania wokół
poło e równowagi. Drgania te rozchodz si w postaci fal po całym krysztale,
a kwant energii tej fali nosi wła nie nazw wy ej wspomnianego fononu. Fonony
mo na traktowa jako do niezwykły gaz, który charakteryzuje si tym, e wraz ze
wzrostem temperatury wzrasta równie ilo fononów. Energia ruchu drgaj cych
atomów kryształu jest równa sumie energii fononów. Własno ci gazu fononów
okre laj pojemno ciepln kryształów i ich przewodnictwo cieplne i s
odpowiedzialne za hamowanie ruchu elektronów w metalach, tzn. s jednym ze ródeł
oporu elektrycznego.
Je li zało ymy sytuacj tak w której b dziemy mieli zbiornik zawieraj cy gaz
fononów oraz, e na jednym z ko ców ciała stałego podtrzymywana jest temperatura
T
1
, a na drugim T
2
, przy czym T
2
>T
1
wówczas b dzie to oznaczało, e na jednym
z tych ko ców koncentracja fononów jest mniejsza (temperatura T
1
) ni na drugim
(T
2
). Fonony b d przepływa z ko ca o temperaturze wy szej do ko ca
chłodniejszego, d
c do wyrównania koncentracji w całej obj to ci. Przemieszczaj c
si w ciele stałym fonony przenosz energi . Tak wi c przenoszenie kolektywnych
drga sieci w krysztale ma wkład do zjawiska przewodnictwa cieplnego. Z reguły,
przewodnictwo cieplne metali jest wi ksze od przewodnictwa cieplnego dielektryków.
W dielektrykach mechanizm fononowy jest jedynym mechanizmem przenoszenia
ciepła. W tych materiałach współczynnik przewodnictwa cieplnego w niezbyt niskich
temperaturach jest odwrotnie proporcjonalny do pierwszej pot gi temperatury
bezwzgl dnej.

14
Nale y podkre li , e w metalach du y udział w przewodnictwie cieplnym ma gaz
elektronów swobodnych, którego istnienie odró nia metale od innych ciał stałych.
W metalu elektrony walencyjne nie s zlokalizowane, aden z nich nie jest zwi zany
z okre lonym j drem atomowym, lecz porusza si w całym metalu. Elektrony
swobodne w procesie zderze przekazuj energi wnosz c wkład do przewodnictwa
cieplnego. Problem ten b dzie omówiony szerzej w dalszej cz ci pracy.
PRZEPŁYW CIEPŁA W STANIE NIEUSTALONYM ORAZ PRAWA
OPISUJ CE PRZEWODNICTWO CIEPLNE
2.1. Prawa opisuj ce przewodnictwo cieplne.
Jak było wspomniane w rozdziale pierwszym, ciepło mo e przechodzi od
obszaru gor cego do obszaru zimnego w wyniku trzech ró nych procesów –
przewodnictwa, konwekcji i promieniowania. Ostatni proces polega na przenoszeniu
energii cieplnej przez promieniowanie elektromagnetyczne, dwa pozostałe
mechanizmy natomiast wymagaj obecno ci o rodka materialnego. W procesie
konwekcji ciepło jest przenoszone podczas ruchu o rodka materialnego jako cało ci,
a wi c proces ten mo e wyst powa tylko w cieczach i gazach. Z kolei mechanizm
przewodzenia polega na wymianie energii pomi dzy cz steczkami lub jonami
w ciałach stałych, cieczach i gazach. W metalach przewodnictwo cieplne zwi zane jest
głównie z wymian energii mi dzy elektronami przewodnictwa.
Je li w jakiej substancji wyst puje gradient temperatury
x
T
∂
∂
wzdłu osi x,
wówczas przez jednostk powierzchni prostopadł do tej osi w jednostce czasu
przepływa ilo ciepła:
Wzór 1
x
T
dt
dQ
∂
∂
−
=
λ
gdzie
λ
jest współczynnikiem przewodzenia ciepła danej substancji; znak minus
w powy szym wzorze wskazuje, e przepływ ciepła zachodzi w przeciwnym kierunku
ni przyrost temperatury, co oznacza, e pierwsza zasada termodynamiki pozostaje
w tym przypadku w mocy. Wy ej przedstawiony wzór stanowi prawo Fouriera.

15
Posta równania, która okre la przewodnictwo cieplne wykazuje, e proces
przenoszenia
energii
cieplnej
jest
procesem
podlegaj cym
prawom
prawdopodobie stwa. Proces przewodnictwa nie zachodzi w ten sposób, e energia
wprowadzona z jednego ko ca próbki przesuwa si wprost po linii prostej do drugiego
ko ca, lecz no niki energii dyfunduj przez próbk bez odchyle , wówczas wyra enie
na strumie cieplny nie zale ałoby od gradientu temperatury, natomiast zale ałoby
tylko od ró nicy temperatury
∆
T mi dzy ko cami próbki bez wzgl du na jej długo .
Proces przewodnictwa cieplnego podlega prawom prawdopodobie stwa i dlatego
w wyra eniu na strumie ciepła wyst puje gradient temperatury.
Rozpi to w warto ci współczynnika przewodzenia ciepła mi dzy dobrymi
przewodnikami, a dobrymi izolatorami wida w poni szej tabeli.
Współczynnik λλλλ przewodnictwa cieplnego w temperaturze 293 K
Tabela 1
Materiał
λ [W/mK]
Mied
384
elazo
88
Woda
0,609
Bawełna
0,182
Powietrze 0
0
C
0,024
W dalszej cz ci tego rozdziału zostan opisane kolejno: prawo Wiedemana –
Franza, które ł czy w sobie przewodno elektryczn z przewodno ci ciepln oraz
prawo Fouriera – Kierchhoffa.
2.1.1. Prawo Wiedemann – Franza.
Spo ród substancji stałych metale maj najwi kszy współczynnik przewodzenia
ciepła
λ
. Przekazywanie ilo ci ciepła w metalach jest wynikiem ruchu swobodnych
elektronów, a w znacznie mniejszym stopniu drganiami atomów wokół w złów sieci
krystalicznej w kwantach energii, zwanych fononami. Mo na przyj , e
współczynnik przewodzenia ciepła metali jest równy sumie współczynników
przewodzenia ciepła elektronów
λ
e
i fononów
λ
f
:

16
λ=λ
e
+
λ
f
Swobodne elektrony w metalach zachowuj si podobnie jak molekuły gazu
w przestrzeni, dlatego nie bez powodu wprowadzono poj cie gazu elektronowego.
Przewodzenie ciepła przez elektrony jest spowodowane ruchem tych samych
no ników co i przewodzenie pr du elektrycznego. Istnieje wi c pewna zale no
pomi dzy elektronowym współczynnikiem przewodzenia ciepła a przewodno ci
elektryczn
σ
oraz temperatur bezwzgl dn T.
Metale s dobrymi przewodnikami zarówno ciepła jak i pr du. Istnieje do
szeroki zakres temperatur, w którym elektrony s odpowiedzialne nie tylko za
przewodnictwo elektryczne, ale równie za transport energii wewn trznej. Prawo
transportu ładunku, czyli prawo Ohma mo na zapisa w postaci:
gradV
j
σ
−
=
gdzie j jest wektorem g sto ci strumienia ładunków, V – potencjałem elektrycznym,
za współczynnik
σ
nosi nazw przewodno ci elektrycznej wła ciwej.
Dla jednorodnego pr ta przewodz cego pr d elektryczny prawo Ohma mo na
zapisa w postaci:
S
l
I
IR
U
σ
=
=
gdzie:
S
l
R
σ
=
W powy szych wzorach : U oznacza ró nic potencjałów mi dzy ko cami pr ta, I –
nat enie pr du, R – opór elektryczny, l, S – długo i powierzchni przekroju
poprzecznego pr ta,
σ
– przewodno wła ciw .
Przyczyn przepływu ładunków elektrycznych jest ró nica potencjałów U,
natomiast wielko skutku, tj. nat enie pr du, zale y od parametrów geometrycznych
(S, l) oraz stałej materiałowej
σ.
Istnieje prosty zwi zek pomi dzy współczynnikiem przewodzenia ciepła
λ
a przewodno ci wła ciw
σ
, który jako pierwsi wyznaczyli do wiadczalnie
E. Wiedemann i W. Franz.

17
LT
=
σ
λ
gdzie T oznacza temperatur bezwzgl dn , L za jest współczynnikiem
proporcjonalno ci, nazwanym liczb Lorentza.
Prawo Wiedemanna – Franza stwierdza, e dla metali w niezbyt niskich
temperaturach stosunek przewodnictwa cieplnego do przewodnictwa elektrycznego
jest wprost proporcjonalny do temperatury, przy czym warto stałej
proporcjonalno ci jest niezale na od rodzaju metalu. Wynik ten odegrał bardzo wa n
rol w rozwoju teorii metali, poniewa potwierdził model gazu elektronowego.
Stosuj c kwantow statystyk Fermiego – Diraca obliczono liczb Lorentza, co
było potwierdzeniem słuszno ci teorii budowy metali i mechanizmów zachodz cych
w nich zjawisk:
2
2
)
(
3 e
k
L
B
π
=
gdzie : e – ładunek elektronu, k
B
– stała Boltzmana.
Prawo Wiedemanna – Franza jest spełnione przez wi kszo metali
w temperaturach pokojowych. W niskich temperaturach odst pstwa od niego s
bardzo du e, ale w tych temperaturach w przewodnictwie cieplnym dominuj c rol
zaczyna odgrywa mechanizm fononowy.
2.2. Przewodzenie ciepła w stanie nieustalonym.
Przez stan nieustalony pr ta rozumiemy taki jego stan termodynamiczny,
w którym temperatura dowolnego punktu pr ta jest funkcj czasu.
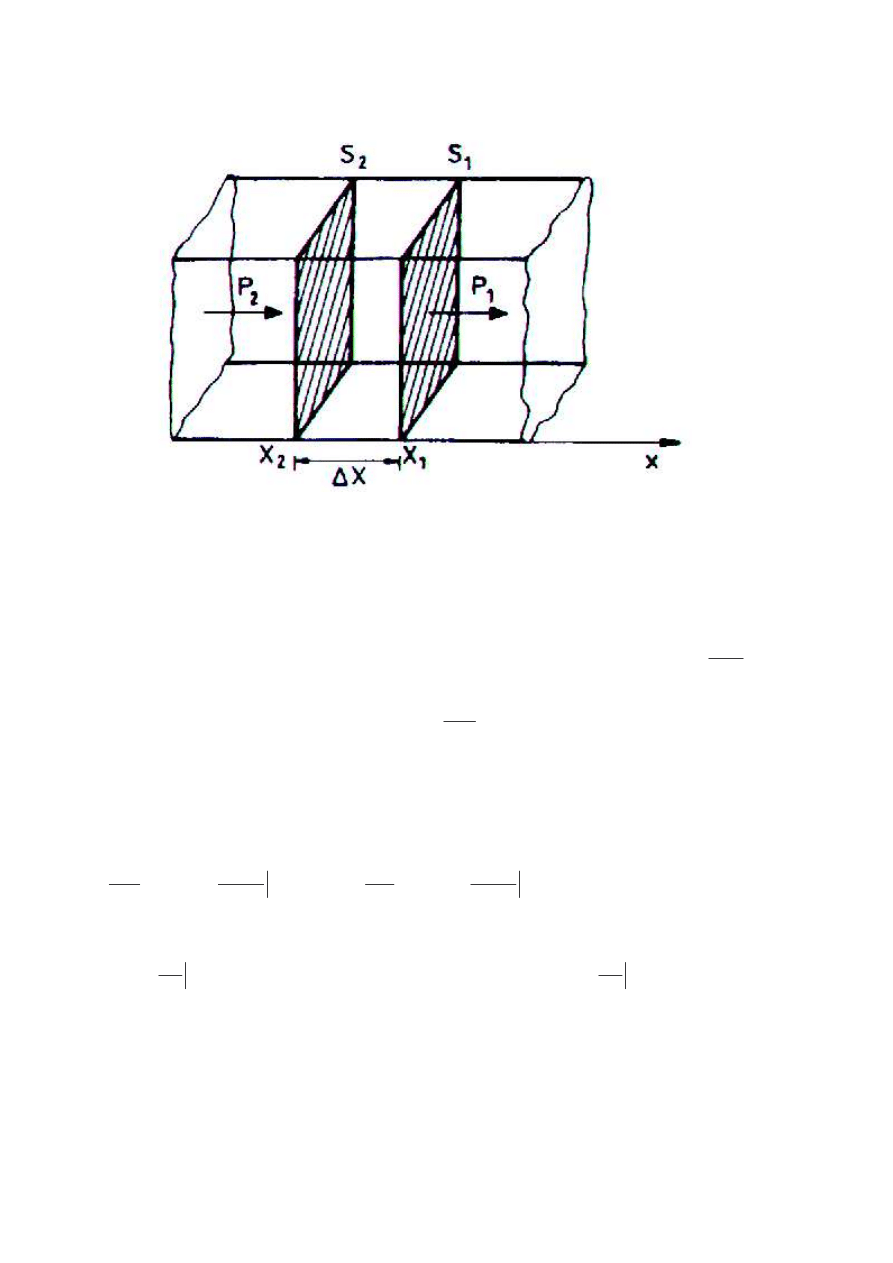
Rozpatrzmy pr t metalowy o przekroju S, długo ci l, którego ko ce maj ró ne
temperatury T
1
i T
2
tak jak to przedstawia poni szy rysunek.
18
Rysunek 2. Przepływ ciepła w pr cie metalowym.
Wybierzmy element pr ta, poło ony wokół punktu x i maj cy długo
∆
x.
Załó my, e do tego elementu przez powierzchni S
2
wpływa moc
dt
dQ
P
2
2
=
, a
przez powierzchni S
1
wypływa
dt
dQ
P
1
1
=
. Zgodnie z równaniem (równanie
okre laj ce prawo Fouriera i strumie cieplny) mo emy zapisa :
Wzór 2
2
)
(
2
2
x
x
dx
x
dT
S
P
dt
dQ
=
=
=
λ
oraz
1
)
(
1
1
x
x
dx
x
dT
S
P
dt
dQ
=
=
=
λ
gdzie
2
x
x
dx
dT
=
jest gradientem temperatury w punkcie x
2
, a
1
x
x
dx
dT
=
jest gradientem
temperatury w punkcie x
1
, przy czym
∆
x=x
1
-x
2
. Energia, któr zgromadzi si
wewn trz elementu o grubo ci
∆
x w czasie dt wyniesie :
Wzór 3

19
dt
dx
x
dT
dx
x
dT
S
dQ
dQ
dQ
x
x
x
x
−
=
−
=
=
=
1
2
)
(
)
(
1
2
λ
Energia ta powoduje przyrost temperatury dT rozpatrywanej warstwy :
Wzór 4
dT
mc
dQ
w
=
gdzie m=S
ρ∆
x ,
ρ
oznacza g sto materiału a c
w
jego ciepło wła ciwe.
Podstawiaj c t warto do równania (wzór 9) oraz dziel c obustronnie przez czas dt
otrzymamy :
Wzór 5
dt
dQ
x
Sc
dt
dT
w
∆
=
ρ
1
Je li długo
∆
x rozpatrywanego elementu pr ta b dzie d y do wielko ci
niesko czenie małej dx (
dx
x
→
∆
) to wzór 8 mo na zapisa w postaci :
Wzór 6
dxdt
x
T
S
dQ
2
2
∂
∂
=
λ
PorTjł35.414 0 Tdł( )Tjłjł/R65.414 0 Tdł( )Tjłjł/R65.414 0 Tdł( )Tjłj0 Tdł( )Tjł35.414 0 Tdł( )Tjł35.414 0 T -7.68 Tdł(=)Tjł/R29 12 Tfł0.99959 0 0.341875 1 100.74 432.2 Tmł(l)Tjł/R12 13.02 Tfł0.999604 0 0 1 159.84 4382B43333 0 0 8 117.3 42B43333 0ł970 0 1

20
2.3. Wnikanie płaskiej fali termicznej.
Przewodzenie ciepła jest jednym ze zjawisk nieodwracalnych i jako takie jest
przejawem reakcji układu termodynamicznego na zakłócenia stanu równowagi.
Reakcja ta zmierza do zlikwidowania zakłócenia.
Zakłócenie, które działa w sposób
trwały, inicjuje pojawienie si procesu nieustalonego. Proces ten nie doprowadza
jednak do stanu równowagi. Je eli zakłócenie nie jest stałe, to po dostatecznie długim
czasie dochodzimy do tzw. stanu ustalonego, w którym temperatury w ró nych
punktach układu s ró ne, ale niezmienne w czasie. Stan ustalony mo e tak e ulec
zakłóceniu. Równie i w tym przypadku zakłócenie inicjuje proces nieustalony, który
mo e doprowadzi do nowego stanu ustalonego czy te do stanu równowagi,
w zale no ci od charakteru zakłócenia. Specjalny charakter maj zakłócenia
periodyczne. Pojawiaj c si w stanie równowagi lub w stanie ustalonym, jako w stanie
pocz tkowym, inicjuj równie proces nieustalony. Po dostatecznie długim czasie
proces ten doprowadza do periodycznego przewodzenia ciepła, przy którym
temperatura w dowolnym punkcie układu jest periodyczn funkcj czasu, o tym
samym okresie co zakłócenie.
Spo ród wielu mo liwych nieustalonych warunków brzegowych najwi ksze znaczenie
praktyczne ma przypadek okresowej zmienno ci temperatury powierzchni, zwi zany
z okresowo zmienn wymian ciepła na granicy ciała. Przypadki takie zachodz przy
wymianie ciepła mi dzy cylindrem silnika tłokowego lub spr arki a czynnikiem
w regeneratorach o okresowym działaniu i w wielu innych urz dzeniach.
W dalszej cz ci b dzie omówiony jeden z prostszych i bardziej typowych
przykładów, mianowicie zostanie rozpatrzone zagadnienie nieustalonego
przewodzenia ciepła w ciele półniesko czonym, gdy temperatura jego powierzchni
ulega okresowym zmianom.
Niech temperatura powierzchni (x=0) półprzestrzeni zmienia si sinusoidalnie:
Wzór 8
θ
=
θ
0
sin(
ω
t)
gdzie:
θ
0
-amplituda zmian temperatury powierzchni,
ω
-cz sto kołowa zmian temperatury.

21
)
(
0
)
,
(
δ
ω
δ
θ
θ
x
t
i
x
e
e
t
x
−
−
=
Dla przypomnienia, jednowymiarowe równanie przewodnictwa cieplnego dla
warunków nieustalonych ma posta :
Wzór 9
2
2
x
C
t
∂
∂
=
∂
∂
θ
λ
θ
gdzie:
λ
- współczynnik przewodnictwa cieplnego,
C - pojemno cieplna jednostki obj to ci (C=
ρ
c
w
,
ρ
– g sto materiału, c
w
– ciepło
wła ciwe). Stosunek
λ
/C=D jak pokazano w poprzednim punkcie nazywamy
współczynnikiem przewodzenia temperatury.
Rozwi zuj c równanie przewodnictwa, mo na przyj ,
e funkcja b d ca
rozwi zaniem tego równania jest iloczynem dwu wyra e , z których jedno jest tylko
funkcj współrz dnej x, drugie za funkcj czasu. Wi c rozwi zaniem równania
(wzór 14) jest funkcja periodyczna:
Wzór 10
Człon
δ
θ
θ
x
e
t
x
−
=
0
)
,
(
oznacza amplitud fali termicznej,
amplituda ta zale y od współrz dnej x i maleje expotencjalnie ze wzrostem x (fala
termiczna jest silnie tłumiona).
W celu wyznaczenia stałej
δ
obliczamy:
)
,
(
)
(
0
t
x
i
x
t
i
e
x
e
i
t
ωθ
δ
ω
δ
ωθ
θ
=
−
−
=
∂
∂
)
1
(
)
,
(
)
,
(
)
,
(
1
+
−
=
−
−
=
∂
∂
i
t
x
t
x
i
t
x
x
δ
θ
θ
δ
θ
δ
θ
oraz
2
2
2
2
2
2
2
)
,
(
2
)
,
(
)
1
2
(
)
1
(
)
,
(
δ
θ
δ
θ
δ
θ
θ
t
x
i
t
x
i
i
i
t
x
x
=
+
+
=
+
=
∂
∂

22
Podstawiaj c pierwsz pochodn temperatury po czasie i drug pochodn po
współrz dnej x do równania (wzór 14) otrzymujemy:
2
)
,
(
2
)
,
(
δ
θ
λ
ωθ
t
x
i
C
t
x
i
=
Z równania powy szego otrzymujemy:
Wzór 11
πν
ωρ
λ
δ
D
c
=
=
2
Wielko
δ
nosi nazw gł boko ci wnikania fali termicznej i oznacza gł boko na
której amplituda fali termicznej maleje e (gdzie e jest podstaw logarytmów
naturalnych) razy.
Analizuj c przesuni cie fazowe pomi dzy zmianami temperatury na
powierzchni i na pewnej gł boko ci mo emy okre li połówkow długo fali. Człon
w nawiasie po prawej stronie równania (wzór 15) oznacza faz fali w punkcie
o współrz dnej x w chwili t.
Obliczaj c x’ dla którego opó nienie fazowe wynosi
π
otrzymujemy nast puj c
zale no na połówkow długo fali:
gdzie
Λ
oznacza długo fali termicznej.
Warto zauwa y , e w odległo ci
Λ
/2 od powierzchni, amplituda fali termicznej
maleje e , czyli 22,6 razy.
πδ
=
=
Λ
'
2
x

23
IDEE POMIAROWE WSPÓŁCZYNNIKA PRZEWODNICTWA
CIEPLNEGO
3.1. Metoda ustalonego przepływu ciepła.
Najprostsze metody pomiaru współczynnika przewodzenia ciepła polegaj na
wytworzeniu ustalonego przepływu ciepła, tak aby rozkład temperatury wewn trz
próbki substancji u ytej do pomiaru nie zmieniał si w czasie. Wtedy wewn trz całej
próbki spełniony jest warunek stacjonarno ci
0
=
∂
∂
t
T
i je li przepływ zachodzi tylko
w jednym kierunku, po scałkowaniu równania opisuj cego przewodno ciepln
otrzymujemy
.
const
x
T =
∂
∂
Obieraj c na osi x dwa punkty w odległo ci L i mierz c
temperatury T
1
i T
2
w tych punktach mo emy wówczas na podstawie równania
(wzór 1) obliczy warto
λ
za pomoc bezpo redniego pomiaru przepływu ciepła
przez jednostk powierzchni, poniewa wtedy:
Wzór 12
L
T
T
x
T
1
2
−
=
∂
∂
oraz
L
T
T
t
Q
1
2
−
=
∂
∂
λ
Dobre przewodniki ciepła.
Post powanie przy wyznaczaniu współczynnika przewodzenia ciepła dobrego
przewodnika upraszcza si dzi ki stosunkowo małej roli strat ciepła. Niemniej jednak
nale y i tu podj pewne rodki ostro no ci, aby poprawki niezb dne dla
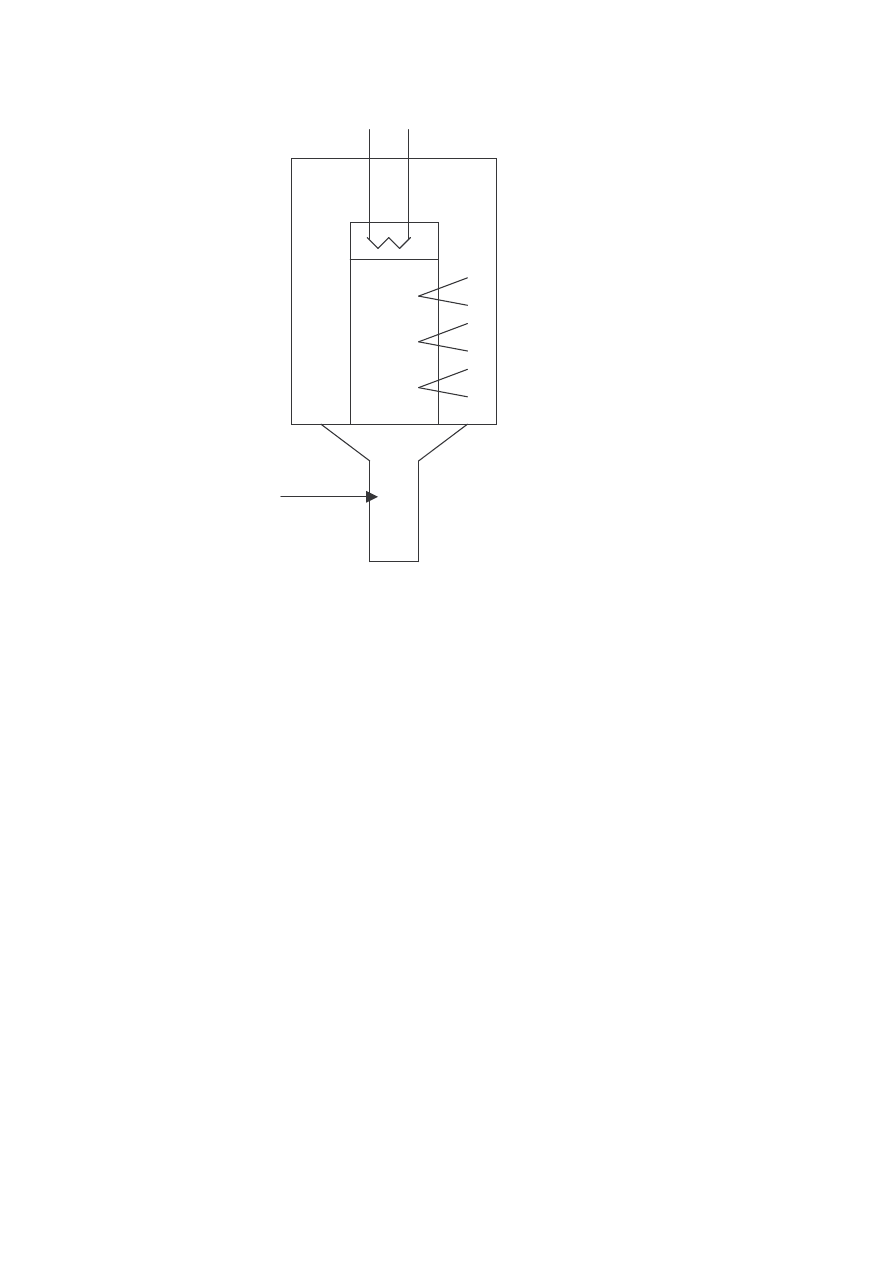
uwzgl dnienia tych strat były jak najmniejsze. Typowe urz dzenie stosowane do
pomiaru współczynnika przewodzenia ciepła pokazano na poni szym rysunku.
24
doprowadzenia grzejnika
upływ ciepła
Rysunek 3 Urz dzenie stosowane do wyznaczania współczynnika przewodzenia ciepła.
Energia elektryczna dostarczana do grzejnika w temperaturze T wytwarza stały
gradient temperatury wzdłu próbki w kształcie pr ta. Wytwarzany gradient
temperatury jest kontrolowany za pomoc termopar T
1
, T
2
, T
3
, mo na go zatem łatwo
okre li . Przekrój pr ta jest znany, mo na wi c za pomoc wzoru (wzór 17) obliczy
λ
, pod warunkiem, e energia dostarczana do pr ta z grzejnika jest znana i e nie ma
adnych istotnych strat ciepła z pr ta. Straty ciepła mo na zmniejszy do minimum
przez izolowanie pr ta i umieszczenie wokół izolowanego pr ta rury osłonowej
z regulowanymi grzejnikami odtwarzaj cymi rozkład temperatury wzdłu pr ta,
zapobiegaj c w ten sposób odpływowi ciepła z pr ta. Ciepło płyn ce wzdłu pr ta
okre la si usuwaj c pr t z przyrz du i wyznaczaj c energi potrzebn wówczas do
utrzymania grzejnika w tej samej temperaturze T. Poniewa energia ta, równa
z grubsza podwojonej energii traconej ze swobodnej powierzchni grzejnika gdy pr t
znajduje si w przyrz dzie, jest obecnie tracona przez powierzchni grzejnika
całkowicie odsłoni t , mo na obliczy ciepło płyn ce wzdłu próbki.
T
T1
T2
próbka
T3
25
Główna trudno wyst puj ca w tej metodzie polega na zapewnieniu dobrego kontaktu
termicznego mi dzy grzejnikami a pr tem. Trudno t pokonuje si zwykle w ten
sposób, e rozkład temperatury wzdłu pr ta przyrównuje si do rozkładu temperatury
wzdłu innego pr ta z substancji o znanym przewodnictwie cieplnym. Kontakt
termiczny jest jednakowy dla obu pr tów. Inny sposób unikni cia wpływu złego
kontaktu termicznego polega na dostarczaniu ciepła przez pr d płyn cy w samym
pr cie.
Złe przewodniki ciepła.
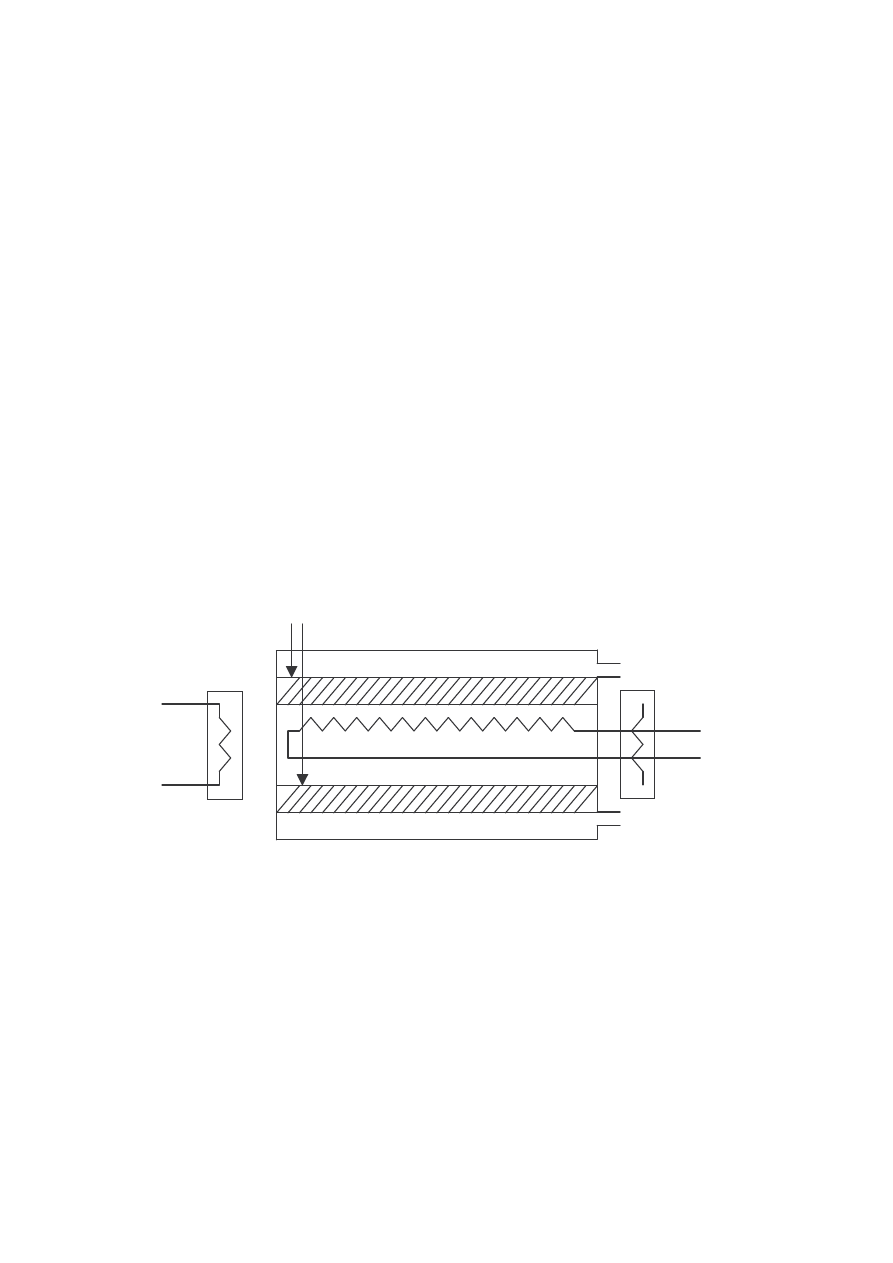
Najprostszy sposób przeprowadzenia dokładnego pomiaru współczynnika
przewodzenia ciepła ciał stałych o małej przewodno ci cieplnej polega na
sporz dzeniu dwóch, mo liwie jednakowych próbek badanej substancji, które
umieszcza si w przyrz dzie pokazanym na poni szym rysunku pomi dzy
miedzianymi walcami.
próbki
woda
pier cie
grzejnik
ochronny
woda
Rysunek 4 Urz dzenie stosowane do wyznaczania współczynnika przewodzenia ciepła złych
przewodników.
Je li rozkład temperatury pier cienia ochronnego jest regulowany tak, aby
odpowiadał rozkładowi w grzejniku i próbkach, to nie ma adnych strat ciepła do
otoczenia i połowa ciepła powstałego w grzejniku popłynie przez ka d z warstw
substancji. Poniewa grubo i przekrój próbek s znane, a temperatur grzejnika
i walców chłodzonych wod mo na łatwo zmierzy , bez trudu oblicza si
współczynnik przewodzenia ciepła.

26
Metoda ogrzewania elektrycznego.
Ogólne równanie przewodnictwa cieplnego dla pr ta przez który przepływa
pr d ma nast puj c posta :
A
c
T
ph
A
c
I
x
T
c
t
T
w
w
w
ρ
σρ
ρ
λ
)
(
2
2
2
2
−
+
∂
∂
=
∂
∂
gdzie:
h(T) – funkcja okre laj ca ilo ciepła traconego w jednostce czasu z jednostki
powierzchni o temperaturze T,
p- obwód pr ta,
c
w
- ciepło wła ciwe,
ρ
−g sto materiału,
σ
-przewodnictwo elektryczne wła ciwe,
Α
−przekrój poprzeczny pr ta,
λ
-współczynnik przewodno ci cieplnej,
2
2
A
I
σ
- ilo ciepła wnoszona do układu przez przepływ pr du,
Dla pr ta dobrze izolowanego dla unikni cia strat ciepła równanie dla stanu
ustalonego przy przepływie pr du przyjmie posta :
Wzór 13
0
2
2
2
2
=
+
∂
∂
A
I
x
T
σ
λ
Je li oba ko ce pr ta b d si znajdowa w stałej temperaturze jak pokazano to na
rysunku poni ej, wówczas rozkład temperatury wzdłu pr ta mo na wyznaczy przez
scałkowanie równania (wzór 18). W przypadku gdy zakres zmian temperatury jest
niewielki, tak e
λ
i
σ
mo na przyj za stałe, wówczas:
)
(
2
0
1
2
2
2
T
T
A
L
I
−
=
σ
λ
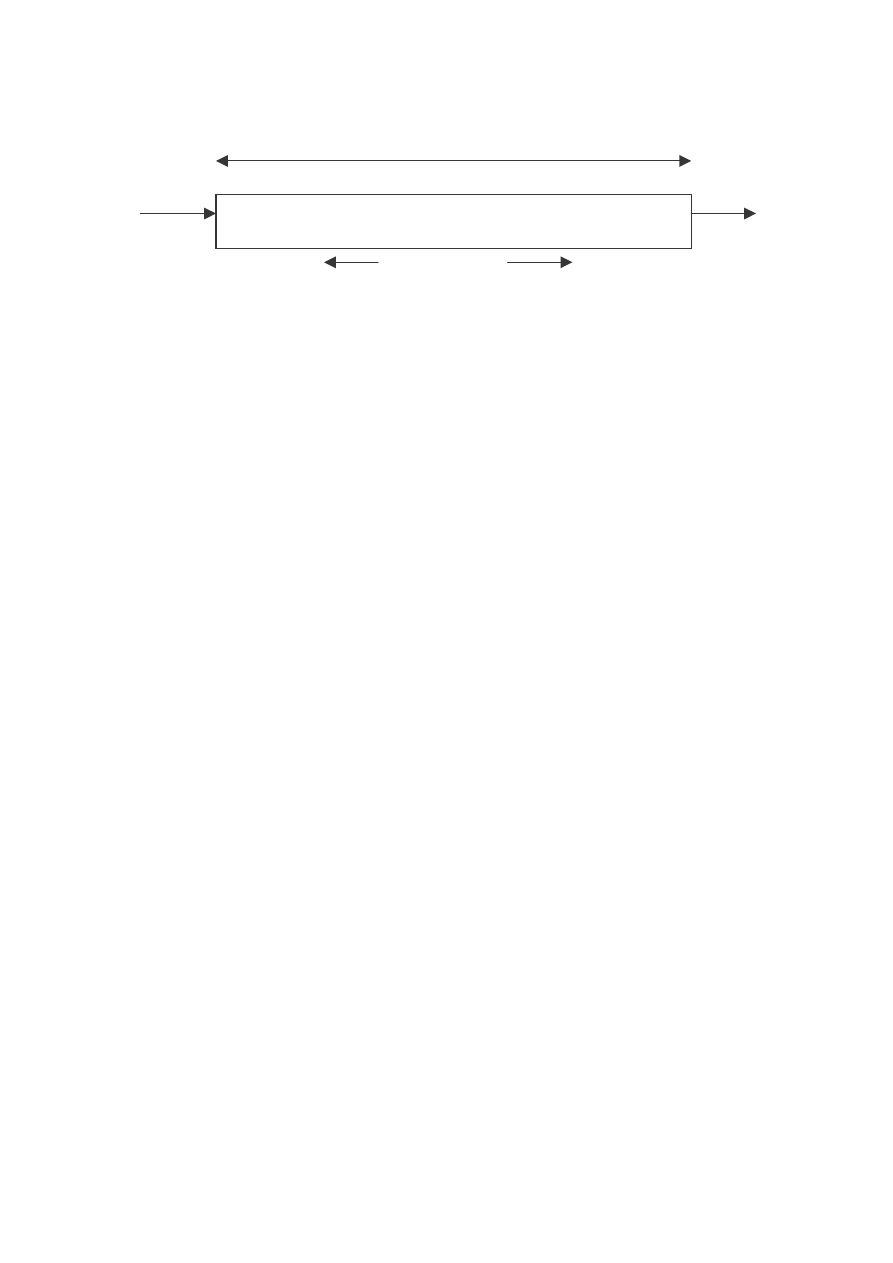
27
2L
T
0
T
1
T
0
I
-x
x=0
+x
Rysunek 5 Rozkład temperatury wzdłu pr ta przewodz cego pr d.
Je li zakres temperatur nie jest mały, wtedy przy całkowaniu trzeba uwzgl dni
zale no
λ
i
σ
od temperatury, a tym samym, tak e zale no od poło enia wzdłu
pr ta.
STANOWISKO LABORATORYJNE DO POMIARU PRZEWODNO CI
CIEPLNEJ METOD DYNAMICZN
4.1. Metoda dynamiczna z okresowym przepływem ciepła.
Celem pracy było zbudowanie zestawu do pomiaru przewodno ci cieplnej
metod dynamiczn . Układ przeznaczony jest do laboratorium Podstaw Fizyki
Politechniki Wrocławskiej.
Pomiar współczynnika przewodno ci cieplnej polega na wygenerowaniu periodycznej
fali termicznej (zbli onej do sinusoidy) w walcu miedzianym i rejestracji zale no ci
rozkładu temperatury od czasu. Fala termiczna wzbudzona jest za pomoc modułu
Peltiera podł czonego do generatora pr du o niskiej cz sto ci.
Walec miedziany ma wymiary:
- długo h=200 [mm]
- rednica
φ=20 [mm]
W walcu s umieszczone termopary które słu do pomiaru rozkładu temperatury
wzdłu walca. Spoina wspólna dla termopar znajduje si na ko cu rozpatrywanego
walca, a wi c siła termoelektryczna termopar jest proporcjonalna do ró nicy
I
I

28
walec wykonany z miedzi
temperatur pr ta na jego ko cu i temperatury pr ta w punkcie w którym umieszczona
jest dana termopara.
Schemat układu pomiarowego przedstawiony jest na rysunku 9.
T1
T2
T3
T4
moduł
Peltiera
tu znajduje si
spoina odniesienia
„przej ciówka”
Rysunek 6 Schemat układu do pomiaru przewodno ci cieplnej.
Podczas wykonywania pomiarów komputer rejestruje zale no temperatury
od czasu T(t) dla dwóch wybranych termopar. Pomiar współczynnika przewodno ci
cieplnej sprowadza si do okre lenia ró nicy czasu po którym fazy dwóch sygnałów
pochodz cych z ró nych termopar s zgodne. Na podstawie równania (wzór 15)
opisuj cego rozchodzenie si fali termicznej w pr cie, mo emy zapisa :
)
(
)
(
1
2
1
1
δ
ω
δ
ω
x
t
x
t
−
=
−
gdzie:
ω
− jest cz sto ci z jak generowana jest fala termiczna
δ
- gł boko wnikania fali termicznej
x
1
, x
2
- odległo ci do rozpatrywanych punktów pomiarowych mierzone od pocz tku
walca
t
1
, t
2
- czasy w których fala jest w tej samej fazie
Jedyn niewiadom w tym równaniu jest
δ
. Po elementarnych przekształceniach
otrzymujemy:
wzór 14
)
(
2
1
2
1
t
t
x
x
−
−
=
ω
δ

29
Znaj c gł boko wnikania fali termicznej, ciepło wła ciwe miedzi oraz jej g sto
mo emy obliczy współczynnik przewodno ci cieplnej. Korzystaj c z zale no ci na
gł boko wnikania fali termicznej (wzór 16) otrzymujemy:
Wzór 15
2
2
ρ
ω
δ
λ
w
c
=
gdzie:
ω
− jest cz sto ci z jak generowana jest fala termiczna
c
w
- ciepło wła ciwe miedzi
ρ
- g sto miedzi
Podstawiaj c wzór 19 do wzoru 20 uzyskujemy ko cow posta wzoru na
współczynnik przewodno ci cieplnej:
Współczynnik przewodno ci cieplnej mo na wyznaczy analizuj c amplitud sygnału
mierzonego przez wybrane termopary w odpowiednich punktach. Pierwszy człon
w rozwi zaniu równania przewodnictwa cieplnego(nr równania) okre la nam zmian
amplitudy sygnału, która maleje expotencjalnie wraz z odległo ci . Znaj c wi c
warto ci temperatur mierzone w dwóch ró nych miejscach w tym samym czasie
mo emy wyliczy gł boko wnikania fali termicznej:
gdzie: T
0
jest temperatur zmierzon przez termopar umieszczon bli ej modułu
Peltiera, T jest temperatur zmierzon przez dalsz termopar za x jest odległo ci
pomi dzy tymi termoparami.
Wstawiaj c t warto do wzoru 20 otrzymujemy wyra enie na współczynnik
przewodno ci cieplnej:
(
)
(
)
2
2
1
2
2
1
2
t
t
x
x
c
w
−
−
=
ω
ρ
λ
=
0
ln
T
T
x
δ
30
Odległo mi dzy kolejnymi spoinami termopar wynosi:
- T1 – T2 58,52 [mm]
- T1 – T3 116,0 [mm]
4.2. Podzespoły tworz ce stanowisko.
4.2.1. Zjawisko Peltiera.
Zjawisko Peltiera z fizycznego punktu widzenia nale y sklasyfikowa do
zjawisk termoelektrycznych, obok zjawiska Seebecka - efekt powstawania ró nicy
potencjałów elektrycznych na styku metali lub półprzewodników (termopary),
zjawiska Thomsona – w którym efekty cieplne towarzysz przepływowi pr du przez
przewodnik, w którym wyst puje gradient temperatury.
Zjawisko Peltiera polega na pochłanianiu lub wydzielaniu ciepła podczas
przepływu pr du przez zł cze metali lub półprzewodników. Cz ciej jednak realizuje
si moduły Peltiera z materiałów półprzewodnikowych, poniewa charakteryzuj si
one silniejsz zale no ci koncentracji no ników pr du od temperatury ni ma to
miejsce w przypadku metali.
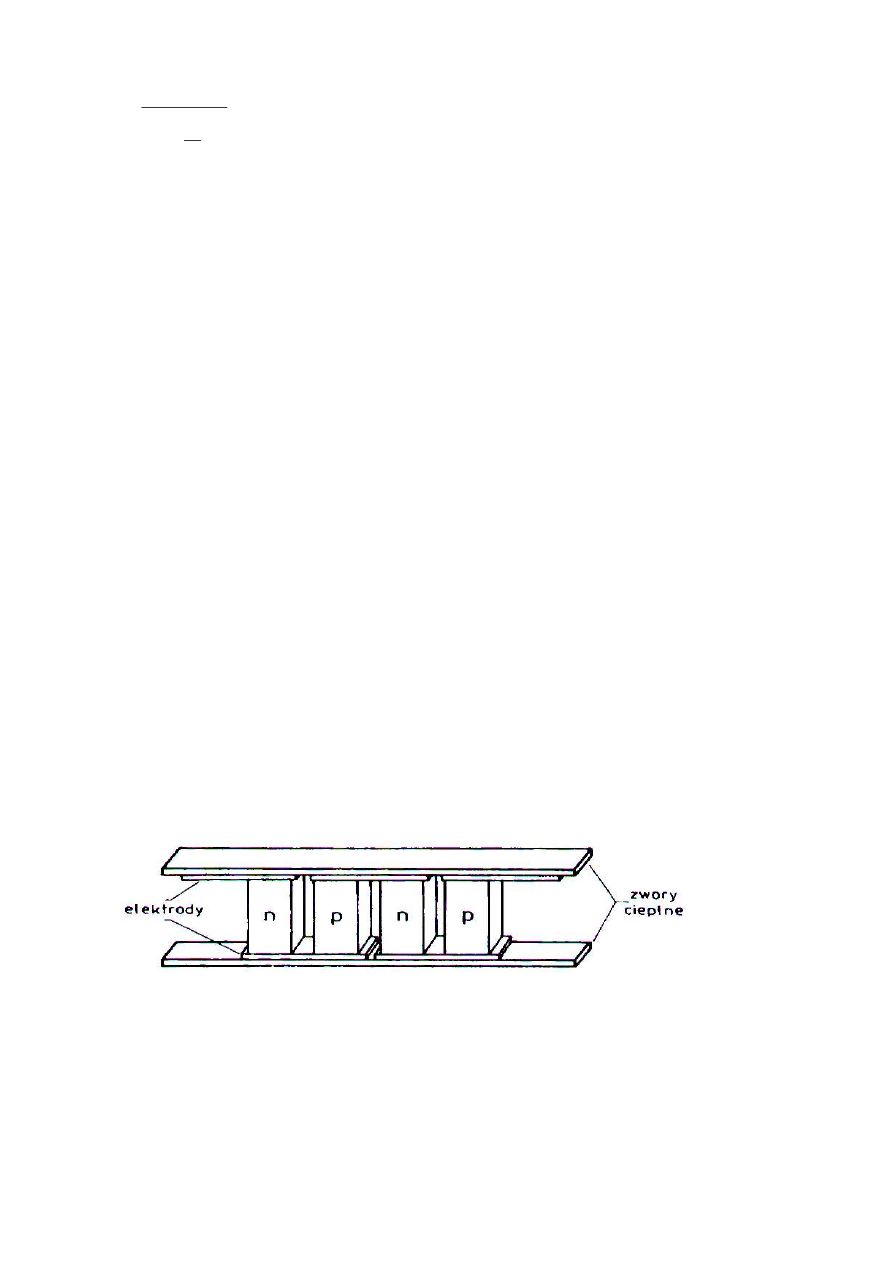
Moduł Peltiera składa si z poł czonych na przemian segmentów wykonanych
z półprzewodnika typu n oraz z półprzewodnika typu p. Elektrycznie segmenty te
poł czone s szeregowo, natomiast cieplnie - równolegle.
Rysunek 7 Budowa półprzewodnikowego modułu Peltiera.
Chłodzenie termoelektryczne oparte jest o prac elementu półprzewodnikowego
zwanego modułem Peltiera i wyst puje, gdy przez element płynie, w odpowiednim
2
0
2
ln
2
=
T
T
x
c
w
ρ
ω
λ
31
kierunku, stały pr d elektryczny. Elementy te wykonuje si w kształcie płaskich
prostok tnych płytek z dwoma elektrycznymi przył czami.
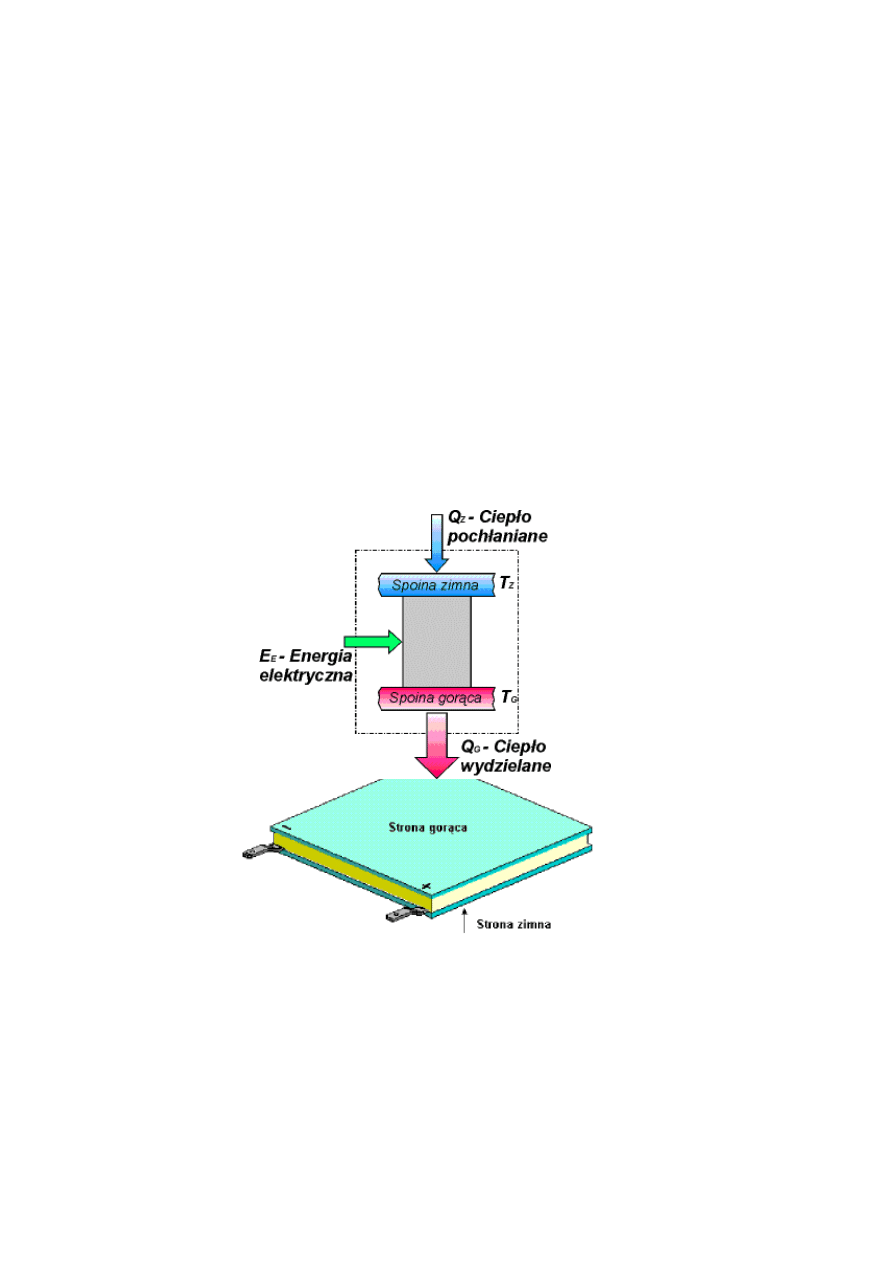
Rysunek 8 Moduł Peltiera.
Moduł Peltiera stanowi bateria pojedynczych ogniw Peltiera umieszczona
mi dzy przeciwległymi okładkami, ceramicznymi płytkami. W ogniwie tym podczas
przepływu pr du zachodz procesy fizyczne, których efektem jest pobieranie energii
cieplnej od otoczenia na spoinie zimnej i jej "przepompowywanie" na spoin gor c .
W module objawia si to schładzaniem jednej "zimnej" strony i ogrzewaniem drugiej
"gor cej" strony (rys.11). Na obie strony przekazywana jest tak e energia cieplna
powstała na skutek przepływu pr du elektrycznego - ciepło Joule’a.
Rysunek 9 Zasada działania modułu Peltiera.
Zjawisko Peltiera, jak zostało wspomniane wcze niej polega na wydzielaniu lub
pochłanianiu ciepła Q
p
podczas przepływu pr du przez zł cze dwóch ró nych metali
lub półprzewodników. Aby przenie ładunek elektryczny q przez zł cze, na którym
wyst puje ró nica potencjałów U
ab
, nale y wykona prac :

32
W celu utrzymania stałej temperatury zł cza nale y doprowadzi lub pobra ciepło:
gdzie:
- Q
p
ciepło Peltiera
-
π
p
stała Peltiera
Warto tej stałej zale y od rodzaju stykaj cych si metali (półprzewodników) oraz
temperatury zł cza. Stała Peltiera jest niezale na od nat enia pr du płyn cego przez
zł cze oraz jego powierzchni. Zmiana kierunku przepływu pr du powoduje zmian
kierunku przekazywania ciepła - podczas przepływu pr du przez zł cze w jednym
kierunku ciepło jest wydzielane, gdy pr d płynie w kierunku przeciwnym ciepło jest
pobierane.
Je eli przez zł cze płynie pr d o nat eniu I, to energia cieplna wydzielana lub
pobierana w jednostce czasu okre lona jest równaniem:
Wzór 16
gdzie:
-
α
współczynnik Seebecka
- T temperatura w skali bezwzgl dnej
Je eli pr d płynie przez przewodnik, w którym wyst puje gradient temperatury, to
w zale no ci od kierunku przepływu pr du nast puje wydzielanie lub pochłanianie
ciepła Thomsona w jednostce czasu:
Wzór 17
gdzie:
-
τ
współczynnik Thomsona
- P
T
ilo ciepła wydzielonego lub pochłoni tego w jednostce czasu
W obwodzie, oprócz ciepła Peltiera oraz ciepła Thomsona, wydzielane jest
ciepło Joule’a o mocy
2
RI
P
=
gdzie R oznacza opór elektryczny przewodnika.
ab
qU
W
=
P
P
q
Q
π
=
TI
I
dt
dQ
P
P
P
P
α
π
=
=
=
dx
dT
I
dt
dQ
P
T
T
τ
=
=

33
Całkowita moc wydzielona w układzie jest sum ciepła Joule’a, ciepła Thomsona oraz
ciepła Peltiera. Nale y pami ta , e ciepło Peltiera mo e by dodatnie lub ujemne,
w zale no ci od kierunku przepływu pr du przez zł cze.
Je eli w przewodniku wyst puje gradient temperatury, to wówczas mamy do
czynienia z przepływem ciepła z cz ci przewodnika o wy szej temperaturze (T
g
),
które b dziemy nazywa gor cym ko cem, do miejsca o ni szej temperaturze (T
z
),
które nazwiemy ko cem zimnym. Ciepło to przekazywane jest dzi ki przewodnictwu
cieplnemu, a moc przekazywanego ciepła jest równa :
gdzie:
-
λ
współczynnik przewodnictwa cieplnego,
- S pole przekroju poprzecznego przewodnika,
- h odległo pomi dzy zimnym i gor cym ko cem przewodnika.
W warunkach ustalonych, zimny koniec w jednostce czasu pobiera z zewn trz
ciepło:
gdzie:
Z
G
T
T
T
−
=
∆
Gor cy koniec w jednostce czasu oddaje na zewn trz ciepło:
Czynnik 1/2 wyst puj cy po prawej stronie powy szych równa wynika z zało enia,
e ciepło Joule’a oraz ciepło Thomsona „dzielone jest równo” pomi dzy zimny
i gor cy koniec.
Moc pobierana ze ródła pr du P
el
jest równa ró nicy mocy wydzielanej przez gor cy
koniec oraz mocy pochłanianej przez koniec zimny:
h
T
T
S
dt
dQ
P
z
g
prz
prz
)
(
−
=
=
λ
h
T
KS
RI
h
T
I
I
T
dt
dQ
P
z
chl
chl
∆
−
−
∆
±
=
=
−
2
2
1
2
1
τ
α
h
T
KS
RI
h
T
I
I
T
dt
dQ
P
g
grz
grz
∆
−
−
∆
=
=
2
2
1
2
1
τ
α
34
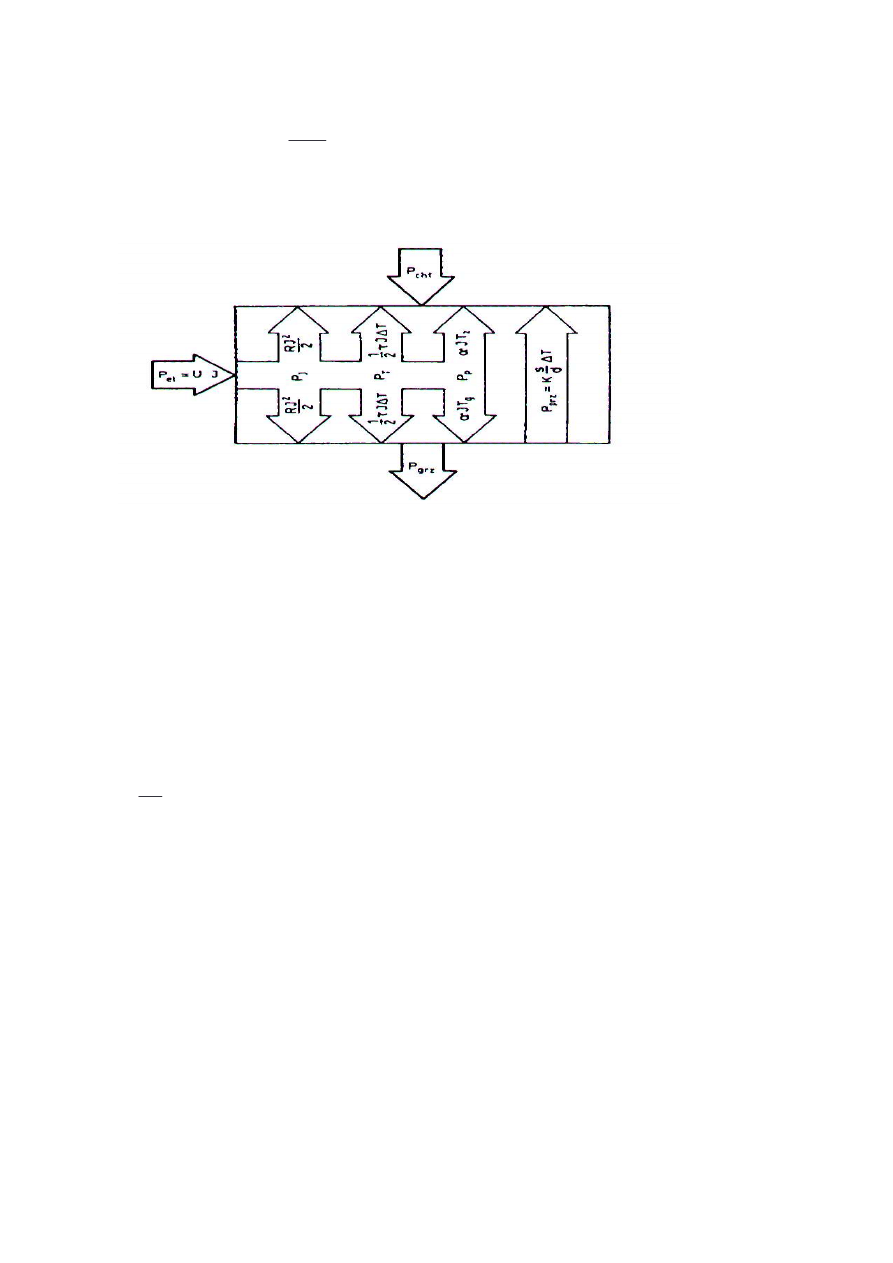
Bilans mocy pobieranej i oddawanej przez moduł Peltiera przedstawia poni szy
rysunek:
Rysunek 10 Bilans mocy w module Peltiera (przyj to, e ciepło Thomsona jest wydzielane).
Termodynamicznie moduł Peltiera stanowi pomp ciepln , która pod wpływem
wło onej energii elektrycznej przepompowuje energi ciepln z jednej strony na
drug . Najwa niejszym jego parametrem jest maksymalna moc cieplna Q
Zmax
, która
jest mo liwa do przepompowania ze strony zimnej na gor c .
Wska nikiem, który okre la przydatno modułu pod wzgl dem chłodniczym
jest współczynnik wydajno ci chłodniczej:
gdzie:
Q
Z
- moc cieplna modułu (energia cieplna pobrana przez stron zimn )
Q
E
- wło ona moc elektryczna potrzebna na przepompowanie energii cieplnej ze
strony zimnej na gor c .
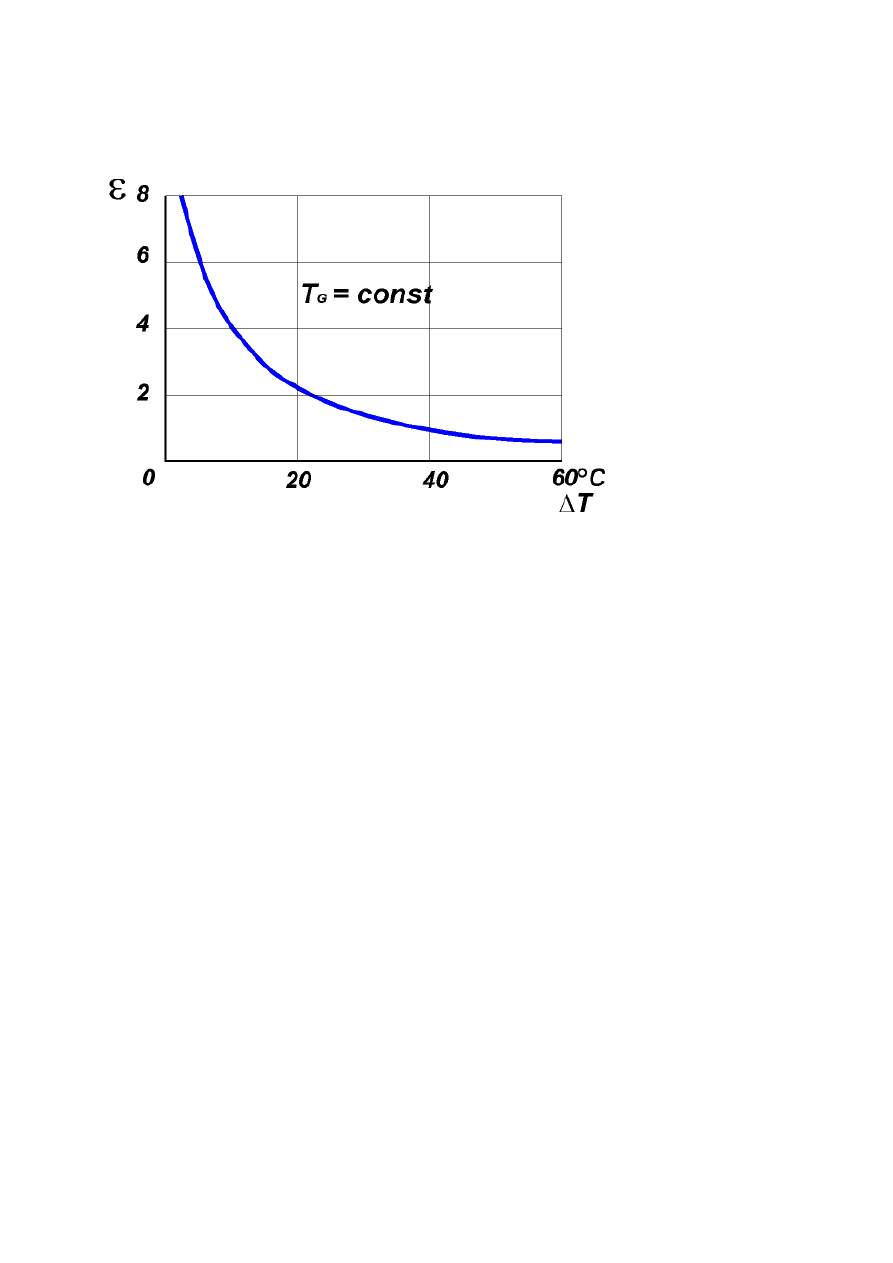
Na rysunku 14 przedstawiono orientacyjn zale no współczynnika
wydajno ci chłodniczej od ró nicy temperatury mi dzy okładkami modułu T=T
G
- T
Z
przy stałej temperaturze strony gor cej T
G
= const. Wynika st d wniosek, e praca
modułu jest najefektywniejsza dla małych warto ci Q
Z
, w zakresie od 0 do 20°C.
W tym zakresie ró nicy temperatury praca modułu jest najbardziej ekonomiczna.
h
T
I
RI
T
I
UI
P
el
∆
+
+
∆
=
=
τ
α
2
E
Z
Q
Q
=
ε
35
Oznacza to, e zu ywaj c porcj energii elektrycznej, moduł przepompowuje
przynajmniej dwukrotnie wi cej energii cieplnej.
Rysunek 11 Zale no współczynnika wydajno ci chłodniczej od ró nicy temperatury ∆∆∆∆T mi dzy
okładkami modułu Peltiera, przy stałej temperaturze strony gor cej T
G
=const.
Na prac modułu ma wpływ wiele parametrów. Najwa niejsze z nich to
parametry elektryczne: nat enie I i napi cie U pr du stałego przepływaj cego przez
moduł, oraz parametry cieplne: temperatura strony gor cej T
G
oraz temperatura strony
zimnej T
Z
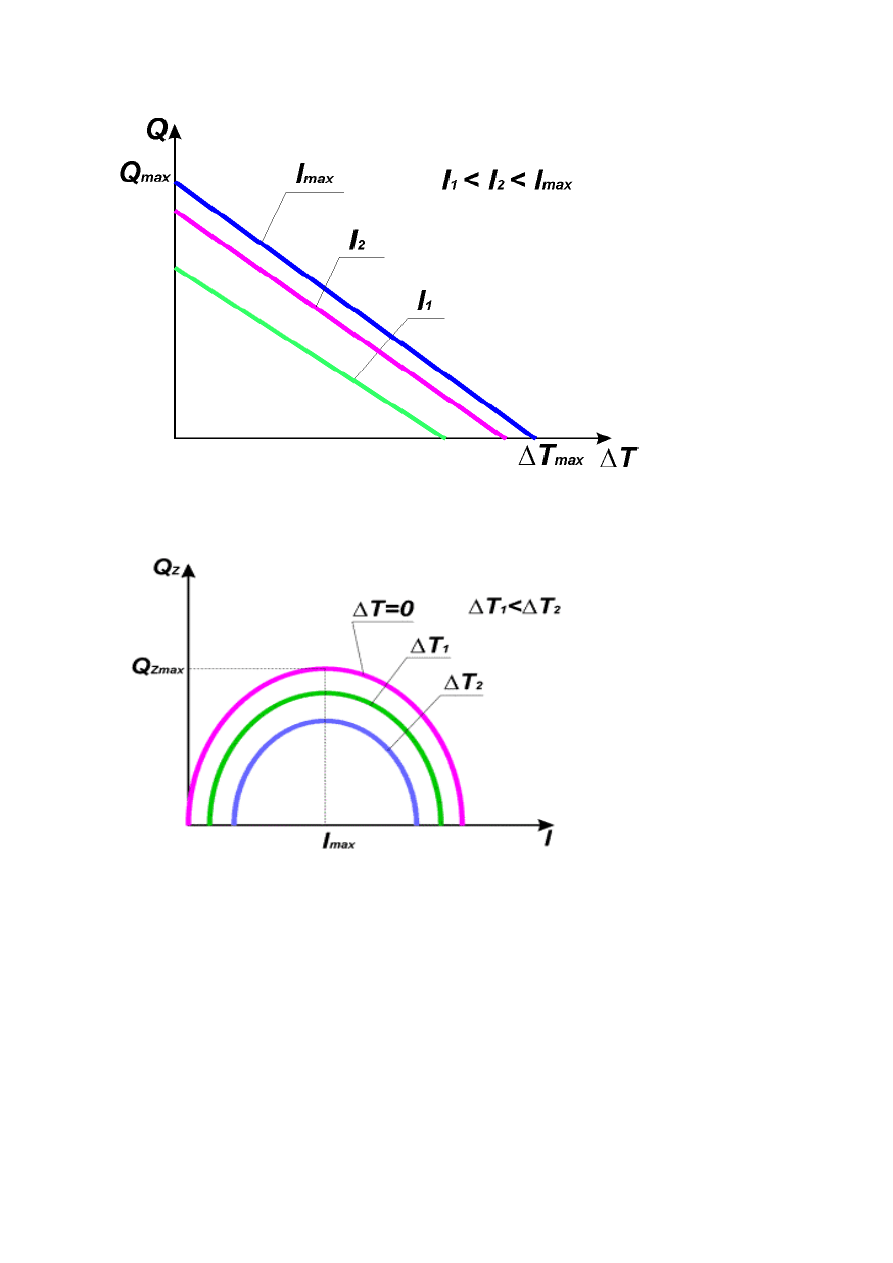
. Rysunek 15 obrazuje przebieg warto ci mocy cieplnej Q
Z
uzale niony od
ró nicy temperatury mi dzy okładkami modułu, przy stałej warto ci nat enia pr du I.
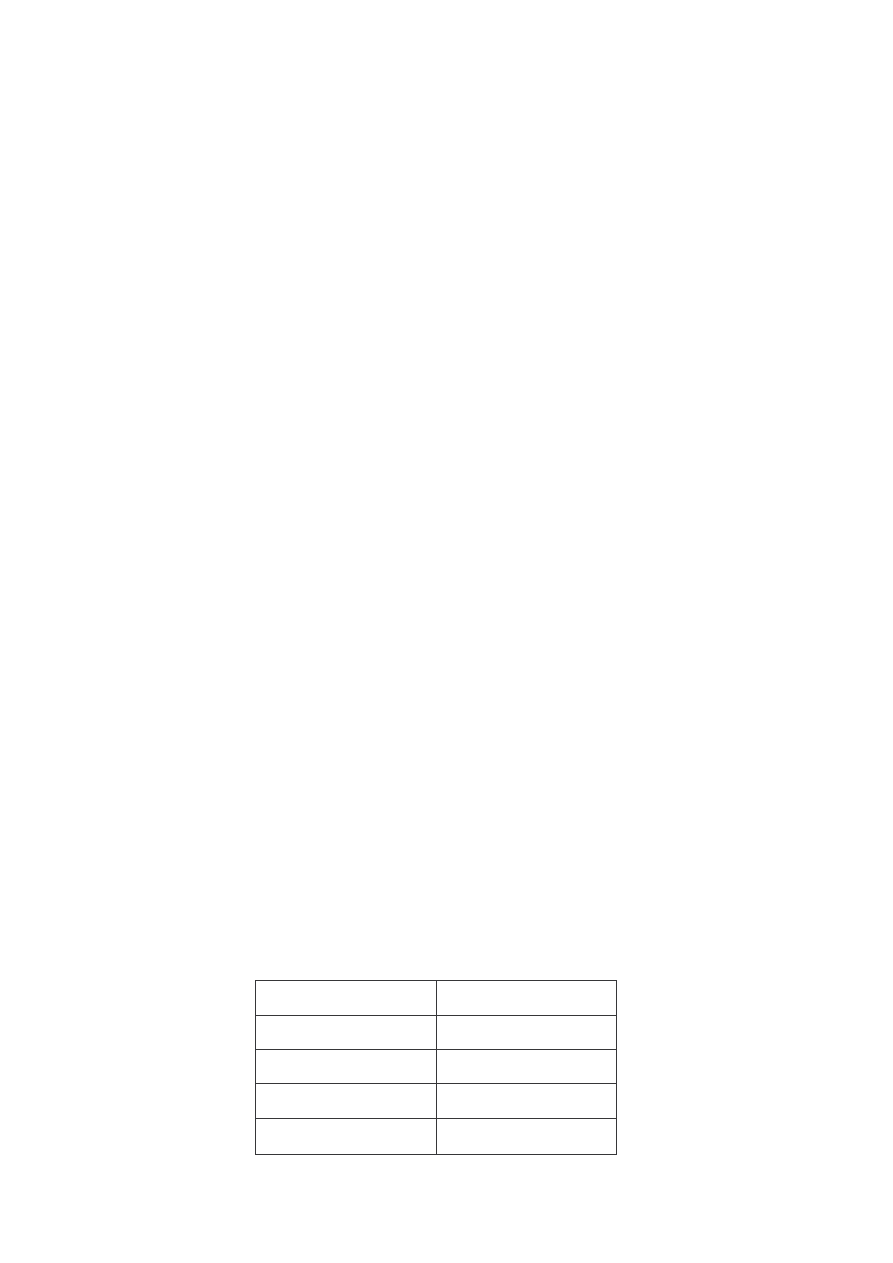
Z kolei na rysunku 16 przedstawiono zale no mocy cieplnej Q
Z
od warto ci
nat enia pr du elektrycznego I, przy stałej ró nicy temperatur
∆
T.
36
Rysunek 12 Zale no mocy cieplnej Q
Z
od
ró nicy temperatur ∆∆∆∆T przy stałym nat eniu pr du I.
Rysunek 13 Zale no mocy cieplnej Q
Z
od pr du I przy stałej warto ci ró nicy temperatur ∆∆∆∆T.
Z charakterystyk tych wida , e moc cieplna modułu Q
Z
maleje wraz ze
wzrostem ró nicy temperatur
∆
T
mi dzy jego okładkami, a maksimum osi ga przy
równej temperaturze strony zimnej i strony gor cej (
∆
T =0). Zmniejszenie nat enia
pr du I powoduje tak e pogorszenie parametrów cieplnych modułu. Dla okre lonej
ró nicy temperatur
∆
T istnieje zawsze taka warto pr du, zwana pr dem
maksymalnym I
max
, daj ca maksymaln warto mocy chłodniczej Q
Zmax
. Zwi kszenie
nat enia pr du ponad I
max
obni a parametry cieplne modułu. Nale y zauwa y , co nie
37
jest pokazane na rysunkach, e wraz ze wzrostem temperatury strony gor cej, maleje
opór wewn trzny modułu, przez co niewiele, ale wzrastaj jego wła ciwo ci cieplne.
Mo liwe jest wówczas uzyskanie wi kszej ró nicy temperatur mi dzy stronami
modułu.
Ze wzgl du na małe rozmiary, szybko uzyskiwania odpowiedniej warto ci
temperatury oraz jej do szerokiego zakresu jak i równie łatwo w zasilaniu tych
elementów, moduły Peltiera znalazły obecnie zastosowanie w wielu dziedzinach nauki
i techniki.
Nale y tutaj wymieni takie zastosowania jak chłodzenie procesorów w komputerach
(pewnym niebezpiecze stwem jest tutaj mo liwo skraplania si pary co mo e
doprowadzi do zwarcia, dlatego procesor powinien by zabezpieczony przed par
wodn oraz dla bezpiecze stwa powinno instalowa si wiatraczek w celu lepszego
odprowadzenia ciepła). Kolejnym zastosowaniem tych modułów s tzw. lodówki
półprzewodnikowe, lodówki samochodowe. Na podstawie wy ej opisanych
elementów realizuje si klimatyzacj w samochodach, chłodzi si skafandry dla
kosmonautów, stoły laboratoryjne itp.
W przedstawionym tutaj zagadnieniu, moduł Peltiera został wykorzystany do
oscylacyjnej zmiany temperatury, który jest sterowany za pomoc generatora małej
cz stotliwo ci.
W tabeli poni ej s przedstawione parametry techniczne wykorzystanego modułu.
Parametry techniczne modułu Peltiera
Tabela 2
Wymiary
30x30x3,6 [mm]
U
zas
14,5 [V]
I
max
3,30 [A]
Q
max
25,7 [W]
∆T
65,0 [C]

38
W poni szej tabeli podane s wyliczone na podstawie wykresów warto ci
współczynnika przewodno ci cieplnej:
Tabela 3
Termopary T1 i T2
Termopary T1 i T3
Okres T [s]
λ
f
λ
a
λ
f
λ
α
60
389,7
982,6
120
388,1
467,3
381,5
352,3
180
381,6
451,7
441,8
240
389,7
376,4
382,8
479,3
gdzie:
λ
f
współczynnik wyliczony z przesuni cia fazowego,
λ
a
współczynnik
wyliczony metod amplitudow .
Dla T=60 [s] i punktów pomiarowych T1 i T3 współczynnik przewodno ci cieplnej
nie został wyliczony, poniewa sygnał docieraj cy do termopary T3 miał tak mał
amplitud i był tak „rozmyty”, e nie mo na było okre li przesuni cia fazowego. Za
dla T=180 [s] i dla tych samych punktów pomiarowych nie mo na było dokładnie
wyznaczy przesuni cia fazowego.
Na poni szych wykresach przedstawione s wyniki pomiarów dla temperatur
odczytywanych z termopar: T1 - T2 i T1-T3 z ró nymi okresami zmian.
Wyszukiwarka
Podobne podstrony:
przewodnictwo cieplne id 407051 Nieznany
przewodnik biofizyka id 407075 Nieznany
przewodnik pulmonologia id 4073 Nieznany
przewodnik jalowka id 407107 Nieznany
przewodzenie motywowanie id 407 Nieznany
przewodnik dydaktyczny 2 id 407 Nieznany
Przewody krAltkie id 407363 Nieznany
Przewod pokarmowy id 406888 Nieznany
przewoz morskie id 407380 Nieznany
przewodnik dydaktyczny id 40709 Nieznany
obrobka cieplna id 328368 Nieznany
przewodnik dwf id 407097 Nieznany
przewodnik biofizyka id 407075 Nieznany
5 Srodki przewozowe id 39652 Nieznany
przewodnik praca ue[1] id 40732 Nieznany
Przewoznik osob 832204 id 40702 Nieznany
Patomorfologia przewodnik id 35 Nieznany
operator przewoznikiem id 33640 Nieznany
więcej podobnych podstron