- 1 -

Konspekt wykładu dla IEIP - 4

Obwody prądu sinusoidalnie zmiennego - cz. 2.

Idealne elementy pasywne jako odbiorniki w obwodach prądu
sinusoidalnie zmiennego.

Dla odbiorników pasywnych, liniowych w obwodach prądu sinusoidalnie zmiennego słuszne

są zależności (zwane prawem Ohma dla obwodów sinusoidalnych):







=

ϕ

=

Ψ

−

Ψ

⋅

=

const

I

Z

U

I

U

i







=

ϕ

−

=

Ψ

−

Ψ

⋅

=

const

U

Y

I

U

I

Przy zastosowaniu metody symbolicznej przybierają one postać:

I

Z

U

⋅

=

i

U

Y

I

⋅

=

Zbadajmy teraz jakie impedancje, admitancje i przesunięcia fazowe mają odbiorniki złożone z

idealnych liniowych elementów pasywnych.

Rezystor (idealny):

i

(t)

u

R(t)

R

Rezystor w obwodzie prądu

sinusoidalnie zmiennego

Opis matematyczny (z prawa Ohma):

)

t

(

i

R

)

t

(

R

u

⋅

=

.

Gdy prąd jest sinusoidalnie zmienny:

)

t

sin(

I

2

i

I

)

t

(

ψ

+

ω

⋅

=

również napięcie jest

sinusoidalnie zmienne:

)

t

sin(

U

2

u

U

R

)

t

(

R

ψ

+

ω

⋅

⋅

=

.

Napięcie to daje się wyliczyć z prawa Ohma jako:

)

t

sin(

I

R

2

i

R

u

I

)

t

(

)

t

(

R

ψ

+

ω

⋅

⋅

⋅

=

⋅

=

Stąd (porównując ostatnie wzory) mamy:







ψ

=

ψ

⋅

=

I

U

R

I

R

U

z czego wynika:









ψ

=

ψ

⋅

=

⋅

=

U

I

R

R

U

G

U

R

1

I

Jest to tzw. prawo Ohma dla rezystora poddanego wymuszeniu sinusoidalnie zmiennemu.

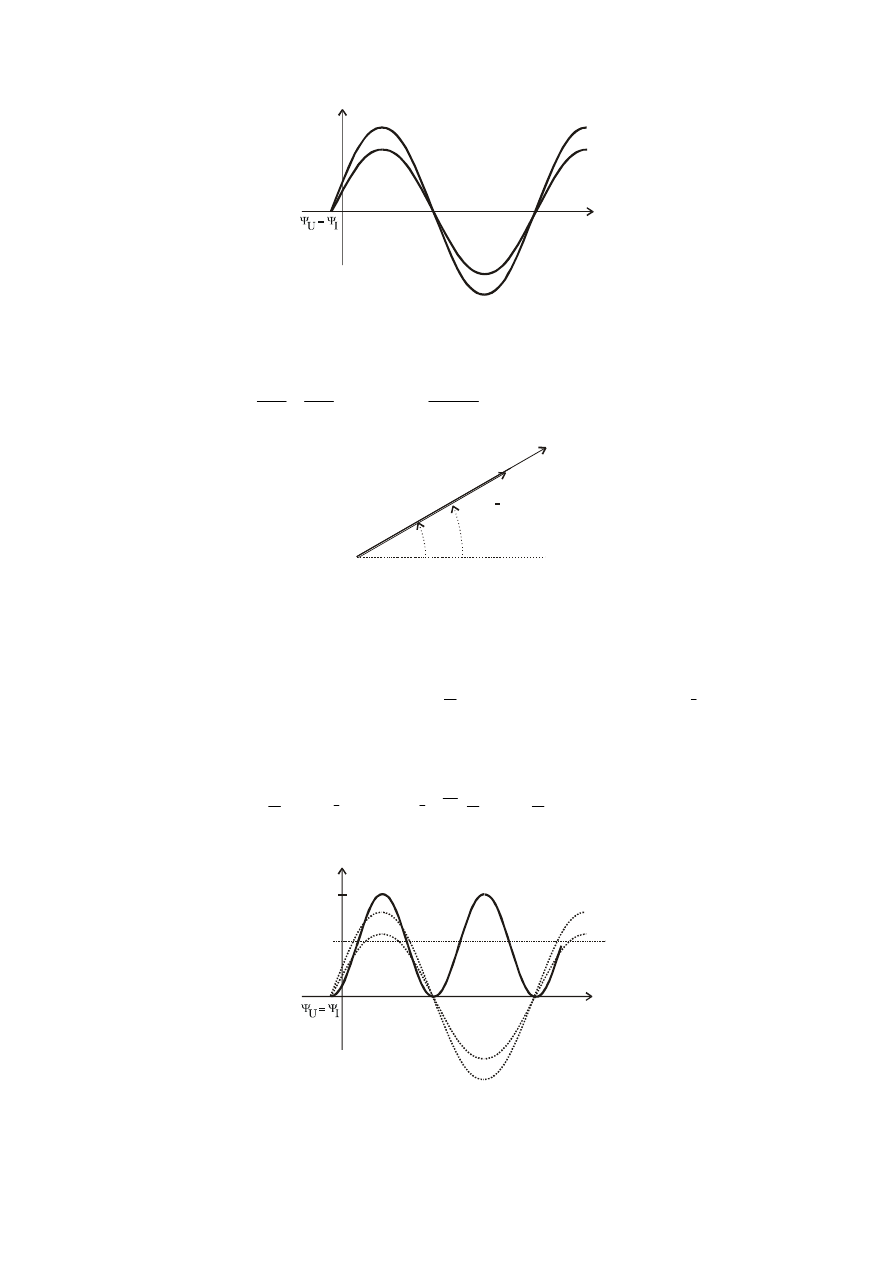
- 2 -

Przebiegi napięcia i prądu rezystora

u, i

R(t)

u

(t)

i

ωt

Impedancja, admitancja i kąt przesunięcia fazowego odbiornika złożonego z idealnego

rezystora wynoszą:

R

I

I

R

I

U

Z

R

R

=

⋅

=

=

,

G

U

G

U

Y

R

R

R

=

⋅

=

,

0

U

I

I

U

=

Ψ

−

Ψ

=

Ψ

−

Ψ

=

ϕ

I

ΨU

ΨI

U = R I

R

.

Wykres wskazowy prądu

i napięcia rezystora

Metoda symboliczna:

Z zależności







=

ψ

−

ψ

⋅

=

0

I

R

U

I

U

R

wynika:

I

R

e

I

R

e

U

U

I

j

U

j

R

R

⋅

=

⋅

⋅

=

⋅

=

ψ

ψ

Jest zatem:

I

R

R

U

⋅

=

i

R

R

U

G

U

R

1

I

⋅

=

⋅

=

Moc:

Przebieg wartości chwilowych mocy rezystora

u, i

U I

R

.

2U I

R

.

R(t)

u

R(t)

p

(t)

i

ωt

- 3 -

W każdej chwili czasowej jest:

)

t

(

)

t

(

R

)

t

(

R

i

u

p

⋅

=

)]

t

(

2

cos

1

[

2

1

I

U

2

)

t

(

sin

I

U

2

)

t

sin(

I

2

)

t

sin(

U

2

p

I

R

I

2

R

I

I

R

)

t

(

R

ψ

+

ω

−

⋅

⋅

=

ψ

+

ω

⋅

⋅

=

=

ψ

+

ω

⋅

⋅

⋅

ψ

+

ω

⋅

=

Ostatecznie:

)]

2

t

2

cos(

I

U

I

U

)]

2

t

2

cos(

1

[

I

U

p

I

R

R

I

R

)

t

(

R

ψ

+

ω

⋅

−

=

ψ

+

ω

−

⋅

=

Wartość średnia mocy za okres, a więc moc czynna:

2

R

R

I

R

I

U

P

⋅

=

=

Mówi się, że rezystor pobiera moc czynną. (Jest to określenie nieścisłe chociaż powszechnie

stosowane: przecież moc to szybkość przepływu energii zatem nie może być ona „pobierana”.)

Induktor idealny (idealna cewka indukcyjna)

i

(t)

L

Induktor w obwodzie prądu

sinusoidalnie zmiennego

u

L(t)

Opis matematyczny (prawo Faraday’a w zastosowaniu do zjawiska samoindukcji):

dt

)

t

(

di

L

)

t

(

L

u

⋅

=

.

Gdy prąd jest sinusoidalnie zmienny:

)

t

sin(

I

2

i

I

)

t

(

ψ

+

ω

⋅

=

również napięcie jest

sinusoidalnie zmienne:

)

t

sin(

U

2

u

U

L

)

t

(

L

ψ

+

ω

⋅

⋅

=

.

Napięcie to daje się wyliczyć z równania cewki jako:

)

2

t

sin(

I

L

2

)

t

cos(

I

2

L

dt

di

L

u

I

I

)

t

(

)

t

(

L

π

+

ψ

+

ω

⋅

⋅

ω

⋅

=

ψ

+

ω

⋅

⋅

ω

⋅

⋅

=

⋅

=

Stąd (porównując ostatnie wzory) mamy:









π

+

ψ

=

ψ

⋅

ω

=

2

I

L

U

I

U

L

z czego wynika:











π

−

ψ

=

ψ

⋅

ω

=

2

U

L

1

I

U

I

L

Jest to tzw. prawo Ohma dla idealnej cewki indukcyjnej poddanej wymuszeniu sinusoidalnie

zmiennemu.

Współczynnikom proporcjonalności pomiędzy wartościami skutecznymi prądu i napięcia

nadaje się status wielkości fizycznych. Charakteryzują one właściwości cewki w obwodach prądu
sinusoidalnego. Są nimi:

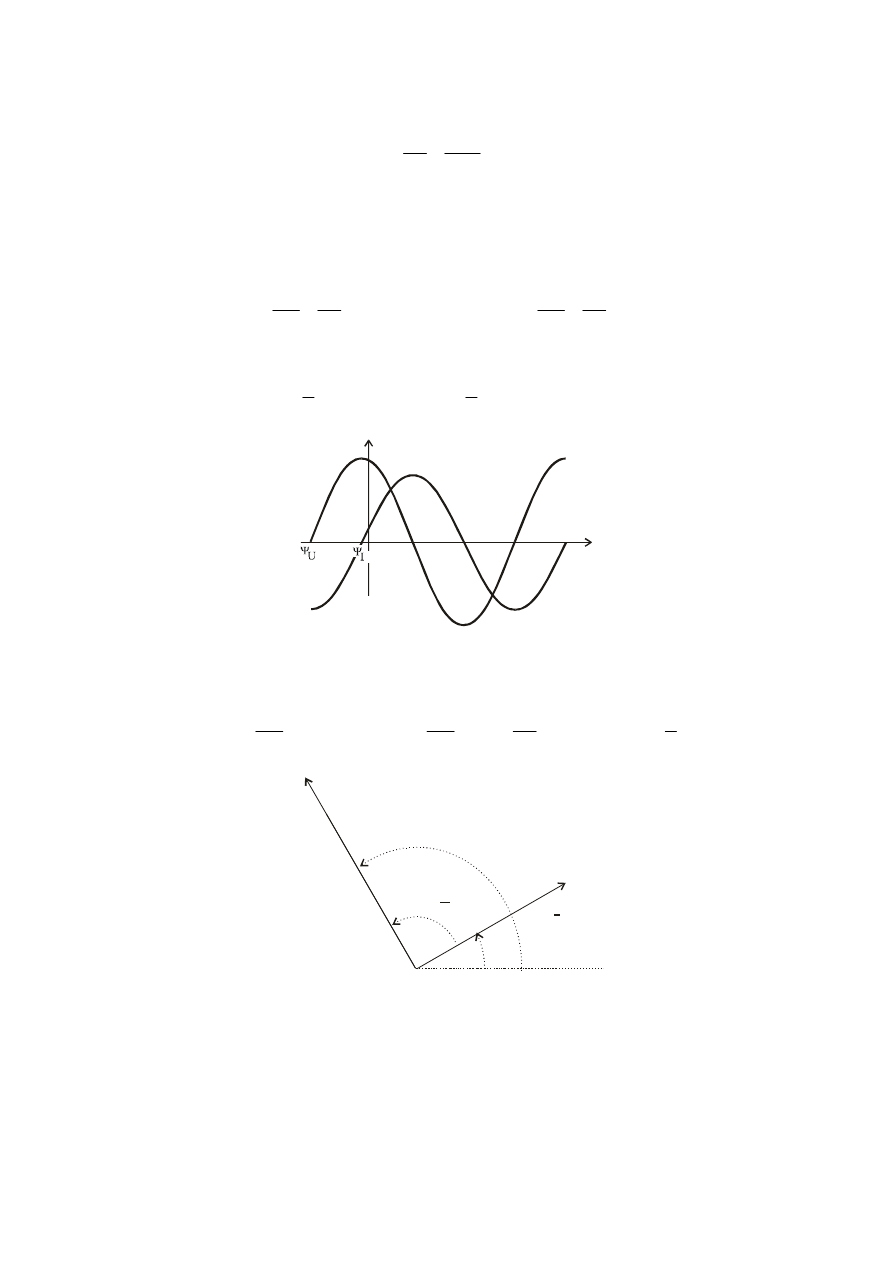
- 4 -

- reaktancja indukcyjna:

fL

2

L

X

L

π

=

ω

=

;

- susceptancja indukcyjna:

fL

2

1

L

1

B

L

π

=

ω

=

.

Terminy „reaktancja” i „susceptancja” pochodzą od łacińskich:
- re-ago - przeciw-działać;
- suscipio - podtrzymywać, popierać.

Jednostki:

Ω

=

=

=

1

A

1

V

1

]

i

[

1

]

u

[

1

]

X

[

1

L

S

1

1V

A

1

]

u

[

1

]

i

[

1

]

B

[

1

L

=

=

=









π

+

ψ

=

ψ

⋅

=

2

I

X

U

I

U

L

L

i









π

−

ψ

=

ψ

⋅

=

2

U

B

I

U

I

L

L

Przebiegi napięcia i prądu induktora

u, i

L(t)

u

(t)

i

ωt

Impedancja, admitancja i kąt przesunięcia fazowego odbiornika złożonego z idealnej cewki

indukcyjnej wynoszą:

L

X

I

U

Z

L

L

L

ω

=

=

=

,

L

1

B

U

I

Y

L

L

L

ω

=

=

=

,

2

I

U

π

=

Ψ

−

Ψ

=

ϕ

I

ΨU

ΨI

U = L I

ω

L

.

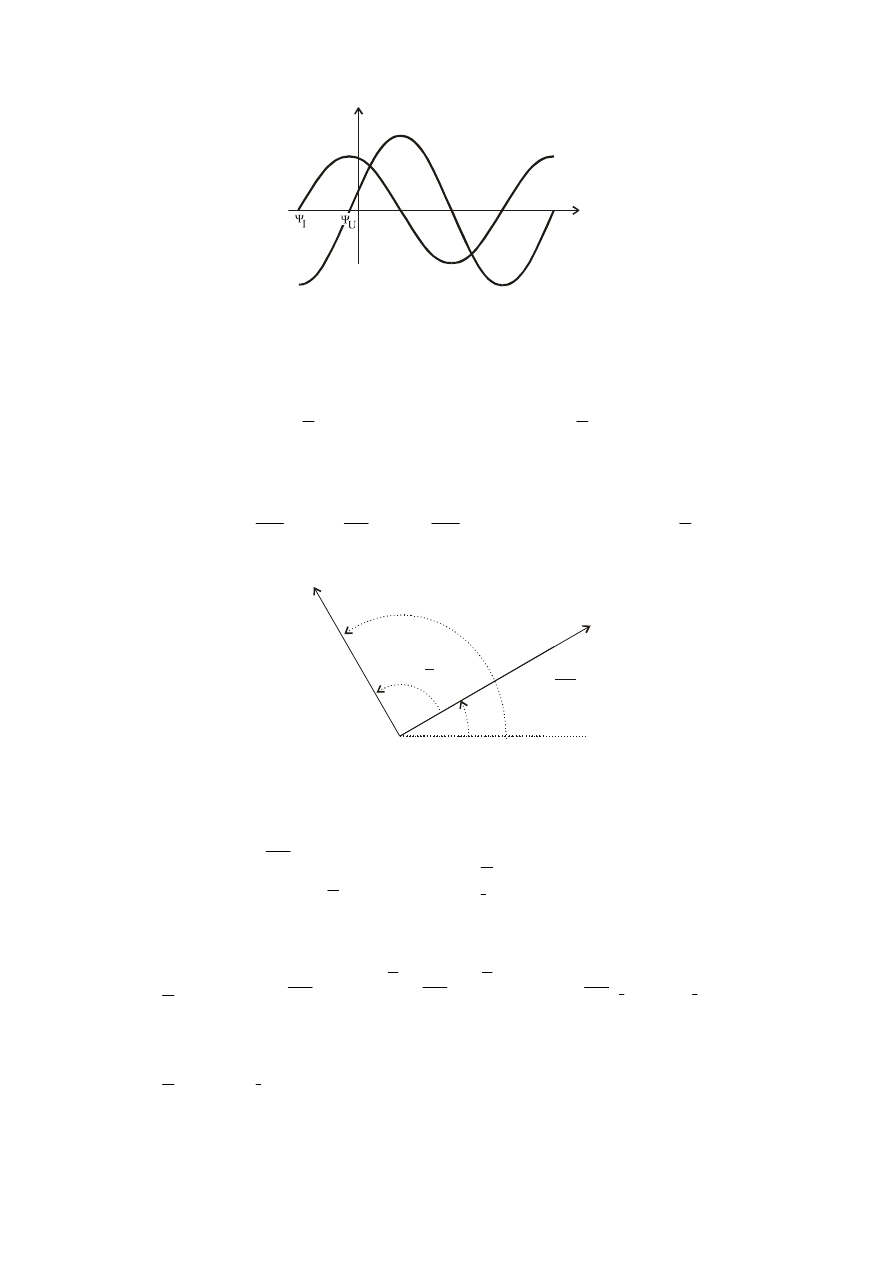
Wykres wskazowy prądu i napięcia induktora

π

2

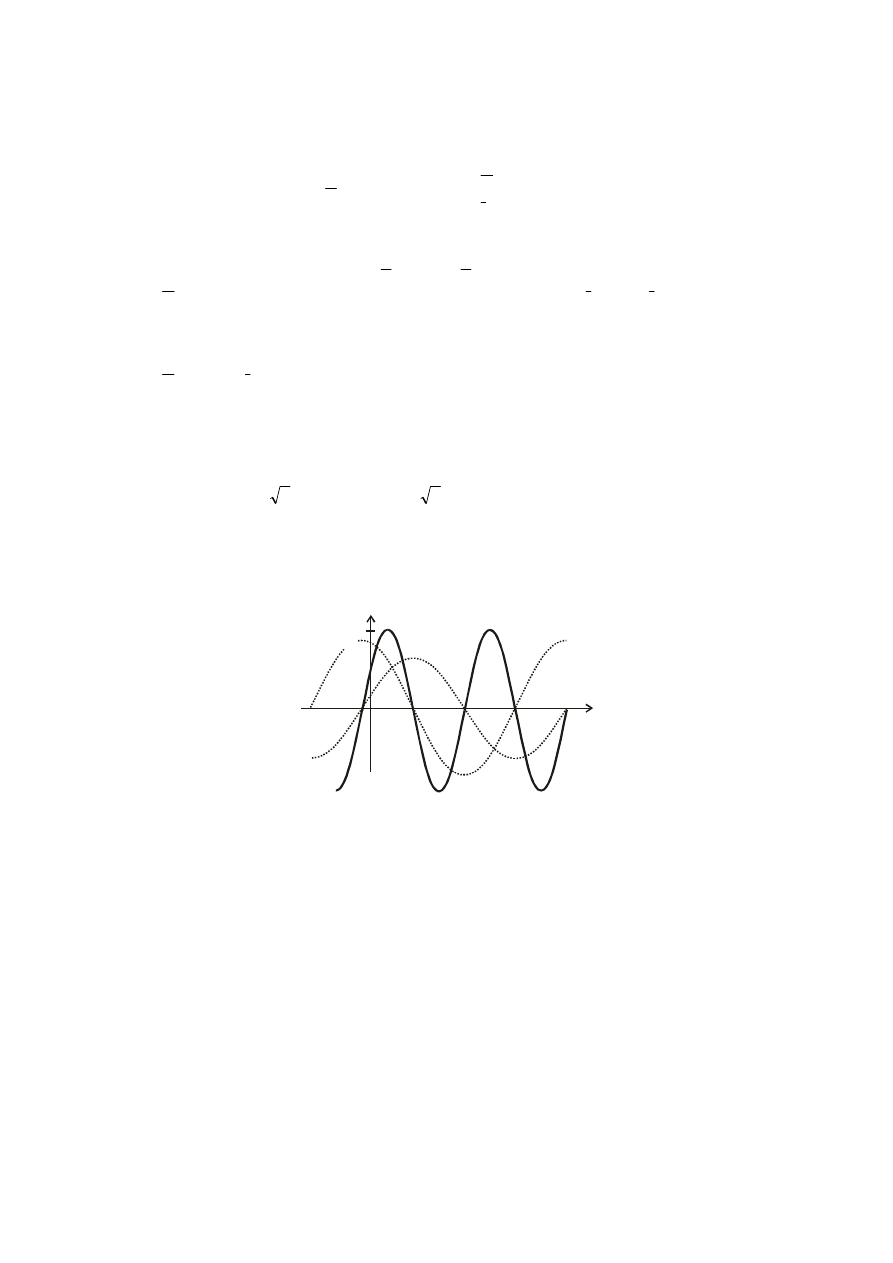
- 5 -

Metoda symboliczna:

Jest:









π

+

ψ

=

ψ

⋅

=

⋅

ω

=

2

I

X

I

L

U

I

U

L

L

oraz

I

j

U

j

L

L

e

I

I

e

U

U

Ψ

Ψ

⋅

=

⋅

=

Stąd:

I

jX

I

L

j

e

I

e

L

e

I

L

e

U

U

L

I

j

2

j

)

2

I

(

j

U

j

L

L

⋅

=

⋅

ω

=

⋅

⋅

⋅

ω

=

⋅

⋅

ω

=

=

Ψ

π

π

+

Ψ

Ψ

Prawo Ohma dla induktora dla metody symbolicznej:

I

jX

U

L

L

⋅

=

Moc:

W każdej chwili czasowej jest:

)

t

(

)

t

(

L

)

t

(

L

i

u

p

⋅

=

)

t

(

2

sin

I

U

)

t

sin(

)

t

cos(

I

U

2

)

t

sin(

I

2

)

t

cos(

U

2

p

I

L

I

I

L

I

I

L

)

t

(

L

ψ

+

ω

⋅

=

ψ

+

ω

⋅

ψ

+

ω

⋅

=

=

ψ

+

ω

⋅

⋅

ψ

+

ω

⋅

=

Ostatecznie:

)

I

2

t

2

sin(

I

L

U

)

t

(

L

p

ψ

+

ω

=

Przebiegi wartości chwilowych mocy induktora

p, u, i

-

-

+

+

L(t)

u

L(t)

p

(t)

i

ωt

U I

L

.

Wartości chwilowe mocy induktora (cewki indukcyjnej) oscylują sinusoidalnie. W różnych

częściach okresu są one dodatnie lub ujemne. Gdy moc jest dodatnia cewka pobiera energię: energia
elektryczna zamieniana jest w energię magnetyczną. Gdy moc jest ujemna cewka staje się źródłem
energii: energia magnetyczna zamieniana jest w energię elektryczną, która zwracana jest do źródła.

Wartości chwilowe mocy cewki oscylują z amplitudą:

I

U

L

.

Wartość średnia mocy za okres, a więc moc czynna:

0

P

L

=

Idealna cewka indukcyjna „średnio” nie pobiera energii. Całą energię, którą pobrała w jednej

części okresu w następnej części zwraca do źródła.

Cewka indukcyjna klasyfikowana jest jako element zachowawczy: energia magazynowana

(zachowywana) jest w jej polu magnetycznym i może być z powrotem zamieniona w energię
elektryczną. Inna nazwa elementu zachowawczego: element reaktancyjny.

Zjawiska energetyczne zachodzące w cewce charakteryzowane są przez moc bierną.

- 6 -

W przypadku cewki jest to moc bierna indukcyjna:

L

Q .

Definiuje się ją jako amplitudę pulsowania mocy na cewce:

2

L

L

L

I

X

I

U

Q

=

=

Mówi się (niezbyt ściśle), że cewka indukcyjna nie pobiera mocy czynnej lecz pobiera moc

bierną (indukcyjną).

Jednostką mocy biernej - inną niż dla „zwykłej”, „prawdziwej” mocy, by podkreślić, że to nie

jest taka „prawdziwa” moc - jest 1 var (czyt.: war). Jest to skrót od: Volt-Amper-reaktancyjny:

var

1

A

V

1

]

i

[

]

u

[

]

Q

[

1

L

=

⋅

=

⋅

=

Niekiedy stosuje się zapis:

ind

var

.

kondensator (idealny)

i

(t)

C

Kondensator w obwodzie prądu

sinusoidalnie zmiennego

u

C(t)

Opis matematyczny:

dt

)

t

(

du

C

)

t

(

i

⋅

=

.

Gdy napięcie jest sinusoidalnie zmienne:

)

t

sin(

U

2

u

U

C

)

t

(

C

ψ

+

ω

⋅

⋅

=

również prąd jest

sinusoidalnie zmienny:

)

t

sin(

I

2

i

I

)

t

(

ψ

+

ω

⋅

⋅

=

.

Prąd ten daje się wyliczyć z równania kondensatora jako:

)

2

U

t

sin(

C

U

C

)

U

t

cos(

C

U

C

dt

)

t

(

C

du

C

)

t

(

i

π

+

ψ

+

ω

⋅

ω

=

ψ

+

ω

⋅

ω

=

⋅

=

Stąd (porównując ostatnie wzory) mamy:









π

+

ψ

=

ψ

⋅

ω

=

2

U

C

I

U

I

C

z czego wynika:











π

−

ψ

=

ψ

⋅

ω

=

2

I

C

1

U

I

U

C

Jest to tzw. prawo Ohma dla kondensatora idealnego poddanego wymuszeniu sinusoidalnie

zmiennemu.

Podobnie jak dla induktora wprowadza się wielkości fizyczne charakteryzujące właściwości

kondensatora w obwodach prądu sinusoidalnego:

- reaktancja pojemnościowa:

fC

2

1

C

1

C

X

π

=

ω

=

- susceptancja pojemnościowa:

fC

2

C

B

C

π

=

ω

=

Jednostki:

Ω

=

=

1

]

i

[

1

]

u

[

1

]

C

X

[

1

S

1

]

u

[

1

]

i

[

1

]

C

B

[

1

=

=

- 7 -

Przebiegi napięcia i prądu kondensatora

u, i

C(t)

u

(t)

i

ωt









π

+

ψ

=

ψ

⋅

=

2

U

B

I

U

I

C

C

z czego wynika:









π

−

ψ

=

ψ

⋅

=

2

I

X

U

I

U

C

C

Impedancja, admitancja i kąt przesunięcia fazowego odbiornika złożonego z idealnego

kondensatora wynoszą:

C

1

X

I

U

Z

C

C

C

ω

=

=

=

,

C

B

U

I

Y

C

C

C

ω

=

=

=

,

2

I

U

π

−

=

Ψ

−

Ψ

=

ϕ

I

ΨU

ΨI

Wykres wskazowy prądu i napięcia kondensatora

π

2

U = I

C

.

ωC

1

Metoda symboliczna:

Jest:











π

−

ψ

=

ψ

⋅

=

⋅

ω

=

2

I

X

I

C

1

U

I

U

C

C

oraz

I

j

U

j

C

C

e

I

I

e

U

U

Ψ

Ψ

⋅

=

⋅

=

Stąd:

I

jX

I

C

1

e

I

e

C

1

e

I

C

1

e

U

U

C

I

j

2

j

)

2

I

(

j

U

j

C

C

⋅

−

=

⋅

ω

−

=

⋅

⋅

⋅

ω

=

⋅

⋅

ω

=

=

Ψ

π

−

π

−

Ψ

Ψ

Prawo Ohma dla kondensatora dla metody symbolicznej:

I

jX

U

C

C

⋅

−

=

- 8 -

Moc:

W każdej chwili czasowej jest:

)

t

(

)

t

(

C

)

t

(

C

i

u

p

⋅

=

)

2

t

2

sin(

I

U

)

t

sin(

)

t

cos(

I

U

2

)

t

cos(

I

2

)

t

sin(

U

2

p

U

C

I

U

C

U

U

C

)

t

(

C

ψ

+

ω

⋅

=

ψ

+

ω

⋅

ψ

+

ω

⋅

=

=

ψ

+

ω

⋅

⋅

⋅

ψ

+

ω

⋅

=

)

2

t

2

sin(

I

U

)

2

2

2

t

2

sin(

I

U

)

2

t

2

sin(

I

U

p

I

C

I

C

U

C

)

t

(

C

ψ

+

ω

−

=

π

+

ψ

+

ω

=

ψ

+

ω

=

Ostatecznie:

)

2

t

2

sin(

I

U

)

2

t

2

sin(

I

U

p

I

C

U

C

)

t

(

C

ψ

+

ω

−

=

ψ

+

ω

=

p, u, i

U I

C

.

C(t)

u

C(t)

p

(t)

i

ωt

-

-

+

+

Przebiegi wartości chwilowych mocy kondensatora

Wartości chwilowe mocy kondensatora oscylują sinusoidalnie. W różnych częściach okresu są

one dodatnie lub ujemne. Gdy moc jest dodatnia kondensator pobiera energię: energia gromadzona
jest w jego polu elektrycznym. Gdy moc jest ujemna cewka staje się źródłem energii: energia pola
elektrycznego zwracana jest do źródła.

Podobnie jak cewka indukcyjna kondensator też jest elementem zachowawczym,

reaktancyjnym.

Wartości chwilowe mocy kondensatora oscylują z amplitudą:

I

U

C

.

Wartość średnia mocy za okres, a więc moc czynna:

0

P

C

=

Idealny kondensator (mówiąc niezbyt poprawnie) nie pobiera mocy czynnej. Pobiera

natomiast moc bierną. Wielkością charakteryzującą zjawiska energetyczne zachodzące w
kondensatorze jest moc bierna pojemnościowa:

C

Q .

Definiuje się ją jako amplitudę pulsowania mocy na kondensatorze:

2

C

C

C

I

X

I

U

Q

=

=

Jednostka jak dla mocy biernej indukcyjnej (tj. 1 var).
Niekiedy stosuje się zapis:

poj

var

albo

cap

var

(od : capacitance).

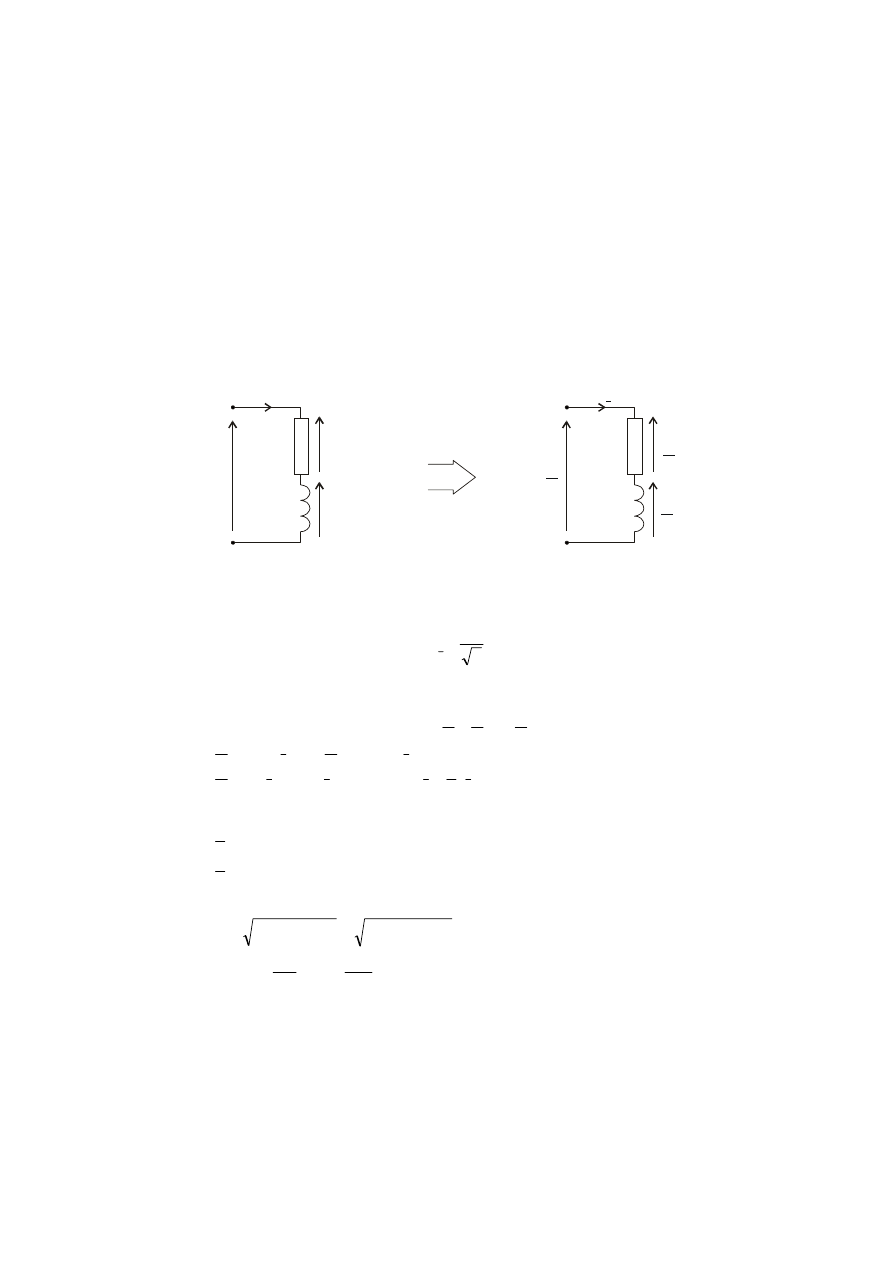
- 9 -

Cewka indukcyjna rzeczywista - gałąź szeregowa RL

W idealnej cewce indukcyjnej zachodzi tylko jedno zjawisko: opisywane prawem Faraday’a

zjawisko samoindukcji związane z istnieniem pola magnetycznego..

Dla rzeczywistych cewek jest to zbyt daleko idąca idealizacja, uwzględniane powinno być

jeszcze co najmniej zjawisko zamiany energii elektrycznej na energię cieplną.

Zjawisko zamiany energii elektrycznej na energię cieplną opisywane jest prawami Ohma oraz

Joule’a i odwzorowywane jest przez idealny rezystor. Zatem schemat zastępczy cewki rzeczywistej
powinien składać się z induktora i rezystora.

Tempo rozpraszania energii na rezystorze (tj. moc “pobierana” przez rezystor) zależy od

wartości natężenia prądu. Również zjawiska zachodzące w induktorze zależą od natężenia prądu. Stąd
w schemacie rezystor i induktor powinny być połączone tak, by przepływał przez nie ten sam prąd, a
więc szeregowo.

i

(t)

u

R(t)

R

R

u

L(t)

L

u

(t)

I

U

j L

ω

UR

UL

Schemat zastępczy cewki rzeczywistej (gałęzi szeregowej RL)

Prąd płynący przez gałąź ma przebieg sinusoidalny:

I

j

I

j

m

I

m

)

t

(

e

I

e

2

I

I

)

t

sin(

I

i

ψ

ψ

⋅

=

⋅

=

⇒

ψ

+

ω

=

Wyznaczmy przebieg wartości chwilowych napięcia.
Najprościej zrobić to stosując metodę symboliczną:

L

R

)

t

(

L

)

t

(

R

)

t

(

U

U

U

u

u

u

+

=

⇒

+

=

I

R

U

R

⋅

=

,

I

L

j

U

L

⋅

ω

=

I

Z

I

)

L

j

R

(

I

L

j

I

R

U

⋅

=

⋅

ω

+

=

⋅

ω

+

⋅

=

Odbiornik ma zatem impedancję zespoloną:

L

jX

R

L

j

R

Z

+

=

ω

+

=

- postać algebraiczna;

ϕ

⋅

=

j

e

Z

Z

- postać wykładnicza,

gdzie:

2

L

2

2

2

)

X

(

R

)

L

(

R

Z

+

=

ω

+

=

R

X

tg

ar

R

L

tg

ar

L

=

ω

=

ϕ

ϕ

⋅

=

cos

Z

R

,

ϕ

⋅

=

ω

=

sin

Z

L

X

L

- 10 -

ϕ

π

2

Im

Z

Re

R

X

L

= ω

L

Impedancja zespolona cewki rzeczywistej

Wartość skuteczna napięcia i przesunięcie fazowe między prądem i napięciem:









ω

+

ψ

=

ψ

⋅

ω

+

=

⋅

=

R

L

tg

ar

I

)

L

(

R

I

Z

U

I

U

2

2

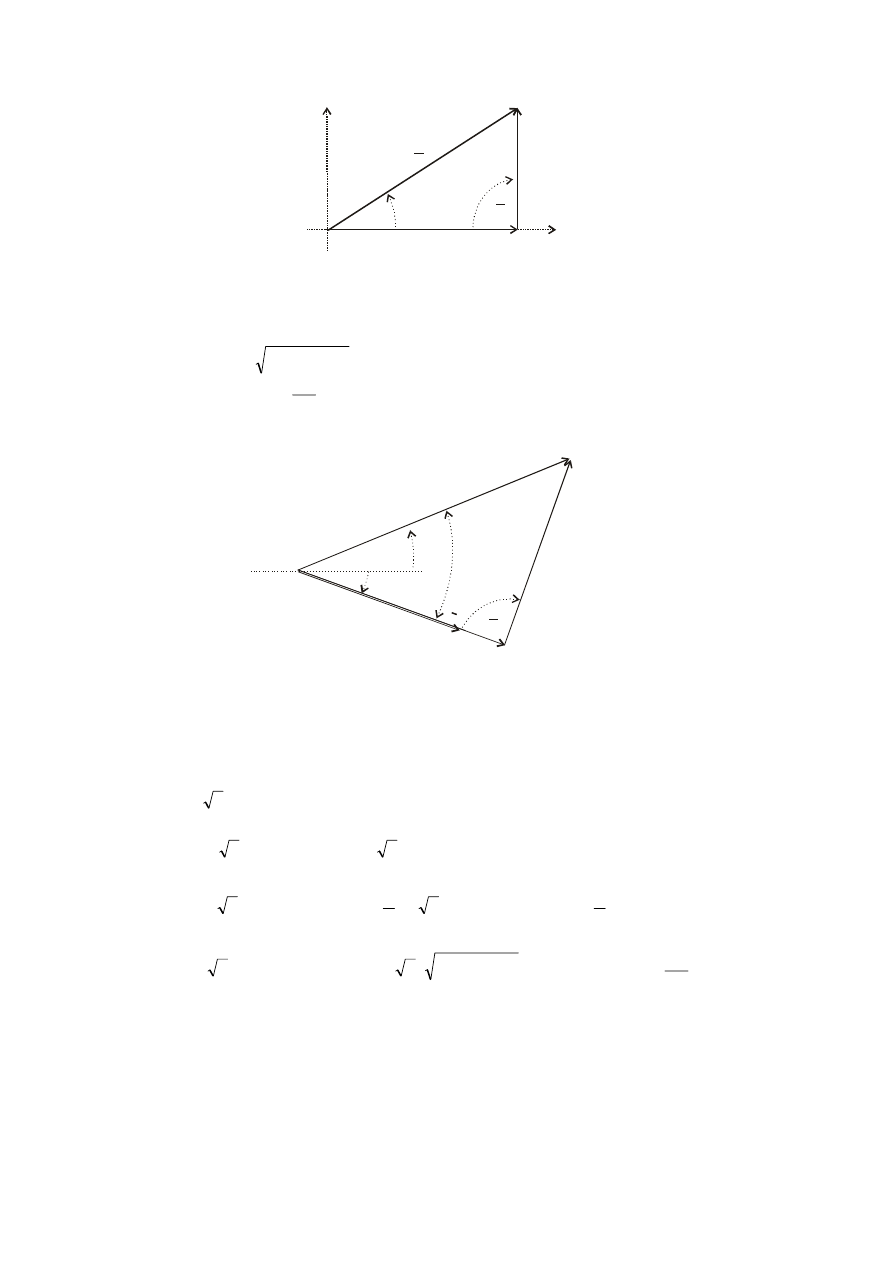
Wykres wskazowy:

I

ϕ

π

2

ΨU

ΨI

U = Z

I

.

U = L I

ω

L

.

U = R

I

R

.

Wykres wskazowy prądu i napięć cewki rzeczywistej

ϕ

⋅

=

⋅

=

cos

U

I

R

U

R

,

ϕ

⋅

=

⋅

=

sin

U

I

X

U

L

L

Przebiegi wartości chwilowych prądu i napięć:

)

t

sin(

I

2

i

I

)

t

(

ψ

+

ω

⋅

=

)

t

sin(

cos

U

2

)

t

sin(

I

R

2

u

I

I

)

t

(

R

ψ

+

ω

⋅

ϕ

⋅

⋅

=

ψ

+

ω

⋅

⋅

=

)

2

t

sin(

sin

U

2

)

2

t

sin(

I

L

2

u

I

I

)

t

(

L

π

+

ψ

+

ω

⋅

ϕ

⋅

=

π

+

ψ

+

ω

⋅

⋅

ω

⋅

=

)

R

L

tg

ar

t

sin(

I

)

L

(

R

2

)

t

sin(

I

Z

2

u

I

2

2

I

)

t

(

ω

+

ψ

+

ω

⋅

⋅

ω

+

⋅

=

ϕ

+

ψ

+

ω

⋅

⋅

⋅

=

- 11 -

u, i

R(t)

u

L(t)

u

(t)

u

ωt

Przebiegi prądu i napięć cewki rzeczywistej

(t)

i

W cewce rzeczywistej nie ma żadnych odrębnych części, z których jedna byłaby idealnym

rezystorem, a druga idealnym induktorem. Takie odrębne części występują jedynie w schemacie
zastępczym, a więc w schemacie pewnego obwodu złożonego z idealnych elementów, będącego
fizycznym modelem cewki rzeczywistej.

Moc:

Moc jaką pobiera gałąź RL:

)

t

(

)

t

(

)

t

(

i

u

p

⋅

=

)

2

t

2

sin(

I

U

)]

2

t

2

cos(

1

[

I

U

i

u

i

u

i

)

u

u

(

p

I

L

I

R

)

t

(

)

t

(

L

)

t

(

)

t

(

R

)

t

(

)

t

(

L

)

t

(

R

)

t

(

Ψ

+

ω

⋅

⋅

+

Ψ

+

ω

−

⋅

⋅

=

=

⋅

+

⋅

=

⋅

+

=

Pierwszy człon tego wyrażenia to przebieg wartości chwilowych mocy rezystora, człon drugi

to przebieg wartości chwilowych mocy induktora.

Moc czynna czyli wartość średnia mocy chwilowej za okres:

I

U

p

P

R

śr

⋅

=

=

Zatem moc czynna gałęzi RL to moc czynna występującego w niej rezystora.
Jest:

ϕ

⋅

=

ϕ

⋅

⋅

=

⋅

=

cos

U

cos

Z

I

R

I

U

R

Stąd znana postać wyrażenia na moc czynną:

ϕ

⋅

=

cos

UI

P

NIE JEST to definicja mocy czynnej, a jedynie wzór na obliczanie mocy czynnej w obwodach

prądu sinusoidalnego.

O wartości „prawdziwej” mocy pobieranej przez odbiornik, tj. mocy czynnej, przy danych

wartościach skutecznych prądu i napięcia decyduje kosinus kąta przesunięcia fazowego pomiędzy

prądem i napięciem

UI

P

cos =

ϕ

. Nosi on nazwę współczynnika mocy. W praktyce elektrotechniki

przemysłowej współczynnikiem mocy nazywany bywa

P

Q

tg =

ϕ

.

Moc bierną (indukcyjną) gałęzi RL definiuje się jako:

ϕ

⋅

=

sin

UI

Q

L

Jest nią zatem amplituda oscylacji mocy na induktorze:

I

U

sin

UI

Q

L

L

=

ϕ

=

Przez analogię do mocy w obwodach prądu stałego w obwodach prądu zmiennego wprowadza

się jeszcze jedną wielkość: moc pozorną S.

Definiuje się ją wzorem:

I

U

S

⋅

=

a więc jako iloczyn wartości skutecznych prądu i napięcia.

- 12 -

Jednostką mocy pozornej - inną niż dla „zwykłej”, „prawdziwej” mocy, by podkreślić, że to

nie jest taka „prawdziwa” moc - jest 1VA (Volt-amper).

VA

1

]

i

[

]

u

[

]

S

[

1

=

⋅

=

Jest:

I

U

S

⋅

=

,

ϕ

⋅

=

ϕ

⋅

=

cos

S

cos

UI

P

oraz:

ϕ

⋅

=

ϕ

⋅

=

sin

S

sin

UI

Q

L

Stąd tzw. równanie mocy:

2

L

2

2

L

2

2

Q

P

S

Q

P

S

+

=

⇒

+

=

Poszczególne rodzaje mocy definiowanych dla gałęzi RL są nawzajem uzależnione od siebie

tak jak boki trójkąta prostokątnego:

ϕ

π

2

S =

UI

P = UI cos

ϕ

Q = UI sin

ϕ

L

Trójkąt mocy g ałęzi RL

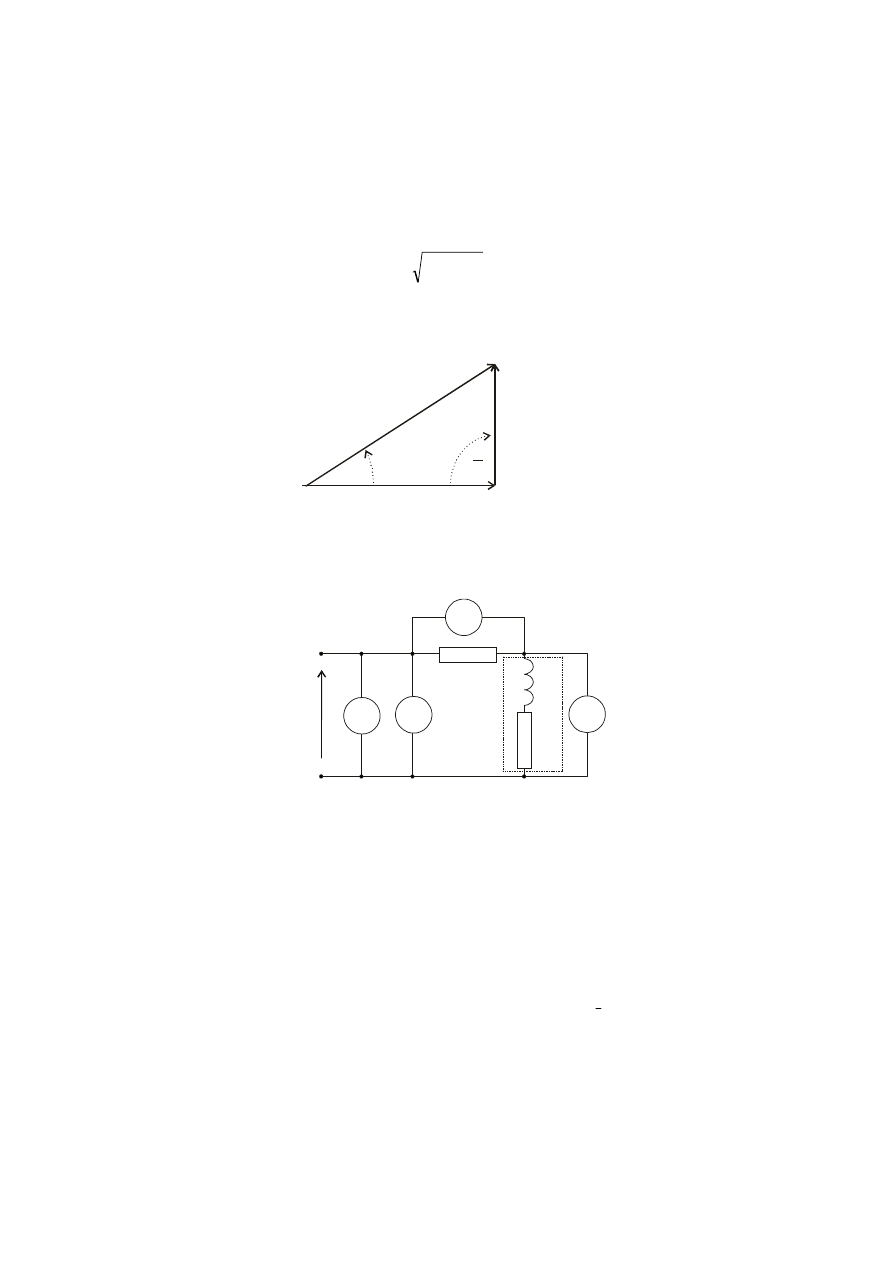
PRZYKŁAD

u(t)

RL

L

R

Hz

V

1

V

2

V

Schemat układu do pomiaru parametrów cewki

Celem wyznaczenia parametrów cewki połączono ją w szereg z rezystorem o znanej

rezystancji

Ω

=

10

R

i układ ten zasilono napięciem sinusoidalnym. Pomierzono napięcia i

częstotliwość.

Wskazania przyrządów:

V

220

U

=

;

V

40

U

1

=

;

V

200

U

2

≈

;

Hz

50

f

≈

.

Mierniki są idealne, mierzą wartości skuteczne.
Obliczyć indukcyjność L i rezystancję

L

R cewki.

Załóżmy, że początkowy kąt fazowy prądu wynosi 0. Jest zatem:

I

e

I

I

0

j

=

⋅

=

⋅

.

Obwód jest szeregowy - ten sam prąd płynie przez wszystkie elementy. Napięcie na

rezystorach jest w fazie z prądem, napięcie na induktorze wyprzedza prąd o ćwierć okresu (

o

90 ).

Pokazuje to wykres wskazowy.

- 13 -

Szkic wykresu wskazowego napięć do przykładu

I

U

UL

UR

L

U1

U2

Napięcie

2

U jest sumą napięć

L

U i

L

R

U

zaś napięcie U - napięć

1

U i

2

U . Dodawania są

(oczywiście) geometryczne i ich obrazem są dwa trójkąty prostokątne. Wykorzystując twierdzenie
Pitagorasa można ułożyć dla nich dwa równania:









+

=

+

+

=

2

L

2

L

R

2

2

2

L

2

L

R

1

2

U

U

U

U

)

U

U

(

U

Tworzą one układ dwu równań z dwoma niewiadomymi.
Rozwiązaniem są wartości:

V

181

U

L

≈

i

V

85

U

L

R

≈

.

Wartość skuteczną prądu można wyliczyć z prawa Ohma:

A

4

10

40

R

U

I

1

=

=

=

Stąd:

Ω

=

=

=

25

,

21

4

85

I

U

R

L

R

L

Ω

≈

≈

=

26

,

45

4

181

I

U

X

L

L

H

m

144

H

144

,

0

314

26

,

45

X

L

L

=

≈

≈

ω

=