Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

1

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Wprowadzenie, bł dy oblicze numerycznych

Bł dy

Sposób zapisu liczb

Na pocz tek zajmiemy si sposobem zapisu liczb w pami ci komputera. Wszyscy oczywi cie wiedz , e komputer

posługuje si zapisem w systemie dwójkowym, jednak aby bli ej zaj si tym zagadnieniem potrzebujemy wi cej

szczegółów. Zajmiemy si wymy lonym komputerem prowadz cym obliczenia na liczbach rzeczywistych i przeznaczaj cym

na ka d liczb 1 bajt (8 bitów) – jest wi c to komputer o mio bitowy. W rzeczywisto ci np. w Turbo Pascalu liczba typu

real zajmuje 6 bajtów (48 bitów). Bity słowa naszego wymy lonego komputera s interpretowane nast puj co:

1

— bit znaku liczby — warto 0 oznacza plus, warto 1 oznacza minus.

2,3,4,5

— bity mantysy (okre lenie to nie ma wła ciwie nic wspólnego ze znan nam mantys logarytmu).

Interpretuje si je jako cztery cyfry po kropce „dziesi tnej” (w układzie dwójkowym nale ałoby j mo e

nazwa „kropk dwójkow ”).

6

— bit znaku wykładnika, interpretacja taka sama jak bitu znaku liczby.

7,8

— bity wykładnika (zwanego te czasem „cech ”, podobnie jak w przypadku logarytmów). Cyfry te

interpretuje si jako liczb całkowit .

W ten sposób bajt postaci 11111111 (zazwyczaj b dziemy to zapisywa bior c bity znaków w nawiasy: (1)1111(1)11

— jest to ten sam bajt, tylko łatwiejszy do zinterpretowania „na oko”) zostanie zinterpretowany jako:

(tu

0.1111

2

2

11

2

i dalej dolne indeksy

2

b d oznacza , e mamy do czynienia z liczb zapisan w układzie dwójkowym)

0.1111

2

2

1

2

2

2

3

2

4

1
2

1
4

1
8

1

16

15
16

0.9375

11

2

2

1

2

0

3

;

2

3

1
8

0.9375

1
8

0.1171875

Jest to wi c –0.1171875.

Rozwa my teraz dwie bliskie sobie liczby: (1)1101 (0)10 oraz (1)1100 (0)10 (jak wida nie mog mniej si od siebie

ró ni ). Obliczmy ich warto ci:

(1)1101 (0)10

0.1101

2

2

10

2

1
2

1
4

1

16

4

3.25

(1)1100 (0)10

0.1100

2

2

10

2

1
2

1
4

4

3

Jak wida w aden sposób nie uda nam si zapisa liczby –3.1 (!) — maszyna musi zapami ta j jako –3.0 (jest bli sze

prawidłowej warto ci ni –3.25).

Ogólnie wprowadzane liczby mog ró ni si od siebie o nie wi cej ni

2

liczba bitów mantysy

2

cecha

Mo emy wi c przyj , e ka da wprowadzona do komputera liczba musi by obarczona jakim bł dem — jego warto

bezwzgl dna zale y od wielko ci liczby, ale jego warto odniesiona do warto ci wpisywanej liczby jest zawsze podobna

— w naszym przykładzie jest to około 2

–4

(1/16 czyli 0,0625). Inaczej mo na to zinterpretowa jako ograniczenie liczby

cyfr znacz cych wprowadzanych liczb. I tu przechodzimy do pierwszego rodzaju bł dów:

Bł dy wej ciowe

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

2

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Nazwa od razu kojarzy nam si z sytuacj gdy dane wej ciowe s np. wynikami pomiarów fizycznych, które z natury

rzeczy obarczone s bł dami. Ale chodzi tu przede wszystkim o bł dy wynikaj ce z

wst pnego zaokr glenia

wprowadzanych (nawet zupełnie dokładnych!) warto ci (dotyczy to zwłaszcza liczb niewymiernych) — a wynika z powy ej

opisanego sposobu zapisu liczb.

Przykład: Rozwa amy nadal 5-cio bitow mantys (wraz z bitem znaku) i 3-y bitowy wykładnik (te wraz z bitem

znaku).

Chcemy zsumowa 3 liczby (w zapisie dziesi tnym):

0.48

0.24

0.12

(wynik powinien oczywi cie wynosi 0.84).

W zapisie dwójkowym maj one niesko czone rozwini cia:

0.(01111010111000010100)

0.0(01111010111000010100)

0.00(01111010111000010100)

Poniewa jednak nasz wymy lony komputer dysponuje tylko czterema bitami dla przedstawienia warto ci liczby,

b dzie musiał wprowadzane liczby zapami ta jako:

(0)1111 (1)01

(0)1111 (1)10

(0)1111 (1)11

czyli tak naprawd b dziemy sumowa : 0.46875, 0.234375 i 0.1171875

!

Gdyby my liczby te mogli dokładnie doda w systemie dwójkowym to wynik powinien wynosi 0.8203125. A zatem

tylko z powodu wyst powania bł dów wej ciowych popełnimy bł d bezwzgl dny wynosz cy około 0.02

! (a

odpowiadaj cy mu bł d wzgl dny wynosi 2,3%).

Bł dy zaokr gle

Kontynuujmy poprzedni przykład: w wyniku zsumowania liczb dwójkowych:

0.01111

2

+ 0.001111

2

+ 0.0001111

2

powinni my otrzyma wynik:

0.1101001

2

(czyli 0.8203125

10

)

Jednak poniewa mamy do dyspozycji tylko 5 cyfr mantysy (a tak na prawd tylko 4, bo jedna jest przeznaczona

na znak) b dziemy sumowa liczby:

0.01111

2

+ 0.00111

2

+ 0.00011

2

(to, e zapisane liczby maj po pi cyfr po przecinku jest najzupełniej zgodne z zało eniem o przeznaczeniu 4 cyfr

na mantys . Liczby te ró ni si wykładnikami. Faktem jest, e drug i trzeci liczb mo na by zapisa dokładniej

(z innymi wykładnikami), ale w celu ich dodania musimy najpierw uzgodni wykładniki — w przeciwnym razie

procesor nie zdoła doda wszystkich liczb.

W wyniku tej operacji otrzymaliby my

0.11001

2

(czyli 0.78125

10

!)

ale liczba ta ma 5 cyfr (dwójkowych) — tyle nasz komputer nie jest w stanie zapami ta . Wynik zostanie wi c

zapisany jako:

(0)1100(0)00 czyli 0.11

2

(w zapisie dziesi tnym: 0.75).

Bł d bezwzgl dny wynosi wi c –0.09 (bł d wzgl dny –10.7% !).

Kolejn ilustracj mo e by nast puj cy przykład: chcemy doda liczby:

1.87

0.93

0.47

(w zapisie maszynowym (przez zapis maszynowy b dziemy rozumie zapis dwójkowy z uwzgl dnieniem

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

3

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

ograniczenia liczby cyfr):

(0)1111 (0)01

(0)1111 (0)00

(0)1111 (1)01

co odpowiada faktycznie warto ciom:

1.875

0.9375

0.46875

Mamy wi c faktycznie dodawanie takich liczb dwójkowych:

1.111

2

0.1111

2

0.01111

2

Po ich dodaniu powinni my dosta :

11.01001

2

czyli: 3.28125 (nawiasem mówi c zamiast 3.27).

Tymczasem ze wzgl du na obecno ograniczonej liczby cyfr znacz cych wykładnika maszyna b dzie musiała

przedstawi wszystkie te liczby z jednakowym wykładnikiem. W przypadku dodawania jakichkolwiek liczb

uzgodnienie wykładników zawsze b dzie polega na zrównaniu ich do najwy szego. Gdy zmieniamy wykładnik

liczby na wy szy (tzn. gdy mno ymy j przez dodatni pot g podstawy — 2) jej cyfry przesuwamy w prawo, a

przed nimi dopisujemy zera. Z powodu ograniczonej liczby cyfr ostatnie z nich „gin ” powoduj c powstanie

pewnego bł du. Gdyby my chcieli uzgodni wykładniki „w dół” — do którego z ni szych (tzn. pomno y liczb

przez ujemn pot g dwójki), musieliby my przesuwa cyfry w lewo, przy czym, znów z powodu ograniczenia

liczby cyfr musieliby my „gubi ” cyfry pocz tkowe, a to spowodowałoby znacznie wi ksze bł dy. Je li wi c

zaczniemy dodawanie od liczby najwi kszej to b dzie to:

(0)1111 (0)01 + (0)1111 (0)00 + (0)1111 (1)01

po dopasowaniu wykładników:

(0)1111 (0)01 + (0)0111 (0)01 + (0)0011 (0)01 = (0)1100 (0)10

1.111

2

+ 0.111

2

+ 0.011

2

= 11.00

2

(byłoby to 11.001

2

ale ostatnia „1” została obci ta)

1.875 + 0.875 + 0.375 = 3 (na prawd 3.125, ale „patrz wy ej”).

Bł d bezwzgledny wynosi 0.27 (a wzgl dny ok. 8%).

Je li za dodawanie zaczniemy od najmniejszego składnika dostaniemy:

(0)1111 (1)01 + (0)1111 (0)00

po dopasowaniu wykładników:

(0)0111 (0)00 + (0)1111 (0)00 = (0)1011 (0)01

0.0111

2

+ 0.1111

2

= 1.011

2

(faktycznie: 1.01101

2

, ale obci te)

0.4375 + 0.9375 = 1.375

i w drugim kroku (nie trzeba dopasowywa pierwszej z liczb bo wykładniki si zgadzaj ):

(0)1011 (0)01 + (0)1111 (0)01 = (0)1101 (0)10

1.011

2

+ 1.111

2

= 11.01

2

1.375 + 1.875 = 3.25

dostajemy wi c wynik wyra nie lepszy ni dodaj c w niewła ciwej kolejno ci — bł d bezwzgl dny wynosi 0.02,

a wzgl dny 0.6%.

Z powy szych rozwa a wynika praktyczna reguła:

Podczas sumowania wielu liczb nale y zadba o to aby dodawa liczby w kolejno ci rosn cej

(najpierw małe potem du e).

Jeszcze wi ksze bł dy wzgl dne mo emy uzyska w przypadku odejmowania liczb o zbli onych warto ciach. Np.

chcemy wykona działanie:

0.5

– 0.46875

0.1

2

– 0.01111

2

= 0.00001

2

(dokładnie: 1/32)

(0)1000 (0)00

– (0)1111 (1)01

=

(0)1000 (0)00

– (0)0111 (0)00

= (0)0001 (0)00 (czyli 1/16

!)

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

4

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

w ten sposób otrzymali my bł d wzgl dny wynosz cy 100%!. Na takie sytuacje wła ciwie nie ma rady — trzeba

o tym pami ta pisz c programy i tak zapisywa algorytmy, aby nie zachodziła konieczno odejmowania liczb o

zbli onych warto ciach.

Zróbmy jeszcze jeden „eksperyment”: sprawdzimy czy 3.2 – 3.0 = 0.3 – 0.1 .

Pierwsze odejmowanie. Najpierw sprawdzimy jak obie liczby zostan zapisane w pami ci naszego komputera

(podkre lona została warto obarczona mniejszym bł dem):

3.2

10

= 11.00110011

2

= (0)1100(0)10 = 3.0

= (0)1101(0)10 = 3.25

Liczba 3.2 zostanie zapisana jako (0)1101(0)10 — czyli jako 3.25.

3.0

10

= 11

= (0)1100(0)10 = 3.0 (zapis dokładny)

(0)1101(0)10 – (0)1100(0)10 = (0)0001(0)10 = 0.25

Wynikiem pierwszgo odejmowania b dzie 0.25 (zamiast 0.2 !).

Drugie odejmowanie. Najpierw zapis obu liczb:

0.3 = 0.01001100110

= (0)1001(1)01

= 0.28125

= (0)1010(1)01

= 0.3125

0.1 = 0.00011001100

= (0)1100(1)11

= 0.09375

= (0)1101(1)11

= 0.1015625

Obie liczby zostan zapisane z bł dami.

(0)1010(1)01 – (0)1101(1)11 = (0)1010(1)01 – (0)0011(1)01 = (0)0111(1)01 = 0.21875

Jak wida wynik tym razem wynosi 0.21875 — te z bł dem, ale tym razem innym.

Z „eksperymentu” tego wynika pewnien „morał”: W przypadku liczb zmiennoprzecinkowych nale y unika sprawdzania

ich równo ci – jest bowiem bardzo prawdopodobne, e liczby o których wiemy na pewno, e s sobie równe (bo dwa ró ne

ci gi działa arytmetycznych przeprowadzone analitycznie (=na karteczce) dały identyczny wynik), w pami ci komputera

wcale równe by nie musz .

W opisie Turbo Pascala mo na znale informacj , e liczba bajtów przeznaczanych na zapis liczb rzeczywistych i ich

zakresy wynosz odpowiednio:

real

6

od 2.9×10

–39

do 1.7×10

38

single

4

od 1.5×10

–45

do 3.4×10

38

double

8

od 5.0×10

–324

do 1.7×10

308

extended

10

od 3.4×10

–4932

do 1.1×10

4932

)

Jednak oczywi cie nie znaczy to, e dodanie najmniejszej mo liwej liczby do najwi kszej cokolwiek zmieni! Liczby

z dopuszczalnego zakresu pami tane s tylko z okre lon liczb cyfr znacz cych (real — 11, single — 7, double — 15

i extended — 19).

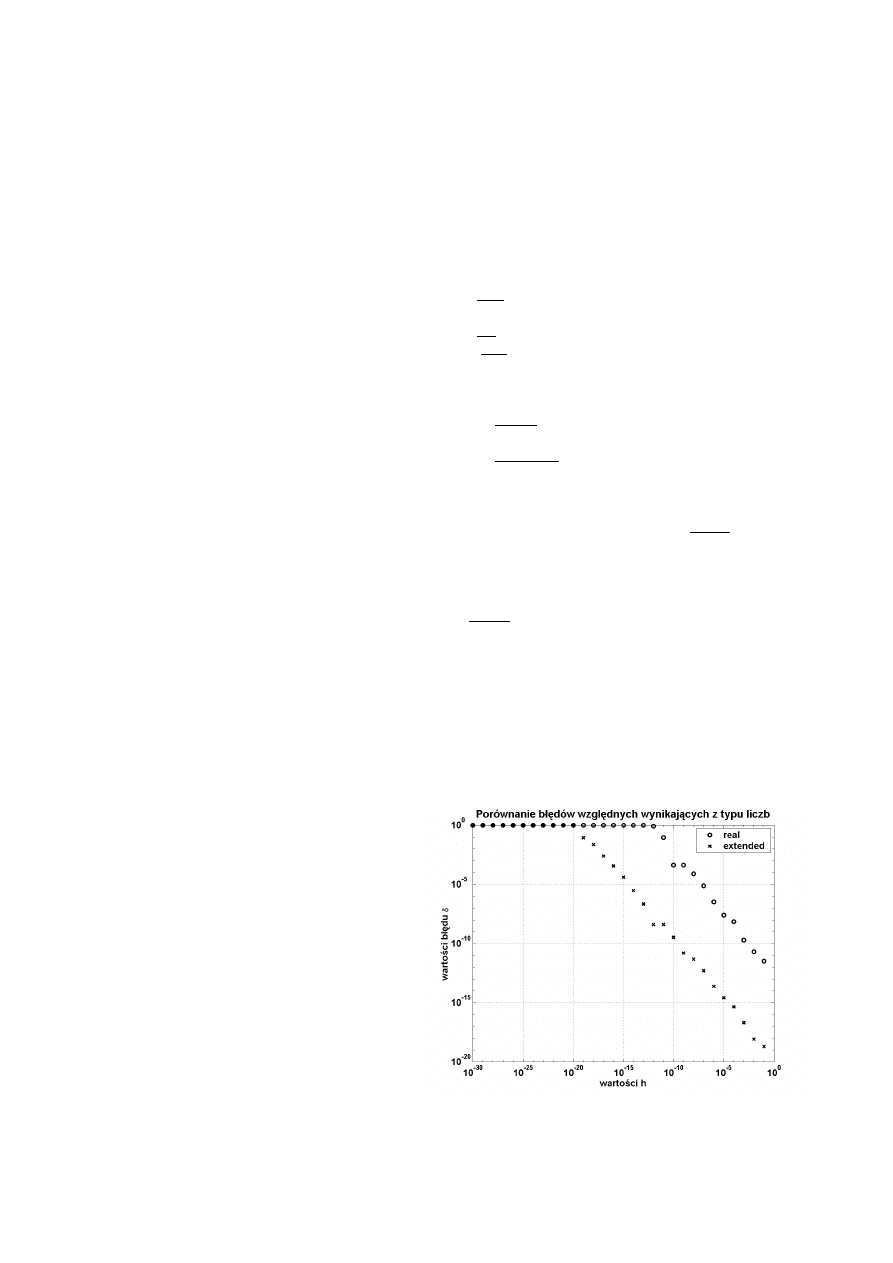
Przykładem skutków bł dów wynikaj cych z

ograniczonego zakresu komputerowej reprezentacji

liczb rzeczywistych mo e by wykonanie nast puj cej

operacji: do jednostki (danego typu) dodajemy mał

liczb h (tego samego typu) po czym od wyniku

odejmujemy jednostk . Oczekujemy, e w wyniku

otrzymamy wła nie mał liczb h. Analitycznie jest to

twierdzenie bezwzgl dnie prawdziwe, jednak kiedy

przeprowadzimy t operacj na komputerze,

stwierdzimy, e gdy tylko h stanie si odpowiednio

małe zaczn wyst powa bł dy. Wykres obok przed-

stawia bł dy wzgl dne uzyskiwane podczas działania

programu w j zyku Turbo Pascal wykonuj cego

wła nie tak operacj . Bł dy o warto ci 1 odpowiadaj

całkowicie bł dnym wynikom (tzn. gdy dodanie h do

jedynki daje w wyniku jedynk ). Wykonywan przez

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

5

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

program procedur mo na przedstawi tak:

h

1

h

1

h

Analogiczn „operacj ” mo na przeprowadzi w Scilabie. Posłu y nam do tego nast puj cy program:

// Ilustracja bł dów wynikaj cych z ograniczonej dokładno ci zapisu liczb.

//

clear

xdel(winsid());

//

h = logspace(-17,-13,100);

delta = (h - abs((h+1)-1) )./h;

xinit()

xset('thickness',2);

plot2d(h,zeros(h),logflag='ln',style=5);

xset('thickness',3);

plot2d(h,delta,logflag='ln',style=13)

xset('thickness',1);

a = get("current_axes");

// równie dobrze a = gca;

a.font_size = 4;

xtitle(sprintf('Wykres bł dów wynikaj cych z dokładno ci zapisu liczb\nwarto

%%eps =

%g',%eps));

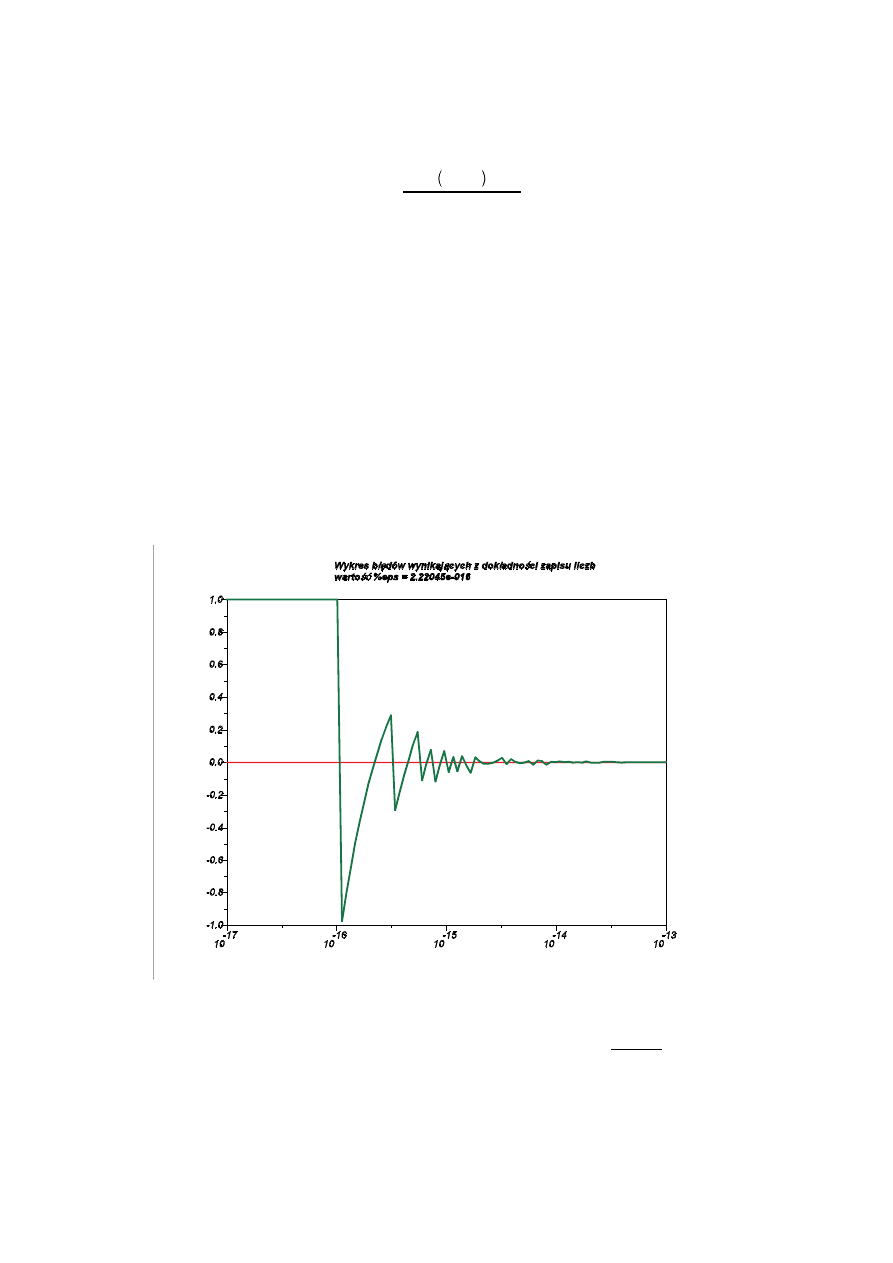
W wyniku jego działania otrzymamy nast puj cy wykres:

Jak wida wprawdzie zmienna

%eps

Scilaba, która w zasadzie informuje nas o dokładno ci wynosi około 10

–16

to jednak

bł dy wyra enia przekraczaj 10% ju o rz d wielko ci wcze niej. Oczywi cie warto parametru h, przy której bł d

całego wyra enia przestanie by akceptowalnie mały zale y od rozmiaru słowa maszynowego. Przy okazji warto zwróci

uwag , e %eps mo na zinterpretowa jako najmniejsz liczb jak uda si doda do jedno ci i zauwa y skutek tego

dodawania. Je eli chcieliby my dodawa j do liczby wi kszej (np. do 1000) to oczywi cie taka najmniejsza „zauwa alna

liczba” b dzie odpowiednio wi ksza (o trzy rz dy wielko ci).

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

6

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Bł dy obci cia

Tak okre lay bł dy wyst puj ce przy obliczaniu sum szeregów niesko czonych za pomoc sko czonej liczby wyrazów

(wła ciwie wszystkie funkcje s obliczane jako sumy szeregów, np. e

x

= 1 + x + ½x

2

+ ... + 1/N! x

N

). Wielko takiego bł du

zale y od tego jak szybko zbie ny jest wykorzystywany szereg. Szczególnie łatwe jest oszacowanie bł du obci cia w

przypadku szeregu, którego wyrazy s monotonicznie malej ce i maj przemienne znaki — w takiej sytuacji bł d jest

dokładnie oszacowany z góry przez warto pierwszego odrzuconego składnika.

Przykład: W przykładzie tym zrezygnujemy z przeprowadzania oblicze w układzie dwójkowym i w reprezentacji

maszynowej. Zało ymy po prostu, e ka da liczba jest zaokr glana do trzech cyfr znacz cych (nie do zadanego

miejsca po przecinku, a wła nie do zadanej liczby cyfr znacz cych — tzn. 5.67 + 7.89 = 13.6 (chocia dokładnie

powinno by 13.56)). Chcemy obliczy e

x

za pomoc rozwini cia e

x

= 1 + x + x

2

/2! + x

3

/3! + ... Rozwa my

obliczenia dla x = 0.5.

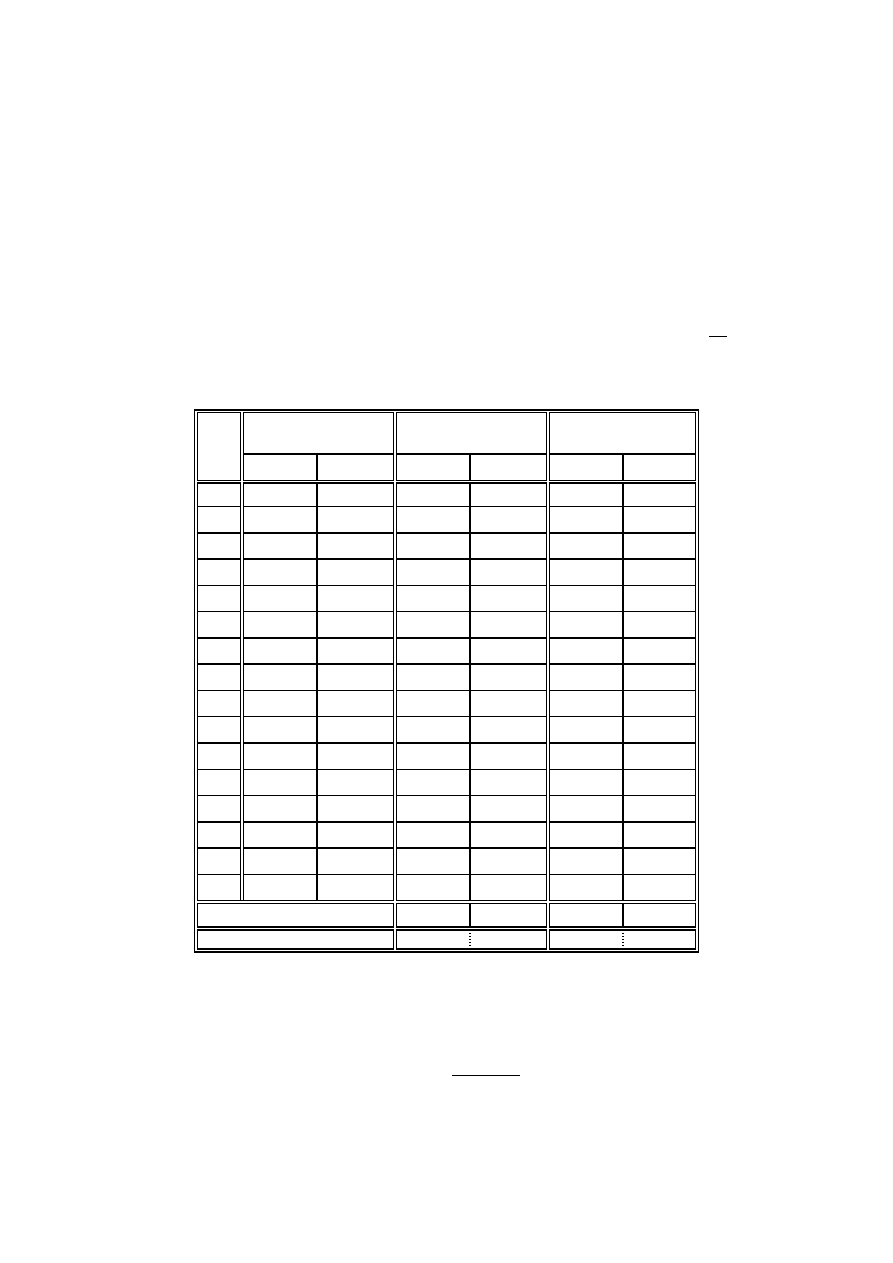
n

warto ci

wyrazów

suma

w dół

suma

w gór

dokł.

zaokr.

dokł.

zaokr.

dokł.

zaokr.

0

1

1

1

1

1.64872

1.648

1

0.5

0.5

1.5

1.5

0.64872

0.648

2

0.125

0.125

1.625

1.62

0.14872

0.148

3

0.02083

0.0208

1.64583

1.64

0.02372

0.0236

4

0.0026

0.0026

1.64844

1.64

0.00289

0.00288

5

0.00026

0.00026

1.6487

1.64

0.00028

0.00028

6

0.00002

0.00002

1.64872

1.64

0.00002

0.00002

7

1.6e-06

1.6e-06

1.64872

1.64

1.7e-06

1.7e-06

8

9.7e-08

9.7e-08

1.64872

1.64

1.0e-07

1.0e-07

9

5.4e-09

5.4e-09

1.64872

1.64

5.7e-09

5.7e-09

10

2.7e-10

2.7e-10

1.64872

1.64

2.8e-10

2.8e-10

11

1.2e-11

1.2e-11

1.64872

1.64

1.3e-11

1.3e-11

12

5.1e-13

5.1e-13

1.64872

1.64

5.3e-13

5.3e-13

13

2.0e-14

2.0e-14

1.64872

1.64

2.0e-14

2.0e-14

14

7.0e-16

7.0e-16

1.64872

1.64

7.2e-16

7.2e-16

15

2.3e-17

2.3e-17

1.64872

1.64

2.3e-17

2.3e-17

sumy

1.64872

1.64

1.64872

1.648

bł dy bezwzgl dne/wzgl dne

0.00872

0.529%

0.00072

0.044%

Inne ródła bł dów

Omówiłem ju przyczyny wyst powania bł dów wynikaj ce z samej istoty działania komputera. Nic nie wspomniałem

jednak o „czynniku ludzkim” (który, nawiasem mówi c, jest najcz stsz ich przyczyn ).

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

7

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Załó my na pocz tek, e mamy program obliczaj cy warto powierzchni koła o promieniu r (mam nadziej , e wszyscy

pami taj , e wynosi ona r

2

). Bł d jaki program b dzie konsekwentnie popełnia b dzie wynika ze sko czono ci zapisu

rozwini cia dwójkowego warto ci i warto ci promienia r oraz z bł dów obci cia popełnianych podczas podnoszenia r

do kwadratu i mno enia obu warto ci. Nic na to nie mo emy poradzi (poza oczywi cie u yciem maszyny b d kompilatora

o dłu szym słowie), ale bł dy te b d w rzeczywisto ci bardzo małe (pami tajmy, e w przedstawionych wcze niej

przykładach u ywali my słowa o miobitowego — tak prymitywnych komputerów w rzeczywisto ci nie ma). Co jednak si

stanie je li programista za warto podstawi 3.141 ? Spodziewany bł d b dzie wynosi około 0.0005 (

!) — b dzie wi c

wielokrotnie wi kszy ni wszystkie bł dy jakie zdoła popełni komputer... Przykład ten wskazuje do dobitnie na fakt,

e programista, u ywaj c niedokładnych stałych, jest w stanie spowodowa bł dy o wiele rz dów wielko ci wi ksze ni

byłby to w stanie zrobi sam komputer. Je eli zale y nam na dokładno ci i za pomoc wyszukanych sztuczek zdołali my

zmusi kompilator do działania na liczbach o (np.) dwukrotnie wi kszej precyzji ni robi to zazwyczaj „sam z siebie”, to

powinni my si równie upewni , e zdefiniowane w nim warto ci stałych w rodzaju albo e równie maj wystarczaj c

dokładno . Podobnie wygl da sytuacja z funkcjami zdefiniowanymi w kompilatorze. W starszych wersjach Turbo Pascala

(np.) funkcje trygonometryczne mogły zwraca warto ci o podwy szonej dokładno ci, ale liczyły je zawsze z dokładno ci

„normaln ” (a cyfry znacz ce brakuj ce do podwy szonej dokładno ci uzupełniały „ mieciami”, które akurat znajdowały

si w tym miejscu w pami ci). Mo na oczywi cie dyskutowa czy bł dy spowodowane w ten sposób s zawinione przez

programist (który wykazał si nadmiernym zaufaniem do kompilatora) czy przez producenta kompilatora, ale pami tajmy,

e za bł dy w wynikach programu przed zleceniodawc odpowiada b dzie autor programu, a „opowiadanie” o bł dach

kompilatora i tak b dzie wygl da na nieudoln prób „zwalenia winy” na kogo innego.

Podczas omawiania wszystkich dotychczasowych bł dów zakładali my, e komputer faktycznie liczy to co powinien.

Tymczasem ródła bł dów (i to tych najwi kszych) pojawiaj si ju na etapie analizy rozwi zywanego zagadnienia.

Posłu si tu „nie miertelnym” przykładem rzutu uko nego: nale y rozwi za równania ruchu ciała rzuconego uko nie.

Ju na etapie formułowania równa ró niczkowych ruchu (czyli nawet jeszcze przed wyborem algorytmu rozwi zywania)

musimy podj nast puj ce decyzje:

a) czy uwzgl dnia opór powietrza czy nie (oczywi cie tak — w przeciwnym razie wyniki b d stosowalne co najwy ej

na Ksi ycu b d w komorze pró niowej),

b) w jaki sposób opór powietrza zale y od pr dko ci: zale no liniowa — zgodna z wzorami Stokesa odnosi si do

cieczy, zale no kwadratowa lepiej pasuje do powietrza (dla niej przynajmniej mamy wyprowadzone wzory, jednak

do wiadczenia pokazuj , e w gr mog wchodzi te wy sze pot gi pr dko ci),

c) w tym miejscu wida , e musimy zdecydowa czy dopuszczamy wyst powanie wiatru czy nie, a je li tak to czy b dzie

on zawsze wia dokładnie poziomo czy te jego pr dko mo e mie składow pionow ,

d) jaki współczynnik proporcjonalno ci zastosowa we wzorze na opór powietrza (zakładaj c, e wzór ju wybrali my)

— jego warto zale y od kształtu ciała (trzebaby wi c przyj jak warto do wiadczaln ) na dodatek wiadomo, e sama

warto tego współczynnika jest funkcj pr dko ci ciała (wzgl dem powietrza — wi c z uwzgl dnieniem wiatru) ,

e) we wzorze na sił oporu (jakiego by my nie przyj li) wyst puje g sto powietrza trzeba wi c zdecydowa czy

uwzgl dniamy zmiany siły oporu z wysoko ci na jak wzniesie si pocisk czy nie, a na dodatek nale ałoby si zastanowi

czy b dziemy uwzgl dnia aktualne ci nienie atmosferyczne i wilgotno powietrza,

f) powinni my si zastanowi czy nasz pocisk b dzie wykonywa jakie ruchy obrotowe czy nie — je li tak to

nale ałoby uwzgl dni efekt Magnusa, który doda nam now składow siły działaj cej na pocisk skierowan prostopadle

do wektora pr dko ci pocisku (wzgl dem powietrza) i do wektora jego pr dko ci obrotowej,

g) warto byłoby te zastanowi si jaki wpływ na trajektori ciała b dzie mie siła Coriolisa (w ko cu Ziemia jest

układem nieinercjalnym).

Tego rodzaju rozwa ania mo na ci gn dalej — pocisk mo e rozgrzewa si w wyniku tarcia o powietrze (zale nie

od swej pr dko ci wzgl dem powietrza) zatem zmienia si mo e jego pole przekroju, zmieni si te prawdopodobnie

lepko powietrza (bo ono te si rozgrzeje tu przy cianie pocisku) itd. itp.. Jak wi c wida , ju analizuj c samo zadanie

musimy przyj wiele zało e upraszczaj cych, a to powoduje, e wła ciwie nie mo na mówi o rozwi zaniach dokładnych

(w jakim abstrakcyjnym, bezwzgl dnym sensie). Ka de rozwi zanie b dzie mie swój szczególny zakres w jakim mo na

b dzie z grubsza poda oszacowanie jego dokładno ci. W powy szym przykładzie je li np. zaniedbamy zale no g sto ci

powietrza od ci nienia, powinni my uprzedzi u ytkownika do jakich wysoko ci dopuszczamy stosowanie naszego

przybli onego rozwi zania (a sam program powinien „lojalnie” informowa , e wprowadzono takie parametry wej ciowe,

przy których pocisk wznosi si na tak wysoko , na jakiej zastosowane w programie przybli enia spowoduj zbyt wielkie

bł dy).

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

8

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

No i jeszcze ostatnia przyczyna — milcz co zało yli my, e autor programu w ogóle umiał rozwi za postawiony przed

nim problem i miał wiadomo stosowanych przybli e . W kra cowym przypadku (mo e nieco humorystycznym, ale

chyba dobrze ilustruj cym problem), kto kto znajomo z fizyk zako czył w szkole podstawowej, a miałby akurat

rozwi za omawiany powy ej problem, przygotowałby program doskonale licz cy przypadek bez oporu powietrza i bez

siły Coriolisa i w ogóle nie powiadomiłby u ytkownika o istniej cych ograniczeniach stosowalno ci swego programu (bo

po prostu nie byłby ich wiadomy).

Podczas zaj z Metod Numerycznych b dziemy zakłada , e naszym jedynym problemem s „psikusy” płatane nam

przez metod (algorytm) rozwi zania. O „psikusach” płatanych nam przez komputer, a wynikaj cych z jego cyfrowej

natury, b dziemy, pisz c programy, zawsze pami ta (ale nie b d do nich ju wraca w dalszym ci gu wykładu). Natomiast

nie b d przypomina o kwestiach, o których wspomniałem przed chwil – innymi słowy zakładam, e programista

dysponuje dostateczn wiedz fizyczn aby problem rozwi za poprawnie. Cały czas musimy jednak pami ta (mo e nawet

zwłaszcza po uko czeniu studiów), e nawet najlepszy algorytm numeryczny nie „uratuje” programu, którego zało enia

s bł dne.

Niestabilno metod obliczeniowych (powodowana przez bł dy obci cia)

We my jako przykład nast puj ce zadanie: Nale y obliczy warto ci całek postaci:

y

n

1

0

x

n

x 5

dx

dla n = 0,1,...,8. Zauwa ymy, e mo na zastosowa wzór rekurencyjny:

y

n

5y

n 1

1
n

co wynika z:

y

n

5y

n 1

1

0

x

n

5x

n 1

x 5

dx

1

0

x

n 1

(x 5)

x 5

dx

1

0

x

n 1

dx

1
n

W przykładzie obliczenia b dziemy wykonywa z trzema cyframi po przecinku, a bł d wynikaj cy z obci cia oznaczymy

przez . Wykonuj c obliczenia kolejno od y

0

b dziemy otrzymywa :

y

o

1

0

dx

x 5

ln(x 5)

1

0

ln6

ln5

y

0

= = 0.182

(bł d )

y

1

= 1 – 5y

0

= 0.090

(bł d 5 )

y

2

= ½ – 5y

1

= 0.050

(bł d 25 )

y

3

= – 5y

2

= 0.083

(bł d 125 )

y

4

= ¼ – 5y

3

= –0.165 (sic

!)

(bł d 625 )

W tym miejscu zatrzymujemy si , bo przecie z samej postaci obliczanej całki wynika, e dla ka dego n powinni my

otrzyma warto dodatni !

Bł d wynika tu z faktu, e przy ka dym kolejnym działaniu nie tylko dodajemy nowy (bardzo mały) bł d zwi zany z

wykonanym mno eniem i dodawaniem, ale równocze nie, poniewa poprzedni wynik mno ymy przez 5, pi ciokrotnie

powi kszamy bł d jakim obarczona była poprzednio obliczona liczba — dla ka dej kolejnej bł d pocz tkowy b dzie 5 razy

wi kszy (wypisane w kolumnie obok).

Aby tego unikn nale y wykorzysta wzór rekurencyjny w przeciwnym kierunku:

y

n 1

1

5n

1
5

y

n

— w tym przypadku bł d popełniany w poprzednich krokach b dzie zawsze dzielony przez 5 — b dzie wi c male .

Przy takiej metodzie oblicze problemem b dzie przyj cie warto ci pocz tkowej (któr musi by jakie y

n

— dla

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

9

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

dostatecznie du ej warto ci n). Istniej dwie mo liwo ci: zało enie, e poczynaj c od jakiej warto ci n warto ci szeregu

y

n

malej tak wolno, e dwie kolejne b d równe sobie, albo e dla wystarczaj co du ego n warto c y

n

wynosi zero.

1. Załó my, e y

10

y

9

, wówczas:

y

9

+ 5y

9

1/10 y

9

1/60 0.017

y

8

= 1/45 – y

9

/5 0.019

y

7

= 1/40 – y

8

/5 0.021

y

6

0.025

y

5

0.028

y

4

0.034

y

3

0.043

y

2

0.058

y

1

0.088

y

0

0.182

(to samo co z obliczenia dokładnego)

2. Załó my, e y

10

= 0, wówczas dostajemy:

y

9

= 0.020

y

8

= 0.018

a pozostałe warto ci jak wy ej.

Warto zapami ta , echo oba przedstawione wzory rekurencyjne s z matematycznego punktu widzenia poprawne,

to jednak jeden z nich z samej swej natury nie nadaje si do oblicze numerycznych. Z takimi przypadkami b dziemy si

jeszcze spotyka . Istniej metody pozwalaj ce przewidzie czy dany algorytm obliczeniowy b dzie powodowa wzrost

bł dów (czyli b dzie „niestabilny”) czy te wr cz przeciwnie — b dzie ogranicza bł dy. Zapoznamy si z nimi pó niej.

wiczenie: Napisa wzór rekurencyjny dla obliczania całek:

y

n

1

0

x

n

4x 1

dx

Poda i przeanalizowa algorytm działaj cy dobrze i algorytm działaj cy le.

Pr dko wykonywania operacji arytmetycznych

Interesuj ce mo e by porównanie pr dko ci wykonywania poszczególnych operacji arytmetycznych. W przypadku

Scilaba warto przy okazji porówna pr dko wykonywania operacji na macierzach z pr dko ci wykonywania p tli.

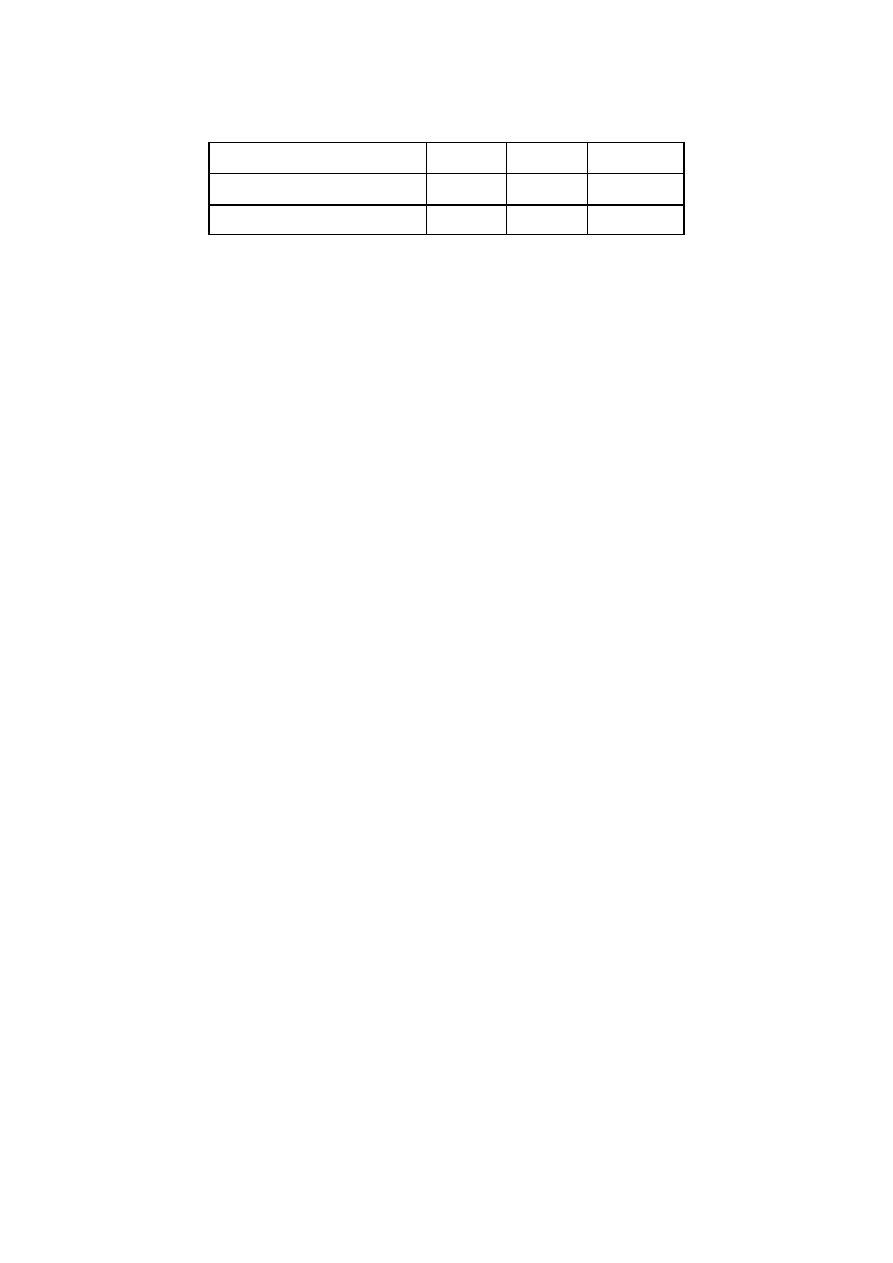
Tabela poni ej podaje czasy wymagane do wykonania miliona operacji na przykładowym (moim;) komputerze.

Kolumna „p tla” odnosi si do działania na pojedynczym skalarze (powtórzonego oczywi cie milion razy), dane z kolumny

„macierz” dotycz jednej operacji za to wykonanej na wektorze zawieraj cym milion elementów.

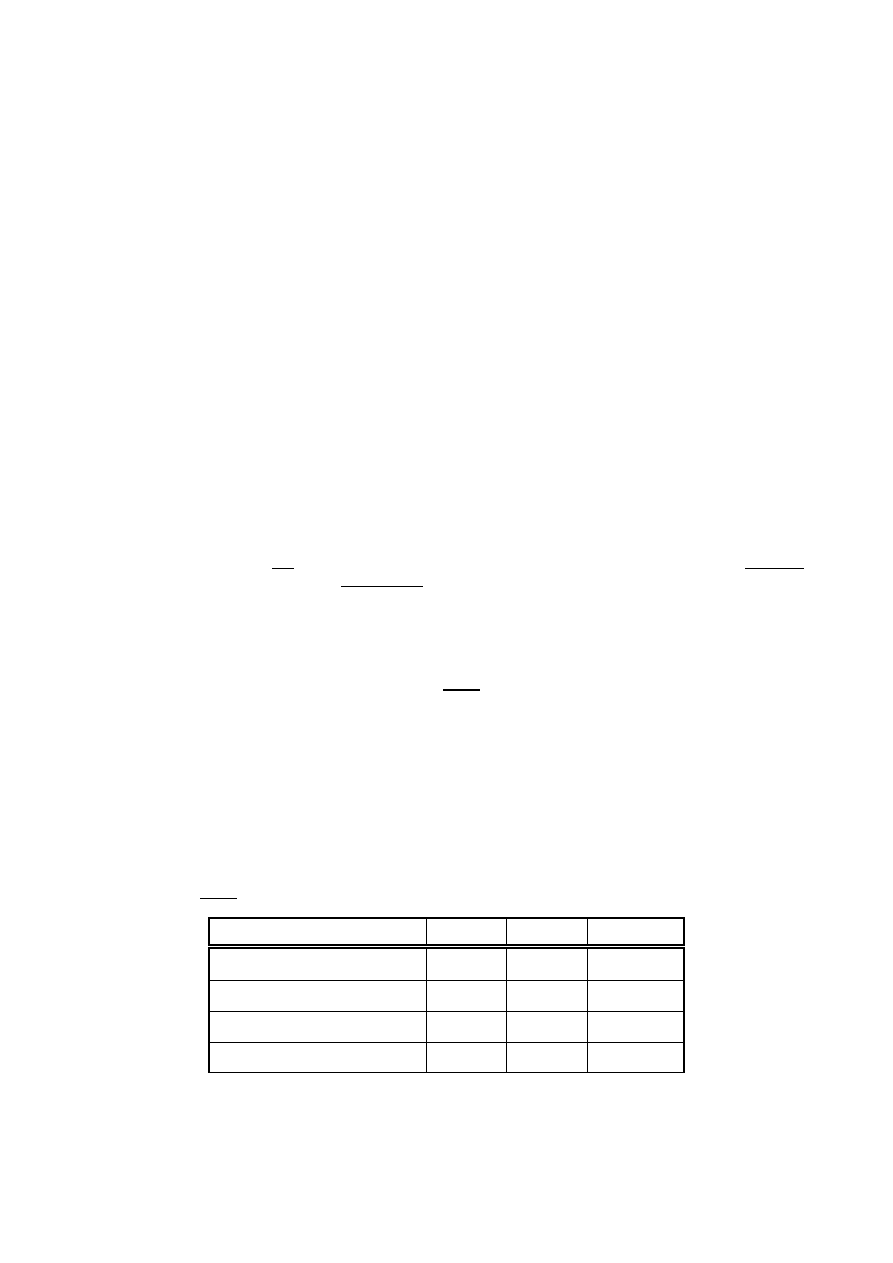
operacja

p tla

macierz

krotno

dodawanie

7.859375

0.078125

100.6

odejmowanie

7.921875

0.09375

84.5

mno enie

7.390625

0.078125

94.6

dzielenie prawostronne

7.28125

0.09375

77.6666667

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

10

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

dzielenie lewostronne

7.328125

0.09375

78.1666667

podnoszenie do dowolnej pot gi

7.859375

0.40625

19.3461538

podnoszenie do kwadratu

7.34375

0.171875

42.7272727

Wida do wyra nie, e warto pozna i stosowa operacje macierzowe. W tabeli nie przedstawiłem wyników dla

przypadku gdy w p tli oblicza si kolejne warto ci wektora równocze nie go powi kszaj c (ostrzegałem przed tak metod

na zaj ciach) — czasy s ok. dziesi ciokrotnie dłu sze ni czasy realizacji p tli (wi c te 10000 razy dłu sze od prawidłowo

realizowanych operacji macierzowych — jak wida ostrze enie nie było bezpodstawne).

Wyniki przedstawione w powy szej tabeli uzyskano za pomoc prostego programu, którego fragment znajduje si

poni ej (aby samodzielnie przeprowadzi takie testy wystarczy powieli go dla ka dego działania, którego pr dko

wykonywania chcemy sprawdzi ).

clear

xdel(winsid())

stacksize(10000000)

// Tu nale ałoby pogada o poleceniu "stacksize".

//

rand('seed',.123456);

n = 10000 // liczba powtórze

//

// dodawanie

a = rand(1,1);

b = rand(1,1);

timer();

for i = 1:n

c = a + b;

end

dodawanie_petla = timer()

clear c

aa = ones(1,n)*a;

bb = ones(1,n)*b;

timer();

cc = aa + bb;

dodawanie_macierz = timer()

clear cc

timer();

for i = 1:n

ccc(i) = a + b;

end

dodawanie_petla_macierz = timer()

clear ccc

Schemat Hornera

Inny sposób usprawnienia oblicze — wzory algebraiczne mo na zapisywa w ró nych postaciach, które mog lepiej

lub gorzej nadawa si do obliczania. Dobrym przykładem jest schemat Hornera — sposób obliczania warto ci wielomianu.

Wielomian postaci:

w(x) = a

n

x

n

+ a

n–1

x

n–1

+ a

n–2

x

n–2

+ ... + a

1

x + a

o

nale y zapisa nast puj co:

w(x) = ((...((a

n

x + a

n–1

)x + a

n–2

)x + ... + a

1

)x + a

o

)

i oblicza w taki sposób:

w

1

= a

n

x + a

n–1

w

2

= xw

1

+ a

n–2

.............

w

n

= xw

1

+ a

o

= w(x)

Uzyskujemy w ten sposób znaczn oszcz dno czasu oblicze : potrzeba b dzie n mno e i n dodawa (zakładaj c,

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

11

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

e wszystkie współczynniki a

i

s niezerowe) — podczas gdy obliczaj c ka d pot g z osobna nale ałoby wykona n

2

/2

mno e i n dodawa .

Pisanie programów

Styl programowania

Komentarze

Istnieje wzór empiryczny:

t

s

t

N

z

gdzie: t

s

jest czasem straconym z powodu braku komentarzy podczas próby poprawienia lub zmienienia programu, t

z

jest

czasem zaoszcz dzonym dzi ki ich nie pisaniu, a N jest liczb tygodni jakie upłyn ły od napisania programu.

Jest to oczywi cie art, ale zawiera spor doz prawdy — pod koniec semestru, podczas pisania programów

rozwi zuj cych równania ró niczkowe cz stkowe metod ró nic sko czonych konieczne b dzie posłu enie si procedurami

rozwi zuj cymi układy równa algebraicznych (które b d opracowywane na pocz tku semestru). B dzie to najlepszy test

prawdziwo ci powy szego wzoru.

Powtórne wykorzystywanie procedur i funkcji

Je li pisane s jakie procedury, które maj znaczenie ogólne i mo na by je wykorzysta w innych programach

(procedury do rozwi zywania układów równa algebraicznych b d pod koniec semestru potrzebne do rozwi zywania

równa ró niczkowych, ale dotyczy to równie ew. procedur komunikowania si z u ytkownikiem itp.) to trzeba je pisa

szczególnie starannie – zaznaczaj c w komentarzach jakie maj wymagania: tzn. np. jakich stałych globalnych spodziewaj

si w programie (w zasadzie nie powinny), w jakiej postaci przyjmuj dane i w jakiej postaci zwracaj wyniki, jakie s ich

ograniczenia (np. maksymalny rozmiar czy ilo danych) itd.

Sposób nazywania zmiennych i stałych

Stosowanie nazw w rodzaju: „c”, „p17”, „k3” znakomicie utrudnia pó niejsze zrozumienie programu. Obecnei, z reguły

nazwy mog mie niemal dowoln długo , ale do ich rozró niania wykorzystywanych jest tylko pewna liczba

pocz tkowych znaków. W Turbo Pascalu s to pierwsze 63 znaki, w Scilabie pierwsze 24 znaki — jesto to wystarczaj ca

liczba by mo na było posługiwa si nazwami w rodzaju: „wyznacznik”, „pierwiastek_1” (ew. „pierw_1”), „x_start”,

„x_koniec” itd. co z kolei bardzo ułatwia pó niejsz interpretacj zapisanych wyra e .

Usuwanie bł dów

Wła ciwie nie istnieje co takiego jak program napisany od razu bezbł dnie. Popełnianie bł dów podczas pisania

programu jest rzecz normaln i nieuniknion (mo emy oczywi cie popełnia ich wi cej lub mniej zale nie od tego jak

powa nie podejdziemy do unikania bł dów). Istotnym problemem jest jednak przede wszystkim znajdowanie i usuwanie

bł dów. W zale no ci od tego jak napisali my program mo e to by łatwiejsze lub trudniejsze. Je li rozwi zywany problem

wymaga długotrwałych oblicze warto na pocz tek zacz pisa program dla mniejszego zakresu, o mniejszej dokładno ci

itp. W ten sposób mo na szybciej stwierdzi wyst powanie bł dów. W ostatecznej wersji programu, dla przyspieszenia jego

działania cz sto rezygnujemy z jakichkolwiek komunikatów ekranowych, w wersji pocz tkowej nie powinni my z nich

rezygnowa , wr cz przeciwnie: nale y generowa znaczn ich liczb — w ten sposób b dzie wiadomo co program akurat

robi i podczas wykonywania jakiej procedury „padł”. Oczywi cie wygodnymi narz dziami do poszukiwania bł dów s

debuggery wbudowane np. w Borland Pascal czy Borland C++ (ale trzeba si najpierw nauczy nimi sprawnie posługiwa ),

natomiast komunikaty wypisywane przez program podczas pracy, umo liwiaj c szybkie zidentyfikowanie bł dnie

działaj cej procedury cz sto pozwalaj bardzo szybko zidentyfikowa i usun bł d.

Zawsze warto pami ta o tym, e bł dy w programie s w 99% zawinione przez programist , a w pozostałym 1%

Metody Numeryczne w Fizyce 1

Bł dy oblicze numerycznych

12

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

równie , tylko, e on o tym jeszcze nie wie. Wiadomo oczywi cie, e istniej bł dy kompilatorów, systemów operacyjnych,

a nawet procesorów, jednak prawdopodobie stwo, e wyst pił który z tych bł dów „niezale nych” od programisty jest

znikome. Mówi c o bł dach popełnionych przez programist miałem na my li nie tylko trywialn zamian plusa na minus

albo mno enia na dzielenie (które to bł dy niestety zazwyczaj bardzo trudno znale , jako e program działa bardzo dobrze,

tylko e daje bezsensowne wyniki) ale tak e (a mo e przede wszystkim) bł dy polegaj ce na niewła ciwym doborze metody

rozwi zania czy niewła ciwej implementacji algorytmu, a nawet wyborze niewła ciwej metody podejmowania decyzji o

zatrzymaniu programu.

Sporz dzanie wykresów

Ten podpunkt pozostał „z dawnych czasów” – gdy studenci pisali swoje programy na MNF1 jeszcze w DOS-owych

kompilatorach C lub Turbo Pascal, daj cych mo liwo c wykorztystywania tylko najbardziej podstawowych procedur

graficznych – w rodzaju wy wietlenia pojedynczego punktu b d narysowania odcinka pomi dzy punktami o zadanych

współrz dnych. Gdy wykorzystujemy Scilaba wiadomo ci te nie b d potrzebne, bo mo na (i nale y) posłu y si

odpowiednimi procedurami Scilaba.