Procesy Rozdzielania

projekt II

wariant nr 28

Michał Kuśmierczyk gr. 2

Prowadzący:

DR INŻ

.

J

AN

N

OWOSIELSKI

Warszawa, grudzień 2008

Zadanie 1.

1.1. Tre

ść

zadania

Sól (siarczan amonu) oczyszcza si

ę

z niewielkiej ilo

ś

ci nierozpuszczalnych zanieczyszcze

ń

poprzez ługowanie

rozcie

ń

czonym roztworem tej soli. Roztwór ługuj

ą

cy (ubogi) jest podgrzany do temperatury t1 = 375 K. Otrzymany

w wyniku ługowania roztwór bogaty jest chłodzony w regeneratorze ciepła, a nast

ę

pnie w dodatkowej chłodnicy do

temperatury t2 = 293 K. Po ochłodzeniu wykrystalizowana sól jest oddzielana, za

ś

roztwór ubogi zawracany

poprzez regenerator ciepła i zagrzewacz do ługowania. Temperatura soli surowej wynoci t2. Okre

ś

li

ć

ciepło

wymienione w regeneratorze, ciepło dostarczane w zagrzewaczu, ilo

ść

roztworu ubogiego oraz ilo

ść

roztworu

bogatego przypadaj

ą

ce na kilogram wydzielonej soli. W obliczeniach pomin

ąć

pojemno

ść

ciepln

ą

zanieczyszcze

ń

i przyj

ąć

wyrównanie temperatur na odpowiednim ko

ń

cu regeneratora.

1.2. Dane projektowe

t1

85

:=

[

ο

C]

t2

20

:=

[

ο

C]

1.3. Obliczenia i rozwi

ą

zanie

Wprowadzamy nast

ę

puj

ą

ce oznaczenia stanów w układzie:

1. Wylot z rozdzielacza - roztwór nasycony o temp. t

2

2. Wylot cieczy ubogiej z regeneratora - roztwór o temp. t

2

'

3. Wylot cieczy ubogiej z dogrzewacza - roztwór o temp. t

1

4. Wylot cieczy bogatej ze zbiornika gdzie nast

ę

puje rozpuszczanie - roztwór nasycony o temp. t

1

'=t

2

'

5. Wylot cieczy bogatej z regeneratora - roztwór nasycony + kryształy o temperaturze t

1

".

6. Wylot cieczy bogatej z chłodnicy - roztwór nasycony + kryształy o temperaturze t

2

.

7. Wlot solli zanieczyszczonej o temperaturze t

2

.

Dochodzi do zrównania temperatur na wylocie strumienia o mniejszej pojemno

ś

ci cieplnej (tzn. o mniejszym

strumieniu cieplnym). Jest to ciecz uboga.

Na podstawie powy

ż

szych oznacze

ń

znane jest poło

ż

enie punktów 1, 3, 7. S

ą

one nanoszone na wykres. Znaj

ą

c

poło

ż

enie punktu 1 odczytujemy skład cieczy ubogiej:

xL

0.42

:=

Na przeci

ę

ciu si

ę

odcinka 3–7 z lini

ą

roztworu nasyconego wyznaczamy poło

ż

enie punktu 4, a tym samym

temperatur

ę

oraz skład cieczy bogatej:

t2p

74

:=

[

ο

C]

xR

0.47

:=

Na linii 1–7 le

ż

y dla x=x

R

le

ż

y stan 6.

Punkt 2 znajdujemy poprzez znalezienie punktu przeci

ę

cia izotermy t

2p

oraz prostej x=x

L

.

Odcinek 2–3 okre

ś

la ciepło dostarczone w dogrzewaczu w przeliczeniu na 1 kg (Q/L) cieczy ubogiej. Odcinek 1–2

natomiast okre

ś

la ciepło wymienione w regeneratorze, równie

ż

w przeliczeniu na 1 kg cieczy ubogiej (Q

reg

/L)

Q

L

30

=

[kJ/kg]

Qreg

L

163

=

[kJ/kg]

Qreg

K

1867

=

[kJ/kg]

Ciepło dostarczone do dogrzewacza w przeliczeniu na 1 kg masy kryształów wyznaczamy
graficznie.

Q

K

259

=

[kJ/kg]

Na koniec wyznaczamy stosunki masowe cieczy ubogiej L, ubogiej R oraz kryształów.

Zakładamy 1 kg wydzielonych kryształów.

K

1

:=

L

1

:=

R

1

:=

warto

ś

ci startowe

Given

R

L

K

+

=

R xR

⋅

K

L xL

⋅

+

=

vec

Find L R

,

(

)

:=

K

1

=

[kg]

L

vec

0

10.6

=

:=

[kg]

R

vec

1

11.6

=

:=

[kg]

Zadanie 2.

2.1. Tre

ść

zadania

Krystalizacj

ę

soli (siarczan amonu) prowadzi si

ę

w warniku pod ci

ś

nieniem P = 100 kPa.

Surówka wpływaj

ą

ca do regeneratora ciepła m atemperatur

ę

t

0

= 20

ο

C i st

ęż

enie x

0

= 0,12

(uł.mas.). Okre

ś

li

ć

ciepło wymieniane w regeneratorze, ciepło doprowadzane w warniku, ilo

ść

surówki, ilo

ść

roztworu ubogiego oraz ilo

ść

roztworu bogatego, przypadaj

ą

ce na kilogram

wydzielonej soli je

ś

li w wyniku procesu powinno wykrystalizowa

ć

a = 45% całkowitej ilo

ś

ci soli

doprowadzonej pod postaci

ą

surówki. W obliczeniach przyj

ąć

wyrównanie temperatur na

odpowiednich ko

ń

cach wymiennika.

2.2. Dane projektowe

P

100

:=

[kPa]

t0

20

:=

[

ο

C]

x0

0.12

:=

a

45

:=

2.3. Obliczenia i rozwi

ą

zanie

Wprowadzamy nast

ę

puj

ą

ce oznaczenia stanów w układzie:

1. Wlot surówki do regeneratora – roztwór (t

0

,x

0

)

1'. Wylot podgrzanej surówki z regeneratora - roztwór (temp. 1')

2. Mieszanina trójfazowa w wyparce

3. Roztwór nasycony 3' i kryształy 3'' opuszczaj

ą

ce warnik (x

R

).

4. Para opuszczaj

ą

ca warnik.

5. Schłodzone kryształy i roztwór nasycony, opuszczaj

ą

ce regenerator (x

R,

temp. t

0

*)

6. Wylot kryształów soli o temperaturze t

0

.

7. Wylot roztworu nasyconego o temperaturze t

0

.

Na wykres nanosimy punkty 1, 6, 7.

Z izobary P odczytujemy temperatur

ę

wrzenia (czyli punkt znajduj

ą

cy si

ę

na linii nasycenia).

t

110

:=

[

ο

C]

Znaj

ą

c t

ą

temperatur

ę

wyznaczamy entalpi

ę

pary dla t i P. Mo

ż

emy dzi

ę

ki temu wyznaczy

ć

punkt 4.

i t

( )

2698

:=

[kJ/kg]

Zaznaczamy na wykresie obszar trójfazowy okre

ś

lany przez punkty 4–3'–3".

Znaj

ą

c izoterm

ę

t0 oraz stan 7 wyznaczamy xL.

xL

0.43

:=

W celu wyznaczenia xR rozwi

ą

zujemy poni

ż

szy równa

ń

. Wszystko b

ę

dzie liczone na 1 kg

wykrystalizowanej soli.

K

1

:=

[kg]

S

1

:=

R

1

:=

xR

0.5

:=

L

1

:=

warto

ś

ci startowe

Given

K

a

100

S

⋅

x0

⋅

=

S x0

⋅

R xR

⋅

=

R

K

L

+

=

R xR

⋅

L xL

⋅

K

+

=

vec

Find S R

,

L

,

xR

,

(

)

:=

S

vec

0

:=

R

vec

1

:=

L

vec

2

:=

xR

vec

3

:=

S

18.519

=

[kg]

L

2.842

=

[kg]

R

3.842

=

[kg]

xR 0.578

=

[kg]

Skład mieszaniny cieczy i kryształów opuszczaj

ą

cych warnik to x

R

. Jeste

ś

my w stanie dzi

ę

ki

temu wyznaczy

ć

punkt 3 na izotermie wrzenia oraz punkt 5 na izotermie t

0

. Stan 2 znajduje si

ę

na przeci

ę

ciu linii ł

ą

cz

ą

cej punkty 3 i 4 dla składu x

0

.

Odcinek 3–5 to ciepło oddane w regeneratorze liczone na 1 kg cieczy bogatej.

Qreg

R

259

=

[kJ/kg]

Odcinek 1–1' okre

ś

la ilo

ść

ciepła oddan

ą

w regeneratorze w przeliczeniu na 1 kg surówki.

Qreg

S

59

=

[kJ/kg]

Ciepło dostarczone do wyparki liczone na 1 kg kryształów zostało wyznaczone metod

ą

graficzn

ą

korzystaj

ą

c

jednak z zale

ż

no

ś

ci na podobie

ń

stwo trójk

ą

tów.

Q

K

20061

=

[kJ/kg]

Zadanie 3.

3.1. Tre

ść

zadania

Korzystaj

ą

c z wykresu entalpowego dla układu alkohol etylowy - woda dla surówki o składzie pocz

ą

tkowym

x

0

= 0.15 uł.mol. alkoholu etylowego i temperaturze pocz

ą

tkowej t

0

= 40

ο

C znajduj

ą

cej si

ę

pod ci

ś

nieniem

0,1 MPa, nale

ż

y wyznaczy

ć

:

a) Dla procesu destylacji równowagowej przy stopniu oddestylowania Z

d

= 0,5; składy produktów; temperatur

ę

destylacji; ciepło dostarczone podczas procesu przypadaj

ą

ce na 1 kg surówki, cieczy wyczerpanej i destylatu;

efekty cieplne w chłodnicach, je

ż

eli temperatura ko

ń

cowa produktów wynosi t = 25

ο

C.

b) Dla procesu destylacji ekspansyjnej (surówka zostaje spr

ęż

ona do si

ć

nienia 0.2 MPa, ogrzana do temperatury

wrzenia i po przej

ś

ciu przez zawór dławi

ą

cy rozpr

ęż

ona do ci

ś

nienia 0.1 MPa): składy otrzymanych produktów;

stopie

ń

oddestylowania; temperatur

ę

w separatorze; ciepło dostarczone do zagrzewacza przypadaj

ą

ce na 1 kg

surówki, cieczy wyczerpanej i destylatu; efekty cieplne w chłodnicach je

ś

li temperatura ko

ń

cowa produktów

wynosi t = 25

ο

C.

c) Dla destylacji rózniczkowej przy stopniu oddestylowania Z

d

= 0,35: składy produktów; ciepło dostarczone do

procesu przypadaj

ą

ce na 1 kg surówki, cieczy wyczerpanej i destylatu oraz efekt cieplny w chłodnicy, je

ś

li

temperatura ko

ń

cowa destylatu wynosi t = 25

ο

C.

d) Dla destylacji rózniczkowej półci

ą

głej: stopie

ń

oddestylowania Z

d

, je

ś

li skład cieczy wyczerpanej x

w

= 0.042

uł.mol. etanolu, a stosunek nat

ęż

enia przepłytu surówki do destylatora jest stały i wynosi S/D =

ψ

= 0,5.

3.2. Dane projektowe

x0

0.40

:=

[uł.mol. etanolu]

skład surówki

t0

30

:=

[

ο

C]

temperatura pocz

ą

tkowa

P

0.1

:=

[MPa]

ci

ś

nienie w układzie

Przeliczenie ułamka molowego na masowy:

ME

46

:=

[g/mol] masa molowa etanolu

Mw

18

:=

[g/mol] masa molowa wody

Xmas x

( )

ME x

⋅

1

x

−

(

) Mw

⋅

x ME

⋅

+

:=

ułamek masowy w funkcji ułamka molowego

x0

Xmas x0

( )

:=

x0 0.63

=

[uł.mas. etanolu]

3.3. Obliczenia

a) Destylacja równowagowa

Zd

0.25

:=

stopie

ń

oddestylowania

t

20

:=

[

ο

C]

temperatura ko

ń

cowa

Zapisujemy bilans masowy oraz składnika dla destylarki. S - ilo

ść

surówki, W - ilo

ść

cieczy wyczerpanej, D - ilo

ść

destylatu oraz x

s

=x

0

, x

w

, x

d

odpowiednio ich ułamki masowe.

S

D

W

+

=

S x0

⋅

D y0

⋅

W xw

⋅

+

=

Eliminacja W:

S x0

⋅

D yD

⋅

S xw

⋅

+

D xw

⋅

−

=

Stopie

ń

oddestylowania

Zd

D

S

=

x0 xw

−

yD xw

−

=

Dane równowagi dla układu alkohol etylowy – woda s

ą

stabelaryzowane pod ci

ś

nieniem 0,1 MPa.

Tworzymy zale

ż

no

ść

funkcyjn

ą

interpoluj

ą

c

ą

warto

ś

ci z tabeli.

Y

0

0.350

0.500

0.580

0.630

0.665

0.690

0.705

0.723

0.737

0.748

0.761

0.770

0.795

0.812

0.857

0.917

1.00





































































































:=

X

0.00

0.05

0.10

0.15

0.20

0.25

0.30

0.35

0.40

0.45

0.50

0.55

0.60

0.65

0.70

0.80

0.90

1.00





































































































:=

S

cspline X Y

,

(

)

:=

f x

( )

interp S X

,

Y

,

x

,

(

)

:=

Zale

ż

no

ść

t

ą

mo

ż

na przedstawi

ć

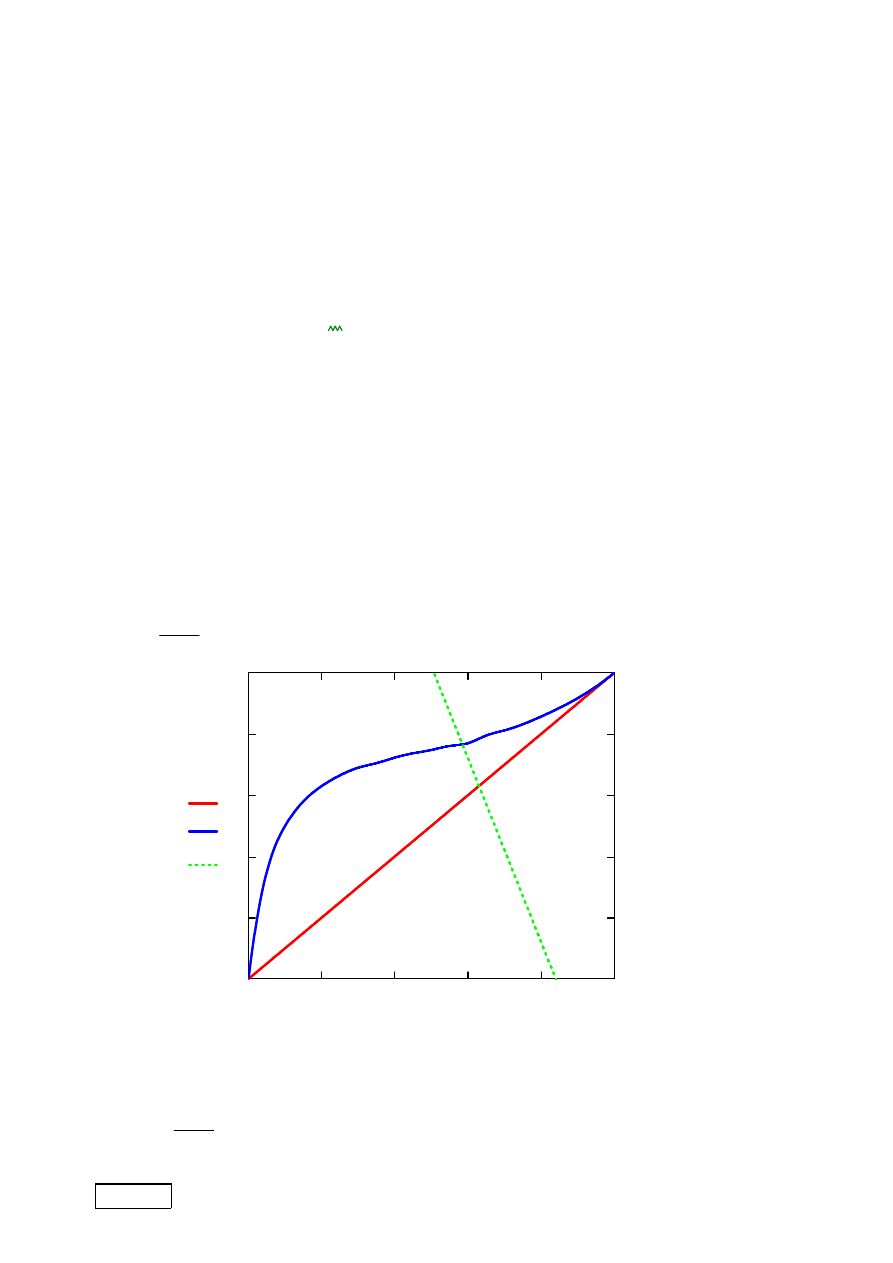
na wykresie.

y x

( )

x

:=

yZd x

( )

x0 x

−

Zd

x

+

:=

przekształcenie stopnia oddestylowania na zale

ż

no

ść

w funkcji x

0

0.2

0.4

0.6

0.8

0

0.2

0.4

0.6

0.8

y x

( )

f x

( )

yZd x

( )

x

Obliczenie składów produktów

Szukamy takiego x spełniaj

ą

cego zadane Z

d

, czyli punktu przeci

ę

cia si

ę

zale

ż

no

ś

ci na y(x) z lini

ą

równowagi.

funcja x

( )

x0 x

−

Zd

x

+

f x

( )

−

:=

xw

root funcja x

( ) x

,

0

,

1

,

(

)

:=

xw 0.585

=

skład cieczy wyczerpanej

Szukamy zatem składu destylatu.

yD

1

:=

warto

ść

startowa dla składu destylatu

Given

Zd

x0 xw

−

yD xw

−

=

yD

Find yD

( )

:=

yD 0.766

=

sklad destylatu

Obliczenie temperatury destylacji

Temperatura destylacji odczytana jest z wykresu i-x. Jest to temperatura izotermy okre

ś

laj

ą

cej równowag

ę

pomi

ę

dzy składem cieczy, a składem pary.

tdest

80.7

:=

[

ο

C]

Obliczanie ciepła dostarczanego podczas procesu

Korzystamy z konstrukcji na wykresie i okre

ś

lamy.

– Ciepło dostarczone podczas procesu na 1kg surówki

Q

S

417

=

[kJ/kg]

– Ciepło dostarczone podczas procesu na 1kg cieczy wyczerpanej

Q

W

583

=

[kJ/kg]

– Ciepło dostarczone podczas procesu na 1kg destylatu

Q

D

1917

=

[kJ/kg]

Obliczanie efektów cieplnych w chłodnicach

Korzystamy z konstrukcji na wykresie.

W chłodnicy destylatu:

QD 1366

=

[kJ/kg]

W chłodnicy cieczy wyczerpanej:

QW 233

=

[kJ/kg]

b) Destylacja ekspansyjna

t

20

:=

[st.C]

temperatura ko

ń

cowa produktów

P1

0.2

:=

[MPa]

ci

ś

nienie po spr

ęż

eniu

P

0.1

=

[MPa]

ci

ś

nienie po rozpr

ęż

eniu

x0 0.63

=

[uł.mas. etanolu]

t0 30

=

[st.C]

temperatura pocz

ą

tkowa

Konstrukcja na wykresie w celu wyznaczenia składów y

d

oraz x

w

na które nast

ą

pi rozdzielenie po zdławieniu.

Surówka zostaje najpierw zagrzana do temperatury wrzenia.

Wyznaczenie składów

Z linii równowagi otrzymano nast

ę

puj

ą

ce składy:

xw

0.616

:=

yD

0.88

:=

Wyznaczenie stopnia oddestylowania

Zd

x0 xw

−

yD xw

−

:=

Zd 0.054

=

Obliczenie ciepła dostarczonego podczas procesu

Korzystamy z konstrukcji na wykresie i okre

ś

lamy.

– Ciepło dostarczone podczas procesu na 1kg surówki

Q

S

260

=

[kJ/kg]

– Ciepło dostarczone podczas procesu na 1kg cieczy wyczerpanej

Q

W

280

=

[kJ/kg]

– Ciepło dostarczone podczas procesu na 1kg destylatu

Q

D

3700

=

[kJ/kg]

Obliczanie efektów cieplnych w chłodnicach

Korzystamy z konstrukcji na wykresie.

W chłodnicy destylatu:

QD 1360

=

[kJ/kg]

W chłodnicy cieczy wyczerpanej:

QW 220

=

[kJ/kg]

c) Destylacja ró

ż

niczkowa

Zd

0.35

:=

stopie

ń

oddestylowania

t

25

:=

[

ο

C]

temperatura ko

ń

cowa

Zapisujemy bilans masowy na deflegmatorze.

L – chwilowa zawarto

ść

moli cieczy w kotle

x – chwilowe st

ęż

enie molowe składnika bardziej lotnego

Cała ilo

ść

moli która uwywa z kotła przechodzi do destylatu, zatem:

dL

−

dD

=

Mo

ż

emy zatem zapisa

ć

:

d L x

⋅

(

)

y x

( ) dL

⋅

=

L dx

⋅

x dL

⋅

+

y x

( ) dL

⋅

=

L dx

⋅

dL y x

( )

x

−

(

)

⋅

=

dL

L

dx

y x

( )

x

−

=

Pocz

ą

tkowa ilo

ść

moli to surówka S, natomiast ko

ń

cowa to ciecz wyczerpana W:

S

W

L

1

L

⌠





⌡

d

x0

xw

x

1

y x

( )

x

−

⌠





⌡

d

=

ln

W

S









x0

xw

x

1

y x

( )

x

−

⌠





⌡

d

=

Zapisuj

ą

c to jako zale

ż

ne od stopnia oddestylowania:

W

S

S

D

−

S

=

1

D

S

−

=

1

Zd

−

=

ln 1

Zd

−

(

)

x0

xw

x

1

y x

( )

x

−

⌠





⌡

d

=

Znaj

ą

c stopie

ń

oddestylowania wyznaczamy skład cieczy wyczerpanej:

xw

0.02

:=

warto

ść

startowa dla składu cieczy wyczerpanej

Given

ln 1

Zd

−

(

)

x0

xw

x

1

f x

( )

x

−

⌠





⌡

d

=

xw

Find xw

( )

:=

xw 0.554

=

skład cieczy wyczerpanej

Z definicji stopnia oddestylowania wyznaczamy skład destylatu:

Given

Zd

x0 xw

−

yD xw

−

=

yD

Find yD

( )

:=

yD 0.771

=

skład destylatu

Obliczenie ciepła dostarczonego podczas procesu

Korzystamy z konstrukcji na wykresie i okre

ś

lamy.

– Ciepło dostarczone podczas procesu na 1kg surówki

Q

S

600

=

[kJ/kg]

– Ciepło dostarczone podczas procesu na 1kg cieczy wyczerpanej

Q

W

840

=

[kJ/kg]

– Ciepło dostarczone podczas procesu na 1kg destylatu

Q

D

1800

=

[kJ/kg]

Obliczanie efektów cieplnych w chłodnicy

Korzystamy z konstrukcji na wykresie.

W chłodnicy destylatu:

QD 1400

=

[kJ/kg]

d) Destylacja półci

ą

gła

xw

0.13

:=

[uł.mol.] etanolu w cieczy wyczerpanej

xw

Xmas xw

( )

:=

xw 0.276

=

[uł.mas.] etanolu w cieczy wyczerpanej

S

D

ψ

=

ψ

0.7

:=

stosunek nat

ęż

enia przepływu surówki do destylatora

Wyznaczenie stopnia oddestylowania

Zapisujemy bilans masowy:

L – wkład do kotła [mol]

S – strumie

ń

podawanej surówki [mol/s]

D – strumie

ń

destylatu [mol/s]

Liczba moli w kotle zmienia si

ę

w czasie:

dL

S dt

⋅

D dt

⋅

−

=

S

S

ψ

−









dt

=

ψ

1

−

ψ









S

⋅

dt

⋅

=

L0

L

L

1

⌠



⌡

d

0

t

t

ψ

1

−

ψ









S

⋅

⌠





⌡

d

=

Zatem otrzymujemy zale

ż

no

ść

na aktualn

ą

liczb

ę

moli w kotle po czasie t:

L t

( )

L0

ψ

1

−

ψ

S

⋅

t

⋅

+

=

W danej chwili składnika bardziej lotnego jest L

.

x:

d L x

⋅

(

)

S x0

⋅

dt

⋅

D y

⋅

dt

⋅

−

=

S x0

⋅

dt

⋅

S

ψ









y

⋅

dt

⋅

−

=

x0

y

ψ

−









S

⋅

dt

⋅

=

Wstawiaj

ą

c wcze

ś

niejsz

ą

zale

ż

no

ść

pod Sdt:

dL

ψ

1

−

ψ









S

⋅

dt

⋅

=

Otrzymujemy:

L dx

⋅

x dL

⋅

+

x0

y

ψ

−









ψ

ψ

1

−









⋅

dL

⋅

=

1

ψ

1

−

L0

L

L

1

L

⌠





⌡

d

⋅

x0

x

x

1

−

y

x

ψ

1

−

(

)

⋅

+

ψ x0

⋅

−

⌠







⌡

d

=

1

ψ

1

−

ln

L

L0













⋅

x0

x

x

1

−

y

x

ψ

1

−

(

)

⋅

+

ψ x0

⋅

−

⌠







⌡

d

=

Proces destylacji prowadzimy tak długo a

ż

osi

ą

gniemy st

ęż

enie cieczy wyczerpanej x

w

:

Przekształcaj

ą

c zale

ż

no

ść

:

L t

( )

L0

ψ

1

−

ψ

S

⋅

t

⋅

+

=

dziel

ą

c j

ą

przez L

0

stronami:

L

L0

L0

ψ

1

−

ψ

S

⋅

t

⋅

+









L0

=

Wiadomo,

ż

e stopie

ń

oddestylowania to ilo

ść

otrzymanego destylatu na ilo

ść

surówki:

Zd

D t

⋅

L0 St

+

=

przekształcaj

ą

c oraz bior

ą

c pod uwag

ę

zale

ż

no

ść

S

D

ψ

=

otrzymujemy:

S t

⋅

ψ L0

⋅

Zd

⋅

1

Zd

−

=

wstawiaj

ą

c t

ą

zale

ż

no

ść

do poprzedniego wzoru otrzymujemy:

L

L0

1

Zd

−

1

ψ Zd

⋅

−

=

Całka przyjmie zatem posta

ć

:

1

ψ

1

−

ln

1

Zd

−

1

ψ Zd

⋅

−













⋅

x0

x

x

1

−

y

x

ψ

1

−

(

)

⋅

+

ψ x0

⋅

−

⌠







⌡

d

=

Nale

ż

y wzi

ąć

pod uwag

ę

, i

ż

y jest opisany równowag

ą

woda-etanol f(x) i jest funkcj

ą

x:

Szukamy takiego Z

d

dla którego x=x

w

danym w zadaniu:

Zd

0.45

:=

warto

ść

startowa stopnia oddestylowania

Given

1

ψ

1

−

ln

1

Zd

−

1

ψ Zd

⋅

−













⋅

x0

xw

x

1

−

f x

( )

x

ψ

1

−

(

)

⋅

+

ψ x0

⋅

−

⌠





⌡

d

=

Zd

Find Zd

( )

:=

Szukany stopie

ń

oddestylowania wynosi zatem:

Zd 0.763

=

Zadanie 4.

4.1. Tre

ść

zadania

Mieszanina gazowa w

ę

glowodorów o składzie: y

01

= 0,4 uł.mol. propanu, y

02

= 0,3 uł.mol. n-butanu, y

03

= 0,3

n-pentanu jest kondensowana pod ci

ś

nieniem P = 1 MPa. Stopie

ń

kondensacji Z

k

= 0,5. Znale

źć

składy

otrzymanych produktów oraz pocz

ą

tkow

ą

temperatur

ę

kondensacji w przypadku:

a) kondensacji równowagowej
b) kondensacji ró

ż

niczkowej

4.2. Dane projektowe

P

1

:=

ci

ś

nienie w układzie

[MPa]

y01

0.4

:=

ułamek molowy propanu w parze

y02

0.3

:=

ułamek molowy butanu w parze

y03

0.3

:=

ułamek molowy n-pentanu w parze

Zk

0.5

:=

stopie

ń

kondensacji

4.3. Blok interpolacyjny

Współczynnik równowagi jest interpolowany wzgl

ę

dem ci

ś

nienia, a nast

ę

pnie temperatury dla wszystkich

składników.

Propan

PROPANdane

0.1

0.2

0.5

1.0

6.8

3.4

1.5

0.8

8.6

4.4

1.8

1.0

10.8

5.5

2.3

1.23

17.0

8.7

3.6

1.9

25.0

13.0

5.3

2.8

















:=

cisnienie

PROPANdane

0

〈 〉

:=

Kprop.T16

PROPANdane

1

〈 〉

:=

Kprop.T66

PROPANdane

4

〈 〉

:=

Kprop.T27

PROPANdane

2

〈 〉

:=

Kprop.T38

PROPANdane

3

〈 〉

:=

Kprop.T93

PROPANdane

5

〈 〉

:=

W1

cspline cisnienie Kprop.T16

,

(

)

:=

KpropT16 p

( )

interp W1 cisnienie

,

Kprop.T16

,

p

,

(

)

:=

W2

cspline cisnienie Kprop.T27

,

(

)

:=

KpropT27 p

( )

interp W2 cisnienie

,

Kprop.T27

,

p

,

(

)

:=

W3

cspline cisnienie Kprop.T38

,

(

)

:=

KpropT38 p

( )

interp W3 cisnienie

,

Kprop.T38

,

p

,

(

)

:=

W4

cspline cisnienie Kprop.T66

,

(

)

:=

KpropT66 p

( )

interp W4 cisnienie

,

Kprop.T66

,

p

,

(

)

:=

W4

cspline cisnienie Kprop.T93

,

(

)

:=

KpropT93 p

( )

interp W4 cisnienie

,

Kprop.T93

,

p

,

(

)

:=

temp

16

27

38

66

93





























:=

Kprop

KpropT16 P

( )

KpropT27 P

( )

KpropT38 P

( )

KpropT66 P

( )

KpropT93 P

( )





























:=

W

cspline temp Kprop

,

(

)

:=

Współczynnik równowagi dla
propanu w funkcji temperatury
dla zało

ż

onego ci

ś

nienia P.

KPR t

( )

interp W temp

,

Kprop

,

t

,

(

)

:=

n-Butan

BUTANdane

0.1

0.2

0.5

1.0

1.8

0.91

0.41

0.24

2.5

1.35

0.55

0.32

3.4

1.7

0.75

0.43

6.4

3.3

1.4

0.8

10.4

5.3

2.3

1.24

















:=

cisnienie

BUTANdane

0

〈 〉

:=

Kbut.T16

BUTANdane

1

〈 〉

:=

Kbut.T66

BUTANdane

4

〈 〉

:=

Kbut.T27

BUTANdane

2

〈 〉

:=

Kbut.T38

BUTANdane

3

〈 〉

:=

Kbut.T93

BUTANdane

5

〈 〉

:=

S1

cspline cisnienie Kbut.T16

,

(

)

:=

KbutT16 p

( )

interp S1 cisnienie

,

Kbut.T16

,

p

,

(

)

:=

S2

cspline cisnienie Kbut.T27

,

(

)

:=

KbutT27 p

( )

interp S2 cisnienie

,

Kbut.T27

,

p

,

(

)

:=

S3

cspline cisnienie Kbut.T38

,

(

)

:=

KbutT38 p

( )

interp S3 cisnienie

,

Kbut.T38

,

p

,

(

)

:=

S4

cspline cisnienie Kbut.T66

,

(

)

:=

KbutT66 p

( )

interp S4 cisnienie

,

Kbut.T66

,

p

,

(

)

:=

S4

cspline cisnienie Kbut.T93

,

(

)

:=

KbutT93 p

( )

interp S4 cisnienie

,

Kbut.T93

,

p

,

(

)

:=

temp

16

27

38

66

93





























:=

Kbut

KbutT16 P

( )

KbutT27 P

( )

KbutT38 P

( )

KbutT66 P

( )

KbutT93 P

( )





























:=

S

cspline temp Kbut

,

(

)

:=

Współczynnik równowagi dla
n-butanu w funkcji
temperatury dla zało

ż

onego

ci

ś

nienia P.

KB t

( )

interp S temp

,

Kbut

,

t

,

(

)

:=

n-Pentan

PENTANdane

0.1

0.2

0.5

1.0

0.48

0.25

0.11

0.062

0.71

0.36

0.16

0.094

1.0

0.53

0.23

0.14

2.3

1.2

0.53

0.31

4.4

2.2

0.97

0.55

















:=

cisnienie

PENTANdane

0

〈 〉

:=

Kpent.T16

PENTANdane

1

〈 〉

:=

Kpent.T66

PENTANdane

4

〈 〉

:=

Kpent.T27

PENTANdane

2

〈 〉

:=

Kpent.T38

PENTANdane

3

〈 〉

:=

Kpent.T93

PENTANdane

5

〈 〉

:=

E1

cspline cisnienie Kbut.T16

,

(

)

:=

KpentT16 p

( )

interp E1 cisnienie

,

Kpent.T16

,

p

,

(

)

:=

E2

cspline cisnienie Kpent.T27

,

(

)

:=

KpentT27 p

( )

interp E2 cisnienie

,

Kpent.T27

,

p

,

(

)

:=

E3

cspline cisnienie Kpent.T38

,

(

)

:=

KpentT38 p

( )

interp E3 cisnienie

,

Kpent.T38

,

p

,

(

)

:=

E4

cspline cisnienie Kpent.T66

,

(

)

:=

KpentT66 p

( )

interp E4 cisnienie

,

Kpent.T66

,

p

,

(

)

:=

E4

cspline cisnienie Kpent.T93

,

(

)

:=

KpentT93 p

( )

interp E4 cisnienie

,

Kpent.T93

,

p

,

(

)

:=

Współczynnik równowagi dla
n-pentanu w funkcji
temperatury dla zało

ż

onego

ci

ś

nienia P.

temp

16

27

38

66

93





























:=

Kpent

KpentT16 P

( )

KpentT27 P

( )

KpentT38 P

( )

KpentT66 P

( )

KpentT93 P

( )





























:=

E

cspline temp Kpent

,

(

)

:=

KPE t

( )

interp E temp

,

Kpent

,

t

,

(

)

:=

4.4. Obliczenia

a) Kondensacja równowagowa

Obliczenie temperatury pocz

ą

tkowej

Zakładamy temperatur

ę

pocz

ą

tkow

ą

kondensacji jako t

p

. B

ę

dzie ona warto

ś

ci

ą

startow

ą

dla oblicze

ń

numerycznych.

tp

60

:=

[

ο

C]

Para musi by

ć

w równowadze z ciecz

ą

, a zatem suma ułamków x=y/K musi by

ć

równa 1. Szukamy takiej

temperatury, dla której jest to spełnione. B

ę

dzie ona temperatur

ą

pocz

ą

tkow

ą

kondensacji. Zk dla pocz

ą

tku

kondensacji jest równy zero.

funcp tp

( )

y01

KPR tp

( )

y02

KB tp

( )

+

y03

KPE tp

( )

+













1

−

:=

tp

root funcp t

( ) t

,

(

)

88.788

=

:=

[

ο

C]

wyznaczona pocz

ą

tkowa temperatura destylacji

Dla tej temperatury wyznaczamy pocz

ą

tkowe ułamki składników w fazie ciekłej.

x01

y01

KPR tp

( )

0.152

=

:=

x02

y02

KB tp

( )

0.257

=

:=

x03

y03

KPE tp

( )

0.591

=

:=

Wyznaczenie ko

ń

cowej temperatury kondensacji

Tak

ż

e na wylocie z kondensatora musi by

ć

spełniona zale

ż

no

ść

x

1

+x

2

+x

3

=1, lecz tym razem bierzemy pod

uwag

ę

zadany stopie

ń

przemiany.

x1 t

( )

y01

Zk KPR t

( ) 1

Zk

−

(

)

⋅

+

:=

x2 t

( )

y02

Zk KB t

( ) 1

Zk

−

(

)

⋅

+

:=

x1 t

( )

y01

Zk KPR t

( ) 1

⋅

+

Z

−

:=

Z

x3 t

( )

y03

Zk KPE t

( ) 1

Zk

−

(

)

⋅

+

:=

Szukamy temperatury, dla których suma ułamków b

ę

dzie równa 1. B

ę

dzie to temperatura

ko

ń

cowa kondensacji.

funck t

( )

y01

Zk KPR t

( ) 1

Zk

−

(

)

⋅

+

y02

Zk KB t

( ) 1

Zk

−

(

)

⋅

+

+

y03

Zk KPE t

( ) 1

Zk

−

(

)

⋅

+

+













1

−

:=

t

20

:=

warto

ść

startowa

tk

root funck t

( ) t

,

(

)

74.562

=

:=

[

ο

C]

Wyznaczamy st

ęż

enia kondensatu i fazy gazowej dla tej temperatury z nast

ę

puj

ą

cych zale

ż

no

ś

ci.

x1 t

( )

y01

Zk KPR t

( ) 1

Zk

−

(

)

⋅

+

:=

x1 tk

( )

0.254

=

y1

KPR tk

( )

x1 tk

( )

⋅

:=

y1 0.546

=

x2 t

( )

y02

Zk KB t

( ) 1

Zk

−

(

)

⋅

+

:=

x2 tk

( )

0.31

=

y2

KB tk

( )

x2 tk

( )

⋅

:=

y2 0.29

=

x1 t

( )

y01

Zk KPR t

( ) 1

⋅

+

Z

−

:=

Z

x3 t

( )

y03

Zk KPE t

( ) 1

Zk

−

(

)

⋅

+

:=

x3 tk

( )

0.436

=

y3

KPE tk

( )

x3 tk

( )

⋅

:=

y3 0.164

=

b) Kondensacja ró

ż

niczkowa

Wyznaczenie temperatury pocz

ą

tkowej

Jest to taka temperatura, dla której para o pocz

ą

tkowym składzie jest par

ą

nasycon

ą

, a zatem jest to ta sama

temperatura jak obliczona dla kondensacji równowagowej.

Wyznaczamy temperatur

ę

ś

redni

ą

mi

ę

dzy wlotem i wylotem, b

ę

d

ą

ca temperatur

ą

obliczeniow

ą

do lotno

ś

ci

wzgl

ę

dnych. Konieczne jest do tego zało

ż

enie temperatury ko

ń

cowej destylacji.

tk

68.2

:=

tsr

tp tk

+

2

78.494

=

:=

[

ο

C]

Lotno

ś

ci składników liczymy wzgl

ę

dem składnika odniesienia – najmniej lotnego n-pentanu

α13

KPR tsr

( )

KPE tsr

( )

5.528

=

:=

α23

KB tsr

( )

KPE tsr

( )

2.422

=

:=

Na wylocie para powinna by

ć

par

ą

nasycon

ą

, zatem suma ułamków molowych w parze powinna by

ć

równa 1.

Zapisujemy zale

ż

no

ść

na ułamki składników w funkcji ułamka składnika odniesienia.

y1 y3

( )

y01

α13

y3

⋅

y03 1 Zk

−

(

)

α13 1

−

⋅





















1

α13

:=

y2 y3

( )

y02

α23

y3

⋅

y03 1 Zk

−

(

)

α23 1

−

⋅





















1

α23

:=

functk y3

( )

y1 y3

( )

y2 y3

( )

+

y3

+

(

)

1

−

:=

Y3

root functk y3

( )

y3

,

(

)

:=

Y1

y1 Y3

( )

:=

Y2

y2 Y3

( )

:=

X3

Y3

KPE tp

( )

:=

X1

Y1

KPR tp

( )

:=

X2

Y2

KB tp

( )

:=

X1 0.224

=

X2 0.256

=

X3 0.219

=

Y1 0.59

=

Y2 0.299

=

Y3 0.111

=

Sprawdzenie, czy dla zadanej temperatury ko

ń

cowej suma ułamków składników w fazie gazowej równa jest 1.

Y1

KPR tk

( )

Y2

KB tk

( )

+

Y3

KPE tk

( )

+

1

=

Temperatura ko

ń

cowa kondensacji wynosi:

tk 68.2

=

[

ο

C]

Zadanie 5.

5.1. Tre

ść

zadania

Prowadzi si

ę

destylacj

ę

z par

ą

wodn

ą

odp

ę

dzaj

ą

c anilin

ę

z jej roztworu z nielotna smol

ą

. Wstad destylacyjny, w

ilo

ś

ci N = 250 kmoli zawiera x

0

= 0,6 uł.mol. aniliny. Mo

ż

na przyj

ąć

stosowalno

ść

roztworu anilina-smoła do prawa

Raoulta. Destylacj

ę

prowadzi si

ę

pod ci

ś

nieniem 0,1 MPa przy u

ż

yciu pary wodnej o entalpii wła

ś

ciwej 2788 kJ/kg.

Nale

ż

y okre

ś

li

ć

zu

ż

ycie pary wodnej niezb

ę

dnej do oddestylowania

η

= 95% anilinny. Pr

ęż

no

ść

pary wodnej oraz

jej entalpi

ę

w zale

ż

no

ś

ci od temperatury oraz pr

ęż

no

ść

pary aniliny w funkcji temperatury zamieszczono w tabeli.

Ś

rednie ciepło wła

ś

ciwe aniliny wynosi 2,35 kJ/kg

.

K, a jej

ś

rednie ciepło parowania równe jest 488 kJ/kg.

5.2. Dane projektowe

N

60

:=

[kmol]

ilo

ść

moli wsadu

x0

0.65

:=

[uł.mol.]

zawarto

ść

aniliny we wsadzie

P

100

:=

[kPa]

ci

ś

nienie w układzie

t

165

:=

[

ο

C]

temperatura pary nasyconej

η

0.79

:=

[-]

stopie

ń

oddestylowania

Lp

488

:=

[kJ/kg

.

K]

ciepło parowania aniliny

Cp

2.35

:=

[kJ/kg]

ciepło wła

ś

ciwe aniliny

Manil

93

:=

[g/mol]

masa molowa aniliny

ANILINAdane

50

60

70

80

90

100

110

120

130

140

150

160

170

184

0.32

0.76

1.41

2.40

3.89

6.09

9.22

12.88

19.26

27.2

37.3

49.3

65.3

101













































































:=

Tanil

ANILINAdane

0

〈 〉

:=

Panil

ANILINAdane

1

〈 〉

:=

Zale

ż

no

ść

pr

ęż

no

ś

ci pary

[kPa] aniliny od

temperatury [

ο

C].

PARAdane

0

10

20

30

40

50

60

70

80

90

100

110

120

130

140

150

160

170

185

190

200

0.613

1.23

2.33

4.24

7.37

12.3

19.9

31.2

47.3

70.1

100

143

198

270

361

476

618

792

1161

1297

1607

2500

2519

2537

2555

2573

2591

2609

2626

2643

2659

2675

2691

2706

2720

2733

2746

2757

2768

2782

2786

2793





















































































































:=

Tpara

PARAdane

0

〈 〉

:=

Ppara

PARAdane

1

〈 〉

:=

ipara

PARAdane

2

〈 〉

:=

Zale

ż

no

ś

c pr

ęż

no

ś

ci pary

wodnej [kPa] i jej entalpii

[kJ/kg] od temperatury [

ο

C].

5.3. Obliczenia

Zapisujemy zale

ż

no

ś

ci funkkcyjne na podstawie danych tabelarycznych:

Sp

cspline Tpara Ppara

,

(

)

:=

p t

( )

interp Sp Tpara

,

Ppara

,

t

,

(

)

:=

pr

ęż

no

ść

pary wodnej w funkcji t

Si

cspline Tpara ipara

,

(

)

:=

i t

( )

interp Si Tpara

,

ipara

,

t

,

(

)

:=

entalpia pary wodnej w funkcji t

Wanil

cspline Tanil Panil

,

(

)

:=

panil t

( )

interp Wanil Tanil

,

Panil

,

t

,

(

)

:=

pr

ęż

no

ść

aniliny w funkcji t

Ilo

ść

uzyskanej aniliny przy danej temperaturze oraz składzie wsadu licz

ą

c na 1 kg pary mo

ż

emy zapisa

ć

jako:

Gm x t

,

(

)

x panil t

( )

⋅

P

x panil t

( )

⋅

−

Manil

18

⋅

:=

[masa aniliny - kg - uzyskanej liczona na 1 kg pary]

Warto

ść

entalpii przypadaj

ą

ca na 1kg pary wodnej jest funkcj

ą

temperatury:

Gi x t

,

(

)

Gm x t

,

(

) Lp Cp t

⋅

+

(

)

⋅

:=

Jako,

ż

e entalpia pary zasilaj

ą

cej musi by

ć

równa entalpii oparów aniliny oraz pary wodnej w temperaturze

destylacji jeste

ś

my w stanie wyznaczy

ć

temperatur

ę

destylacji w funkcji ułamka molowego aniliny.

Entalpia pary zasilaj

ą

cej układ i

p0

:

ip0

i t

( )

2.763

10

3

×

=

:=

[kJ/kg]

func x tdest

,

(

)

Gi x tdest

,

(

)

i tdest

( )

+

ip0

−

:=

Szukamy takiego t

dest

, dla którego funkcja przyjmie warto

ść

zero z przedziału temperatur, dla których

mamy stabelaryzowane warto

ś

ci, czyli 50 - 184.

tdest x

( )

root func x t

,

(

) t

,

50

,

184

,

(

)

:=

tdest 0.65

(

)

91.52

=

[

ο

C]

Nast

ę

pnie wyznaczamy ci

ś

nienie aniliny w funkcji ułamka molowego aniliny we wsadzie.

Panil x

( )

panil tdest x

( )

(

)

x

⋅

:=

zgodnie z prawem Raoulta

Aby uzyska

ć

stopie

ń

oddestylowania obliczamy ko

ń

cowy ułamek molowy aniliny.

Nsmoły

1

x0

−

(

)

N

⋅

21

=

:=

ilo

ść

smoły

xw

1

η

−

(

) x0

⋅

N

⋅

Nsmoły

1

η

−

(

) x0

⋅

N

⋅

+

0.281

=

:=

ko

ń

cowy ułamek molowy aniliny

Nast

ę

pnie obliczamy ilo

ść

kmoli wody zu

ż

utej do przeprowadzenia procesu:

Nwody

x0

xw

x

1

1

x

−

(

)

2

⌠







⌡

d Nsmoły

⋅

Nsmoły P

⋅

x0

xw

x

1

1

x

−

(

)

2

Panil x

( )

⋅

⌠







⌡

d

⋅

−

:=

Przeliczaj

ą

c to na mas

ę

zu

ż

ytej wody otrzymujemy:

Mwody

18 Nwody

⋅

2.172

10

4

×

=

:=

[kg] wody