2014-03-15

1

Podstawy finansów 2014

studia stacjonarne

Warto

ść

tera

ź

niejsza i przyszła pieni

ą

dza.

Koszt pieni

ą

dza. Odsetki proste, zło

ż

one –

kapitalizacja odsetek.

ZADANIA

I CZ

ĘŚĆ

2014-03-15

2

Wartość pieniądza w czasie

Nominalna warto

ść

pieni

ą

dza, pomijaj

ą

c rzadkie przypadki denominacji, nie

ulega zmianie. Zmianie podlega natomiast realna warto

ść

pieni

ą

dza.

Na skutek powszechno

ś

ci zjawisk inflacyjnych najcz

ęś

ciej mo

ż

na spotka

ć

si

ę

z

przykładami spadku warto

ś

ci realnej pieni

ą

dza, o ile pieni

ą

dz nie jest przez

jego wła

ś

cicieli odpowiednio traktowany.

Potocznie konieczno

ść

przeciwdziałania naturalnemu spadkowi pieni

ą

dza w

czasie wyra

ż

a stwierdzenie,

ż

e pieni

ą

dz musi „pracowa

ć

”. Oznacza to w

praktyce konieczno

ść

jego pomna

ż

ania w takim tempie, aby siła nabywcza

powi

ę

kszonej ilo

ś

ci pieni

ą

dza była co najmniej stała, a najlepiej rosła.

Najprostszym wyrazem zmiany warto

ś

ci pieni

ą

dza w czasie s

ą

zmiany

warto

ś

ci konta bankowego. Zmiany te nast

ę

puj

ą

na skutek naliczania na

ró

ż

ne sposoby odsetek.

Z ekonomicznego punktu widzenia odsetki mo

ż

na traktowa

ć

jako zapłat

ę

banku

za udzielenie przez wła

ś

ciciela kapitału prawa dysponowania dan

ą

kwot

ą

.

Kluczowe znaczenie w tym procesie odgrywa tzw. stopa procentowa.

Wartość pieniądza w czasie

2014-03-15

3

Wartość pieniądza w czasie

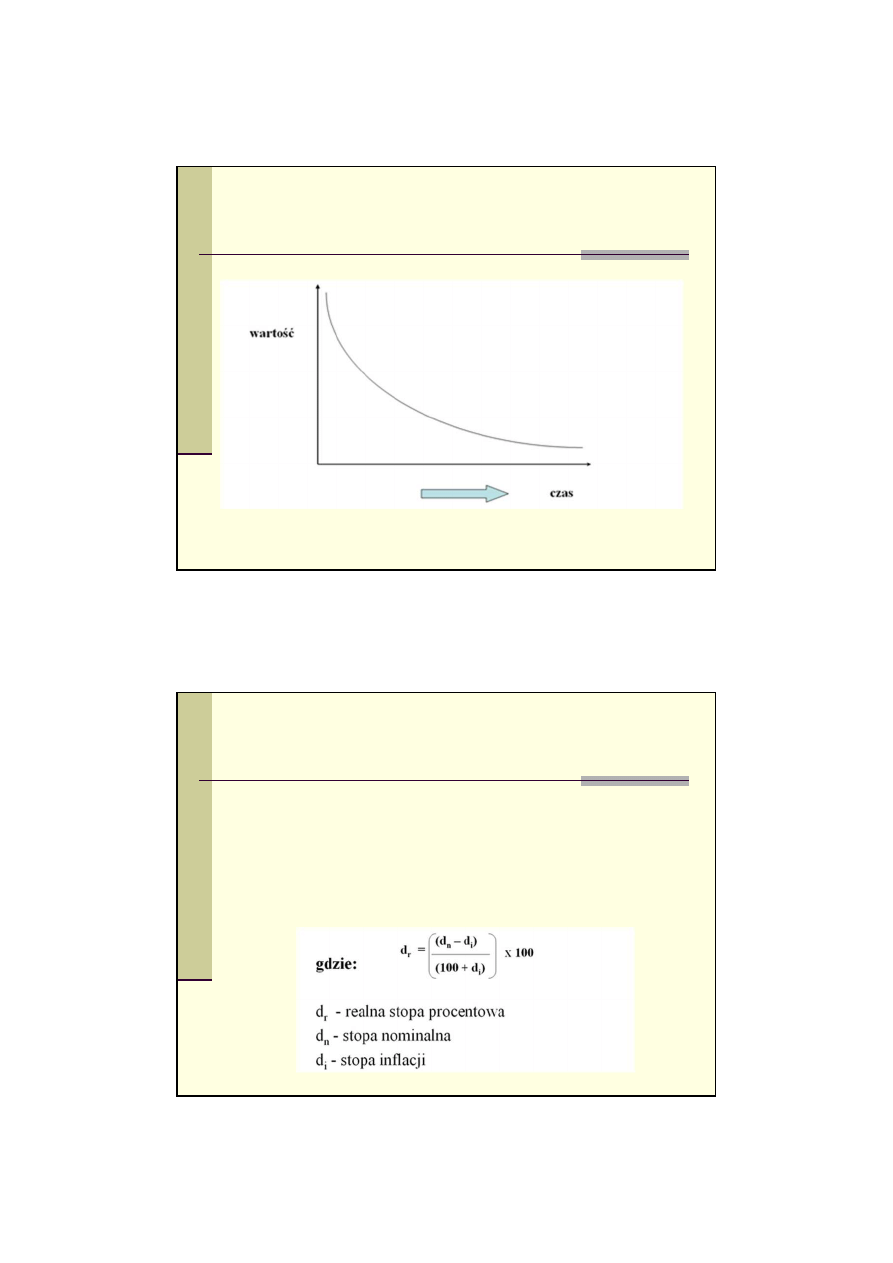
Realna stopa procentowa

To stopa procentowa uwzgl

ę

dniaj

ą

ca inflacyjny wzrost cen, który

prowadzi do deprecjacji pieni

ą

dza.

Realna stopa procentowa pozwala oceni

ć

, czy nominalny przyrost

ilo

ś

ci pieni

ą

dza b

ę

d

ą

cy efektem pobierania odsetek wi

ąż

e si

ę

ze

spadkiem b

ą

d

ź

wzrostem realnej siły nabywczej okre

ś

lonej ilo

ś

ci

pieni

ą

dza.

Realna stopa procentowa mierzy wzrost ró

ż

nego rodzaju obci

ąż

e

ń

finansowych.

2014-03-15

4

Realna stopa procentowa

Zad.1

Oblicz realne oprocentowanie lokaty bankowej je

ś

li:

oprocentowanie lokaty nominalne (roczne) = 12%

stopa inflacji (roczna) = 9%

(2,75%)

Zad.2

Oblicz realne oprocentowanie

ś

rodków a’vista je

ś

li:

oprocentowanie

ś

rodków a’vista (roczne) = 5%

stopa inflacji (roczna) = 9%

(-3,67%)

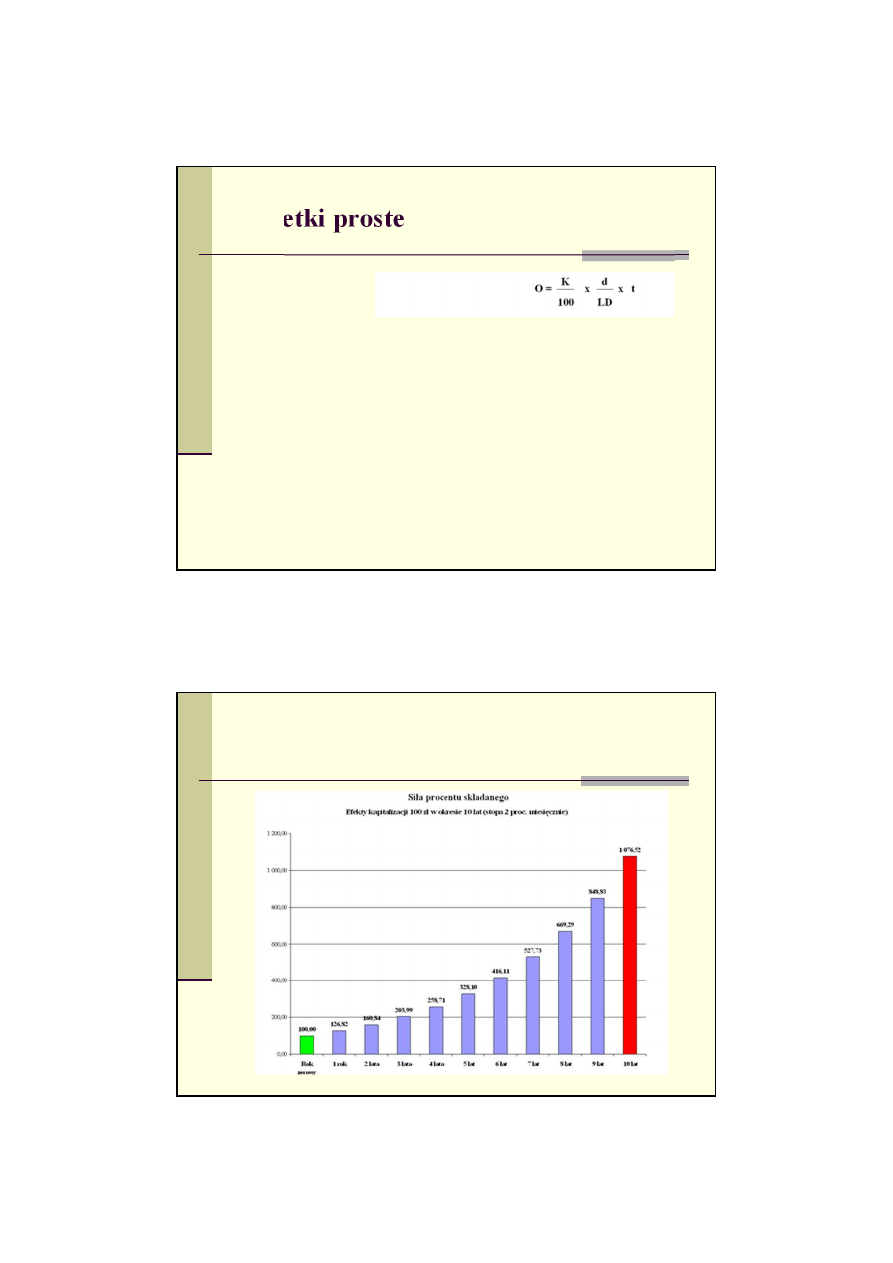
Odsetki proste

Polegaj

ą

na obliczaniu odsetek od stałej kwoty pieni

ęż

nej.

Rachunek odsetek prostych zwykle stosuje si

ę

przy kredytach,

lokatach, depozytach o okresie wykorzystania liczonym w dniach. W
takim przypadku stop

ę

procentow

ą

nale

ż

y sprowadzi

ć

do skali

dziennej.

Czas wykorzystania kapitału liczy si

ę

od dnia nast

ę

pnego, licz

ą

c od

dnia powstania zobowi

ą

zania finansowego, ł

ą

cznie z dniem spłaty.

2014-03-15

5

Odsetki proste

Zad.3

Przedsi

ę

biorstwo zaci

ą

gn

ę

ło krótkoterminowy kredyt 27 maja na

sum

ę

70 tys. zł i spłaciło 10 wrze

ś

nia płac

ą

c 24% w stosunku

rocznym.

Oblicz kwot

ę

odsetek.

(4 878,90 zł)

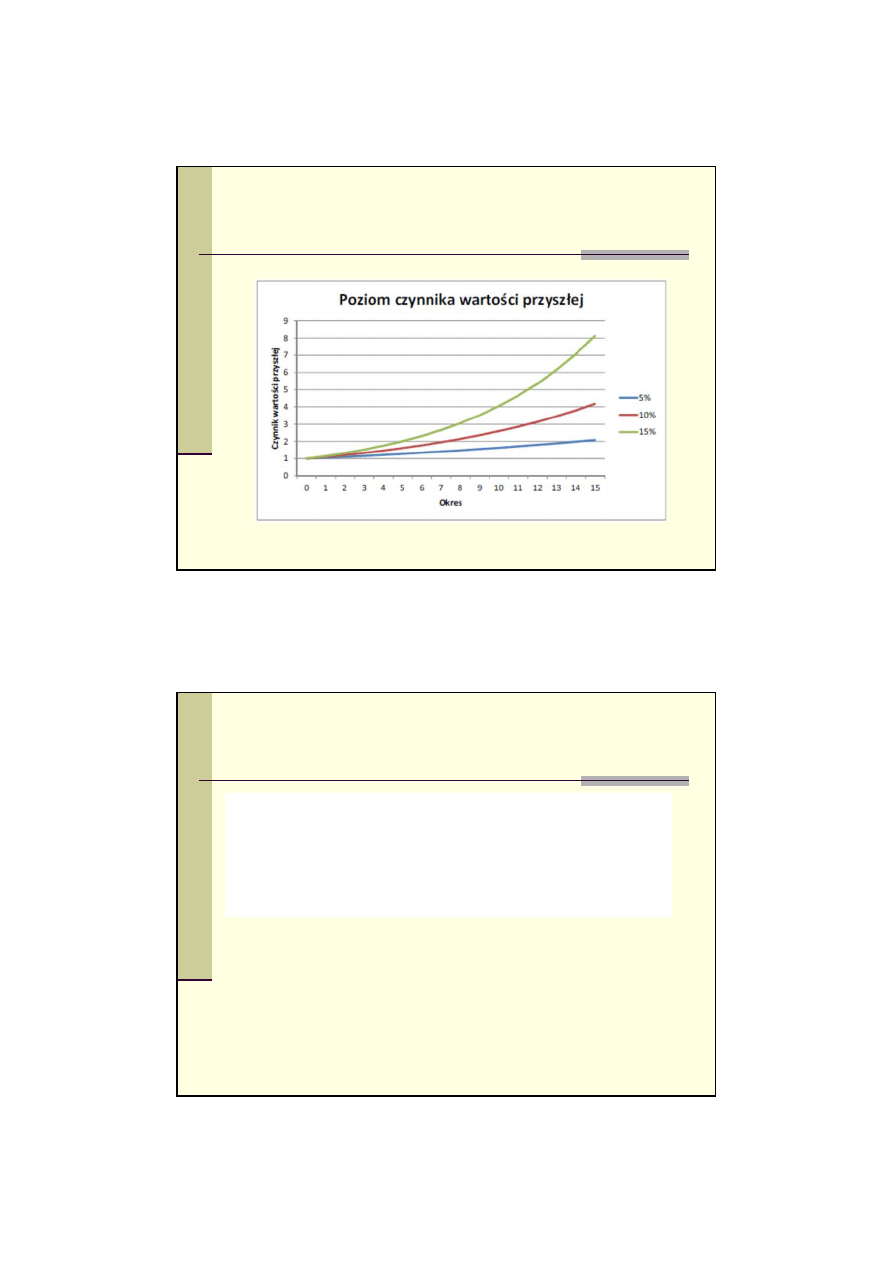
Wartość przyszła (Future Value) - skapitalizowana

2014-03-15

6

Wartość przyszła (Future Value) - skapitalizowana

Wartość przyszła (Future Value) - skapitalizowana

Zad.4

Zad.4

Firma zaci

ą

gn

ę

ła po

ż

yczk

ę

45 tys. zł na 5 lat. Stopa procentowa

przez pierwsze 3 lata wynosi 16%, pozostałe 18%.

Kapitał wraz z odsetkami spłaca si

ę

jednorazowo.

Oblicz koszt po

ż

yczki.

(52 802,62 zł)

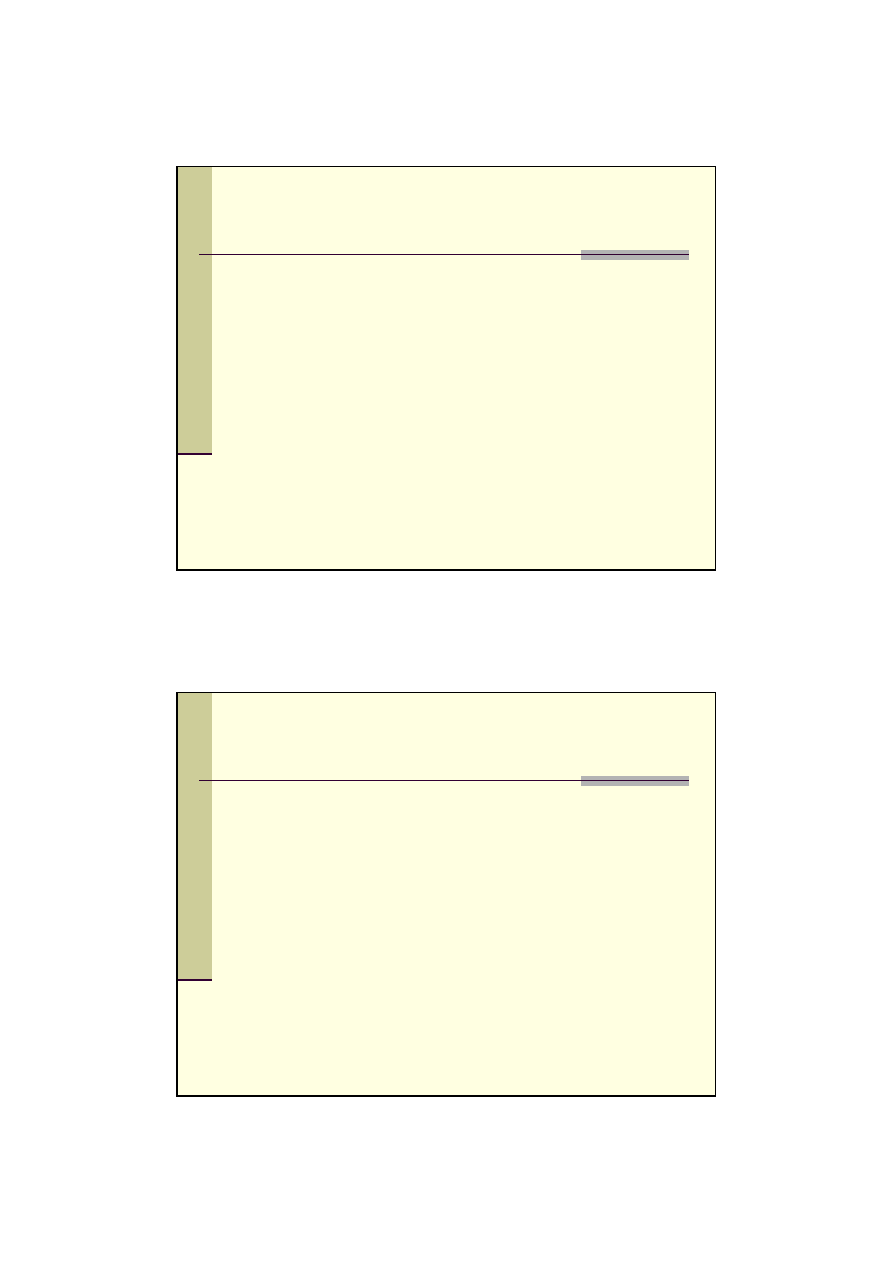
S

kn

= k x (1 + d/100)

n

Gdzie:
k – kapitał podstawowy,
d – stopa procentowa dla okresu kapitalizacji,
n – liczba okresów kapitalizacji,

S

kn

- suma skapitalizowana na koniec n okresów.

2014-03-15

7

Częstotliwość naliczania odsetek

Wzór na stop

ę

% porównywaln

ą

z roczn

ą

[(1 + d/100)

n

-1] x 100

Zad.5

Przedsi

ę

biorstwo rozpatruje oferty lokat trzech banków:

A. Stopa odsetkowa 25% naliczana 1 – razowo z dołu (roczna)

B. Stopa odsetkowa miesi

ę

czna 2% z kapitalizacj

ą

C. Stopa odsetkowa kwartalna 6% z kapitalizacj

ą

Która oferta jest najkorzystniejsza dla przedsi

ę

biorstwa?

(B)

II CZ

ĘŚĆ

2014-03-15

8

Dyskonto

Polega na potr

ą

caniu odsetek z góry.

W przypadku niektórych inwestycji finansowych jest to zasada ( np.
przy lokowaniu wolnych

ś

rodków pieni

ęż

nych w papiery komercyjne).

Dyskonto posiada „wi

ę

ksz

ą

sił

ę

” poniewa

ż

kredytobiorca nie

dysponuje pełn

ą

kwot

ą

kredytu jak przy pobieraniu odsetek z dołu.

Zad.6

(z dołu)

Dyskonto – okresy krótsze niż rok

Zad.6a

(bon)

2014-03-15

9

Skonto

Skonto to procentowe zmniejszenie sumy nale

ż

no

ś

ci, przyznawane nabywcy

towaru na warunkach kredytowych, w razie zapłaty nale

ż

no

ś

ci gotówk

ą

przed

umówionym terminem.

Firma, która nie korzysta ze skonta lecz reguluje swoje zobowi

ą

zania z

odroczonym terminem płatno

ś

ci ponosi koszt kredytu handlowego.

Stopa skonta stanowi zatem wyraz kosztu kredytu handlowego, który
poniesie przedsi

ę

biorstwo, je

ś

li ze skonta nie skorzysta.

Zad.7

(TAK)

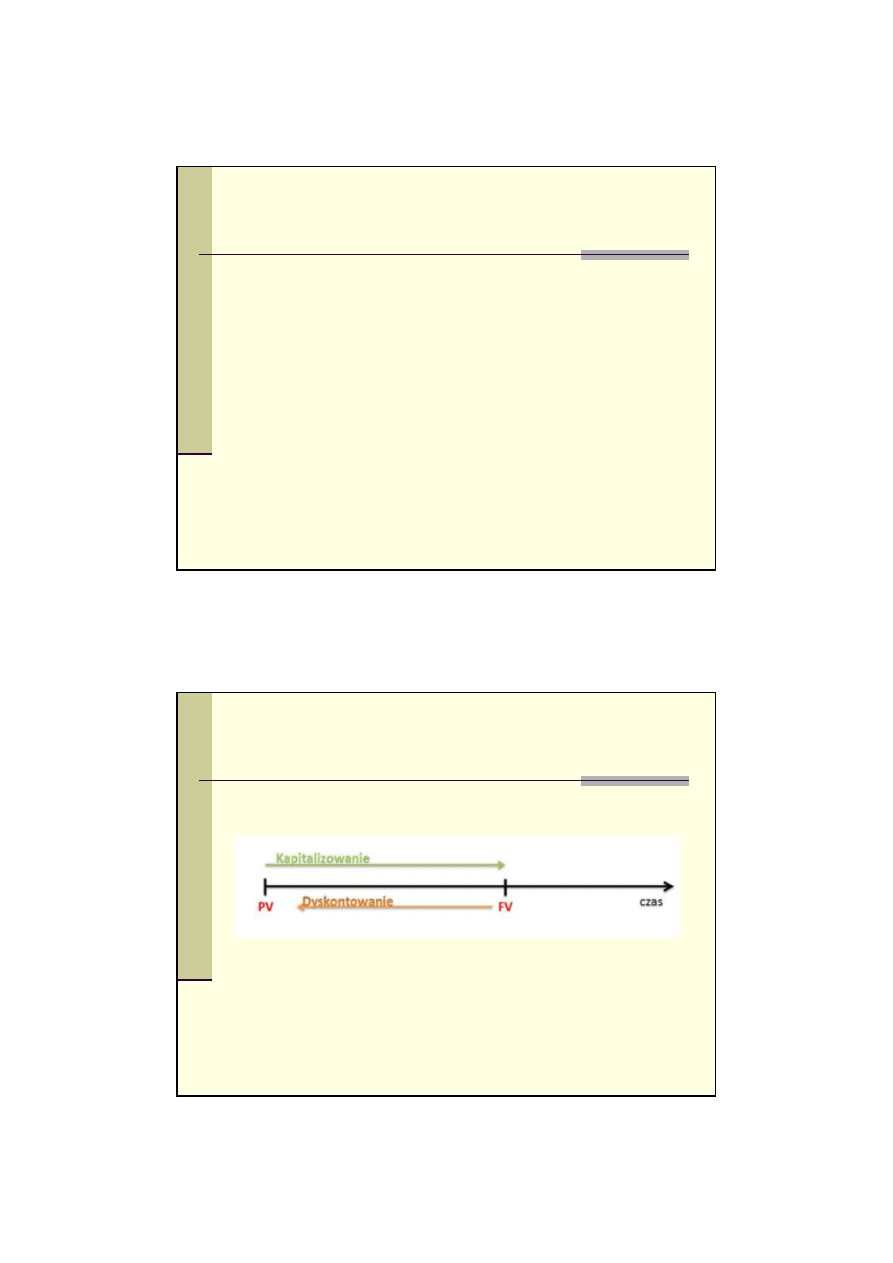
Dyskontowanie (PV – Present Value)

Operacj

ę

odwrotn

ą

do kapitalizacji nazywamy dyskontowaniem.

Dyskontowanie to wyznaczanie wcze

ś

niejszych warto

ś

ci kapitału na

podstawie znajomo

ś

ci warto

ś

ci pó

ź

niejszych.

W szczególno

ś

ci efektem dyskontowania mo

ż

e by

ć

warto

ść

tera

ź

niejsza

(bie

żą

ca, aktualna) kapitału.

Stopa procentowa wykorzystywana przy dyskontowaniu nazywa si

ę

stop

ą

dyskontow

ą

. O ile stopa procentowa wyst

ę

puj

ą

ca przy kapitalizacji

mierzy tempo pomna

ż

ania warto

ś

ci kapitału, o tyle stopa dyskontowa

mierzy tempo pomniejszania warto

ś

ci kapitału w czasie.

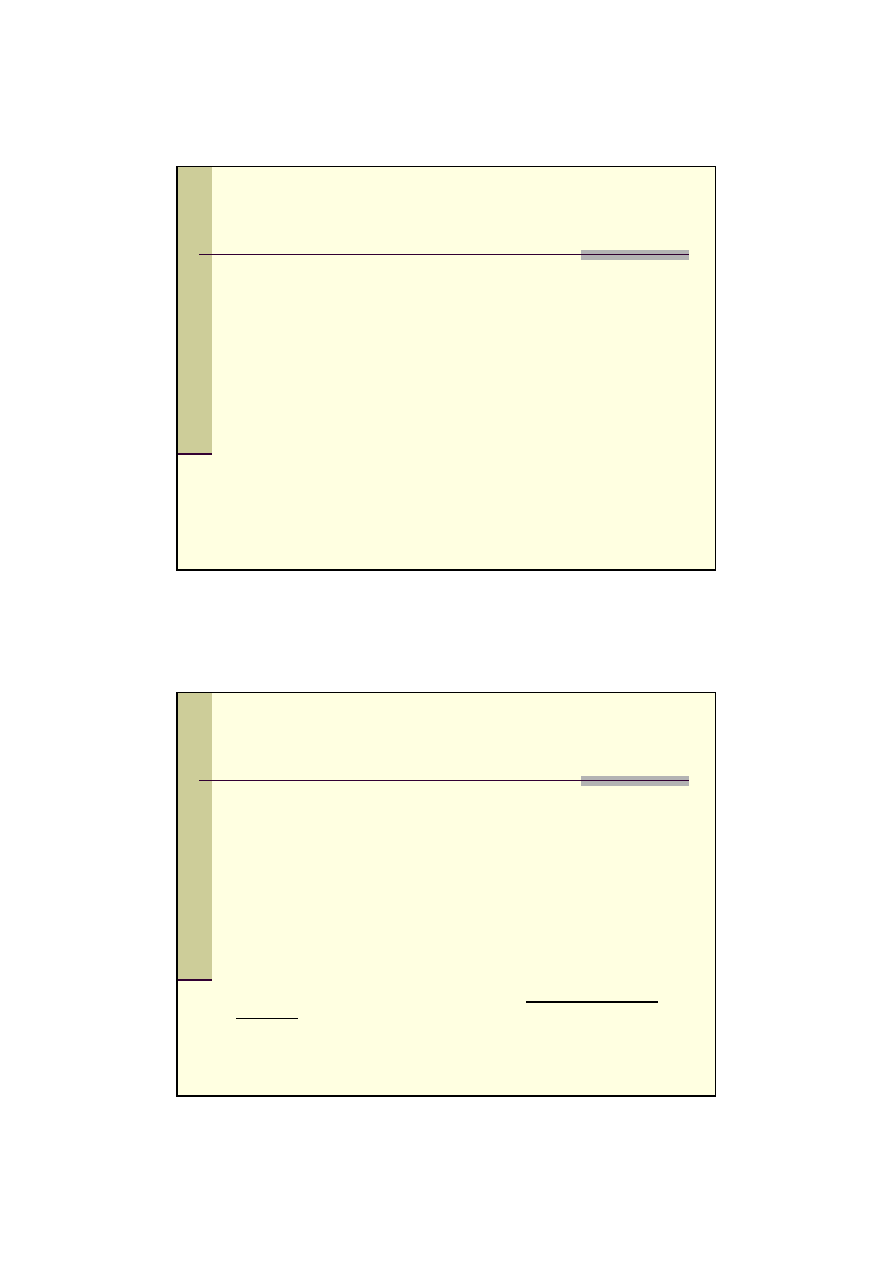
K

d

= K

p

x

(1 + d/100)

-n

gdzie:
K

d

- wartość zdyskontowana przyszłych płatności

K

p

– wartość przyszłych płatności po upływie n okresów

n – liczba okresów dyskontowania

(1 + d/100)

-n

współczynnik dyskonta jednostki kapitału (wartości bieżącej)

2014-03-15

10

Dyskontowanie (PV – Present Value)

Zad.8

Dłu

ż

nik przedsi

ę

biorstwa ogłosił upadło

ść

. Jego zobowi

ą

zania

wobec przedsi

ę

biorstwa wynosz

ą

65 tys. zł, któr

ą

to kwot

ę

b

ę

dzie

mo

ż

na odzyska

ć

dopiero po dwóch latach.

Przedsi

ę

biorstwo korzysta z 24% kredytu długoterminowego, odsetki

kapitalizowane s

ą

co pół roku.

Oblicz obecn

ą

warto

ść

przyszłej płatno

ś

ci.

(41 308,68 zł)

Zad.9

Przedsi

ę

biorstwo pragnie ulokowa

ć

depozyt w banku na procent

składany, aby móc podj

ąć

po upływie 3 lat 50.000 zł, a po upływie

dalszych 2 lat 60.000 zł.

Bank oferuje odsetki za pierwsze 3 lata 16% rocznie.

Za nast

ę

pne dwa lata 18%.

Ile powinna wynosi

ć

ł

ą

czna kwota lokaty pocz

ą

tkowej?

(59 639,50 zł)

Dyskontowanie (PV – Present Value)

Zad.10

Firma budowlana zawarła wieloletni kontrakt na wykonywanie robót
przy budowie elektrowni.

Umowa przewiduje zabezpieczenie zło

ż

one przez firm

ę

w banku, jako

gwarancj

ę

jako

ś

ci wykonywanych robót.

Oblicz wysoko

ść

depozytu, który powinien by

ć

zło

ż

ony w banku,

je

ś

li:

Wysoko

ść

depozytu po upływie 2,5 roku ma mie

ć

warto

ść

200 tys. zł (kwota ta zostanie wypłacona);

Po upływie 4 (tj. 1,5 roku po uprzedniej wypłacie) warto

ść

depozytu ma wynie

ść

150.000 zł .

Zakładamy,

ż

e stopa % od lokat wynosi 20%, kapitalizacja jest za

ś

kwartalna.

(191 499,38 zł)

2014-03-15

11

III CZ

ĘŚĆ

Annuitety

Płatno

ś

ci okresowe o stałej wysoko

ś

ci dokonywane w z góry ustalonych

odst

ę

pach czasu, przy zało

ż

eniu kapitalizacji odsetek, na podstawie danej

stopy procentowej.

Zad.11 - FV

(42 824,62 zł)

2014-03-15

12

Annuitety

Zad.12 – PV

Firma użytkuje na zasadzie leasingu kapitałowego maszyny. Zgodnie z umową powinna
uregulować jeszcze 7 kwartalnych rat leasingowych po 900 zł każda, a po ich zapłacie
maszyny przechodzą na własność leasingobiorcy.

Leasingodawca oferuje natychmiastowe przekazanie przedmiotu leasingu, jeśli
leasingobiorca zapłaci od razu całą sumę 6 300 zł pomniejszoną o kwotę jednej transzy – 5
400 zł.

Przedsiębiorstwo rozważa opłacalność tej propozycji, mając na uwadze, że opłaca odsetki
od wykorzystywanego kredytu bankowego w wysokości 24% rocznie , naliczane
kwartalnie po 6%.

Czy propozycja jest opłacalna?

(NIE)

Annuitety

Zad.13 – PV

Przedsi

ę

biorstwo chce naby

ć

obligacje 5 – letnie na rynku wtórnym

za 90.000 zł, przy czym cena nominalna obligacji wynosi 100.000 zł.

Odsetki proste od tych obligacji wynosz

ą

w stosunku rocznym 16% .

Wykup obligacji nast

ą

pi po 3 latach od daty nabycia wg ceny

nominalnej.

Oblicz czy inwestycja ta jest opłacalna je

ś

li przedsi

ę

biorstwo

zamierza uzyska

ć

zwrot oraz zysk w wysoko

ś

ci co najmniej 20%

rocznie.

(TAK)

2014-03-15

13

Annuitety

Zad.14 – PV

Ile jest dzi

ś

warta obligacja o warto

ś

ci nominalnej 1 000 zł,

oprocentowana w wysoko

ś

ci 15%, o terminie wykupu

przypadaj

ą

cym za pi

ęć

lat.

Stopa dyskontowa wynosi 10%.

Czy warto kupi

ć

t

ę

obligacj

ę

za 1 050 zł?

(TAK)

Annuitety

Zad.15 – PV

Jaka jest warto

ść

obligacji o nominale 1 000 zł, z terminem wykupu

przypadaj

ą

cym za 3 lata, je

ż

eli jej oprocentowanie jest wy

ż

sze od

wska

ź

nika inflacji o 5 punktów procentowych.

Inflacja w pierwszym roku wyniesie 10%, w drugim 8% i w trzecim
7%,

a stopa zwrotu jest wy

ż

sza od stopy inflacji o 4 punkty procentowe.

(1 023,66 zł)