
Projektowanie zbrojenia na skręcanie
Przykład 1 – proste skręcanie
Dane materia
łowe:
Beton C25/30:
fck = 25MPa
fck
fctm =
2.6MPa
Ecm =
31GPa
γC =
fctk
1.4
fcd =
= 17.9 ⋅MPa
γC
fctk = 1.8MPa
fyk
fctd =
= 1.3 ⋅MPa
γC
Stal RB500W:
fyk =
Geometria przekroju:
500MPa
γ
S = 1.15
fyd =
= 434.8 ⋅MPa
γS
Es = 200GPa
b
= 40cm
h
= 40cm
Zbrojenie przekroju:
ϕ = 20mm
ϕs =
10mm
Moment skr
ęcający:
TEd = 75kNm

Projektowanie zbrojenia na skręcanie
Otulina zbrojenia:
Klasa ekspozycji XC3
cmin.dur
25mm
=
cmin.b
ϕ
=
Δcdev 10mm
=
cmin
max
cmin.dur cmin.b 10mm
(
)
(
)
25 mm
⋅
=
=
cnom
cmin Δcdev
+
35 mm
⋅
=
=
a1
cnom ϕs
+
0.5
ϕ
+
5.4 cm
⋅
=
=
d
h
a1
−
34.6 cm
⋅
=
=
Określenie geometrii zastępczego przekroju cienkościennego
tef
max
b h
⋅
2 b
h
+
(
)
2 a1
⋅
10.8 cm
⋅
=
=
2 a1
⋅
10.8 cm
⋅
=
b h
⋅
2 b
h
+
(
)
10 cm
⋅
=
uk
2 b
tef
−
h
tef
−
(
)
+
⋅
116.8 cm
⋅
=
=
Ak
b
tef
−
(
)
h
tef
−
(
)
⋅
852.6 cm
2
⋅
=
=

Projektowanie zbrojenia na skręcanie
2
Wyznaczenie momentu skr
ęcającego, dla którego zbrojenie na skręcanie nie jest potrzebne
TRd.c = 2 ⋅Ak ⋅tef ⋅fctd = 23.8 ⋅kNm
<
TEd = 75 ⋅kNm
Maksymalna si
ła ścinająca ściankę:
TEd
τT =
2
⋅A
k
⋅t
ef
= 4.1 ⋅MPa
VEd.i = τT ⋅tef ⋅
(
h
− t
ef
)
= 129.3 ⋅kN
Dalej projektujemy zbrojenie jak dla przekroju o szeroko
ści t
ef
i wysoko
ści h-t
ef
:
π ⋅ϕs
A
=
= 0.79 ⋅cm
2
ν = 0.6 ⋅
1
−
fck
= 0.54
αcw =
1.0
sw
4
1
2
⋅V
Ed.i
250MPa
θ = ⋅asin
2
α
⋅
ν ⋅f
⋅t ⋅
h
− t
= 28.6 ⋅deg
cot (
θ)
= 1.83
< 2.0
cw
cd ef
(
ef
)

Projektowanie zbrojenia na skręcanie
Przyj
ęto
θ = 28.6deg
cot (
θ) = 1.83
fywd = fyd
s1 =
Asw
VEd.i
⋅
(
h
− t
ef
)
⋅f
ywd ⋅cot (θ)
= 14 ⋅cm
Przyj
ęto strzemiona co: s
1
= 14cm
VRd.s =
Asw
s1
(
h
− t
ef
)
⋅f
ywd ⋅cot (θ)
= 129.7 ⋅kN
>
VEd.i =
129.3
⋅kN
No
śność krzyżulców betonowych
αcw ⋅tef ⋅
(
h
− t
ef
)
⋅
ν ⋅fcd
VRd.max =
cot (
θ)
+ tan (
θ)
= 129.3 ⋅kN
>
VEd.i = 129.3 ⋅kN
Ewentualnie:
TRd.max = 2 ⋅ν ⋅αcw ⋅fcd ⋅Ak ⋅tef ⋅sin (θ) ⋅cos (θ) = 75 ⋅kNm
>
TEd = 75 ⋅kNm

Projektowanie zbrojenia na skręcanie
− 1
− 1
Dodatkowe zbrojenie:
ASL =
TEd
2
⋅A
k
uk
⋅
fyd
⋅cot (
θ)
= 21.8 ⋅cm
2
ASL
π⋅ ϕ
2
4
= 6.9
Przyj
ęto 8 prętów
ϕ20 rozłożonych równomiernie po obwodzie.
Sprawdzenie warunków na minimalny stopie
ń zbrojenia oraz warunków konstrukcyjnych:
2
⋅A
sw
fck ⋅MPa
ρ
w =
s1 ⋅b
= 0.28 ⋅%
>
ρ
w.min = 0.08 ⋅
fyk ⋅MPa
= 0.08 ⋅%
sl.max =
0.75d
=
25.9
⋅cm
min (( b h ))
2(b
+ h)
= 40 ⋅cm
>
s1 = 14 ⋅cm
= 20 ⋅cm
8
Projektowanie zbrojenia na skręcanie i ścinanie
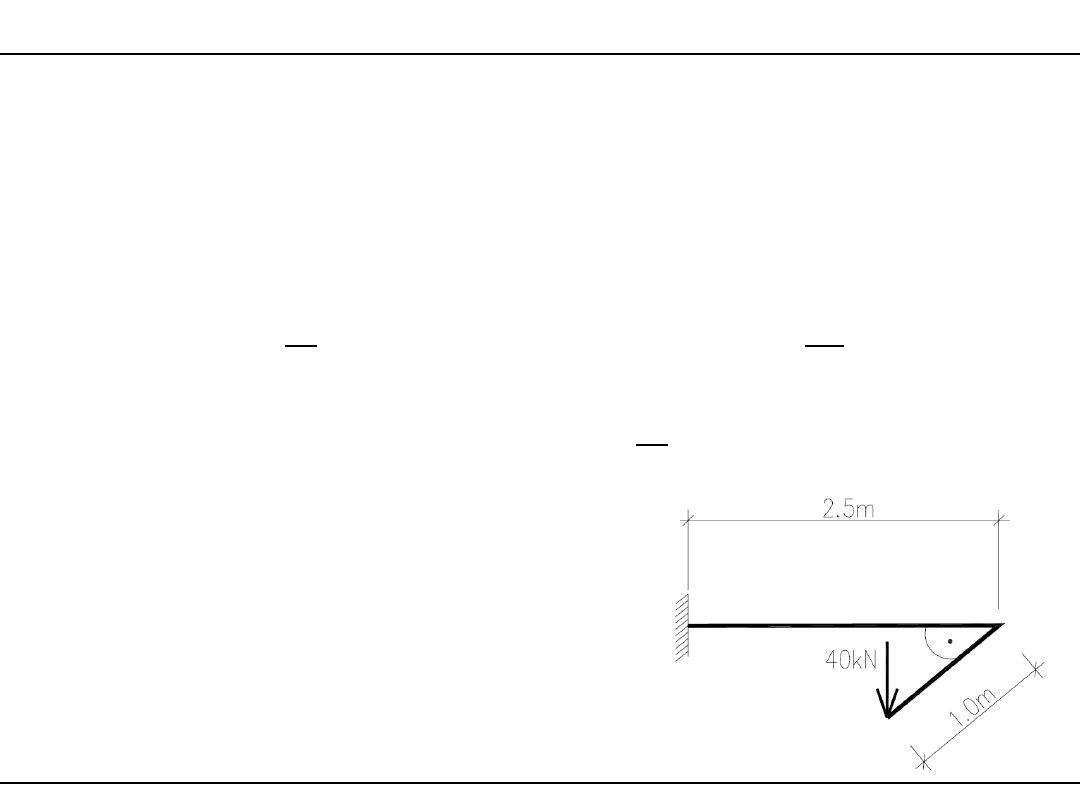
Przykład 2 – belka wspornikowa skręcana i ścinana
Dane materiałowe:
Beton C25/30:
fck
25MPa
=
fctm
2.6MPa
=
Ecm
31GPa
=
γC 1.4
=
fctk
1.8MPa
=
fcd
fck
γC
17.9 MPa
⋅
=
=
fctd
fctk
γC
1.3 MPa
⋅
=
=
Stal RB500W:
fyk
500MPa
=
γS 1.15
=
fyd
fyk
γS
434.8 MPa
⋅
=
=
Es
200GPa
=
Geometria przekroju:
b
30cm
=
h
50cm
=
Zbrojenie przekroju:
ϕd 16mm
=
ϕg 16mm
=
ϕs 8mm
=
Wypadkowe sił wewnętrznych:
TEd
40kNm
=
VEd
40kN
=
MEd
100kNm
=

Projektowanie zbrojenia na skręcanie i ścinanie
Otulina zbrojenia:
Klasa ekspozycji XC3
cmin.dur
25mm
=
cmin.b
ϕd
=
Δcdev 10mm
=
cmin
max
cmin.dur cmin.b 10mm
(
)
(
)
25 mm
⋅
=
=
cnom
cmin Δcdev
+
35 mm
⋅
=
=
a1
cnom ϕs
+
0.5
ϕd
+
5.1 cm
⋅
=
=
d
h
a1
−
44.9 cm
⋅
=
=
a2
cnom ϕs
+
0.5
ϕg
+
5.1 cm
⋅
=
=
Wyznaczenie zbrojenia głównego - metoda uproszczona:
μeff
MEd
fcd b
⋅ d
2
⋅
0.093
=
=
ξeff 1
1
2
μeff
⋅
−
−
0.097
=
=
ξeff.lim 0.8
0.35%
fyd
Es
0.35%
+
⋅
0.493
=
=
ξeff ξeff.lim
<

Projektowanie zbrojenia na skręcanie i ścinanie
As1
b d
⋅
ξeff
⋅
fcd
fyd
⋅
5.38 cm
2
⋅
=
=
As1
π ϕg
2
⋅
4
2.7
=
As1.prov
3
π ϕg
2
⋅
4
⋅
6.03 cm
2
⋅
=
=
Zbrojenie minimalne:
Przyjęto górą 3
ϕ16:
As.min1
0.26
fctm
fyk
⋅
b
⋅ d
⋅
1.82 cm
2
⋅
=
=
As.min2
0.0013 b
⋅ d
⋅
1.75 cm
2
⋅
=
=
As.min3
0.4 0.56
⋅
fctm
fyk
⋅
0.5 b
⋅
⋅
h
⋅
0.874 cm
2
⋅
=
=
As1.prov
max
As.min1 As.min2 As.min3
(
)
(
)
>
Projektowanie zbrojenia na skręcanie i ścinanie
Sprawdzenie czy zbrojenie na skręcanie i ścinanie jest konieczne ze względów obliczeniowych
CRd.c
0.18
γC
0.129
=
=
k
min
1
200mm
d
+
2.0
1.667
=
=
k1
0.15
=
AsL
As1.prov
=
ρL min
AsL
b d
⋅
2%
0.45 %
⋅
=
=
σcp 0MPa
=
νmin 0.035 k
3
2
⋅
fck
MPa
1
2
⋅
MPa
⋅
0.377 MPa
⋅
=
=
VRd.c
CRd.c k
⋅
100
ρL
⋅
fck
MPa
⋅
1
3
⋅
MPa
⋅
k1 σcp
⋅
+
b
⋅ d
⋅
64.6 kN
⋅
=
=
VRd.c >
νmin k1 σcp
⋅
+
(
)
b
⋅ d
⋅
50.8 kN
⋅
=
VRd.c
64.6 kN
⋅
=
>
VEd
40 kN
⋅
=

Projektowanie zbrojenia na skręcanie i ścinanie
tef
max
b h
⋅
2 b
h
+
(
)
2 a1
⋅
10.2 cm
⋅
=
=
uk
2 b
tef
−
h
+
tef
−
(
)
⋅
119.2 cm
⋅
=
=
Ak
b
tef
−
(
)
h
tef
−
(
)
⋅
788 cm
2
⋅
=
=
TRd.c
2 Ak
⋅
tef
⋅
fctd
⋅
20.7 kNm
⋅
=
=
<
TEd
40 kNm
⋅
=
Maksymalna siła ścinająca ściankę:
τT
TEd
2 Ak
⋅
tef
⋅
2.5 MPa
⋅
=
=
τV
VEd
b 0.9 d
⋅
(
)
⋅
0.3 MPa
⋅
=
=
VEd.i
τT τV
+
(
)
tef
⋅
h
tef
−
(
)
⋅
114.4 kN
⋅
=
=

Projektowanie zbrojenia na skręcanie i ścinanie
Dalej projektujemy zbrojenie jak dla przekroju o szerokości t
ef
i wysokości h-t
ef
:
Asw
π ϕs
2
⋅
4
0.5 cm
2
⋅
=
=
ν
0.6 1
fck
250MPa
−
⋅
0.54
=
=
αcw 1.0
=
θ
1
2
asin
2 VEd.i
⋅
αcw ν
⋅ f
cd
⋅
tef
⋅
h
tef
−
(
)
⋅
⋅
17.9 deg
⋅
=
=
cot
θ
( )
3.1
=
>
2
Przyjęto
θ
26.6deg
=
cot
θ
( )
2
=
fywd
fyd
=
s1
Asw
VEd.i
h
tef
−
(
)
⋅
fywd
⋅
cot
θ
( )
⋅
15.2 cm
⋅
=
=
Przyjęto strzemiona
ϕ8 co
s1
15cm
=

Projektowanie zbrojenia na skręcanie i ścinanie
VRd.s.i
Asw
s1
h
tef
−
(
)
⋅
fywd
⋅
cot
θ
( )
⋅
115.8 kN
⋅
=
=
>
VEd.i
114.4 kN
⋅
=
VRd.max.i
αcw tef
⋅
h
tef
−
(
)
⋅
ν
⋅ f
cd
⋅
cot
θ
( )
tan
θ
( )
+
156.7 kN
⋅
=
=
>
VEd.i
114.4 kN
⋅
=
TRd.max
2
ν
⋅
αcw
⋅
fcd
⋅
Ak
⋅
tef
⋅
sin
θ
( )
⋅
cos
θ
( )
⋅
62.1 kNm
⋅
=
=
VRd.max
αcw b
⋅ 0.9
⋅
d
ν
⋅ f
cd
⋅
cot
θ
( )
tan
θ
( )
+
468 kN
⋅
=
=
TEd
TRd.max
VEd
VRd.max
+
0.73
=
< 1.0
Projektowanie zbrojenia na skręcanie i ścinanie
Dodatkowe zbrojenie podłużne:
ASL
TEd
2 Ak
⋅
uk
fyd
⋅
cot
θ
( )
⋅
13.9 cm
2
⋅
=
=
ASL
π ϕg
2
⋅
4
6.9
=
Przyjęto 7 prętów
ϕ16 rozłożonych równomiernie po obwodzie.
Sprawdzenie warunków na minimalny stopień zbrojenia oraz warunków konstrukcyjnych
ρw
2 Asw
⋅
s1 b
⋅
0.22 %
⋅
=
=
>
ρw.min 0.08
fck MPa
1
−
⋅
fyk MPa
1
−
⋅
⋅
0.08 %
⋅
=
=
sl.max
0.75d
33.7 cm
⋅
=
=
min
b h
(
)
(
)
30 cm
⋅
=
s1
15 cm
⋅
=
>
uk
8
15 cm
⋅
=
Projektowanie zbrojenia na skręcanie i ścinanie
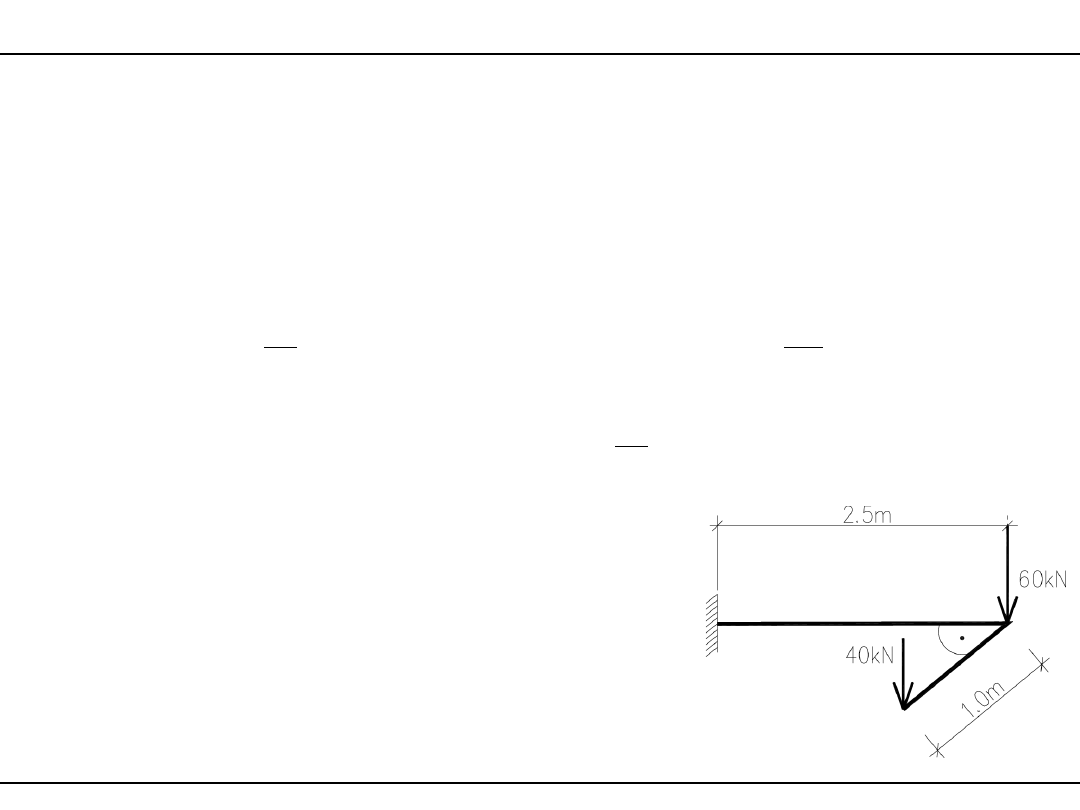
Przykład 3 – belka wspornikowa skręcana i ścinana
Dane materiałowe:
Beton C25/30:
fck
25MPa
=
fctm
2.6MPa
=
Ecm
31GPa
=
γC 1.4
=
fcd
fck
γC
17.9 MPa
⋅
=
=
fctk
1.8MPa
=
fctd
fctk
γC
1.3 MPa
⋅
=
=
Stal RB500W:
fyk
500MPa
=
γS 1.15
=
fyd
fyk
γS
434.8 MPa
⋅
=
=
Es
200GPa
=
Geometria przekroju:
b
30cm
=
h
50cm
=
Zbrojenie przekroju:
ϕd 22mm
=
ϕg 22mm
=
ϕs 8mm
=
Wypadkowe sił wewnętrznych:
TEd
40kNm
=
VEd
100kN
=
MEd
250kNm
=

Projektowanie zbrojenia na skręcanie i ścinanie
Otulina zbrojenia:
Klasa ekspozycji XC3
cmin.dur
25mm
=
cmin.b
ϕd
=
Δcdev 10mm
=
cmin
max
cmin.dur cmin.b 10mm
(
)
(
)
25 mm
⋅
=
=
cnom
cmin Δcdev
+
35 mm
⋅
=
=
a1
cnom ϕs
+
0.5
ϕg
+
5.4 cm
⋅
=
=
d
h
a1
−
44.6 cm
⋅
=
=
a2
cnom ϕs
+
0.5
ϕg
+
5.4 cm
⋅
=
=
Wyznaczenie zbrojenia głównego - metoda uproszczona:
μeff
MEd
fcd b
⋅ d
2
⋅
0.235
=
=
ξeff 1
1
2
μeff
⋅
−
−
0.271
=
=
ξeff.lim 0.8
0.35%
fyd
Es
0.35%
+
⋅
0.493
=
=
ξeff ξeff.lim
<

Projektowanie zbrojenia na skręcanie i ścinanie
As1
b d
⋅
ξeff
⋅
fcd
fyd
⋅
14.92 cm
2
⋅
=
=
As1
π ϕg
2
⋅
4
3.9
=
Przyjęto górą 4
ϕ22 :
As1.prov
4
π ϕg
2
⋅
4
⋅
15.21 cm
2
⋅
=
=
Zbrojenie minimalne:
As.min1
0.26
fctm
fyk
⋅
b
⋅ d
⋅
1.81 cm
2
⋅
=
=
As.min2
0.0013 b
⋅ d
⋅
1.74 cm
2
⋅
=
=
As.min3
0.4 0.86
⋅
fctm
fyk
⋅
0.5 b
⋅
⋅
h
⋅
1.342 cm
2
⋅
=
=
As1.prov
max
As.min1 As.min2 As.min3
(
)
(
)
>

Projektowanie zbrojenia na skręcanie i ścinanie
Sprawdzenie czy zbrojenie na skręcanie i ścinanie jest konieczne ze względów obliczeniowych
CRd.c
0.18
γC
0.129
=
=
k
min
1
200mm
d
+
2.0
1.67
=
=
k1
0.15
=
AsL
As1.prov
=
ρL min
AsL
b d
⋅
2%
1.14 %
⋅
=
=
σcp 0MPa
=
νmin 0.035 k
3
2
⋅
fck
MPa
1
2
⋅
MPa
⋅
0.378 MPa
⋅
=
=
VRd.c
CRd.c k
⋅
100
ρL
⋅
fck
MPa
⋅
1
3
⋅
MPa
⋅
k1 σcp
⋅
+
b
⋅ d
⋅
87.6 kN
⋅
=
=
VRd.c >
νmin k1 σcp
⋅
+
(
)
b
⋅ d
⋅
50.5 kN
⋅
=
VRd.c
87.6 kN
⋅
=
<
VEd
100 kN
⋅
=

Projektowanie zbrojenia na skręcanie i ścinanie
tef
max
b h
⋅
2 b
h
+
(
)
2 a1
⋅
10.8 cm
⋅
=
=
uk
2 b
tef
−
h
+
tef
−
(
)
⋅
116.8 cm
⋅
=
=
Ak
b
tef
−
(
)
h
tef
−
(
)
⋅
752.6 cm
2
⋅
=
=
TRd.c
2 Ak
⋅
tef
⋅
fctd
⋅
20.9 kNm
⋅
=
=
<
TEd
40 kNm
⋅
=
Potrzebne zbrojenie poprzeczne zarówno
na ścinanie i skręcanie

Projektowanie zbrojenia na skręcanie i ścinanie
τT
TEd
2 Ak
⋅
tef
⋅
2.46 MPa
=
=
τV
VEd
b 0.9
⋅
d
⋅
0.83 MPa
=
=
ν
0.6 1
fck
250MPa
−
⋅
0.54
=
=
αcw 1.0
=
θ
1
2
asin
2
τT τV
+
(
)
⋅
ν fcd
⋅
αcw
⋅
⋅
22 deg
=
=
cot
θ
( )
2.536
=
>
2.0
Przyjęto do obliczeń:
θ
26.6deg
=
cot
θ
( )
2
=
TRd.max
2
ν
⋅
αcw
⋅
fcd
⋅
Ak
⋅
tef
⋅
sin
θ
( )
⋅
cos
θ
( )
⋅
62.8 kNm
⋅
=
=
VRd.max
αcw b
⋅ 0.9
⋅
d
⋅
ν
⋅ f
cd
⋅
cot
θ
( )
tan
θ
( )
+
464.9 kN
⋅
=
=
TEd
TRd.max
VEd
VRd.max
+
0.852
=
< 1.0

Projektowanie zbrojenia na skręcanie i ścinanie
Zbrojenie poprzeczne na ścinanie:
Strzemiona
dwucięte
ϕs 8 mm
⋅
=
Asw_V
2
π ϕs
2
⋅
4
1.01 cm
2
⋅
=
=
fywd
fyd
=
sV
Asw_V
VEd
0.9
⋅
d
⋅ f
ywd
⋅
cot
θ
( )
⋅
35 cm
⋅
=
=
Asw_V
sV
2.869
cm
2
m
⋅
=

Projektowanie zbrojenia na skręcanie i ścinanie
Zbrojenie poprzeczne na skręcanie:
Strzemiona obwodowe
ϕs 8 mm
⋅
=
Asw_T
π ϕs
2
⋅
4
0.5 cm
2
⋅
=
=
VEd.i
τT tef
⋅
h
tef
−
(
)
⋅
104.2 kN
⋅
=
=
sT
Asw_T
VEd.i
h
tef
−
(
)
⋅
fywd
⋅
cot
θ
( )
⋅
16.4 cm
⋅
=
=
Asw_T
sT
3.061
cm
2
m
⋅
=

Projektowanie zbrojenia na skręcanie i ścinanie
Superpozycja zbrojenia:
Pole przekroju strzemion potrzebne na 1 mb elementu:
qT_V
Asw_V
sV
2Asw_T
sT
+
8.99
cm
2
m
⋅
=
=
Końcowy rozstaw strzemion na ścinanie i skręcanie:
sT_V
Asw_V
qT_V
11.2 cm
⋅
=
=
Dodatkowe zbrojenie podłużne:
ASL
TEd
2 Ak
⋅
uk
fyd
⋅
cot
θ
( )
⋅
14.3 cm
2
⋅
=
=
Przyjęto 4 pręty
ϕ22 rozłożone równomiernie na obwodzie.
ASL
4
π ϕg
2
⋅
4
⋅
15.2 cm
2
⋅
=
=
Projektowanie zbrojenia na skręcanie i ścinanie
Sprawdzenie warunków na minimalny stopień zbrojenia oraz warunków konstrukcyjnych
Asw
2
π ϕs
2
⋅
4
⋅
1.01 cm
2
⋅
=
=
ρw
Asw
sT_V b
⋅
0.3 %
⋅
=
=
>
ρw.min 0.08
fck MPa
1
−
⋅
fyk MPa
1
−
⋅
⋅
0.08 %
⋅
=
=
sl.max
0.75d
33.5 cm
⋅
=
=
min
b h
(
)
(
)
30 cm
⋅
=
sT_V
11 cm
⋅
=
>
uk
8
15 cm
⋅
=
Document Outline
- Wymiarowanie belki żelbetowej – skręcanie, skręcanie ze ścinaniem Blok IV, projekt
- Projektowanie zbrojenia na skręcanie
- Projektowanie zbrojenia na skręcanie
- Projektowanie zbrojenia na skręcanie
- Projektowanie zbrojenia na skręcanie
- Projektowanie zbrojenia na skręcanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
- Projektowanie zbrojenia na skręcanie i ścinanie
Wyszukiwarka
Podobne podstrony:
01. Skrecanie
TD 01
Ubytki,niepr,poch poł(16 01 2008)
01 E CELE PODSTAWYid 3061 ppt
01 Podstawy i technika
01 Pomoc i wsparcie rodziny patologicznej polski system pomocy ofiarom przemocy w rodzinieid 2637 p
zapotrzebowanie ustroju na skladniki odzywcze 12 01 2009 kurs dla pielegniarek (2)
01 Badania neurologicz 1id 2599 ppt
01 AiPP Wstep
ANALIZA 01
01 WPROWADZENIA
01 piątek
choroby trzustki i watroby 2008 2009 (01 12 2008)
syst tr 1 (2)TM 01 03)13
Analiza 01
04 01 MORBILLO ROSOLIA VaMALATTIA
więcej podobnych podstron