SYSTEMY LICZBOWE

SYSTEMY LICZBOWE

dr inż. Jacek FLOREK

dr inż. Jacek FLOREK

Instytut Informatyki

Instytut Informatyki



Rodzaje informacji (analogowe i cyfrowe)

Rodzaje informacji (analogowe i cyfrowe)



System dwójkowy

System dwójkowy



System heksadecymalny

System heksadecymalny

1

RODZAJE INFORMACJI

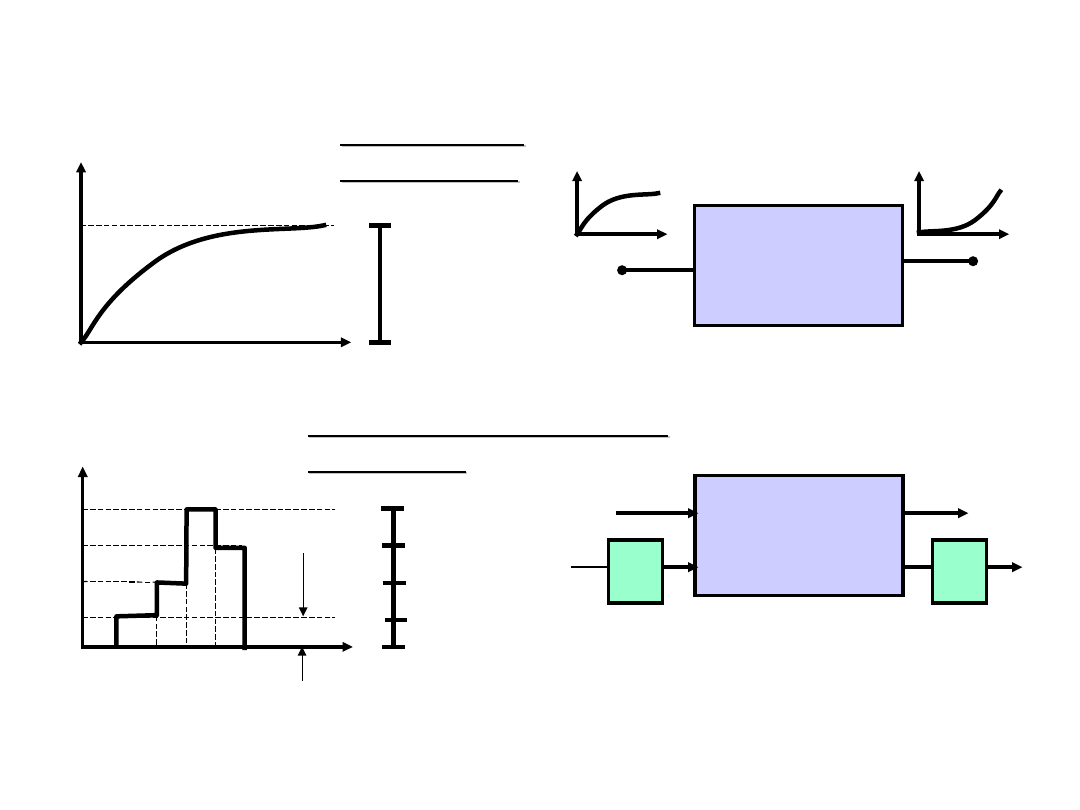
RODZAJE INFORMACJI

Informacje

Informacje

analogowe

analogowe

Informacje dyskretne

Informacje dyskretne

(cyfrowe)

(cyfrowe)

U(t)

Umax

Umax

0

0

R=(0,Umax)

nieskończony

zbiór możliwych

wartości

U(t)

Umaxq

Umax

0

0

R=(

U, 2U,

3U, 4U

)

moc zbioru R

wynosi 4

U - kwant

wartości

MASZYNA

MASZYNA

ANALOGOWA

ANALOGOWA

WE

WY

MASZYNA

MASZYNA

CYFROWA

CYFROWA

#

#

#

#

a/c

c/a





INFORMACJA CYFROWA

INFORMACJA CYFROWA

(1)

(1)

Def.1. Informacją cyfrową nazywamy informację przedstawioną w

Def.1. Informacją cyfrową nazywamy informację przedstawioną w

postaci słów cyfrowych

postaci słów cyfrowych

Def.1. Informacją cyfrową nazywamy informację przedstawioną w

Def.1. Informacją cyfrową nazywamy informację przedstawioną w

postaci słów cyfrowych

postaci słów cyfrowych

Def.2. Słowem cyfrowym nazywamy dowolny ciąg składający się z

Def.2. Słowem cyfrowym nazywamy dowolny ciąg składający się z

symboli 0 i/lub 1

symboli 0 i/lub 1

Def.2. Słowem cyfrowym nazywamy dowolny ciąg składający się z

Def.2. Słowem cyfrowym nazywamy dowolny ciąg składający się z

symboli 0 i/lub 1

symboli 0 i/lub 1

Długość słowa

Długość słowa

Oznaczenie

Oznaczenie

symboliczne

symboliczne

Nazwa

Nazwa

1

1

4

4

8

8

16

16

32

32

64

64

a

a

0

0

a

a

3

3

...a

...a

0

0

a

a

7

7

.....a

.....a

0

0

a

a

15

15

.......a

.......a

0

0

a

a

31

31

.........a

.........a

0

0

a

a

63

63

...........a

...........a

0

0

bit

bit

tetrada, kęs

tetrada, kęs

bajt

bajt

słowo 16-bitowe, słowo

słowo 16-bitowe, słowo

podwójne słowo, dwusłowo

podwójne słowo, dwusłowo

słowo 64-bitowe, czterosłowo

słowo 64-bitowe, czterosłowo

1b - oznacza 1 bit

1b - oznacza 1 bit

1B=8b

1B=8b

1B - oznacza 1 bajt

1B - oznacza 1 bajt

1kB=1024B (2

1kB=1024B (2

10

10

)

)

1MB=1024kB

1MB=1024kB

1GB=1024MB

1GB=1024MB

Przykład: 20 MB jest ilością informacji ośmiokrotnie większą niż 20Mb

Przykład: 20 MB jest ilością informacji ośmiokrotnie większą niż 20Mb

INFORMACJA CYFROWA

INFORMACJA CYFROWA

(2)

(2)

W słowach cyfrowych wyróżnia się najstarszą i najmłodszą pozycję,

W słowach cyfrowych wyróżnia się najstarszą i najmłodszą pozycję,

tj.

tj.

bit najbardziej znaczący

bit najbardziej znaczący

zwany najstarszym (ang.

zwany najstarszym (ang.

MSB

MSB

- Most

- Most

Significant Bit

Significant Bit

)

)

oraz

oraz

bit najmniej znaczący

bit najmniej znaczący

zwany najmłodszym (ang.

zwany najmłodszym (ang.

LSB

LSB

-

-

Least

Least

Significant Bit

Significant Bit

)

)

a

a

n-1

n-1

......................... a

......................... a

0

0

MSB

MSB

LSB

LSB

Analogicznie możemy mówić o starszym i

Analogicznie możemy mówić o starszym i

najmłodszym bajcie lub o starszej lub młodszej

najmłodszym bajcie lub o starszej lub młodszej

tetradzie

tetradzie

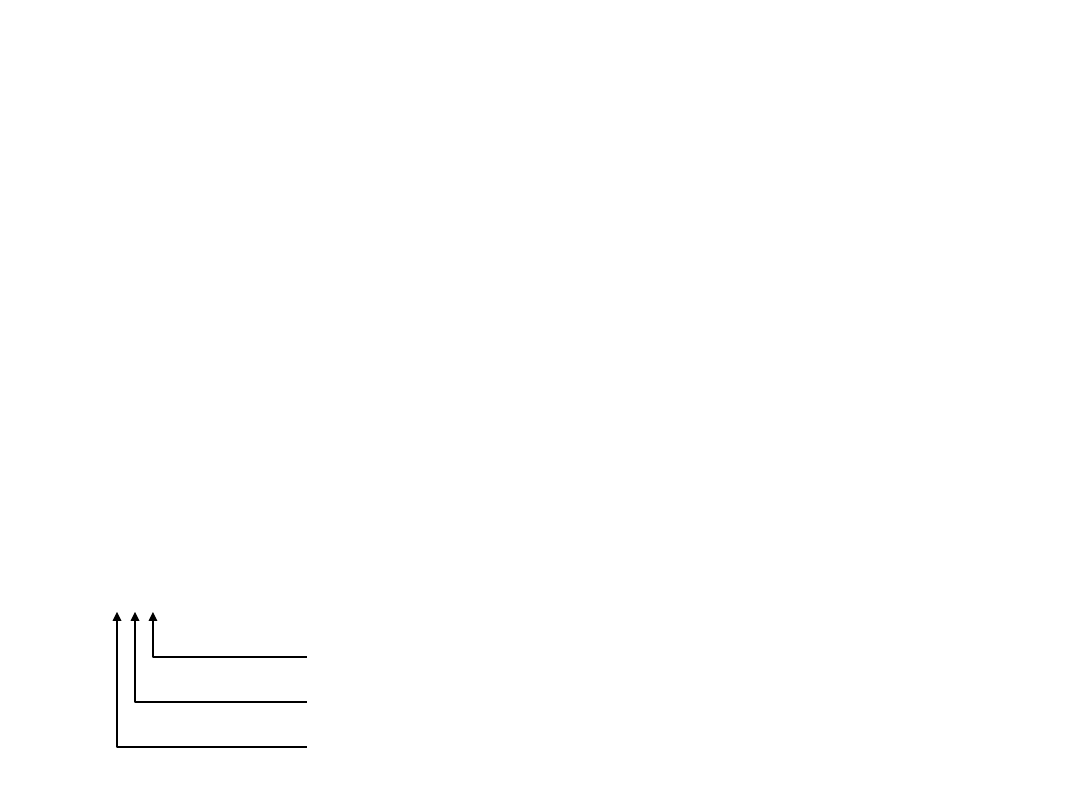
DZIESIĘTNY SYSTEM LICZBOWY

DZIESIĘTNY SYSTEM LICZBOWY

Do zapisu dowolnej liczby system

Do zapisu dowolnej liczby system

wykorzystuje dziesięć symboli (cyfr):

wykorzystuje dziesięć symboli (cyfr):

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Dowolną liczbę w systemie dziesiętnym

Dowolną liczbę w systemie dziesiętnym

możemy przedstawić jako następująca sumę:

możemy przedstawić jako następująca sumę:

(a

(a

n-1

n-1

...a

...a

1

1

a

a

0

0

)

)

D

D

= a

= a

n-1

n-1

*10

*10

(n-1)

(n-1)

+...+ a

+...+ a

1

1

*10

*10

1

1

+ a

+ a

0

0

*10

*10

0

0

=

=

gdzie:

gdzie:

i - numer pozycji w liczbie,

i - numer pozycji w liczbie,

a

a

i

i

- dowolna z cyfr od 0 do 9,

- dowolna z cyfr od 0 do 9,

n - ilość cyfr (pozycji) w liczbie

n - ilość cyfr (pozycji) w liczbie

Przykład:

Przykład:

424

424

D

D

= 4*10

= 4*10

2

2

+ 2*10

+ 2*10

1

1

+ 5*10

+ 5*10

0

0

pozycja jedynek

pozycja jedynek

(0)

(0)

pozycja

pozycja

dziesiątek (1)

dziesiątek (1)

pozycja setek (2)

pozycja setek (2)









1

n

0

i

i

i

10

a

DWÓJKOWY SYSTEM LICZBOWY

DWÓJKOWY SYSTEM LICZBOWY

Do zapisu dowolnej liczby system

Do zapisu dowolnej liczby system

wykorzystuje dwa symbole (cyfry):

wykorzystuje dwa symbole (cyfry):

0, 1

0, 1

Dowolną liczbę w systemie dwójkowym

Dowolną liczbę w systemie dwójkowym

możemy przedstawić jako następująca

możemy przedstawić jako następująca

sumę:

sumę:

(a

(a

n-1

n-1

...a

...a

1

1

a

a

0

0

)

)

B

B

= a

= a

n-1

n-1

*2

*2

(n-1)

(n-1)

+...+ a

+...+ a

1

1

*2

*2

1

1

+ a

+ a

0

0

*2

*2

0

0

=

=

gdzie:

gdzie:

i - numer pozycji w liczbie,

i - numer pozycji w liczbie,

a

a

i

i

- dowolna z cyfr (0 lub 1),

- dowolna z cyfr (0 lub 1),

n - ilość cyfr (pozycji) w liczbie

n - ilość cyfr (pozycji) w liczbie

Przykład:

Przykład:

10100

10100

B

B

= 1*2

= 1*2

4

4

+ 0*2

+ 0*2

3

3

+ 1*2

+ 1*2

2

2

+ 0*2

+ 0*2

1

1

+ 0*2

+ 0*2

0

0









1

n

0

i

i

i

2

a

KONWERSJA LICZB

KONWERSJA LICZB

1.

1.

2.

2.

10100

10100

B

B

= 1*2

= 1*2

4

4

+ 0*2

+ 0*2

3

3

+ 1*2

+ 1*2

2

2

+ 0*2

+ 0*2

1

1

+ 0*2

+ 0*2

0

0

=

=

= 1*16 + 0*8 + 1*4 + 0*2 + 0*1 = 20

= 1*16 + 0*8 + 1*4 + 0*2 + 0*1 = 20

D

D

20:2 = 10

20:2 = 10

10:2 = 5

10:2 = 5

5:2 = 2

5:2 = 2

2:2 = 1

2:2 = 1

1:2 = 0

1:2 = 0

reszta=

reszta=

0

0

reszta=

reszta=

0

0

reszta=

reszta=

1

1

reszta=

reszta=

0

0

reszta=

reszta=

1

1

k

ie

ru

n

e

k

o

d

c

zy

tu

k

ie

ru

n

e

k

o

d

c

zy

tu

w

y

n

ik

u

w

y

n

ik

u

czyli 20

czyli 20

D

D

=

=

10100

10100

B

B

HEKSADECYMALNY (SZESNASTKOWY)

HEKSADECYMALNY (SZESNASTKOWY)

SYSTEM LICZBOWY

SYSTEM LICZBOWY

Do zapisu dowolnej liczby system

Do zapisu dowolnej liczby system

wykorzystuje szesnaście symboli (cyfr i

wykorzystuje szesnaście symboli (cyfr i

liter):

liter):

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Dowolną liczbę w systemie

Dowolną liczbę w systemie

heksadecymalnym możemy przedstawić

heksadecymalnym możemy przedstawić

jako następująca sumę:

jako następująca sumę:

(a

(a

n-1

n-1

...a

...a

1

1

a

a

0

0

)

)

H

H

= a

= a

n-1

n-1

*16

*16

(n-1)

(n-1)

+...+ a

+...+ a

1

1

*16

*16

1

1

+

+

a

a

0

0

*16

*16

0

0

=

=

gdzie:

gdzie:

i - numer pozycji w liczbie,

i - numer pozycji w liczbie,

a

a

i

i

- dowolna cyfra heksadecymalna,

- dowolna cyfra heksadecymalna,

n - ilość cyfr (pozycji) w liczbie

n - ilość cyfr (pozycji) w liczbie

Przykład:

Przykład:

1C2

1C2

H

H

= 1*16

= 1*16

2

2

+ C*16

+ C*16

1

1

+ 2*16

+ 2*16

0

0









1

n

0

i

i

i

16

a

KONWERSJA LICZB

KONWERSJA LICZB

(1)

(1)

1.

1.

2.

2.

1C2

1C2

H

H

= 1*16

= 1*16

2

2

+ C*16

+ C*16

1

1

+ 2*16

+ 2*16

0

0

=

=

= 1*256 + 12*16 + 2*1 = 450

= 1*256 + 12*16 + 2*1 = 450

D

D

450:16 =

450:16 =

28

28

28:16 = 1

28:16 = 1

1:16 = 0

1:16 = 0

reszta=

reszta=

2

2

reszta=

reszta=

C

C

reszta=

reszta=

1

1

k

ie

ru

n

e

k

k

ie

ru

n

e

k

o

d

c

zy

tu

o

d

c

zy

tu

w

y

n

ik

u

w

y

n

ik

u

czyli 450

czyli 450

D

D

=

=

1C2

1C2

H

H

reszty zapisujemy w

reszty zapisujemy w

postaci cyfry

postaci cyfry

heksadecymalnej

heksadecymalnej

KONWERSJA LICZB

KONWERSJA LICZB

(2)

(2)

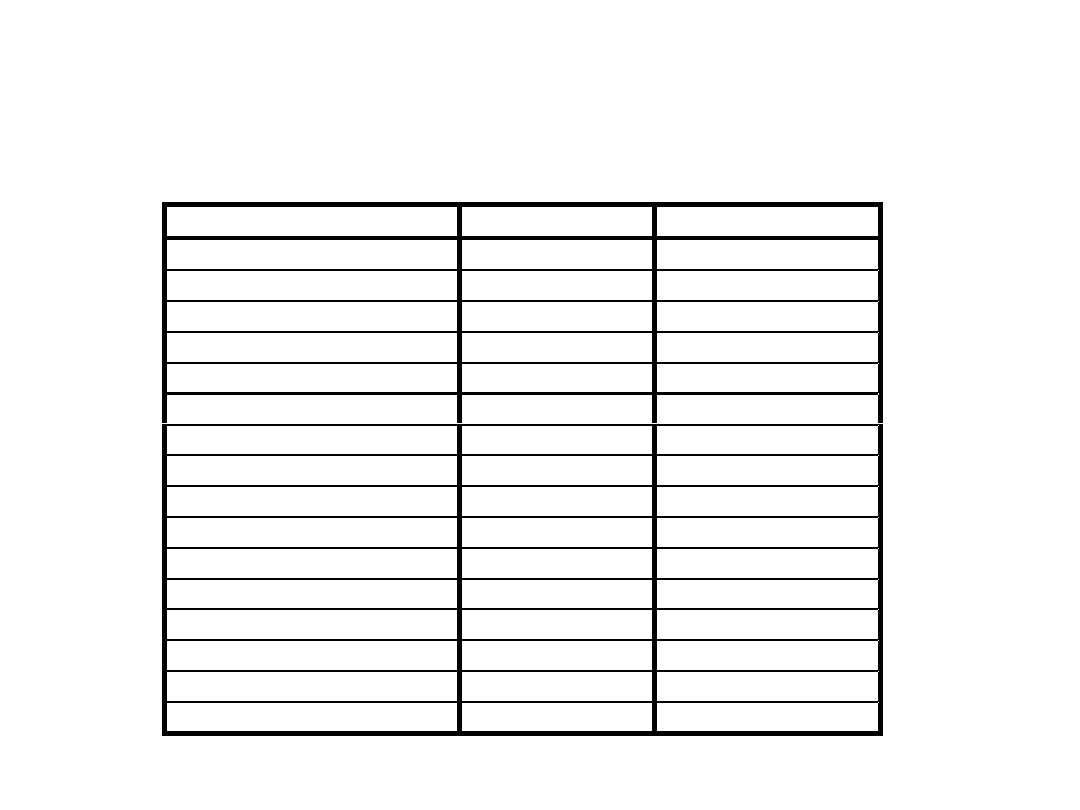
Do konwersji zapisu binarnego na

Do konwersji zapisu binarnego na

heksadecymalny i odwrotnie wykorzystuje

heksadecymalny i odwrotnie wykorzystuje

się tabelę:

się tabelę:

cyfra heksadecymalna liczba binarna liczba dziesiętna

0

0000

0

1

0001

1

2

0010

2

3

0011

3

4

0100

4

5

0101

5

6

0110

6

7

0111

7

8

1000

8

9

1001

9

A

1010

10

B

1011

11

C

1100

12

D

1101

13

E

1110

14

F

1111

15

KONWERSJA LICZB

KONWERSJA LICZB

(3)

(3)

1C2

1C2

H

H

=

=

= 0001 1100

= 0001 1100

0010 =

0010 =

= 000111000010

= 000111000010

=

=

= 111000010

= 111000010

B

B

111000010

111000010

B

B

=

=

=

=

000

000

1 1100 0010

1 1100 0010

B

B

=

=

= 1C2

= 1C2

H

H

każdą cyfrę hex.

każdą cyfrę hex.

zapisujemy w postaci

zapisujemy w postaci

czwórki cyfr binarnych

czwórki cyfr binarnych

odrzucamy nieznaczące

odrzucamy nieznaczące

zera na początku liczby

zera na początku liczby

binarnej

binarnej

1.

1.

2.

2.

liczbę binarną dzielimy od

liczbę binarną dzielimy od

końca na czwórki

końca na czwórki

ewentualnie dopisując

ewentualnie dopisując

nieznaczące zera w

nieznaczące zera w

ostatniej (pierwszej)

ostatniej (pierwszej)

czwórce

czwórce

każdą czwórkę binarną

każdą czwórkę binarną

zapisujemy w postaci cyfry

zapisujemy w postaci cyfry

hex.

hex.

W jakim systemie liczbowym zapisano

W jakim systemie liczbowym zapisano

biografię?

biografię?

Ukończyłem uniwersytet w

Ukończyłem uniwersytet w

44

44

roku życia; po roku,

roku życia; po roku,

jako już

jako już

100

100

-letni młodzieniec, ożeniłem się z

-letni młodzieniec, ożeniłem się z

34

34

-

-

letnią panienką. Nieznaczna różnica wieku –

letnią panienką. Nieznaczna różnica wieku –

11

11

lat

lat

tylko – sprzyjała bardzo harmonijnemu małżeńskiemu

tylko – sprzyjała bardzo harmonijnemu małżeńskiemu

pożyciu. W stosunkowo krótkim czasie mieliśmy już

pożyciu. W stosunkowo krótkim czasie mieliśmy już

10

10

dzieci. Moja miesięczna pensja wynosiła

dzieci. Moja miesięczna pensja wynosiła

13000

13000

zł,

zł,

z których

z których

1/10

1/10

oddawałem siostrze, tak iż na własne

oddawałem siostrze, tak iż na własne

utrzymanie mieliśmy tylko

utrzymanie mieliśmy tylko

11200

11200

zł na miesiąc;

zł na miesiąc;

mimo to byliśmy szczęśliwi.

mimo to byliśmy szczęśliwi.

W systemie dziesiętnym ma ona postać:

W systemie dziesiętnym ma ona postać:

Ukończyłem uniwersytet w

Ukończyłem uniwersytet w

24

24

roku życia; po roku,

roku życia; po roku,

jako już

jako już

25

25

-letni młodzieniec, ożeniłem się z

-letni młodzieniec, ożeniłem się z

19

19

-letnią

-letnią

panienką. Nieznaczna różnica wieku –

panienką. Nieznaczna różnica wieku –

6

6

lat tylko –

lat tylko –

sprzyjała

bardzo

harmonijnemu

małżeńskiemu

sprzyjała

bardzo

harmonijnemu

małżeńskiemu

pożyciu. W stosunkowo krótkim czasie mieliśmy już

pożyciu. W stosunkowo krótkim czasie mieliśmy już

5

5

dzieci. Moja miesięczna pensja wynosiła

dzieci. Moja miesięczna pensja wynosiła

1000

1000

zł, z

zł, z

których

których

1/5

1/5

oddawałem siostrze, tak iż na własne

oddawałem siostrze, tak iż na własne

utrzymanie mieliśmy tylko

utrzymanie mieliśmy tylko

800

800

zł na miesiąc; mimo

zł na miesiąc; mimo

to byliśmy szczęśliwi.

to byliśmy szczęśliwi.

KODOWANIE LICZB I TEKSTÓW

KODOWANIE LICZB I TEKSTÓW

dr inż. Jacek FLOREK

dr inż. Jacek FLOREK

Instytut Informatyki

Instytut Informatyki



Kody binarne

Kody binarne



kod naturalny NKB

kod naturalny NKB



kod BCD

kod BCD



kod Gray’a

kod Gray’a



inne kody

inne kody



Kodowanie znaków (tekstów)

Kodowanie znaków (tekstów)

2

KODOWANIE

KODOWANIE

Zbiorem

Zbiorem

kodowanym może

kodowanym może

być zbiór

być zbiór

dowolnych

dowolnych

obiektów (cyfr,

obiektów (cyfr,

liter, symboli

liter, symboli

graficznych,

graficznych,

stanów

stanów

logicznych,

logicznych,

poleceń do

poleceń do

wykonania itp.)

wykonania itp.)

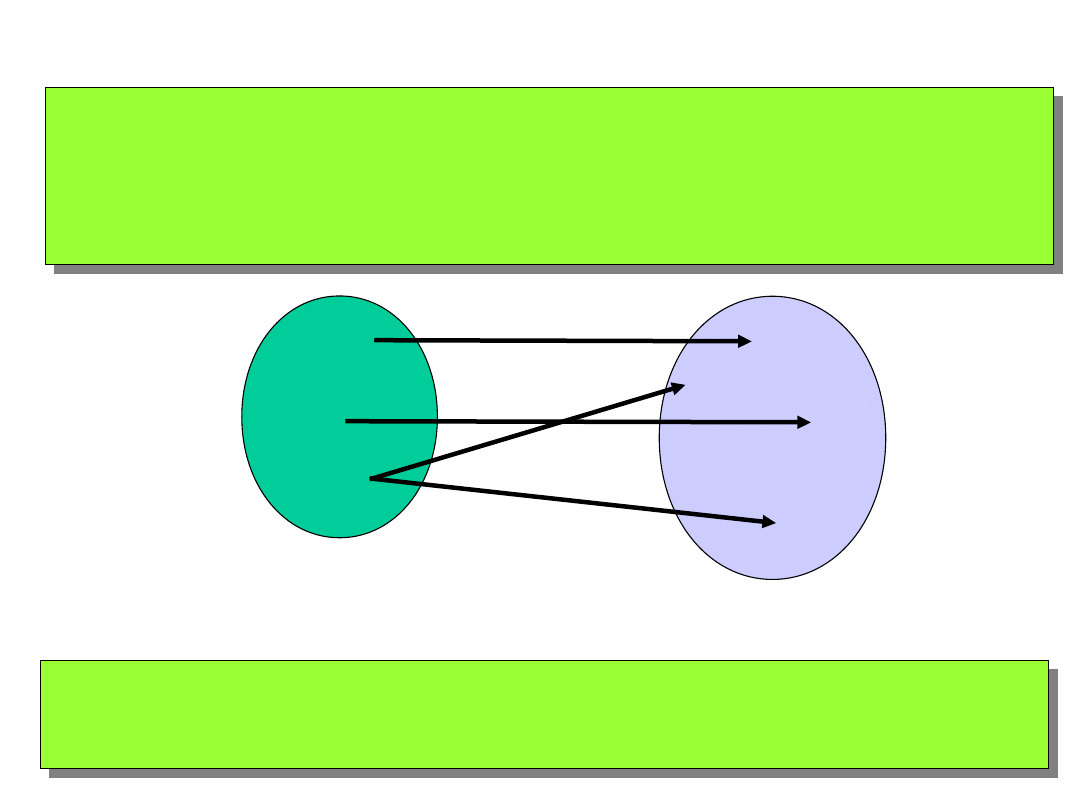
Def.1.

Def.1.

Kodowaniem

Kodowaniem

nazywamy przyporządkowanie

nazywamy przyporządkowanie

poszczególnym obiektom zbioru kodowanego

poszczególnym obiektom zbioru kodowanego

odpowiadających im elementów zwanych słowami kodowymi,

odpowiadających im elementów zwanych słowami kodowymi,

przy czym każdemu słowu kodowemu musi odpowiadać

przy czym każdemu słowu kodowemu musi odpowiadać

dokładnie jeden element kodowany

dokładnie jeden element kodowany

Def.1.

Def.1.

Kodowaniem

Kodowaniem

nazywamy przyporządkowanie

nazywamy przyporządkowanie

poszczególnym obiektom zbioru kodowanego

poszczególnym obiektom zbioru kodowanego

odpowiadających im elementów zwanych słowami kodowymi,

odpowiadających im elementów zwanych słowami kodowymi,

przy czym każdemu słowu kodowemu musi odpowiadać

przy czym każdemu słowu kodowemu musi odpowiadać

dokładnie jeden element kodowany

dokładnie jeden element kodowany

A

A

B

B

C

C

010

010

111

111

100

100

001

001

Proces kodowania może być

Proces kodowania może być

opisem słownym, wzorem

opisem słownym, wzorem

(zależnością matematyczną),

(zależnością matematyczną),

tabelą kodową itp.

tabelą kodową itp.

Def.2. Kodem liczbowym nazywamy taki kod, który liczbom

Def.2. Kodem liczbowym nazywamy taki kod, który liczbom

dowolnego systemu będzie przyporządkowywał słowa

dowolnego systemu będzie przyporządkowywał słowa

kodowe w postaci zerojedynkowej (binarnej)

kodowe w postaci zerojedynkowej (binarnej)

Def.2. Kodem liczbowym nazywamy taki kod, który liczbom

Def.2. Kodem liczbowym nazywamy taki kod, który liczbom

dowolnego systemu będzie przyporządkowywał słowa

dowolnego systemu będzie przyporządkowywał słowa

kodowe w postaci zerojedynkowej (binarnej)

kodowe w postaci zerojedynkowej (binarnej)

NATURALNY KOD BINARNY (NKB)

NATURALNY KOD BINARNY (NKB)

Def. Jeżeli dowolnej liczbie dziesiętnej przyporządkujemy

Def. Jeżeli dowolnej liczbie dziesiętnej przyporządkujemy

odpowiadająca jej liczbę binarną, to otrzymamy naturalny

odpowiadająca jej liczbę binarną, to otrzymamy naturalny

kod binarny (NKB)

kod binarny (NKB)

Def. Jeżeli dowolnej liczbie dziesiętnej przyporządkujemy

Def. Jeżeli dowolnej liczbie dziesiętnej przyporządkujemy

odpowiadająca jej liczbę binarną, to otrzymamy naturalny

odpowiadająca jej liczbę binarną, to otrzymamy naturalny

kod binarny (NKB)

kod binarny (NKB)

Minimalna długość k słowa binarnego reprezentującego liczbę

Minimalna długość k słowa binarnego reprezentującego liczbę

dziesiętną A musi spełniać warunek:

dziesiętną A musi spełniać warunek:

1

2A

2

A

k







Oznacza to, że aby zakodować liczbę dziesiętną w zakresie 0-15

Oznacza to, że aby zakodować liczbę dziesiętną w zakresie 0-15

wystarczy wykorzystać jedną tetradę (długość słowa kodowego

wystarczy wykorzystać jedną tetradę (długość słowa kodowego

k=4) gdyż

k=4) gdyż

31

2

15

4





NKB

0

0000

1

0001

2

0010

3

0011

4

0100

5

0101

6

0110

7

0111

8

1000

9

1001

10

1010

11

1011

12

1100

13

1101

14

1110

15

1111

KOD PROSTY BCD

KOD PROSTY BCD

Gdy w systemie wygodnie jest operować liczbami dziesiętnymi

Gdy w systemie wygodnie jest operować liczbami dziesiętnymi

stosowany jest kod BCD. Liczba terad kodu BCD jest bowiem

stosowany jest kod BCD. Liczba terad kodu BCD jest bowiem

równa liczbie pozycji dziesiętnych reprezentowanej liczby. Np.

równa liczbie pozycji dziesiętnych reprezentowanej liczby. Np.

dziesiętna liczba 6-pozycyjna (000000-999999) jest kodowana

dziesiętna liczba 6-pozycyjna (000000-999999) jest kodowana

na 24 bitach

na 24 bitach

Konstrukcja:

Konstrukcja:

•

każdej cyfrze dziesiętnej przyporządkowujemy czterocyfrową

każdej cyfrze dziesiętnej przyporządkowujemy czterocyfrową

liczbę dwójkową w kodzie NKB

liczbę dwójkową w kodzie NKB

*)

*)

;

;

•

słowo kodowe w kodzie prostym BCD otrzymujemy zapisując

słowo kodowe w kodzie prostym BCD otrzymujemy zapisując

każdą cyfrę liczby dziesiętnej w postaci tetrady binarnej

każdą cyfrę liczby dziesiętnej w postaci tetrady binarnej

463

463

D

D

= 010001100011

= 010001100011

BCD

BCD

67

67

D

D

= 01100111

= 01100111

BCD

BCD

*)

*)

gdybysmy zamiast kodu NKB użyli kodu np. Gray’a wówczas

gdybysmy zamiast kodu NKB użyli kodu np. Gray’a wówczas

otrzymalibysmy kod BCD Gray’a

otrzymalibysmy kod BCD Gray’a

KOD GRAY’A

KOD GRAY’A

Kod Gray’a tworzy się z kodu naturalnego NKB biorąc pod

Kod Gray’a tworzy się z kodu naturalnego NKB biorąc pod

uwagę:

uwagę:

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią się

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią się

tylko na jednej pozycji

tylko na jednej pozycji

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią się

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią się

tylko na jednej pozycji

tylko na jednej pozycji

1

n

2

n

2

n

n

1

n

1

n

n

n

b

b

g

b

b

g

b

g





















NKB

Kod Gray’a

000

000

001

001

010

011

011

010

100

110

101

111

110

101

111

100

INNE KODY BINARNE

INNE KODY BINARNE

NKB BCD Kod Gray’a

1 z 10

J ohnsona

0

0000

0000

0000

0000000001

00000

1

0001

0001

0001

0000000010

00001

2

0010

0010

0011

0000000100

00011

3

0011

0011

0010

0000001000

00111

4

0100

0100

0110

0000010000

01111

5

0101

0101

0111

0000100000

11111

6

0110

0110

0101

0001000000

11110

7

0111

0111

0100

0010000000

11100

8

1000

1000

1100

0100000000

11000

9

1001

1001

1101

1000000000

10000

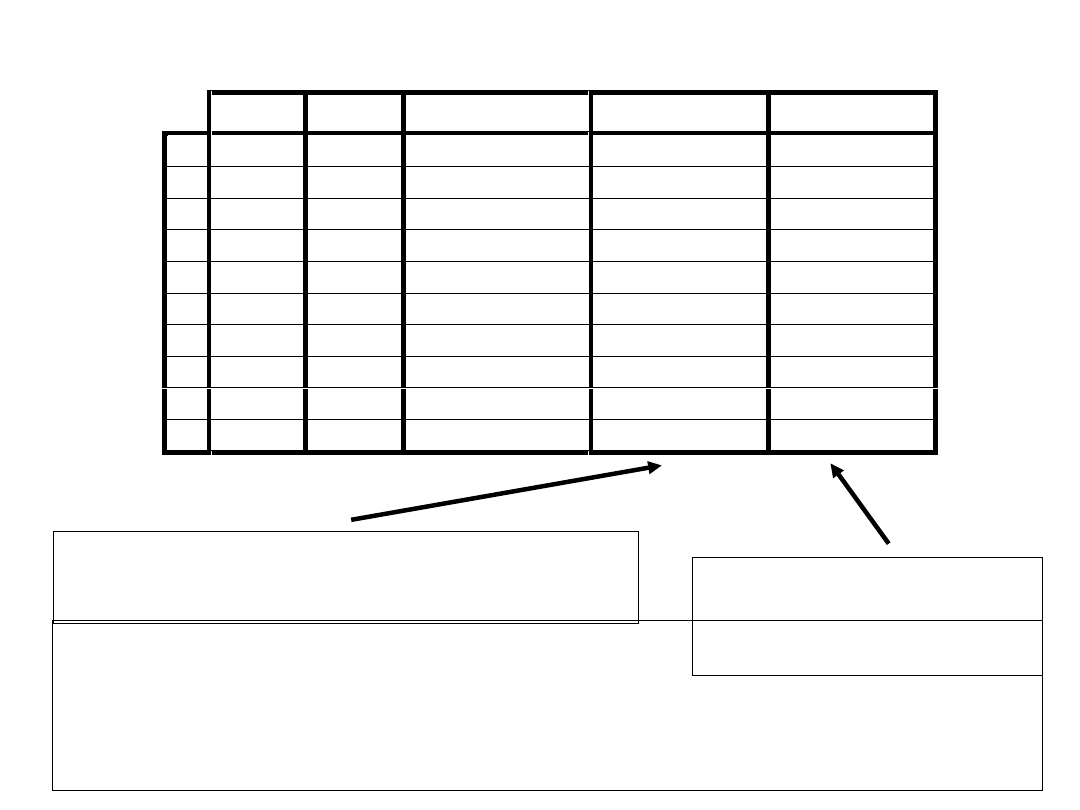
Długość słowa kodu „1 z n” (w tabeli „1 z

Długość słowa kodu „1 z n” (w tabeli „1 z

10”) jest równa n, tj. liczności zbioru

10”) jest równa n, tj. liczności zbioru

kodowanego (liczbie kodowanych słów)

kodowanego (liczbie kodowanych słów)

Kod 5-bitowy

Kod 5-bitowy

stosowany do

stosowany do

kodowania cyfr

kodowania cyfr

dziesiętnych

dziesiętnych

Są to kody nadmiarowe (redundancyjne), w których liczba pozycji

Są to kody nadmiarowe (redundancyjne), w których liczba pozycji

binarnych jest większa niż wynika to z ogólnej zależności

binarnych jest większa niż wynika to z ogólnej zależności

Redundancję można wykorzystać do zwiększenia niezawodności

Redundancję można wykorzystać do zwiększenia niezawodności

operacji wykonywanych na liczbach

operacji wykonywanych na liczbach

1

2A

2

A

k







KODOWANIE ZNAKÓW

KODOWANIE ZNAKÓW

Początki:

Początki:

•

Harald C. M. Morse (kropka - kreska - ....);

Harald C. M. Morse (kropka - kreska - ....);

•

Anatol de Baudot (dalekopis);

Anatol de Baudot (dalekopis);

•

w pierwszych maszynach cyfrowych - kod dalekopisowy

w pierwszych maszynach cyfrowych - kod dalekopisowy

5-bitowy, a potem 8-bitowy (EBCDIC);

5-bitowy, a potem 8-bitowy (EBCDIC);

W 1977 roku kiedy to ANSI (

W 1977 roku kiedy to ANSI (

American National Standards Institute

American National Standards Institute

)

)

zatwierdził

zatwierdził

kod ASCII

kod ASCII

(

(

The American Standard Code for Information

The American Standard Code for Information

Interchange

Interchange

).

).

Jest to 7-bitowy kod (8 bit do kontroli parzystości),

Jest to 7-bitowy kod (8 bit do kontroli parzystości),

definiujący 128-elementowy zestaw znaków (

definiujący 128-elementowy zestaw znaków (

character

character

set

set

) o wartościach kodowych od 0 do 127. Zestaw

) o wartościach kodowych od 0 do 127. Zestaw

zawiera litery łacińskie (duże i małe), cyfry i znaki

zawiera litery łacińskie (duże i małe), cyfry i znaki

interpunkcji

oraz

różne

znaki

specjalne.

interpunkcji

oraz

różne

znaki

specjalne.

Międzynarodowa Organizacja Standaryzacji - ISO,

Międzynarodowa Organizacja Standaryzacji - ISO,

nadała amerykańskiemu systemowi kodowania status

nadała amerykańskiemu systemowi kodowania status

standardu międzynarodowego oznaczonego jako ISO

standardu międzynarodowego oznaczonego jako ISO

646.

646.

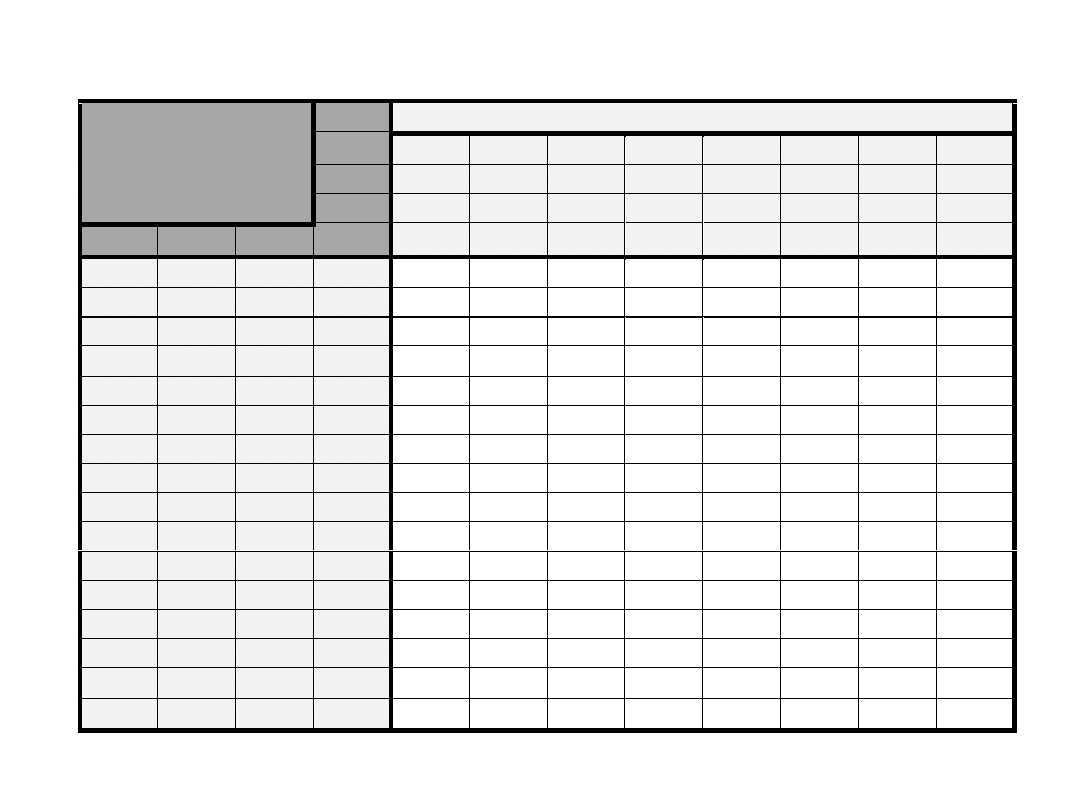
Kod ASCII rozszerzony

Kod ASCII rozszerzony

wprowadza dodatkowe 128 znaków

wprowadza dodatkowe 128 znaków

wykorzystując mało używany bit parzystości:

wykorzystując mało używany bit parzystości:

IBM wprowadza

IBM wprowadza

•

Code Page 474 dla USA

Code Page 474 dla USA

•

Code Page 852 dla Europy Wschodniej

Code Page 852 dla Europy Wschodniej

8

Bit kontroli parzystości

7

0

0

0

0

1

1

1

1

6

0

0

1

1

0

0

1

1

Numery bitów słowa

5

0

1

0

1

0

1

0

1

4

3

2

1

0

0

0

0

NUL

DEL

SP

0

@

P

‘

p

0

0

0

1

SOH DC1

!

1

A

Q

a

q

0

0

1

0

STX

DC2

„

2

B

R

b

r

0

0

1

1

ETX

DC3



3

C

S

c

s

0

1

0

0

EOT DC4

$

4

D

T

d

t

0

1

0

1

ENQ NAK

%

5

E

U

e

u

0

1

1

0

ACK SYN

&

6

F

V

f

v

0

1

1

1

BEL

ETB

`

7

G

W

g

w

1

0

0

0

BS

CAN

(

8

H

X

h

x

1

0

0

1

HT

EM

)

9

I

Y

i

y

1

0

1

0

LF

SUB

*

:

J

Z

j

z

1

0

1

1

VT

ESC

+

;

K

[

k

{

1

1

0

0

FF

FS

,

<

L

\

l

|

1

1

0

1

CR

GS

-

=

M

]

m

}

1

1

1

0

SO

RS

.

>

N



n

~

1

1

1

1

SI

US

/

?

O



o

DEL

KODOWANIE ZNAKÓW

KODOWANIE ZNAKÓW

kod ASCII

kod ASCII

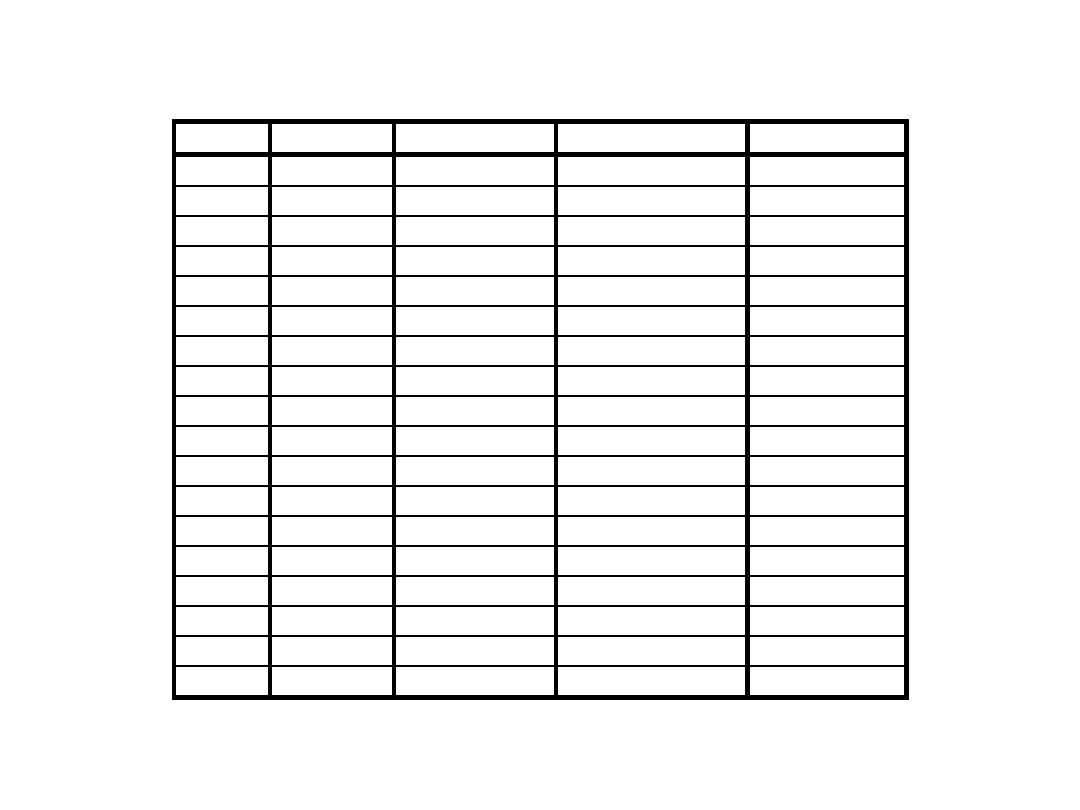
KODOWANIE ZNAKÓW

KODOWANIE ZNAKÓW

problem polskich liter

problem polskich liter

1. W 1987 roku ISO tworzy standard ISO 8859 (rozszerzone ASCII):

1. W 1987 roku ISO tworzy standard ISO 8859 (rozszerzone ASCII):

•

ISO 8859-1 (Latin-1) - Europa zachodnia

ISO 8859-1 (Latin-1) - Europa zachodnia

•

ISO 8859-2 (Latin-2) - Europa wschodnia

ISO 8859-2 (Latin-2) - Europa wschodnia

•

...............................

...............................

•

ISO 8859-5 (cyrlica)

ISO 8859-5 (cyrlica)

•

...............................

...............................

•

ISO 8859-7 (greka)

ISO 8859-7 (greka)

•

...............................

...............................

2. W 1990 roku Instytut Maszyn Matematycznych tworzy

2. W 1990 roku Instytut Maszyn Matematycznych tworzy

kod

kod

Mazovia

Mazovia

(rozpowszechniony w dobie kart graficznych Hercules)

(rozpowszechniony w dobie kart graficznych Hercules)

3. Firma Microsoft tworzy własny zestaw znaków dla Europy

3. Firma Microsoft tworzy własny zestaw znaków dla Europy

wschodniej

wschodniej

Windows CP 1250

Windows CP 1250

KODOWANIE ZNAKÓW

KODOWANIE ZNAKÓW

problem polskich liter

problem polskich liter

Litera Mazovia IBM Latin-2 Windows1250 ISO Latin-2

Ą

143

164

165

161

Ć

149

143

198

198

Ę

144

168

202

202

Ł

156

157

163

163

Ń

165

227

209

209

Ó

163

224

211

211

Ś

152

151

140

166

Ź

160

141

143

172

Ż

161

189

175

175

ą

134

165

185

177

ć

141

134

230

230

ę

145

169

234

234

ł

146

136

179

179

ń

164

228

241

241

ó

162

162

243

243

ś

158

152

156

182

ź

166

171

159

188

ż

167

190

191

191

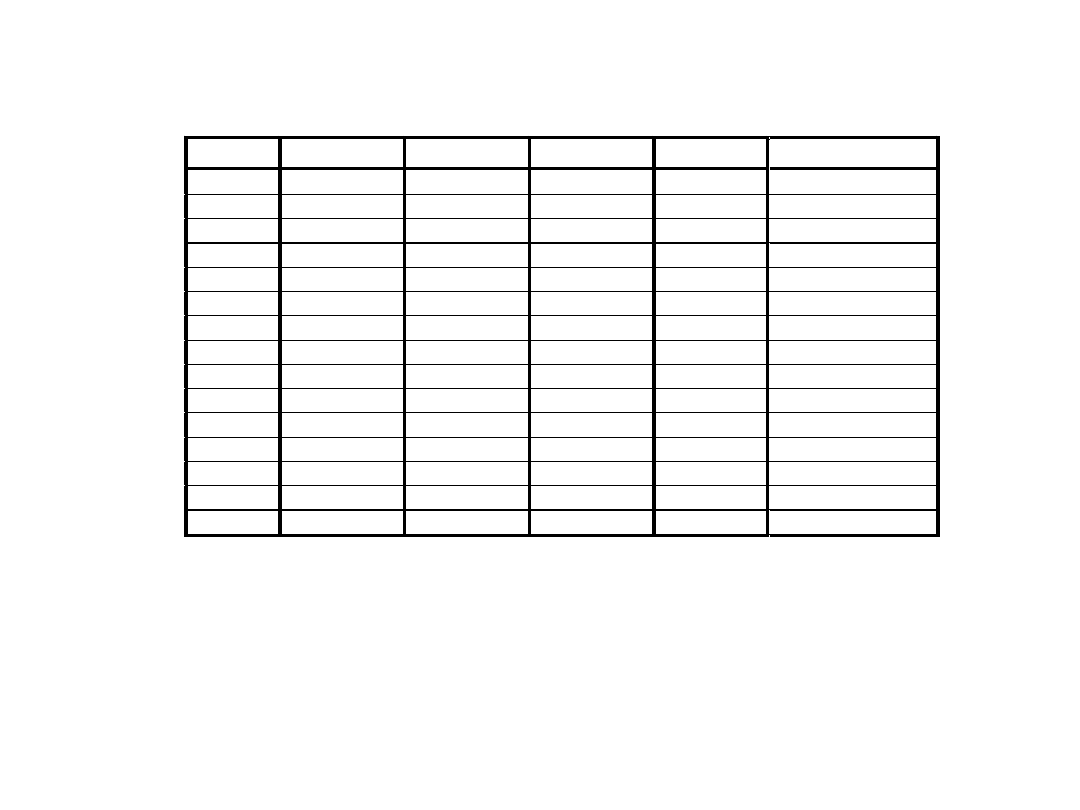
STAŁOPOZYCYJNA REPREZENTACJA

STAŁOPOZYCYJNA REPREZENTACJA

LICZB

LICZB

Do

reprezentacji

liczb

całkowitych

stosowane

są

kody

Do

reprezentacji

liczb

całkowitych

stosowane

są

kody

stałopozycyjne

stałopozycyjne

•

zapis znak-moduł

zapis znak-moduł

•

zapis U1

zapis U1

•

zapis U2

zapis U2

•

zapis polaryzowany (BIAS)

zapis polaryzowany (BIAS)

Zapis

Zapis

U2

U2

(uzupełnień do 2) jest podobny do U1 ale dla liczb ujemnych.

(uzupełnień do 2) jest podobny do U1 ale dla liczb ujemnych.

Moduł liczby ujemnej powstaje tak, że do zanegowanych pozycji słowa jest

Moduł liczby ujemnej powstaje tak, że do zanegowanych pozycji słowa jest

arytmetycznie dodawana jedynka i dopiero tak utworzone słowo odpowiada

arytmetycznie dodawana jedynka i dopiero tak utworzone słowo odpowiada

w NKB modułowi tej liczby.

w NKB modułowi tej liczby.

„

„

0” ma pojedynczą reprezentację: 0000...000

0” ma pojedynczą reprezentację: 0000...000

Zapis

Zapis

U2

U2

(uzupełnień do 2) jest podobny do U1 ale dla liczb ujemnych.

(uzupełnień do 2) jest podobny do U1 ale dla liczb ujemnych.

Moduł liczby ujemnej powstaje tak, że do zanegowanych pozycji słowa jest

Moduł liczby ujemnej powstaje tak, że do zanegowanych pozycji słowa jest

arytmetycznie dodawana jedynka i dopiero tak utworzone słowo odpowiada

arytmetycznie dodawana jedynka i dopiero tak utworzone słowo odpowiada

w NKB modułowi tej liczby.

w NKB modułowi tej liczby.

„

„

0” ma pojedynczą reprezentację: 0000...000

0” ma pojedynczą reprezentację: 0000...000

Zapis

Zapis

BIAS

BIAS

(polaryzowany) przedstawia liczby w taki sposób, że „0” jest

(polaryzowany) przedstawia liczby w taki sposób, że „0” jest

reprezentowane przez n-bitowe słowo 1000..000 czyli przez liczbę 2

reprezentowane przez n-bitowe słowo 1000..000 czyli przez liczbę 2

n-1

n-1

kodu

kodu

NKB. Wszystkie inne liczby A są przedstawione na n pozycjach jako binarne

NKB. Wszystkie inne liczby A są przedstawione na n pozycjach jako binarne

wartości liczby 2

wartości liczby 2

n-1

n-1

+A

+A

Zapis

Zapis

BIAS

BIAS

(polaryzowany) przedstawia liczby w taki sposób, że „0” jest

(polaryzowany) przedstawia liczby w taki sposób, że „0” jest

reprezentowane przez n-bitowe słowo 1000..000 czyli przez liczbę 2

reprezentowane przez n-bitowe słowo 1000..000 czyli przez liczbę 2

n-1

n-1

kodu

kodu

NKB. Wszystkie inne liczby A są przedstawione na n pozycjach jako binarne

NKB. Wszystkie inne liczby A są przedstawione na n pozycjach jako binarne

wartości liczby 2

wartości liczby 2

n-1

n-1

+A

+A

Zapis

Zapis

znak-moduł

znak-moduł

tworzy się przez dodanie przed MSB dodatkowego bitu

tworzy się przez dodanie przed MSB dodatkowego bitu

znaku do zapisu NKB: 0 - liczba dodatnia; 1 - liczba ujemna;

znaku do zapisu NKB: 0 - liczba dodatnia; 1 - liczba ujemna;

„

„

0” ma podwójną reprezentację: 1000...000 lub 0000...000

0” ma podwójną reprezentację: 1000...000 lub 0000...000

Zapis

Zapis

znak-moduł

znak-moduł

tworzy się przez dodanie przed MSB dodatkowego bitu

tworzy się przez dodanie przed MSB dodatkowego bitu

znaku do zapisu NKB: 0 - liczba dodatnia; 1 - liczba ujemna;

znaku do zapisu NKB: 0 - liczba dodatnia; 1 - liczba ujemna;

„

„

0” ma podwójną reprezentację: 1000...000 lub 0000...000

0” ma podwójną reprezentację: 1000...000 lub 0000...000

W zapisie

W zapisie

U1

U1

(uzupełnień do 1) MSB jest także bitem znaku : 0 - liczba

(uzupełnień do 1) MSB jest także bitem znaku : 0 - liczba

dodatnia; 1 - liczba ujemna; ale w zależności od jego wartości dalsze bity

dodatnia; 1 - liczba ujemna; ale w zależności od jego wartości dalsze bity

mają różne znaczenie.

mają różne znaczenie.

Dla „0” (l.dodatnia) dalsze bity reprezentują liczbę w NKB.

Dla „0” (l.dodatnia) dalsze bity reprezentują liczbę w NKB.

Dla „1” (l.ujemna) dalsze bity reprezentują moduł liczby ujemnej, w taki

Dla „1” (l.ujemna) dalsze bity reprezentują moduł liczby ujemnej, w taki

sposób, że zanegowane ich wartości odpowiadają modułowi tej liczby w NKB.

sposób, że zanegowane ich wartości odpowiadają modułowi tej liczby w NKB.

„

„

0” ma podwójną reprezentację: 1111...111 lub 0000...000

0” ma podwójną reprezentację: 1111...111 lub 0000...000

W zapisie

W zapisie

U1

U1

(uzupełnień do 1) MSB jest także bitem znaku : 0 - liczba

(uzupełnień do 1) MSB jest także bitem znaku : 0 - liczba

dodatnia; 1 - liczba ujemna; ale w zależności od jego wartości dalsze bity

dodatnia; 1 - liczba ujemna; ale w zależności od jego wartości dalsze bity

mają różne znaczenie.

mają różne znaczenie.

Dla „0” (l.dodatnia) dalsze bity reprezentują liczbę w NKB.

Dla „0” (l.dodatnia) dalsze bity reprezentują liczbę w NKB.

Dla „1” (l.ujemna) dalsze bity reprezentują moduł liczby ujemnej, w taki

Dla „1” (l.ujemna) dalsze bity reprezentują moduł liczby ujemnej, w taki

sposób, że zanegowane ich wartości odpowiadają modułowi tej liczby w NKB.

sposób, że zanegowane ich wartości odpowiadają modułowi tej liczby w NKB.

„

„

0” ma podwójną reprezentację: 1111...111 lub 0000...000

0” ma podwójną reprezentację: 1111...111 lub 0000...000

STAŁOPOZYCYJNA REPREZENTACJA

STAŁOPOZYCYJNA REPREZENTACJA

LICZB

LICZB

Liczba

ZM

U1

U2

BIAS

BCD

-127

11111111

10000000

10000001

00000001 1000100100111

-126

11111110

10000001

10000010

00000010 1000100100110

...

...

...

...

...

...

...

...

...

...

...

...

-2

10000010

11111101

11111110

11111110 1000000000010

-1

10000001

11111110

11111111

11111111 1000000000001

0

10000000

11111111

00000000

10000000 0000000000000

0

00000000

00000000

00000000

10000000 0000000000000

1

00000001

00000001

00000001

10000001 0000000000001

2

00000010

00000010

00000010

10000010 0000000000010

3

00000011

00000011

00000011

10000011 0000000000011

...

...

...

...

...

...

...

...

...

...

...

...

126

01111110

01111110

01111110

11111110 0000100100110

127

011111111 011111111 011111111 11111111 0000100100111

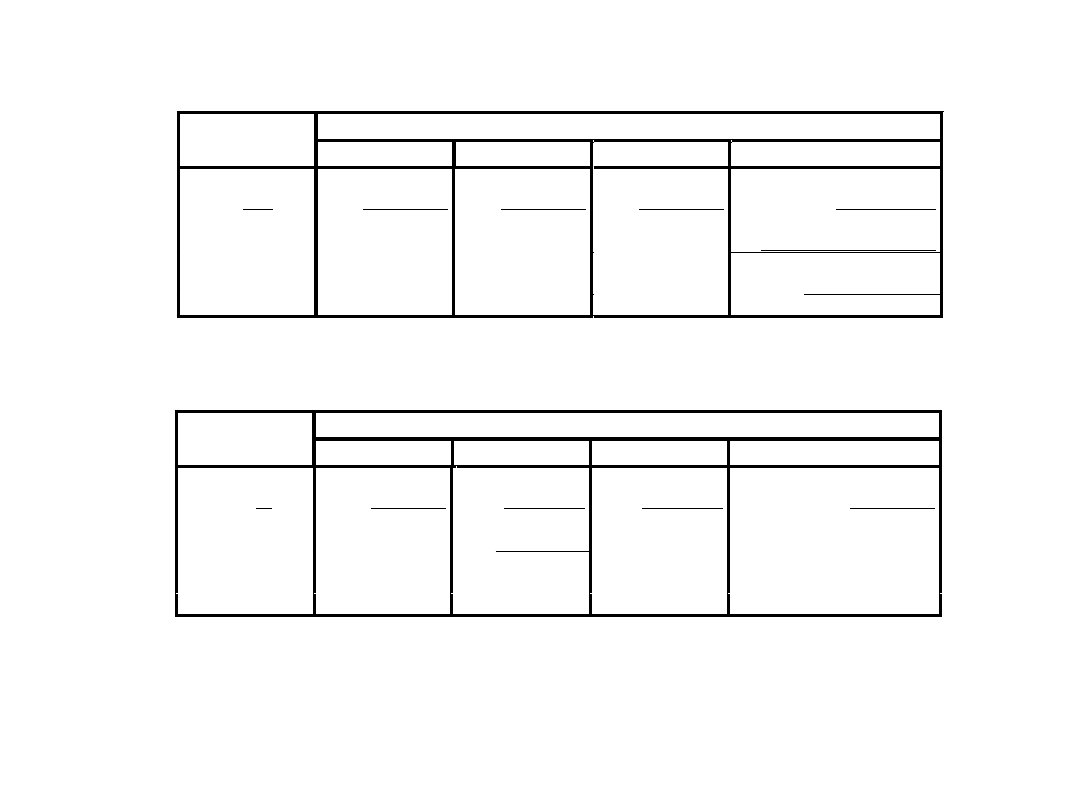
STAŁOPOZYCYJNA REPREZENTACJA

STAŁOPOZYCYJNA REPREZENTACJA

LICZB

LICZB

dodawanie i odejmowanie

dodawanie i odejmowanie

Wartości w zapisach

Wartości

dziesiętne

ZM

U1

U2

BCD

89

+45

0 1011001

0 0101101

0 1011001

0 0101101

0 1011001

0 0101101

0 1000 1001

0 0100 0101

+134

(1) 0 0000110 (1) 0 0000110 (1) 0 0000110

0 1100 1110

Korekcja + 0110 0110

0010 0100

+ (1)

(1) 0011 0100

Wartości w zapisach

Wartości

dziesiętne

ZM

U1

U2

BCD

+9

-7

0 1001

+ 1 0111

0 1001

+ 1 1000

0 1001

+ 1 1001

0 1001

+ 1 0111

+2

0 0010

(1) 0 0001

+ 1

(1) 0 0010

0 0010

0 0010

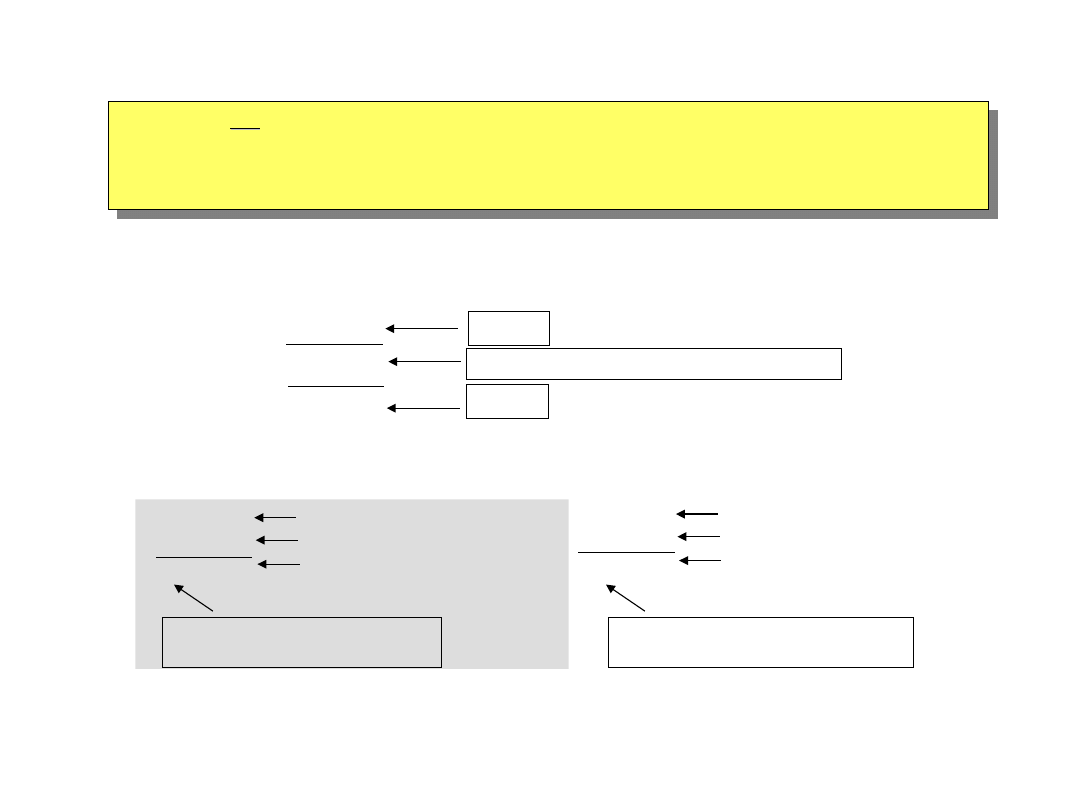
STAŁOPOZYCYJNA REPREZENTACJA

STAŁOPOZYCYJNA REPREZENTACJA

LICZB

LICZB

dodawanie i odejmowanie (kod U2)

dodawanie i odejmowanie (kod U2)

W zapisie

W zapisie

U2

U2

(uzupełnień do 2) liczbę binarną można przedstawić jako:

(uzupełnień do 2) liczbę binarną można przedstawić jako:

a

a

n-1

n-1

...a

...a

0

0

= -a

= -a

n-1

n-1

.

.

2

2

n-1

n-1

+a

+a

n-2

n-2

.

.

2

2

n-2

n-2

+

+

...

...

+a

+a

0

0

.

.

2

2

0

0

Najstarszy bit nie jest tylko bitem znaku ale niesie wraz ze swoją wagą

Najstarszy bit nie jest tylko bitem znaku ale niesie wraz ze swoją wagą

wartość ujemną

wartość ujemną

W zapisie

W zapisie

U2

U2

(uzupełnień do 2) liczbę binarną można przedstawić jako:

(uzupełnień do 2) liczbę binarną można przedstawić jako:

a

a

n-1

n-1

...a

...a

0

0

= -a

= -a

n-1

n-1

.

.

2

2

n-1

n-1

+a

+a

n-2

n-2

.

.

2

2

n-2

n-2

+

+

...

...

+a

+a

0

0

.

.

2

2

0

0

Najstarszy bit nie jest tylko bitem znaku ale niesie wraz ze swoją wagą

Najstarszy bit nie jest tylko bitem znaku ale niesie wraz ze swoją wagą

wartość ujemną

wartość ujemną

1101

1101

U2

U2

= -1

= -1

.

.

2

2

3

3

+1

+1

.

.

2

2

2

2

+0

+0

.

.

2

2

1

1

+1

+1

.

.

2

2

0

0

= -8+4+1

= -8+4+1

= -3

= -3

D

D

0111

0111

U2

U2

= -0

= -0

.

.

2

2

3

3

+1

+1

.

.

2

2

2

2

+1

+1

.

.

2

2

1

1

+1

+1

.

.

2

2

0

0

= 4+2+1

= 4+2+1

= 7

= 7

D

D

Ponieważ: a-b=a+(-b); -a+b=(-a)+b; -a-b=(-a)+(-b) to korzystnie

Ponieważ: a-b=a+(-b); -a+b=(-a)+b; -a-b=(-a)+(-b) to korzystnie

jest stosować liczbę przeciwną (oznaczanej symbolem ~) do danej

jest stosować liczbę przeciwną (oznaczanej symbolem ~) do danej

~0111

~0111

U2

U2

1000

1000

+ 1

+ 1

1001

1001

U2

U2

negacja wszystkich bitów i dodanie 1

negacja wszystkich bitów i dodanie 1

-7

-7

D

D

7

7

D

D

Zakresy liczb w kodzie U2: -2

Zakresy liczb w kodzie U2: -2

n-1

n-1





X

X





2

2

n-1

n-1

-1

-1

np. dla n=5 liczby od -16

np. dla n=5 liczby od -16

D

D

(10000

(10000

U2

U2

) do +15

) do +15

D

D

(01111

(01111

U2

U2

). W

). W

zakresie tym muszą się znaleźć nie tylko argumenty ale i wynik.

zakresie tym muszą się znaleźć nie tylko argumenty ale i wynik.

110111

110111

+111000

+111000

1 101111

1 101111

-9

-9

D

D

=

=

-1

-1

.

.

32+1

32+1

.

.

16+0

16+0

.

.

8+1

8+1

.

.

4+1

4+1

.

.

2+1

2+1

.

.

1

1

-8

-8

D

D

=

=

-1

-1

.

.

32+1

32+1

.

.

16+1

16+1

.

.

8+0

8+0

.

.

4+0

4+0

.

.

2+0

2+0

.

.

1

1

-17

-17

D

D

=

=

-1

-1

.

.

32+0

32+0

.

.

16+1

16+1

.

.

8+1

8+1

.

.

4+1

4+1

.

.

2+1

2+1

.

.

1

1

bit poza zakresem -

bit poza zakresem -

odrzucamy

odrzucamy

10111

10111

+11000

+11000

1 01111

1 01111

-9

-9

D

D

=

=

-1

-1

.

.

16+0

16+0

.

.

8+1

8+1

.

.

4+1

4+1

.

.

2+1

2+1

.

.

1

1

-8

-8

D

D

=

=

-1

-1

.

.

16+1

16+1

.

.

8+0

8+0

.

.

4+0

4+0

.

.

2+0

2+0

.

.

1

1

-17

-17

D

D

=

=

-1

-1

.

.

32+0

32+0

.

.

16+1

16+1

.

.

8+1

8+1

.

.

4+1

4+1

.

.

2+1

2+1

.

.

1

1

bit poza zakresem - nie

bit poza zakresem - nie

odrzucamy

odrzucamy

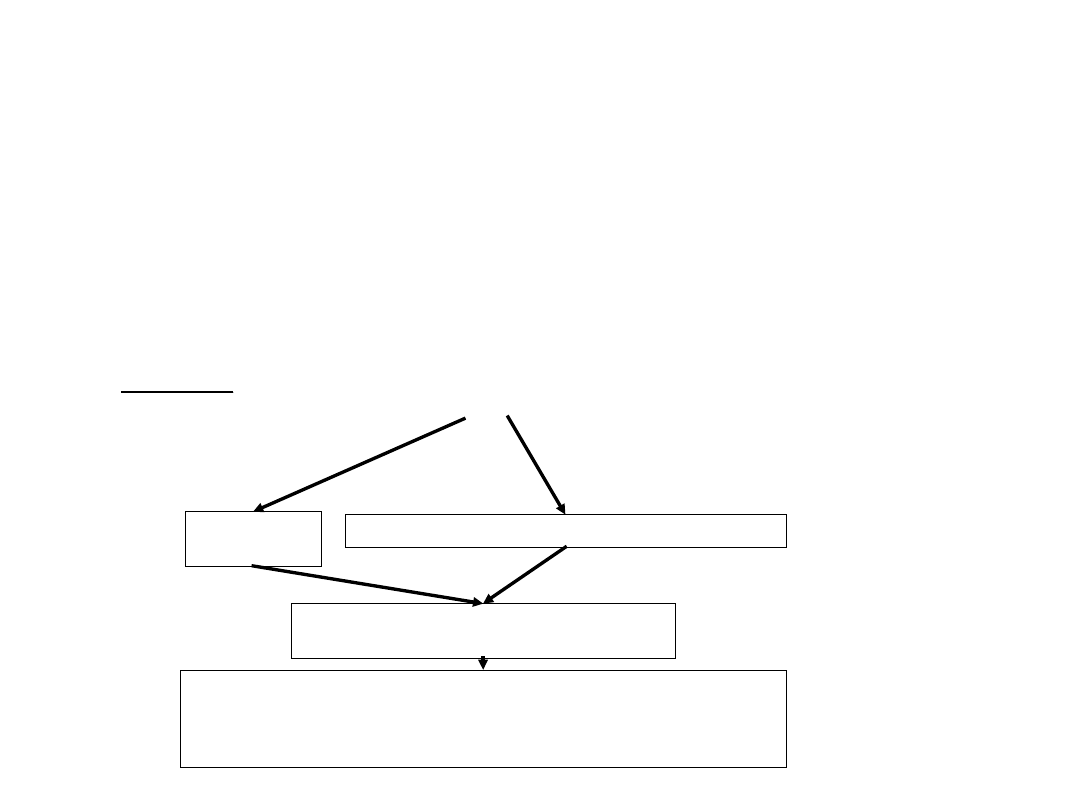
ZMIENNOPOZYCYJNA REPREZENTACJA

ZMIENNOPOZYCYJNA REPREZENTACJA

LICZB

LICZB

Do

reprezentacji

liczb

ułamkowych

stosowany

jest

zapis

Do

reprezentacji

liczb

ułamkowych

stosowany

jest

zapis

zmiennopozycyjny złożony z trzech części:

zmiennopozycyjny złożony z trzech części:

•

jednobitowe pole znaku

jednobitowe pole znaku

•

n-bitowe pole części ułamkowej (mantysy) - S

n-bitowe pole części ułamkowej (mantysy) - S





[0.5, 1.0)

[0.5, 1.0)

tj. dwójkowo 0.1000...0

tj. dwójkowo 0.1000...0





S<0.1111...1

S<0.1111...1

czyli 0.1a

czyli 0.1a

-2

-2

a

a

-3

-3

...a

...a

-(n+2)

-(n+2)

, tj. 1

, tj. 1

.

.

2

2

-1

-1

+a

+a

-2

-2

.

.

2

2

-2

-2

+a

+a

-3

-3

.

.

2

2

-3

-3

+...+a

+...+a

-(n+2)

-(n+2)

.

.

2

2

-(n+2)

-(n+2)

m-bitowe pole części wykładnika (cechy) - E

m-bitowe pole części wykładnika (cechy) - E

A =

A =

±

±

S

S

.

.

B

B

±

±

E

E

B - podstawa (np. 2, 10, 16 itp.)

B - podstawa (np. 2, 10, 16 itp.)

Przykład:

Przykład:

+625,625 =0,625625

+625,625 =0,625625

.

.

10

10

3

3

100111000

100111000

1

1

0,625=0,5+0,125

0,625=0,5+0,125





0,100+0,001 = 0,101

0,100+0,001 = 0,101

1001110001,101

=

1001110001,101

=

0,1001110001101

0,1001110001101

.

.

2

2

10

10

1bit znaku

1bit znaku

mantysa (23 bity)

mantysa (23 bity)

cecha (8 bitów)

cecha (8 bitów)

0 0011 1000 1101 0000 0000 0000

0 0011 1000 1101 0000 0000 0000

10001010

10001010

ELEMENTY ALGEBRY BOOLE’A

ELEMENTY ALGEBRY BOOLE’A

dr inż. Jacek FLOREK

dr inż. Jacek FLOREK

Instytut Informatyki

Instytut Informatyki



Zmienne logiczne i operacje logiczne

Zmienne logiczne i operacje logiczne



Aksjomaty algebry Boole’a i prawa de

Aksjomaty algebry Boole’a i prawa de

Morgana

Morgana



Funkcje logiczne

Funkcje logiczne



Minimalizacja funkcji logicznych

Minimalizacja funkcji logicznych



Realizacja funkcji logicznych

Realizacja funkcji logicznych

3

ZMIENNE LOGICZNE I OPERACJE

ZMIENNE LOGICZNE I OPERACJE

LOGICZNE

LOGICZNE

Algebra Boole’a jest algebrą z trzema operacjami na

Algebra Boole’a jest algebrą z trzema operacjami na

dwuwartościowych

argumentach

(wyniki

też

są

dwuwartościowych

argumentach

(wyniki

też

są

dwuwartościowe)

dwuwartościowe)

•

suma logiczna (alternatywa)

suma logiczna (alternatywa)

•

iloczyn logiczny (koniunkcja)

iloczyn logiczny (koniunkcja)

•

negacja (inwersja)

negacja (inwersja)

działania dwu- lub

działania dwu- lub

więcej argumentowe

więcej argumentowe

działania jedno-argumentowe

działania jedno-argumentowe

Def.1. Jeżeli co najmniej jeden z argumentów jest

Def.1. Jeżeli co najmniej jeden z argumentów jest

równy 1, to wynik sumowania jest równy 1. Suma

równy 1, to wynik sumowania jest równy 1. Suma

jest równa 0 tylko w przypadku, gdy wszystkie

jest równa 0 tylko w przypadku, gdy wszystkie

argumenty są równe 0.

argumenty są równe 0.

Def.1. Jeżeli co najmniej jeden z argumentów jest

Def.1. Jeżeli co najmniej jeden z argumentów jest

równy 1, to wynik sumowania jest równy 1. Suma

równy 1, to wynik sumowania jest równy 1. Suma

jest równa 0 tylko w przypadku, gdy wszystkie

jest równa 0 tylko w przypadku, gdy wszystkie

argumenty są równe 0.

argumenty są równe 0.

Def.2. Wynik iloczynu jest równy 1, wtedy i tylko

Def.2. Wynik iloczynu jest równy 1, wtedy i tylko

wtedy, gdy wszystkie argumenty przyjmują

wtedy, gdy wszystkie argumenty przyjmują

wartość 1.

wartość 1.

Def.2. Wynik iloczynu jest równy 1, wtedy i tylko

Def.2. Wynik iloczynu jest równy 1, wtedy i tylko

wtedy, gdy wszystkie argumenty przyjmują

wtedy, gdy wszystkie argumenty przyjmują

wartość 1.

wartość 1.

Def.3. Negacja polega na zmianie wartości

Def.3. Negacja polega na zmianie wartości

argumentu, tj. jeśli argument ma wartość 1, to

argumentu, tj. jeśli argument ma wartość 1, to

operacja daje w wyniku wartość 0, a jeśli

operacja daje w wyniku wartość 0, a jeśli

argument ma wartość 0, to operacja daje w

argument ma wartość 0, to operacja daje w

wyniku wartość 1.

wyniku wartość 1.

Def.3. Negacja polega na zmianie wartości

Def.3. Negacja polega na zmianie wartości

argumentu, tj. jeśli argument ma wartość 1, to

argumentu, tj. jeśli argument ma wartość 1, to

operacja daje w wyniku wartość 0, a jeśli

operacja daje w wyniku wartość 0, a jeśli

argument ma wartość 0, to operacja daje w

argument ma wartość 0, to operacja daje w

wyniku wartość 1.

wyniku wartość 1.

Def.0. Zmienną logiczną nazywamy zmienną, która

Def.0. Zmienną logiczną nazywamy zmienną, która

może przyjmować jedną z dwóch wartości

może przyjmować jedną z dwóch wartości

logicznych: prawdę lub fałsz („0” lub „1”, „L” lub

logicznych: prawdę lub fałsz („0” lub „1”, „L” lub

„H”).

„H”).

Def.0. Zmienną logiczną nazywamy zmienną, która

Def.0. Zmienną logiczną nazywamy zmienną, która

może przyjmować jedną z dwóch wartości

może przyjmować jedną z dwóch wartości

logicznych: prawdę lub fałsz („0” lub „1”, „L” lub

logicznych: prawdę lub fałsz („0” lub „1”, „L” lub

„H”).

„H”).

AKSJOMATY ALGEBRY BOOLE’A I PRAWA DE MORGANA

AKSJOMATY ALGEBRY BOOLE’A I PRAWA DE MORGANA

1. Przemienność

1. Przemienność

2. Łączność

2. Łączność

3. Rozdzielczość

3. Rozdzielczość

4. Tożsamość

4. Tożsamość

5. Komplementarność

5. Komplementarność

A

B

B

A

A

B

B

A













C)

(B

A

C

B)

(A

C)

(B

A

C

B)

(A





















BC

A

C)

B)(A

(A

C

A

B

A

C)

A(B



















A

A

A

A

A

A

1

1

A

A

1

A

A

0

A

0

0

A

























1

A

A

0

A

A









B

A

B

A

B

A

B

A













Prawa de Morgana

Prawa de Morgana

OPERACJE LOGICZNE

OPERACJE LOGICZNE

A

B

A

B A

+

B A B

0

0 0

0

1

1

1

0 0

1

0

1

0

1 0

1

1

0

1

1 1

1

0

0

)

x

(x

x

x

x

x

x

x

f

x

x

x

x

f

x

x

x

x

x

f

x

x

f

x

x

x

x

x

f

x

x

f

)

x

(x

x

x

f

0

f

1

0

1

0

1

0

1

0

7

1

0

1

0

6

1

0

1

0

1

5

1

0

4

0

1

0

1

0

3

1

0

2

1

0

1

0

1

0































































1

f

x

x

x

x

x

x

x

x

f

x

x

x

x

x

x

f

x

x

x

x

x

f

x

x

x

x

x

x

x

x

f

x

x

x

x

x

f

x

x

x

x

f

x

x

f

15

1

0

1

0

1

0

1

0

14

1

0

1

0

1

0

13

0

1

0

1

0

12

1

0

1

0

1

0

1

0

11

1

1

0

1

0

10

1

0

1

0

9

1

0

8















































































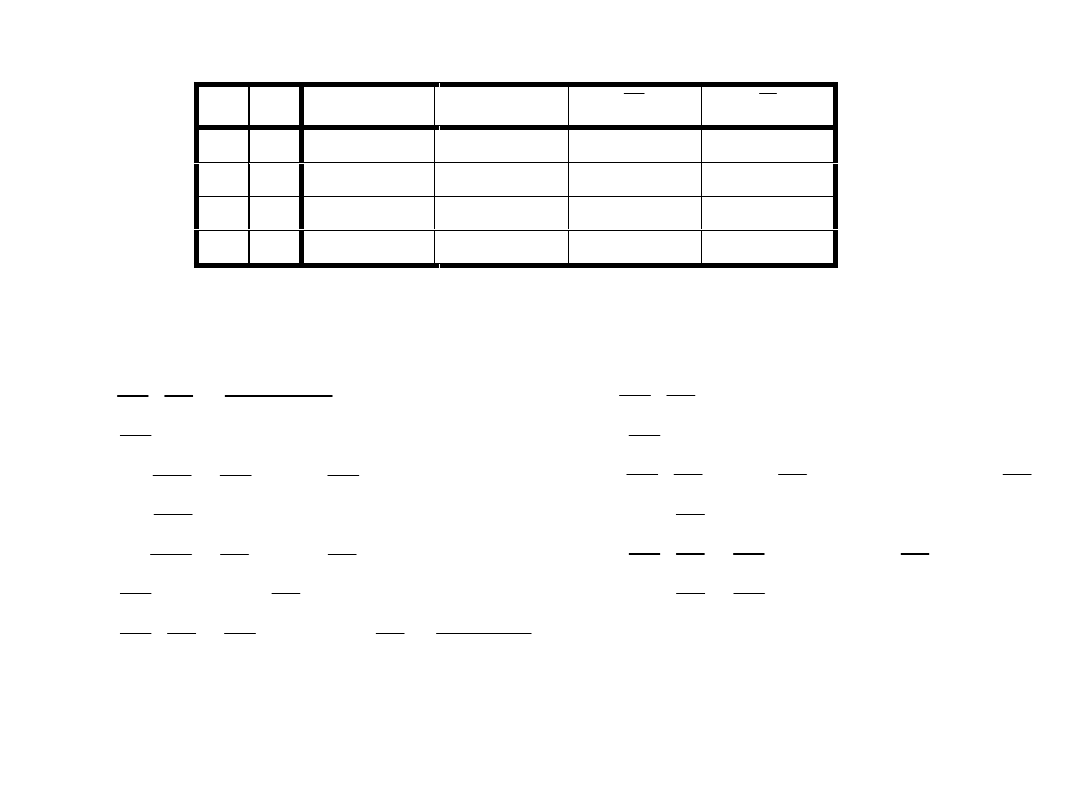
FUNKCJE BOOLE’OWSKIE

FUNKCJE BOOLE’OWSKIE

Istnieją cztery sposoby przedstawienia tych funkcji:

Istnieją cztery sposoby przedstawienia tych funkcji:

•

tablica prawdy

tablica prawdy

•

postać kanoniczna funkcji

postać kanoniczna funkcji

•

dziesiętny zapis funkcji

dziesiętny zapis funkcji

•

mapa Karnaugha

mapa Karnaugha

)

x

x

)(x

x

x

x

)(

x

x

(x

y

lub

x

x

x

x

x

x

x

x

x

x

x

x

y

2

1

0

2

1

0

2

1

0

2

1

0

2

1

0

2

1

0

2

1

0







































0,4,3

y

lub

1,2,5,6,7

y

X

0

X

1

X

2

f

0

0

0

0

0

1

1

0

0

1

2

0

1

0

1

3

1

1

0

0

4

0

0

1

0

5

1

0

1

1

6

0

1

1

1

7

1

1

1

1





-

wskazanie

na

postać

alternatywną

-

wskazanie

na

postać

koniunkcyjną

1.

1.

2.

2.

3.

3.

4.

4.

X

2

X

0

X

1

0

1

0

0

0

0

0

1

1

1

1

1

0

1

1

0

1

1

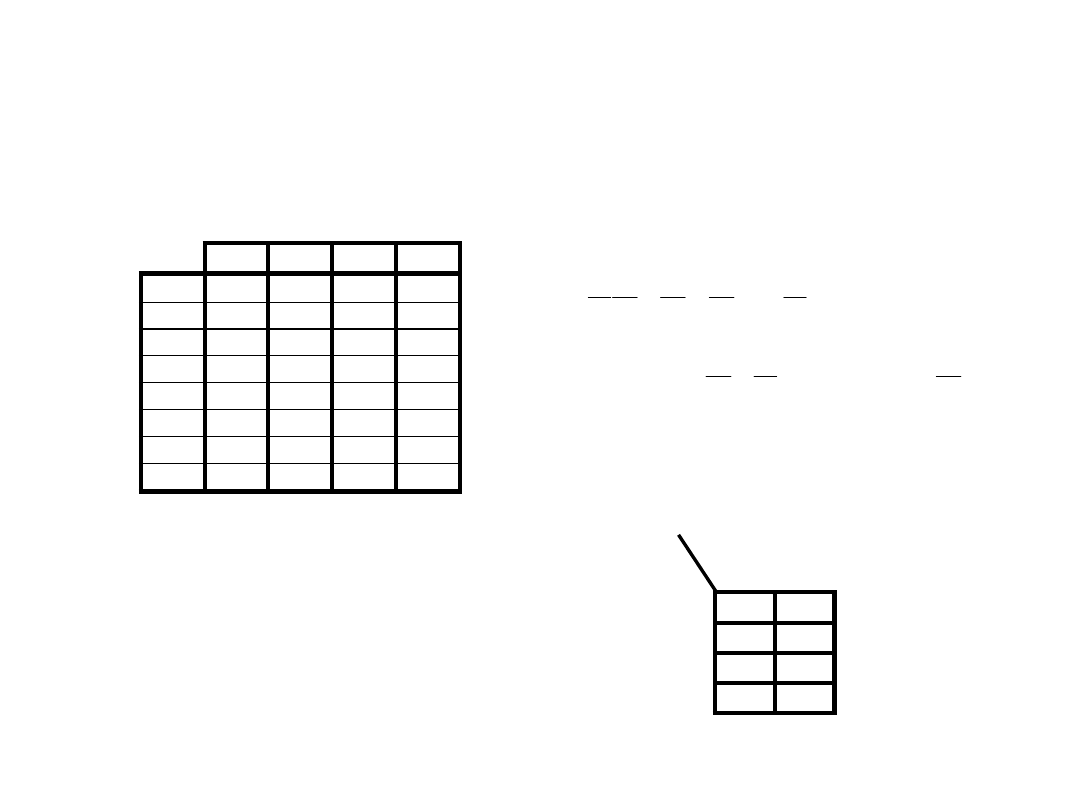
MINIMALIZACJA FUNKCJI LOGICZNYCH

MINIMALIZACJA FUNKCJI LOGICZNYCH

Minimalizację funkcji można przeprowadzić:

Minimalizację funkcji można przeprowadzić:

•

przekształcając postać kanoniczna funkcji

przekształcając postać kanoniczna funkcji

•

wykorzystując mapy Karnaugha

wykorzystując mapy Karnaugha

•

metodą Quine’a

metodą Quine’a

•

metodą Quine’a-McCluskeya

metodą Quine’a-McCluskeya

•

metodą tablic harwardzkich

metodą tablic harwardzkich

•

metodą Patricka

metodą Patricka

•

metodą Blake’a

metodą Blake’a

Przykład: Zminimalizować funkcję f(A,B,C,D)=

Przykład: Zminimalizować funkcję f(A,B,C,D)=





(5,7,13,15)

(5,7,13,15)

A

B

C

D

f

0

0

0

0

0

0

1

0

0

0

1

0

2

0

0

1

0

0

3

0

0

1

1

0

4

0

1

0

0

0

5

0

1

0

1

1

6

0

1

1

0

0

7

0

1

1

1

1

8

1

0

0

0

0

9

1

0

0

1

0

10

1

0

1

0

0

11

1

0

1

1

0

12

1

1

0

0

0

13

1

1

0

1

1

14

1

1

1

0

0

15

1

1

1

1

1

00 01 11 10

00

0

0

0

0

01

0

1

1

0

11

0

1

1

0

10

0

0

0

0

AB

AB

CD

CD

f(A,B,C,D)=BD

f(A,B,C,D)=BD

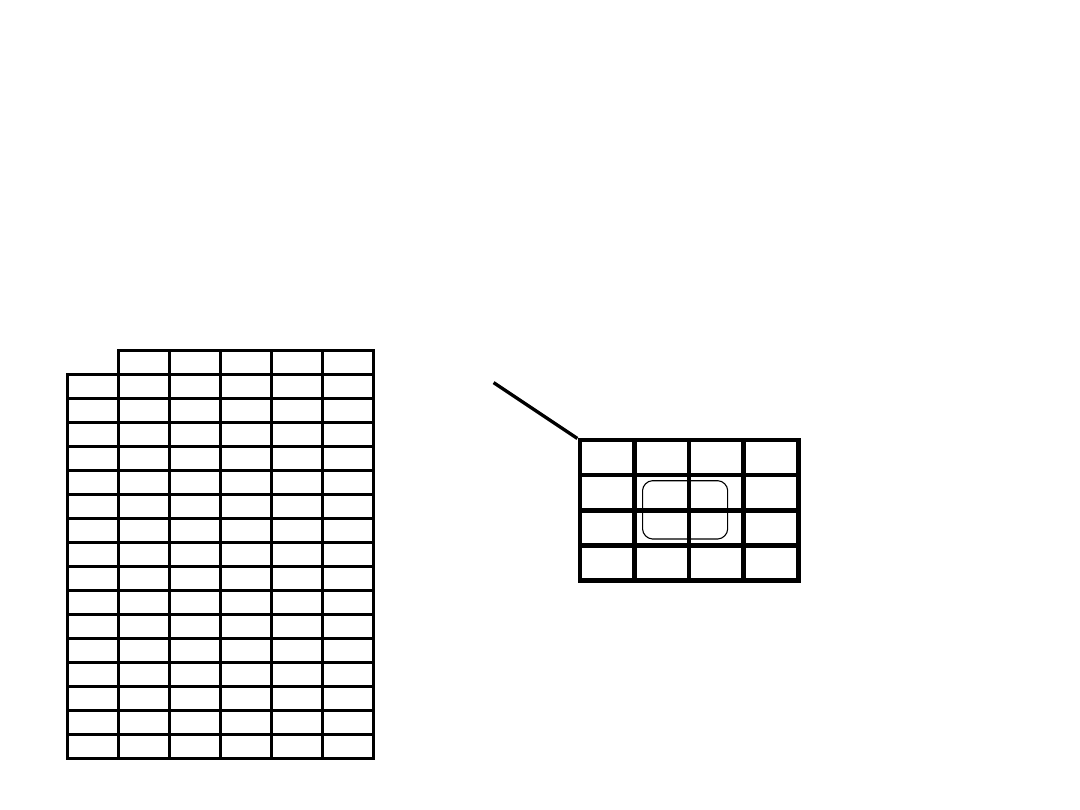
MINIMALIZACJA FUNKCJI LOGICZNYCH

MINIMALIZACJA FUNKCJI LOGICZNYCH

Przykład: Zminimalizować funkcję f(A,B,C,D)=

Przykład: Zminimalizować funkcję f(A,B,C,D)=





(5,7,13,15)

(5,7,13,15)

A

B

C

D

f

0

0

0

0

0

0

1

0

0

0

1

0

2

0

0

1

0

0

3

0

0

1

1

0

4

0

1

0

0

0

5

0

1

0

1

1

6

0

1

1

0

0

7

0

1

1

1

1

8

1

0

0

0

0

9

1

0

0

1

0

10

1

0

1

0

0

11

1

0

1

1

0

12

1

1

0

0

0

13

1

1

0

1

1

14

1

1

1

0

0

15

1

1

1

1

1

00 01 11 10

00

0

0

0

0

01

0

1

1

0

11

0

1

1

0

10

0

0

0

0

AB

AB

CD

CD







DB

B)

D)(B

(D

B

)

A

B(A

D

)

C

D(C

B)

B

A

D)(AB

D

C

(CD

BB)

B

A

AB

A

DD)(A

D

C

CD

C

(C

B)

A

B)(

D)(A

C

D)(

(C

D)

C,

B,

f(A,





























































lub

lub

00 01 11 10

00

0

0

0

0

01

0

1

1

0

11

0

1

1

0

10

0

0

0

0

AB

AB

CD

CD

DB

D)

C,

B,

f(A,



00 01 11 10

00

0

0

1

1

01

0

1

0

1

11

0

1

1

0

10

0

0

0

0

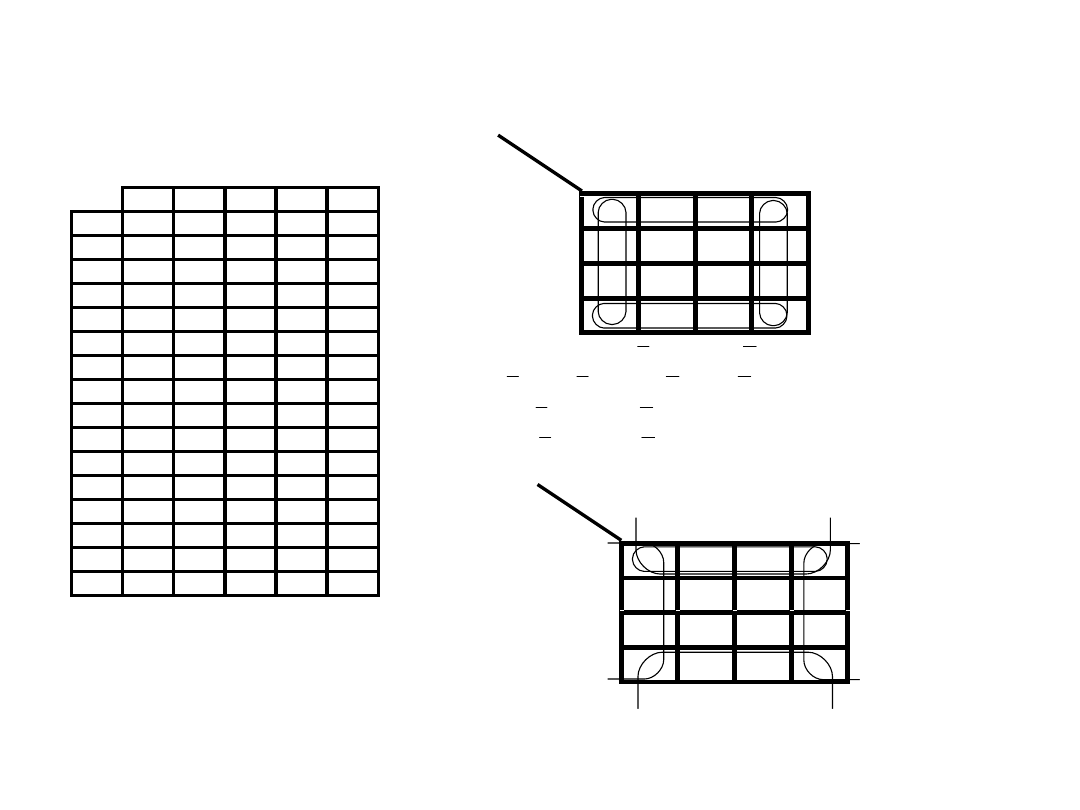
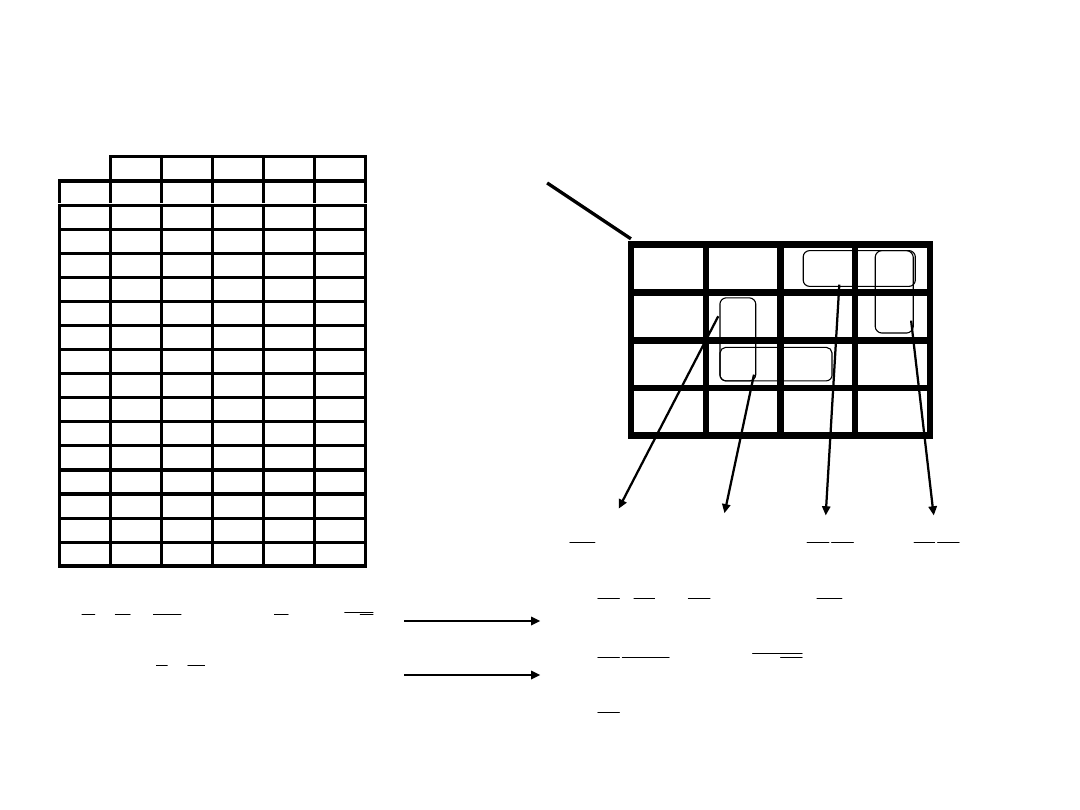
Przykład:

Zminimalizować

funkcję

Przykład:

Zminimalizować

funkcję

f(A,B,C,D)=

f(A,B,C,D)=





(5,7,8,9,12,15)

(5,7,8,9,12,15)

AB

AB

CD

CD

f(A,B,C,D)

f(A,B,C,D)

=

=

A

B

C

D

f

0

0

0

0

0

0

1

0

0

0

1

0

2

0

0

1

0

0

3

0

0

1

1

0

4

0

1

0

0

0

5

0

1

0

1

1

6

0

1

1

0

0

7

0

1

1

1

1

8

1

0

0

0

1

9

1

0

0

1

1

10

1

0

1

0

0

11

1

0

1

1

0

12

1

1

0

0

1

13

1

1

0

1

0

14

1

1

1

0

0

15

1

1

1

1

1

ABD+BCD+ACD+ABC =
AC(B D) BD(A C)
ACBD BDAC
AC BD















B D BD

i

A C AC

 

 

XY XY X Y



 

MINIMALIZACJA FUNKCJI LOGICZNYCH

MINIMALIZACJA FUNKCJI LOGICZNYCH

REALIZACJA FUNKCJI BOOLE’OWSKICH

REALIZACJA FUNKCJI BOOLE’OWSKICH

X

0

X

1

X

2

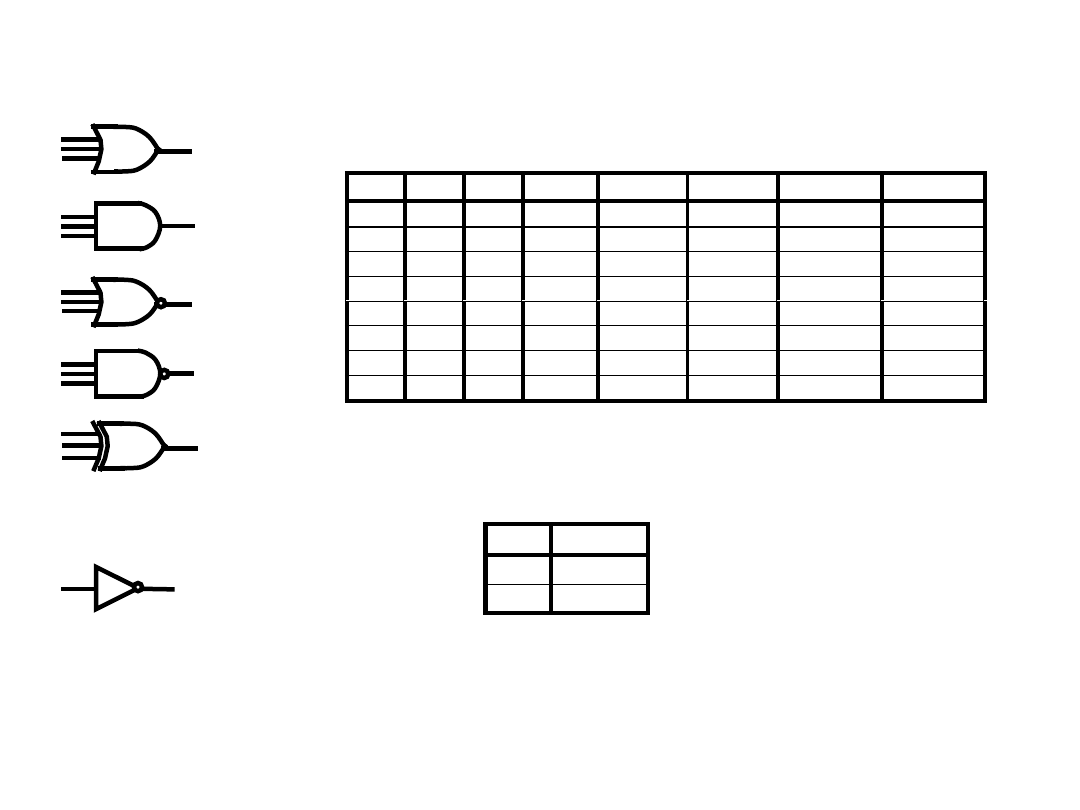
f(OR) f(AND) f(NOR) f(NAND) f(EXOR)

0

0

0

0

0

1

1

0

0

0

1

1

0

0

1

1

0

1

0

1

0

0

1

1

0

1

1

1

0

0

1

1

1

0

0

1

0

0

1

1

1

0

1

1

0

0

1

1

1

1

0

1

0

0

1

1

1

1

1

1

1

0

0

0

OR

OR

AND

AND

NOR

NOR

NAND

NAND

EXOR

EXOR

NOT

NOT

X

1

f(NOT)

0

1

1

0

PROJEKTOWANIE UKŁADÓW LOGICZNYCH

PROJEKTOWANIE UKŁADÓW LOGICZNYCH

dr inż. Jacek FLOREK

dr inż. Jacek FLOREK

Instytut Informatyki

Instytut Informatyki



Podział układów logicznych

Podział układów logicznych



Realizacja funkcji logicznych układów

Realizacja funkcji logicznych układów

kombinacyjnych

kombinacyjnych



Realizacja układu sekwencyjnego

Realizacja układu sekwencyjnego

4

PODZIAŁ UKŁADÓW LOGICZNYCH

PODZIAŁ UKŁADÓW LOGICZNYCH

Układy logiczne można podzielić (w zależności od przyjętego

Układy logiczne można podzielić (w zależności od przyjętego

kryterium) na:

kryterium) na:

Def.1. Układem kombinacyjnym nazywamy taki układ

Def.1. Układem kombinacyjnym nazywamy taki układ

cyfrowy, w którym stan wejść jednoznacznie

cyfrowy, w którym stan wejść jednoznacznie

określa stan wyjść układu.

określa stan wyjść układu.

Def.1. Układem kombinacyjnym nazywamy taki układ

Def.1. Układem kombinacyjnym nazywamy taki układ

cyfrowy, w którym stan wejść jednoznacznie

cyfrowy, w którym stan wejść jednoznacznie

określa stan wyjść układu.

określa stan wyjść układu.

Def.2. Układem sekwencyjnym nazywamy taki układ

Def.2. Układem sekwencyjnym nazywamy taki układ

cyfrowy, w którym stan wyjść zależy od stanu

cyfrowy, w którym stan wyjść zależy od stanu

wejść oraz od poprzednich stanów układu.

wejść oraz od poprzednich stanów układu.

Def.2. Układem sekwencyjnym nazywamy taki układ

Def.2. Układem sekwencyjnym nazywamy taki układ

cyfrowy, w którym stan wyjść zależy od stanu

cyfrowy, w którym stan wyjść zależy od stanu

wejść oraz od poprzednich stanów układu.

wejść oraz od poprzednich stanów układu.

•

układy kombinacyjne

układy kombinacyjne

•

układy sekwencyjne

układy sekwencyjne

•

układy asynchroniczne

układy asynchroniczne

•

układy synchroniczne

układy synchroniczne

Def.3. Układem asynchronicznym nazywamy taki

Def.3. Układem asynchronicznym nazywamy taki

układ cyfrowy, dla którego w dowolnym

układ cyfrowy, dla którego w dowolnym

momencie jego działania stan wejść

momencie jego działania stan wejść

oddziaływuje na stan wyjść.

oddziaływuje na stan wyjść.

Def.3. Układem asynchronicznym nazywamy taki

Def.3. Układem asynchronicznym nazywamy taki

układ cyfrowy, dla którego w dowolnym

układ cyfrowy, dla którego w dowolnym

momencie jego działania stan wejść

momencie jego działania stan wejść

oddziaływuje na stan wyjść.

oddziaływuje na stan wyjść.

Def.4. Układem synchronicznym nazywamy taki układ

Def.4. Układem synchronicznym nazywamy taki układ

cyfrowy, dla którego stan wejść wpływa na stan

cyfrowy, dla którego stan wejść wpływa na stan

wyjść w pewnych określonych odcinkach czasu

wyjść w pewnych określonych odcinkach czasu

zwanych

zwanych

czasem czynnym

czasem czynnym

, natomiast w

, natomiast w

pozostałych odcinkach czasu zwanych

pozostałych odcinkach czasu zwanych

czasem

czasem

martwym

martwym

stan wejść nie wpływa na stan wyjść.

stan wejść nie wpływa na stan wyjść.

Def.4. Układem synchronicznym nazywamy taki układ

Def.4. Układem synchronicznym nazywamy taki układ

cyfrowy, dla którego stan wejść wpływa na stan

cyfrowy, dla którego stan wejść wpływa na stan

wyjść w pewnych określonych odcinkach czasu

wyjść w pewnych określonych odcinkach czasu

zwanych

zwanych

czasem czynnym

czasem czynnym

, natomiast w

, natomiast w

pozostałych odcinkach czasu zwanych

pozostałych odcinkach czasu zwanych

czasem

czasem

martwym

martwym

stan wejść nie wpływa na stan wyjść.

stan wejść nie wpływa na stan wyjść.

PODZIAŁ UKŁADÓW LOGICZNYCH

PODZIAŁ UKŁADÓW LOGICZNYCH

układy kombinacyjne:

układy kombinacyjne:

–

sumatory

sumatory

–

komparatory

komparatory

–

dekodery, kodery, transkodery

dekodery, kodery, transkodery

–

multipleksery, demultipleksery

multipleksery, demultipleksery

–

.....

.....

•

układy matrycowe

układy matrycowe

•

........

........

•

układy zbudowane z bramek

układy zbudowane z bramek

•

bloki kombinacyjne

bloki kombinacyjne

układy sekwencyjne:

układy sekwencyjne:

•

przerzutniki

przerzutniki

•

rejestry

rejestry

•

liczniki

liczniki

•

.....

.....

A={X,Y,

A={X,Y,





: X

: X





Y}

Y}

X-

zbiór

stanów

sygnałów

X-

zbiór

stanów

sygnałów

wejściowego

wejściowego

Y - zbiór stanów sygnałów

Y - zbiór stanów sygnałów

wyjściowego

wyjściowego





- funkcja opisująca działanie

- funkcja opisująca działanie

układu

układu

A={X, Y, S,

A={X, Y, S,





: X

: Xx

S

S





S,

S,





:

:

X

Xx

S

S





Y}

Y}

X-

zbiór

stanów

sygnałów

X-

zbiór

stanów

sygnałów

wejściowego

wejściowego

Y

-

zbiór

stanów

sygnałów

Y

-

zbiór

stanów

sygnałów

wyjściowego

wyjściowego

S - zbiór stanów wewnętrznych

S - zbiór stanów wewnętrznych





- funkcja przejść (określa zmiany

- funkcja przejść (określa zmiany

stanów

układu

wszystkich

stanów

układu

wszystkich

wzbudzeń)

wzbudzeń)





-

funkcja

wyjść

-

funkcja

wyjść

(przyporządkowuje

sygnały

(przyporządkowuje

sygnały

wyjściowe

stanom

układu

i

wyjściowe

stanom

układu

i

wzbudzeniom)

wzbudzeniom)

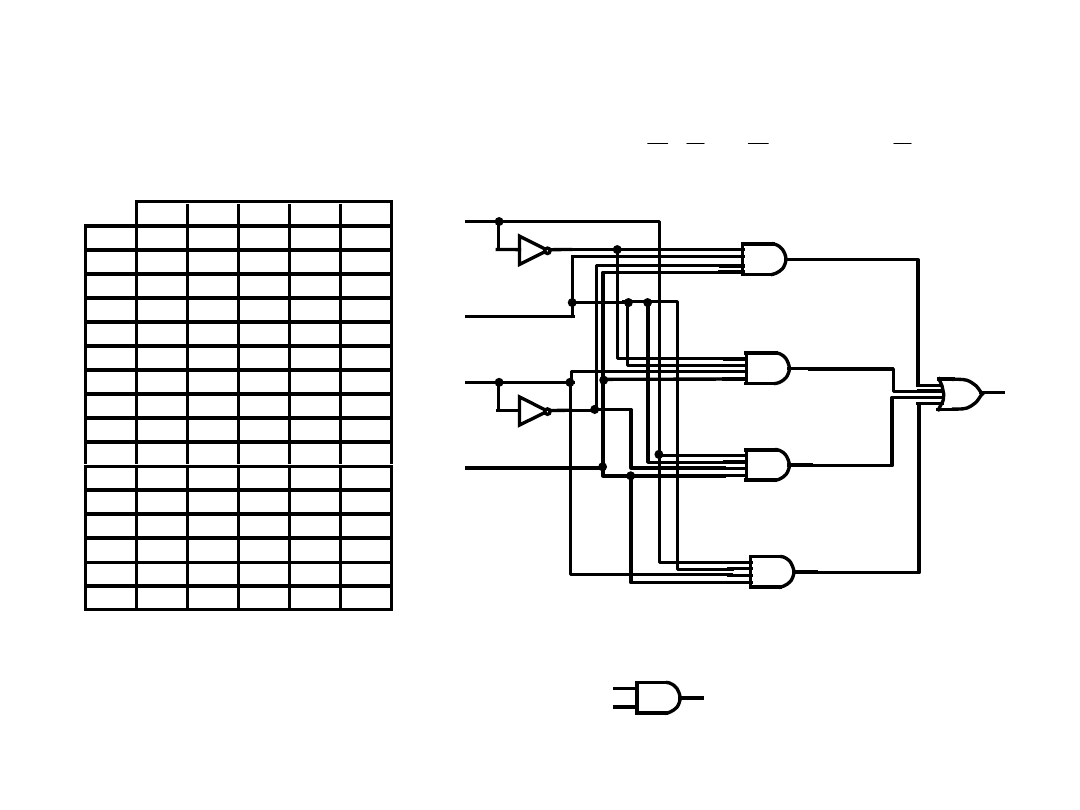
REALIZACJA FUNKCJI LOGICZNYCH

REALIZACJA FUNKCJI LOGICZNYCH

Przykład:

Zaprojektować

układ

realizujący

funkcję

Przykład:

Zaprojektować

układ

realizujący

funkcję

f(A,B,C,D)=

f(A,B,C,D)=





(5,7,13,15)

(5,7,13,15)

A

B

C

D

f

0

0

0

0

0

0

1

0

0

0

1

0

2

0

0

1

0

0

3

0

0

1

1

0

4

0

1

0

0

0

5

0

1

0

1

1

6

0

1

1

0

0

7

0

1

1

1

1

8

1

0

0

0

0

9

1

0

0

1

0

10

1

0

1

0

0

11

1

0

1

1

0

12

1

1

0

0

0

13

1

1

0

1

1

14

1

1

1

0

0

15

1

1

1

1

1

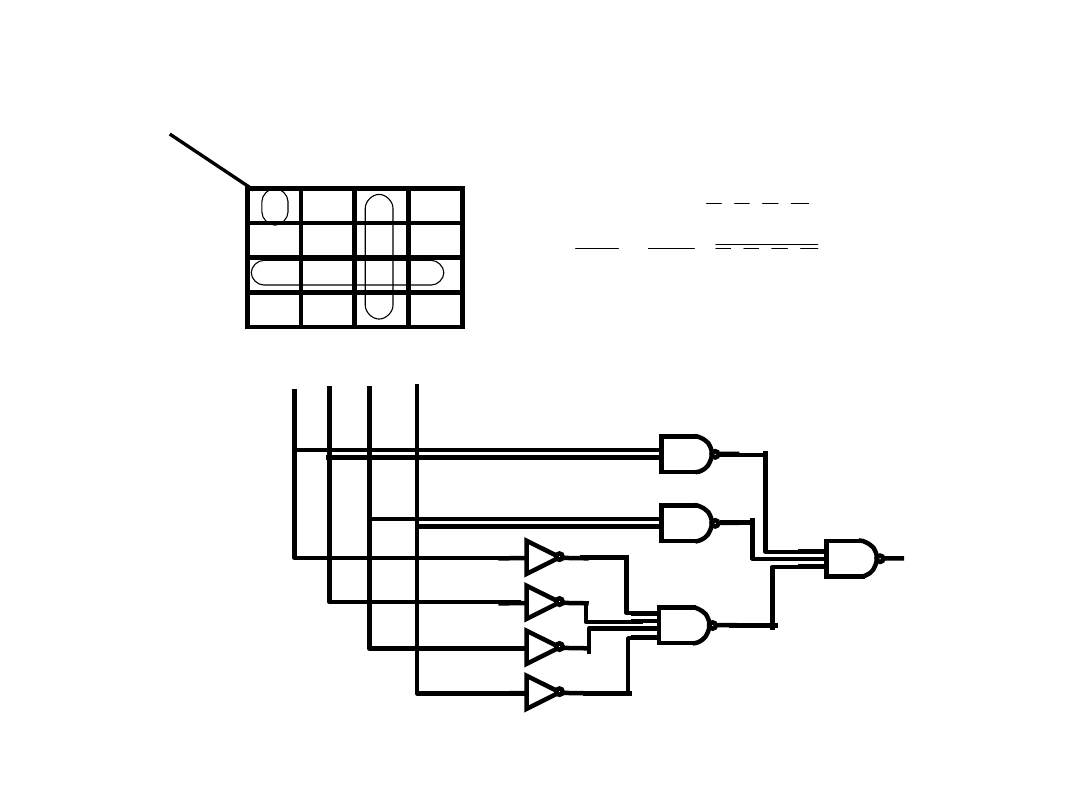
f(A,B,C,D)=(5,7,13,15)=

ABCD+ABCD+ABCD+ABCD

A

B

C

D

lub

na

podstawie

tablic

Karnaugha

B

D

REALIZACJA FUNKCJI LOGICZNYCH

REALIZACJA FUNKCJI LOGICZNYCH

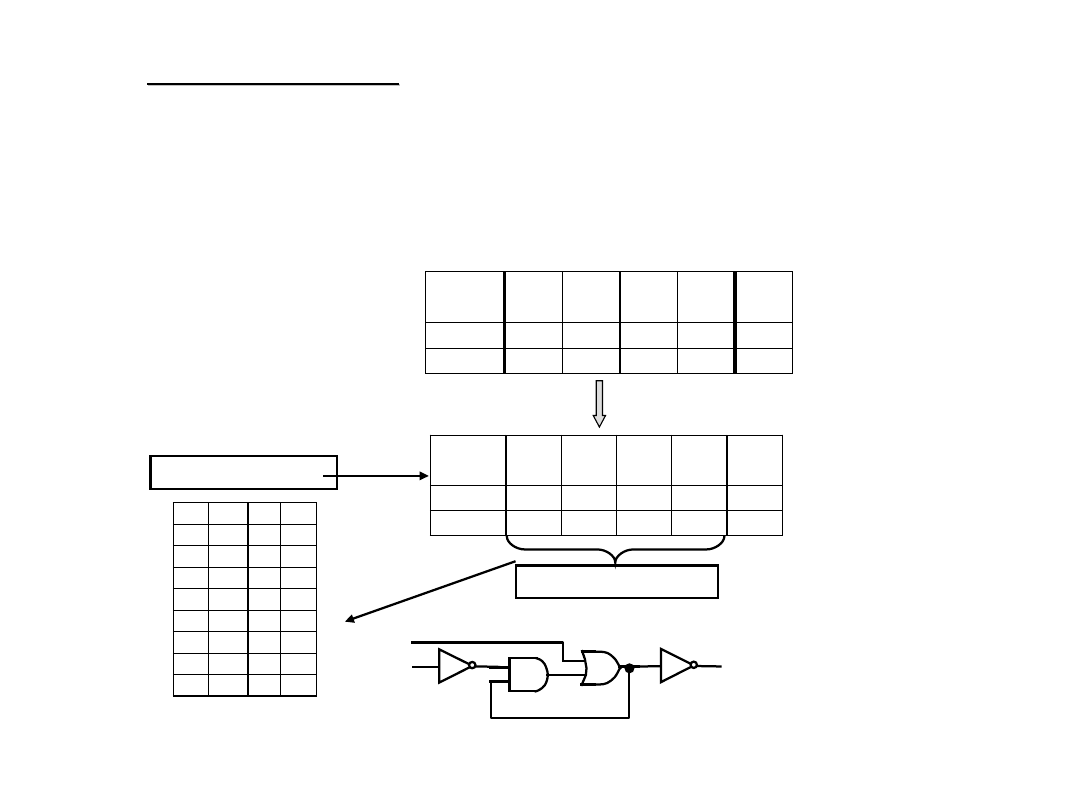
Przykład: Zaprojektować układ realizujący funkcję

Przykład: Zaprojektować układ realizujący funkcję

00 01 11 10

00

1

0

1

0

01

0

0

1

0

11

1

1

1

1

10

0

0

1

0

AB

AB

CD

CD

D

C

B

A

D

C

B

A

D

C

B

A

D

C

B

A

Y



































)

(

)

(

A B C D

A B C D

REALIZACJA UKŁADU SEKWENCYJNEGO

REALIZACJA UKŁADU SEKWENCYJNEGO

Założenia (przykład):

Założenia (przykład):

układ dwustanowy S={S

układ dwustanowy S={S

1

1

=0, S

=0, S

2

2

=1}

=1}

o czterech pobudzeniach X={X

o czterech pobudzeniach X={X

1

1

=00, X

=00, X

2

2

=01, X

=01, X

3

3

=10, X

=10, X

4

4

=11}

=11}

i dwóch stanach sygnałów wyjściowych Y={Y

i dwóch stanach sygnałów wyjściowych Y={Y

1

1

=1,Y

=1,Y

2

2

=0}

=0}

oraz funkcjach

oraz funkcjach





: X

: X

1

1

x S

x S

1

1

= S

= S

1

1





: S

: S

1

1

= Y

= Y

2

2

X

X

2

2

x

x

S

S

1

1

= S

= S

1

1

S

S

2

2

= Y

= Y

1

1

X

X

3

3

x S

x S

1

1

= S

= S

2

2

X

X

4

4

x

x

S

S

1

1

= S

= S

2

2

X

X

1

1

x S

x S

2

2

= S

= S

2

2

X

X

2

2

x

x

S

S

2

2

= S

= S

1

1

X

X

3

3

x S

x S

2

2

= S

= S

2

2

X

X

4

4

x

x

S

S

2

2

= S

= S

2

2

X

i

X

1

X

2

X

3

X

4

Y

i

S

i

S

1

S

1

S

1

S

2

S

2

Y

2

S

2

S

2

S

1

S

2

S

2

Y

1

x

1

x

2

00

01

11

10

Y

i

S

i

0

0

0

1

1

1

1

1

0

1

1

0

zakodowana

zakodowana

tabela przejść i wyjść

tabela przejść i wyjść

stany pierwotne

stany pierwotne

stany następne S

stany następne S

t

t

x

1

x

2

S

S

t

0

0

0

0

1

0

0

1

0

1

0

0

1

1

0

1

0

0

1

1

1

0

1

1

0

1

1

0

1

1

1

1

x

2

x

1

S

y

PODSTAWY DZIAŁANIA UKŁADÓW CYFROWYCH

PODSTAWY DZIAŁANIA UKŁADÓW CYFROWYCH

dr inż. Jacek FLOREK

dr inż. Jacek FLOREK

Instytut Informatyki

Instytut Informatyki



Cyfrowe układy arytmetyczne

Cyfrowe układy arytmetyczne



Przerzutniki

Przerzutniki



Rejestry

Rejestry



Liczniki

Liczniki



Dzielniki

Dzielniki



Bramki trójstanowe

Bramki trójstanowe



Multipleksery i demultipleksery

Multipleksery i demultipleksery



Magistrale danych

Magistrale danych

5-6

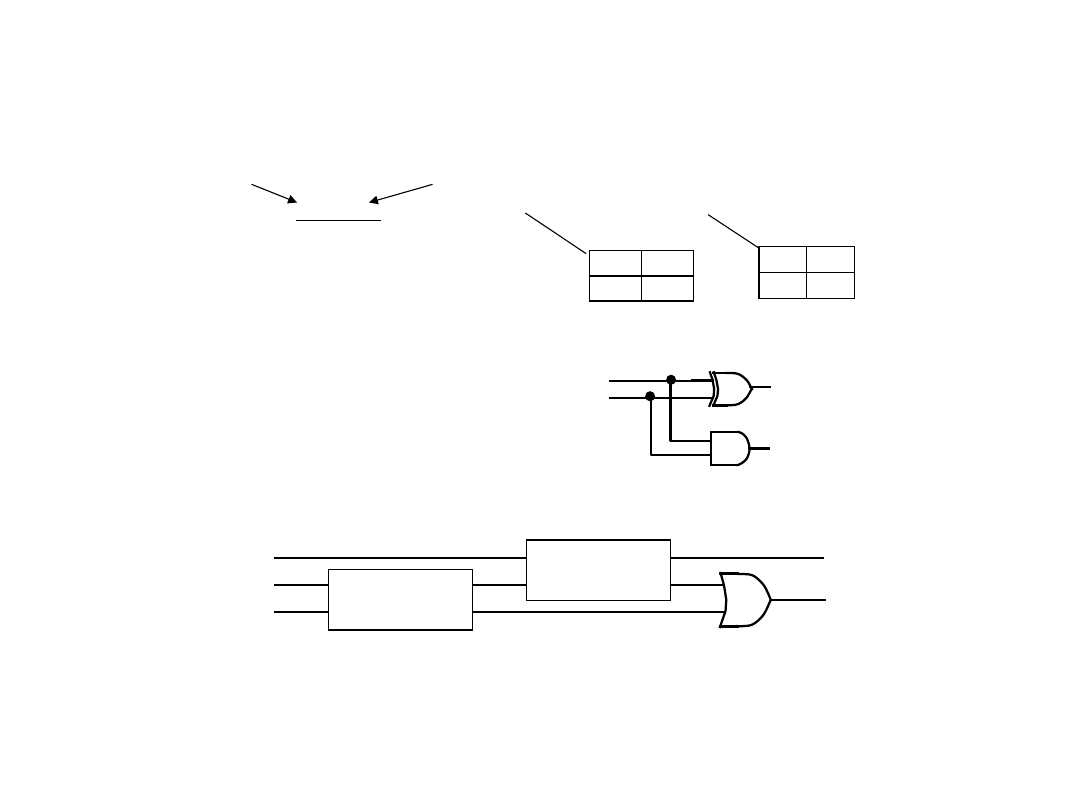
Przykład projektowania układu kombinacyjnego

Przykład projektowania układu kombinacyjnego

(jednobitowy półsumator)

(jednobitowy półsumator)

Dodawanie binarne dwóch bitów

Dodawanie binarne dwóch bitów

C

Y

0+0= 0

0

0+1= 0

1

1+0= 0

1

1+1= 1

0

przeniesienie

przeniesienie

wynik sumowania

wynik sumowania

0

1

0

0

1

1

1

0

0

1

0

0

0

1

0

1

a

a

b

b

a

a

b

b

C=ab

C=ab

b

a

Y





C

C

Y

Y

a

a

b

b

półsumator

półsumator

sumator

sumator

półsumator

półsumator

półsumator

półsumator

a

a

i

i

a

a

a

a

b

b

b

b

y

y

y

y

c

c

c

c

b

b

i

i

y

y

i

i

c

c

i

i

C

C

i+1

i+1

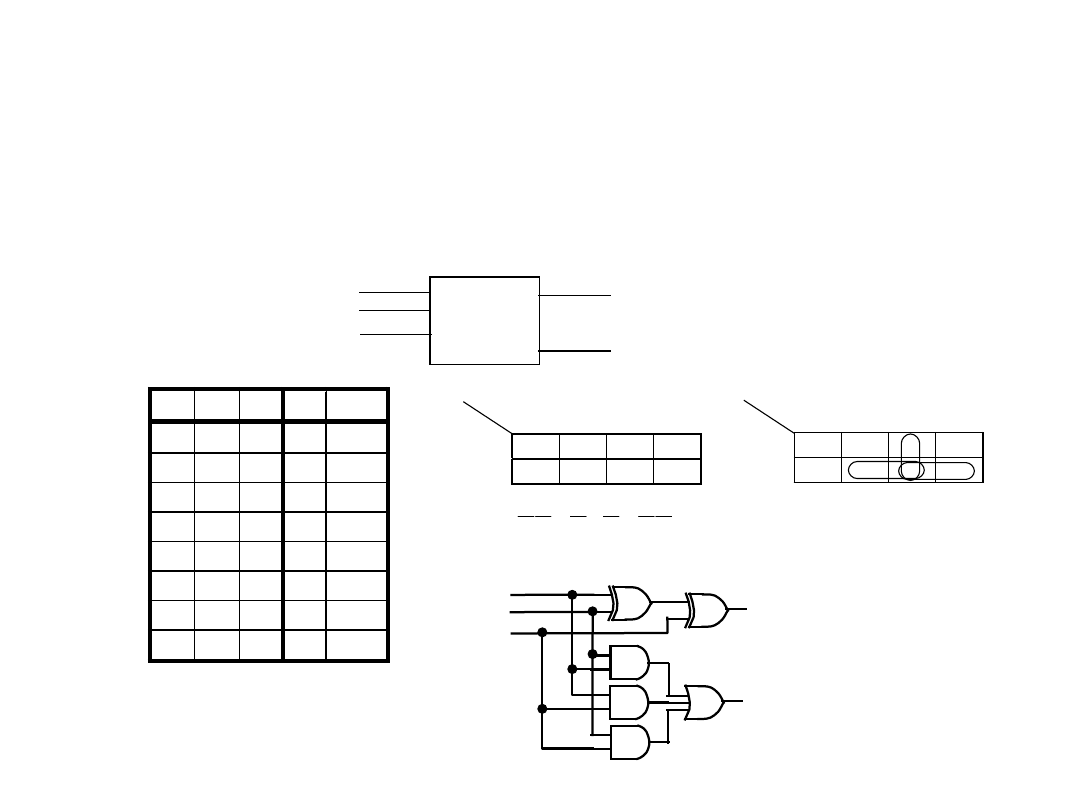
Przykład projektowania układu kombinacyjnego

Przykład projektowania układu kombinacyjnego

(jednobitowy sumator)

(jednobitowy sumator)

1. Dane są dwie liczby w kodzie NKB:

1. Dane są dwie liczby w kodzie NKB:













i

i

i

i

i

i

b

B

a

A

2

2

2. Jak znaleźć sumę?

2. Jak znaleźć sumę?

Dodawać poszczególne pozycje (począwszy od pozycji najmniej

Dodawać poszczególne pozycje (począwszy od pozycji najmniej

znaczących) uwzględniając przeniesienie. Czyli obliczyć dwie

znaczących) uwzględniając przeniesienie. Czyli obliczyć dwie

funkcje: y

funkcje: y

i

i

- binarny wynik dodawania oraz c

- binarny wynik dodawania oraz c

i+1

i+1

- wartość

- wartość

przeniesienia

przeniesienia

3. Tabela prawdy

3. Tabela prawdy

a

i

b

i

c

i

y

i

c

i+1

0

0

0 0

0

1

0

0 1

0

0

1

0 1

0

1

1

0 0

1

0

0

1 1

0

1

0

1 0

1

0

1

1 0

1

1

1

1 1

1





c

c

i+1

i+1

y

y

i

i

c

c

i

i

a

a

i

i

b

b

i

i

4. Mapy Karaugha

4. Mapy Karaugha

00 01 11 10

0

0

1

0

1

1

1

0

1

0

00 01 11 10

0

0

0

1

0

1

0

1

1

1

c

c

i

i

a

a

i

i

b

b

i

i

c

c

i+1

i+1

y

y

i

i

a

a

i

i

b

b

i

i

c

c

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

c

b

a

c

b

a

c

b

a

c

b

a

c

b

a

y

















i

i

i

i

i

i

1

i

c

b

c

a

b

a

c









c

c

i

i

c

c

i+1

i+1

y

y

i

i

a

a

i

i

b

b

i

i

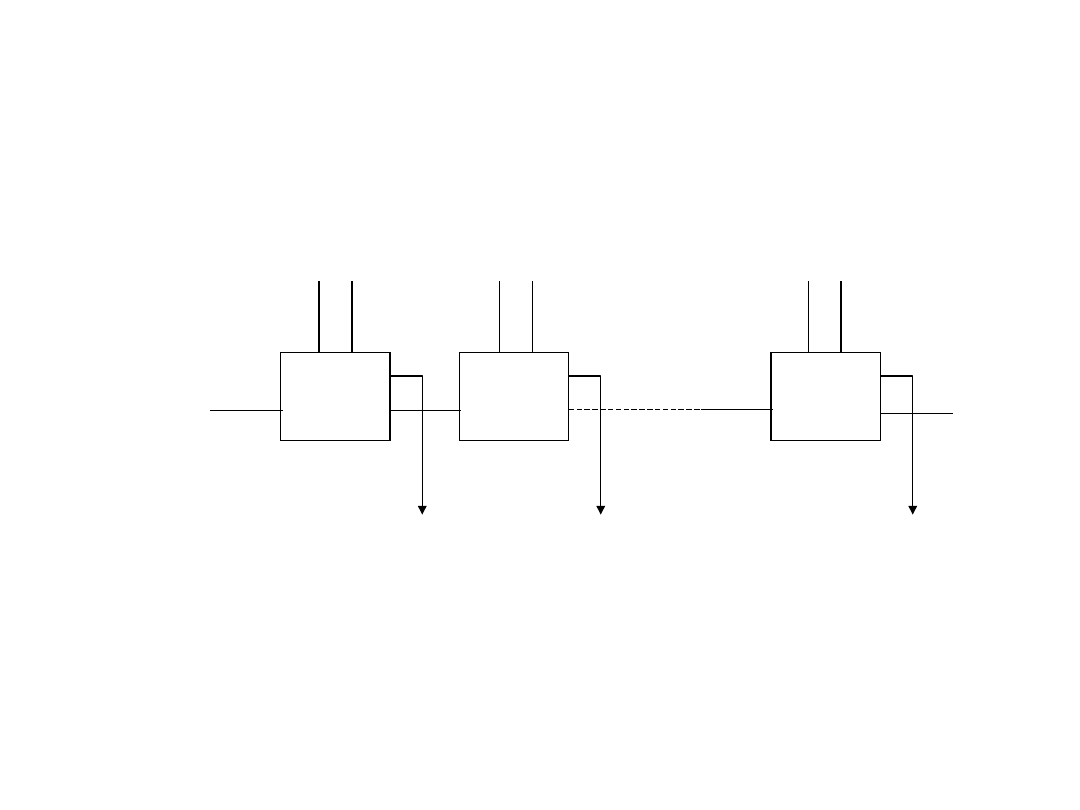
Przykład projektowania układu kombinacyjnego

Przykład projektowania układu kombinacyjnego

(sumator wielobitowy)

(sumator wielobitowy)

Aby zrealizować sumowanie dwóch k-bitowych liczb należy

Aby zrealizować sumowanie dwóch k-bitowych liczb należy

połączyć ze sobą k sumatorów jednobitowych

połączyć ze sobą k sumatorów jednobitowych





y

y

0

0

c

c

0

0

=0

=0

a

a

0

0

b

b

0

0









c

c

k

k

a

a

1

1

b

b

1

1

a

a

k-1

k-1

b

b

k-1

k-1

y

y

1

1

y

y

k-1

k-1

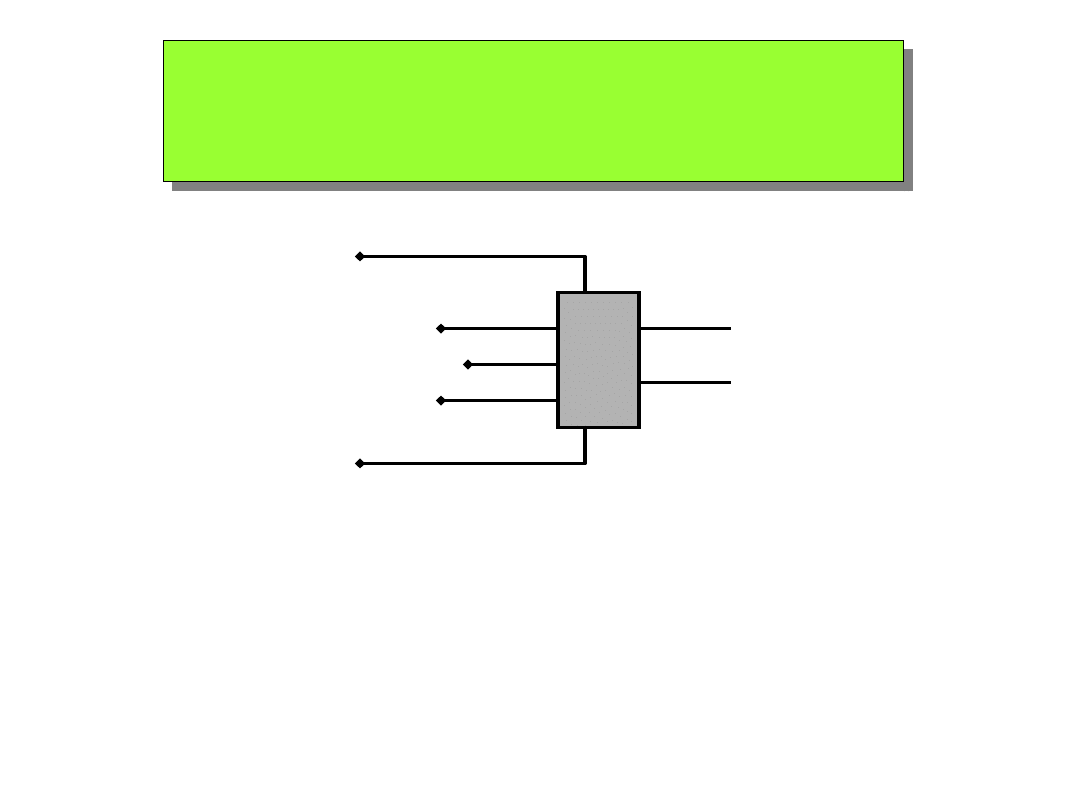
PRZERZUTNIKI

PRZERZUTNIKI

Posiada co najmniej dwa wejścia i z reguły dwa

Posiada co najmniej dwa wejścia i z reguły dwa

wyjścia

wyjścia

w

e

jś

c

ia

w

e

jś

c

ia

p

ro

g

ra

m

u

ją

c

e

p

ro

g

ra

m

u

ją

c

e

w

e

jś

c

ia

w

e

jś

c

ia

i

n

fo

rm

a

c

y

jn

e

i

n

fo

rm

a

c

y

jn

e

wejście

wejście

zegarowe

zegarowe

w

y

jś

c

ia

w

y

jś

c

ia

Zasadnicze typy przerzutników:

Zasadnicze typy przerzutników:

RS, JK, D

RS, JK, D

i

i

T

T

Def.1. Przerzutniki są podstawowymi

Def.1. Przerzutniki są podstawowymi

elementami układów sekwencyjnych,

elementami układów sekwencyjnych,

których zasadniczym zadaniem jest

których zasadniczym zadaniem jest

pamiętanie jednego bitu informacji

pamiętanie jednego bitu informacji

Def.1. Przerzutniki są podstawowymi

Def.1. Przerzutniki są podstawowymi

elementami układów sekwencyjnych,

elementami układów sekwencyjnych,

których zasadniczym zadaniem jest

których zasadniczym zadaniem jest

pamiętanie jednego bitu informacji

pamiętanie jednego bitu informacji

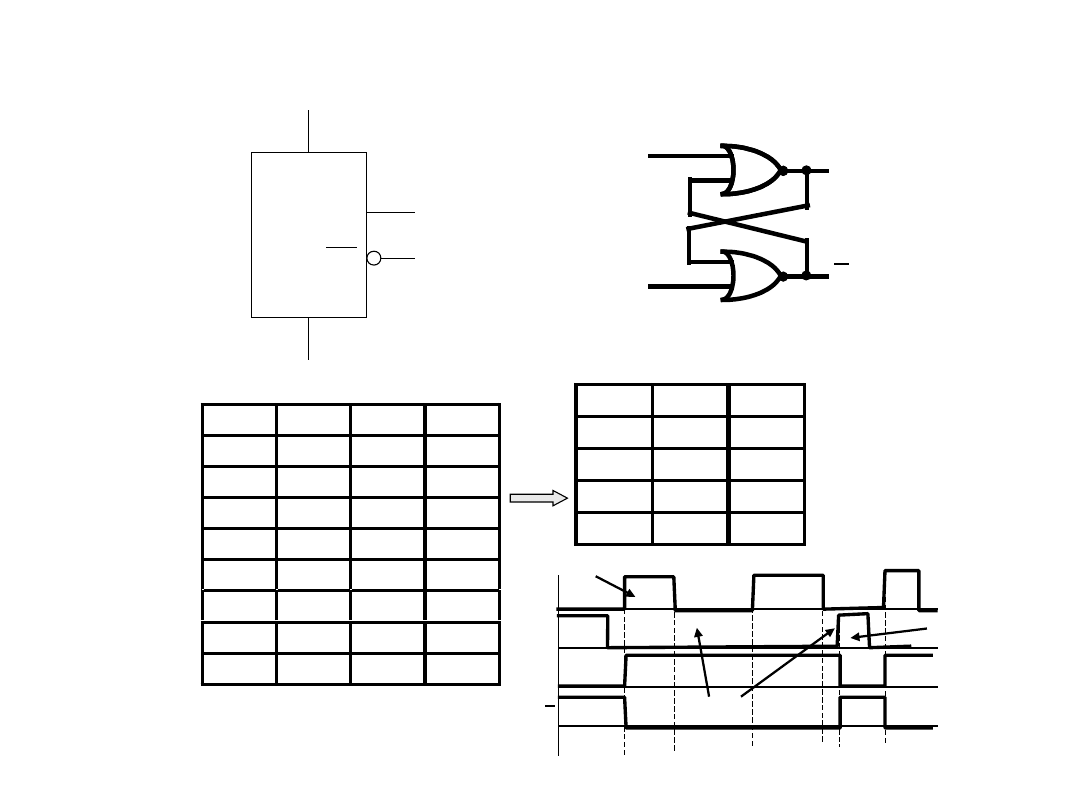
ASYNCHRONICZNY PRZERZUTNIK

ASYNCHRONICZNY PRZERZUTNIK

RS

RS

R

R

S

S

Q

Q

Q

Q

w

e

jś

c

ia

w

e

jś

c

ia

in

fo

rm

a

c

y

jn

e

/p

ro

g

ra

m

u

ją

c

e

in

fo

rm

a

c

y

jn

e

/p

ro

g

ra

m

u

ją

c

e

w

y

jś

c

ia

w

y

jś

c

ia

R

S

Q

n

Q

n-1

0

0

0

0

0

0

1

1

0

1

0

1

0

1

1

1

1

0

0

0

1

0

1

0

1

1

0

-

1

1

1

-

S

S

R

R

Q

Q

Q

Q

wyjście

wyjście

proste

proste

wyjście

wyjście

zanegowane

zanegowane

wejście

wejście

zerujące (RESET)

zerujące (RESET)

wejście

wejście

ustawiające (SET)

ustawiające (SET)

R

S

Q

n+1

0

0

Q

n

0

1

1

1

0

0

1

1

-

pamiętanie

pamiętanie

zerowanie

zerowanie

ustawianie

ustawianie

stan

stan

zabroniony

zabroniony

S

S

R

R

Q

Q

Q

Q

wpis jedynki

wpis jedynki

zerowanie

zerowanie

pamiętanie

pamiętanie

czas

czas

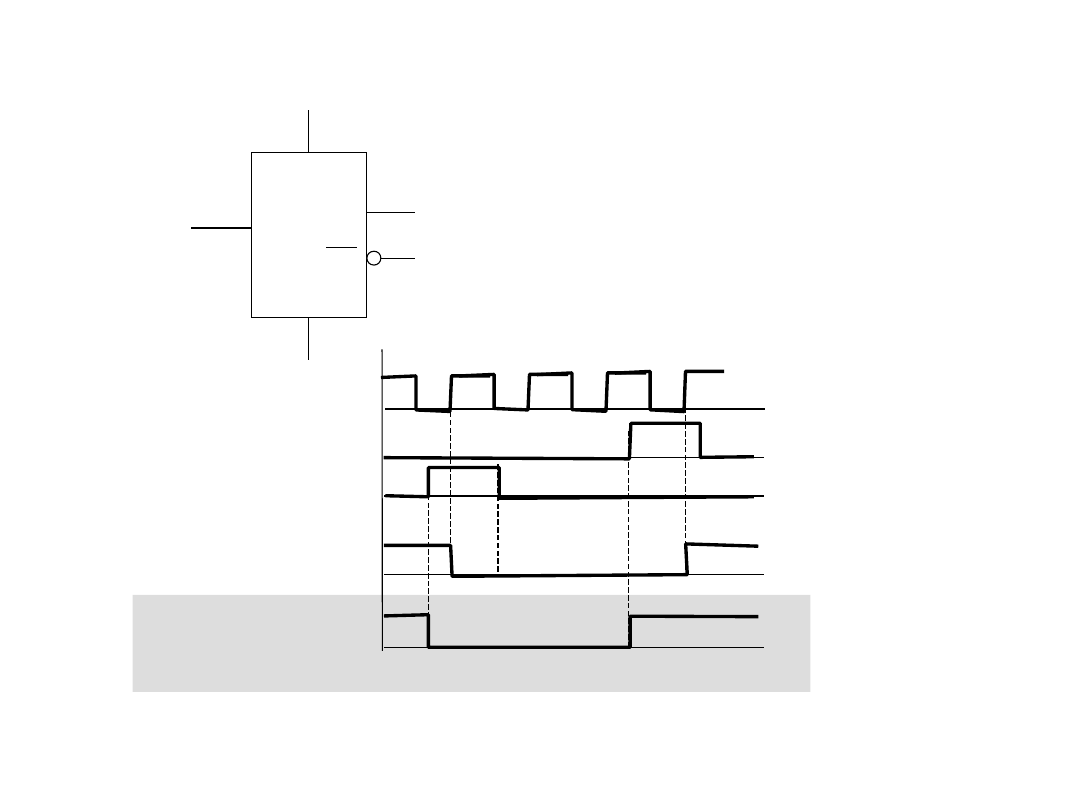
SYNCHRONICZNY PRZERZUTNIK

SYNCHRONICZNY PRZERZUTNIK

RS

RS

S

S

R

R

Q

Q

Q

Q

wyjście

wyjście

proste

proste

wyjście

wyjście

zanegowane

zanegowane

wejście

wejście

zerujące (RESET)

zerujące (RESET)

wejście

wejście

ustawiające (SET)

ustawiające (SET)

zegar

zegar

CK

CK

S

S

R

R

Q

Q

czas

czas

CK

CK

Q

Q

asynchroniczny

asynchroniczny

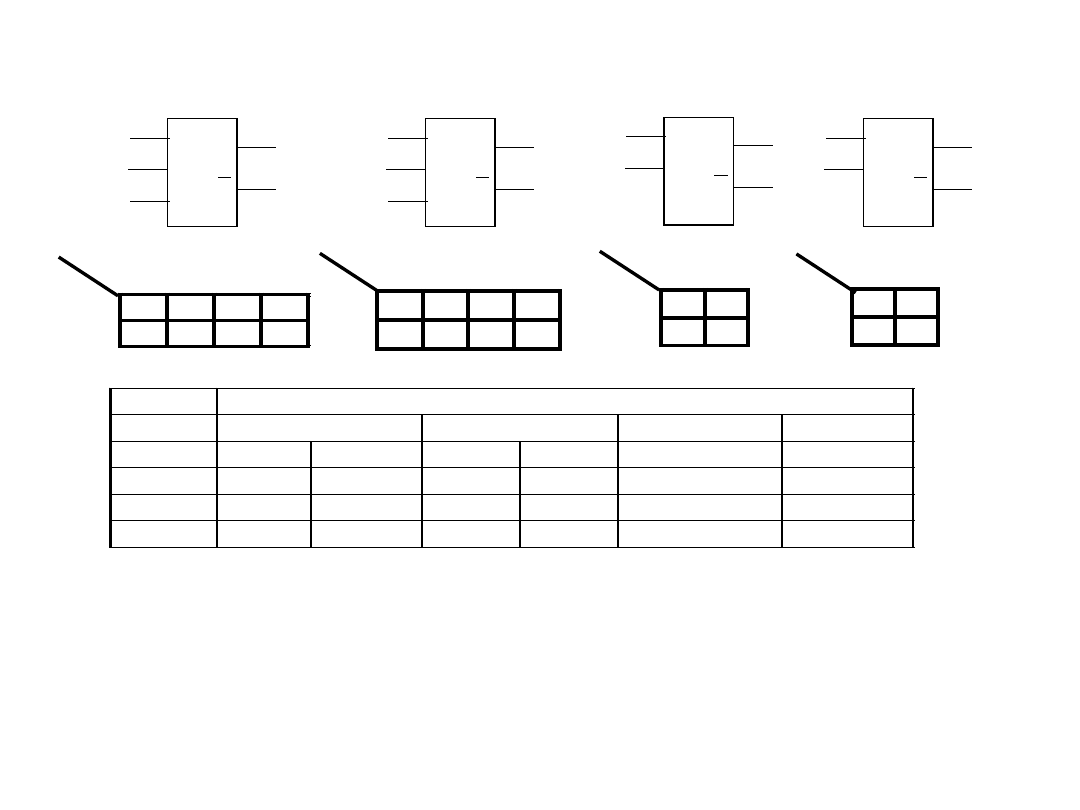
INNE PRZERZUTNIKI

INNE PRZERZUTNIKI

S

S

R

R

Q

Q

Q

Q

zegar

zegar

K

K

J

J

Q

Q

Q

Q

zegar

zegar

D

D

Q

Q

Q

Q

zegar

zegar

T

T

Q

Q

Q

Q

zegar

zegar

00 01 11 10

0

0

1

-

0

1

1

1

-

0

Q

Q

RS

RS

00 01 11 10

0

0

0

1

1

1

1

0

0

1

Q

Q

JK

JK

0

1

0

0

1

1

0

1

Q

Q

D

D

0

1

0

0

1

1

1

0

Q

Q

T

T

t

t+

1

Q

RS

J K

D

T

0

-

0

0

-

0

0

0

0

1

1

-

1

1

1

1

0

-

1

0

1

1

0

-

-

0

1

0

Przerzutnik JK działa podobnie jak RS, z tą różnicą, że gdy J=K=1,

Przerzutnik JK działa podobnie jak RS, z tą różnicą, że gdy J=K=1,

to sygnał zegara zmienia stan. W innych przypadkach J działa jak

to sygnał zegara zmienia stan. W innych przypadkach J działa jak

S, a K jak R.

S, a K jak R.

Przerzutnik D zapamiętuje stan wejścia D w chwili impulsu zegara.

Przerzutnik D zapamiętuje stan wejścia D w chwili impulsu zegara.

Przerzutnik T zmienia swój stan w czasie impulsu zegarowego,

Przerzutnik T zmienia swój stan w czasie impulsu zegarowego,

jeżeli T=1 a pozostaje w stanie pierwotnym, gdy T=0

jeżeli T=1 a pozostaje w stanie pierwotnym, gdy T=0

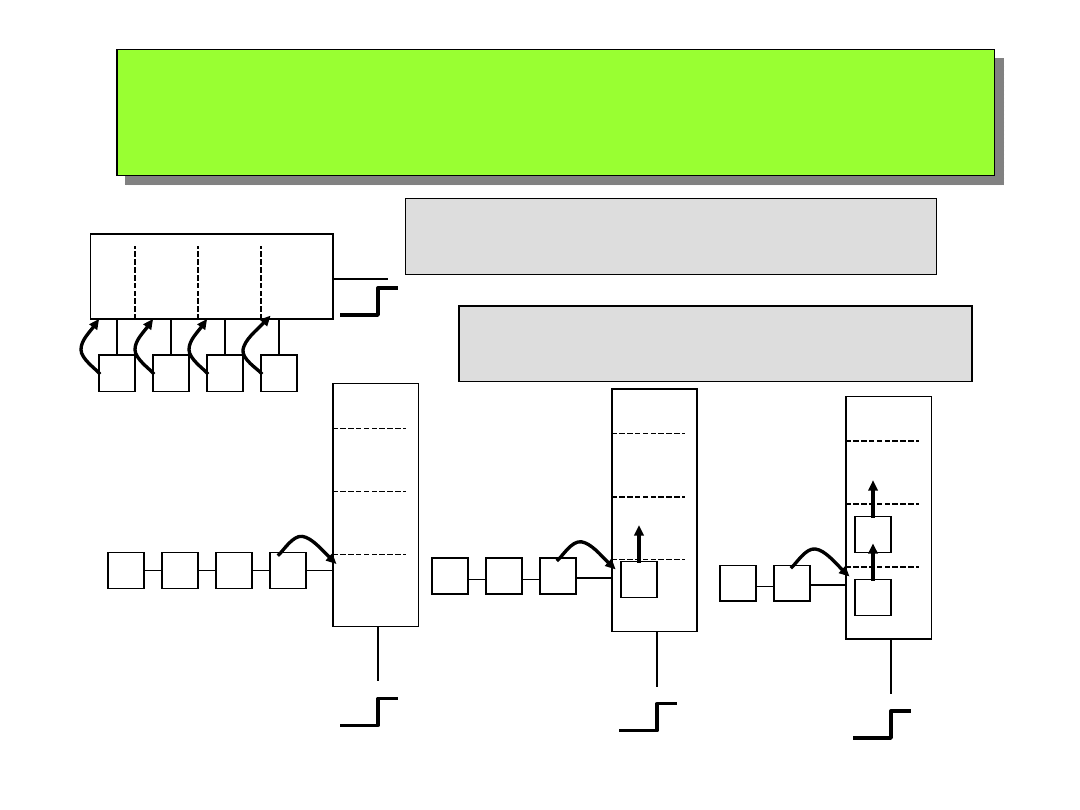
REJESTRY

REJESTRY

Def.1. Rejestrem nazywamy układ cyfrowy przeznaczony do

Def.1. Rejestrem nazywamy układ cyfrowy przeznaczony do

krótkoterminowego przechowywania niewielkich

krótkoterminowego przechowywania niewielkich

informacji lub do zamiany postaci informacji z

informacji lub do zamiany postaci informacji z

równoległej na szeregową lub odwrotnie.

równoległej na szeregową lub odwrotnie.

Def.1. Rejestrem nazywamy układ cyfrowy przeznaczony do

Def.1. Rejestrem nazywamy układ cyfrowy przeznaczony do

krótkoterminowego przechowywania niewielkich

krótkoterminowego przechowywania niewielkich

informacji lub do zamiany postaci informacji z

informacji lub do zamiany postaci informacji z

równoległej na szeregową lub odwrotnie.

równoległej na szeregową lub odwrotnie.

a

a

1

1

a

a

2

2

a

a

3

3

W

e

W

e

3

3

W

e

W

e

2

2

W

e

W

e

1

1

W

e

W

e

0

0

CLK

CLK

a

a

0

0

rejestr

rejestr

CLK

CLK

a

a

0

0

a

a

1

1

a

a

2

2

a

a

3

3

rejestr

rejestr

CLK

CLK

a

a

0

0

a

a

1

1

a

a

2

2

a

a

3

3

rejestr

rejestr

CLK

CLK

a

a

0

0

a

a

1

1

a

a

2

2

a

a

3

3

rejestr

rejestr

...

...

T1

T1

T3

T3

T2

T2

Wprowadzanie równoległe - wszystkie bity słowa
informacji wprowadzamy jednocześnie , w jednym
takcie zegara

Wprowadzanie szeregowe - informację
wprowadzamy bit po bicie (jeden bit na jeden
takt zegara)

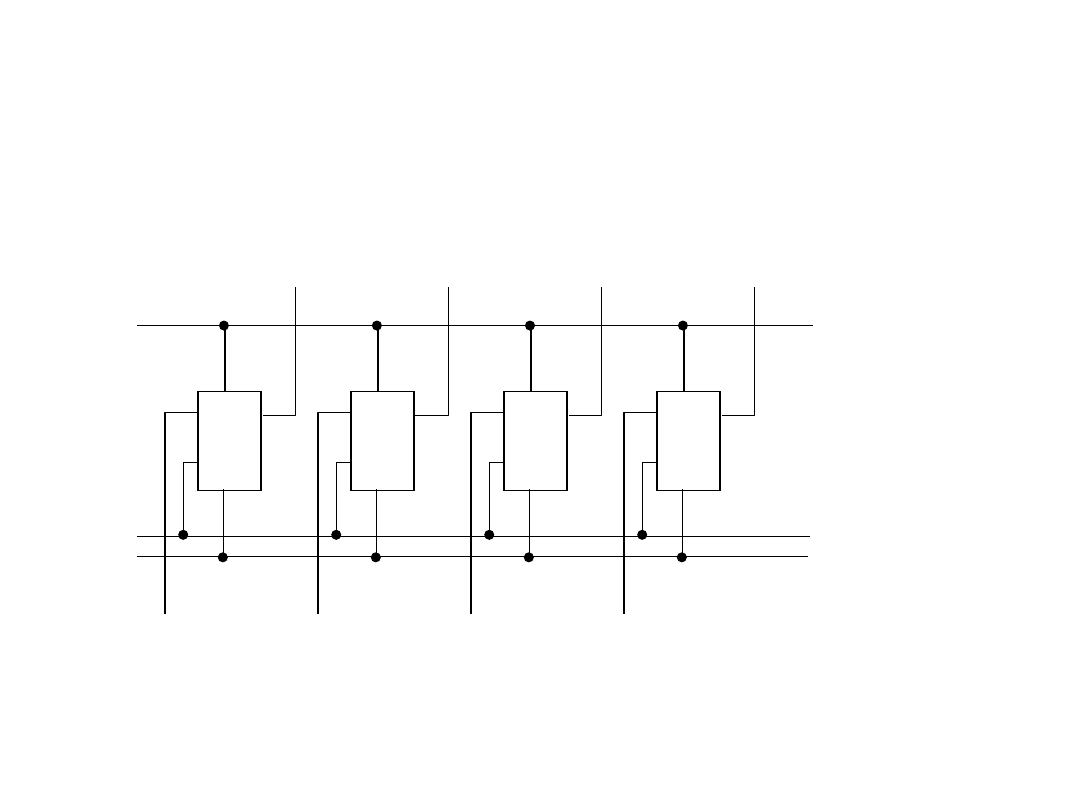
REJESTRY

REJESTRY

•

PIPO - parallel input, parallel output - z wejściem i wyjściem

PIPO - parallel input, parallel output - z wejściem i wyjściem

równoległym (rejestry buforowe)

równoległym (rejestry buforowe)

•

SISO - serial input, serial output - wejście i wyjście szeregowe

SISO - serial input, serial output - wejście i wyjście szeregowe

(rejestry przesuwające)

(rejestry przesuwające)

•

SIPO - serial input, parallel output - z wejściem szeregowym i

SIPO - serial input, parallel output - z wejściem szeregowym i

równoległym wyjściem

równoległym wyjściem

•

PISO - parallel input, serial output - z wejściem równoległym i

PISO - parallel input, serial output - z wejściem równoległym i

szeregowym wyjściem

szeregowym wyjściem

P1

P1

Q1

Q1

D1

D1

P2

P2

Q2

Q2

D2

D2

P3

P3

Q3

Q3

D3

D3

P4

P4

Q4

Q4

D4

D4

CLK

CLK

UST

UST

ZER

ZER

LICZNIKI

LICZNIKI

Def.1. Licznikiem nazywamy układ cyfrowy, na którego

Def.1. Licznikiem nazywamy układ cyfrowy, na którego

wyjściu pojawia się zakodowana liczba impulsów

wyjściu pojawia się zakodowana liczba impulsów

podanych na jego wejście zliczające.

podanych na jego wejście zliczające.

Musi być znany:

Musi być znany:

•

stan początkowy licznika (zero)

stan początkowy licznika (zero)

•

pojemność licznika

pojemność licznika

•

kod zliczania

kod zliczania

Def.1. Licznikiem nazywamy układ cyfrowy, na którego

Def.1. Licznikiem nazywamy układ cyfrowy, na którego

wyjściu pojawia się zakodowana liczba impulsów

wyjściu pojawia się zakodowana liczba impulsów

podanych na jego wejście zliczające.

podanych na jego wejście zliczające.

Musi być znany:

Musi być znany:

•

stan początkowy licznika (zero)

stan początkowy licznika (zero)

•

pojemność licznika

pojemność licznika

•

kod zliczania

kod zliczania

Rodzaje liczników:

Rodzaje liczników:

•

liczące w przód (następnikowe)

liczące w przód (następnikowe)

•

liczące w tył (poprzednikowe)

liczące w tył (poprzednikowe)

•

rewersyjne (mozliwość zmiany kierunku zliczania)

rewersyjne (mozliwość zmiany kierunku zliczania)

•

szeregowe (asynchroniczne)

szeregowe (asynchroniczne)

•

równoległe (synchroniczne)

równoległe (synchroniczne)

D0

D0

D1

D1

D2

D2

D3

D3

Q0

Q0

Q1

Q1

Q2

Q2

Q3

Q3

TC

TC

CEP

CEP

CET

CET

CLK

CLK

LD

LD

CLR

CLR

LICZNIK

LICZNIK

D0 - D3 - wejścia danych

D0 - D3 - wejścia danych

CLK - wejście zegarowe

CLK - wejście zegarowe

CLR - wejście zerujące

CLR - wejście zerujące

LD - wejście sterujące do wpisywania

LD - wejście sterujące do wpisywania

danych z wejść D0-D1

danych z wejść D0-D1

CEP - wejście dostępu (umożliwia

CEP - wejście dostępu (umożliwia

zliczanie)

zliczanie)

CET - wejście dostępu (umożliwia

CET - wejście dostępu (umożliwia

powstanie przeniesienia TC)

powstanie przeniesienia TC)

Q0 - Q3 - wyjścia

Q0 - Q3 - wyjścia

TC - wyjście przeniesienia (umożliwia

TC - wyjście przeniesienia (umożliwia

rozbudowę)

rozbudowę)

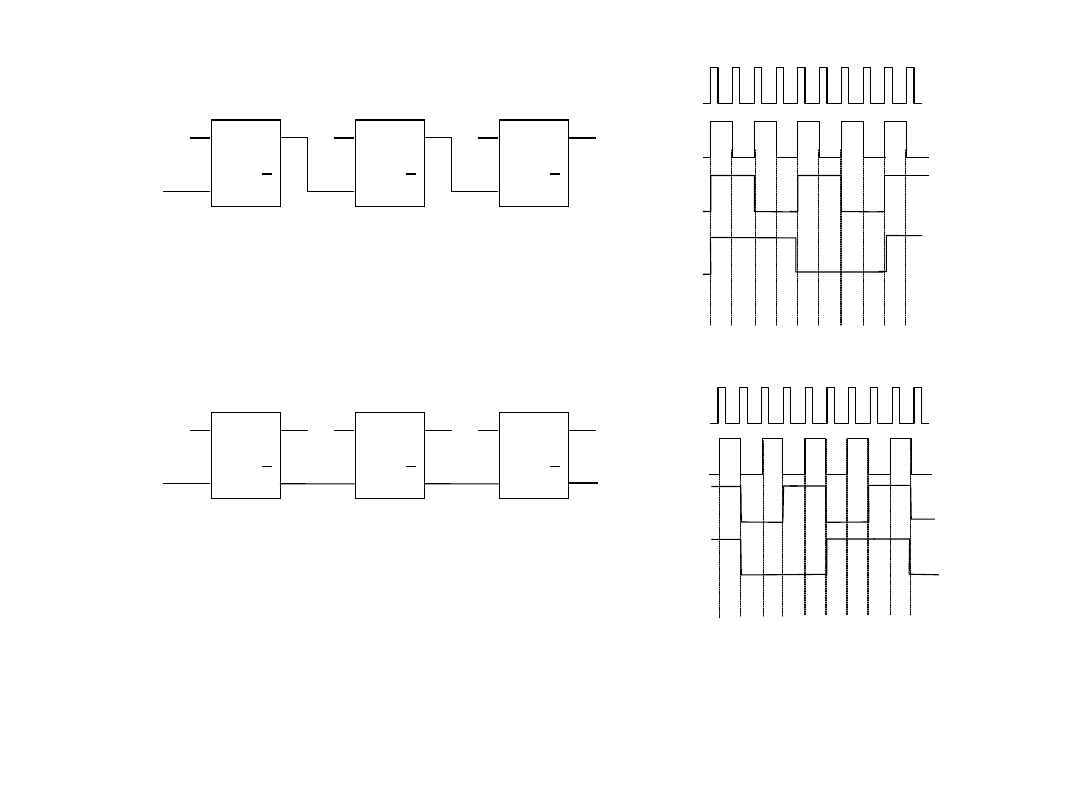
LICZNIKI

LICZNIKI

Q

Q

Q

Q

T

T

CLK

CLK

Q

Q

Q

Q

T

T

CLK

CLK

Q

Q

Q

Q

T

T

CLK

CLK

CLK

CLK

Q1

Q1

Q2

Q2

Q3

Q3

Q1

Q1

Q2

Q2

Q3

Q3

Q

Q

Q

Q

T

T

CLK

CLK

Q

Q

Q

Q

T

T

CLK

CLK

Q

Q

Q

Q

T

T

CLK

CLK

Q1

Q1

Q2

Q2

Q3

Q3

CLK

CLK

Q1

Q1

Q2

Q2

Q3

Q3

001

001

110

110

101

101

111

111

100

100

011

011

010

010

000

000

001

001

110

110

101

101

111

111

100

100

011

011

010

010

000

000

Licznik poprzednikowy (liczący w

Licznik poprzednikowy (liczący w

tył)

tył)

Licznik następnikowy (liczący w

Licznik następnikowy (liczący w

przód)

przód)

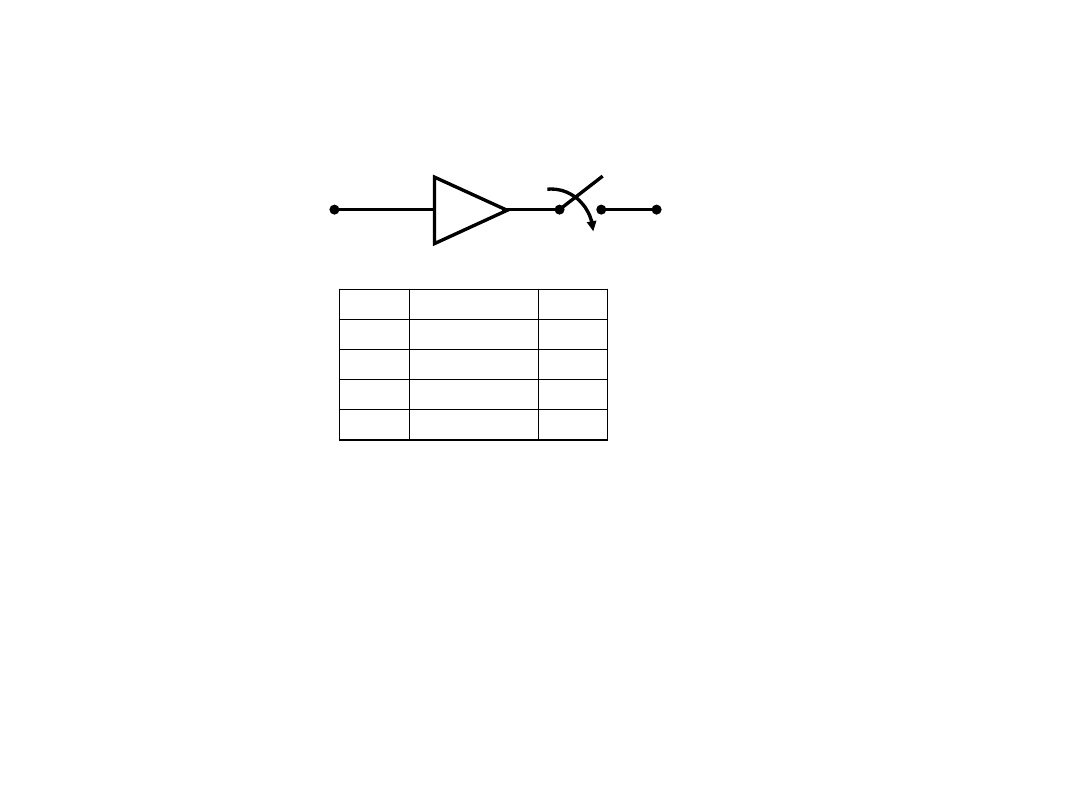
BRAMKI TRÓJSTANOWE

BRAMKI TRÓJSTANOWE

Bramka trójstanowa jest narzędziem umożliwiającym

Bramka trójstanowa jest narzędziem umożliwiającym

odseparowanie elektryczne dwóch lub więcej punktów w systemie,

odseparowanie elektryczne dwóch lub więcej punktów w systemie,

np. wyjścia pewnego układu i wspólnego przewodu , po którym

np. wyjścia pewnego układu i wspólnego przewodu , po którym

przesyłane są dane.

przesyłane są dane.

WE

WE

WY

WY

ENABLE

ENABLE

WE ENABLE

WY

0

1

0

1

1

1

0

0

Z

1

0

Z

Na wyjściu mogą pojawić się trzy stany:

Na wyjściu mogą pojawić się trzy stany:

•

stany logiczne przekazywane z wejścia bramki (0 lub 1)

stany logiczne przekazywane z wejścia bramki (0 lub 1)

•

stan Z tzw. wysokiej impedancji (brak wzajemnego wpływu

stan Z tzw. wysokiej impedancji (brak wzajemnego wpływu

wartości elektrycznych na wejściu na wartości elektryczne

wartości elektrycznych na wejściu na wartości elektryczne

na wyjściu bramki

na wyjściu bramki

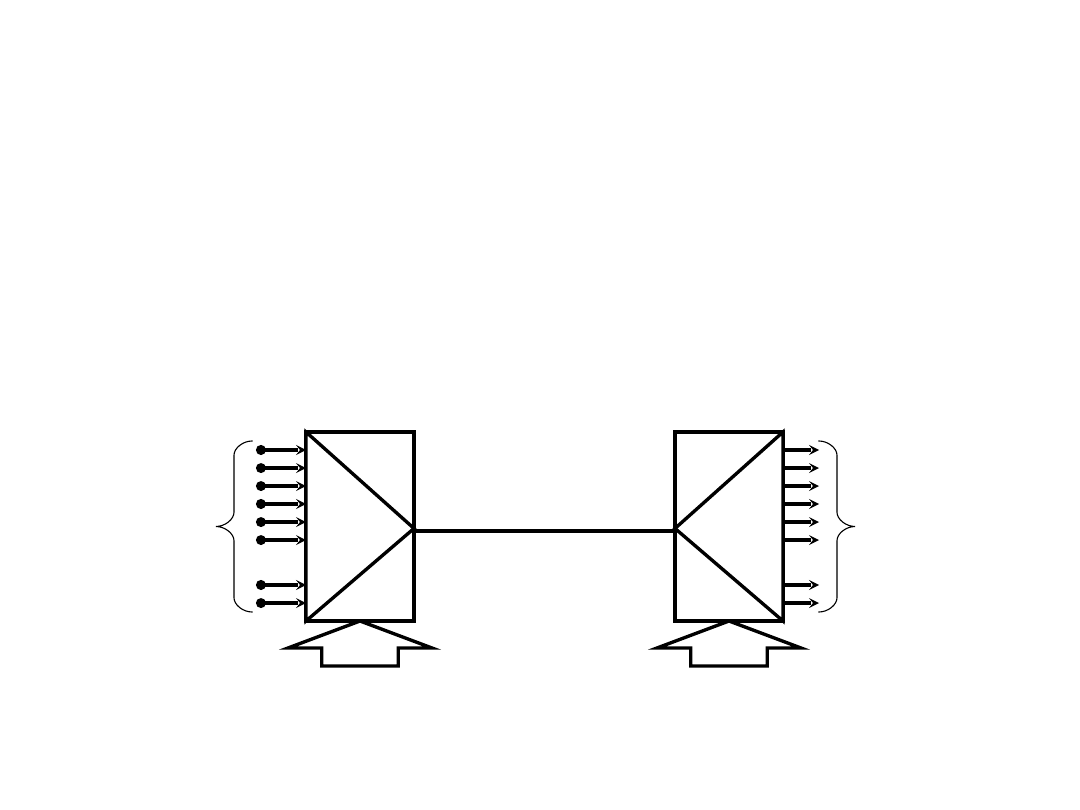
Mutipleksery i demutipleksery są układami umożliwiającymi

Mutipleksery i demutipleksery są układami umożliwiającymi

zrealizowanie systemu transmisji.

zrealizowanie systemu transmisji.

Po stronie nadawczej występuje przetwornik formatu słów z

Po stronie nadawczej występuje przetwornik formatu słów z

równoległego na szeregowy - mutiplekser. Umożliwia on

równoległego na szeregowy - mutiplekser. Umożliwia on

przesłanie (w postaci prostej lub zanegowanej) na wyjście

przesłanie (w postaci prostej lub zanegowanej) na wyjście

tego z sygnałów podanych na wejście informacyjne, który

tego z sygnałów podanych na wejście informacyjne, który

jest doprowadzony do wejścia o numerze określonym przez

jest doprowadzony do wejścia o numerze określonym przez

stan wejść adresowych.

stan wejść adresowych.

Po

stronie

odbiorczej

przetwornik

słów

z

formatu

Po

stronie

odbiorczej

przetwornik

słów

z

formatu

szeregowego na równoległy - demutiplekser. Umożliwia on

szeregowego na równoległy - demutiplekser. Umożliwia on

przesłanie (w postaci prostej lub zanegowanej) sygnału z

przesłanie (w postaci prostej lub zanegowanej) sygnału z

wejścia na to wyjście, które zostało wyróżnione przez stan

wejścia na to wyjście, które zostało wyróżnione przez stan

wejść adresowych.

wejść adresowych.

MULTIPLEKSERY I DEMULTIPLEKSERY

MULTIPLEKSERY I DEMULTIPLEKSERY

WE

WE

WY

WY

MULTIPLEKSER

MULTIPLEKSER

Linia przesyłowa

Linia przesyłowa

Adres

Adres

Adres

Adres

DEMULTIPLEKSE

DEMULTIPLEKSE

R

R

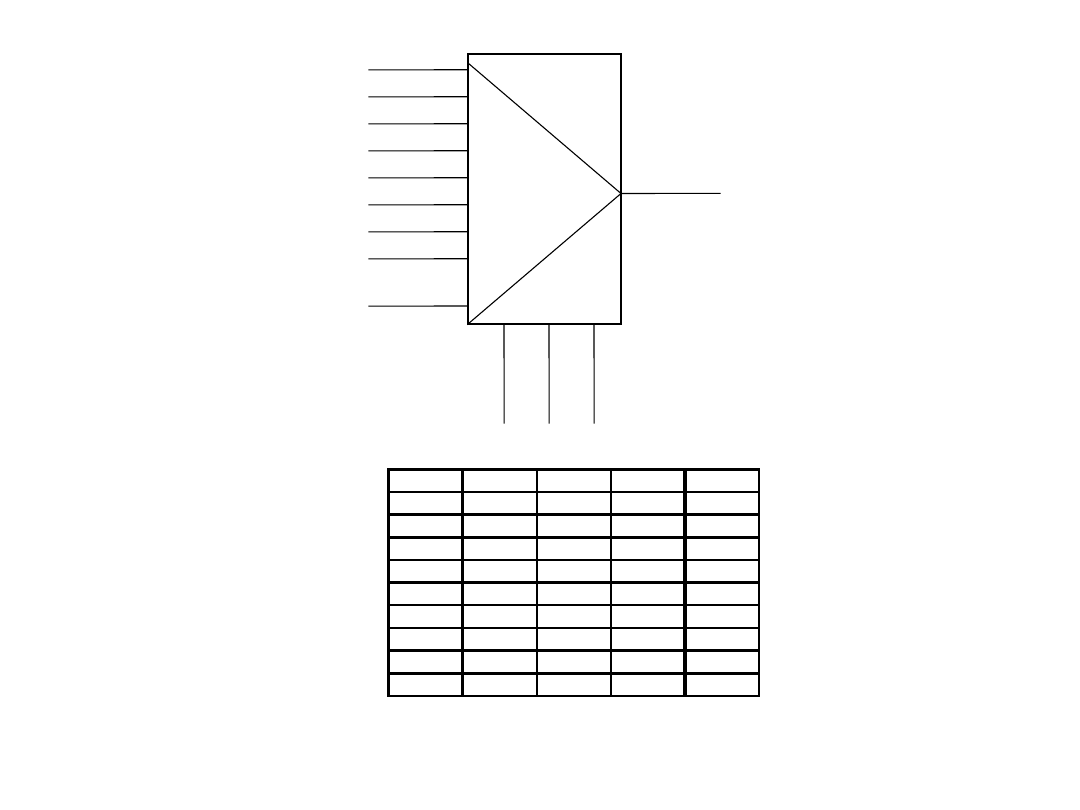
MULTIPLEKSERY

MULTIPLEKSERY

D0

D0

D1

D1

D2

D2

D3

D3

D4

D4

D5

D5

D6

D6

D7

D7

A

A

B

B

C

C

W

W

Strob

Strob

.

.

C

B

A

Strob.

W

x

x

x

1

0

0

0

0

0

D0

0

0

1

0

D1

0

1

0

0

D2

0

1

1

0

D3

1

0

0

0

D4

1

0

1

0

D5

1

1

0

0

D6

1

1

1

0

D7

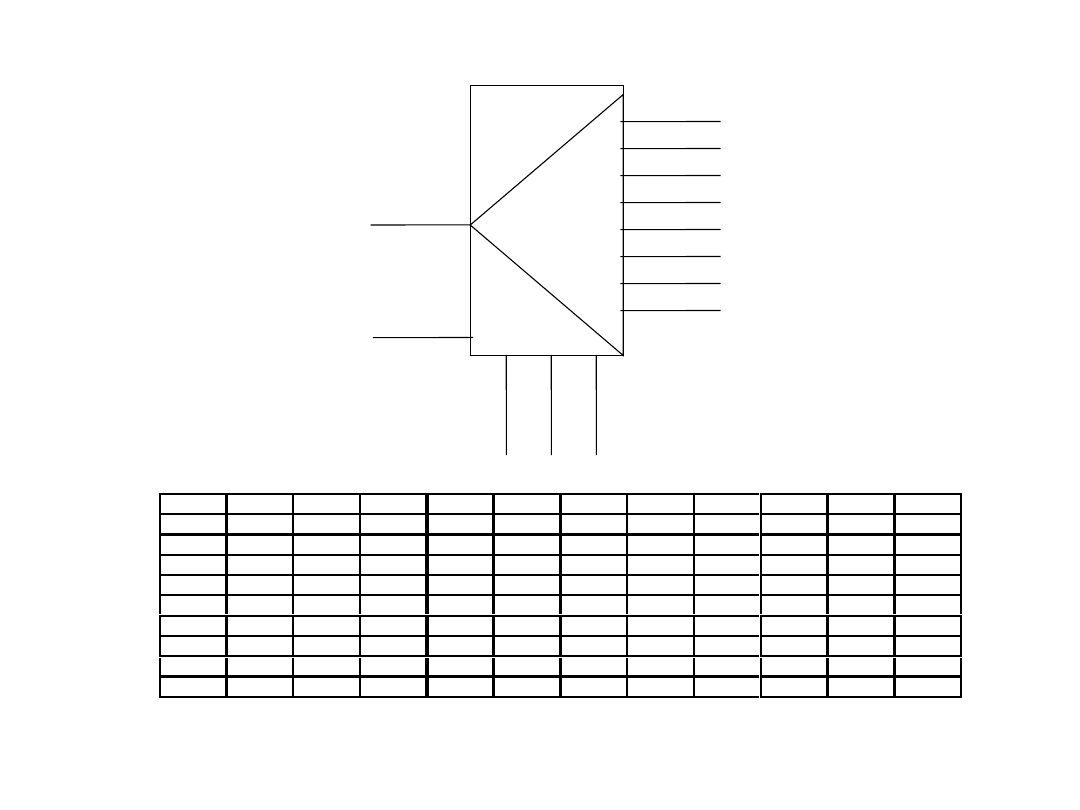
DEMULTIPLEKSERY

DEMULTIPLEKSERY

Y0

Y0

Y1

Y1

Y2

Y2

Y3

Y3

Y4

Y4

Y5

Y5

Y6

Y6

Y7

Y7

A

A

B

B

C

C

W

W

Strob

Strob

.

.

C

B

A

Strob.

Y0

Y1

Y2

Y3

Y4

Y5

Y6

Y7

x

x

x

1

1

1

1

1

1

1

1

1

0

0

0

0

0

1

1

1

1

1

1

1

0

0

1

0

1

0

1

1

1

1

1

1

0

1

0

0

1

1

0

1

1

1

1

1

0

1

1

0

1

1

1

0

1

1

1

1

1

0

0

0

1

1

1

1

0

1

1

1

1

0

1

0

1

1

1

1

1

0

1

1

1

1

0

0

1

1

1

1

1

1

0

1

1

1

1

0

1

1

1

1

1

1

1

0

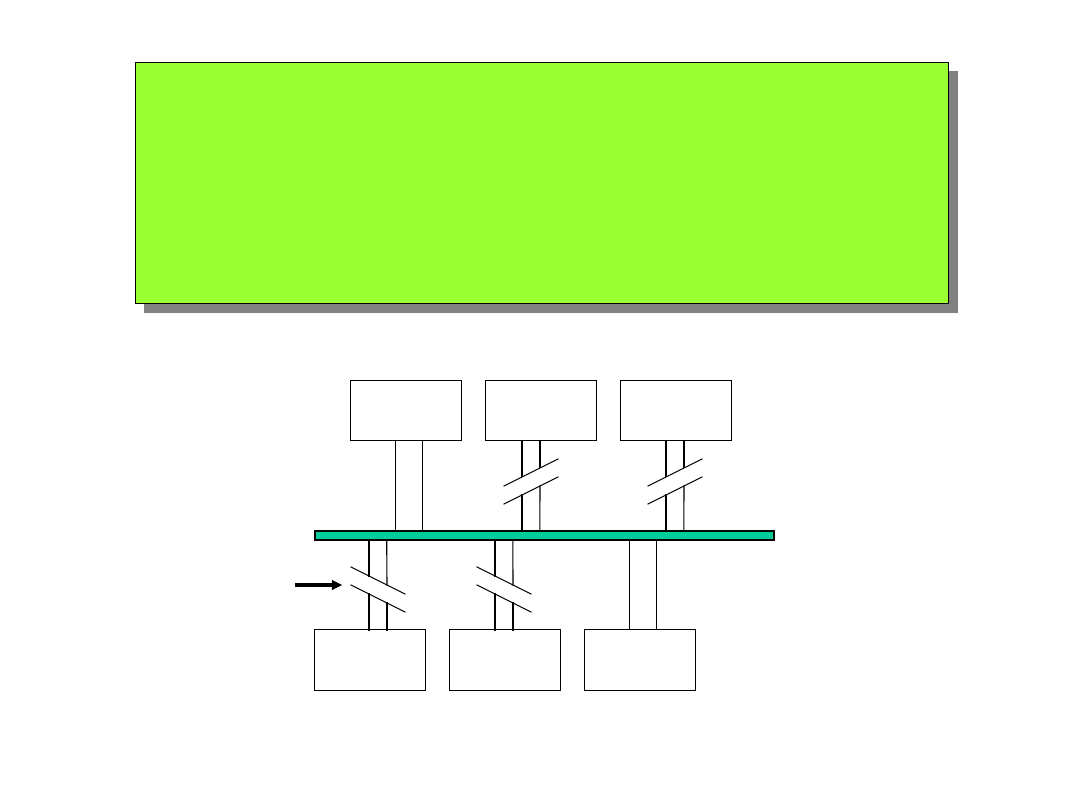
MAGISTRALE DANYCH

MAGISTRALE DANYCH

Def.1. Magistralą nazywamy zestaw linii oraz układów

Def.1. Magistralą nazywamy zestaw linii oraz układów

przełączających, łączących dwa lub więcej układów

przełączających, łączących dwa lub więcej układów

mogących być nadajnikami lub odbiornikami informacji.

mogących być nadajnikami lub odbiornikami informacji.

Przesyłanie informacji zachodzi zawsze pomiędzy

Przesyłanie informacji zachodzi zawsze pomiędzy

dokładnie jednym układem będącym nadajnikiem a

dokładnie jednym układem będącym nadajnikiem a

dokładnie jednym układem będącym odbiornikiem, przy

dokładnie jednym układem będącym odbiornikiem, przy

pozostałych układach odseparowanych od linii

pozostałych układach odseparowanych od linii

przesyłających.

przesyłających.

Def.1. Magistralą nazywamy zestaw linii oraz układów

Def.1. Magistralą nazywamy zestaw linii oraz układów

przełączających, łączących dwa lub więcej układów

przełączających, łączących dwa lub więcej układów

mogących być nadajnikami lub odbiornikami informacji.

mogących być nadajnikami lub odbiornikami informacji.

Przesyłanie informacji zachodzi zawsze pomiędzy

Przesyłanie informacji zachodzi zawsze pomiędzy

dokładnie jednym układem będącym nadajnikiem a

dokładnie jednym układem będącym nadajnikiem a

dokładnie jednym układem będącym odbiornikiem, przy

dokładnie jednym układem będącym odbiornikiem, przy

pozostałych układach odseparowanych od linii

pozostałych układach odseparowanych od linii

przesyłających.

przesyłających.

NAD

NAD

ODB

ODB

Układ

Układ

odseparowany

odseparowany