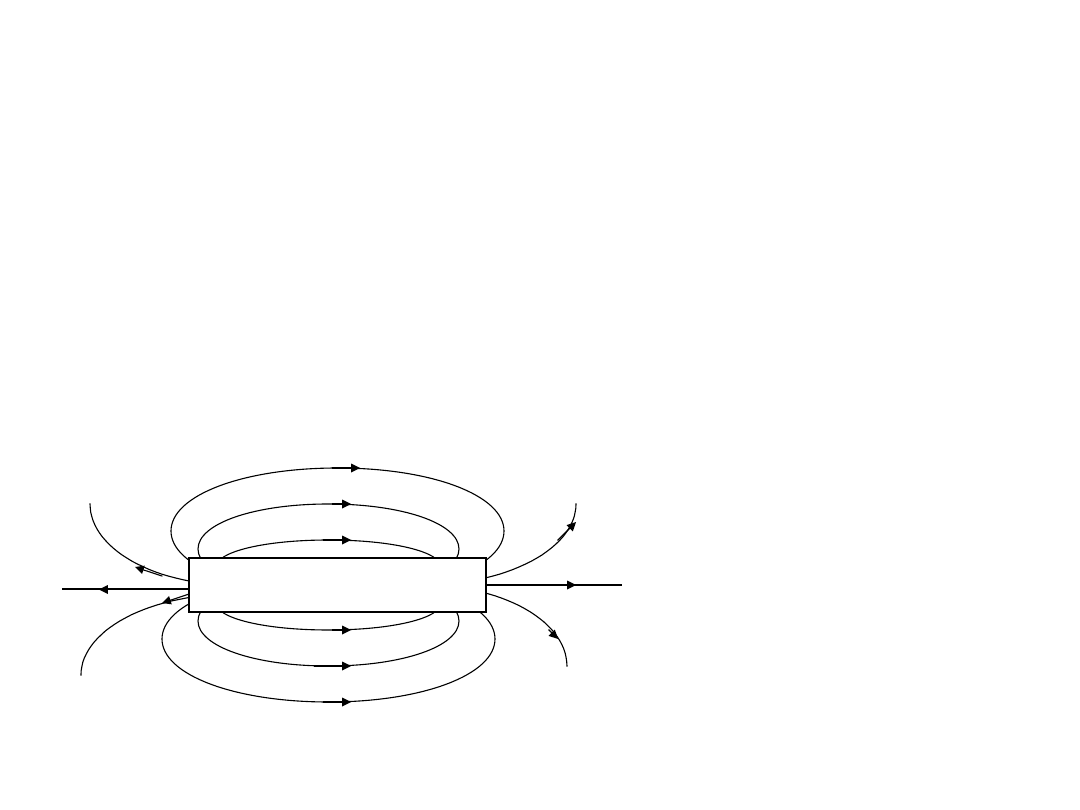
Pole magnetyczne

Polem magnetycznym nazywamy
przestrzeń otaczającą magnes trwały
lub przewodnik przewodzący prąd.

N

S

Liniom sił pola
przyjęto nadawać
taki zwrot, w jakim
skierowane jest
ostrze igły
wskazujące w polu
magnetycznym
ziemskim kierunek
północny.

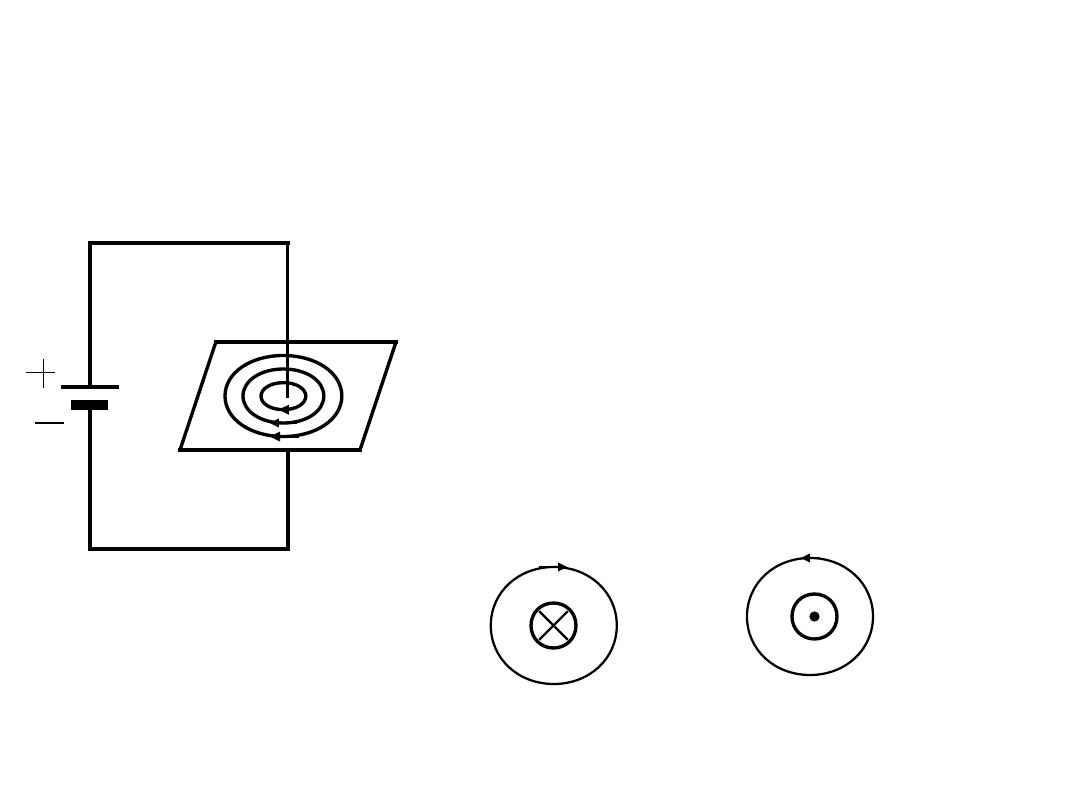
Pole magnetyczne

B

Zwrot linii sił pola
określa się za pomocą
reguły śruby
prawoskrętnej.

Prąd: wpływa
wypływa

Wielkości pola magnetycznego

- Strumień magnetyczny
- Indukcja magnetyczna
- Napięcie magnetyczne
- Natężenie pola magnetycznego

Strumień magnetyczny

Strumień magnetyczny -  - suma wszystkich

linii pola, przechodzących przez określony
przekrój.

Ponieważ strumień magnetyczny wiąże się z
przepływem prądu, który jest efektem
występowania napięcia, jednostką strumienia
jest woltosekunda (lub weber).

1[Wb] = 1 V 1s = 1 Vs

Jednostką podwielokrotną jest makswel.

1[Mx] = 10

-8

Wb

Indukcja magnetyczna

Gęstość strumienia magnetycznego, określona
liczbą linii sił pola przypadającą na jednostkę
powierzchni – to indukcja magnetyczna.

dS

d

B





Indukcja magnetyczna jest wektorem
skierowanym zgodnie z osią igły magnetycznej
swobodnie zawieszonej w polu magnetycznym.
Zwrot – od bieguna południowego do
północnego.
Jeżeli pole jest równomierne:

S

B 



Indukcja magnetyczna

Strumień magnetyczny w całym obwodzie ma tę
sama wartość. Linie strumienia są zamknięte i w
żadnym punkcie pola nie mogą zniknąć ani
powstać.
Własność ta jest analogiczna do własności prądu
elektrycznego, określanej I prawem Kirchhoffa.

0

1





n

i

- w punkcie węzłowym rozgałęzionego
obwodu magnetycznego suma strumieni
równa się zeru.

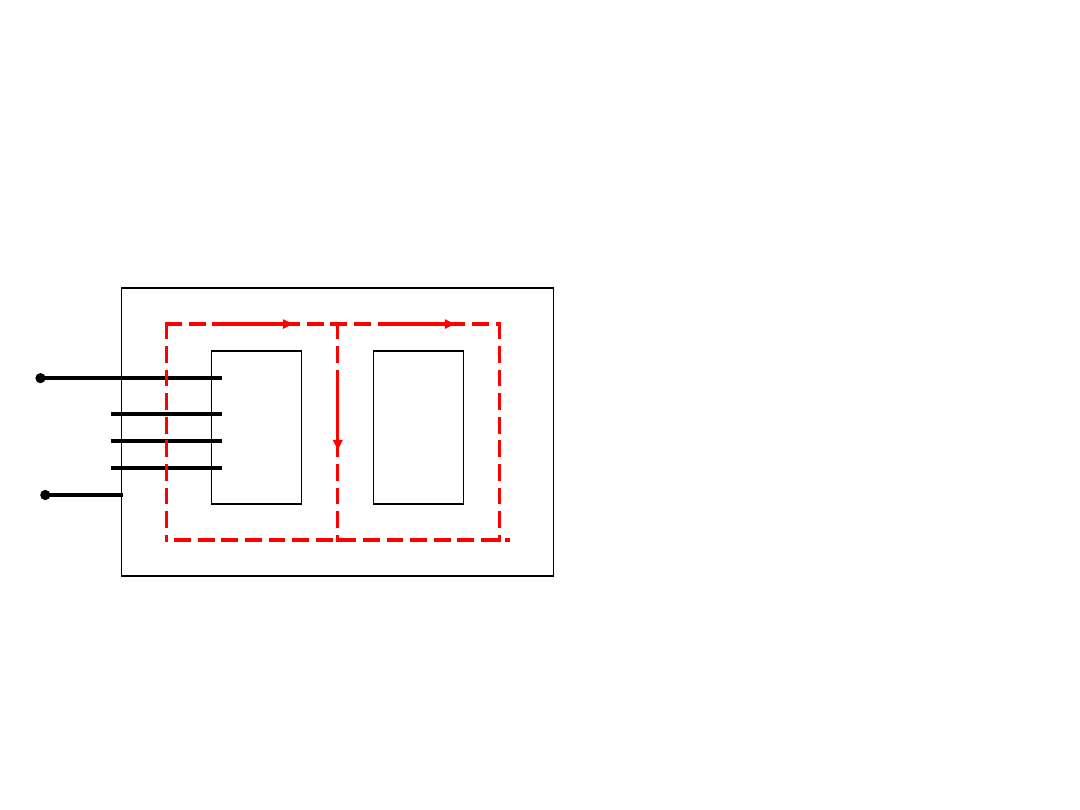
Indukcja magnetyczna



3



2



1

0

3

2

1













Zwykle strumień
dopływający do
węzła ma znak „+”,
a odpływający –
znak „-”.

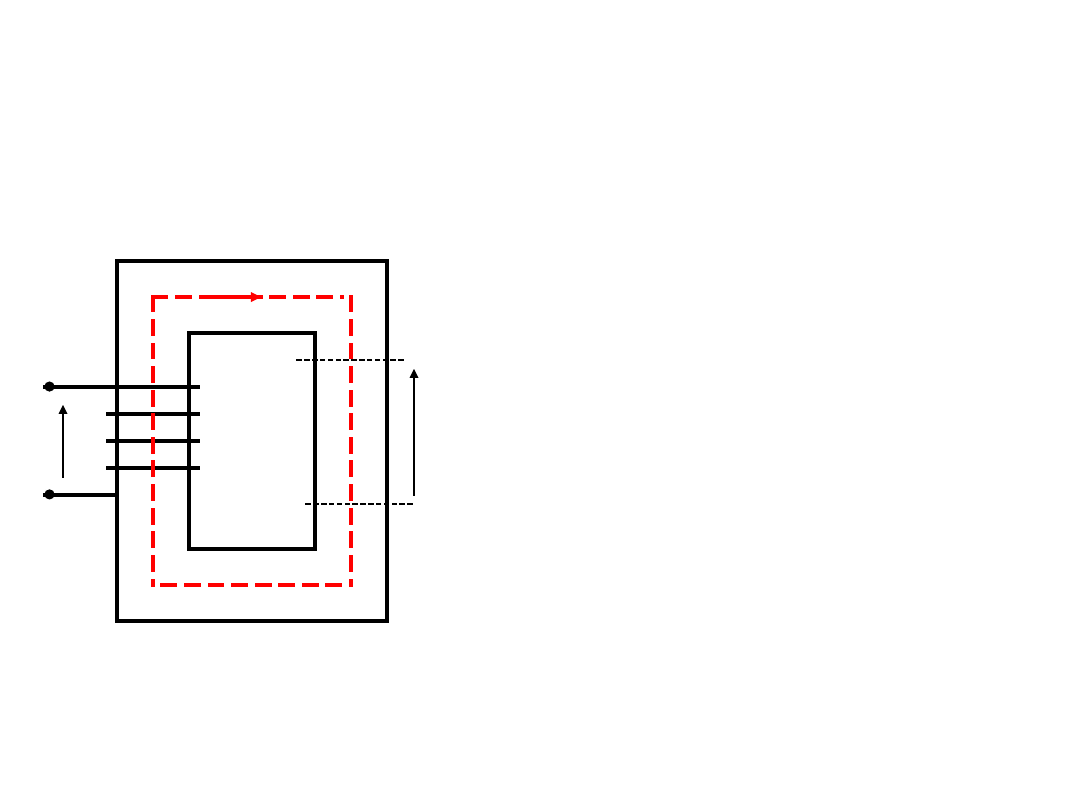
Napięcie magnetyczne





U

mAB

B

A

- napięcie
magnetyczne
źródłowe - 
- spadek napięcia
magnetycznego - U

m

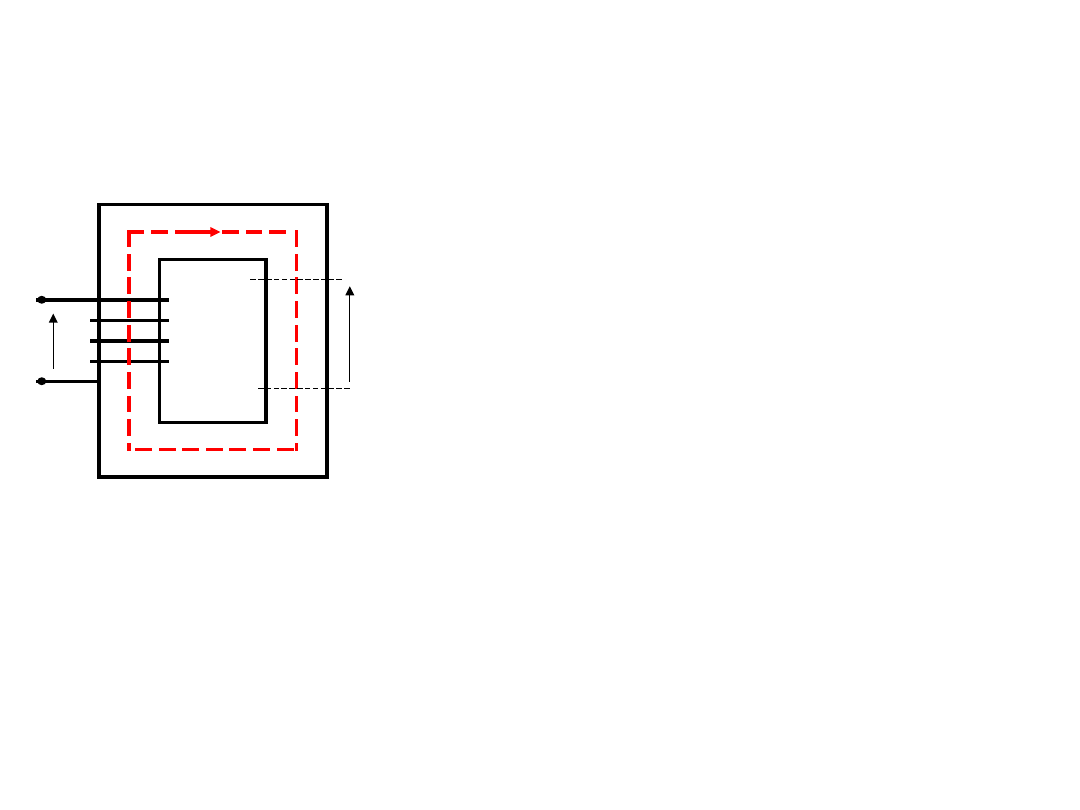
Napięcie magnetyczne źródłowe





U

mA

B

B

A

Napięcie magnetyczne
źródłowe – przepływ (lub
SMM), które jest
przyczyną powstania
strumienia
magnetycznego tak jak
SEM jest przyczyną
powstania prądu.

Przepływ można wytworzyć albo za pomocą
magnesów trwałych albo za pomocą prądu
elektrycznego płynącego przez cewkę o
liczbie zwojów z.

Iz





[A]

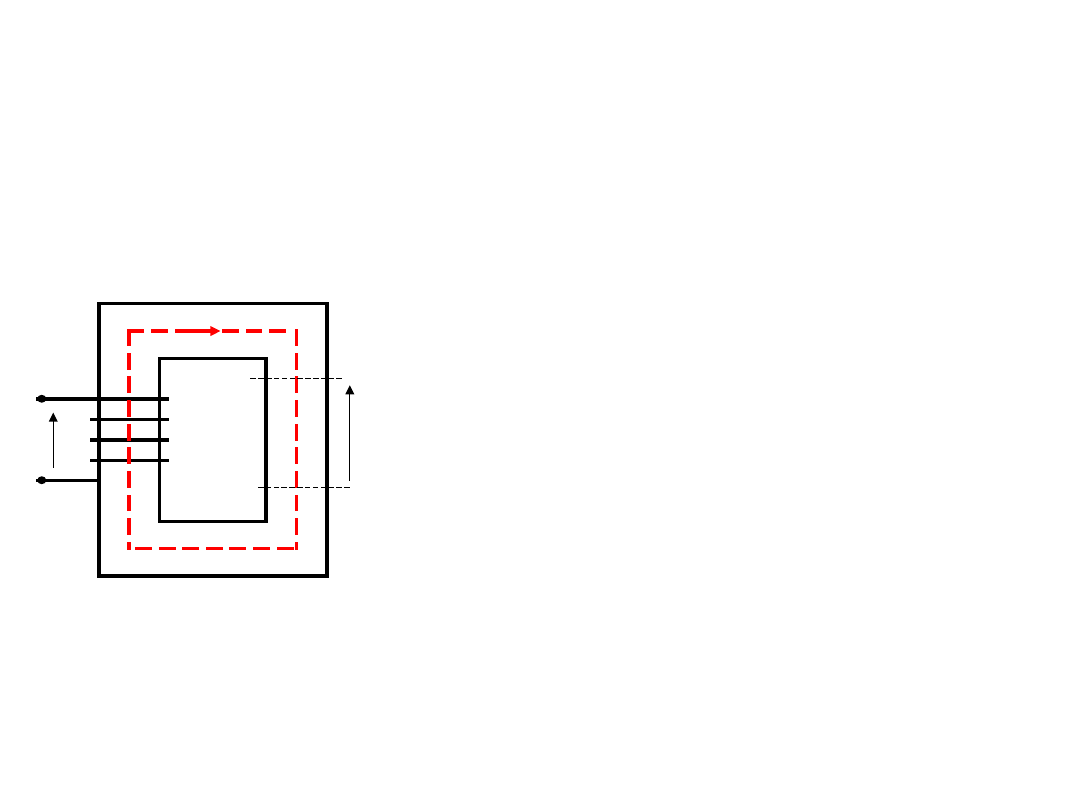
Spadek napięcia magnetycznego





U

mA

B

B

A

Spadek napięcia
magnetycznego U

m

wzdłuż odcinka obwodu
magnetycznego –
odpowiada on
elektrycznemu napięciu
na odbiorniku lub
spadkowi napięcia..

Spadek napięcia magnetycznego

Prawo Ohma dla obwodu magnetycznego:







m

R

R

m

[A/Vs] – opór magnetyczny (lub

reluktancja)

Odwrotność reluktancji, to przewodność
magnetyczna (lub permeancja).









[H
]

s

A

Vs

H







1

1

1

Opór magnetyczny

Opór magnetyczny jest zależny od wymiarów

geometrycznych i właściwości środowiska

tworzącego obwód magnetyczny:

S

l

R

m





l – długość linii pola,

S – przekrój, przez który przenika strumień 
 - przenikalność magnetyczna bezwzględna

środowiska

Przenikalność magnetyczna

Jednostką przenikalności
magnetycznej jest henr na metr.

 

 

   

m

H

m

s

Am

mVs

m

Vs

A

m

s

R

l

m

1

1

1

1

1

1

1

1

2

2















Przenikalność magnetyczna

Przenikalność magnetyczna bezwzględna

określana jest w zależności od przenikalności

próżni i przenikalności względnej.

r

o









m

H

o

7

10

4













r

– przenikalność magnetyczna względna:



r

< 1

– dla diamagnetyków



r

> 1

– dla paramagnetyków



r

>> 1 – dla ferromagnetyków

Natężenie pola magnetycznego

Analogicznie do natężenia pola elektrycznego,
natężenie pola magnetycznego wyraża się zależnością:

dl

dU

H

m





]

[

1

]

[

1

m

A

H 

Dla równomiernego pola, wzbudzonego przez
długi przewód lub długą cewkę, w której
długość jest dużo większa od promienia
zwoju:

l

Iz

H 

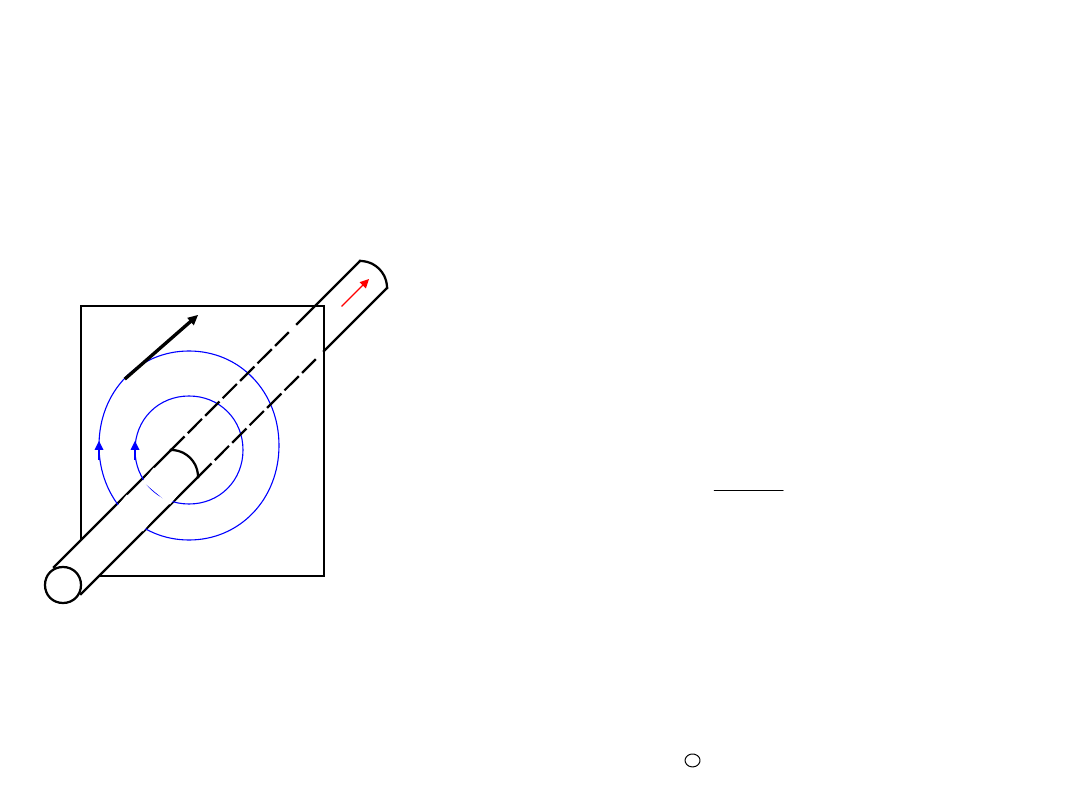
Natężenie pola magnetycznego

B

I

Długi przewód z prądem,
który jest źródłem pola
magnetycznego. Indukcja
magnetyczna takiego pola:

r

I

B





2



r – odległość od osi
przewodu

Jest to prawo Ampere’a, którego ogólna
postać jest:



 I

l

d

B







Prawo Biota-Savarta

Prawo Ampere’a możemy łatwo stosować do
znajdowania pola magnetycznego (indukcji
magnetycznej) tylko wtedy, gdy rozkład
prądów jest symetryczny. Jeżeli pole jest
tworzone przez prąd płynący w
krzywoliniowym przewodniku lub przez
wiele prądów o różnych wartościach i różnej
orientacji w przestrzeni, zastosowanie
prawa Ampere’a może sprawiać trudności i
wówczas stosujemy prawo Biota-Savarta.

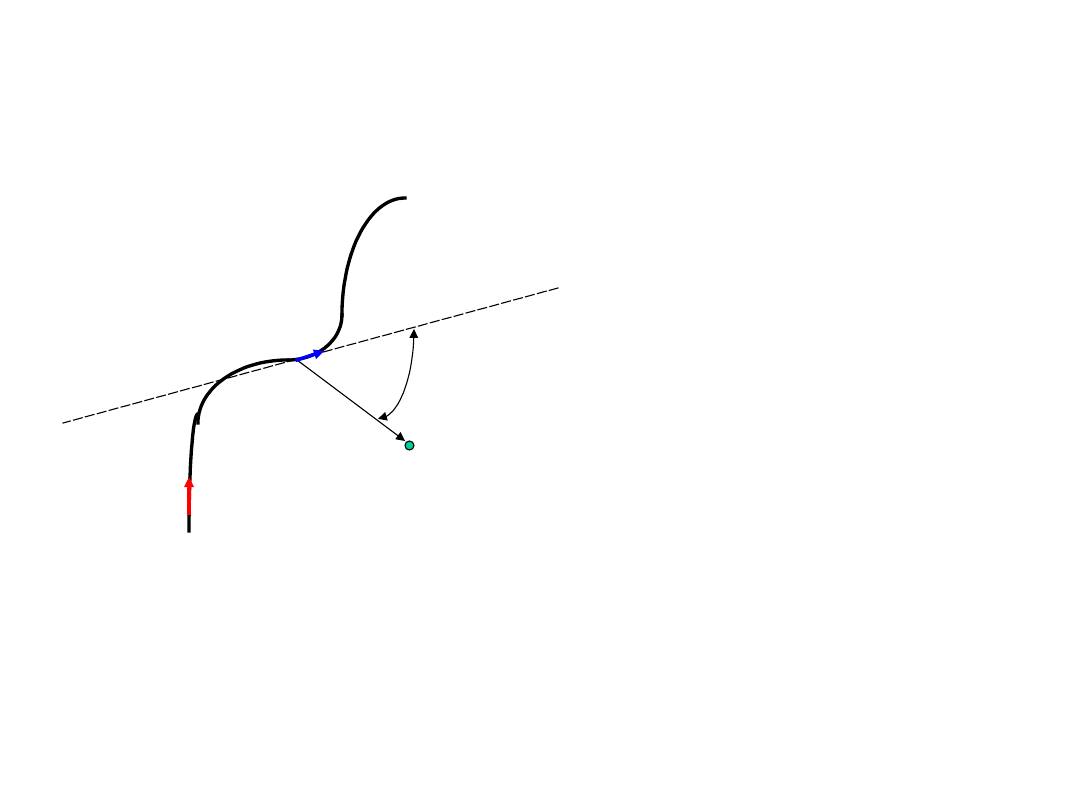
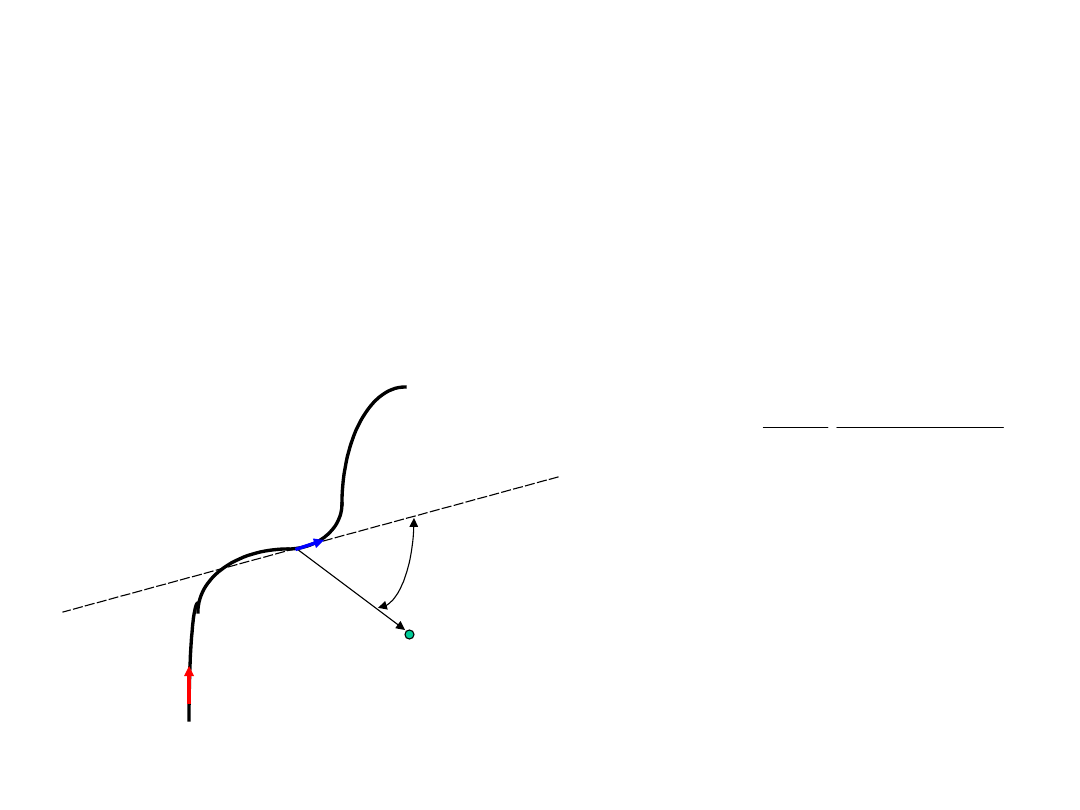
Prawo Biota-Savarta

x

x

i

P

r



dl

dB

Obliczając indukcję
B pola
magnetycznego w
dowolnym punkcie
P dzielimy prąd na
dowolnie małe
elementy – odcinki
dl przewodu z
prądem o
natężeniu i (mają
one kierunek

stycznej do przewodu) i obliczamy wkłady dB
wnoszone do wartości indukcji pola przez
każdy z tych nieskończenie małych elementów.

Prawo Biota-Savarta

Zgodnie z prawem Biota-Savarta, wartość
liczbowa elementarnej indukcji dB pola
wytworzonego przez elementarny prąd idl:

x

x

i

P

r



dl

dB

2

sin

4

r

dl

i

dB











 dB

B

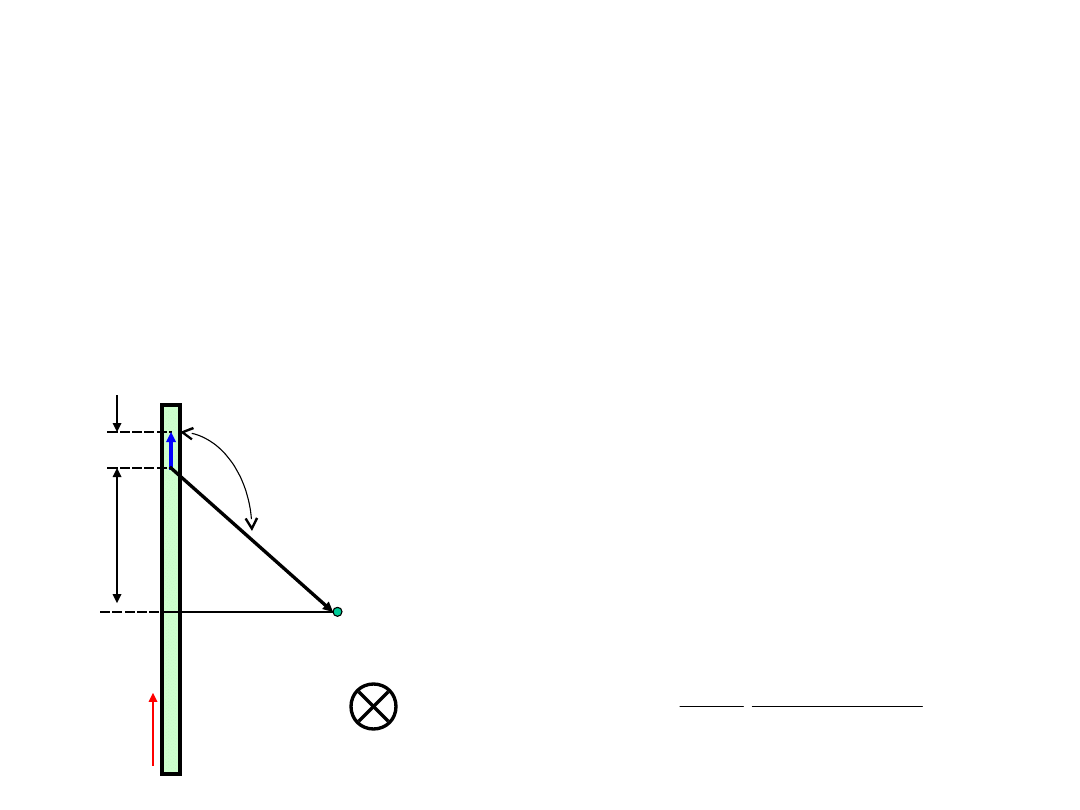
Prawo Biota-Savarta -przykład

Obliczmy indukcję magnetyczną B w
dowolnym punkcie pola magnetycznego P
jakie wywoła prąd o natężeniu i płynący
przez długi prostoliniowy przewód.

i

P

R

d

x

x

r

dB



Wielkość wkładu dB do
indukcji pola
magnetycznego w
punkcie P pochodząca
od elementu dx:

2

sin

4

r

dx

i

dB









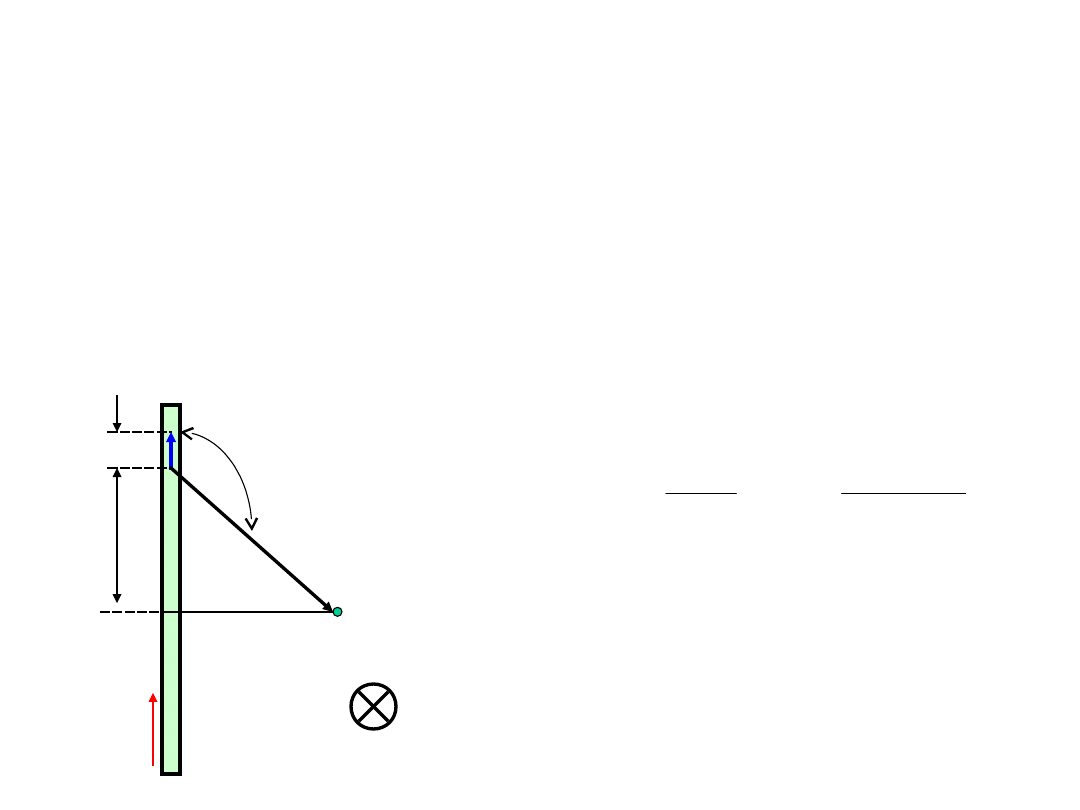
Prawo Biota-Savarta -przykład

Wszystkie wektory dB w punkcie pola P są
tak samo skierowane (poza rysunek,
prostopadle do jego płasz-czyzny). Zatem
całkowita indukcja B:

i

P

R

d

x

x

r

dB



dx

r

i

dB

B

x

x

















2

sin

4







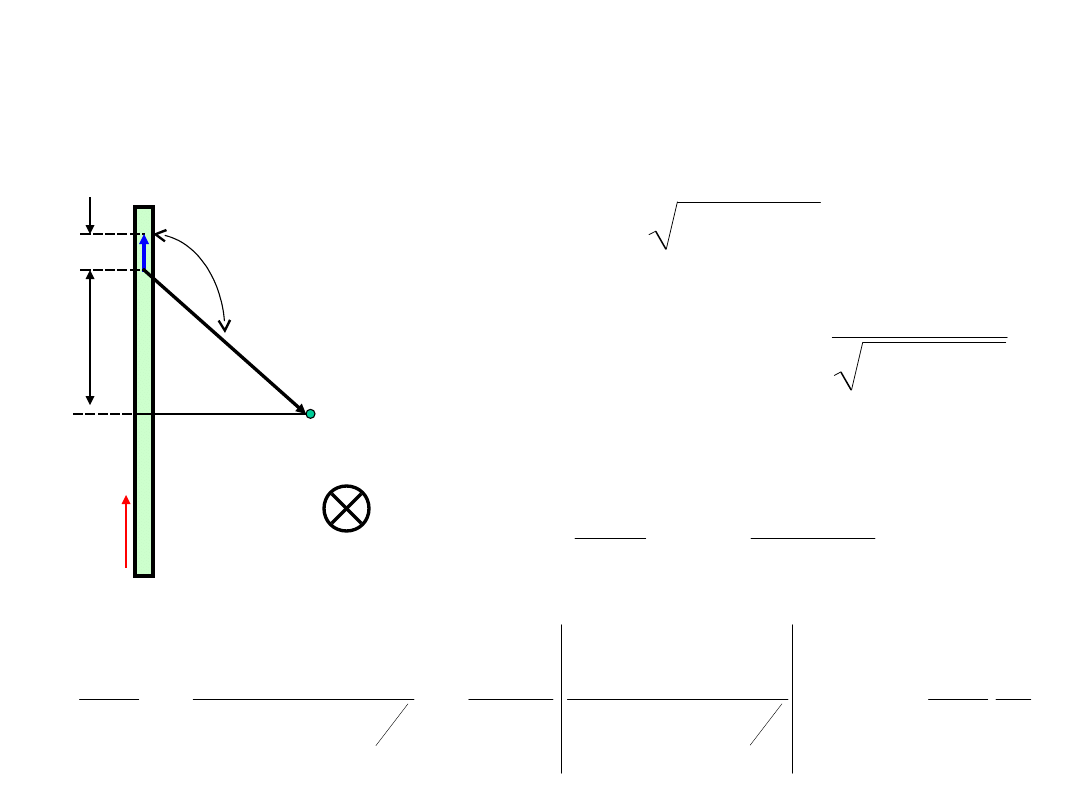
Prawo Biota-Savarta -przykład

i

P

R

d

x

x

r

dB

















dx

r

i

B

x

x

2

sin

4







2

2

R

x

r









2

2

sin

sin

R

x

R























R

i

R

x

x

R

i

R

x

Rdx

i

x

x













2

4

4

2

1

2

2

2

3

2

2





























Natężenie pola magnetycznego

B

Dla długiej cewki:

gdzie: l – długość cewki

l

Iz

B





Natężenie pola magnetycznego

Wektor indukcji magnetycznej
B i wektor natężenia pola
magnetycznego są z sobą
związane zależnością:

H

B





Prawo przepływu

Napięcie magnetyczne równomiernego pola na
odcinku obwodu magnetycznego o długości l:

i

mi

Hl

U 

W całym obwodzie magnetycznym, dla k
odcinków:







k

i

k

mi

Hl

U

1

1

Ponieważ suma wszystkich spadków
napięcia wzdłuż obwodu magnetycznego
jest równoważona przez przepływ:







Iz

Hl

k

i

1

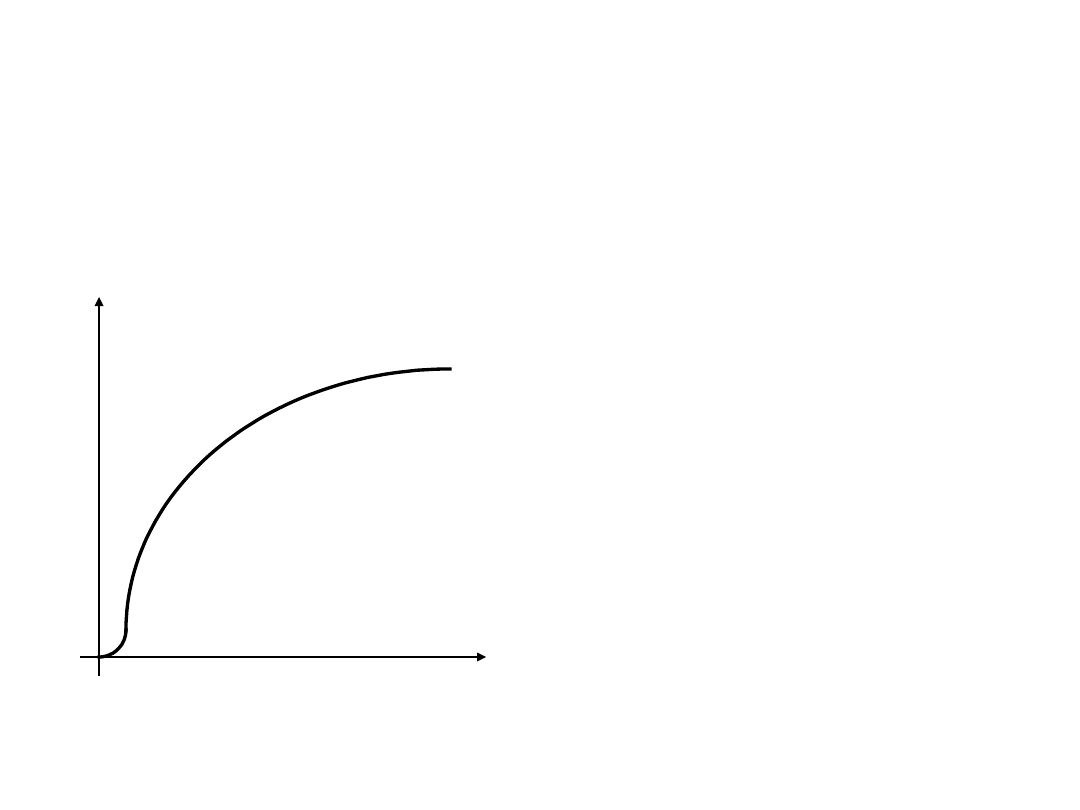
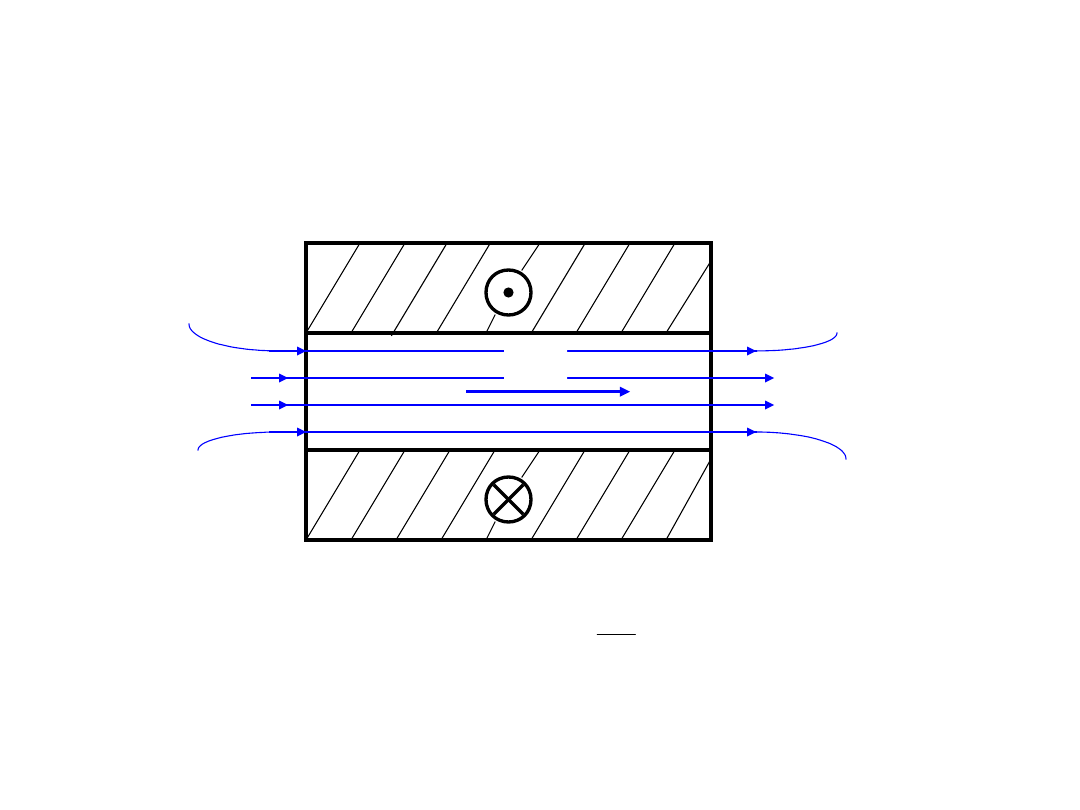
Pole magnetyczne w materiałach

ferromagnetycznych

H

B

0

H

B





Pierwotna
charakterystyka
magnesowania –
wyznaczana dla próbki
całkowicie
rozmagnesowanej.

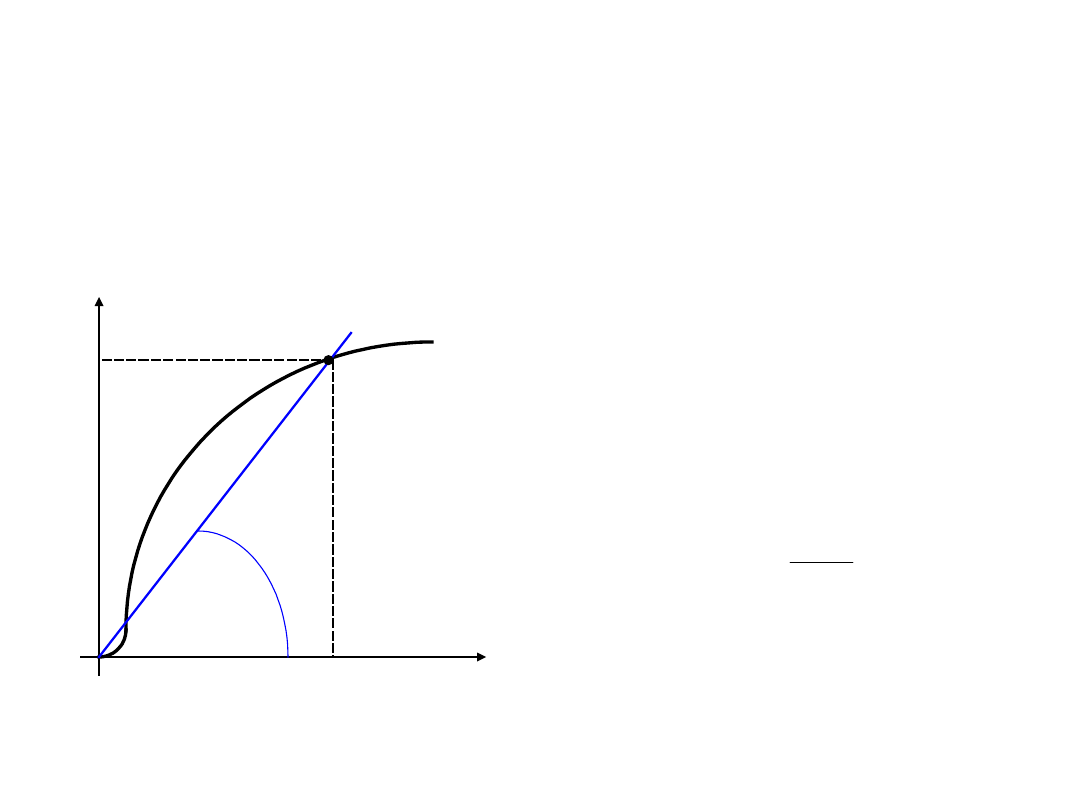
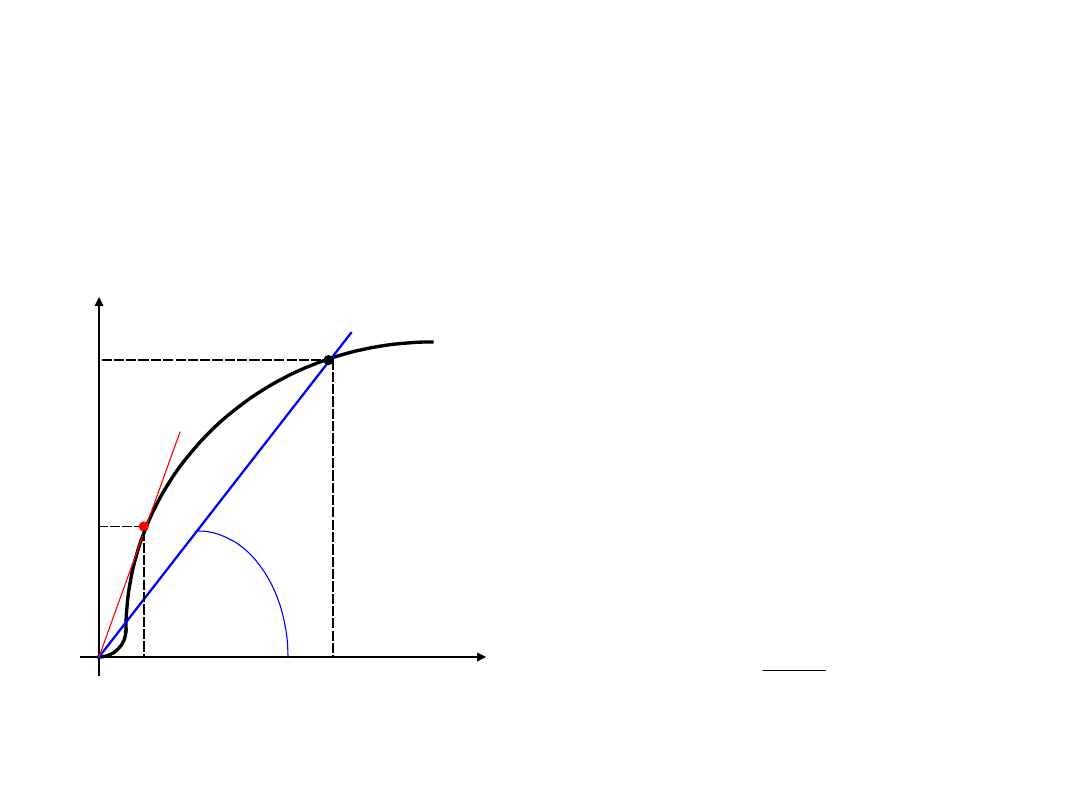
Pole magnetyczne w materiałach

ferromagnetycznych

H

B

0

A

H

A

B

A



-

przenikalność

magnetyczna statyczna

określana w dowol-nym
punkcie A
charakterystyki
magnesowania:

A

A

st

H

B





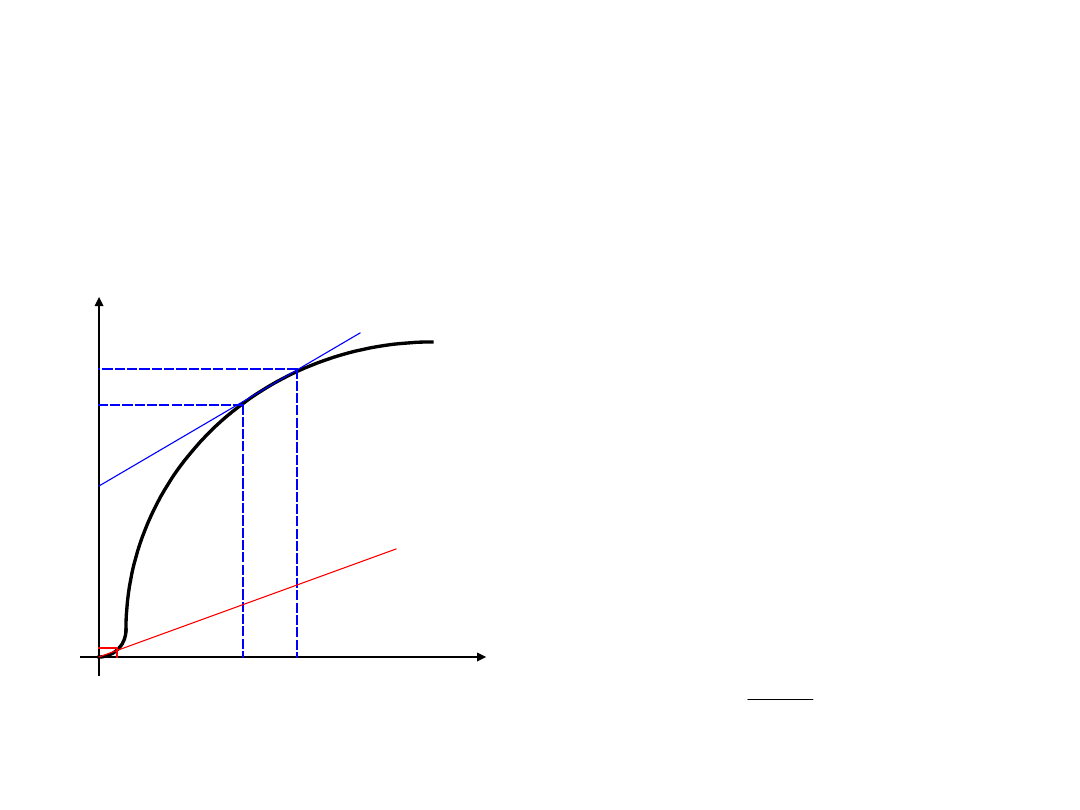
Pole magnetyczne w materiałach

ferromagnetycznych

-

przenikalność

magnetyczna
maksymalna

określana w

punkcie styczności
pierwotnej
charakterystyki
magnesowania i prostej
przechodzącej przez
początek układu
współrzędnych.

B

B

m

H

B





H

B

0

A

H

A

B

A



B

B

B

H

B

Pole magnetyczne w materiałach

ferromagnetycznych

-

przenikalność

magnetyczna dynamiczna

określana jako nachylenie
pierwotnej
charakterystyki
magnesowania:

dH

dB

H

B

H

d













lim

0



H

B

0

dH

dB

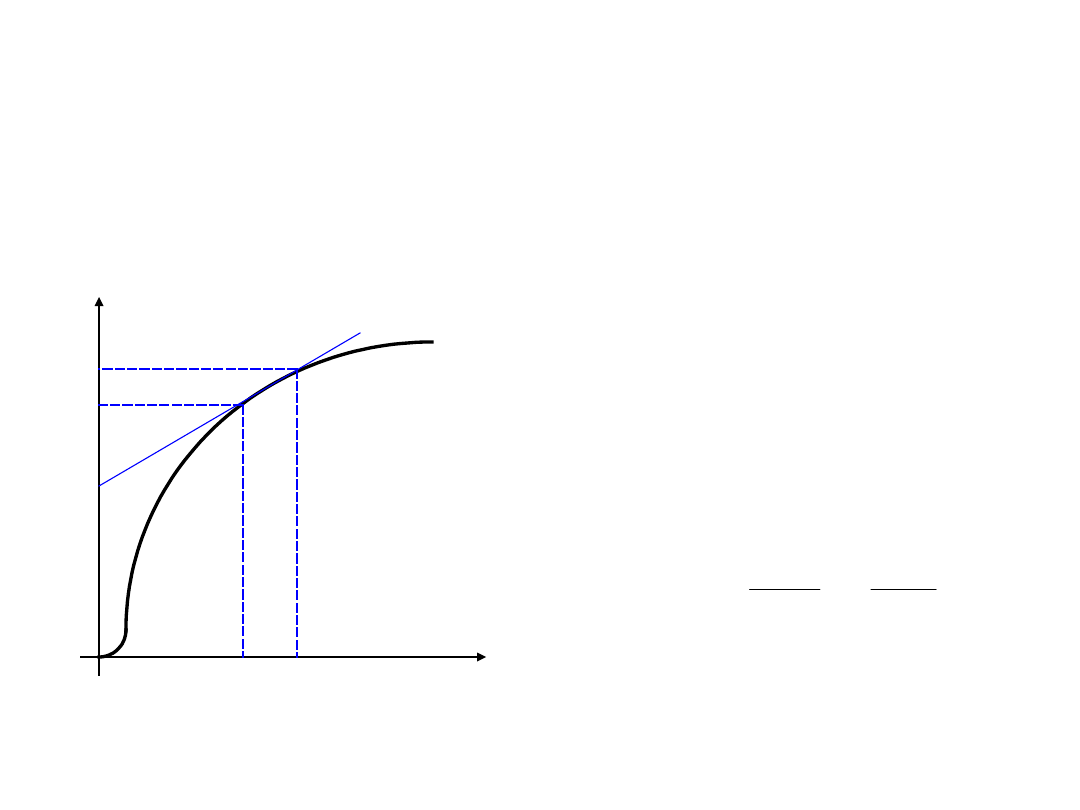
Pole magnetyczne w materiałach

ferromagnetycznych

-

przenikalność

magnetyczna
początkowa

–

przenikalność
dynamiczna w punkcie
H=0, czyli nachylenie
stycznej do pierwotnej
charakterystyki
magnesowania w
początku układu
współrzędnych:

0

0

















H

r

dH

dB



H

B

0

dH

dB

d

B

d

H

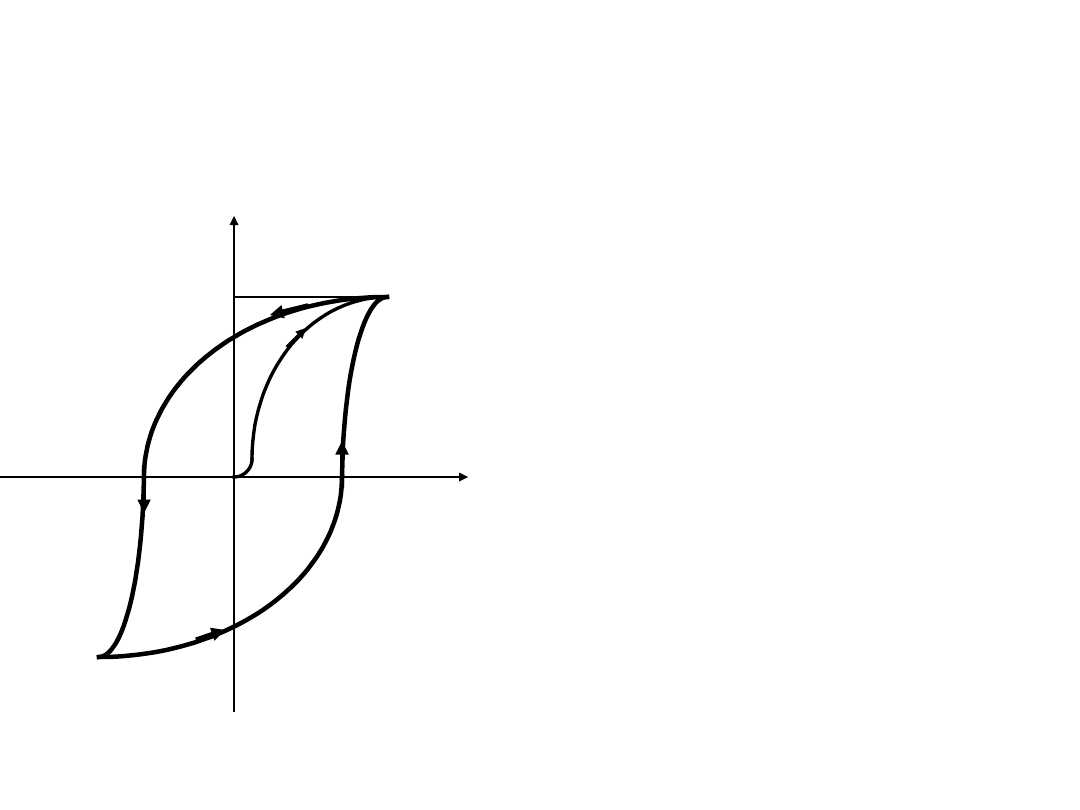
Pętla histerezy

+ H – w punkcie a,

- H – w punkcie d.

Gdy H do 0, B = B

r

-

induk- cja pozostałości

magnetycznej

(remanencja).

B = 0 (w punkcie c) gdy
natężenie H

c

= - H -

natężenie powściagające
(koercja).

Maksymalna wartość
indukcji – indukcja
nasycenia (B

s

)

0

a

b

c

d

B

H

B

s

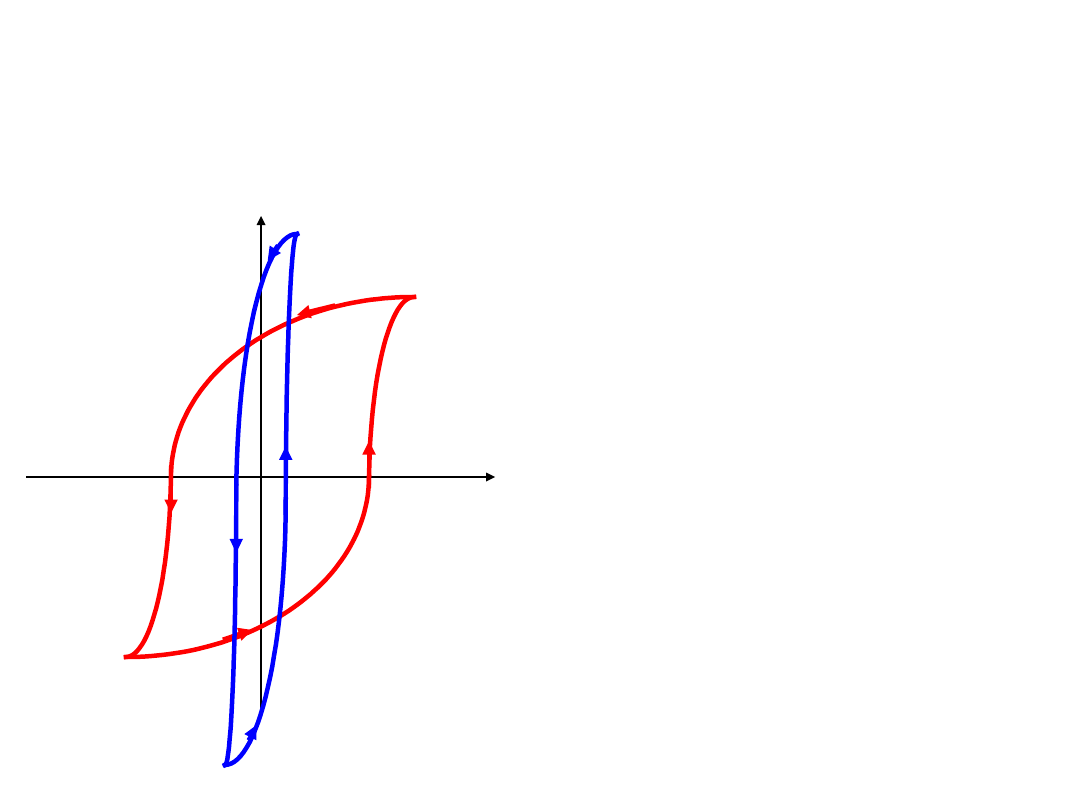
Pętla histerezy

b

a

a

– pętla z małymi

stratami dla
materiałów magnetycz-
nych miękkich

b

- pętla z dużymi

stratami, dla
materiałów magnetycz-
nych twardych

Rodzaj

materiału

B

s

[T]

B

r

[T]

H

c

[A/m]

Zastosowanie

Materiały magnetyczne miękkie

Żeliwo

1,6

0,5

400

Korpusy maszyn

elektrycznych

Permaloj A

0,95

0,6

3,5

Wzmacniacze

magnetyczne,

przekaźniki, przyrządy

pomiarowe

Materiały magnetyczne twarde

Blacha

gorąco-

walcowana

2,0

1,1

20 - 70

Obwody magnetyczne

maszyn

Blacha

zimno-

walcowana

2,0

12

Transformatory

Stop AlNiCo

11,

5

0,5

1

2000065

000

Magnesy trwałe

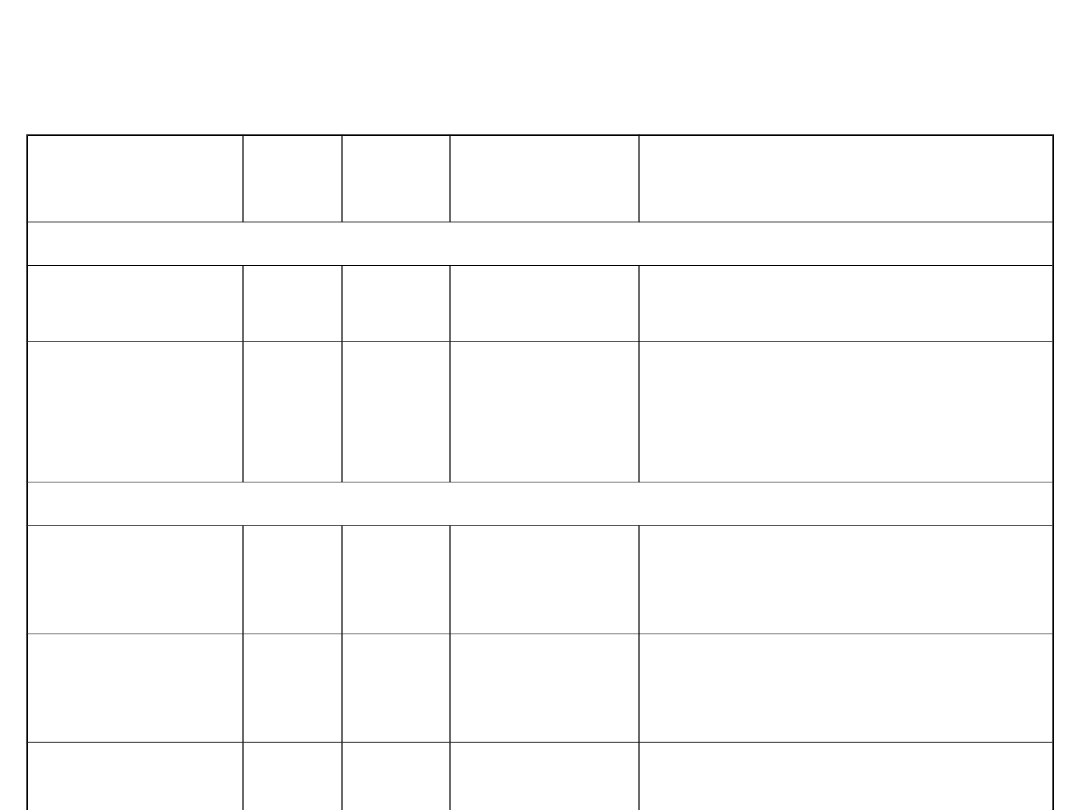
Parametry materiałów

magnetycznych

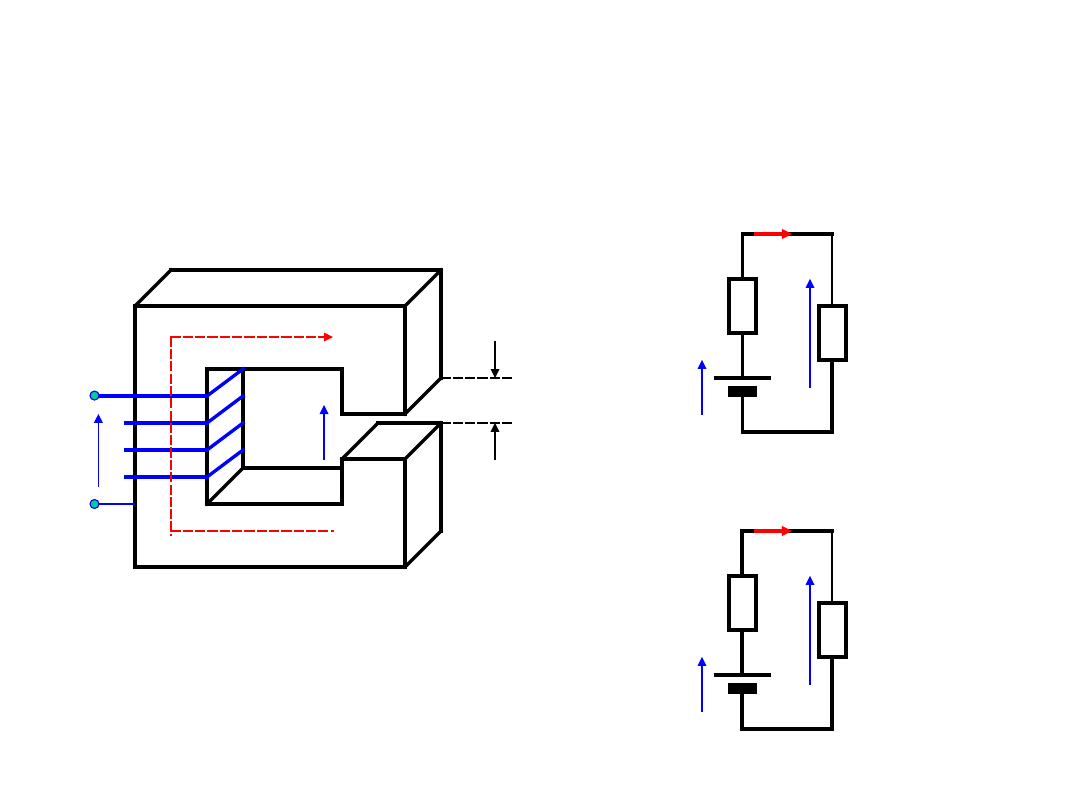
Obliczanie obwodów

magnetycznych

=I

z





R

m

=R

m

R

mFe

=R

mw

U

m

R

w

R

U

E

I

R

mw

R

m

U

m





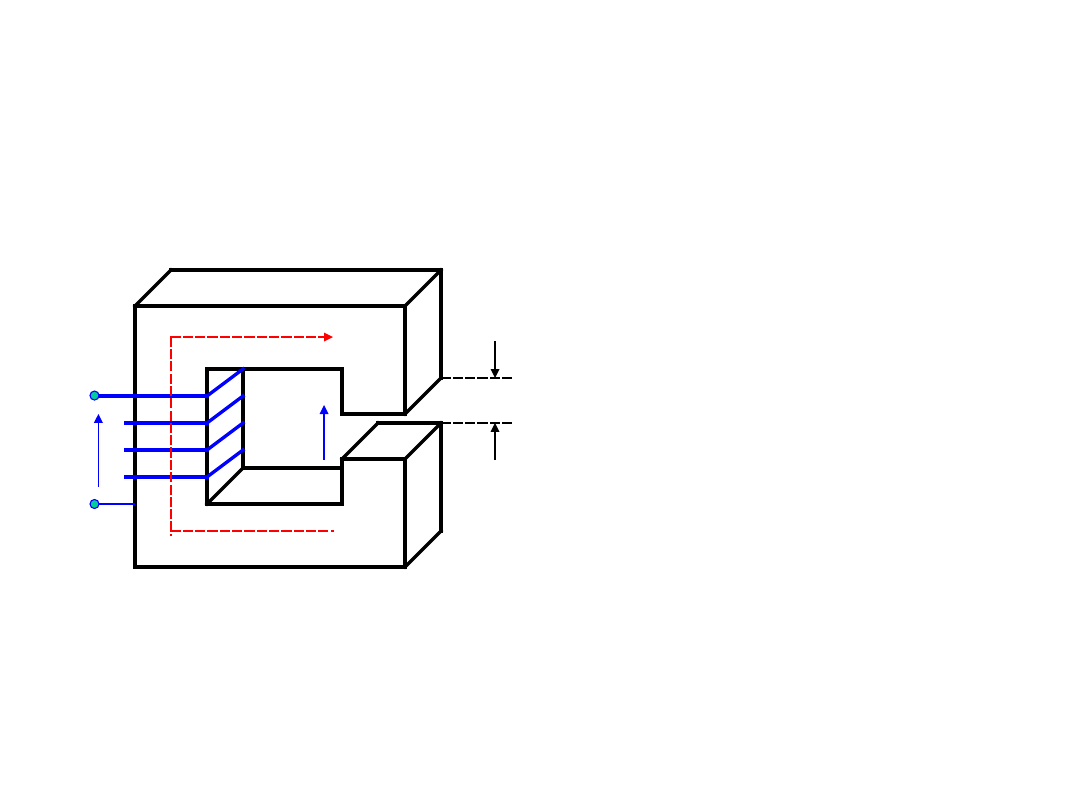
Obliczanie obwodów

magnetycznych

=I

z





R

m

=R

m

R

mFe

=R

mw

U

m

Obliczanie obwodu
magnetycznego
polega głównie na
wyznaczeniu siły
magnetomotoryczne
j (przepływu



= Iz)

niezbędnej do
wytworze- nia
strumienia
magnetycz- nego



przy określonym
materiale i
wymiarach
geometrycznych
obwodu.

Obliczanie obwodów

magnetycznych

W obwodzie nierozgałęzionym złożonym z
szeregowo połączonych odcinków o różnej
przenikalności magnetycznej lub o różnym
przekroju, mając dany strumień  oblicza

się:

1. Indukcję B dla każdego odcinka: B =  / S
2. Natężenie pola H z krzywej B(H) dla
poszczególnych gatunków materiałów.

3. Przepływ I

ż

= H

1

l

1

+ H

2

l

2

+ ....

+ H

n

l

n

potrzebny do wytworzenia żądanego
strumienia.

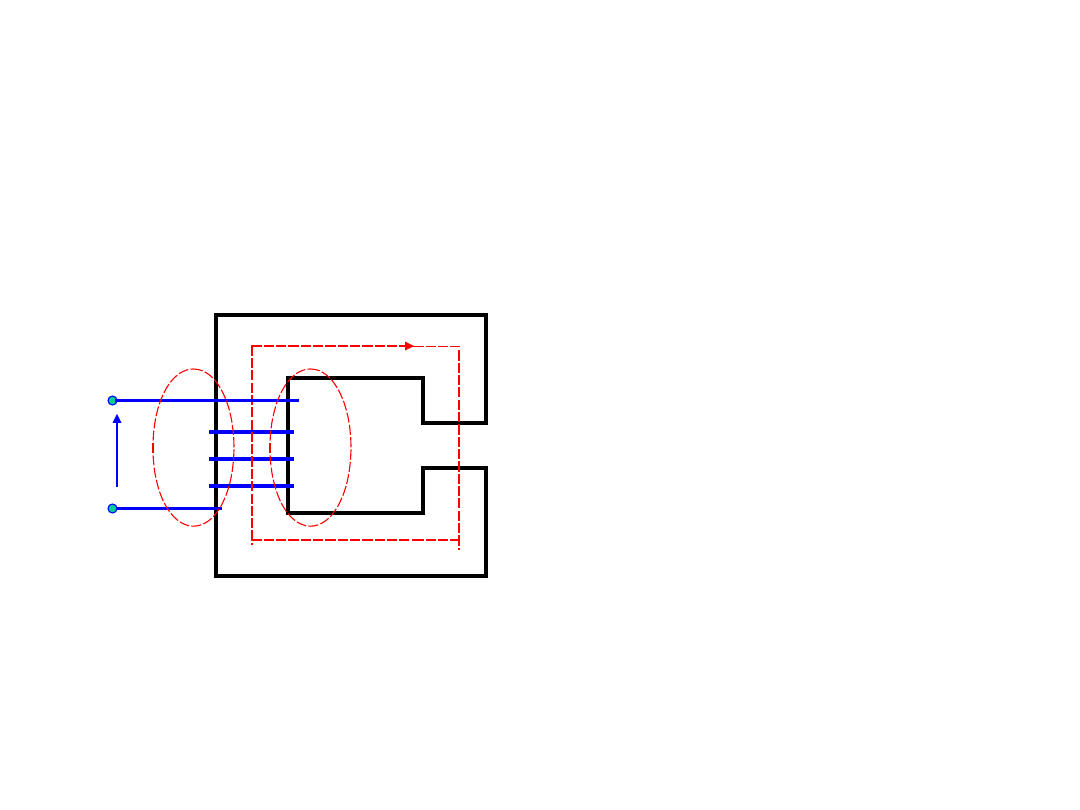
Obliczanie obwodów

magnetycznych

Jeżeli w obwodzie
magnetycznym jest
szczelina
powietrzna, należy
w obliczeniach
uwzględnić
dodatkowo
strumień
rozproszenia, czyli
około 10 ÷ 20%
całkowitego
strumienia.







r

Indukcja elektromagnetyczna

Prawo przepływu określa zależność między
prądem elektrycznym

(przyczyna)

a

wywołanym przez niego polem
magnetycznym

(skutek).

Prawo indukcji elektromagnetycznej opisuje

proces odwrotny

- prawidłowość, przy której

w pewnych warunkach pole magnetyczne
wywołuje napięcie a zatem i prąd
elektryczny.

Indukcja elektromagnetyczna

Indukowane napięcie może być
wytwarzane:
- w nieruchomych przewodach przez
zmienne w czasie pole magnetyczne,
- w ruchomych przewodach przez stałe
w czasie pole magnetyczne,
-w ruchomych przewodach przez
zmienne w czasie pole magnetyczne.

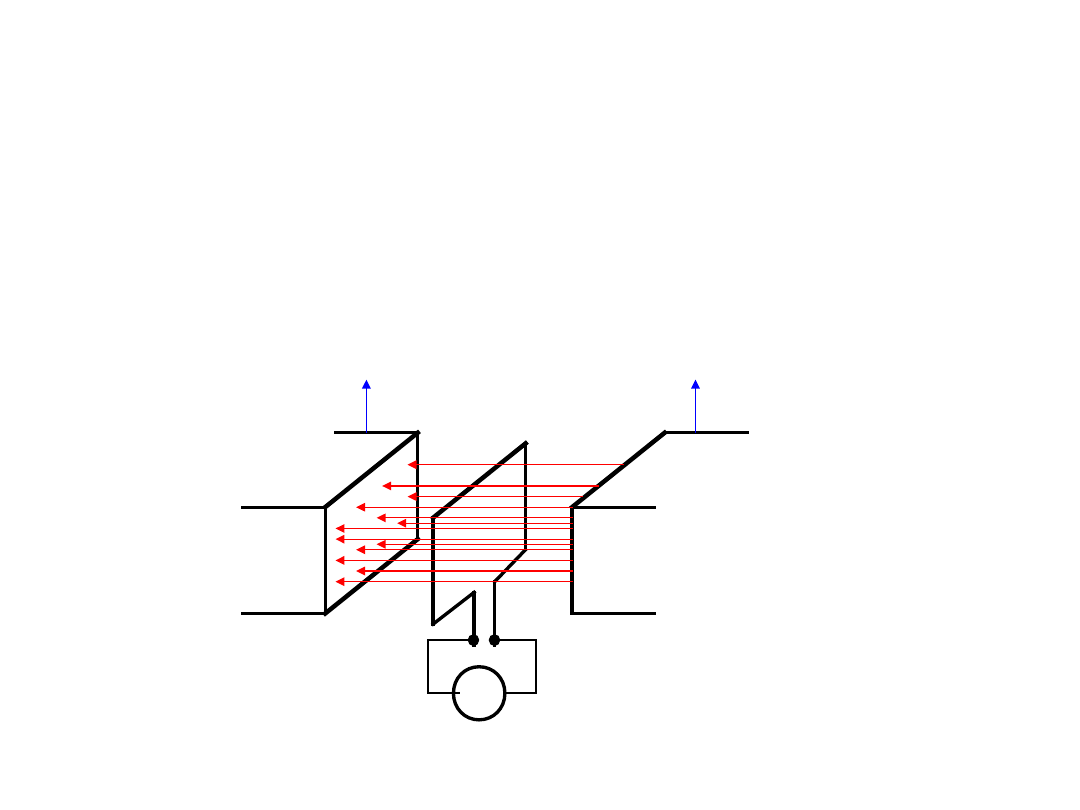
Indukcja elektromagnetyczna

Nieruchomy przewód w zmiennym w czasie polu

magnetycznym.

V



v

v

N

S

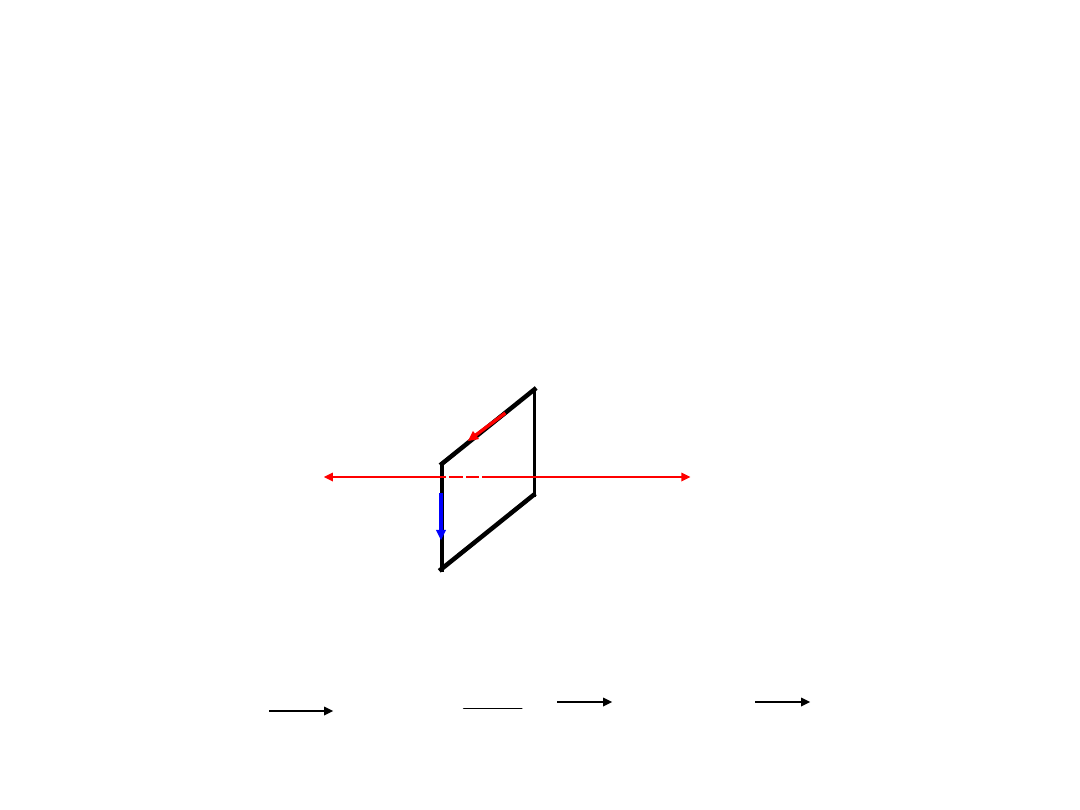
Indukcja elektromagnetyczna

Nieruchomy przewód w zmiennym w czasie polu

magnetycznym.

d

i

d

i

e

dt

d

e







i

 =

var



i

Indukcja elektromagnetyczna

Nieruchomy przewód w zmiennym w czasie polu

magnetycznym.

dt

d

e







Jeżeli obwód elektryczny składa się nie z
jednego , a z z zwojów, to z obwodem
skojarzony jest strumień pola  obejmujący

wszystkie zwoje. Wówczas:

z

z





i prawo indukcji ma postać:

czyli:

dt

d

z

e

z







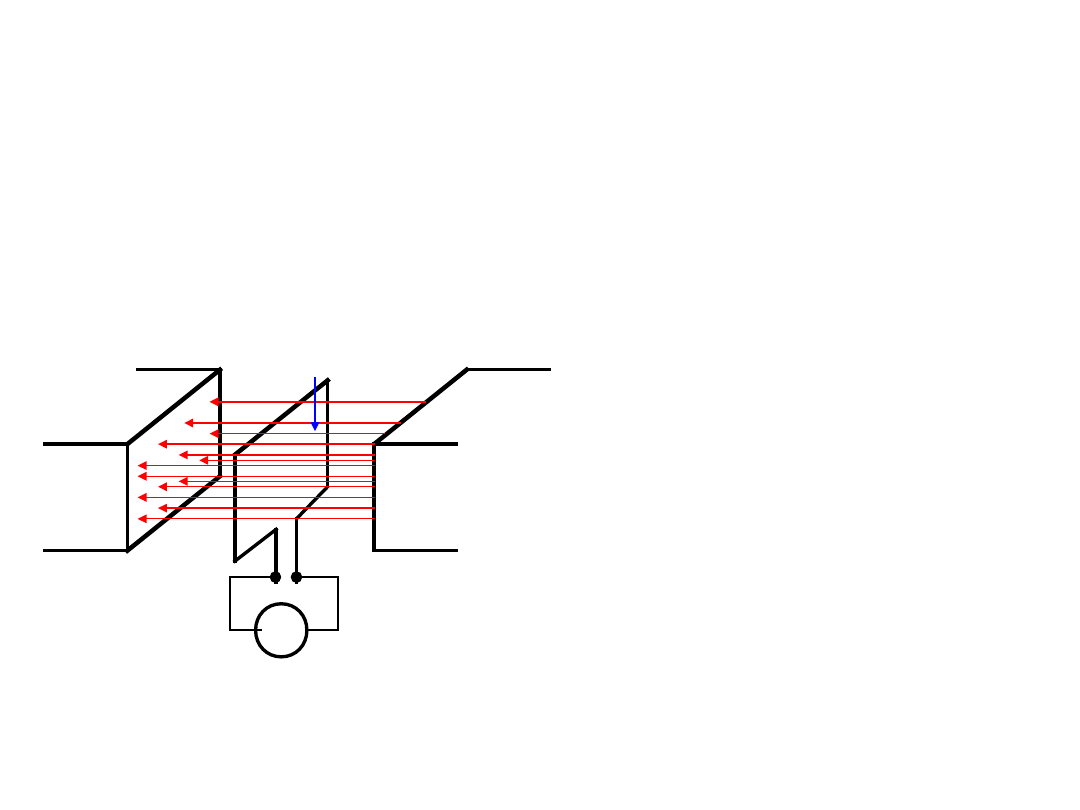
Indukcja elektromagnetyczna

Ruchomy przewód w stałym w czasie polu

magnetycznym.

V



v

N

S

Zmiana strumienia
sprzężonego ze
zwojem o długości l
w polu określonym
przez wartość
indukcji
magnetycznej B:

Bldx

BdS

d







Indukcja elektromagnetyczna

Ruchomy przewód w stałym w czasie polu

magnetycznym.

Bldx

BdS

d







poniewa
ż:

Blv

dt

dx

Bl

dt

d







wobec tego
SEM:

Blv

e 



Jeżeli prędkość ruchu przewodu jest stała, to
napięcie indukowane też ma wartość stałą.

Blv

E





Indukcja elektromagnetyczna

Indukowane napięcie musi mieć taki zwrot,
aby wywołany przez nie w obwodzie
zamkniętym prąd przeciwdziałał przyczynie,
czyli nie pozwalał na wzrost strumienia.

Zwrot tego napięcia określa reguła prawej
dłoni:

jeżeli linie strumienia pola

magnetycznego zwrócone są ku otwartej dłoni
prawej ręki, a kciuk wskazuje ruch prze-wodu,
to pozostałe palce wskazują zwrot
indukującego się napięcia.

Ruchomy przewód w stałym w czasie polu

magnetycznym.

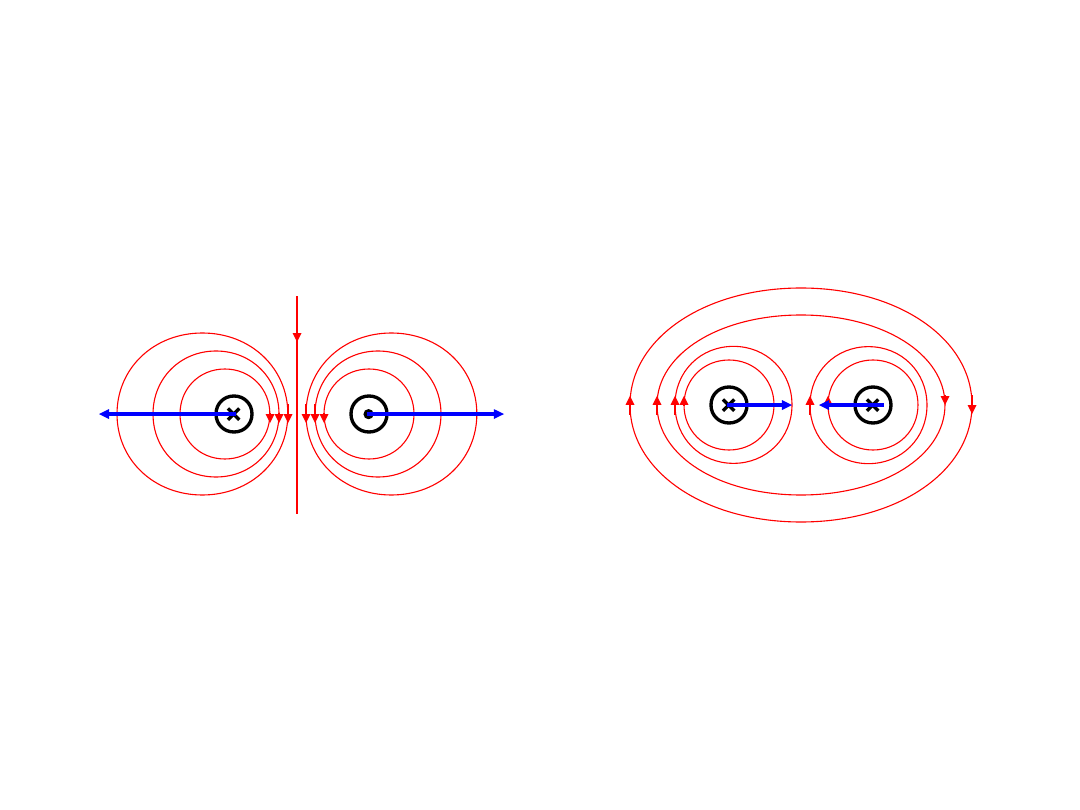
Siła oddziaływania dwóch

przewodów równoległych

F

F

F

F

Siły oddziaływania między przewodami są
prostopadłe do kierunku linii strumienia pola
magnetycznego i do kierunku prądu.

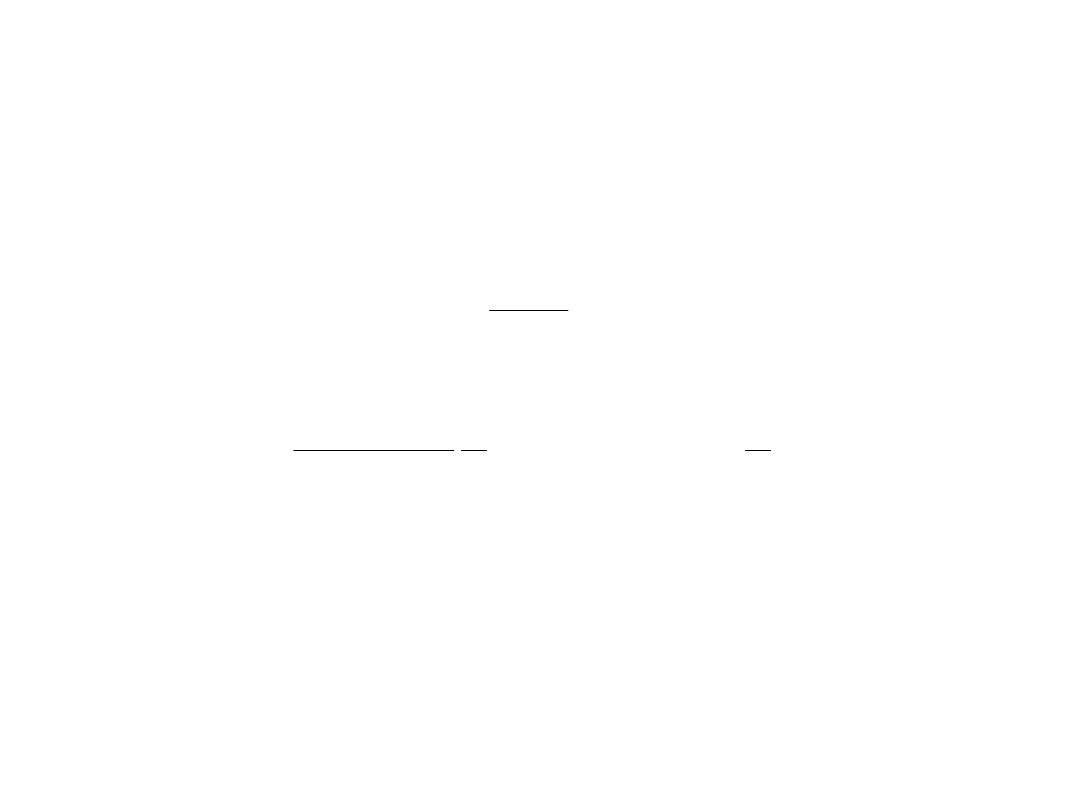
Siła oddziaływania dwóch

przewodów równoległych

a – odstęp między
przewodami

l – długość przewodów

2

1

0

2

I

I

a

l

F







2

1

7

2

1

7

10

2

2

10

4

I

I

a

l

I

I

a

l

F

















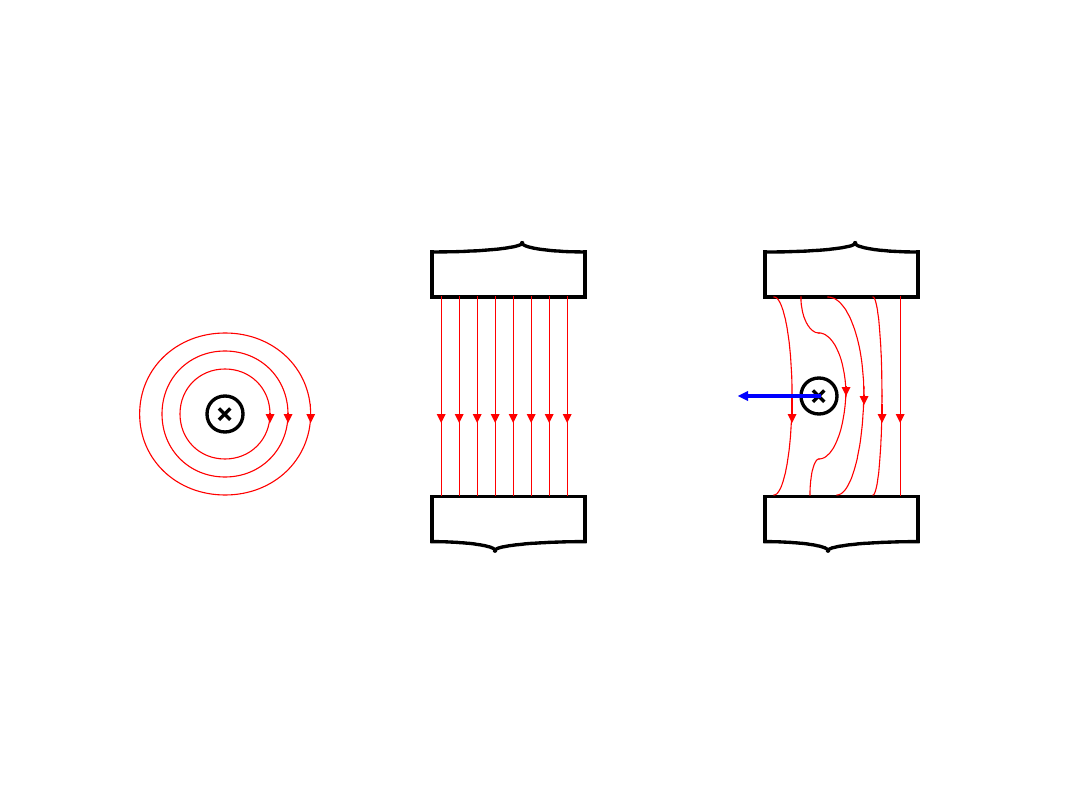
Prawo Laplace’a

N

S

N

S

F

Pole
przewodu

Pole
wypadkowe

Pole drugiego
przewodu
traktowane jako
pole magnetyczne
zewnętrzne

Prawo Laplace’a

Wzajemne oddziaływanie dwóch przewodów z
prądem można przedstawić jako oddziaływanie
na przewód o długości l wiodący prąd I pola
magnetycznego o gęstości linii sił, czyli indukcji
B wywołanego przez drugi przewód.
Ponieważ:

a

I

H

B







2

2

0

0





a

2

1

0

2

I

I

a

l

F







to
dla

I

I 

1

lIB

F 

Prawo Laplace’a

Ogólnie l i B są wektorami, przy czym ma
zwrot i kierunek prądu tworzącego pole
magnetyczne zewnętrzne (I

2

).

Iloczyn wektorowy daje w wyniku
wektor skierowany pod kątem prostym do
płaszczyzny utworzonej przez wektory.

l







B

l











B

l

I

F











Prawo Laplace’a





B

l

I

F











Ponieważ
:

t

q

I 

to:





B

v

q

F











gdzie: - prędkość w m/s

v

Prawo Laplace’a

Układy wektorów:

lub:

tworzą trojkę prawoskrętną.

Kierunek można wyznaczyć odnosząc do
iloczynu wektorowego lub
regułę śruby prawoskrętnej lub lewej
dłoni:

-

jeżeli wektor indukcji wchodzi do

otwartej dłoni lewej ręki, a wyciągnięte cztery
palce pokrywają się ze zwrotem prądu, to
wyciągnięty kciuk wskazuje zwrot siły
działającej na przewód.

F

B

l







,

,

F

B

v





 ,

,

F







B

l











B

v





B



Indukcyjność własna

Siła elektromotoryczna indukuje się niezależnie
od przyczyny zmiany strumienia
magnetycznego. Zmianę strumienia objętego
przez obwód może wywołać prąd płynący w tym
samym obwodzie, jeżeli w dowolnie małym
czasie dt wystąpi zmiana prądu o di.
Zmianę prądu można wywołać jednorazowo
przez proces łączeniowy (przerywanie lub
załączanie obwodu) lub okresowo, jeśli płynący
prąd jest prądem przemiennym.

Indukcyjność własna

Przy zmianie prądu w obwodzie indukuje się siła
elektromotoryczna samoindukcji, której wartość
określa prawo indukcji elektromagnetycznej.

dt

d

z

e







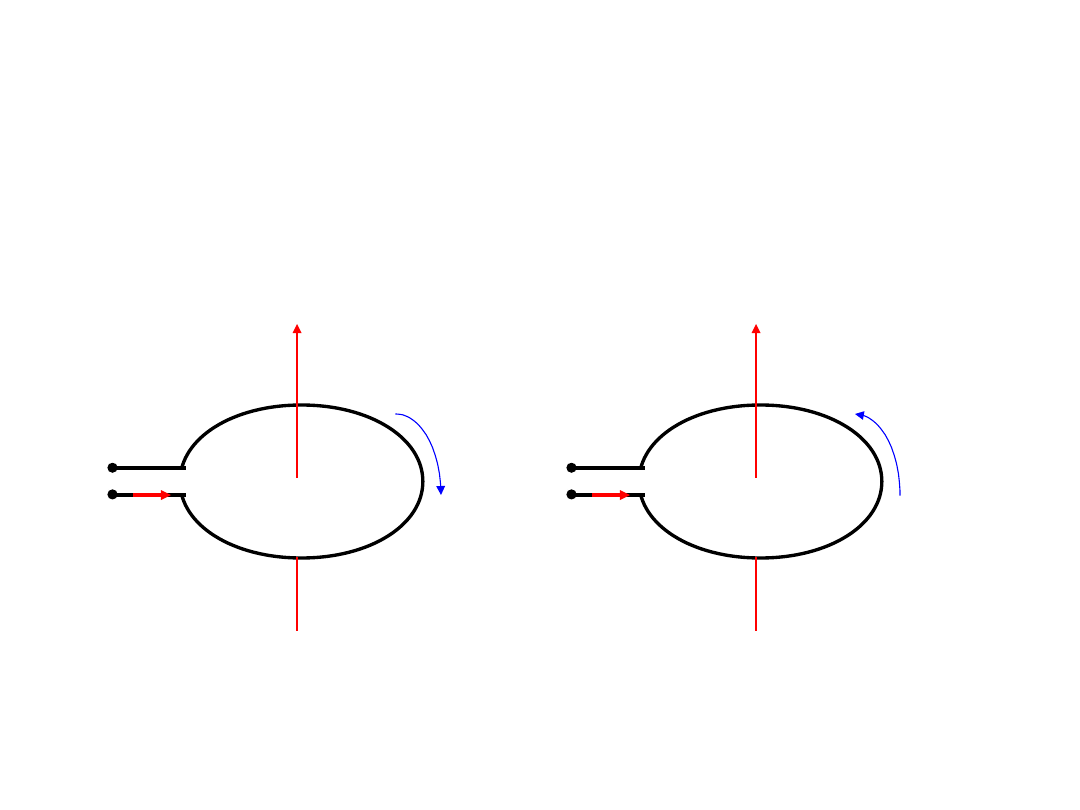
Indukcyjność własna

I+di



+d

e

L

I-di

 -d

e

L

Indukcyjność własna

Poniew
aż:

m

m

R

Iz

R









dt

di

L

dt

di

R

z

e

m

L









2

gdzie:

L - indukcyjność własna

przewodu (lub cewki)

l

S

z

R

z

L

r

m





0

2

2





 

   

 

H

s

A

Vs

i

t

e

L

1

1

1

1

1

1

1













Indukcyjność własna

Zgodnie z regułą Lenza SEM e

L

przeciwdziała

zmianom prądu, a więc przy wzroście prądu
(I+di) e

L

ma zwrot przeciwny do prądu; przy

zanikaniu prądu (I-di) e

L

ma zwrot zgodny z

prądem.
Aby wzrastający prąd mógł przepłynąć przez
odcinek obwodu o indukcyjności L , musi
przezwyciężyć przeciwdziałającą mu siłę
elektromotoryczną samoindukcji, co oznacza, że
napięcie występujące na indukcyjności:

L

L

e

u





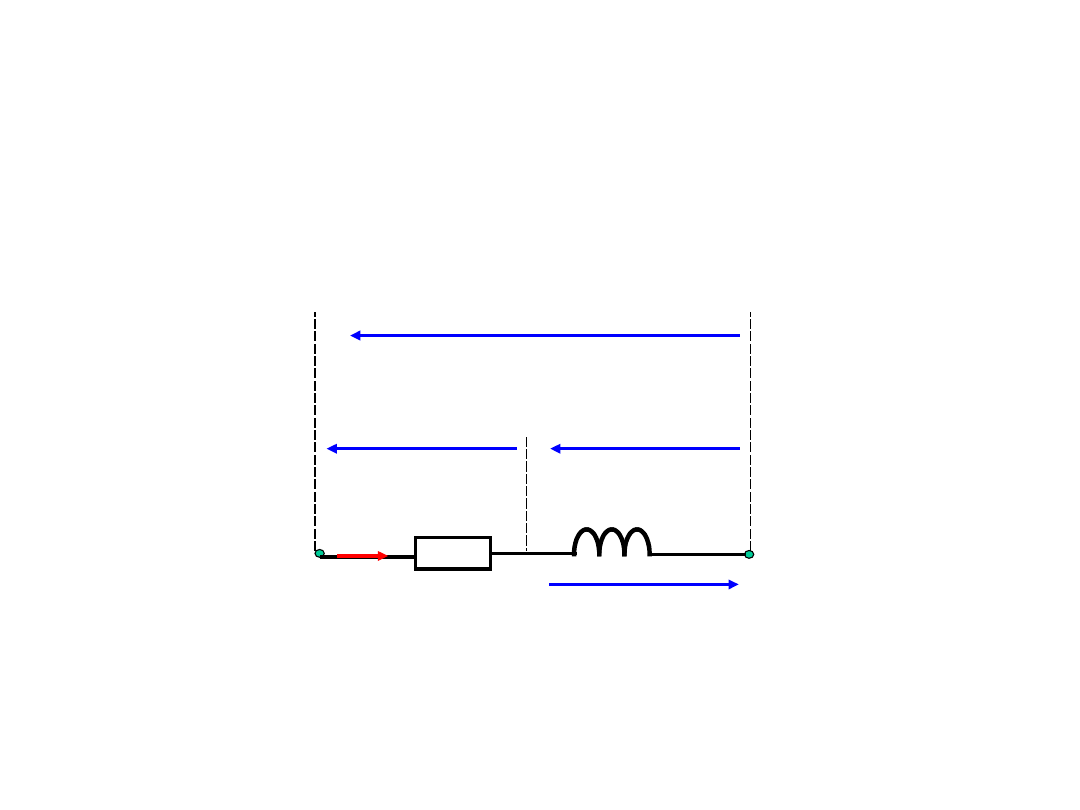
Indukcyjność własna

R

i

u

L

u

R

u

L

=L di/dt

e

L

= - L di/dt

Indukcyjność własna

l

S

z

L

r





0

2



Indukcyjności pojedynczych przewodów są
małe w porów-naniu z indukcyjnością cewek -
duży wpływ liczby zwojów.Indukcyjność zależy
również od przenikalności magnetycznej:

-

cewka nawinięta na rdzeniu magnetycznym ma
większą indukcyjność niż umieszczona w
powietrzu,

- indukcyjność cewki nawiniętej

na rdzeniu nie jest stała lecz zależy od
nasycenia obwodu magnetycznego.

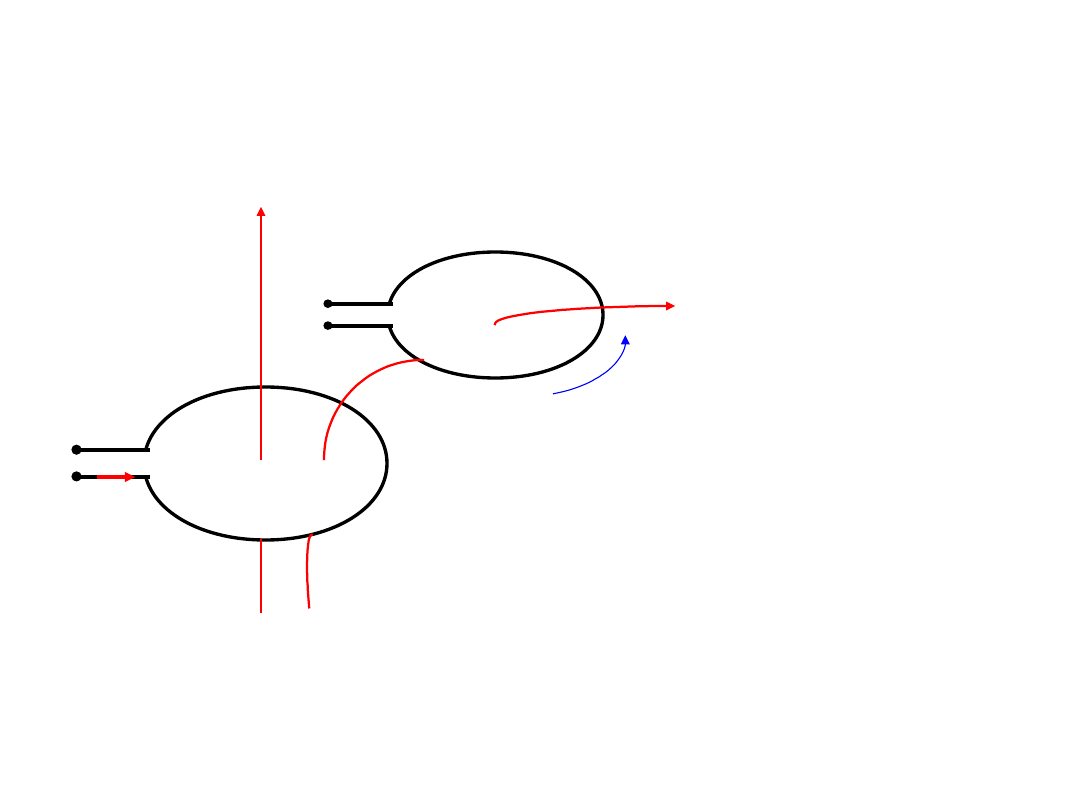
Indukcyjność wzajemna

i

1



11

e

2



12

1

2

Indukowanie SEM w cewce,
która znajduje się w polu
magnetycznym
wytworzonym przez drugą
cewkę nazywa się

indukcją

wzajemną

.

Indukcyjność wzajemna

1

1

1

1

1

1

12

m

R

z

i

k

k









dt

d

z

e

12

2

2







dt

di

L

dt

di

R

z

z

k

e

m

1

12

1

1

2

1

1

2











12

– część strumienia wytworzonego przez

cewkę 1 a oddziałującego na cewkę 2.

Indukcyjność wzajemna

dt

di

L

dt

di

R

z

z

k

e

m

2

21

2

2

2

1

2

1









Analogiczne byłoby oddziaływanie cewki 2 na
cewkę 1. Wówczas w cewce 1 indukowałaby
się SEM, przy zmianie prądu i

2

.

21

12

L

L 

- indukcyjności wzajemne

Indukcyjność wzajemna

Gdy cewki są w pełni sprzężone, tzn. nie
występuje strumień rozproszenia:

2

1

12

L

L

L





Przy niecałkowitym sprzężeniu:

2

1

12

L

L

k

L





Gdzie:

- współczynnik

sprzężenia.

2

1

k

k

k





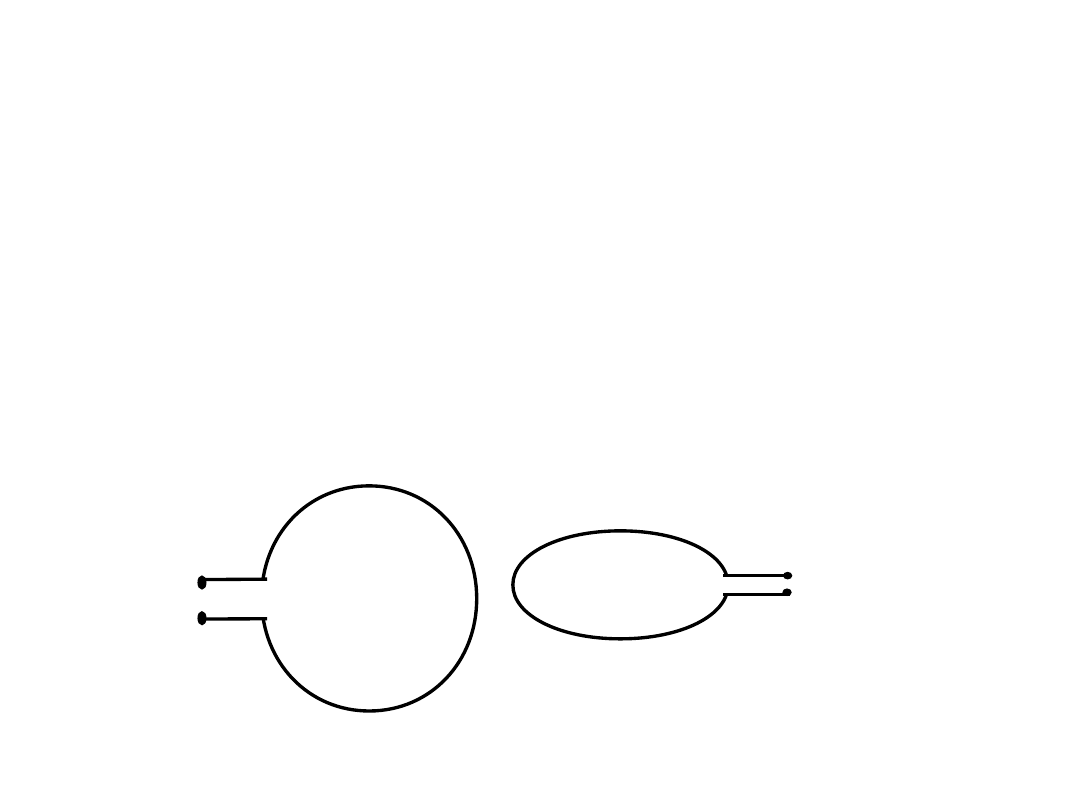
Indukcyjność wzajemna

Współczynnik
sprzężenia:

1

0 

k

0

min



k

- dla cewek, których
powierzchnie są do siebie
prostopadłe

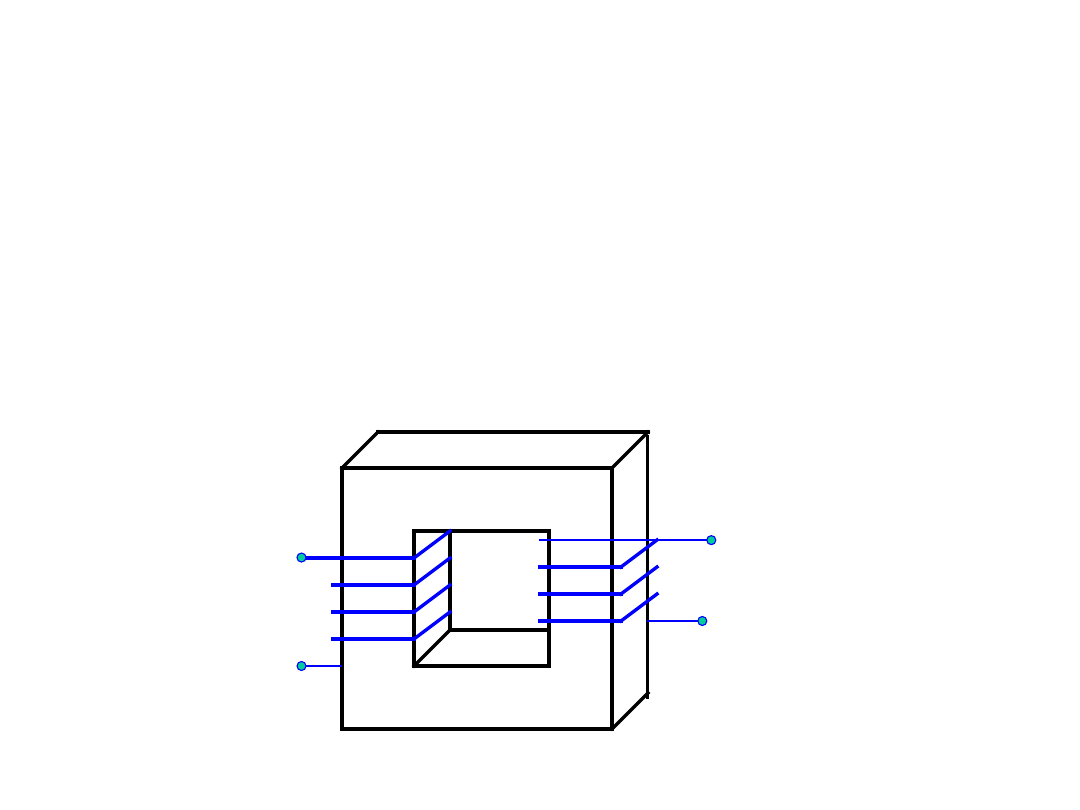
Indukcyjność wzajemna

1

min



k

- dwa uzwojenia nawinięte
współosiowo na wspólnym
rdzeniu z materiału
farromagnetycznego

1



k

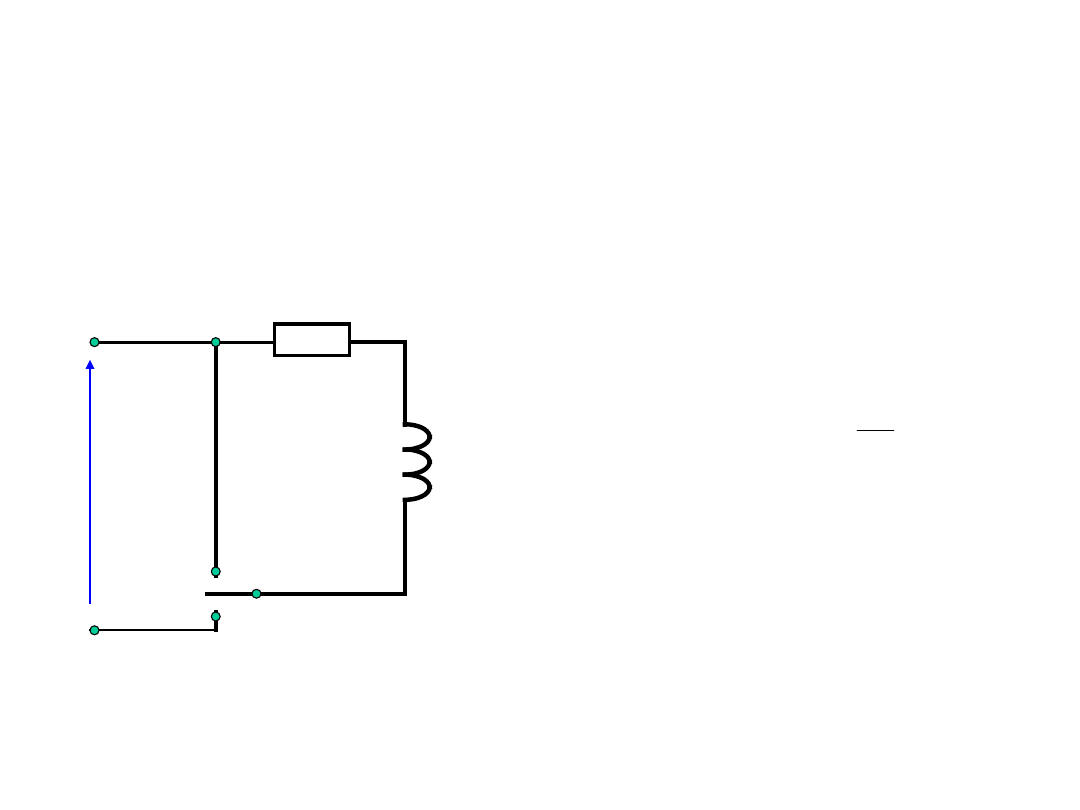
Przebiegi łączeniowe

Obwód z cewka indukcyjną

R

L

U

1

2

Przełącznik p w pozycji
1. Ustalona po pewnym
czasie wartość prądu:

p

R

U

I 

Prąd nie osiągnie tej
wartości od razu,
ponieważ narastaniu
prądu przeciwstawia
się SEM samoindukcji.

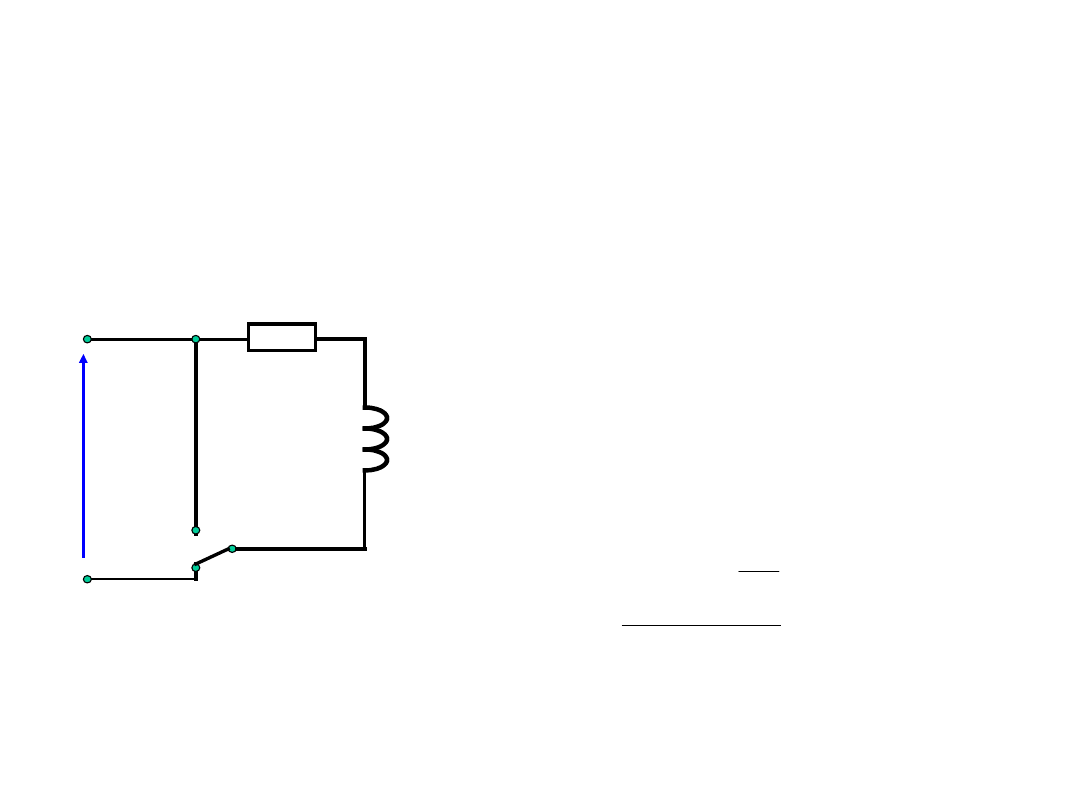
Przebiegi łączeniowe

Obwód z cewka indukcyjną

W czasie narastania prądu
w obwodzie działa
napięcie U i SEM
samoindukcji, wobec
czego, zgodnie z prawem
Ohma:

L

R

U

1

2

p

R

dt

di

L

U

i





Przebiegi łączeniowe

Obwód z cewka indukcyjną

R

dt

di

L

U

i





I

R

U



T

R

L







i

I

T

dt

di





1

dla

0



t

0



i



















T

t

e

I

i

1

T - stała czasowa obwodu

Przebiegi łączeniowe

Obwód z cewka indukcyjną



tg

T



1



















T

t

e

I

i

1

i

t





I

Narastanie
prądu jest tym
szybsze im
mniejsza jest
stała czasowa
obwodu.

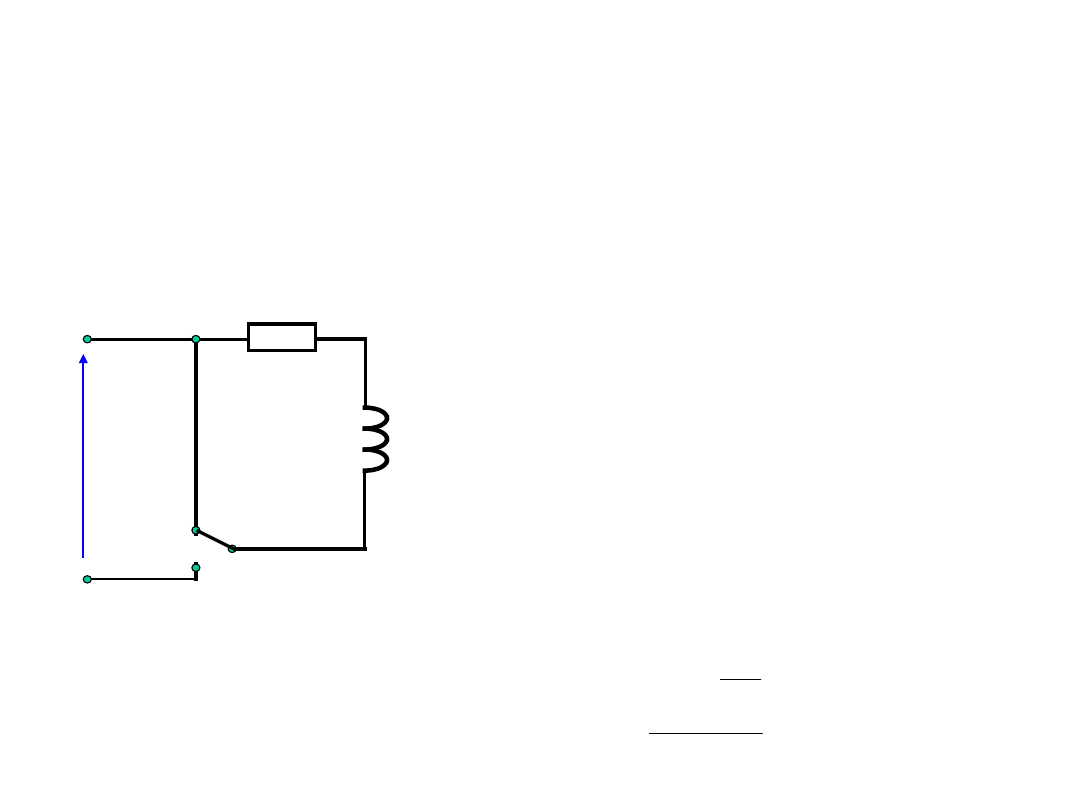
Przebiegi łączeniowe

Obwód z cewka indukcyjną

Przełącznik p w
położeniu 2 – obwód RL
zostaje zwarty, czyli:

L

R

U

1

2

p

0



U

Prąd musi zmaleć do 0,
ale zmniejszaniu się
prądu przeciw-działa
SEM samoindukcji.

Zgodnie z prawem
Ohma:

R

dt

di

L

i





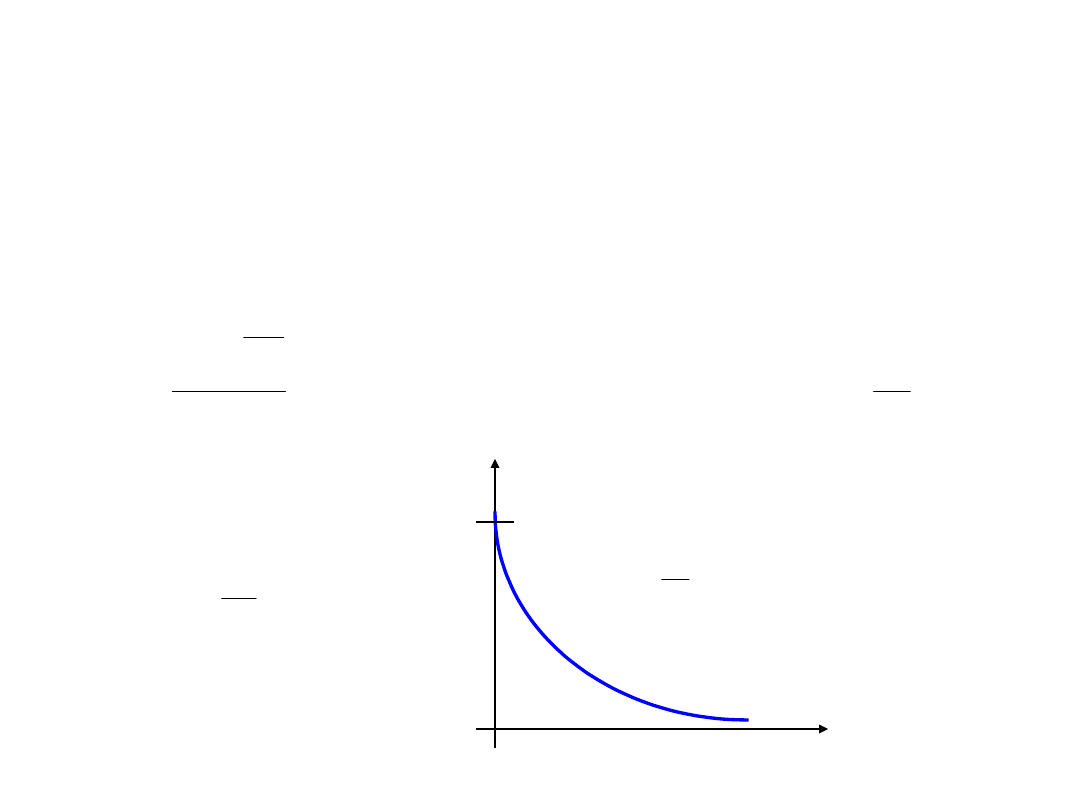
Przebiegi łączeniowe

Obwód z cewka indukcyjną

R

dt

di

L

i





dla

0



t

R

U

I

i





T

t

Ie

i





i

t

I

T

t

Ie

i





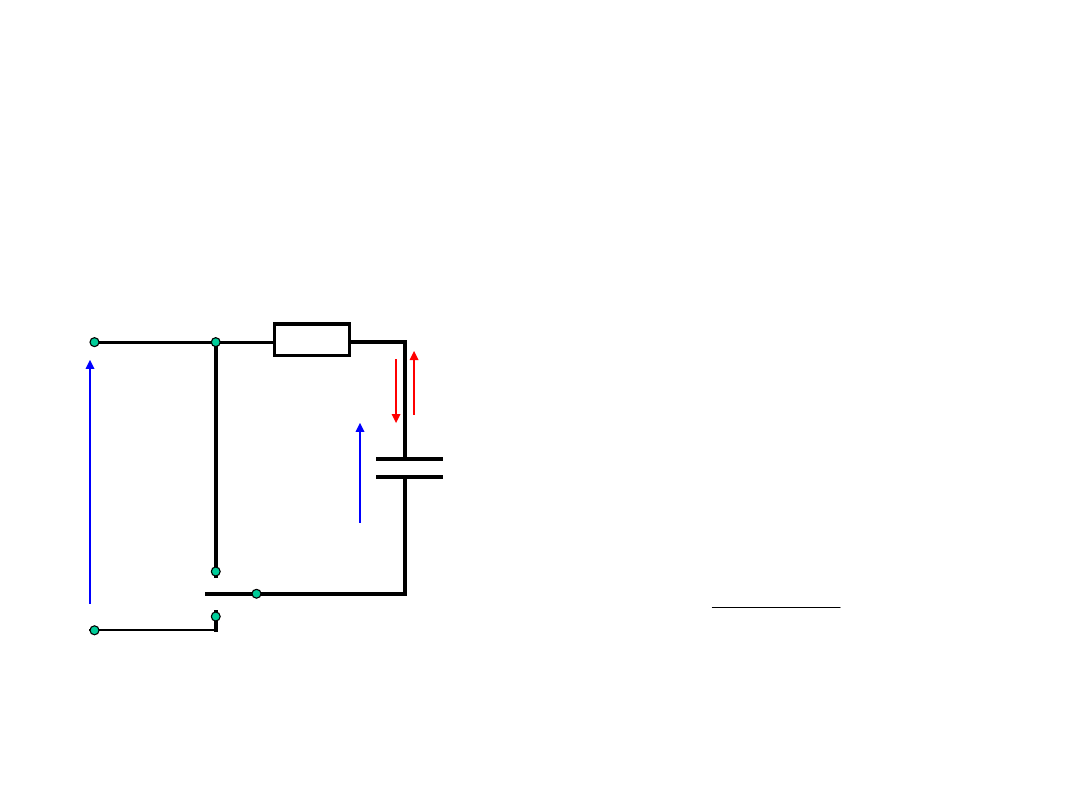
Przebiegi łączeniowe

Obwód z kondensatorem

Przełącznik p w pozycji
1. Popłynie prąd
ładujący kondensator
do uzyskania ładunku
q:

R

u

U

i

C





R

C

U

1

2

u

C

i

C

i

p

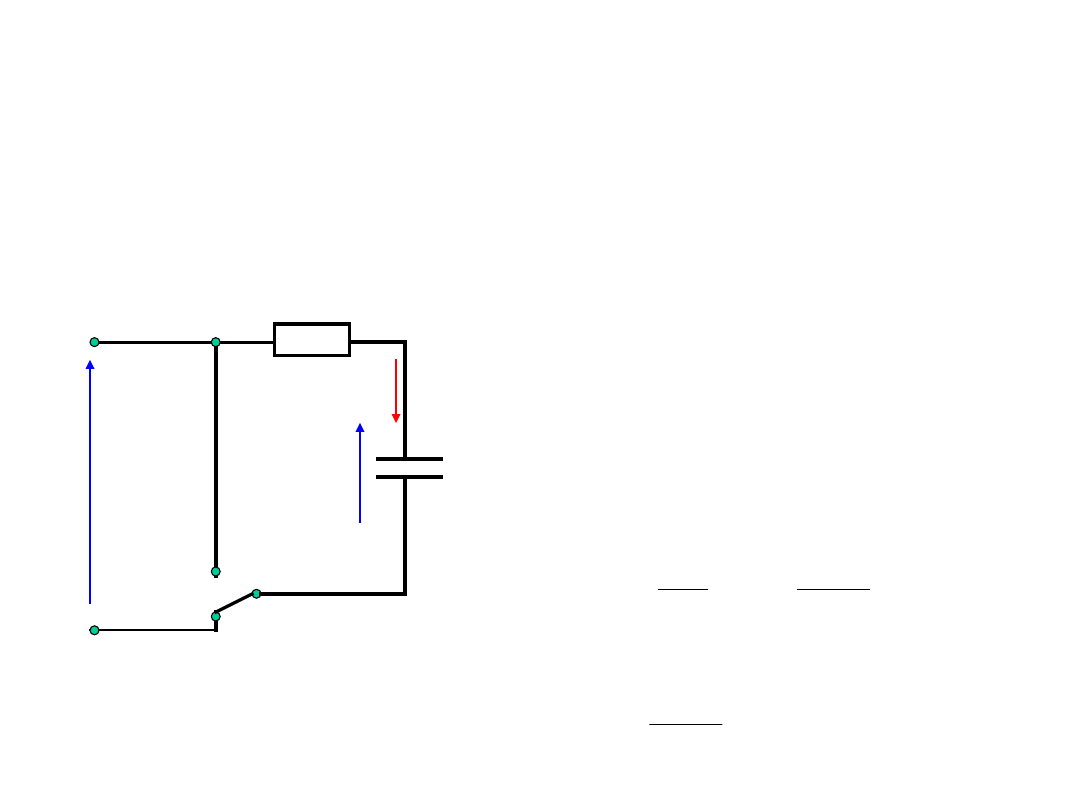
Przebiegi łączeniowe

Obwód z kondensatorem

Napięcie u

C

wzrasta

przy ładowaniu, aż do
wartości U, przy której
prąd przestaje płynąć.

R

C

U

1

2

u

C

i

p

dt

du

C

dt

dq

i

C





czyli:

C

C

u

U

dt

du

RC





Przebiegi łączeniowe

Obwód z kondensatorem

C

C

u

U

dt

du

RC





W
chwili

0



t

0



C

u

wię
c



















RC

t

C

e

U

u

1

oraz

RC

t

C

e

R

U

R

u

U

i









Przebiegi łączeniowe

Obwód z kondensatorem

Prąd w obwodzie z kondensatorem
maleje od

R

U

i 

przy

0



t

do

0



i

przy





t

Napięcie na kondensatorze rośnie od

0



C

u

dla

0



t

do

U

u

C



dla





t

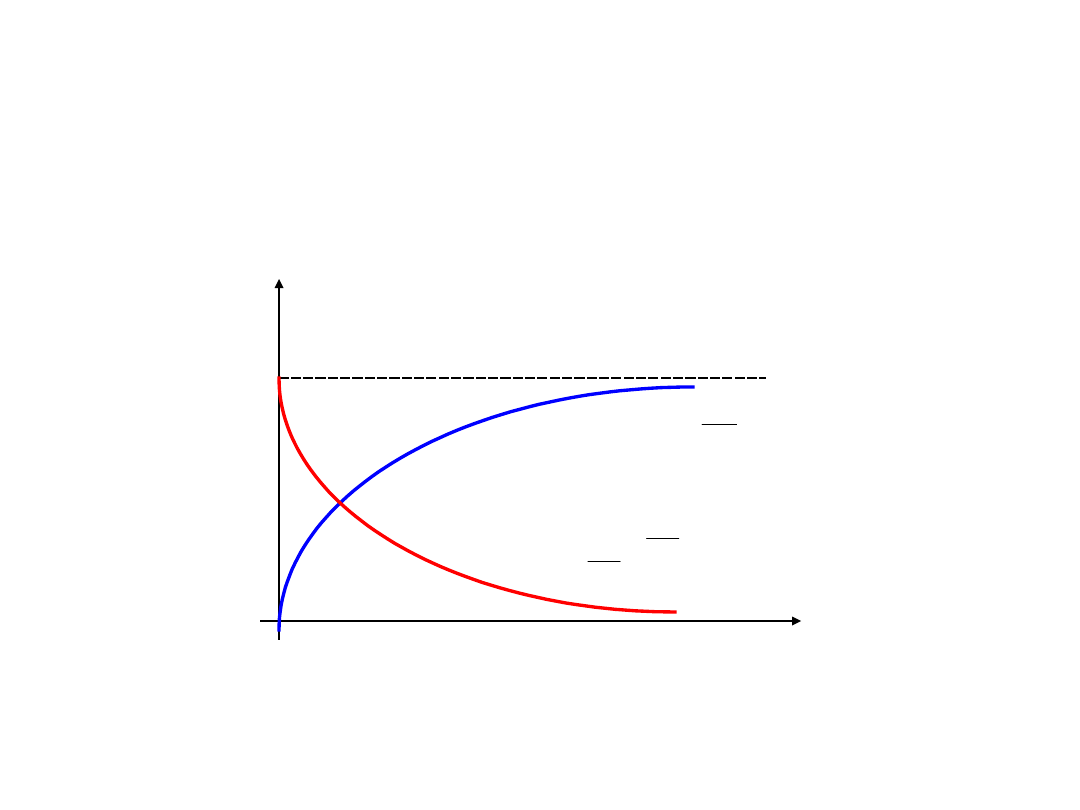
Przebiegi łączeniowe

Obwód z kondensatorem

U

U/R

u

C

i

t

RC

t

e

R

U

i























RC

t

C

e

U

u

1

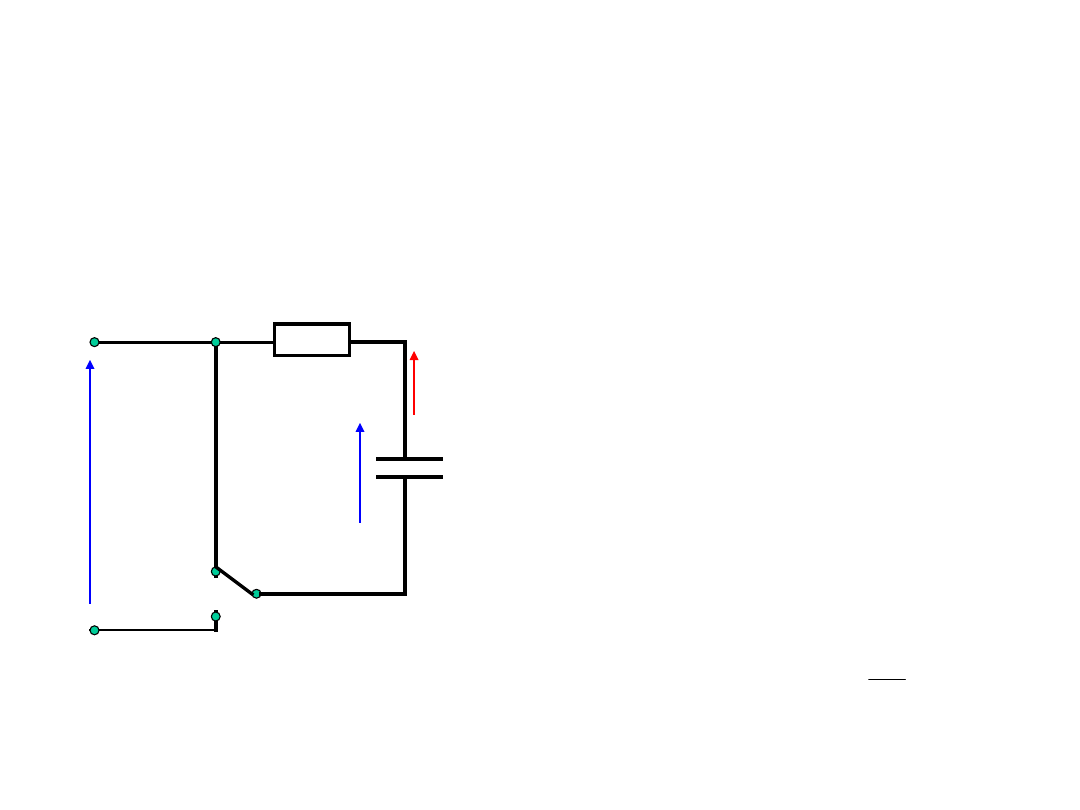
Przebiegi łączeniowe

Obwód z kondensatorem

Przełącznik p w pozycji
2 – następuje
rozładowanie
kondensatora. W
obwodzie istnieje
napięcie

R

C

U

1

2

u

C

i

C

p

U

u

C



i płynie prąd:

R

U

i

C



Przebiegi łączeniowe

Obwód z kondensatorem

Ładunek

maleje, prąd również

C

Cu

q

dt

dq

i 



Na podstawie prawa
Ohma

Ri

u

C



czyli:

dt

du

RC

dt

dq

R

u

C

C









C

C

u

RC

dt

du

1





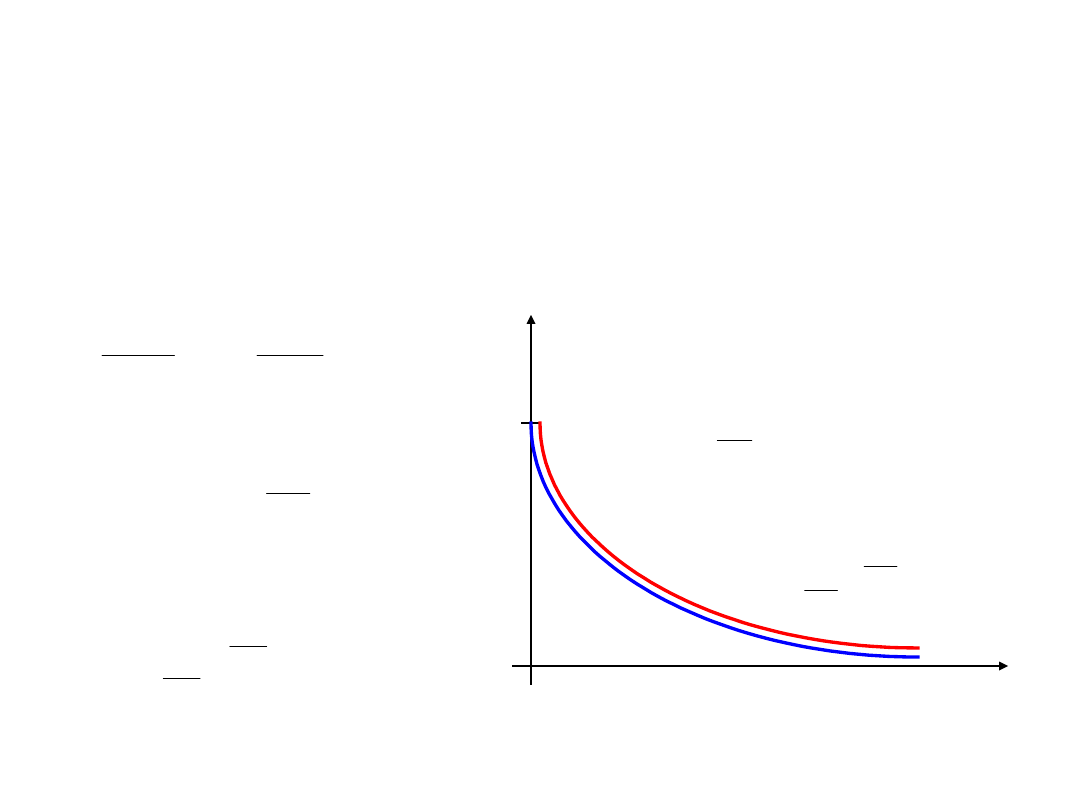
Przebiegi łączeniowe

Obwód z kondensatorem

C

C

u

RC

dt

du

1





RC

t

C

Ue

u





RC

t

e

R

U

i





T=RC – stała czasowa obwodu

u

C

i

U

U/

R

RC

t

C

Ue

u





RC

t

e

R

U

i





t

Przebiegi łączeniowe

Obydwa elementy bierne – cewka i
kondensator w obwodzie prądu stałego
nie pozwalają na gwałtowną zmianę prądu
(cewka) lub napięcia (kondensator).

Są więc elementami zachowawczymi
(konserwa-tywnymi).

Wytwarzanie prądów

przemiennych

l

d





Prądnica prądu
przemiennego – jej
najprostszym modelem
jest zwój wirujący w
równomiernym polu
magnetycznym ze stałą
prędkością kątową .

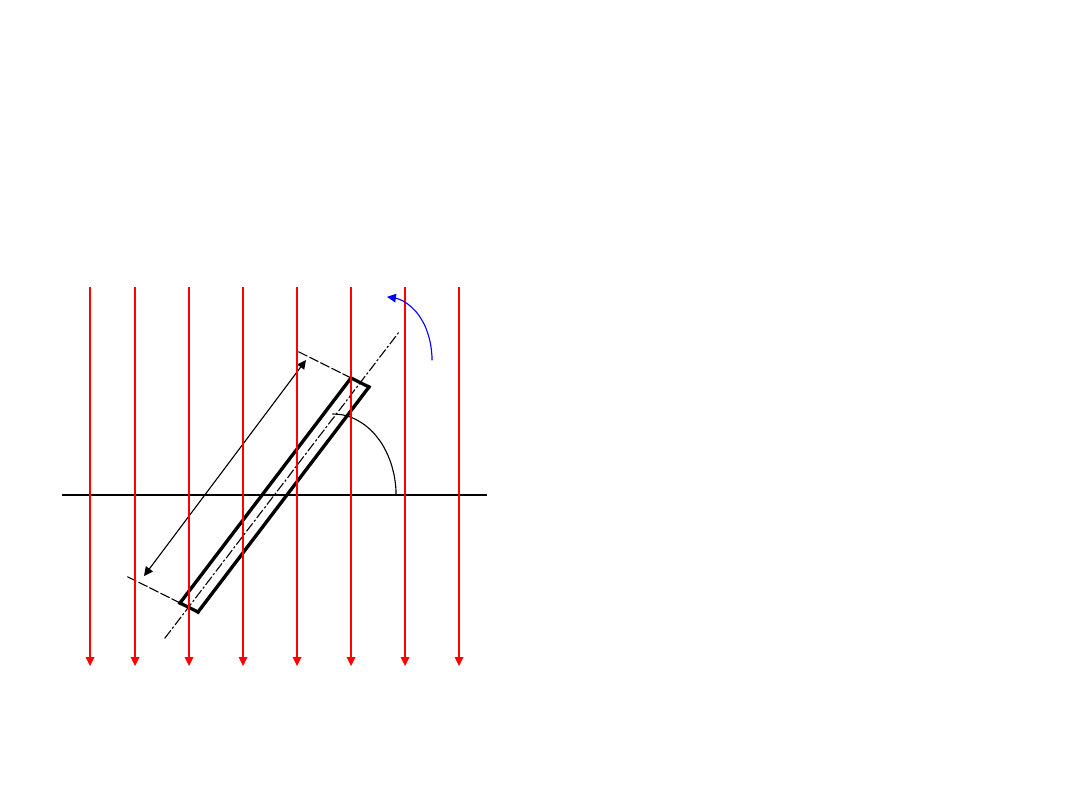
Wytwarzanie prądów

przemiennych

d

a

a





B

Zwój o średnicy d i
długoś-ci l z
wyjściowego położe-
nia poziomego (=0)

zaczyna wirować w
kierun-ku przeciwnym
do ruchu wskazówek
zegara. W poło-żeniu
wyjściowym zwój
przenika strumień o
największej wartości:

Bld

m





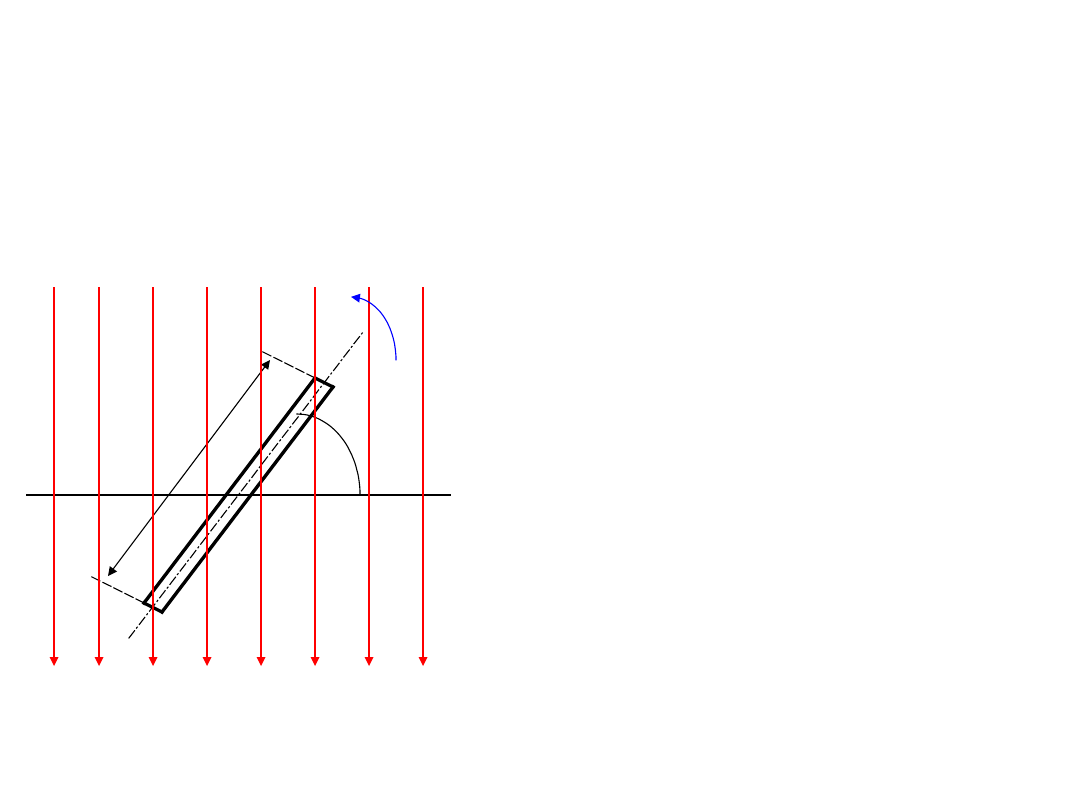
Wytwarzanie prądów

przemiennych

d

a

a





B

Przy wirowaniu
powierzchnia
przenikania strumienia
maleje i można ją
określić jako rzut
powierzchni objętej
ramką na powierzchnię
prostopadłą do
kierunku pola (a-a).
Zatem w dowolnym
położeniu:

t

Bld

m

m







cos

cos

cos













Wytwarzanie prądów

przemiennych

Indukowane napięcie można określić z
ogólnego prawa indukcji
elektromagnetycznej dla określonej zmiany
strumienia. Przy wzroście napięcia zgodnym
z regułą śruby prawoskrętnej:





t

E

t

z

dt

t

d

z

dt

d

z

e

m

m

m









sin

sin

cos





















Wytwarzanie prądów

przemiennych

Wartość maksymalna napięcia
indukowanego dla danej maszyny jest stała
przy stałej prędkości obrotowej i równa:

ldB

z

E

m





Obojętne jest czy wiruje uzwojenie, w
którym wytwarza się napięcie (twornik) a
uzwojenie wytwarzające strumień jest
nieruchome, czy odwrotnie