
Wykład 7
Myślenie i rozwiązywanie
problemów

Czym jest myślenie?
Proces łączenia elementów poznawczej
reprezentacji świata (obrazów, pojęć lub
sądów) w dłuższe ciągi
Reprezentacje poznawcze mogą być
trwałe (pojęcia, sądy) lub nietrwałe
(spostrzeżenia, wyobrażenia), ale
zawsze są strukturami poznawczymi, a
nie procesami
Jeśli struktury poznawcze podlegają
dalszemu przetwarzaniu, mamy do
czynienia z procesem myślenia

Funkcje myślenia
Zastępowanie jawnego zachowania
Działanie na niby, zachowanie symboliczne
Bezpieczne, bez konsekwencji
Sprawdzanie różnych wariantów
Eksperyment myślowy
Myślenie jako internalizacja zachowania
jawnego

Pożytki z myślenia
Zdolność do rozwiązywania
WSZELKICH problemów
realnych, możliwych, hipotetycznych
konkretnych i abstrakcyjnych
absurdalnych
np. co jest czym czego?
dlaczego ogórek nie śpiewa?

Myślenie u ludzi i u zwierząt
U ludzi
Niezależne od działania
Niezależne od kontekstu
U zwierząt
Tylko w działaniu
Zawsze w kontekście (np. w naturalnych
warunkach życia gatunku)
Pies “myślący” na polowaniu przestaje
myśleć w supermarkecie

Złudzenie
Myślenie jest procesem świadomym i
całkowicie kontrolowanym
W rzeczywwistości:
Świadomi jesteśmy skutków
Niektórych operacji (nie zawsze)
Myśli niekontrolowane (intruzywne): efekt
białych niedźwiedzi

Struktura myślenia
Materiał
Np. werbalny, obrazowy
Operacje
Przekształcenia, np. kojarzenie, negacja
Reguły
Ograniczenia nakładane na operacje (np.
zakaz dzielenia przez zero)

Rozumowanie
Wyciąganie wniosków z przesłanek
Koty mają cztery łapy
Moje zwierzę ma cztery łapy
Więc…
Z przesłanek może NIC nie wynikać

Rodzaje rozumowań
Indukcja
Kumulacja wiedzy
Obserwacja szczegółowe sąd ogólny
Dedukcja
Cała wiedza zawarta w przesłankach
Wiedza niejawna wiedza jawna
Abdukcja
Wnioskowanie o przyczynach na podstawie
skutków
(śledztwo, diagnoza lekarska, badanie naukowe)

Zalety i wady rozumowań
Dedukcja
Niezawodne
Lecz często trywialne
Indukcja i abdukcja
Zawodne
Ale płodne
INDUKCJA PODSTAWĄ SUKCESU
NOWOŻYTNEJ NAUKI

Rodzaje dedukcji
Sylogizmy
Relacje kategorialne (kwantyfikatory:
wszyscy, nikt, niektórzy)
Relacje nierówności (wyższy, mądrzejszy)
Rozumowanie warunkowe
Funktory rachunku zdań (np. implikacja,
koniunkcja, dysjunkcja, negacja,
równoważność)
Jeśli … to …

Przykłady sylogizmów
Niektóre zwierzęta są ssakami
Każdy ssak oddycha płucami
Zatem niektóre zwierzęta oddychają
płucami
Adam jest wyższy od Bartka
Bartek jest niższy od Cezarego
Więc Bartek jest z całej trójki najniższy

Przykłady rozumowań
warunkowych
Jeśli p to q
p
więc q
Jeśli p to q
nieprawda, że q
więc nieprawda, że p

Jak to jest w nauce?
Jeśli TEORIA to FAKT
TEORIA
Więc FAKT (bez sensu, tego nie
potrzebujemy)
Jeśli TEORIA to FAKT
FAKT
Więc TEORIA (bez sensu, to rozumowanie
jest błędne)

Weryfikacja hipotez
naukowych
Jeśli TEORIA to FAKT
Nie FAKT
Więc NIE TEORIA (falsyfikacja, wiedza
negatywna)

Jak uzyskać wiedzę
pozytywną?
Jeśli TEORIA to FAKT
Jeśli NIE TEORIA, to FAKT ALTERNATYWNY
NIE TEORIA = hipoteza zerowa
Nieprawda, że FAKT ALTERNATYWNY
Nieprawda, że NIE TEORIA
(Odrzucamy hipotezę zerową jako mało
prawdopodobną, p<0,05)
Więc TEORIA (dowód nie wprost)

Weryfikacja hipotez poza
nauką
Jeśli kocha, to nie zapomni o rocznicy
Nie zapomniał(a)
Więc kocha
BŁĄD W ROZUMOWANIU!
Jeśli kocha to nie zapomni o rocznicy
Zapomniał(a)
Więc nie kocha
ROZUMOWANIE POPRAWNE!

Błędy w rozumowaniu
• Skąd wynikają?
• Brak kompetencji
• Tendencyjność
• Wpływ treści i kontekstu

Tendencyjność w
rozumowaniu
Systematyczne błędy
Uniwersalne
Typowe dla wiekszości ludzi
Pojawiają się w charakterystycznych
momentach procesu myślenia

Przykłady tendencyjności
Efekt konwersji przesłanek
• Wszystkie A są B
• Więc wszystkie B są A
• Wszystkie psy są
kudłate
• Wszystkie kudłacze są
psami?
Efekt atmosfery
• Wszystkie A są B
• Wszystkie C są B
• Więc wszystkie A są C
• Wszystkie wróble są
ptakami
• Wszystkie sikorki są
ptakami
• Więc wszystkie wróble
są sikorkami

Dlaczego tak łatwo się
pomylić?
• Wszyscy uczeni są dobrze wykształceni
• Wszyscy eksperci są dobrze wykształceni
• Więc wszyscy uczeni są ekspertami
• Wniosek prawdziwy „sam w sobie”
sprawia wrażenie, jak gdyby był
poprawny logicznie

Efekt treści i kontekstu
• (1) Żadne papierosy nie są tanie
• Niektóre używki są tanie
• Zatem, niektóre używki nie są
papierosami
• (2) Żadne używki nie są tanie
• Niektóre papierosy są tanie
• Zatem, niektóre papierosy nie są
używkami
•

• (3) Żadne używki nie są tanie
• Niektóre papierosy są tanie
• Zatem, niektóre używki nie są
papierosami
• (4) Żadne papierosy nie są tanie
• Niektóre używki są tanie
• Zatem, niektóre papierosy nie są
używkami

Jak dobrze sobie radzimy z
konfliktem miedzy logiką a
zdrowym rozsądkiem?
1. wniosek logiczny i prawdziwy (92%)
2. wniosek logiczny i absurdalny (46%)
3. wniosek nielogiczny, ale prawdziwy
(92%)
4. wniosek nielogiczny, i absurdalny
(8%)
Evans, Barston i Pollard (1983)

Wason: zadanie selekcyjne

Typowe wyniki badań
Jeśli G, to liczba nieparzysta
G89% (dobrze)
9 62% (źle)
6 25% (dobrze)
A 16% (źle)
Jeśli H
0
, to wynik X. Stwierdzam nie X.
Zatem nie H
0

Wersja realistyczna
Wyobraź sobie, że jesteś policjantem na służbie.
Twoja praca polega na kontroli respektowania
obowiązujących norm. Karty leżące przed tobą
zawierają informacje o czterech osobach
siedzących przy stole. Na jednej stronie karty
podany jest wiek osoby, a na drugiej stronie –
co dana osoba pije. Obowiązuje następująca
reguła: Jeżeli ktoś pije piwo, to musi mieć
ukończone 18 lat. Wskaż kartę albo karty,
które koniecznie musisz odwrócić, aby ustalić,
czy reguła została naruszona.

Wyniki w wersji realistycznej
73% podaje poprawne odpowiedzi
Nikt nie podał poprawnego rozwiązania
w wersji abstrakcyjnej
Efekt materiału tematycznego

Rozwiązywanie problemów
Stan wyjściowy (problematyczny)
Stan docelowy (idealny)
Rozwiązywanie problemu do
zbudowanie ścieżki między stanem
wyjściowym a docelowym
Operacje
Ograniczenia
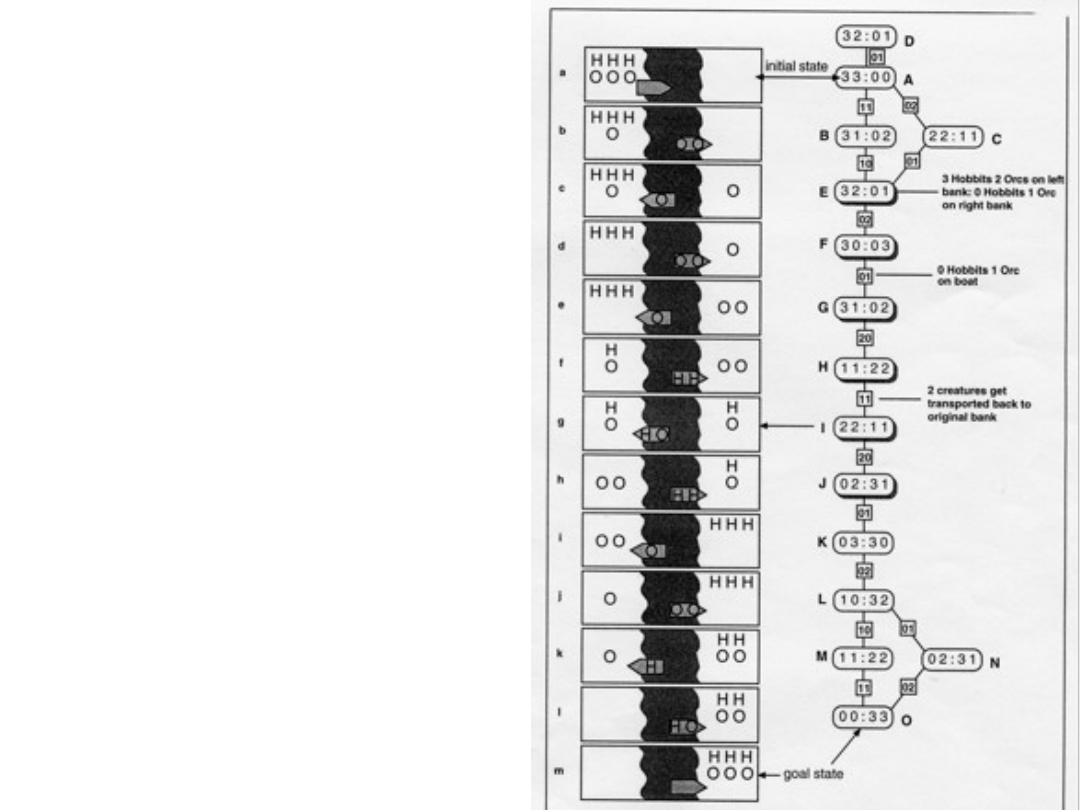
Hobbici i Orki

Rodzaje problemów
Proste lub złożone
Jak złożona musi być reprezentacja
problemu
Dobrze lub źle określone
Jak dokładnie są określone parametry
stanu wyjsciowego i docelowego
np.jak zwiększyć bezpieczeństwo ruchu
drogowego?

Problem dziewięciu kropek:
prosty, ale trudny
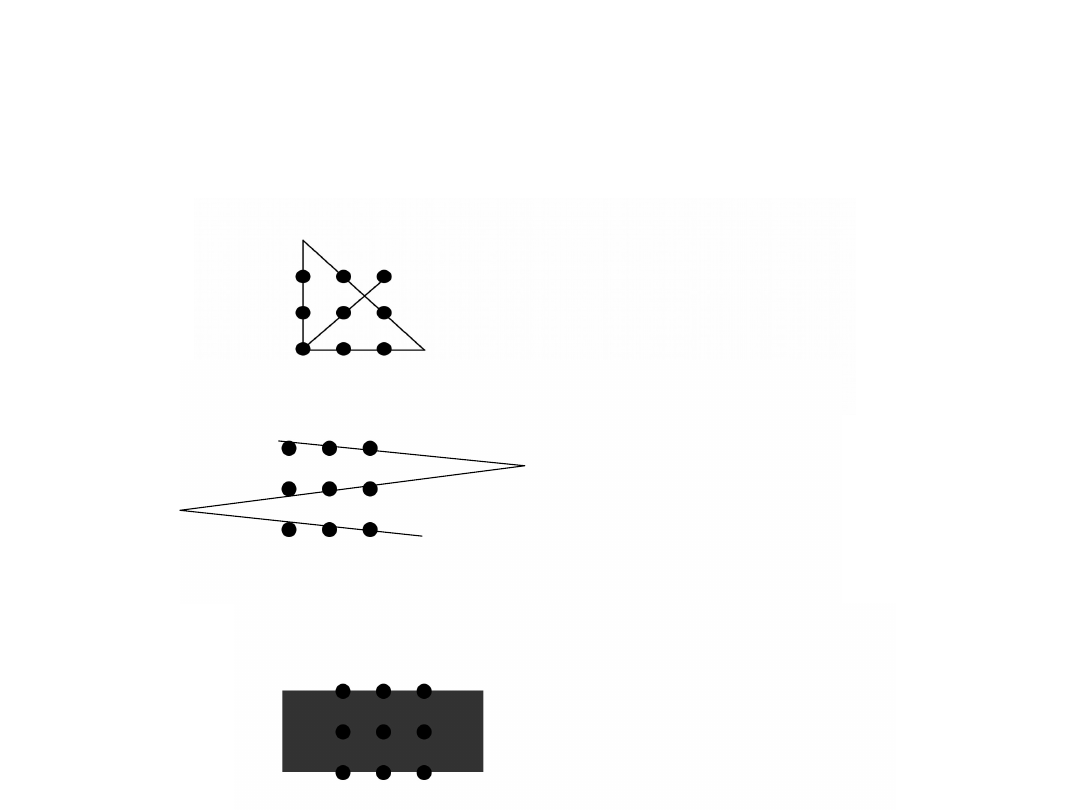
Problem 9 kropek: prosty, ale
źle określony

Problem uszkodzonej szachownicy:
rola właściwej reprezentacji
poznawczej

Karl Duncker: Problem
świecy

Fazy procesu rozwiązywania
problemów wg RJ
Sternberga
1.
Identyfikacja problemu
2.
Definiowanie problemu
3.
Wybór właściwej strategii
4.
Zdobywanie informacji
5.
Mobilizacja (alokacja) zasobów
poznawczych
6.
Monitorowanie postępu
7.
Sprawdzenie poprawności
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
Wyszukiwarka
Podobne podstrony:
Myślenie i rozwiązywanie problemów, Psychologia Ogólna, Referaty
SCIAGA1 myslenie rozwiazywanie problemow, AWF, I rok, Psychologia
Psychologia notatki na egzamin myslenie rozwiazywanie problemow, AWF, I rok, Psychologia
Myślenie i rozwiązywanie problemów
myslenie i rozwiazywanie problemow, Psychologia
Myślenie i rozwiązywanie problemów, Psychologia, Psychologia poznawcza
Myślenie i rozwiązywanie problemów
Myślenie i rozwiązywanie problemów, Psychologia Ogólna, Referaty
Myślenie i rozwiazywanie problemow
T 3[1] METODY DIAGNOZOWANIA I ROZWIAZYWANIA PROBLEMOW
ROZWIĄZYWANIE PROBLEMÓW
Rozwiazywanie problemów
Rehabilitacja jako pomoc w rozwiązywaniu problemów życiowych niepełnosprawnych
Coaching mentoring i zarzadzanie Jak rozwiazywac problemy i budowac zespol
telekomunikacja rozwiązania problemów z cienkiej książki
03 Kształtowanie umiejętności rozwiązywania problemówid 4402
14 rozwiazywanie problemow
więcej podobnych podstron