WYTRZYMAŁOŚĆ MATERIAŁÓW

prowadzący

prof. dr hab. inż. Kazimierz WÓJS

Wykład 14

Opracował

Andrzej Sitka

PEŁZANIE I RELAKSACJA

PEŁZANIE I RELAKSACJA

PEŁZANIE I RELAKSACJA

Pełzanie

– zjawisko zmiany odkształcenia

elementu w czasie pod wpływem stałego naprężenia
działającego w stałej temperaturze.

Pełzanie jest zjawiskiem

reologicznym

.

PEŁZANIE I RELAKSACJA

Reologia

–

nauka,

która

zajmuje

się

powstawaniem odkształceń w materiałach i zmianą
tych odkształceń wraz z upływem czasu.

Relaksacja

– zmniejszanie się naprężeń w miarę

upływu czasu przy zachowaniu niezmienionych

wymiarów ciała.

PEŁZANIE I RELAKSACJA

Reologiczne równanie stanu dla jednoosiowego

rozciągania ma postać: 

gdzie:



– naprężenie,



– odkształcenie,

t – czas,

T – temperatura.

PEŁZANIE I RELAKSACJA





0

,

,



const

T

t

F





(1)

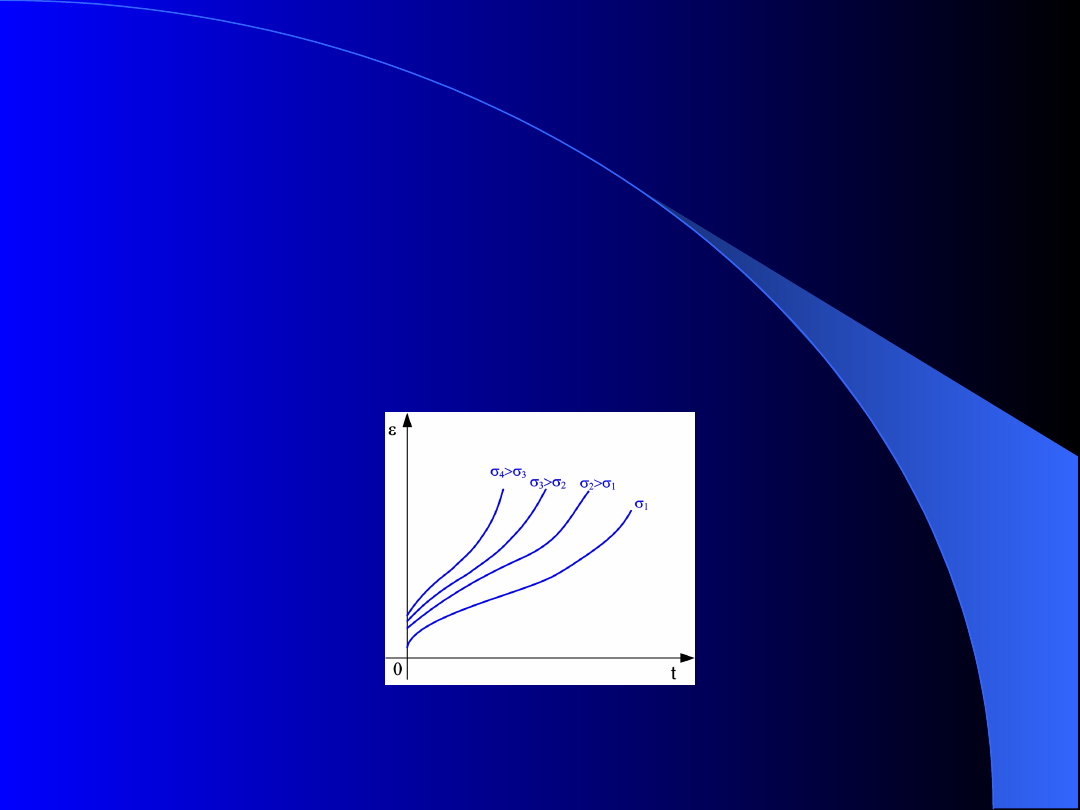
Rys. 1. Krzywe pełzania

W określonej temperaturze istnieje pewna

powierzchnia we współrzędnych



,



, t. Po przecięciu

tej powierzchni płaszczyznami prostopadłymi do
poszczególnych osi układu



,



, t otrzymuje się trzy

rodzaje krzywych:

•

Krzywe pełzania – przecięcie powierzchni F(



,



,

t) płaszczyznami



=const (rys. 1),

•

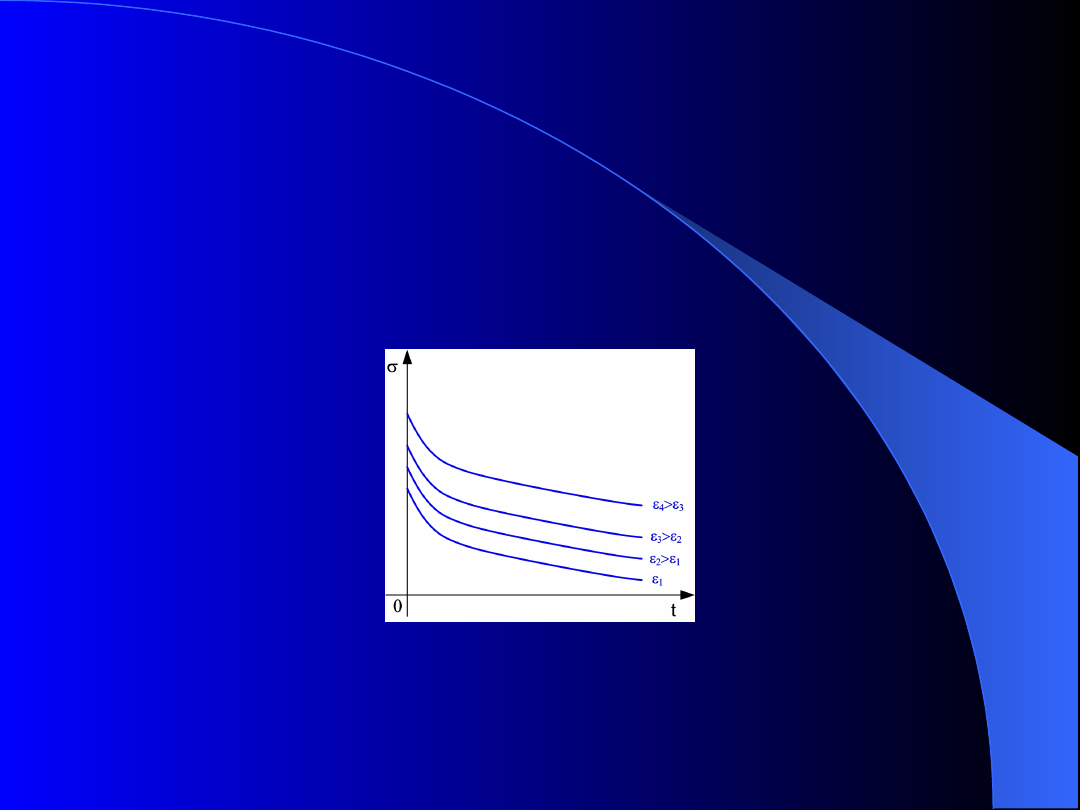
Krzywe relaksacji – przecięcie powierzchni F(



,



,

t) płaszczyznami



=const (rys. 2),

Rys. 2. Krzywe relaksacji

PEŁZANIE I RELAKSACJA

•

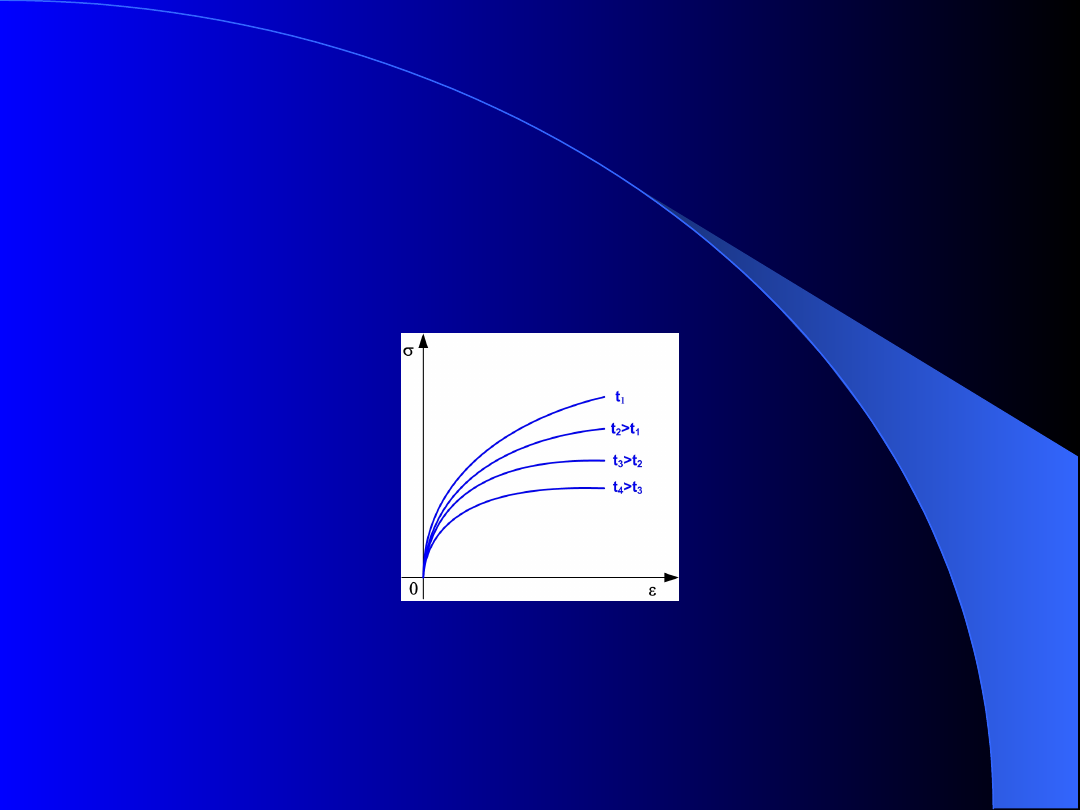
Izochroniczne krzywe pełzania – przecięcie
powierzchni F(



,



, t) płaszczyznami t=const (rys.

3).

PEŁZANIE I RELAKSACJA

Rys. 3. Izochroniczne krzywe pełzania

W temperaturze ok. 20C zjawisko pełzania

można zaobserwować w tworzywach sztucznych i w

stopach

metali

lekkich,

w

temperaturach

podwyższonych również w stalach.

PEŁZANIE I WYTRZYMAŁOŚĆ

NA PEŁZANIE

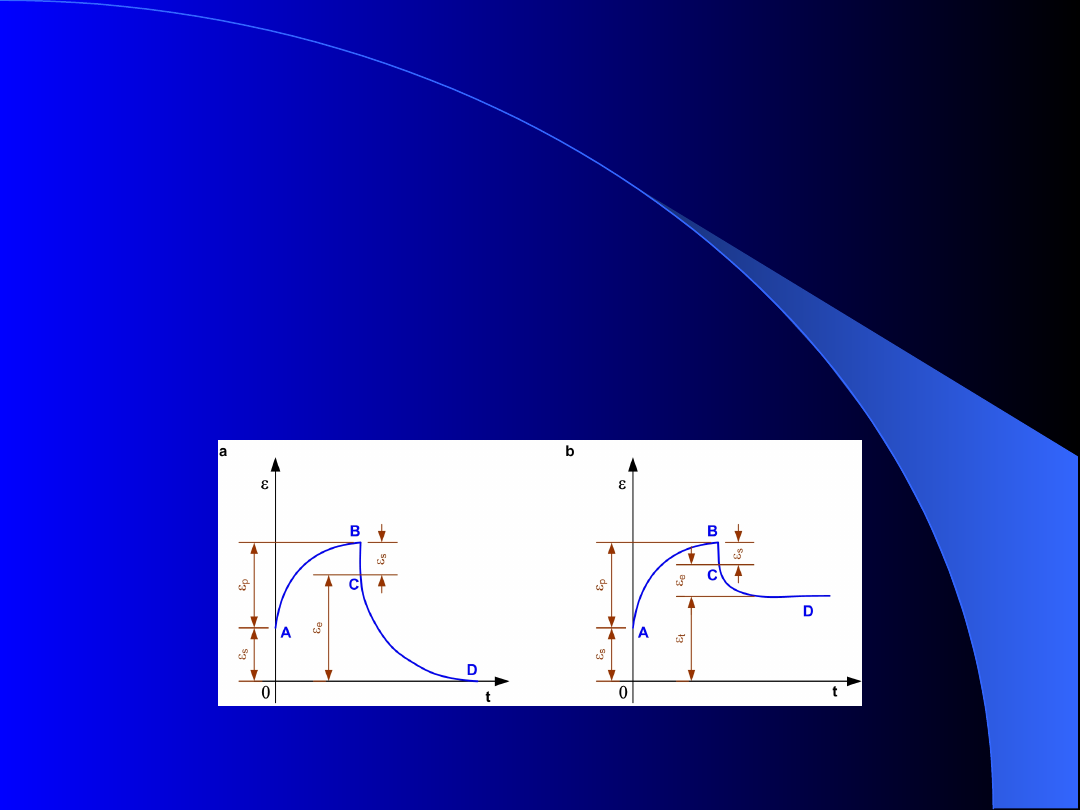
Pełzanie może być:

Sprężyste

– odkształcenia zmniejszają się po

odciążeniu najpierw bardzo szybko, a następnie powoli
do całkowitego ich zaniku (rys. 4a).

Plastyczne

– odkształcenia nie znikają całkowicie (rys.

4b).

PEŁZANIE I WYTRZYMAŁOŚĆ

NA PEŁZANIE

Rys. 4. Pełzanie, a) – sprężyste, b) - plastyczne

•

0A – odkształcenie sprężyste 

s

(2)

•

AB – odkształcenie pełzania 

p

•

BC – powrót sprężysty 

s

PEŁZANIE I WYTRZYMAŁOŚĆ

NA PEŁZANIE

E

s







E

s







•

CD – powrót niesprężysty 

e

, odkształcenie trwałe 

t

.

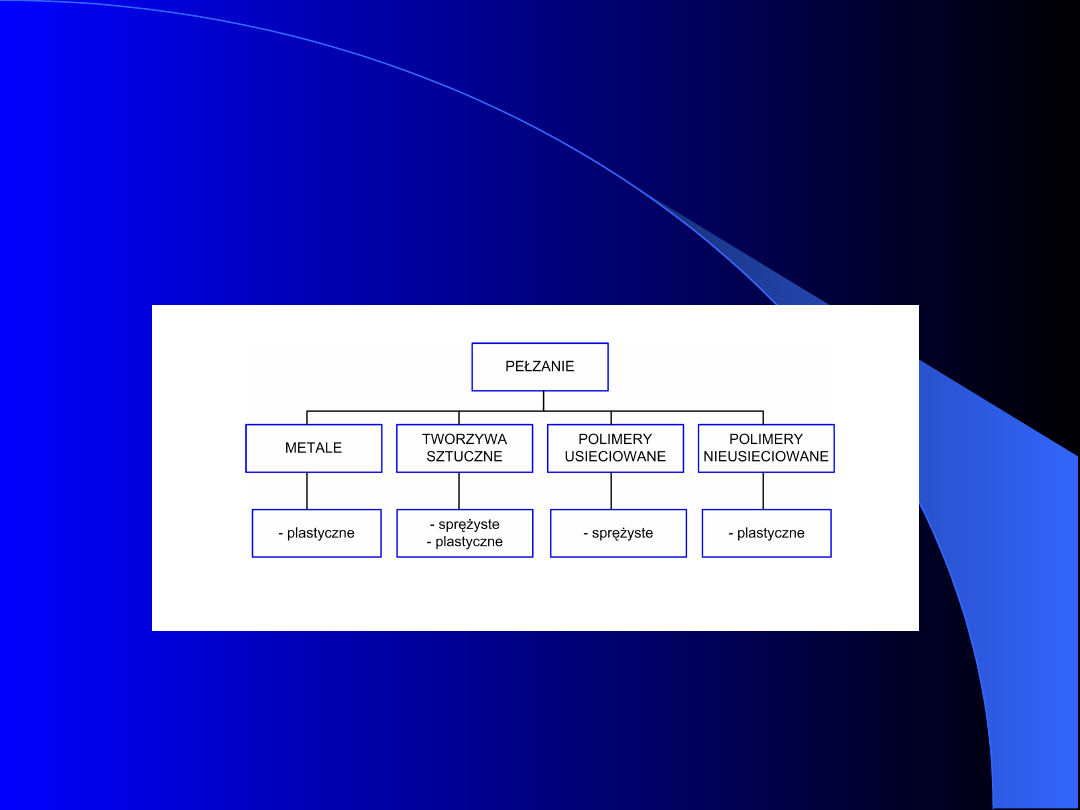
W materiałach można zaobserwować rodzaje pełzania:

PEŁZANIE I WYTRZYMAŁOŚĆ

NA PEŁZANIE

Warunki bezpiecznej pracy części maszyn wymagają
znajomości zmian odkształcenia i naprężenia. Należy
wyznaczyć następujące zależności:

PEŁZANIE I WYTRZYMAŁOŚĆ

NA PEŁZANIE

 





.

,T

const

dla

t















 





gdzie:



- pełzanie,

- prędkość pełzania.





WYKRES PEŁZANIA

Próby pełzania przeprowadza się następująco:

badaną

próbkę

umieszcza

się

w

komorze

zapewniającej utrzymanie stałej temperatury t i
obciąża się stałą, co do wartości siłą rozciągającą. W
określonych

odstępach

czasu

–

za

pomocą

tensometrów mechanicznych, czujników zegarowych,
itp. – mierzy się wydłużenie trwałe próbki. Na
podstawie wyników pomiarów sporządza się wykres
pełzania (rys. 5).

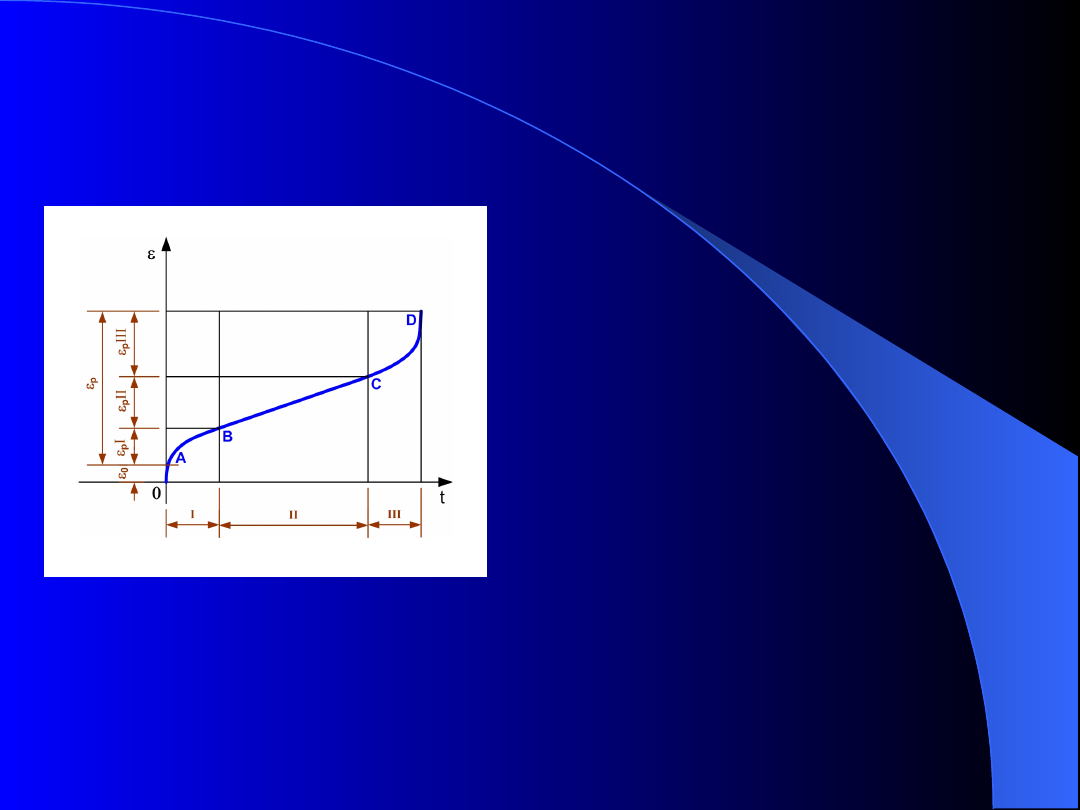
WYKRES PEŁZANIA

Rys. 5. Wykres pełzania stali

W czasie próby pełzania
można wyróżnić trzy okresy:

•

I – przyrost wydłużenia

trwałego maleje w miarę
upływu czasu (odcinek AB),

•

II – okres pełzania

ustalonego (odcinek BC),

•

III – szybkość przyrostów

długości znacznie wzrasta
(odcinek CD).

WYKRES PEŁZANIA

Odkształcenie można podzielić na odkształcenie

początkowe



0

(sprężyste lub plastyczne) oraz na

odkształcenie pełzania



p

(trzy zakresy pełzania:



pI

,



pII

,



pIII

).

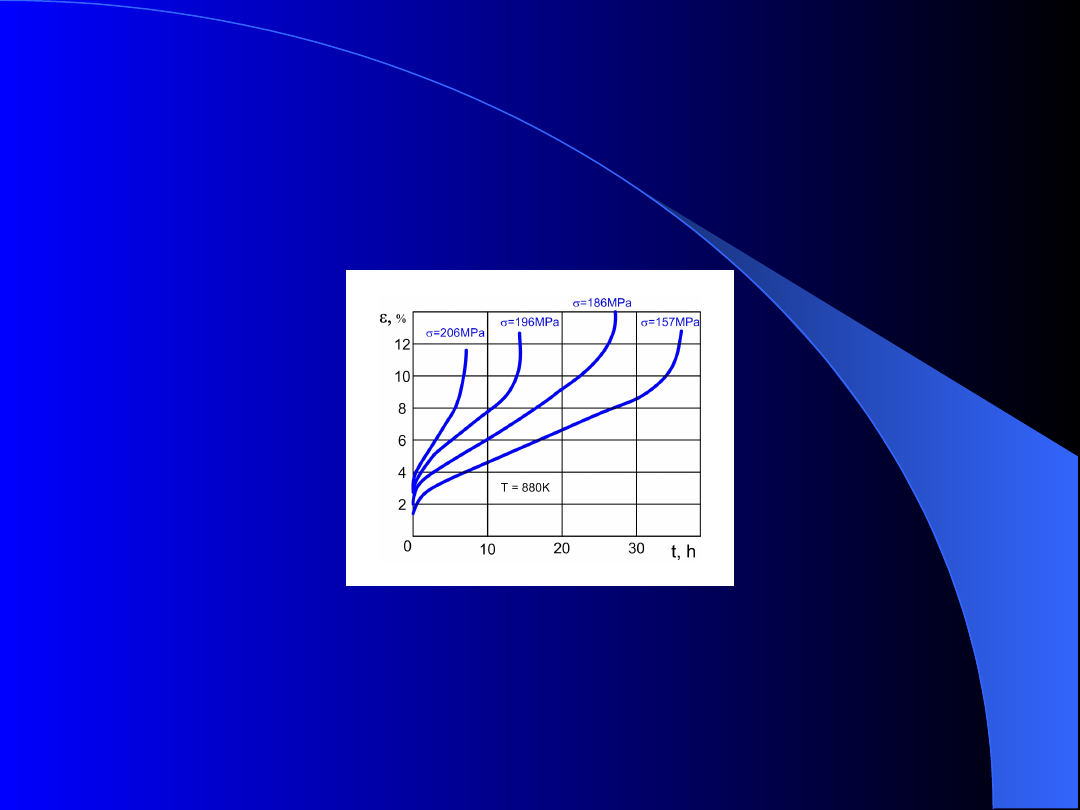
Rys. 6. Wykresy pełzania stali H23N18 w stałej

temperaturze przy różnych naprężeniach

WYKRES PEŁZANIA

Doświadczalne wykresy pełzania próbek wykonanych

ze stali H23N18:

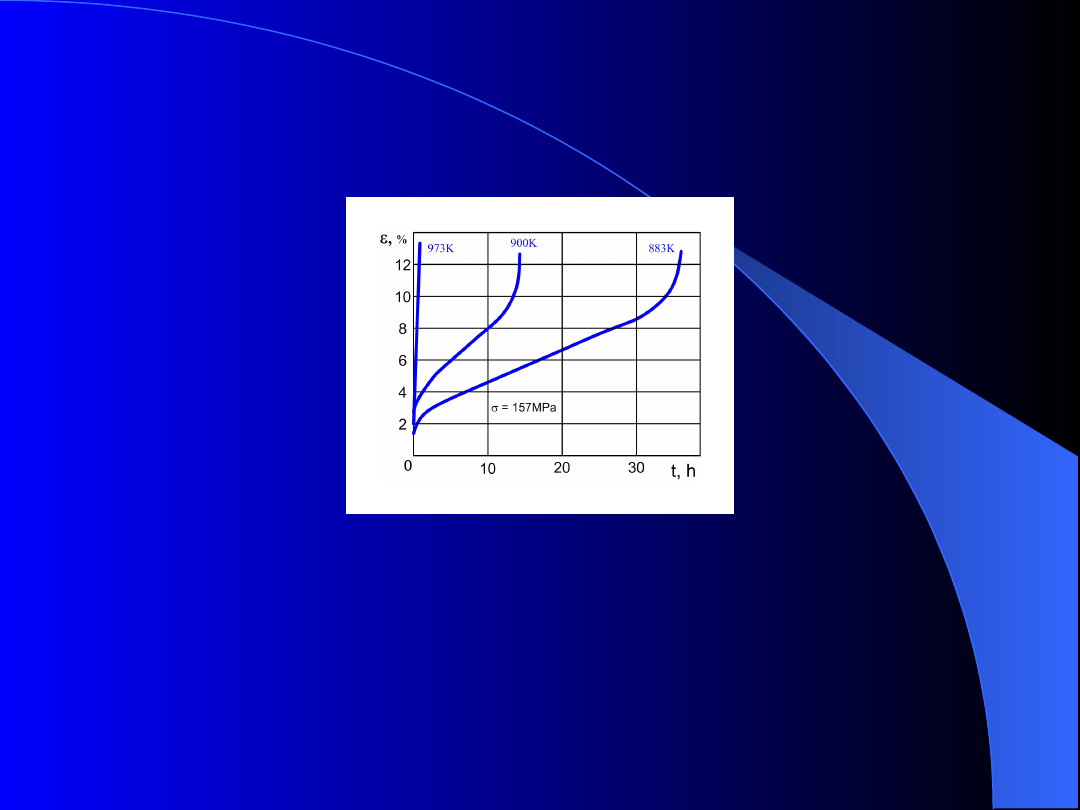
WYKRES PEŁZANIA

Rys. 7. Wykresy pełzania stali H23N18 w różnych

temperaturach przy stałym naprężeniu

 Pełzanie można podzielić na:

1.

Pełzanie w niskich temperaturach – zmniejszanie
się prędkości odkształcenia na skutek umocnienia
w wyniku odkształceń trwałych.

2.

Pełzanie w wysokich temperaturach – stała
prędkość

odkształcenia

na

skutek

braku

umocnienia.

MECHANIZM ZNISZCZENIA

MECHANIZM ZNISZCZENIA

Pełzanie w wysokich temperaturach ze względu na

wartości naprężenia dzieli się na:

1.

Pełzanie dyslokacyjne wywołane przez duże
naprężenia,

2.

Pełzanie dyfuzyjne odpowiadające mniejszym
naprężeniom.

Wytrzymałość trwała

na rozciąganie R



-

największe

naprężenie,

które

nie

spowoduje

rozerwania próbki po dowolnie długim czasie (wartość
niemożliwa do określenia).

Należy posługiwać się wielkościami umownymi
(czasowymi):

•

Granica pełzania,

•

Wytrzymałość na pełzanie.

WYTRZYMAŁOŚĆ TRWAŁA

Granica pełzania R

xTt

– iloraz stałego

obciążenia F

xTt

przez przekrój początkowy próbki S

0

(obciążenie to po upływie określonego czasu t w stałej
temperaturze T spowoduje trwałe wydłużenie próbki):

(3)

WYTRZYMAŁOŚĆ TRWAŁA

0

S

F

R

xTt

xTt



Wytrzymałość na pełzanie

R

zTt

– iloraz stałego

obciążenia F

zTt

przez przekrój początkowy próbki S

0

(obciążenie to po upływie określonego czasu t w stałej
temperaturze T spowoduje rozerwanie próbki):

(4)

WYTRZYMAŁOŚĆ TRWAŁA

0

S

F

R

zTt

zTt



Trwałość t

z

próbki (czas do jej zniszczenia) –

uzyskuje się całkując prędkość pełzania lub na

podstawie

doświadczeń.

Doświadczalna

wartość

Monkmana - Granta ma postać:

(5)

WYTRZYMAŁOŚĆ TRWAŁA

m

pII

z

C

t









gdzie:

C,m – stałe materiałowe.

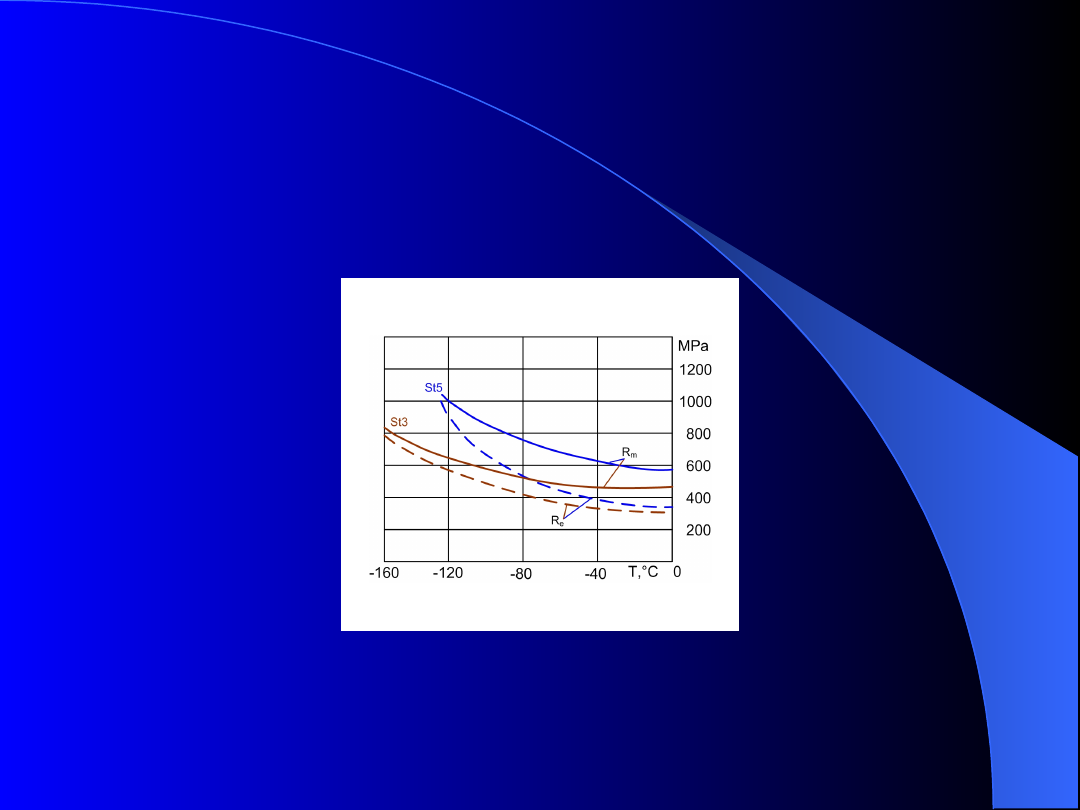
Rys. 8. Własności stali St3 i St5 w temperaturach

obniżonych

Przykładowe własności wytrzymałościowe stali w

zależności od temperatury:

WYTRZYMAŁOŚĆ TRWAŁA

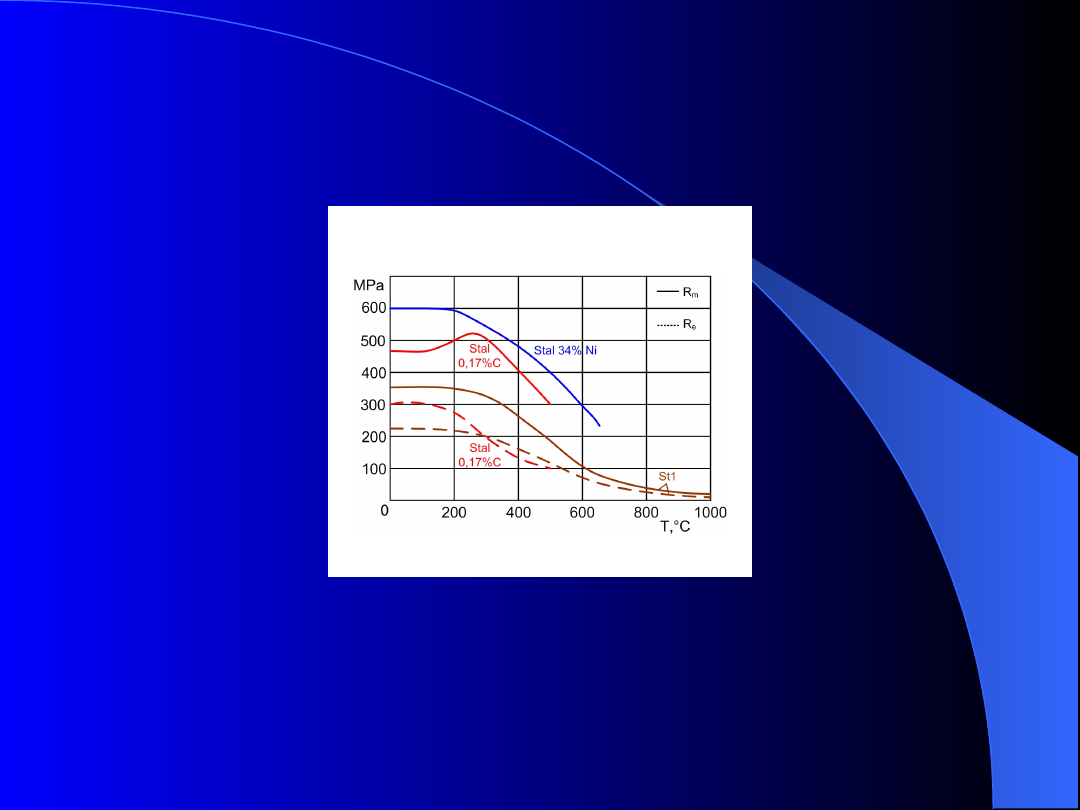
Rys. 9. Zmiany własności stali w temperaturach

podwyższonych

WYTRZYMAŁOŚĆ TRWAŁA

W miarę obniżania się temperatury bardzo szybko
spada udarność – materiały plastyczne wykazują
wówczas cech materiałów kruchych i przy udarnym
działaniu sił łatwo ulegają pękaniu (rys. 10).

Udarnością

nazywamy iloraz energii potrzebnej do

złamania próbki o określonych wymiarach przez pole
przekroju poprzecznego próbki.

Warunki równowagi

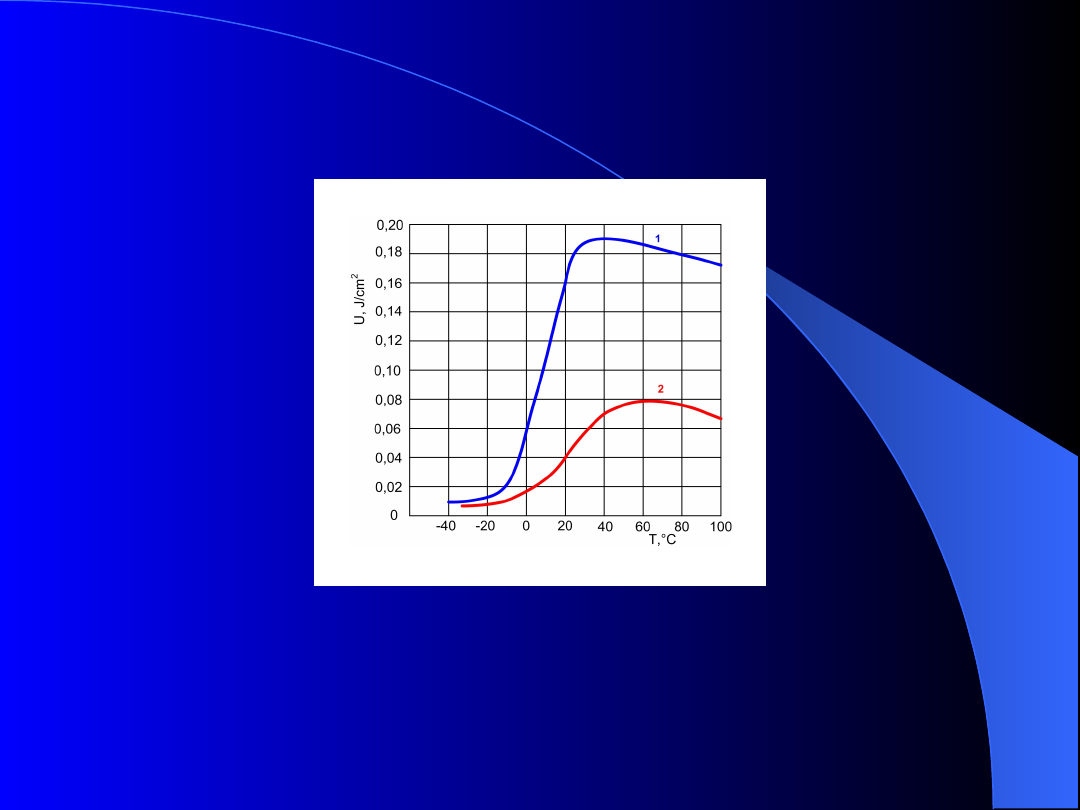
Rys. 10. Zmiany udarności stali; 1 – bez zgniotu, 2 – po zgniocie

70%

Warunki równowagi

Naprężenia dopuszczalne



dop

ustala się na

podstawie przyjęcia dopuszczalnego odkształcenia
pełzania



dop

po upływie określonej liczby godzin.

Pomijając

pierwszy

okres

pełzania

(pełzanie

nieustalone) odkształcenie całkowite będzie wynosić:

OBLICZENIA WYTRZYMAŁOŚCIOWE

 

Rozciąganie

dop

dop

n

T

pII

t

k

E























0

0

(6)

gdzie:



0

– naprężenie początkowe,

E

T

– moduł Younga w danej temperaturze T.

Przyjmując



0

=



=



dop

, równanie (6) przyjmie postać:

Rozciąganie

(7)

Rozwiązując równanie (7) otrzymamy poszukiwane
naprężenia dopuszczalne



dop

. Rozwiązanie przybliżone

otrzymamy pomijając odkształcenie natychmiastowe:

(8)

dop

dop

n

dop

T

dop

t

k

E











n

dop

dop

dop

kt

1





















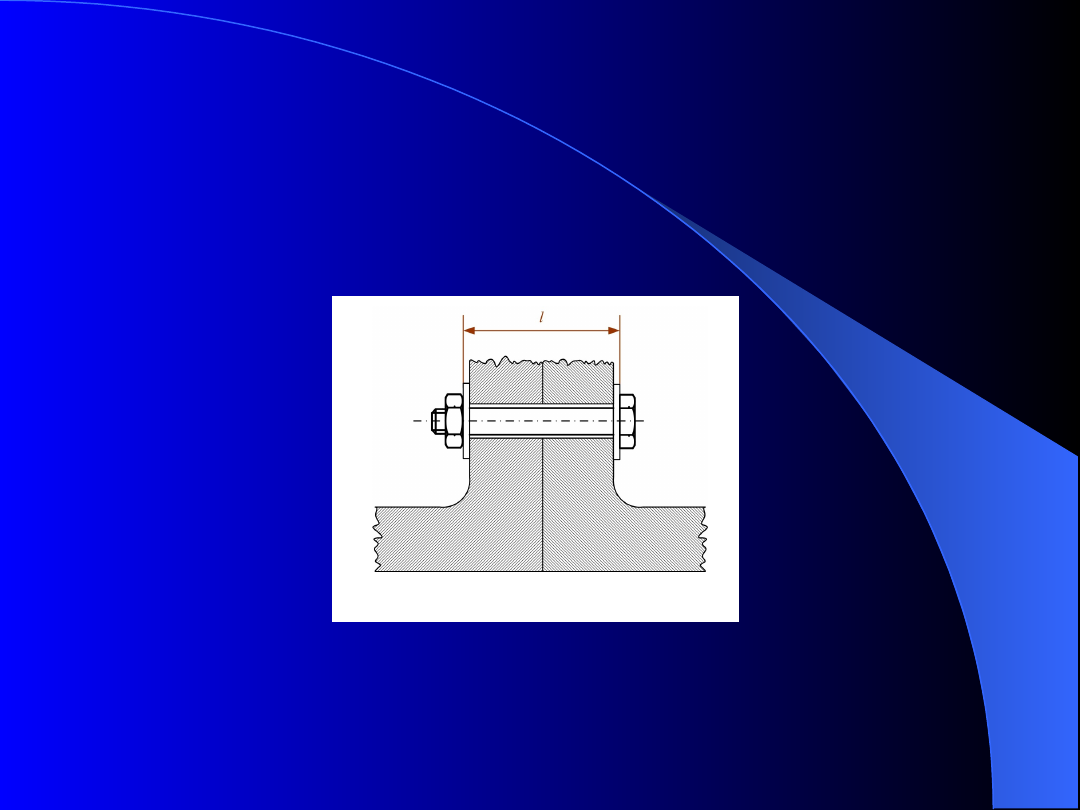
Typowym przykładem relaksacji jest zmniejszenie
naprężeń w śrubach łączących kołnierze rurociągów
pracujących w podwyższonych temperaturach (rys.
11).

Relaksacja naprężeń

Rys. 11. Śruba łącząca kołnierze rurociągów

Połączenie kołnierzy jest sztywne – l = const.

Uwzględniono tylko pełzanie samej śruby – obliczenia
uproszczone.

 

Suma odkształcenia sprężystego



s

=



/E i odkształcenia

pełzania



p

nie zmieni się, gdyż odkształcenie całkowite



jest stałe i równe odkształceniu początkowemu



0

=



0

/E ze względu na stały naciąg śruby.

(9)

Relaksacja naprężeń

E

E

p

0















Uwzględnijmy tylko zakres pełzania ustalonego:

po przekształceniu:

.

Po zróżniczkowaniu równania (22) względem czasu i
uwzględnieniu równania (23) mamy:

(10)

Relaksacja naprężeń

n

pII

p

k









 



0









n

p

k

E

E















dt

d

E

k

n





1





(12)

(11)

a stąd:

(13)

(14)

Relaksacja naprężeń

n

d

Ek

dt





1





Całkując względem czasu otrzymamy:

C

n

Ek

t

n











1

1

1



i ostatecznie zależność czasu od naprężenia:

Relaksacja naprężeń

(16)









n

n

n

Ek

t











1

1

0

1

1





(15)

Stałą całkowania C wyznaczymy z warunku:



=



0

dla

t =0

n

Ek

C

n







1

1

1

0



ZMĘCZENIE MATERIAŁÓW

ZMĘCZENIE MATERIAŁÓW

Zmęczenie materiałów

– zjawisko obniżania się

wytrzymałości materiału przy działaniu naprężeń
zmiennych.

 

W zależności od rodzaju obciążeń zmęczenie można
podzielić na:

•

zmęczenie mechaniczne – wywołane zmiennym

polem sił,

•

zmęczenie cieplne – wywołane zmiennym polem

temperatury i ograniczeniem swobody odkształceń
cieplnych.

ZMĘCZENIE MATERIAŁÓW

Zmienność

naprężeń

w

poszczególnych

elementach maszyn w większości przypadków ma
charakter sinusoidalny:

(1)

gdzie:



m

– naprężenie średnie cyklu,



a

– amplituda zmian naprężeń,

 - prędkość kołowa lub pulsacja zmian naprężeń.

ZMĘCZENIE MECHANICZNE

Naprężenia zmęczeniowe

t

a

m









sin





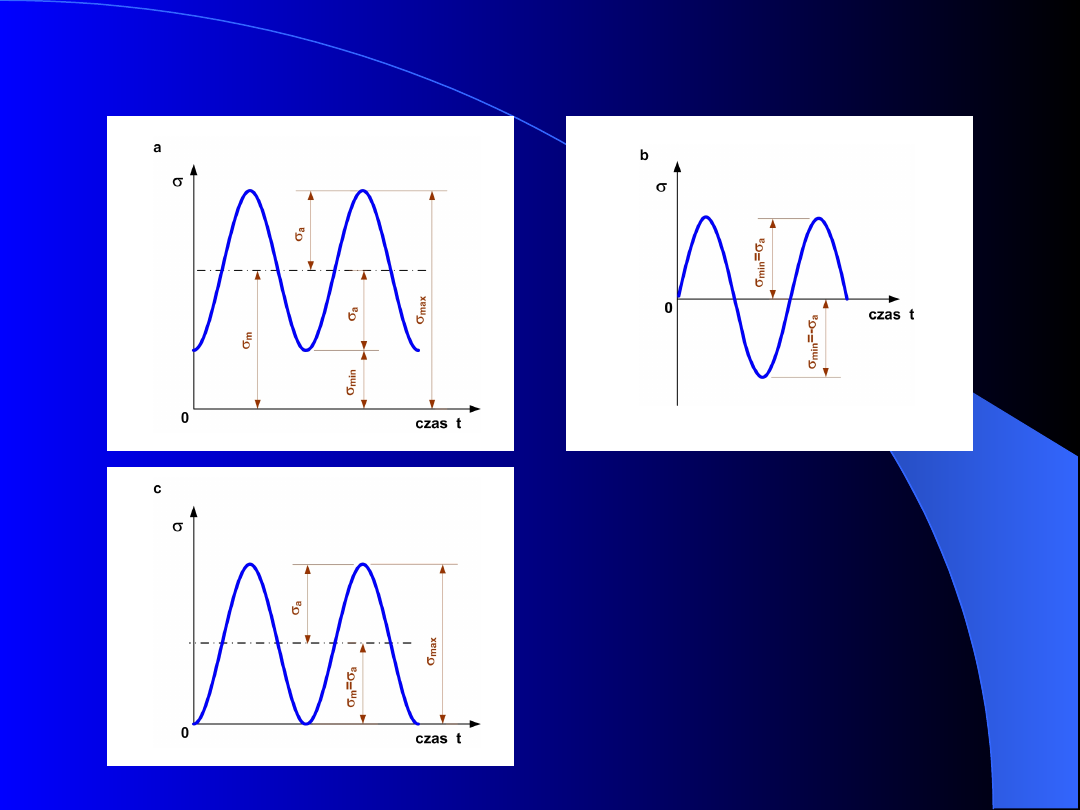
Naprężenia zmęczeniowe

Rys. 1. Podstawowe cykle

naprężeń: a) sinusoidalny dowolny,

b) obustronny (symetryczny), c)

jednostronny (pulsujący, tętniący)

Zgodnie z równaniem (1) naprężenia cyklu zmieniają
się od wartości maksymalnej:

(2)

do wartości minimalnej

(3)

Naprężenie średnie cyklu wynosi:

Naprężenia zmęczeniowe

a

m











max

a

m











min

2

min

max











m

(4)

Spośród różnego rodzaju cyklów zmian naprężeń

można wyróżnić:

•

cykl

obustronny

symetryczny

(zwany

wahadłowym lub obustronnym). Naprężenie średnie

jest równe zeru (



m

=0), a wówczas naprężenia

zmieniają się od



min

=-



a

do



max

=



a

;

•

cykl jednostronny-tętniący

(zwany pulsującym

lub jednostronnym). Naprężenia zmieniają się od zera

do



max

=2



a

. Naprężenie średnie cyklu wynosi



m

=½



max

=



a

.

Naprężenia zmęczeniowe

Asymetrię cyklu określa współczynnik asymetrii cyklu
R:

Naprężenia zmęczeniowe

max

min







R

(5)

oraz współczynnik stałości naprężenia H:

(6)

a

m

H







przy czym:

(7)

(8)

Naprężenia zmęczeniowe

R

R

H







1

1

1

1







H

H

R

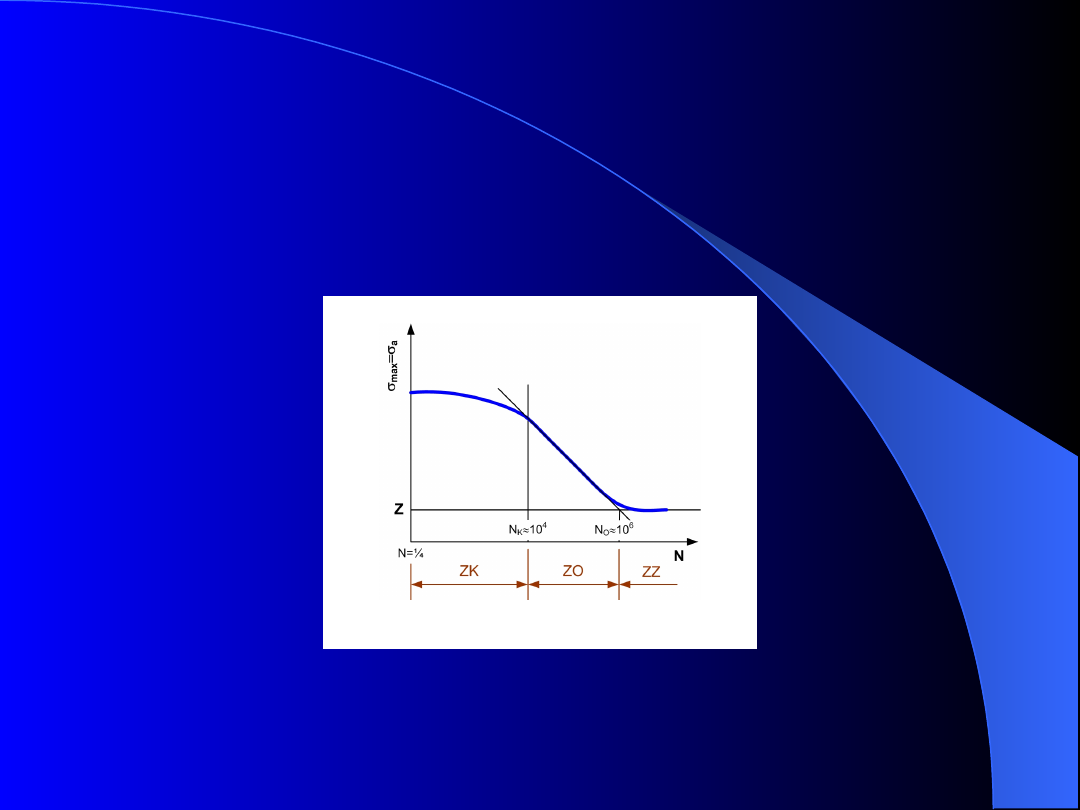
Wykres zależności między naprężeniem



max

a liczbą

cykli potrzebną do zniszczenia próbki N

z

nazywa się

wykresem Wőhlera

(rys. 2).

Wykres Wőhlera

Rys. 2. Wykres Wőhlera

Na wykresie Wőhlera można wyróżnić trzy

zakresy wytrzymałości zmęczeniowej:

•

ZK – zakres małej liczby cykli,

•

ZO

–

zakres

ograniczonej

wytrzymałości

zmęczeniowej,

•

ZZ – zakres nieograniczonej wytrzymałości

zmęczeniowej.

Wykres Wőhlera

Nieograniczona wytrzymałość zmęczeniowa Z

–

największe naprężenie



max

(dla określonego rodzaju

cyklu), przy którym element nie ulegnie zniszczeniu po

osiągnięciu umownej, granicznej liczby cykli N

G

.

Nieograniczona wytrzymałość zmęczeniowa jest więc

granicą zmęczenia

.

Wykres Wőhlera

Graniczną liczbę cykli N

G

(podstawa próby

zmęczeniowej) przyjmuje się w zależności od rodzaju
materiału i sposobu obciążenia:

•

10  10

6

– dla stali konstrukcyjnych i innych stopów

żelaza,

•

100  10

6

– dla stopów metali nieżelaznych,

•

2  10

6

– dla różnych elementów konstrukcji.

Wykres Wőhlera

Wykres Smitha

Wykres Smitha stosuje się do przedstawienia

wyników badań zmęczeniowych przy ustalonej
granicznej liczbie cykli i dla dowolnej wartości
współczynnika stałości obciążenia H.

 

Na podstawie wykresu można stwierdzić, że:

naprężenia maksymalne



max

i naprężenia minimalne



min

są funkcją naprężeń średnich



m

:

 

m

f





1

max



 

m

f





2

min



(9)

(10)

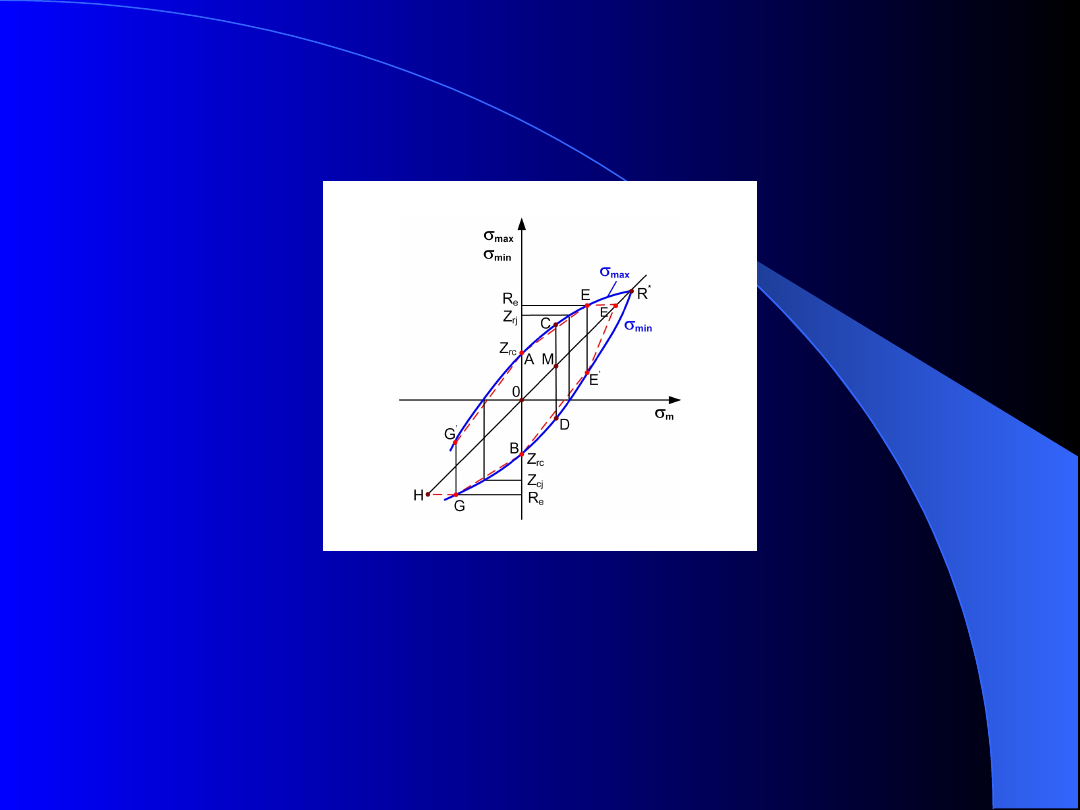
Wykres Smitha

Rys. 3. Wykres Smitha

Na wykresie Smitha dla jednoosiowego stanu
naprężenia, zaznaczono charakterystyczne wartości
naprężeń granicznych:

•

Z

rc

– cykl wahadłowy,

•

Z

rj

– cykl odzerowo tętniący (dodatni),

•

Z

cj

– cykl odzerowo tętniący (ujemny),

•

R

*

- wartość rzędnej wykresu Smitha przy



a

=0 (w

praktyce R

*

=R

m

dla rozciągania)

Wykres Smitha

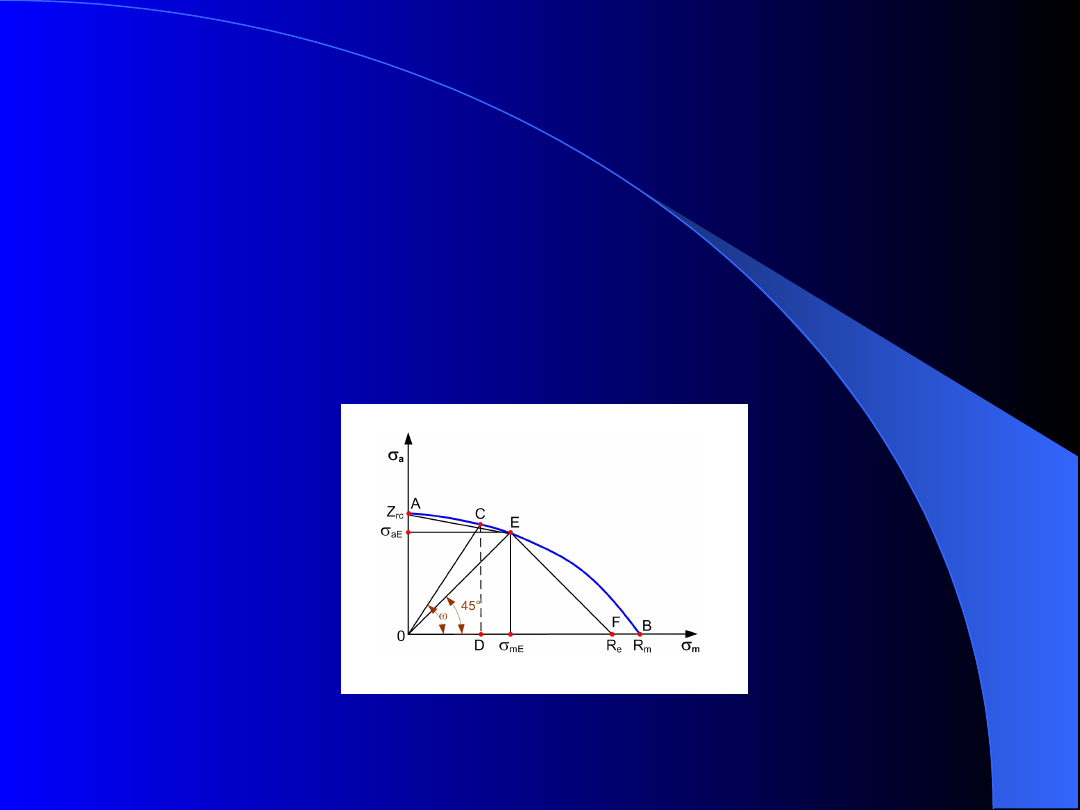
Wykres Haigha (rys. 4) powstaje przez obrót o kąt 45
prostej OR* na wykresie Smitha. Na osiach
współrzędnych odmierzamy



m

i



a

. Na obu wykresach

tym

samym

punktom

odpowiadają

te

same

oznaczenia.

Wykres Haigha

Rys. 4. Wykres Haigha

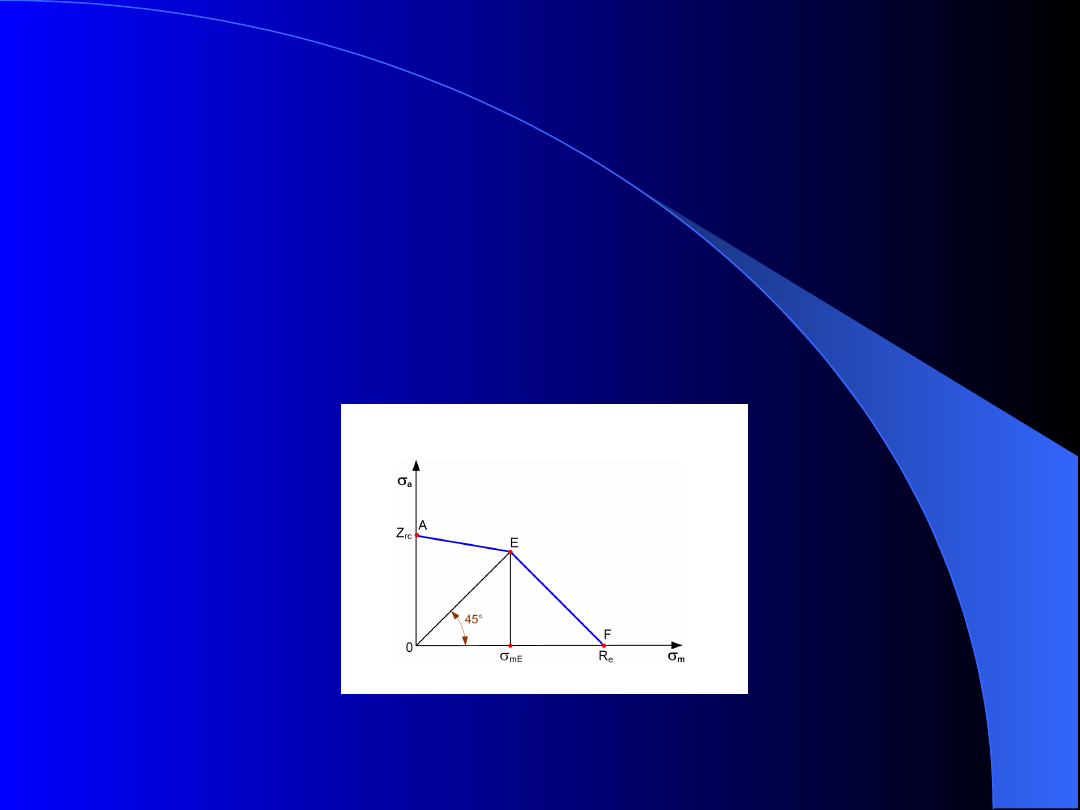
Rys. 5. Uproszczony wykres Haigha

Dla przypadku rozciągania – ściskania można

zastosować uproszczony wykres Haigha (rys. 5). Do
sporządzenia tego wykresu wystarczą następujące
dane: Z

rc

(punkt A), granica plastyczności R

e

(punkt G)

oraz

wytrzymałość

zmęczeniowa

przy

cyklu

jednostronnym Z

rj

.

Wykres Haigha

Prosta wychodząca z początku układu i nachylona pod
kątem  do osi odciętych wyznacza na wykresie
Haigha punkt C, gdzie:

Wykres Haigha

R

R

tg

m

a









1

1







(11)

Suma rzędnej



a

i odciętej



m

tego punktu jest

wytrzymałością zmęczeniową Z, gdyż:

(12)

Z

DC

OD

a

m











max







Przebieg krzywej AB dla materiałów w stanie
sprężysto- plastycznym można opisać równaniem:

Wykres Haigha

(13)































2

1

m

m

rc

a

R

Z





Prosta przechodząca przez punkty E oraz F ogranicza
wartości stosowanych naprężeń, gdyż:

(14)

m

m

a

R













max

Rozpatrzmy pręt o przekroju kołowym poddany

zginaniu

obrotowemu.

Amplitudę

naprężeń

normalnych



an

wyznaczamy z zależności:

Uproszczone obliczenia

wytrzymałościowe

W

M

g

an





gdzie:

M

g

– moment gnący,

W – wskaźnik wytrzymałości na zginanie obliczone
względem średnicy pręta.

(15)

Warunkiem niezawodności elementu konstrukcji, czyli
jej odpowiedniej trwałości jest spełnienie następującej
zależności:

(16)

gdzie:

•



k

– współczynnik działania karbu,

(Z

rc

– wytrzymałość zmęczeniowa próbek gładkich;

Z

rck

– wytrzymałość zmęczeniowa próbek z karbem).

(



k

– współczynnik wrażliwości na

działanie karbu;



k

– współczynnik kształtu)

Uproszczone obliczenia

wytrzymałościowe

go

p

k

an

Z

n









rck

rc

k

Z

Z









1

1







k

k

k







•

n – współczynnik bezpieczeństwa.

•



- współczynnik określający wpływ wymiarów

elementów

(Z

d

– wytrzymałość zmęczeniowa

elementu lub próbki o dowolnej średnicy; Z –
wytrzymałość zmęczeniowa próbki o średnicy 7-10
mm).

•



p

– współczynnik stanu powierzchni, (Z

’

–

wytrzymałość zmęczeniowa przy danym rodzaju
obróbki

powierzchniowej;

Z

–

wytrzymałość

zmęczeniowa próbki polerowanej).

•

Z

go

– wytrzymałość zmęczeniowa przy zginaniu

obrotowym.

Z

Z

d





Z

Z

p

'





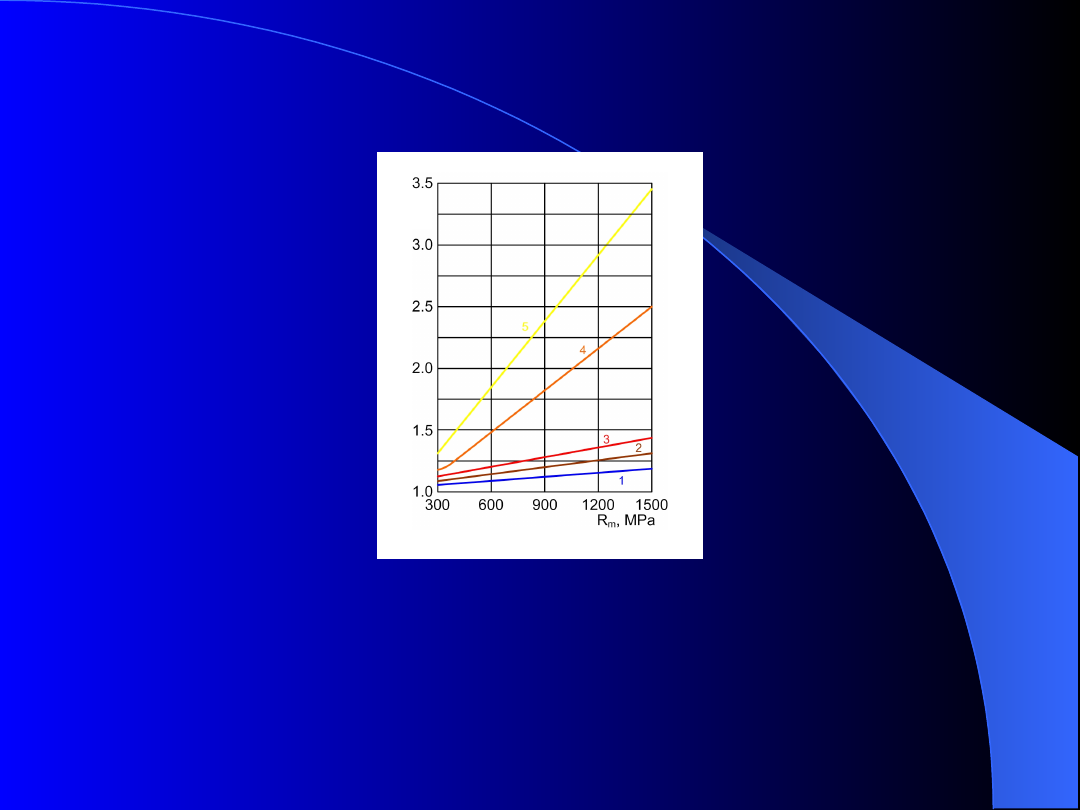
Uproszczone obliczenia

wytrzymałościowe

Rys. 7. Współczynnik stanu powierzchni dla stalowych części:

rozciąganych lub zginanych



p

. 1 – 9 klasa chropowatości

powierzchni (szlifowanie wykończające), 2 – 7 klasa

chropowatości (frezowanie), 3 – 5 klasa chropowatości

(toczenie zwykłe), 4 – ostry karb o kącie rozwarcia 60 i

głębokości 0,1 mm na próbce o średnicy 7,5 mm, 5 – część

pokryta naskórkiem walcowniczym



p

Amplitudę naprężeń nominalnych wyznacza się z
zależności:

Uproszczone obliczenia

wytrzymałościowe

n

Z

k

go

p

an









(16)

Prawa strona tego równania wyraża naprężenie
dopuszczalne na zmęczenie dla rozpatrywanego
przypadku zginania obrotowego.

REGUŁA MINERA

Warunki pracy różnych części maszyn są często

takie, że muszą one przenosić cykliczne obciążenia o
zmiennej amplitudzie.

Reguła Minera przedstawia liniowy sposób sumowania
uszkodzeń:

(17)

gdzie:

N

i

– liczba cykli o danej amplitudzie naprężenia,

N

zi

– liczba cykli do zniszczenia odpowiadająca tej

amplitudzie naprężenia,

i – liczba różnych amplitud naprężenia występujących
w procesie

1

1







k

i

zi

i

N

N

Założenie reguły Minera polega na tym, że

stopień uszkodzenia w procesie zmęczenia (dla danej

amplitudy naprężenia) określa stopień uszkodzenia dla

każdej innej amplitudy naprężenia.

REGUŁA MINERA

Zmęczenie cieplne – proces powstawania i

rozwoju uszkodzeń w materiałach części maszyn i

konstrukcji na skutek zmian energii wewnętrznej pod

wpływem

wielokrotnych

okresowych

zmian

temperatury.

 

Ze względu na sposób hamowania odkształcen

cieplnych zmeczenie cieplne można podzielić na:

•

zmęczenie

cieplne

z

ograniczeniami

zewnętrznymi,

•

zmęczenie

cieplne

z

ograniczeniami

wewnętrznymi.

ZMĘCZENIE CIEPLNE

Ograniczenia zewnętrzne – reakcje więzów (siły

przyłożone do powierzchni elementu).

Ograniczenia wewnętrzne – gradient temperatury,

anizotropia

struktury

i

różne

wartości

współczynników rozszerzalności cieplnej sąsiednich
ziaren, faz lub też elementów składowych
kompozytów.

ZMĘCZENIE CIEPLNE

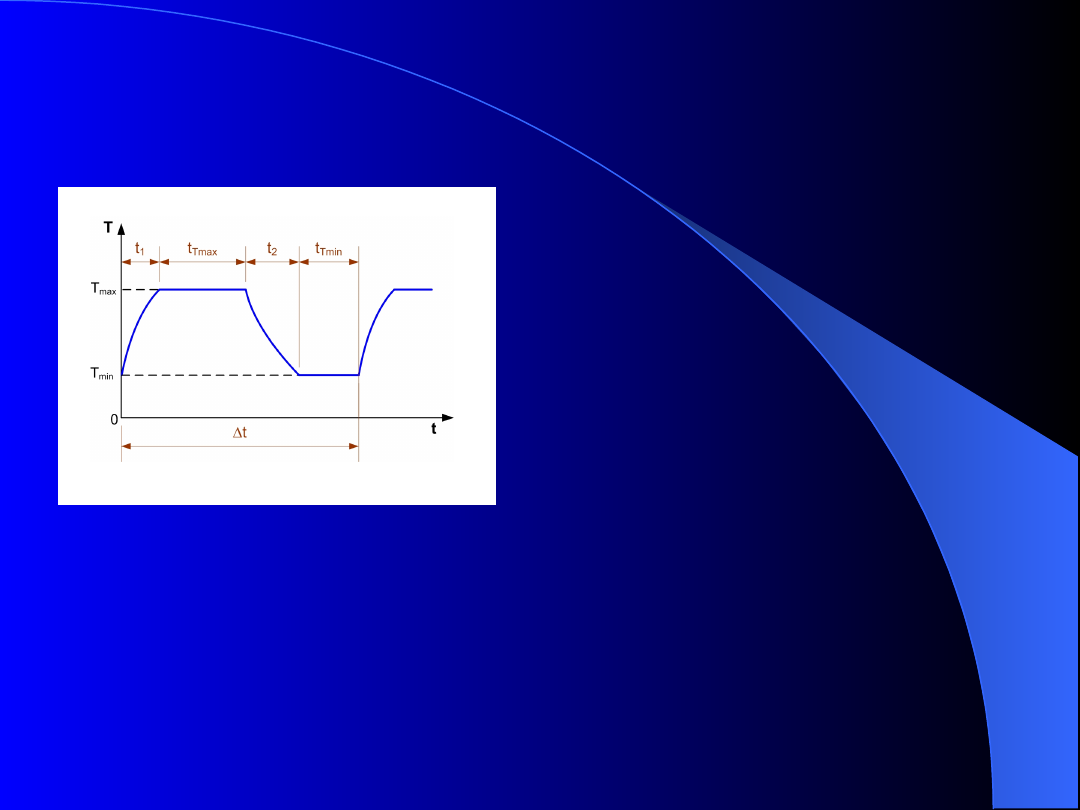
Rys. 8. Kształt cyklu cieplnego

ZMĘCZENIE CIEPLNE

Cykl cieplny składa się z:

•

nagrzanie do temperatury
maksymalnej T

max

w czasie t

1

,

•

wytrzymanie

w

temperaturze maksymalnej w
czasie t

Tmax

,

•

chłodzenie do temperatury
minimalnej T

min

w czasie t

2

,

•

wytrzymanie

w

temperaturze minimalnej w
czasie t

Tmin

.

Zmęczenie cieplne należy do procesów o małej

liczbie cykli (N

z

 5



10

4

).