Temat:

Produkcja

Jest procesem, w którym czynniki produkcji są
przekształcane w wyroby gotowe
Dla celów naszej analizy posługujemy się trzema
szeroko rozumianymi kategoriami czynników
produkcji:
•materiałami

(obejmują m. in. Surowce, dobra pośrednie, wodę,

elektryczność i inne źródła energii)

•pracą

(oznacza wszystkie kategorie pracowników zatrudnianych

przez przedsiębiorstwo)

•kapitałem

(obejmuje m. in. budynki, maszyny, i urządzenia oraz

zapasy

Najważniejszą prawidłowością występującą w procesie

produkcji jest ścisły związek między wielkością
produkcji a kosztami. Głównym zadaniem każdego
menedżera odpowiedzialnego za sprawy produkcji
jest wybór takiej metody wytwarzania, która pozwoli
osiągnąć dany wolumen produkcji przy najniższych
kosztach całkowitych.

Dlatego też efektywna produkcja wymaga stworzenia

odpowiedniej infrastruktury produkcyjnej oraz
dokładnej oceny zapotrzebowania na materiały i
czynniki wytwórcze. Oznacza to również konieczność
zwracania uwagi na koszty tych czynników i
nieustannego poszukiwania tańszych metod
wytwarzania dóbr oraz świadczenia usług przez
przedsiębiorstwo.

1. Funkcja produkcji

- Określa maksymalną wielkość produkcji, jaką

może wytworzyć przedsiębiorstwo przy różnych

kombinacjach czynników wytwórczych

- Można ją przedstawić w formie równania, wykresu

lub tabeli

- Ogólna postać: Q = F(M,L,K

)

Zapis ten oznacza, że wielkość produkcji przedsiębiorstwa

zależy odpowiednio od ilości materiałów (M), pracy (L) i

kapitału (K) zastosowanych w procesie wytwarzania.

- Cel maksymalizacji zysku (najczęściej przyjmowany

przez menedżerów) wymaga przyjęcia założenia, iż
produkcja jest efektywna z technicznego punktu widzenia

,

oznacza to, że ani czynniki produkcji, ani wyroby gotowe nie są

marnotrawione lub niewłaściwie wykorzystywane. Oznacza to również, że

menedżerowie nie powinni decydować się na dalsze stosowanie

nieefektywnej metody produkcji, jeśli istnieje lepsza metoda, która daje

możliwości zwiększania produkcji przy tej samej wielkości nakładów

czynników wytwórczych.

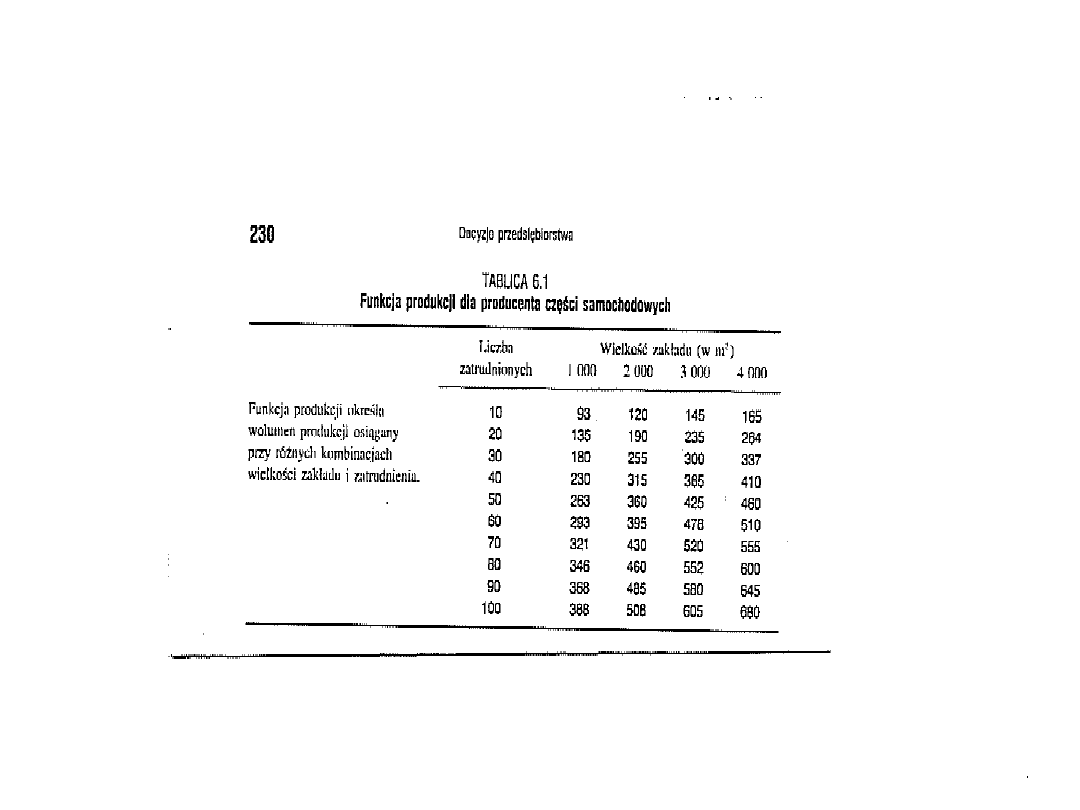
Przykład:

Funkcja produkcji producenta

części samochodowych

Tablica z poprzedniego slajdu pokazuje funkcję

produkcji przedsiębiorstwa
wieloasortymentowego dostarczającego
części dwóm z trzech największych
producentów samochodów w Stanach
Zjednoczonych. Tablica zawiera dane
oznaczające wielkości produkcji, które
można wytworzyć przy zastosowaniu
różnych kombinacji dwóch czynników
wytwórczych – pracy i kapitału. Każda z liczb
odzwierciedla wielkość produkcji osiąganą
przy zastosowaniu danej ilości pracy
(podanej w wierszach) i określonej wielkości
zakładu (dane w kolumnach).

2. Produkcja przy jednym zmiennym

czynniku wytwórczym

a)

Produkcja w krótkim i długim okresie

Okres krótki oznacza czas, w którym ilość jednego lub więcej

czynników produkcji stosowanych przez przedsiębiorstwo

jest stała, innymi słowy nie podlega zmianom.

Czynniki, których

nakład w krótkim okresie się nie zmienia, nazywamy stałymi. Typowym

stałym czynnikiem produkcji jest kapitał, zmiana jego zasobu wymaga

bowiem czasu.

Okres długi jest czasem niezbędnym aby

przedsiębiorstwo mogło dostosować wielkość

wszystkich nakładów czynników produkcji.

W długim

okresie przedsiębiorstwo może dokonać zmian wielkości (skali) swojego

zakładu (podobnie jak i ilości wszystkich pozostałych czynników produkcji).

Nie istnieje żadna uniwersalna reguła pozwalająca

wyznaczyć granicę między krótkim i długim

okresem; linia podziału musi raczej być określana

w każdym przypadku z osobna. Dla rafinerii może

to być kilka lat, dla banku kilka miesięcy.

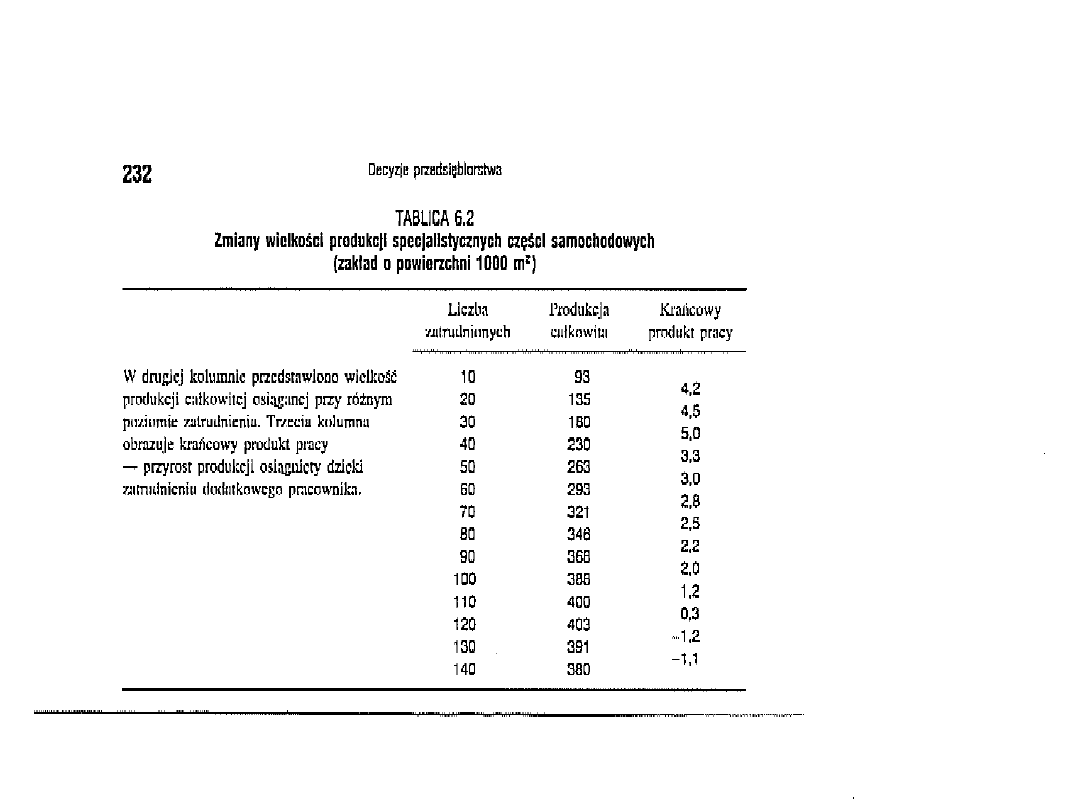
b) Produkt krańcowy

Zakładamy, że zmienny jest tylko jeden czynnik

produkcji, więc produkt krańcowy:

-to dodatkowa wielkość produkcji otrzymana dzięki

zatrudnieniu dodatkowej jednostki zmiennego

czynnika produkcji przy założeniu stałości

wszystkich pozostałych czynników wytwórczych

-jeśli tym zmiennym czynnikiem jest praca, jak w

naszym przykładzie, to:

Marginal product of labour: MP

L

MP

L

=dQ/dL,

innymi słowy

krańcowy produkt pracy jest równy zmianie wielkości

produkcji na jednostkę przyrostu zatrudnienia

l

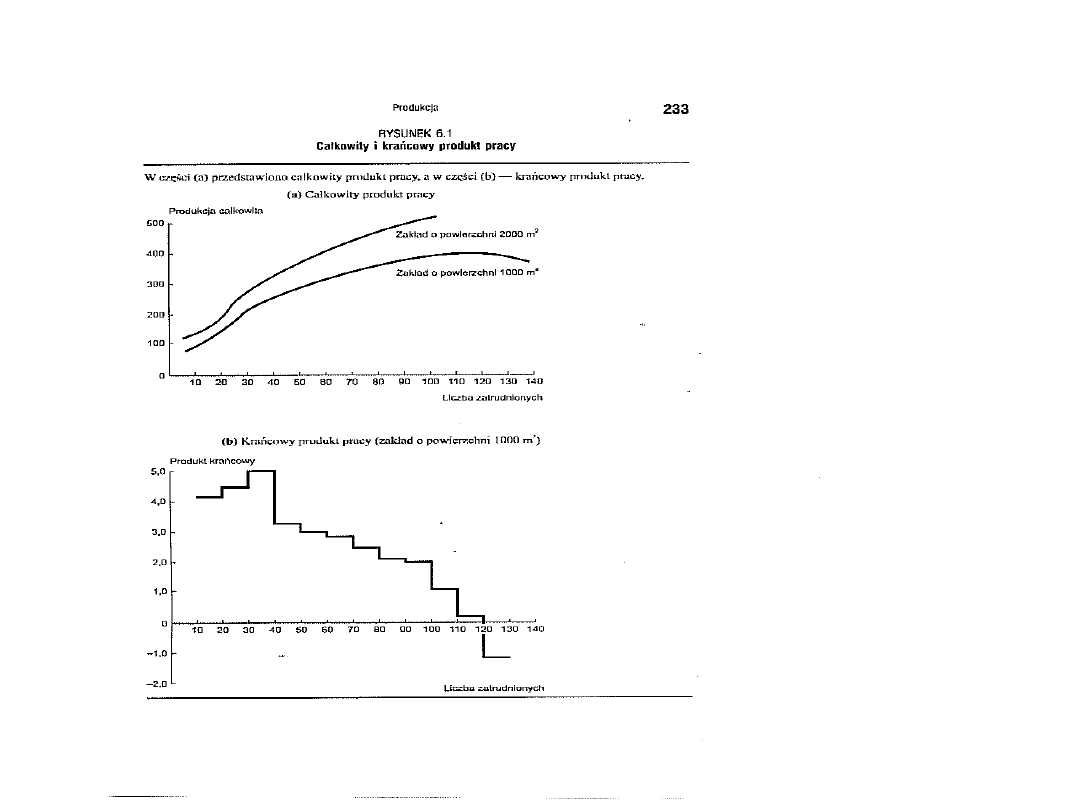
Zauważmy, że MP

L

najpierw rośnie ( przy zwiększaniu

zatrudnienia do 40 osób), a następnie maleje.

Istnieje kilka przyczyn wyjaśniających rosnącą

produktywność krańcową (przy niskim
zatrudnieniu). Gdy zasób siły roboczej jest
niewielki, każdy pracownik musi być „specjalistą
od wszystkiego” (i w efekcie niczego nie potrafi
robić dobrze). Zwiększenie zatrudnienia stwarza
możliwość specjalizacji – poszczególni pracownicy
wykonują tylko określone zajęcia – dzięki czemu
wzrasta produkcja.

Co więcej, wykorzystując bardziej efektywnie

istniejący zasób maszyn i urządzeń, dodatkowi
pracownicy będą w zwiększonym stopniu
przyczyniać się do wzrostu produkcji.

3. Prawo malejących przychodów

Malejący produkt krańcowy zmiennego czynnika produkcji

wskazuje na działanie jednego z najbardziej znanych i
najważniejszych empirycznych „praw” produkcji,

Głosi ono, że jeżeli następuje wzrost nakładów

jednego czynnika produkcji (przy założeniu
stałości pozostałych czynników), to
począwszy od pewnego poziomu przyrosty
produkcji zaczynają maleć; oznacza to, że
zmniejsza się produkt krańcowy.

W omawianym przykładzie malejące przychody z pracy występują przy

zatrudnieniu przekraczającym 40 osób. Przy tym poziomie
zatrudnienia są już obsadzone najbardziej produktywne stanowiska ,
co oznacza, że kolejni pracownicy są przydzielani do mniej
produktywnych zajęć.

Optymalne wykorzystanie czynnika produkcji

Prawo malejących przychodów oznacza, że w

procesie podejmowania decyzji o wielkości

produkcji przedsiębiorstwo ma do czynienie z

klasycznym dylematem decyzyjnym. Poprzez

zastosowanie większej ilości zmiennego czynnika

wytwórczego osiąga ono bezpośrednią korzyść w

postaci zwiększonej produkcji całkowitej, która

zostaje okupiona dodatkowym kosztem

związanym z tym czynnikiem.

Jaki jest optymalny poziom wykorzystania czynnika

zmiennego?

Jak zwykle odpowiedź znajdujemy, obliczając zysk

krańcowy przedsiębiorstwa. Tym razem zysk ten

jest wynikiem zwiększania nakładu czynnika

produkcji o jednostkę.

Krańcowy przychód z czynnika produkcji

(MRP) jest to przyrost utargu wynikający ze

zwiększenia nakładu tego czynnika o

jednostkę.

MRP

L

=MR

x

MP

L

MRP

L

– krańcowy przychód z pracy

MR – utarg krańcowy na jednostkę produktu
MP

L

– krańcowy produkt pracy w jednostkach fizycznych

Zatrudnienie powinno być zwiększane do

momentu, gdy krańcowy przychód z pracy

zrówna się z krańcowym kosztem pracy, tzn:

MRP

L

=

MC

L

Rekomendacja:

Dążące do maksymalizacji zysku przedsiębiorstwo powinno

zwiększać nakład zmiennego czynnika produkcji dopóty, dopóki

krańcowy przychód z tego czynnika nie zrówna się z krańcowym

kosztem tego czynnika

4. Produkcja w długim okresie

Przedsiębiorstwo może dowolnie zmieniać wielkość

nakładów wszystkich czynników produkcji. Na
podkreślenie zasługują dwa aspekty tej elastyczności:

Po pierwsze: przedsiębiorstwo staje wobec kilku ważnych

dylematów dotyczących stosowanej technologii.
Najważniejsze z nich wiąże się z określeniem proporcji,
w jakich w procesie produkcji wykorzystywane są
czynniki wytwórcze. Na przykład przedsiębiorstwo
może stwierdzić, że opłacalne jest zmniejszenie
zatrudnienia w administracji i zainwestowanie w nowy
sprzęt komputerowy oraz zakup specjalistycznego
oprogramowania dla pracowników. W rezultacie
przedsiębiorstwo to zastępuje pracę kapitałem.

Po drugie: przedsiębiorstwa muszą

podejmować istotne decyzje dotyczące

skali swoich inwestycji.

Pytania:
Jaka jest najbardziej opłacalna metoda

rozszerzania działalności firmy w długim

okresie?

Czy istnieją jakieś granice wielkości

przedsiębiorstwa, po przekroczeniu

których efektywność drastycznie maleje?

Są to ważne pytania, na które można

odpowiedzieć odwołując się do pojęcia

korzyści skali.

Skala produkcji przedsiębiorstwa oznacza wielkość wszystkich

stosowanych przez nie czynników produkcji. Zmiana skali

jest z kolei rozumiana jako określona procentowa zmiana

nakładów wszystkich czynników produkcji.

Kluczowe dla menedżera jest pytanie, o ile zmieni się

wolumen produkcji przedsiębiorstwa przy proporcjonalnym

wzroście zaangażowania czynników produkcji? W

odpowiedzi na to pytanie pomocne jest pojęcie

przychodów skali. Przychody skali to miara procentowej

zmiany wielkości produkcji wynikającej z danej procentowej

zmiany nakładów czynników produkcji. Musimy zauważyć

trzy przypadki:

• Stałe przychody ze skali – występują wówczas gdy dana

procentowa zmiana nakładów wszystkich czynników

produkcji przynosi dokładnie taką samą procentową

zmianę wolumenu produkcji.

Powszechnym przypadkiem występowania stałych

przychodów ze skali produkcji jest sytuacja, w której

przedsiębiorstwo może łatwo powielać swój proces

produkcji.

•

Rosnące przychody ze skali produkcji, występują wówczas,

gdy dana procentowa zmiana nakładów wszystkich

czynników wytwórczych przynosi większą procentową

zmianę wolumenu produkcji (przypadek taki często

określany jest w skrócie jako

korzyści skali).

• Zmniejszające się przychody ze skali, występują

wówczas, gdy dany procentowy wzrost nakładów

wszystkich czynników wytwórczych przynosi mniejszy

procentowy wzrost produkcji. Najczęściej malejące

przychody ze skali wynikają ze struktury organizacyjnej

w bardzo dużych przedsiębiorstwach. Wraz ze wzrostem

skali przedsiębiorstwa mnożą się też problemy związane

z koordynacja i kontrolą na wielu poziomach zarządzania.

Wygodną miarą dla korzyści skali jest elastyczność

produkcji. Elastyczność produkcji jest to procentowa

zmiana wielkości produkcji wywołana wzrostem nakładów

wszystkich czynników wytwórczych o 1%. Dla stałych

przychodów ze skali elastyczność jest równa 1; dla

rosnących przychodów ze skali jest ona większa od 1,

wreszcie dla zmniejszających się przychodów ze skali jest

ona mniejsza od 1.

Produkcja po najniższych kosztach

W długim okresie przedsiębiorstwo może zmienić wielkość zużycia

wszystkich czynników produkcji. Ponieważ z czynnikami

wytwórczymi związane są koszty, pojawia się pytanie: w jaki

sposób przedsiębiorstwo może określić taką kombinację czynników

produkcji, która pozwoli zminimalizować koszty wytworzenia danej

wielkości produkcji?

Q = F(L, K)

TC = P

L

L + P

K

K

W długim okresie przedsiębiorstwo produkuje po najniższych kosztach

wówczas, gdy relacje produktów krańcowych do kosztów czynników

wytwórczych są równe dla wszystkich czynników produkcji

MP

L

MP

K

------------ = -------------

P

L

P

K

W bardziej ogólnej postaci, tj. dla wielu czynników, prawidłowość ta przyjmuje

formę odpowiednio długiego ciągu równości relacji produktów krańcowych i

cen czynników produkcji.

5. Mierzenie funkcji produkcji

a) Liniowa funkcja produkcji

Q = aL + bK + c

a, b, c są parametrami, które należy oszacować na

podstawie dostępnych danych

Bezpośrednią implikacją liniowości jest to, że

produkt krańcowy każdego z czynników
produkcji jest stały: MP

L

=a i MP

K

=b

Ponadto liniowość powoduje, że czynniki produkcji

są w stosunku do siebie doskonałymi
substytutami.

b) Funkcja produkcji o stałych proporcjach, jest

przeciwieństwem funkcji liniowej.

- Zamiast doskonałej substytucyjności, mamy tu do

czynienie z całkowitym brakiem substytucji

czynników produkcji.

Nadmiar któregokolwiek z czynników nie jest dobry.

Wzrost produkcji wymaga zrównoważonego

wzrostu nakładów wszystkich czynników

wytwórczych.

Istnieje jednak ważna implikacja wynikająca z

założenia produkcji o stałych proporcjach. W

przypadku wzrostu ceny jednego z czynników

wytwórczych, przedsiębiorstwo nie może

zaoszczędzić na tym czynniku, zastępując go

innym.

c) Wielomianowe funkcje produkcji

W funkcjach tych zmienne podnoszone są do potęgi wyrażonej

dodatnimi liczbami całkowitymi, gdzie np. a i b są
dodatnimi parametrami funkcji.

2

2

K

bL

aLK

Q





d) Funkcja Cobba- Douglasa

- Wygodnie jest estymować tą funkcję w

postaci logarytmicznej:





K

cL

Q 

K

L

c

Q

log

log

log

log











6. Inne decyzje dotyczące produkcji

a)

Przedsiębiorstwo wielozakładowe – dysponujemy
dwoma zakładami przetwórczymi – jaka powinna
być skala produkcji w każdym z nich?

Odpowiedź:

MP

A

= MP

B (produkty krańcowe w obu firmach są równe)

b) Wiele produktów –

przedsiębiorstwo staje przed problemem

alokacji ograniczonej ilości zasobu pomiędzy różne produkty!

Rekomendacja:

Wszystkie produkty dają jednakowy zysk krańcowy na jednostkę

czynnika produkcji