Metody i techniki badań

społecznych i pedagogicznych

Bartłomiej Walczak

Dobór próby

Metody doboru próby

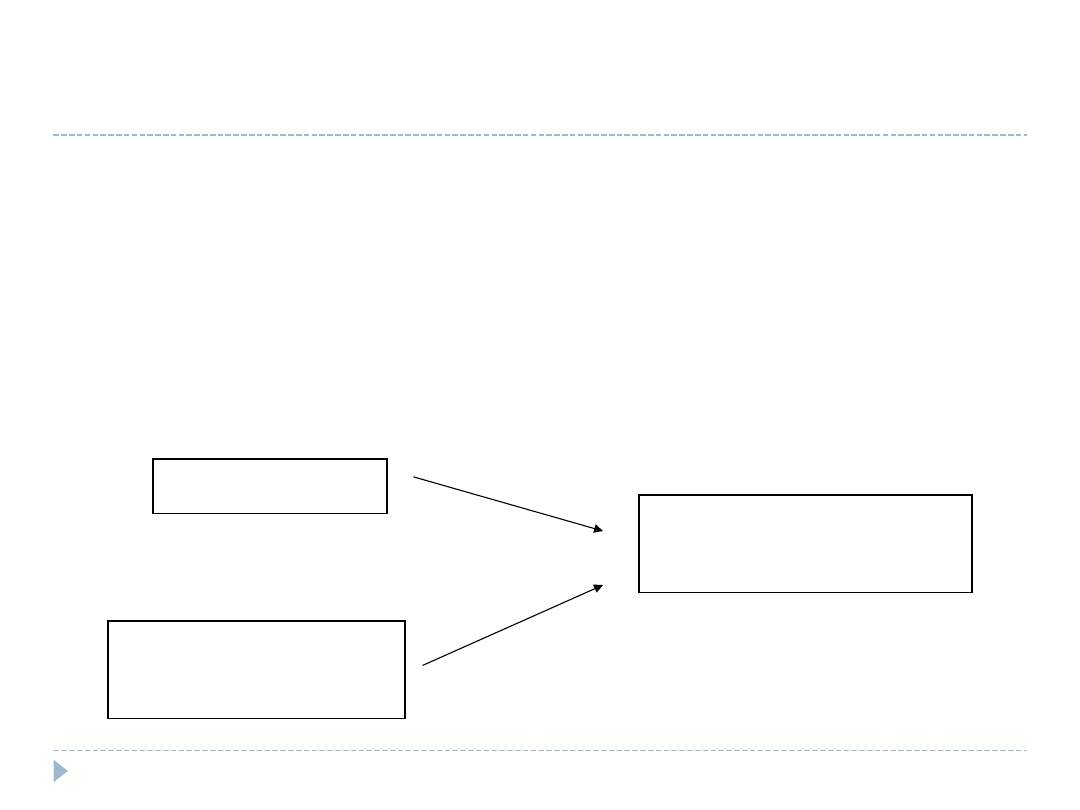
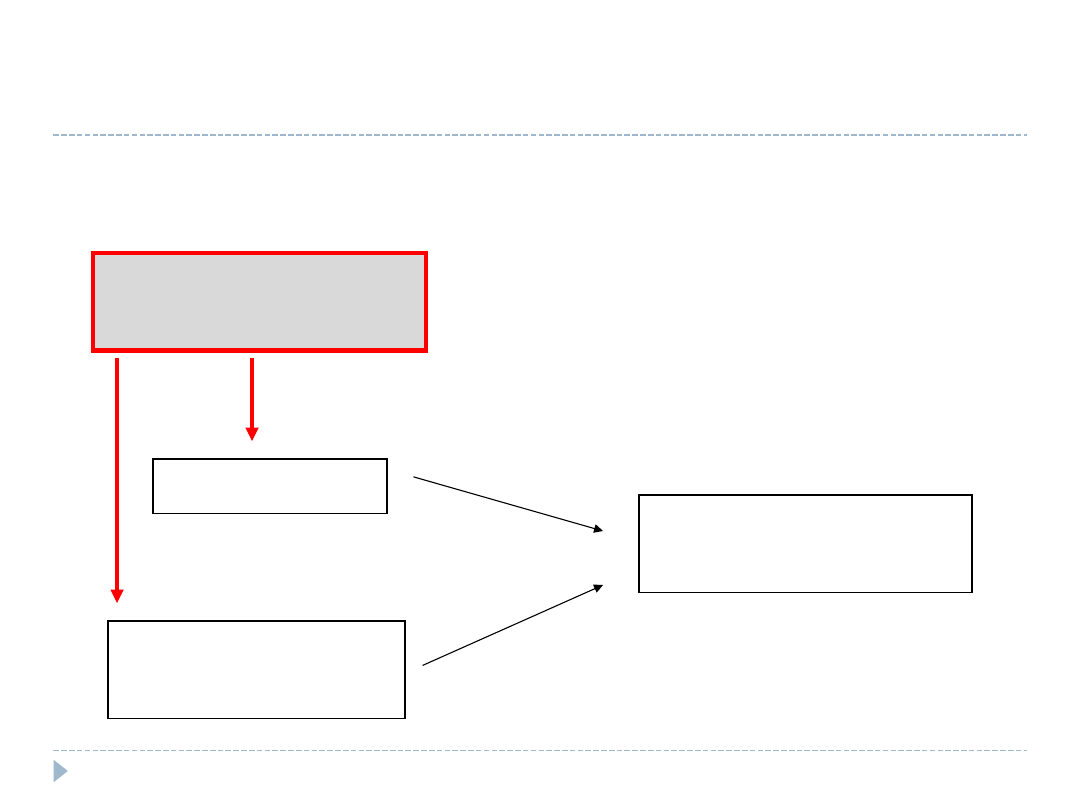
Dobór próby



Probabilistyczny



Nieprobabilistyczny

Nieprobabilistyczny dobór próby



Oparty na dostępności badanych



Celowy lub arbitralny



Metoda kuli śnieżnej



Dobór kwotowy

Dobór kwotowy

płeć

Ocena sytuacji

gospodarczej

Miejsce

zamieszkania

Dobór kwotowy

płeć

Ocena sytuacji

gospodarczej

Miejsce

zamieszkania

Zmienne
niezależne

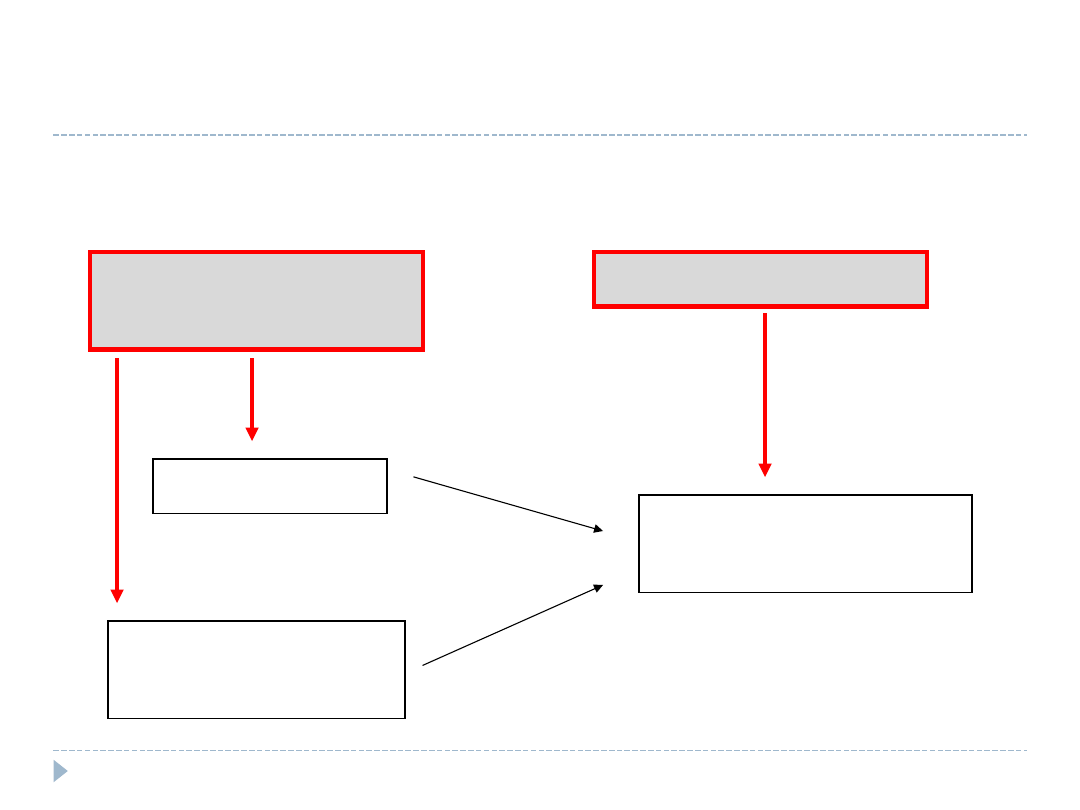
Dobór kwotowy

płeć

Ocena sytuacji

gospodarczej

Miejsce

zamieszkania

Zmienne
niezależne

Zmienna zależna

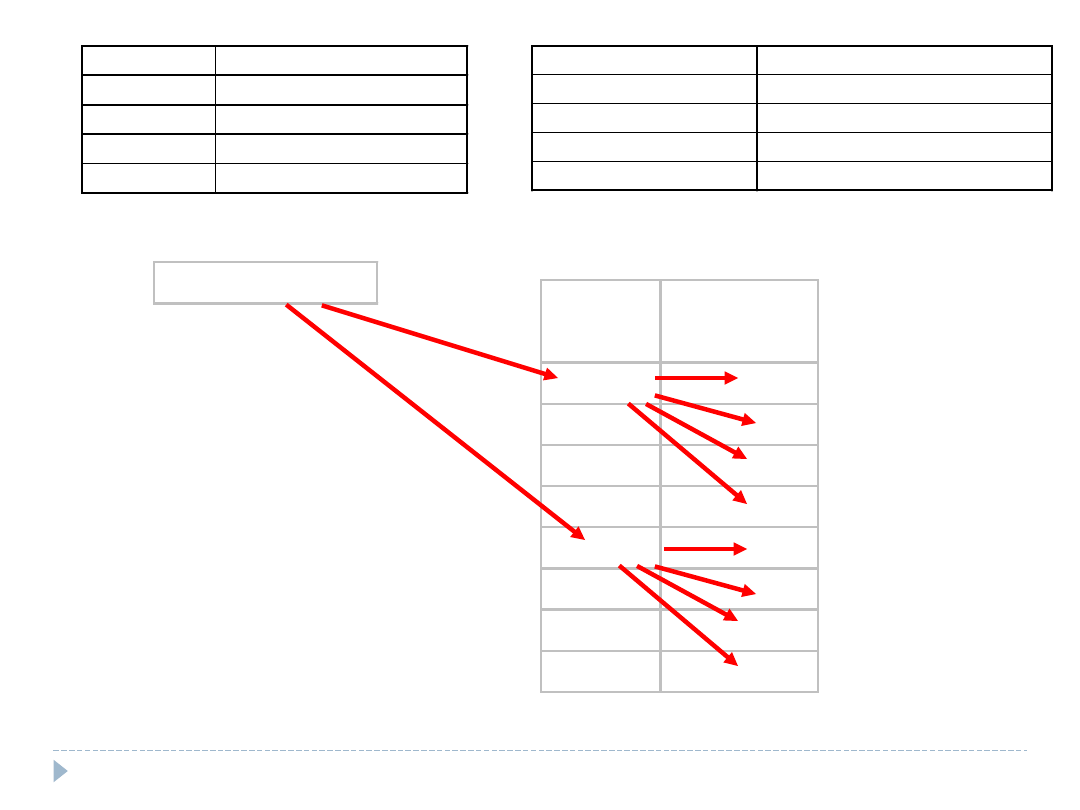
płeć

miejsce zamieszkania

kobieta

wieś

mężczyzna miasto do 10 tys

10 tys - 499 tys
powyżej 499 tys

płeć

miejsce zamieszkania

kobieta (60%)

wieś (30%)

mężczyzna (40%)

miasto do 10 tys (15%)
10 tys - 499 tys (25%)
powyżej 499 tys (30%)

1000 osób:

płeć

miejsce
zam/płeć

600

180

90

150
180

400

120

60

100
120

30% z 600=180

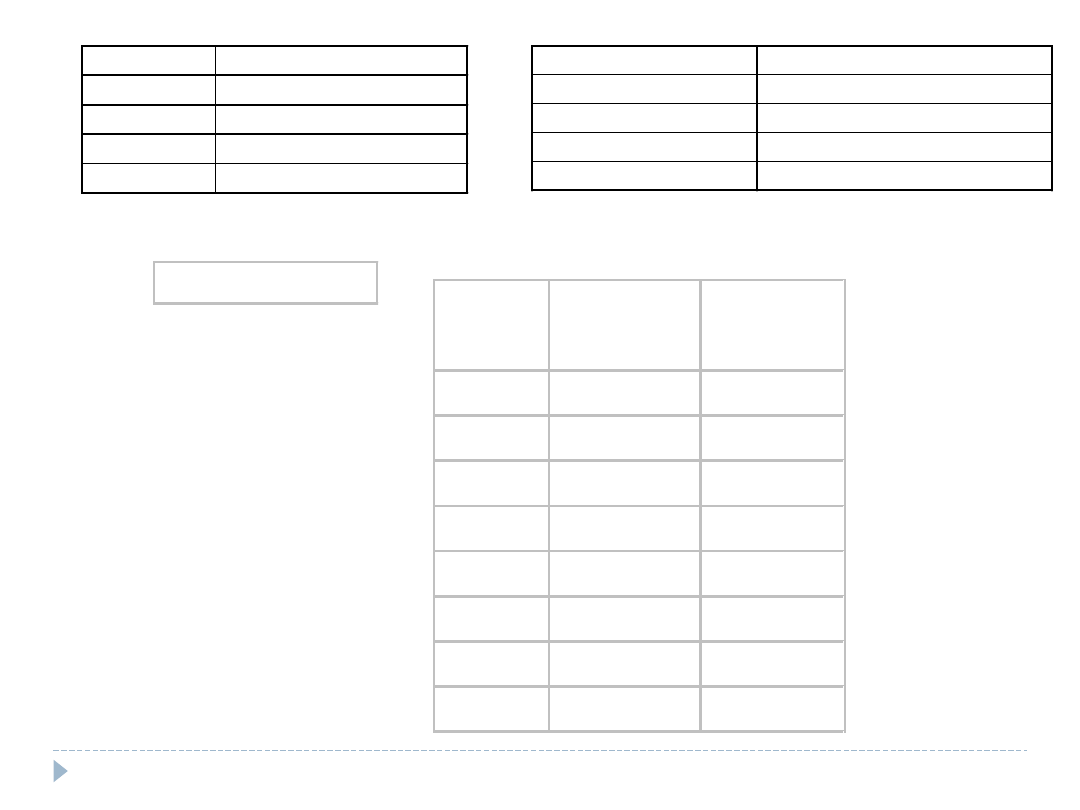
płeć

miejsce zamieszkania

kobieta

wieś

mężczyzna miasto do 10 tys

10 tys - 499 tys
powyżej 499 tys

płeć

miejsce zamieszkania

kobieta (60%)

wieś (30%)

mężczyzna (40%)

miasto do 10 tys (15%)
10 tys - 499 tys (25%)
powyżej 499 tys (30%)

1000 osób:

płeć

miejsce
zam/płeć wagi

600

180 10os*18

90 10os*9

150 10os*15
180 10os*18

400

120 10os*12

60 10os*6

100 10os*10
120 10os*12

Założenia probabilistycznego doboru próby

10PLN

20PLN

0PLN

90PLN

80PLN

70PLN

60PLN

30PLN

50PLN

40PLN

Ozł

10zł

20 zł

30 zł

40zł

50 zł

60zł

70 zł

80 zł

90zł

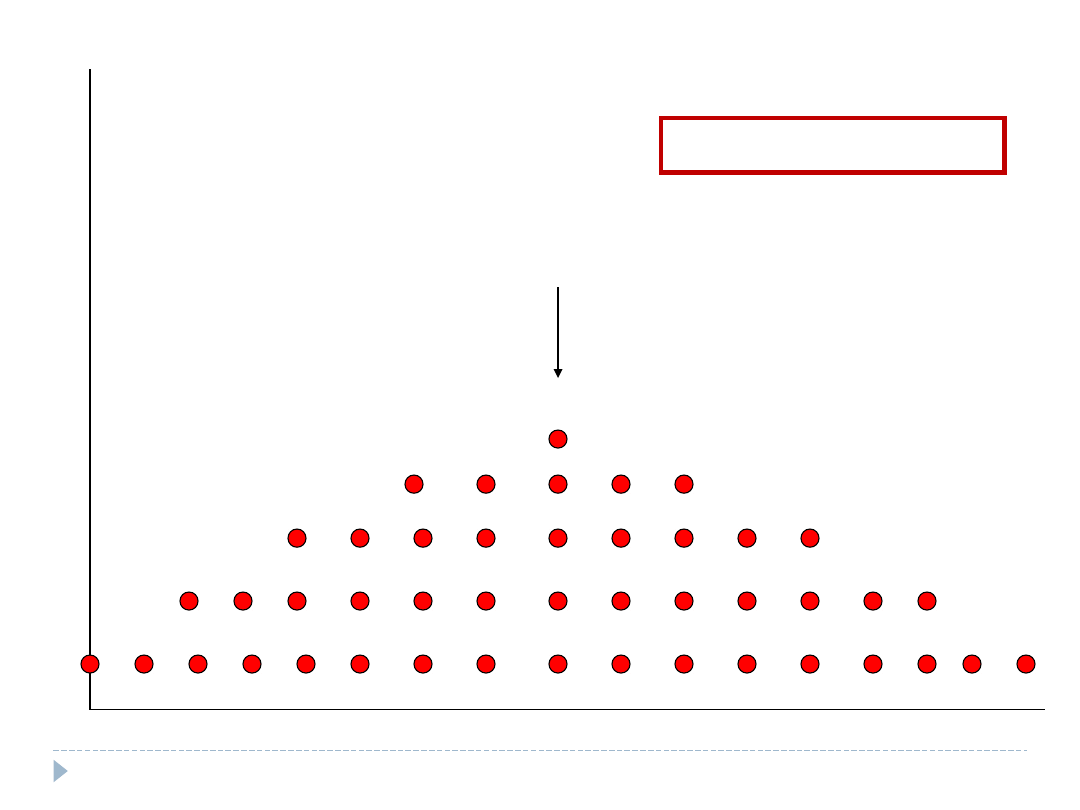
Estymatory średniej (wielkość
próby=1)

10

9

8

7

6

5

4

3

2

1

L

ic

zb

a

p

ró

b

(

ra

ze

m

=

1

0

)

Rzeczywista średnia=45zł

Ozł

10zł

20 zł

30 zł

40zł

50 zł

60zł

70 zł

80 zł

90zł

Estymatory średniej (wielkość
próby=2)

10

9

8

7

6

5

4

3

2

1

L

ic

zb

a

p

ró

b

(

ra

ze

m

=

4

6

)

Rzeczywista średnia (parametr)=45zł

Rozkład normalny

Błąd standardowy



błąd z próby lub błąd losowy (najczęściej mierzony
błędem standardowym) pozwala na określenie



Poziom ufności



Przedział ufności



Rachunek prawdopodobieństwa:



34% estymatorów odchyla się 1 BS w górę, 34% w dół od
rzeczywistego parametru



95% estymatorów odchyla się +/- 1,96 BS



99,9 estymatorów odchyla się +/- 2,58 BS

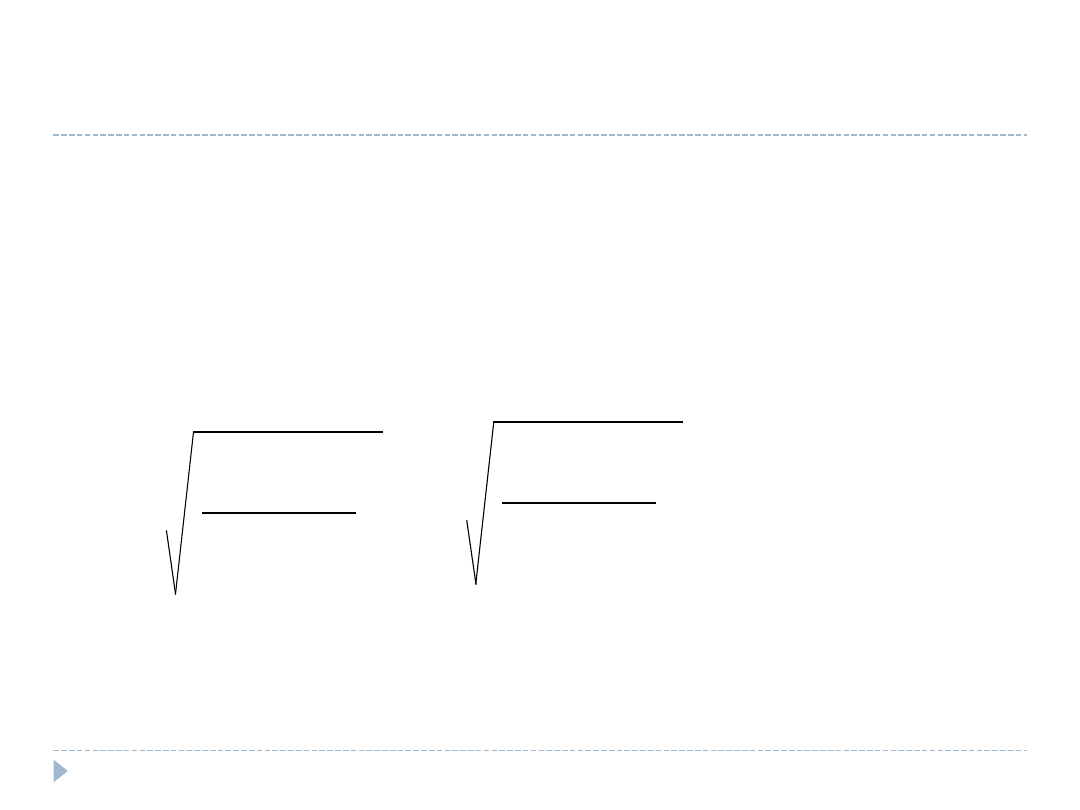
Przykład:

W grupie 100 studentów 50% jest za

podwojeniem liczby zajęć z teorii doboru
próby, 50% jest przeciw

50 x 50

100

s

p

=

= 0,05 (5% )

Błąd standardowy proporcji wynosi 5%

0,5x 0,5

100

=

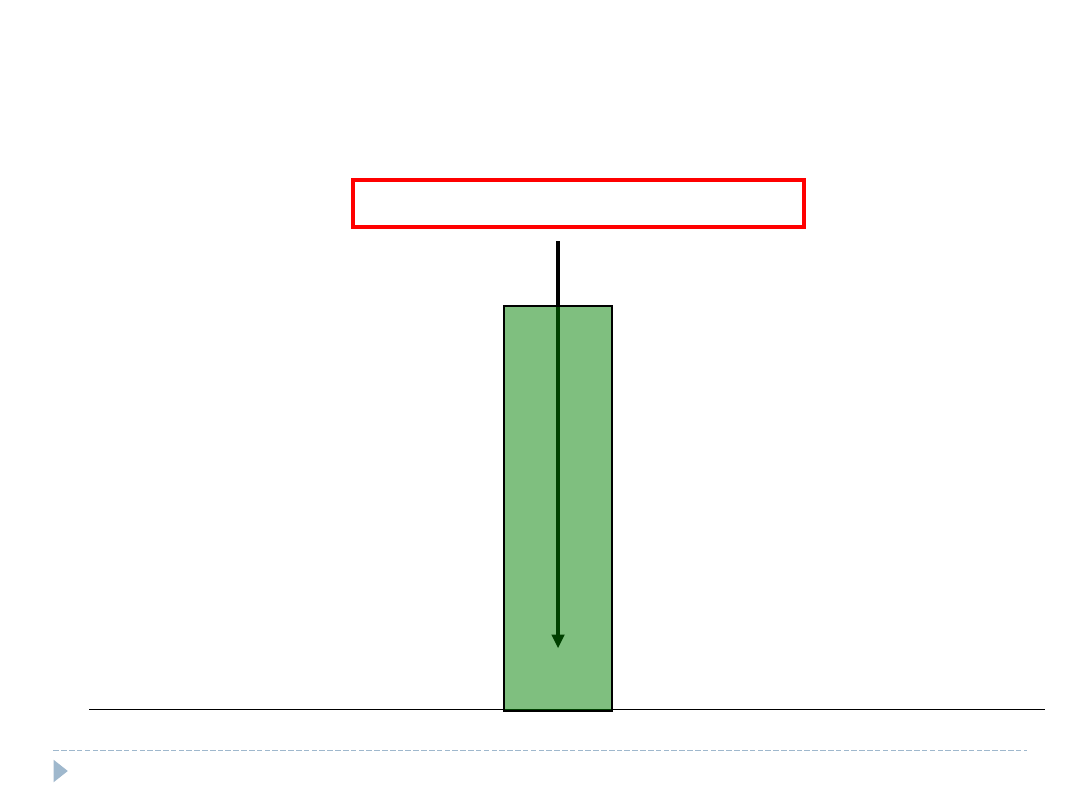
Co to znaczy?

Po pierwsze: 68% estymatorów zmieści się w przedziale
+/- 5% od rzeczywistego parametru. Innymi słowy: Przy
poziomie ufności 68% przedział ufności wynosi 45%-55%

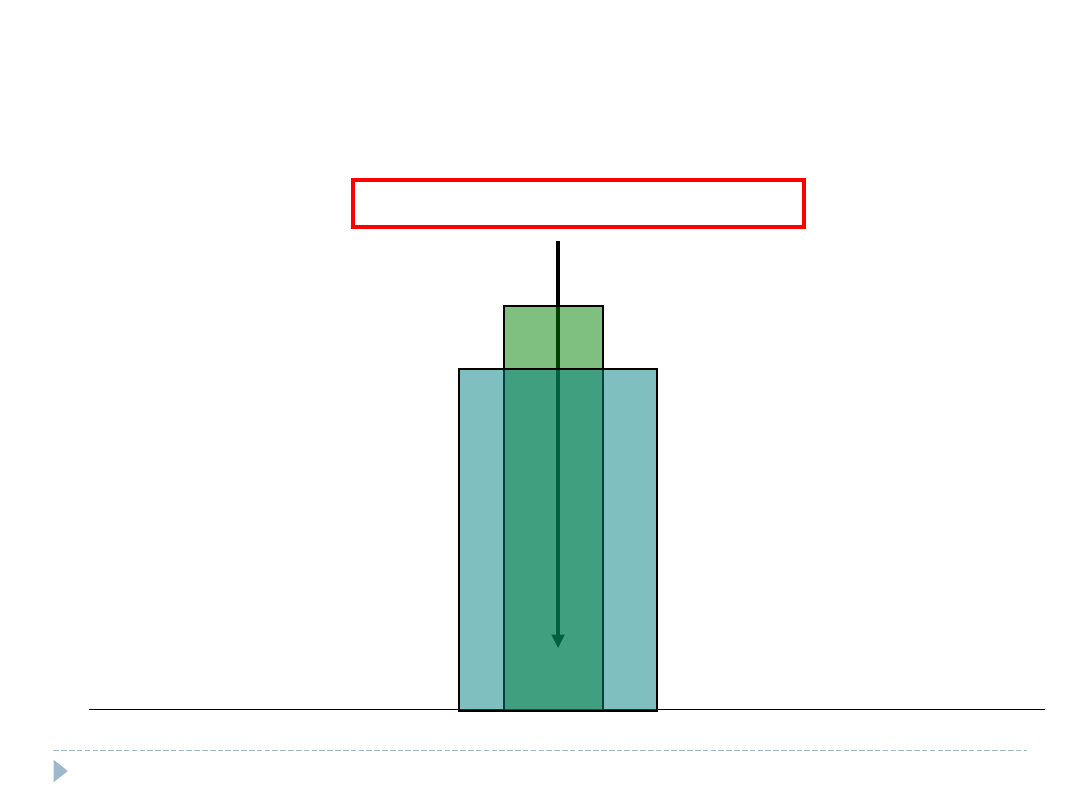
Po drugie: 95% estymatorów zmieści się w przedziale +/-
10% od rzeczywistego parametru (w zaokrągleniu: 1,96
wielkości błędu standardowego) . Innymi słowy: Przy
poziomie ufności 95% przedział ufności wynosi 40%-60%

Po trzecie: 99,9% estymatorów zmieści się w przedziale
+/- 15% od rzeczywistego parametru (tj. +/- 2,58 błędu
standardowego). Innymi słowy: Przy poziomie ufności
99,9% przedział ufności wynosi 35%-65%

O 10 20 30 40 50 60 70 80 90 100

Odsetek popierających (%)

Rzeczywisty parametr=50%

68% pomiarów

-5% +5%

45

55

O 10 20 30 40 50 60 70 80 90 100

Odsetek popierających (%)

Rzeczywisty parametr=50%

68% pomiarów

95% pomiarów

-5% +5%

-10%

+10%

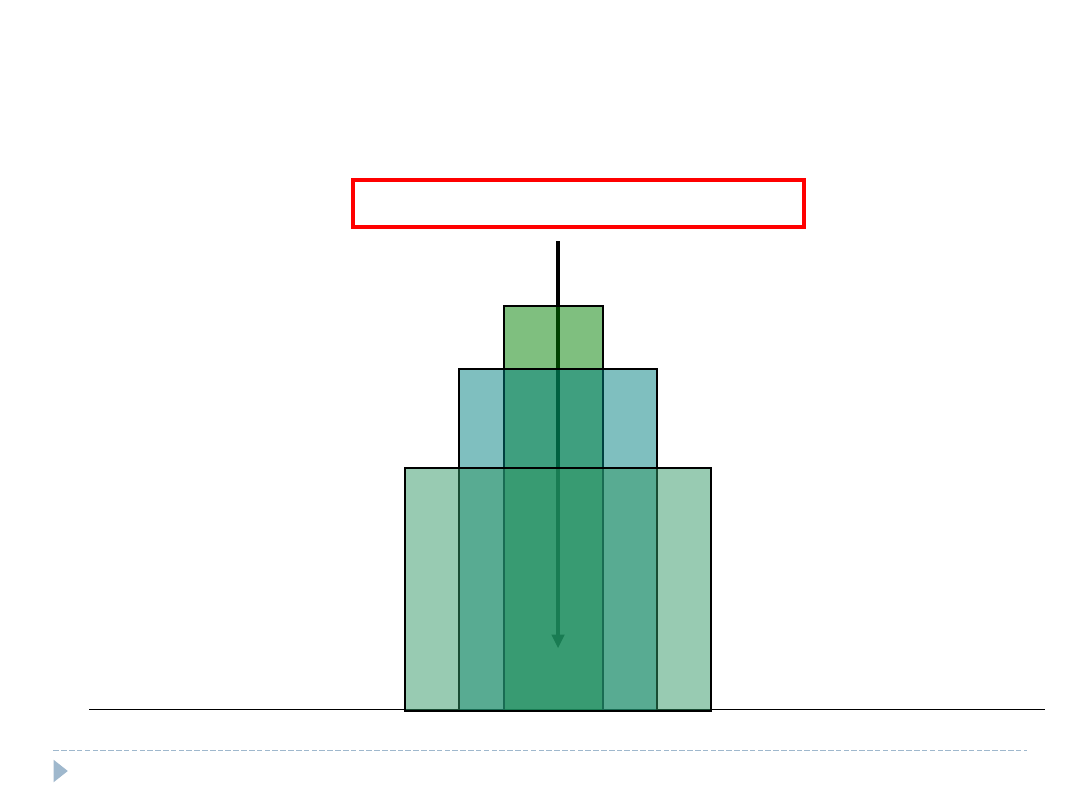
O 10 20 30 40 50 60 70 80 90 100

Odsetek popierających (%)

Rzeczywisty parametr=50%

68% pomiarów

95% pomiarów

-5% +5%

-10%

+10%

99,9% pomiarów

-15%

+15%

35

65

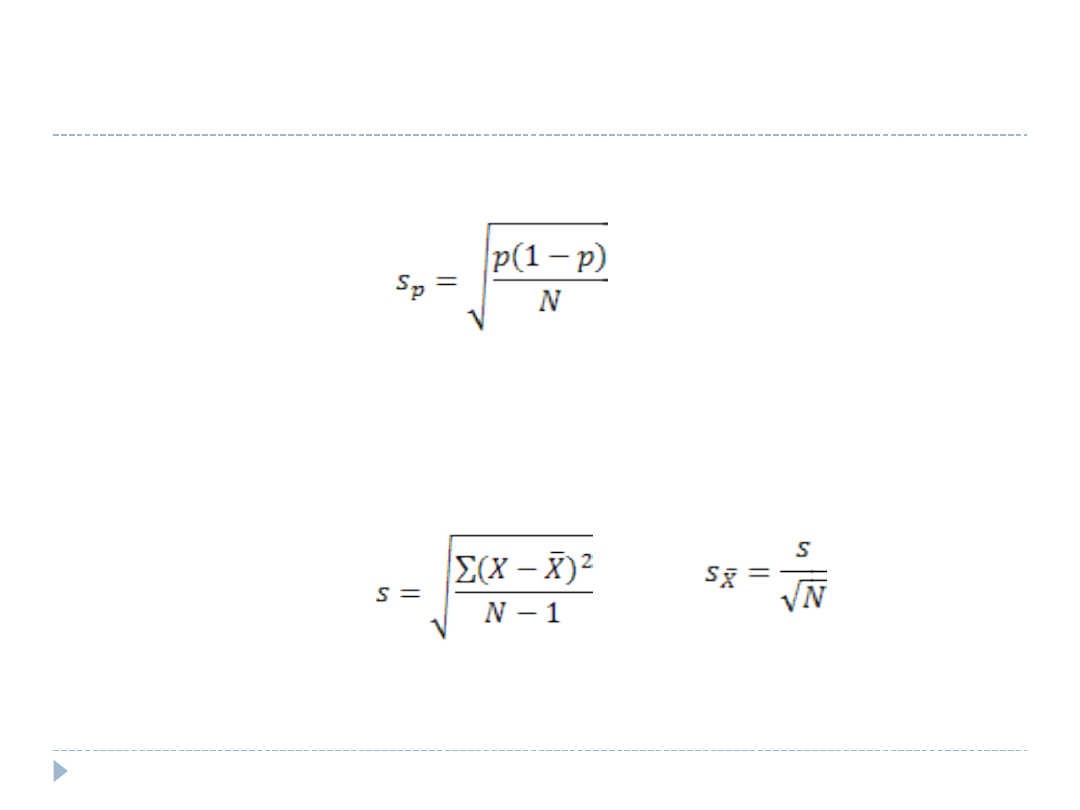
Dwa najważniejsze wzory



Szacowanie błędu standardowego proporcji



s

p

– błąd standardowy, p – proporcja, N –

liczebność próby



Szacowanie błędu standardowego średniej



s – odchylenie standardowe z próby, N –
liczebność średniej

Obliczanie przedziałów ufności

Mamy 95% prawdopodobieństwo, że parametr (w całej populacji)
znajduje się 1,96 wielkości błędu standardowego w górę i w dół od
estymatora (wyniku z próby)

Mamy 99% prawdopodobieństwo, że parametr (w całej populacji)
znajduje się 2,58 wielkości błędu standardowego w górę i w dół od
estymatora (wyniku z próby)

Typy doboru próby w doborze
probabilistycznym



Tworzenie operatu losowania



Prosty dobór losowy



Dobór systematyczny



Dobór wartstwowy

Operat losowania



Pełna, ponumerowana lista elementów w
populacji



Np. lista dzieci w grupie

1.

Jaś

2.

Marysia

3.

Stefan

4.

Asia

5.

Marta

6.

Ania

7.

Piotruś

8.

Krzyś

Prosty dobór losowy



Podstawowa metoda doboru



Nieskuteczna, jeśli populację różnicuje
zmienna niezależna



Niepraktyczna, gdy próba jest bardzo liczna



Podstawowe metody losowania:



Tablica liczb losowych



Generatory liczb losowych

Przykład tablicy liczb losowych

1.

Jaś

2.

Marysia

3.

Stefan

4.

Asia

5.

Marta

6.

Ania

7.

Piotruś

8.

Krzyś

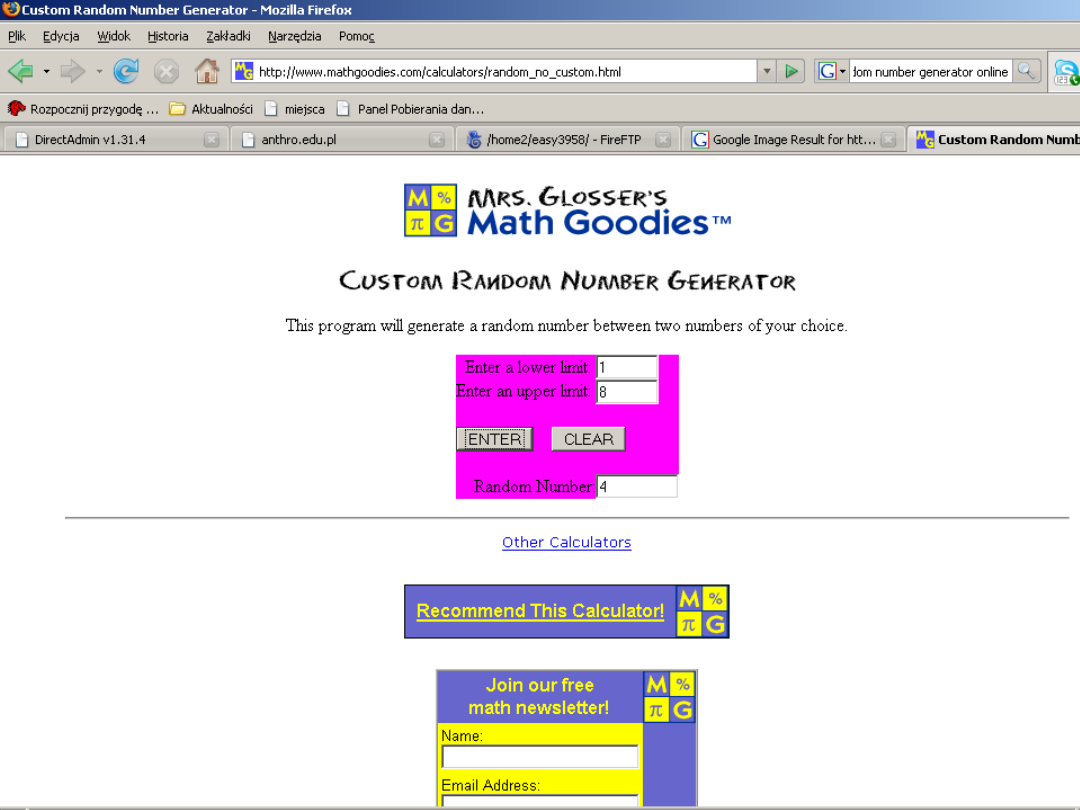
Generatory liczb losowych



Funkcja RANDBETWEEN w MS EXCEL



RANDBETWEEN(najmniejsza wartość; największa
wartość)

1.

Jaś

2.

Marysia

3.

Stefan

4.

Asia

5.

Marta

6.

Ania

7.

Piotruś

8.

Krzyś

=RANDBETWEEN(1;8)

Dobór systematyczny



Wygodna metoda przy większych próbach



Umożliwia łatwe wartstwowanie



Bierzemy n-ty element z operatu



Pierwszą liczbę losujemy



Ustalamy interwał losowania (wielkość
populacji/zakładana wielkość próby)



Do próby bierzemy pierwszy, wylosowany
element, następnie dodajemy do jego
numeru porządkowego wartość interwału
losowania, dokładamy kolejny element do
próby, dodajemy interwał itd.



Populacja: 1000 elementów



Próba: 100

Warstwowany dobór próby

Dobór warstwowy (warstwowany)

Liczba kobiet

5

Liczba mężczyzn

15

25%

75%

Przykładowy operat, założona
próba=15 klas

1gimnazjum sportowa 1A

2gimnazjum sportowa 1B

3gimnazjum sportowa 1C

4gimnazjum pułaskiego 1A

5gimnazjum pułaskiego 1B

6gimnazjum pułaskiego 1C

7gimnazjum pułaskiego 1D

8gimnazjum sportowa 2A

9gimnazjum sportowa 2B

10gimnazjum pułaskiego 2A

11gimnazjum pułaskiego 2B

12gimnazjum pułaskiego 2C

13gimnazjum pułaskiego 2D

14gimnazjum sportowa 3A

15gimnazjum sportowa 3B

16gimnazjum sportowa 3C

17gimnazjum pułaskiego 3A

18gimnazjum pułaskiego 3B

19gimnazjum pułaskiego 3C

20gimnazjum pułaskiego 3D

21 ZSZ

mickiewicza

1A

22 ZSZ

mickiewicza

1B

23 ZSZ

mickiewicza

1C

24 ZSZ

mickiewicza

2A

25 ZSZ

mickiewicza

2B

26 ZSZ

mickiewicza

2C

27 LO

kopernika

1A

28 LO

kopernika

1B

29 LO

kopernika

1C

30 LO

kopernika

1D

31 LO

kopernika

1E

32 LO

kopernika

1F

33 LO

mickiewicza

1a

34 LO

mickiewicza

1B

35 LO

kopernika

2A

36 LO

kopernika

2B

37 LO

kopernika

2C

38 LO

kopernika

2D

39 LO

kopernika

2E

40 LO

mickiewicza

2A

41 LO

mickiewicza

2B

42 LO

kopernika

3A

43 LO

kopernika

3B

44 LO

kopernika

3C

45 LO

kopernika

3D

46 LO

kopernika

3E

47 LO

kopernika

3F

48 LO

mickiewicza

3A

49 LO

mickiewicza

3B

50 LO

mickiewicza

3C

51 LP

mickiewicza

1A

52 LP

mickiewicza

1B

53 LP

mickiewicza

2A

54 LP

mickiewicza

2B

55 LP

mickiewicza

2C

56 LP

mickiewicza

2D

57 LP

mickiewicza

3A

58 LP

mickiewicza

3B

59 LP

mickiewicza

3C

60 Tch mickiewicza

1A

Przykładowy operat, założona
próba=15 klas

1gimnazjum sportowa 1A

2gimnazjum sportowa 1B

3gimnazjum sportowa 1C

4gimnazjum pułaskiego 1A

5gimnazjum pułaskiego 1B

6gimnazjum pułaskiego 1C

7gimnazjum pułaskiego 1D

8gimnazjum sportowa 2A

9gimnazjum sportowa 2B

10gimnazjum pułaskiego 2A

11gimnazjum pułaskiego 2B

12gimnazjum pułaskiego 2C

13gimnazjum pułaskiego 2D

14gimnazjum sportowa 3A

15gimnazjum sportowa 3B

16gimnazjum sportowa 3C

17gimnazjum pułaskiego 3A

18gimnazjum pułaskiego 3B

19gimnazjum pułaskiego 3C

20gimnazjum pułaskiego 3D

21 ZSZ

mickiewicza

1A

22 ZSZ

mickiewicza

1B

23 ZSZ

mickiewicza

1C

24 ZSZ

mickiewicza

2A

25 ZSZ

mickiewicza

2B

26 ZSZ

mickiewicza

2C

27 LO

kopernika

1A

28 LO

kopernika

1B

29 LO

kopernika

1C

30 LO

kopernika

1D

31 LO

kopernika

1E

32 LO

kopernika

1F

33 LO

mickiewicza

1a

34 LO

mickiewicza

1B

35 LO

kopernika

2A

36 LO

kopernika

2B

37 LO

kopernika

2C

38 LO

kopernika

2D

39 LO

kopernika

2E

40 LO

mickiewicza

2A

41 LO

mickiewicza

2B

42 LO

kopernika

3A

43 LO

kopernika

3B

44 LO

kopernika

3C

45 LO

kopernika

3D

46 LO

kopernika

3E

47 LO

kopernika

3F

48 LO

mickiewicza

3A

49 LO

mickiewicza

3B

50 LO

mickiewicza

3C

51 LP

mickiewicza

1A

52 LP

mickiewicza

1B

53 LP

mickiewicza

2A

54 LP

mickiewicza

2B

55 LP

mickiewicza

2C

56 LP

mickiewicza

2D

57 LP

mickiewicza

3A

58 LP

mickiewicza

3B

59 LP

mickiewicza

3C

60 Tch mickiewicza

1A

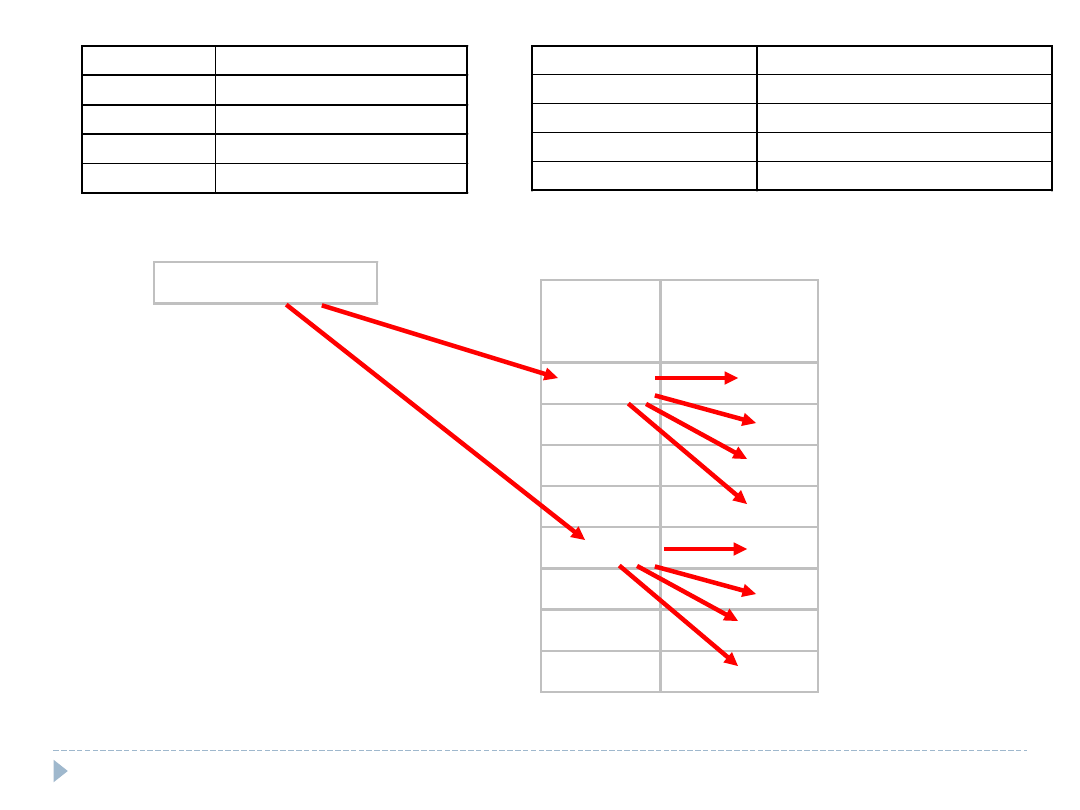
płeć

miejsce zamieszkania

kobieta

wieś

mężczyzna miasto do 10 tys

10 tys - 499 tys
powyżej 499 tys

płeć

miejsce zamieszkania

kobieta (60%)

wieś (30%)

mężczyzna (40%)

miasto do 10 tys (15%)
10 tys - 499 tys (25%)
powyżej 499 tys (30%)

1000 osób:

płeć

miejsce
zam/płeć

600

180

90

150
180

400

120

60

100
120

30% z 600=180