TYPY WIDMOWE GWIAZD

Typ widmowy

Temperatura

barwa

gwiazda

typowa

O

25 - 30 10

3

°

K

}

λ

Oriona

B

15 - 25 10

3

°

K

}

niebieskie

ε

Oriona

A

11 10

3

°

K

}

α

Duż ego Psa

P

7.5 10

3

°

K

niebiesko-białe

α

Małego Psa

R - N - C

←

G

6.0 10

3

°

K

biało-ż ółte

Słoń ca

S

←

K

5.0 10

3

°

K

czerwone

α

Arktur

M

2 - 3 10

3

°

K

czerwone

α

Oriona

WIELKOŚ CI GWIAZDOWE

Zapis

9

m

Obserwacje pokazują ż e

I

I

m

m

+

=

5

100

Zatem

log

log

I

I

m

m

−

=

+

5

2

log

log

.

I

I

m

m

−

= =

+

1

2

5

0 4

;

(

)

log

log

.

I

I

m

m

m

m

−

+

=

⋅

∆

∆

0 4

(

)

log

.

.

I

I

m

m

m

m

m1

1

0 4

0 4

=

⋅

=

−

∆

;

m m

I

I

m

m

−

= −

⋅

1

1

2 512

.

log

m = 0

96 gwiazd N. P. S

top atm

fot

lux

.

.

.

∼

⋅

∼

⋅

−

−

2 54 10

2 5 10

10

6

;

1

13 98

lux

m

∼ = −

.

Gdy I w luxach

m=-2.5 log(I) -13.98

Wielkoś ć absolutna

M m

L

L

R

R

R

− = −

⋅

⋅

= −

= −

+

2 5

4

10

4

5

10

5

5

2

2

. log

log

log

π

π

( )

M

m

R a r

= + −

−

5 5 log

m

¤

= -26

m

,8;

M

¤

+4

m

8 -dla Słoń ca

+24

m

0 kraniec widzialnoś ci

GWIAZDY ZMIENNE

1.Układy podwójne
2.Cefejdy np.

δ

Cefejda M

υ

min = 74,3; M

υ

max = 3,6

- Rozpowszechnienie.
- Okres - wielkoś ć absolutna, zależ noś ć .
- Wyznaczanie odległoś ci.

GWIAZDY NOWE

Krzywe blasku , Model wybuchu - otoczka

Moc wybuchu

P = 10

42

- 10

41

ergów

lub wielkoś ci absolutne

M = 9

Częstoś ć wybuchów - 30 rocznie w Galaktyce

GWIAZDY SUPERNOWE

Krzywa blasku: dwa typy I, II

Model wybuchu - cała objętoś ć

Moc wybuchu

10

50

- 10

51

ergów

CZĘ STOŚĆ WYBUCHÓ W

TYP

GALAKTY

KI

ELIPTYCZNY SPIRALNY

NIEREGULARNY

Masa w 10

11

M

¤

720

130

40

Liczba wybuchów na 100lat

na 10

11

M

¤

0.007

2

4

Obserwowana liczba Ityp/IItyp

6/1

17/44

7/0

REMANENTY PO WYBUCHACH.

Pulsary.

DOWODY ISTNIENIA MATERII

ROZPROSZONEJ

1.Istnienie jasnych mgławic widocznych na fotografii.
2.Występowanie ciemnych obłoków.
3.Nieobserwowanie galaktyk w pobliż u płaszczyzny Drogi Mlecznej.
4.Rosną ce z odległoś cią poczerwienienie ś wiatła gwiazd.
5.Występowanie w widmach gwiazd linii pochodzenia międzygwiezdnego.
6.Polaryzacja ś wiatła gwiazd.
7.Obserwacje promieniowania radiowego (linia 21 cm).
E = 13.6 eV;

ν

= 1.42

⋅

10

9

Hz;

λ

= 21 cm; P

o

= 1420.4058 MH

z

λ

0

= 21.1 cm

Praw. przejś cia

A = 2.85 x 10

-15

s

-1

N

N

g

g

h

kT

2

1

2

1

0

=











−









exp

υ

gdzie g

1

/g

2

wagi statyst.

g

g

1

2

3

=

k

g

g

g

N A h

N A h

H

H

=

+

=

1

1

2

0

0

3

4

υ

υ

( )

s

k

r

r d

=

∫

υ

π

υ

4

2

2

Ω

s

I

h

N d

H

Ω

= =

∫

3

16

0

0

υ

υ

[ ]

υ

π

p

e

e

e

e N

E m

N

Hz

=









 =

⋅

2

2

0

3

1

2

4

9 1 10

.

υ

υ

g

<<

• υ

υ

υ

grup

p

c

=

−





















1

1

2

• υ

g

cz

−

ęstoś ć rotacji

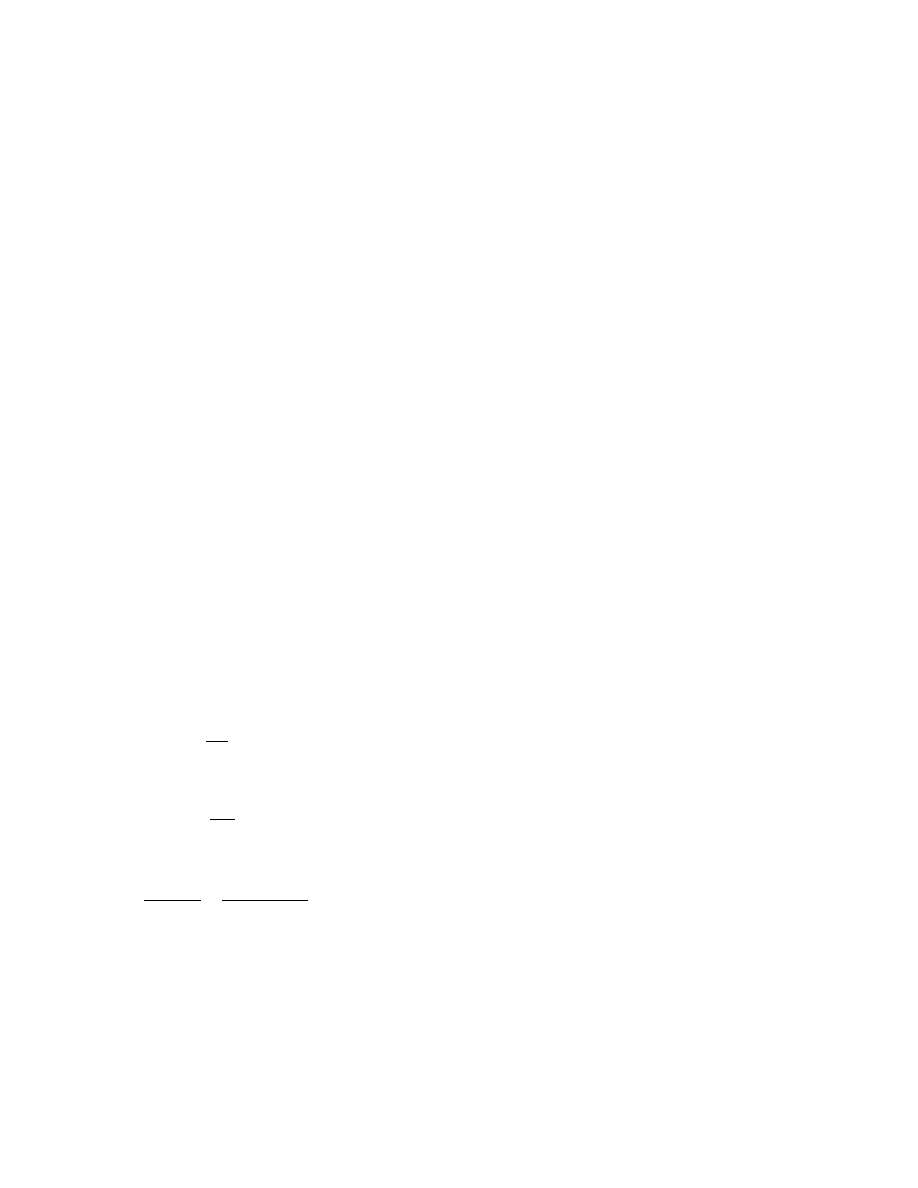
PRZESTRZENNE ROZŁ OŻ ENIE GWIAZD.

a)gromady kuliste

n

g

>

1000 (M13 w Herkulesie)

b)gromady otwarte

n

g

<

1000 (Plejady)

Ewolucja gwiazd
Droga ewolucyjna Słoń ca.
Budowa i dynamika Drogi Mlecznej.
a)składowe Galaktyki

Gwiazdy

0.075 M

¤

/pc

3

I 0.06 ~ || ~

II

0.015 ~ || ~

gaz H

e

+ H 0.025 ~ || ~

pył z

r

<10

-5

cm

0.0002 ~ || ~

prom cosm

0.5 eV/cm

3

pole magn. H ~ 3·10

-6

G 0.2 eV/cm

3

promieniowanie elektro-magnet.(fotony)

0.5 eV/cm

3

ROTACJA GALAKTYKI

Stała Orta

υ

rad

rA

l

.

sin

≅

2

υ

rad .

- prędkoś ć w układzie słonecznym

r - odległoś ć od u. s.

A - 15 km s

-1

kpc

-1

B

A

R

km s kpc

= −

= −

−

−

υ

0

0

1

1

10

υ

0

0

, R

−

prędkoś ć i odległoś ć od Słoń ca

υ

0

250

=

km

s

R

kpc

0

10

=

Wyznaczanie masy Galaktyki z rotacji

M

R

GM M

R

G

¤

¤

υ

0

2

0

0

2

=

M

M

G

≅

10

11

¤

ODLEGŁOŚ CI

1AU = 1.495979 10

13

cm

1ps = 1pc = 3.015678 10

18

cm

1kpc = 10

3

pc

BUDOWA GWIAZDY STACJONARNEJ

( )

( )

( )

ρ ρ

=
=
=

r z

p

r t

T T r t

,

,

,

dla symetrii kulistej

( )

( )

∂

∂

πρ

M r t

r

r t r

,

,

=

4

2

(1)

( )

( )

M r t

r t

r dr

r

,

,

=

⋅

∫

ρ

π

0

2

4

( ) ( )

dp

dr

g r

r

= −

ρ

(2)

bo

( )

( )

( )

F r

g r dM r

= −

⋅

( )

( )

dM r

r

r dr

=

4

2

π ρ

( )

( ) ( )

dp r

dr

g r

r

= −

⋅

ρ

gdzie

( )

( )

g r

G

M r

r

=

2

zatem

( )

( ) ( )

dp r

dr

GM r

r

r

= −

2

ρ

(2’)

Dla gazu niezdegenerowanego

( )

( ) ( )

p r

R

r

T r

= ⋅

⋅

µ

ρ

(3)

bo

( )

p v

R

M

T r

v

⋅ =

⋅

µ

PRODUKCJA ENERGII W JĄ DRZE

GWIAZDY

Grawitacyjna

Obliczanie energii potencjalnej dla chmury gazu o masie M skupionej do
rozmiarów kuli o promieniu R

( )

( )

( )

( )

dE

G M r

dM r

dr

r

G M r dM r

r

p

r

= −

⋅

= −

∞

∫

2

dM(R) - masa warstewki o promieniu (r, r+dr)

( ) ( )

E

G

M r dM r

r

G

r

r dr

p

R

R

= −

=

−

⋅

=

∫

∫

0

3

0

4

3

4

π ρ π ρ

( )

( )

M r

r

dM r

r

dr

=

=

4

3

4

3

2

π ρ

π ρ

( )

( )

M r dM r

r

r

dr

⋅

=

⋅

⋅

4

3

4

3

2

π ρ π ρ

= ⋅

⋅

= − ⋅

⋅

= − ⋅

⋅

⋅ =

−

= −

G

r

r

G

R

R

G

R

R

R

G

M

R

GM

R

R

4

3

4

1

5

4

3

4

1

5

4

3

4

3

3

5

3

5

3

5

3

2

0

3

2

3

3

2

2

π ρ π

ρ

π ρ π

ρ

π ρ

π ρ

Termiczna skala czasu dla Słoń ca (Kelvina)

τ

~

E

2

p

¤

1

4

10

4 10

5 10

15 10

48

23

14

6

L

x

erg

erg s

s

lat

=

⋅

⋅

= ⋅

= ⋅

/

WIEK UKŁADU SŁONECZNEGO

Metoda radio izotopów

U

lat

P

U

lat

P

b

b

92

238

9

206

92

235

8

207

1
2

1
2

4 5 10

7 07 10

τ

τ

=

⋅

→

=

⋅

→

.

.

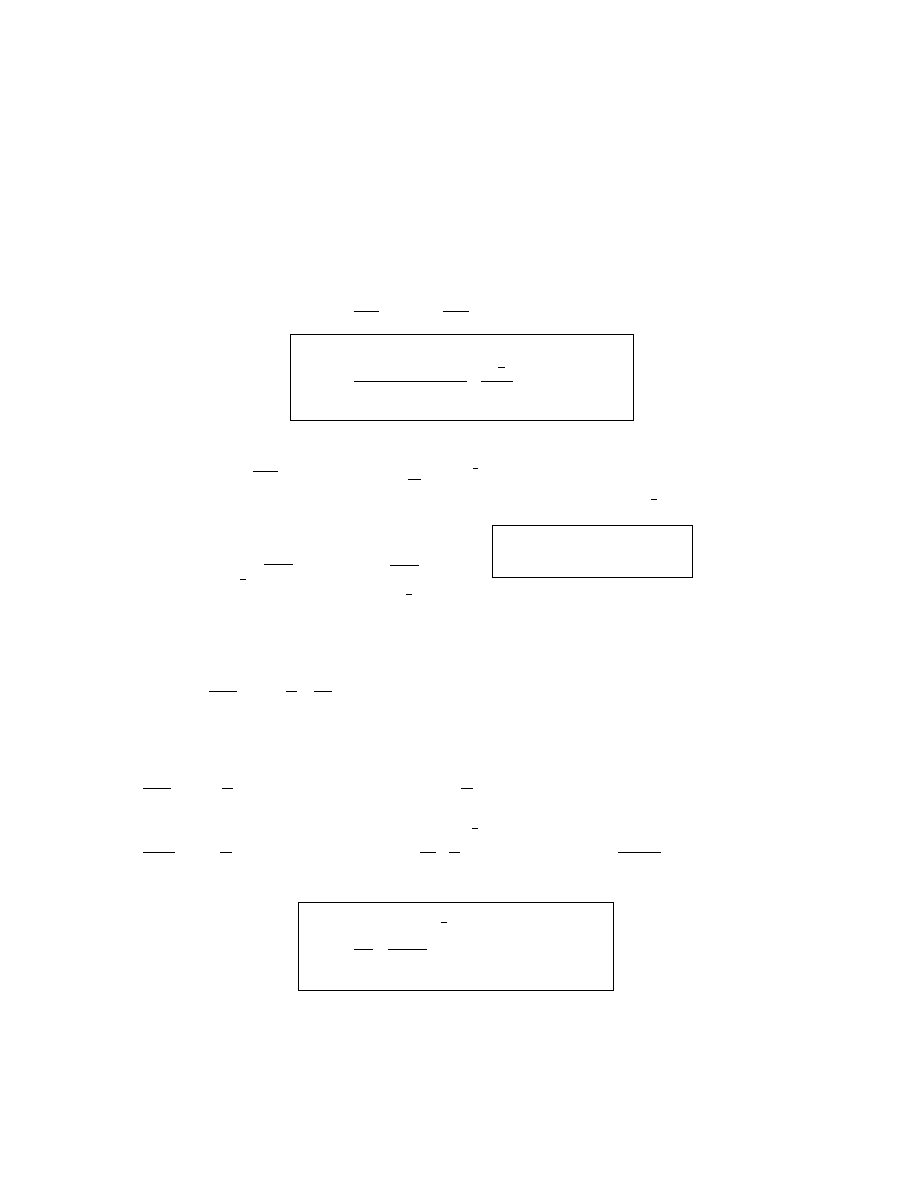
Niech

N

liczba zawartoś ci atomów uranu

M

M

M

U

P

P

P

238

b

b

b

−

=

−

206

206

206

s

¤

N

N

M

P

U

U

P

238

238

b

=

+

206

N N e

t

=

-

⋅

λ

− =

λ

t

N

N

ln

0

dN

N

t

= −λ

t

N

N

M

lat

U

U

P

b

=

+

















=

⋅

ln

ln

.

238

238

206

1

2

9

2

4 6 10

τ

dN

N

t

= − λ

;

1

2

1

2

=

−

e

λτ

;

−

= −

ln2

1

2

λτ

;

τ

λ

1

2

2

=

ln

;

λ

τ

=

ln2

1

2

;

t

lat

=

⋅

4 6 10

9

.

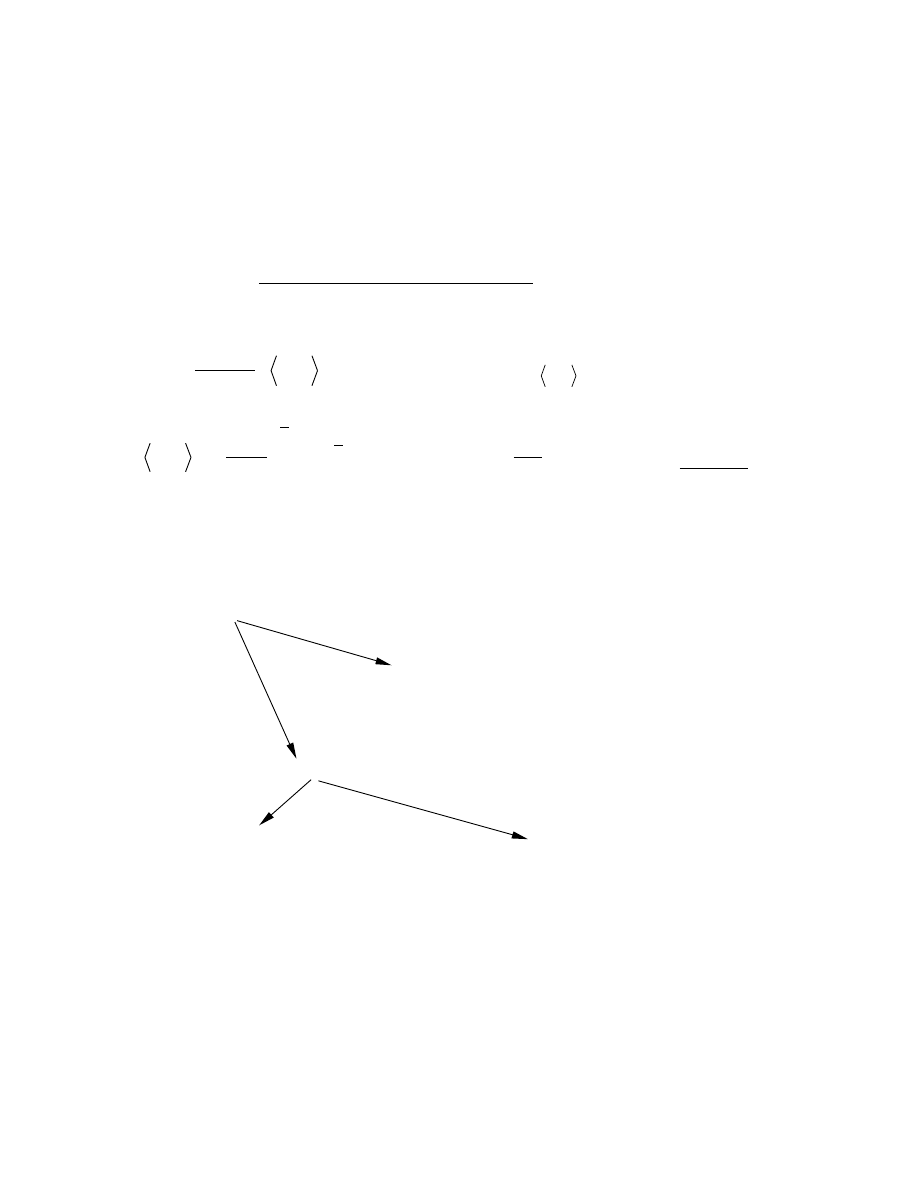
CZAS SWOBODNEGO SPADKU

m

d r

dt

G

r

r

2

2

3

2

4

3

= −

π ρ

Równanie oscylacji punktu materialnego w polu

grawitacyjnym Ziemi

d r

dt

G

r

2

2

4

3

= −

ρπ

ω

ρ π

2

4

3

=

G

4

4

3

2

2

π

ρ π

T

G

=

T

G

=











1 1

1

2

ρ

ρ

π

=

3

4

3

R

M

T

G

R

GM

s

lat

= 






= ⋅

=

1

5 10

20

3

1

2

8

Ją drowa

Częstoś ć zderzeń dwóch typów czą stek o rozkładzie pędów Maxwell’a
Reakcje ją drowe syntezy.

Defekt masy.

Założ enie:

( )

( )

n

n

1

1

2

2

ν

ν

,

( ) ( )

(

)

E

n

n

Q

=

⋅

⋅ ⋅

⋅

+

∞

∞

∫

∫

1

1

2

2

12

1

2

2

1

1

ν

ν

σ ν

δ

ν ν

ν

ν

min

min

gdy n

1

= n

2

E

n n

Q

= ⋅ ⋅

⋅

1

2

2

σ ν

gdzie

( )

σ ν

σ ν ω

ν

ν

=

⋅

∞

∫

f

d

min

3

( )

( )

σ υ

π

σ

υ

=











⋅

−









∞

∫

8

1

2

3

2

m

kT

E

E

E

kT

dE

E

min

exp

gdzie m

M m

M

m

υ

=

+

1

2

1

2

CYKL PROTONOWY

H

1

+ H

1

→

D

2

+ e

+

+

ν

e

2.38 MeV lub

H

1

+ e

-

+ H

1

→

D

2

+

ν

e

[

σ

= 10

-47

cm

2

]

D

2

+ p

→

He

3

+

γ

10.98 MeV

He

3

+ He

3

→

He

4

+ 2p

12.85 MeV

→

He

3

+ He

4

→

Be

7

+

γ

Be

7

+ e

-

→

Li

7

+

ν

e

Be

7

+p

→

B

8

+

γ

Li

7

+ p

→

He

4

+ He

4

B

8

→

Be

8

+ e

+

+

ν

e

Be

8

→

2 He

4

4p

→

1He + 26.72 MeV; 0.51 MeV w neutrino

(2.38 + 10.98 + 12.85) + 0.51 = 26.72 MeV

ε

pp

= A

ρ

X

2

T

n

A = 1.05 10

-29

T

≈

(12-15) 10

6

°

K

n = 4

X =

%

H

CYKL CNO

C

12

+ H

1

1

→

N

13

+

γ

N

13

→

C

13

+ e

+

+

ν

e

C

13

+ H

1

1

→

N

14

→

γ

N

14

+ H

1

1

→

O

15

+

γ

O

15

→

N

15

+ e

+

+

ν

e

N

15

+ H

1

1

→

C

12

+ He

4

ε

= 6.4

⋅

10

18

erg/g

He

ε

CNO

=

β

ρ

X Z

CNO

T

n

β

= 1.6 10

-142

X =

%

M

Z =

%

CNO

n = 20

÷

13

( )

L r

r dr

r

=

∫

4

2

0

π ρε

(4)

lub

( )

( )

d L r

dr

r

r

=

4

2

π ρ ε

(4

’

)

OKREŚ LENIE

µ DLA GWIAZDY

X

M

H

=

ρ

;

Y

M

He

=

ρ

;

Z

M

A

=

ρ

; X+Y+Z = 1

L

Y

m

H

H

=

3

4

ρ

bo

m

He

= 4 m

H

;

L

Z

m

A

H

=

1

2

ρ

bo

m

A

= A m

H

liczba elektronów = 1/2 A

N

X

Y

Z

m

H

=

+

+









⋅

2

3

4

1

2

ρ

µ

ρ

=

=

+

+









−

N m

X

Y

Z

H

2

3

4

1

2

1

Produkcja energii w gwieździe.

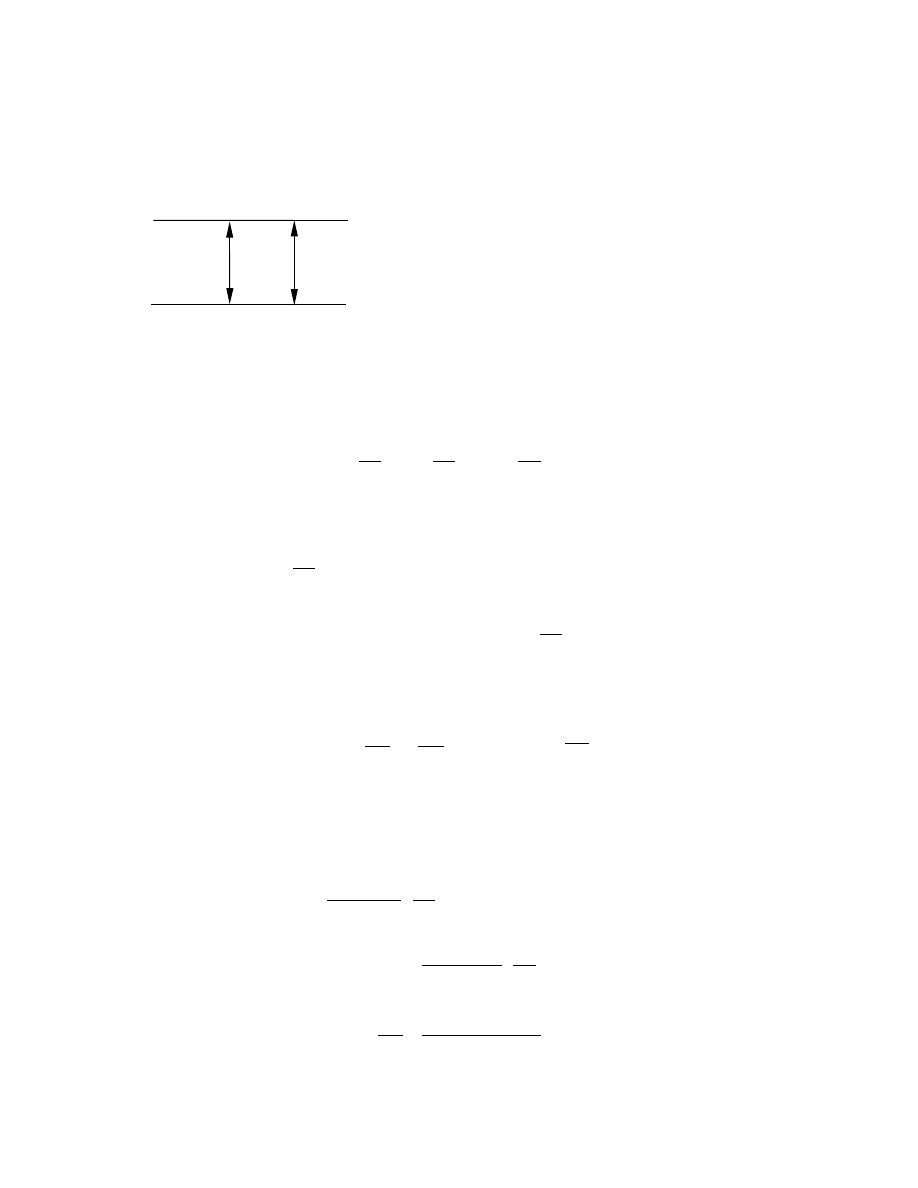
TRANSPORT ENERGII W GWIEŹ DZIE

Przez promieniowanie

T

σ

ε

⋅

=

T

4

H

dr

(

)

σ

ε

T dT

+

=

4

T+dT

H

T dT

=

4

3

σ

bo

( )

d

dT

T

dT

dr

T

dT

dr

dr

σ

σ

4

3

4

=

I I

e

k x

= ⋅

−

0

ρ

k - współczynnik absorbcji

1

k

ρ

- gruboś ć optyczna

moż na przyją ć

dr

k

=

1

ρ

a =

ε

H

ac

k

T

dT

dr

=

ρ

3

bo

σ =

ac

4

[

]

a

CGS

=

⋅

−

7 7 10

15

.

( )

L r

r

H

=

⋅

4

2

π

( )

L r

r acT

k

dT

dr

=









4

2

3

π

ρ

lub dokładniej

( )

L r

r acT

k

dT

dr

=









16

3

2

3

π

ρ

( )

( )

( )

dT

dr

L r

k

r

r ac T r

=

3

16

2

3

ρ

π

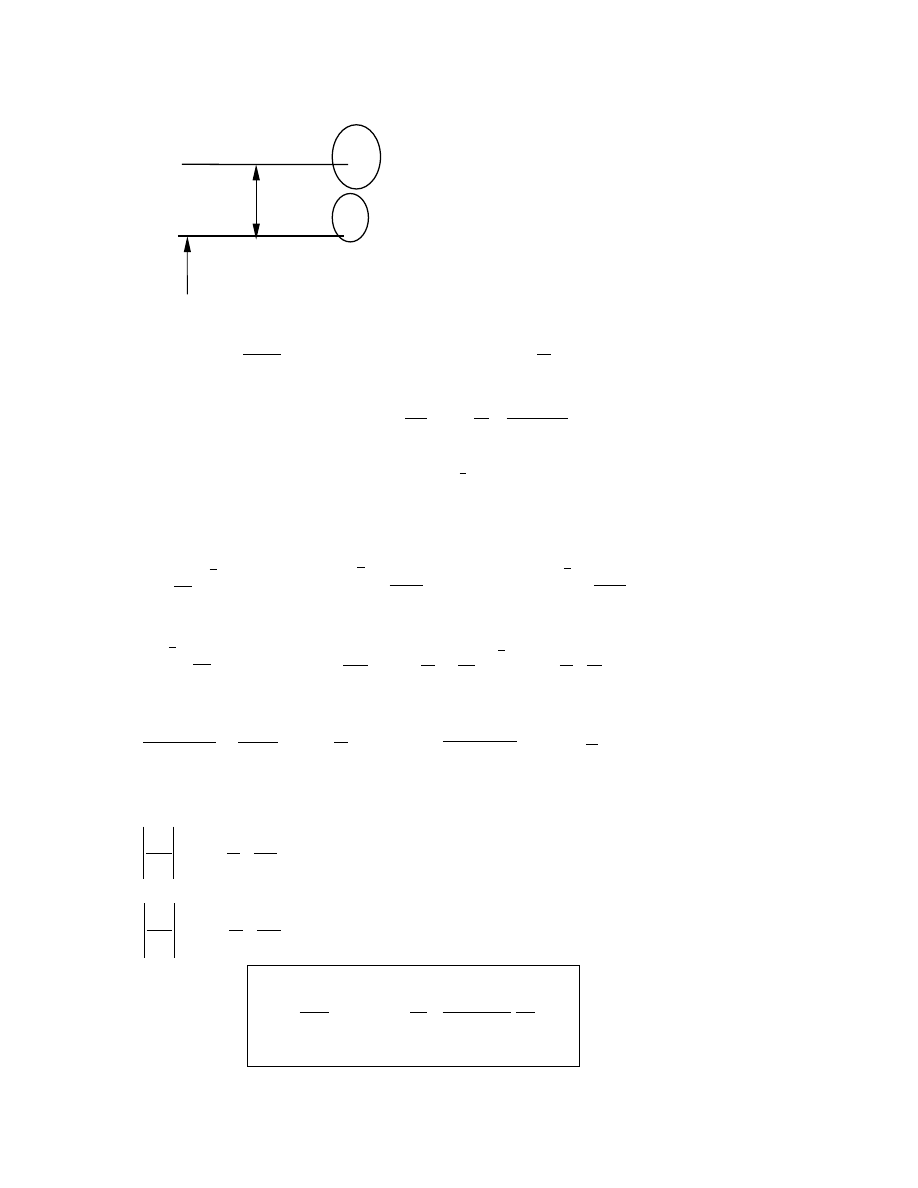
Konwekcja

ρ

•

•

•

p

T

dr

ρ p

T

(

)

ρ

ρ

•

<

+

r

dr

r

Przemiana adiabatyczna

( )

( ) ( )

dp r

dr

g r

r

= −

ρ

( )

( ) ( )

p r

R

r T r

=

µ

ρ

otrzymamy

( )

−

=

⋅











dT

dr

g r

R

d

T

d

p

µ

(log )

(log )

dla adiabaty

p

=ρ

γ

zatem

ρ

γ

=

p

1

Wstawiamy do równania gazu

p

R

p T

=

µ

γ

1

p

p

RT

1

γ

µ

=

p

RT

p

−

=

1

γ

µ

p

R

T

1

1

−

⋅ =

γ

µ

dT

dp

R

p

T

p

= −







⋅

= −







−

1

1

1

1

1

γ

µ

γ

γ

d

T

d

p

p dT

T dp

(log )

(log )

=

= −







1

1

γ

gdy

d

T

d

p

(log )

(log )

< 1

1

−

γ

nie zachodzi

> zachodzi konwekcja

dT

dr

dp

dr

= −







1

1

γ

przypadek adiabaty

dT

dr

dp

dr

< −







1

1

γ

nie rozwinie się konwekcja

( )

dT

dr

GM r

r

R

= − −











1

1

2

γ

µ

(5’)

RÓWNANIA

( )

( )

dM r

dr

r t r

=

4

2

πρ ,

(1)

( ) ( )

dp

dr

G

M r

r

r

= −

2

ρ

(2’)

( )

( ) ( )

p r

R

r T r

=

µ

ρ

(3)

( )

( )

dL r

dr

r

r

=

4

2

πρ ε

(4’)

( )

( )

( )

dT

dr

L r

k

r

r acT r

=

3

16

2

3

ρ

π

(5)

lub

wymiennie

( )

dT

dr

GM r

r

R

= − −











1

1

2

γ

µ

(5’)

Warunki brzegowe

dla r > R

( )

p R

=

0,

M(R) = M

L(R) = L

T(R) = T

dla r = 0

M = 0;

L = 0;

G

AZ ZDEGENEROWANY

ZASADA NIEOZNACZNONOŚCI

∆ ∆

p

x

h

⋅

=

=

2

π

h

∆

∆

x

p

=

h

∆

x

n

=

1

1

3

n

x

p

≥

≥







−

∆

∆

3

3

h

(

)

n mkT

mk

T

e

3

2

3

2

3

2

3

2

1

⋅

= 







⋅

h

h

dokładniej

( )

n

m

kT

e

> 







⋅







20

3

2

3

2

3

2

h

π

ρ≥

−

2 4 10

8

3

2

. x

T

T

K

= ⋅

16 10

6

ρ= ⋅

15 10

3

3

.

g

cm

ρ

dla kar ów

g

cm

g

cm

ł

2 10

4 10

10

3

12

3

⋅

⇔ ⋅

M

M

c

c

=









144

2

2

.

¤

µ

µ

c

=

2