Wartość przyszła wielkość do jakiej
wzrośnie inwestycja w przyszłości

Procent prosty

Procent składany

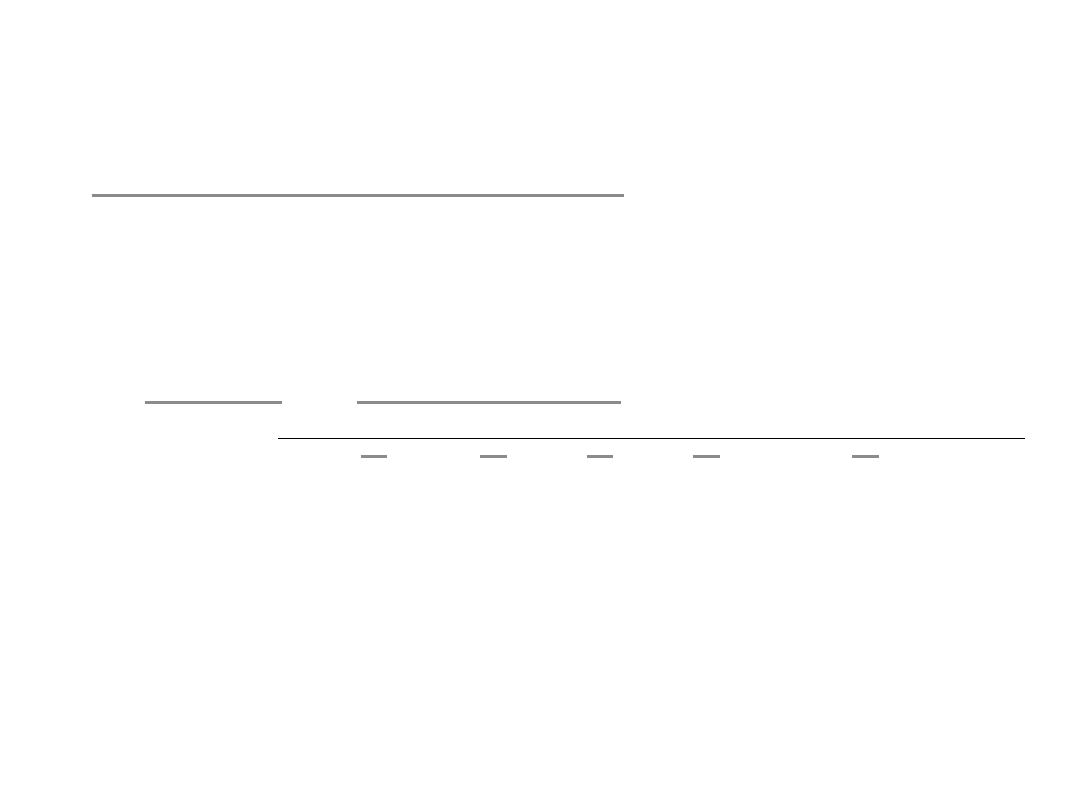
Przykład – Procent prosty
Ile zyskamy przez 5 lat na kapitale

początkowym równym 100

Dzisiaj

Przyszłe lata

1 2 3 4

5

Odsetki
Wart. kap. 100

6

10

6

6

11

2

6

11

8

6

12

4

6

13

0

Wartość na koniec 5. roku = 130

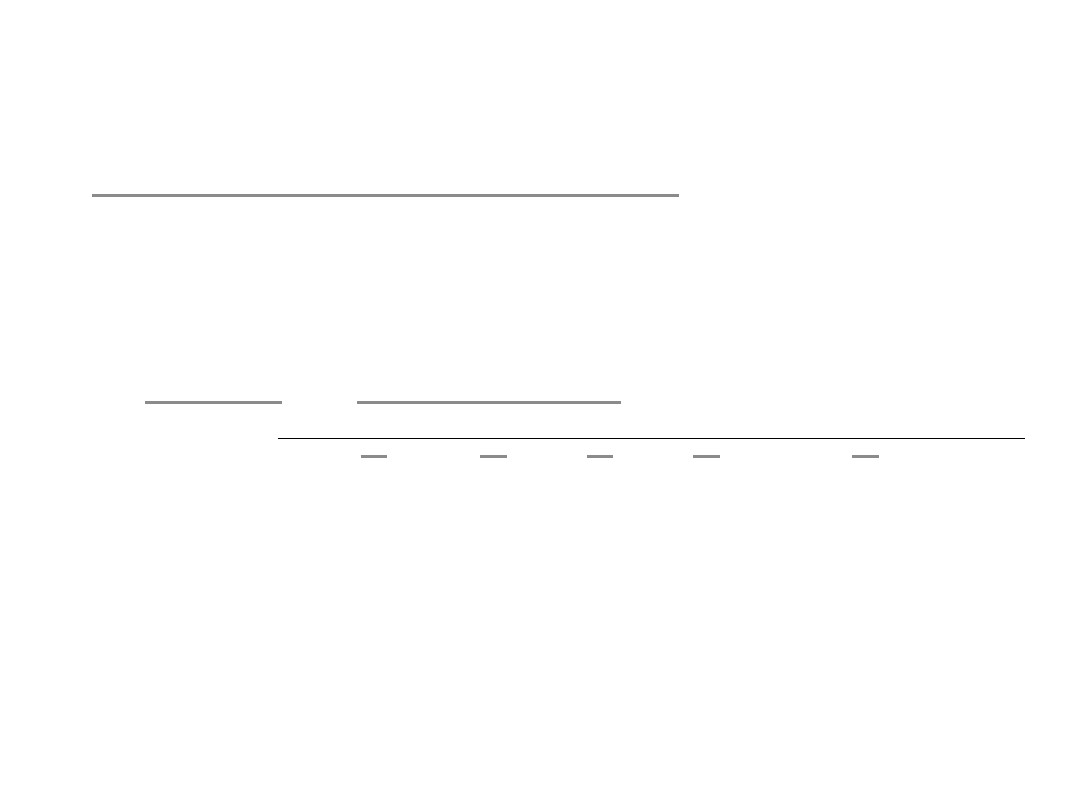
Przykład – Procent składany
Ile zyskamy przez 5 lat na kapitale

początkowym równym 100

Dzisiaj

Przyszłe lata

1 2 3 4

5

Odsetki
Wart. kap. 100

6

106

6,36
112,

36

6,74
119,

10

7,15
126,

25

7,57
133,

82

Wartość na koniec 5. roku = 133,82

Wartość przyszła 100 = FV

t

r

FV

)

1

(

100







t

r

FV

)

1

(

100 





Przykład - FV
Jaka jest przyszła wartość 100 zł jeżeli
odsetki sa kapitalizowane rocznie przy
stopie procentowej 6% przez pięć lat?

82

.

133

$

)

06

.

1

(

100

$

5









FV

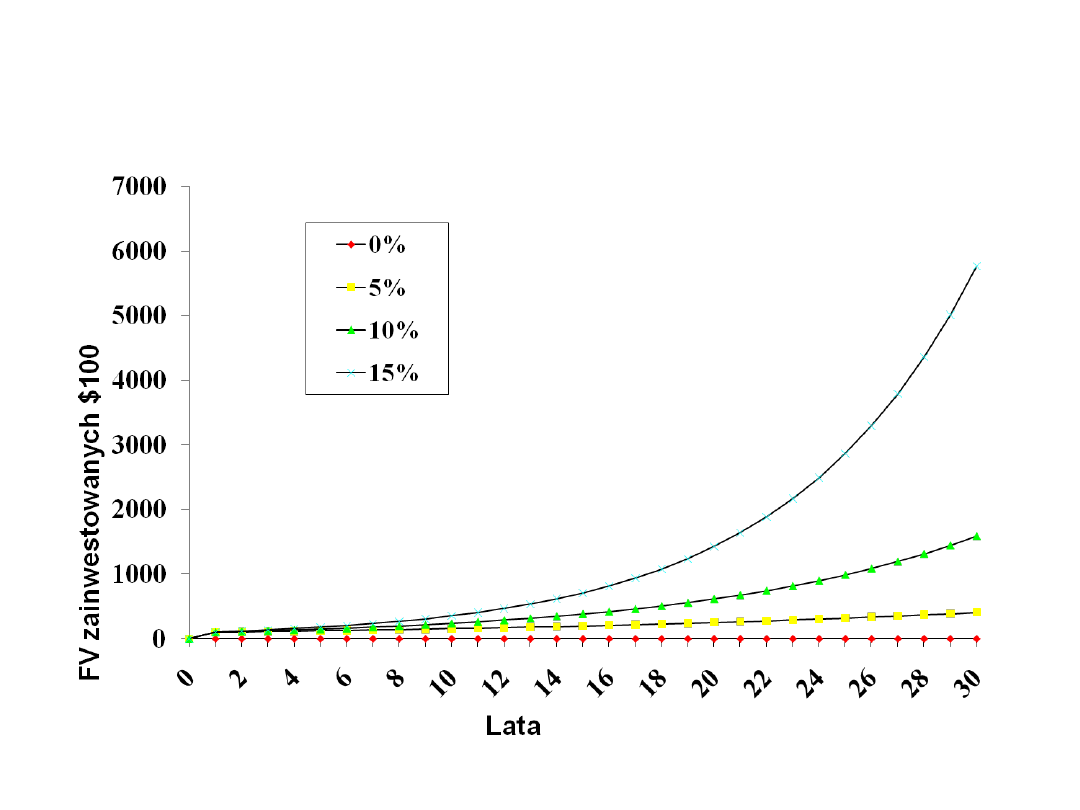
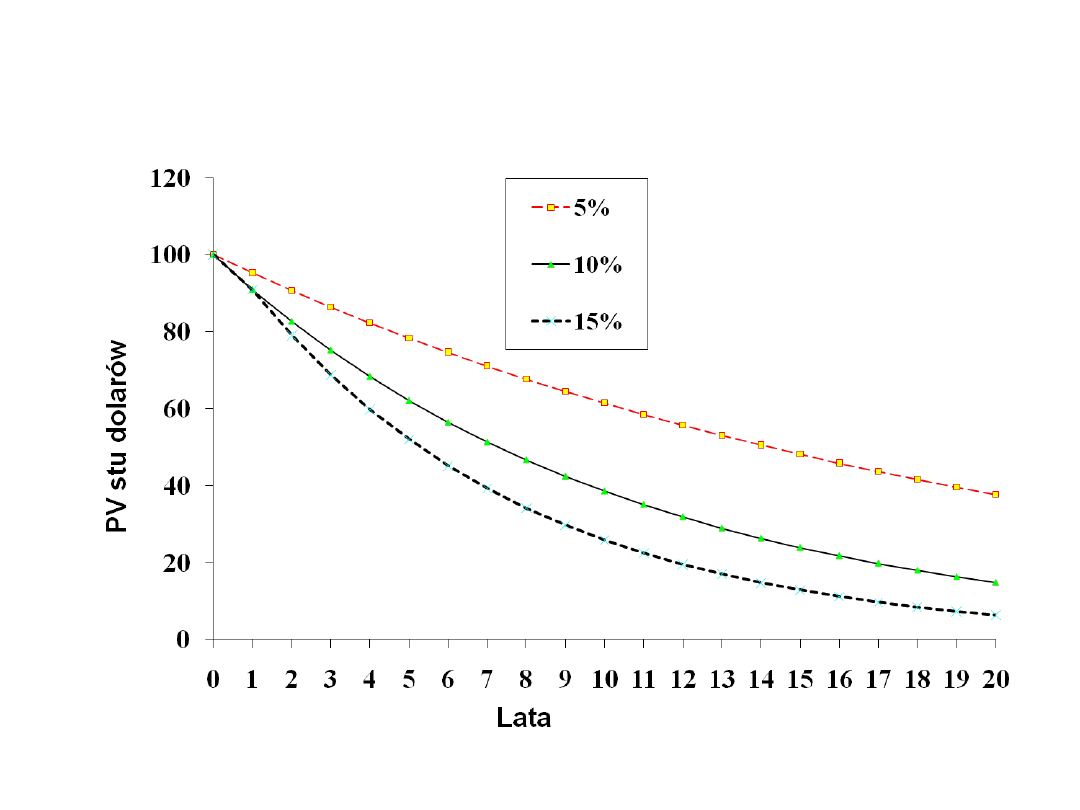
Wartość przyszła przy procencie

składanym

Stopy
procentowe

Sprzedaż Manhattan Island

Peter Minuit kupił Manhattan Island za $24
w 1626 r. Czy zrobił dobry interes?

dolarów

bilionów

57

.

120

)

08

.

1

(

24

$

380









FV

Dla r = 3.5

FV = 11 416

794

Present Value

Present

Value

Bieżąca

wartość

przyszłego

przepływu

pieniężnegoStopa dyskontowa

Stopa procentowa

wykorzystywana do

obliczania bieżących wartości

przyszłych przepływów

Wskaźnik

dyskontowy

Wartość bieżąca

przyszłej

płatności równej

1 zł

Wskaźnik dyskontowy = DF = PV

przepływu $1

Wartość bieżąca

D

F

r

t





1

1

( )

P

V

F

V

r

t







1

1

( )

Stopy
dyskontowe

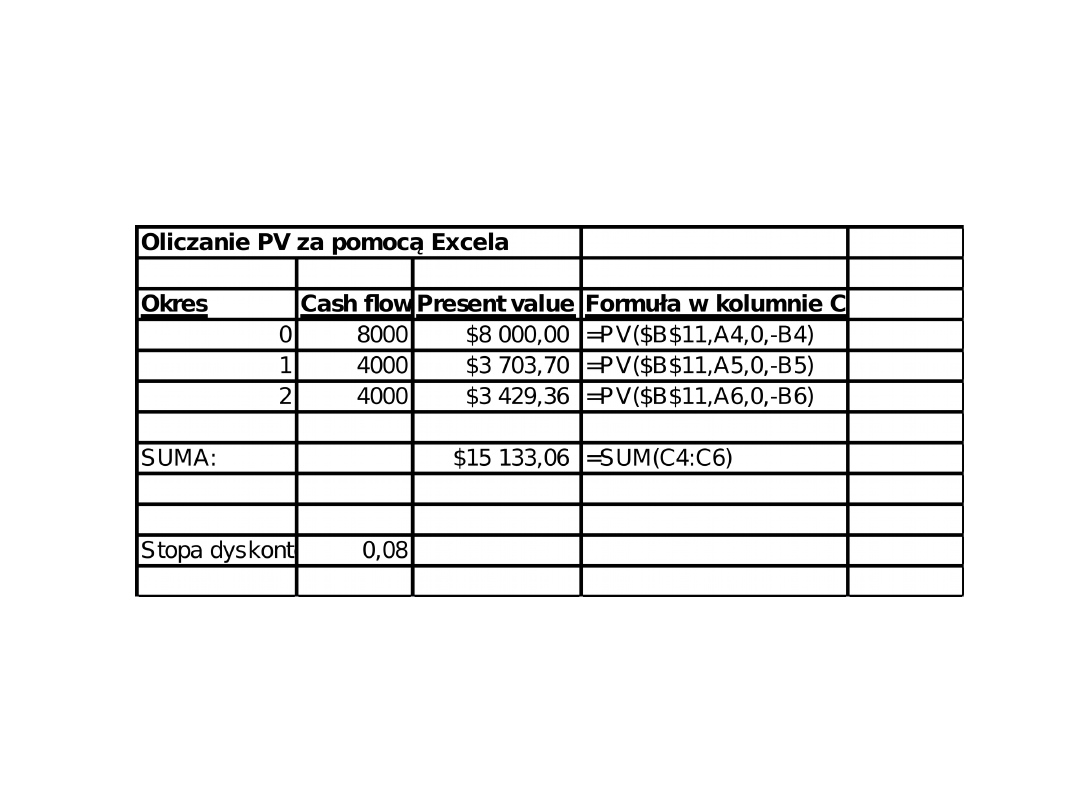
Przykład

Dealer samochodowy proponuje Ci wybór jednej
z dwóch form płatności za kupowany samochód
1) $15 500 dzisiaj
2) trzy raty: $8 000 dzisiaj i po $4 000 pod
koniec każdego roku.
Którą opcję należy wybrać?

$15,133.06

36

.

429

,

3

70

.

703

,

3

8,000.00

2

1

)

08

.

1

(

000

,

4

2

)

08

.

1

(

000

,

4

1















PV

PV

PV obliczane dla wielu przepływów

pieniężnych

PV

C

r

C

r











1

1

2

2

1

1

(

)

(

)

....

Renta dożywotnia (Perpetuity)

Annuitet (Annuity)

PV

C

r







PV C

r

r

r

t







1

1

1

(

)





PVAF

r

r

r

t

 



1

1

1

(

)

Wskaźnik dyskontowy annuitetu

wartość bieżąca 1 zł otrzymywanego co roku przez t lat

Przykład
Jaką kwotę należy zainwestować przy
stopie procentowej 10% , aby otrzymać
rentę dożywotnią na poziomie 100 000
rocznie?

PV 



100 000

10

000000

,

.

$1,

,

Przykład – cd…
Jeżeli pierwsza roczna płatność ma być
wypłacona za 3 lata, jaką kwotę należy
odłożyć dzisiaj?

PV 





1 000 000

1 10

3

315

,

,

( . )

$751,

Przykład
Kupujesz samochód, za który masz
zapłacić w trzech rocznych ratach po 4
000. Ile kosztuje Cię ten sposób płatności?





PV

PV









4 000

94741

1

10

1

10 1 10

3

,

$9,

.

.

. ( . )





FV

C PVAF

r

t

 

 

(

)

1

Przykład
Planujesz oszczędzać 4 000 rocznie przez
20 lat.
Ile uzbierasz przy stopie proc. 10%





FV

FV





 





4 000

1 10

100

1

10

1

10 1 10

20

20

,

( . )

$229,

.

. (

. )

Net Present Value

Wartość bieżąca netto (Net Present

Value) – suma bieżących wartości
wszystkich przepływów
pieniężnych

Koszt alternatywny kapitału –

oczekiwana stopa zwrotu, z jakiej
rezygnujemy inwestując w projekt

Net Present Value

N

P

VC

C

r

t

t





0

1

( )

N

P

V

C

C

r

C

r

C

r

t

t

















0

1

1

2

2

11

1

()

()

.

.

.

()

Net Present Value

Przykład
Możesz zainwestować w
budynek z powierzchnią
biurową. Za wynajem możesz
dostać rocznie 16 000 (po
opodatkowaniu). Za trzy lata
będziesz mógł sprzedać
budynek za 450 000.
Ile jesteś skłonny wydać
dzisiaj na tę inwestycję? (st.
dyskontowa: 7%)

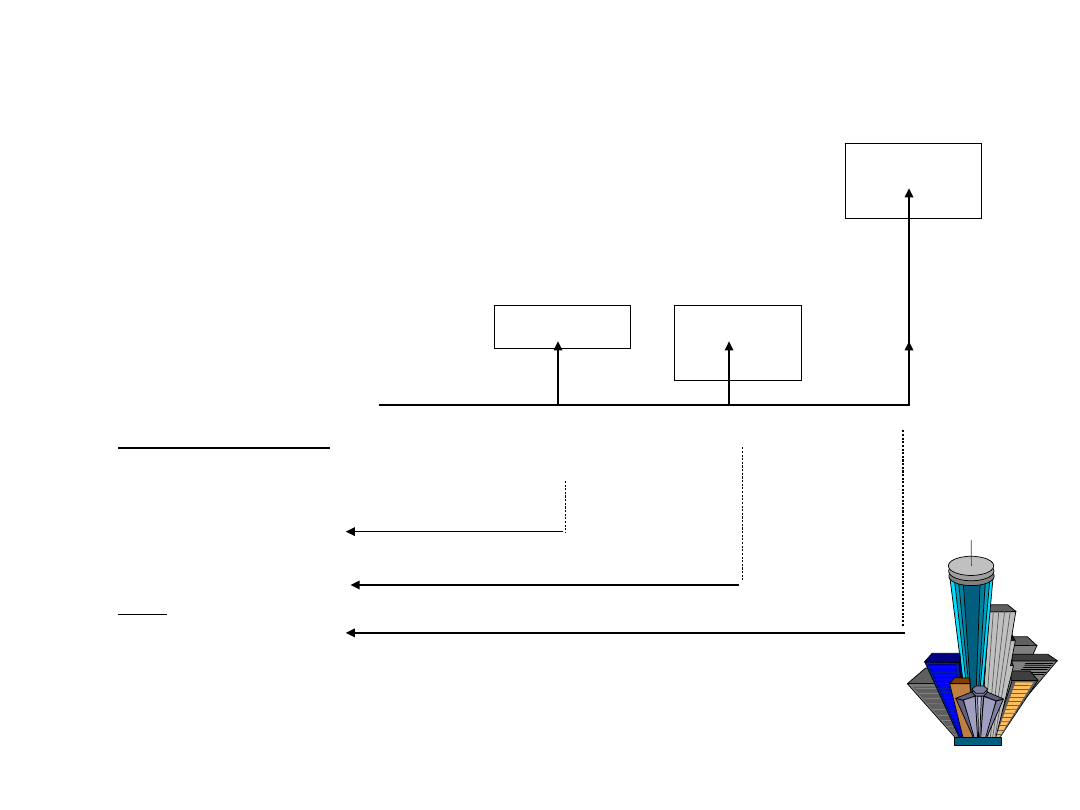
$16,00
0

$16,00
0

$16,000

$450,00
0

$466,00
0

0

1 2

3

Present Value

?

?
?
$409,323 (?)

Gdyby budunek kosztował 350 000…

NPV

NPV











350 000

16 000

107

16 000

107

466000

107

323

1

2

3

,

,

( . )

,

( . )

,

( . )

$59,

Example
The three project below are available. The
company accepts all projects with a 2 year or less
payback period. Show how this decision will
impact our decision.

Projekt C

0

C

1

C

2

C

3

Okr. Zwr.

NPV

@10%

A -2000+1000 +1000 +10000
B -2000+1000 +1000 0
C -2000 0 +2000 0

Okres zwrotu

+ 7,249
- 264
- 347

2
2
2

Wewnętrzna stopa zwrotu - Internal
Rate of Return (IRR) – stopa
dyskontowa, przy której NPV = 0.

Opłaca się zainwestować w każdy projekt
inwestycyjny oferujący stopę zwrotu
wyższą niż alternatywny koszt kapitału

Możesz zainwestować w budynek z powierzchnią
biurową, który kosztuje 350 000. Za wynajem
możesz dostać rocznie 16 000 (po
opodatkowaniu). Za trzy lata będziesz mógł
sprzedać budynek za 450 000.

Ile wynosi wewnętrzna stopa zwrotu tego
przedsięwzięcia?

0

350 000

16 000

1

16 000

1

466 000

1

1

2

3















,

,

(

)

,

(

)

,

(

)

IRR

IRR

IRR

IRR = 12.96%

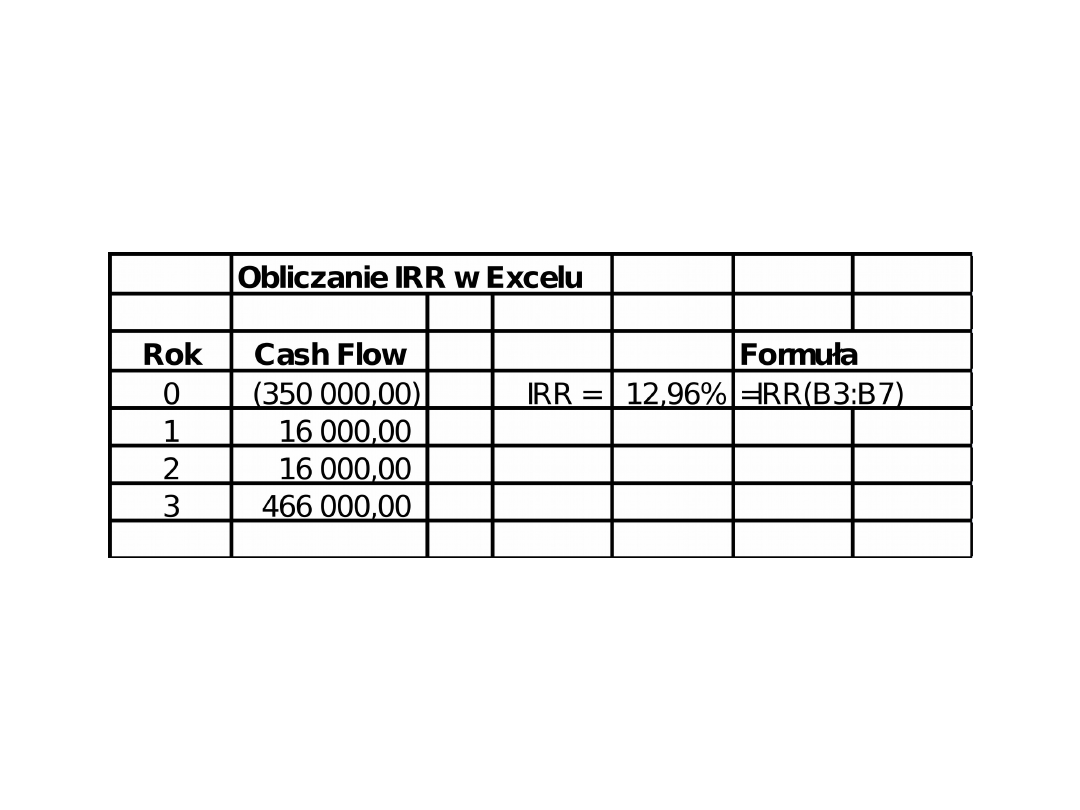
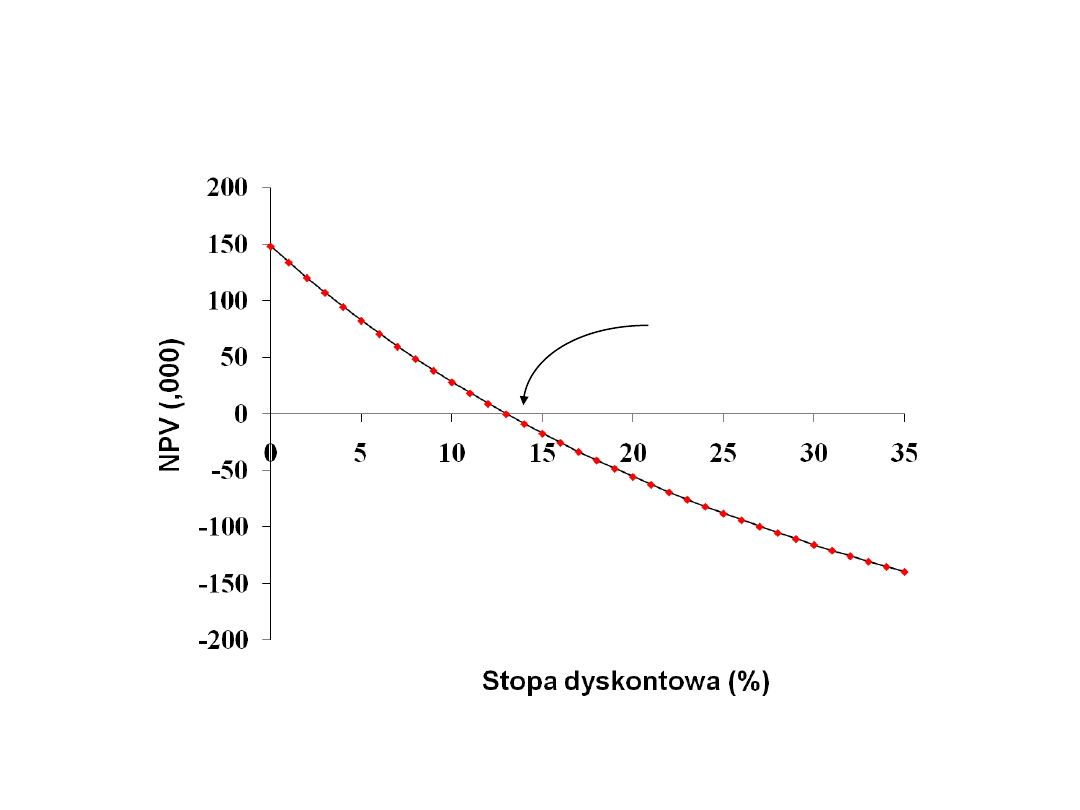
IRR=12.96%

Przykład
Możesz wybrać pomiędzy dwiema
możliwościami zadysponowania
zakupionym budynkiem. Nową propozycją
jest sprzedaż budynku po roku za 400
000.

%

29

.

14

0

)

1

(

400

350

1













IRR

NPV

%

96

.

12

0

)

1

(

466

)

1

(

16

)

1

(

16

350

3

2

1





















IRR

IRR

IRR

NPV

Ekwiwalentny przepływ roczny

Equivalent Annual Annuity

Przykład
Zakładając, ceny oraz roczne koszty
użytkowania dwóch maszyn, wybierz tą, którą
opłaca się kupić (koszt kapitału wynosi 6%)

rok

Masz.

0 1 2 3 PV

@6%

EAA

F

-15 -4 -4 -4

G

-10 -6 -6

-25.69
-21.00

- 9.61
-11.45

Ekwiwalentny przepływ roczny

Equivalent Annual Annuity

Przykład
Zakładając, ceny oraz roczne koszty
użytkowania dwóch maszyn, wybierz tą, którą
opłaca się kupić (koszt kapitału wynosi 6%)

rok

Masz.

1 2 3 4 PV

@6%

E.A.A.

F

-15 -4 -4 -4

G

-10 -6 -6

-25.69
-21.00

- 9.61
-11.45

Przykład

Wybierz jeden z projektów bazując na EEA
(r=9%).

4

.

10

7

.

8

1

.

8

20

2

.

6

9

.

5

2

.

5

9

.

4

15

Projekt

4

3

2

1

0





B

A

EAA

NPV

C

C

C

C

C

2.82
2.78

.87

1.10

Wskaźnik zyskowności (Profitability Index)