Modelowanie i

identyfikacja

procesów

Studia doktoranckie

Wykład

Prof. Jerzy Lipski

Treść wykładu



Opis procesów i postacie modeli;



Analiza właściwości dynamicznych

wyznaczonych modeli;



Podstawy wyznaczania modeli;



Przygotowanie sygnałów do przetwarzania w

procesie identyfikacji parametrów modelu;



Przykłady modelowania procesów

dynamicznych;



MatLab jako narzędzie do modelowania

procesów

Literatura



Janiszewski Krzysztof : Identyfikacja modeli

parametrycznych, Akademicka Oficyna
Wydawnicza EXIT, 2002;



Stranneby Dag : Cyfrowe przetwarzanie

sygnałów, Wyd. btc 2004;



Mrozek B., Mrozek Z. : MATLAB i Simulink

Poradnik Użytkownika, Wyd. Helion 2004;



Ljung Lennart: System Identification

TOOLBOX, Wyd. The MATH WORKS Inc.

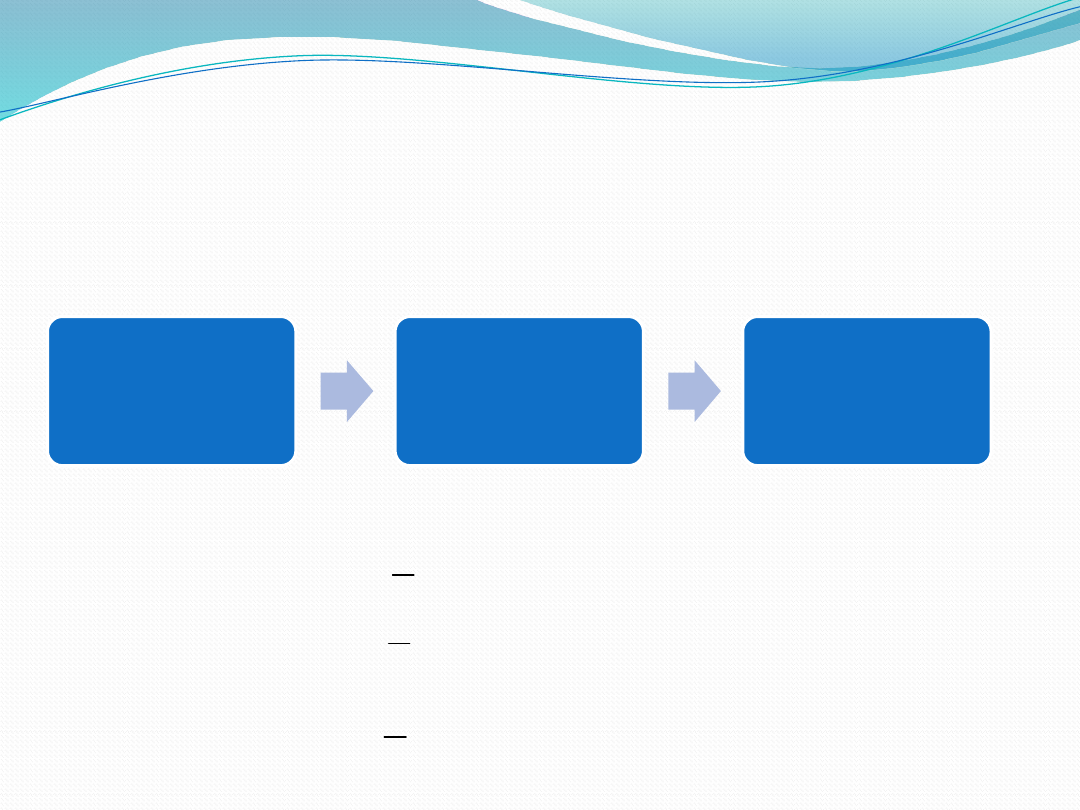
Cele identyfikacji i zasady
wyznaczania modeli

Wektor

wejść U

Wektor

stanu X

Wektor

wyjść Y









p

u

u

u

U

,...,

,

2

1









m

x

x

x

X

,...,

,

2

1









r

y

y

y

Y

,...,

,

2

1





t

U

X

f

t

x

dt

d

,

,

)

(

1

1







t

U

X

f

t

x

dt

d

,

,

)

(

2

2







t

U

X

f

t

x

m

m

dt

d

,

,

)

( 

...





t

U

X

g

t

y

,

,

)

(

1

1







t

U

X

g

t

y

,

,

)

(

2

2







t

U

X

g

t

y

r

r

,

,

)

( 

...

•Sterowania

•Sygnały mierzalne

•Zakłócenia
procesowe

Równania stanu

Równania wyjść

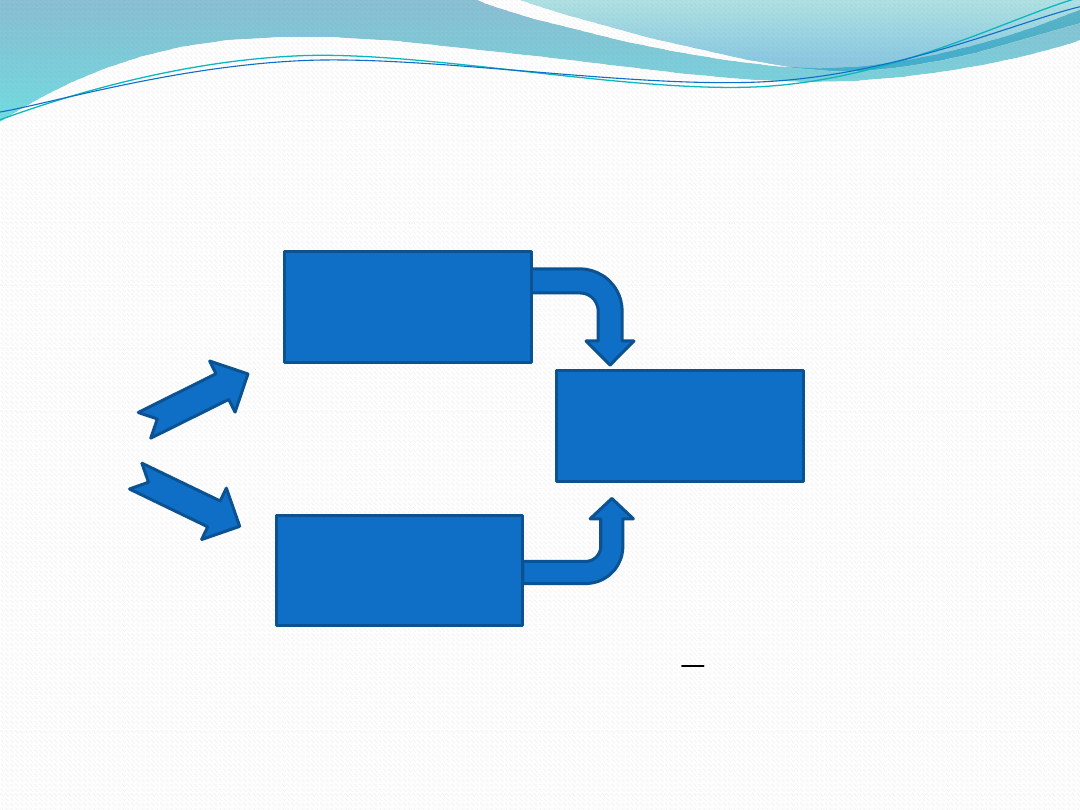
Modelowanie
symulacyjne

U





t

U

X

f

t

x

i

i

dt

d

,

,

ˆ

ˆ

)

(

ˆ







t

U

X

g

t

y

j

j

,

,

ˆ

ˆ

)

(

ˆ



MODEL

Porównanie

PROCES

Identyfikacja
parametryczna



Przyjęcie adekwatności opisu

deterministycznego dla naśladowania
procesu:





t

P

U

Y

O

Y

,

,

,



Gdzie: P – parametry (współczynniki) dopasowujące model

w sensie przyjętego kryterium

Zastosowanie modeli
parametrycznych



Regulacja stałowartościowa;



Regulacja programowa;



Zastosowanie algorytmów predykcyjnych w

zadaniach regulacji;



Umożliwienie celowej ingerencji w proces;



Ocena stanu procesu w celach

diagnostycznych;



Prognozowanie stanów przyszłych;



Odtworzenie tych stanów procesu, które są

niedostępne pomiarowo.

Sygnały i ich właściwości



Nośnikiem informacji jest sygnał;



Każdy sygnał ciągły można przedstawić w

postaci szeregu Fouriera w formie sumy
przebiegów sinusoidalnych o postaci:



Przedstawienie w postaci szeregu pozwala na

obliczenie energii niesionej przez sygnał jako
całkę z kwadratu jego wartości:





,...,

1

,

0

,

,

sin

)

(

2

0















k

t

A

t

T

k

k

k

k

k

k





























0

2

0

2

1

2

0

2

)

(

)

(

k

k

T

A

A

T

d

E







Próbkowanie sygnałów



Sygnały ciągłe są przez systemy pomiarowe

próbkowane ze stałym okresem



Sygnał po przetworzeniu jest funkcją

wielokrotności okresu



Twierdzenie Shannona

Wartości sygnału pomierzone z okresem

stanowią jednoznaczną reprezentację dla
sygnału ciągłego, który można przedstawić
jako sumę przebiegów sinusoidalnych o
częstotliwościach



)

( k





)

( k











s

f

f

,

0





2

1

s

f

dla