1. Opis techniczny.

Przedmiot opracowania

Przedmiotem opracowania jest żelbetowy, monolityczny strop płytowo-żebrowy o

konstrukcji szkieletowej. Przeznaczenie budynku - biurowiec.

Charakterystyka konstrukcji

Budynek o konstrukcji szkieletowej ma stropy żelbetowe w formie płyty żelbetowej

jednokierunkowo zbrojonej opartej na układzie żeber i podciągów. Projektowany jest jako
czterokondygnacyjny biurowiec, zlokalizowany w Katowicach, w związku z czym, ze względu
na kategorię użytkowania, owa siedziba zaliczona zostaje do kategorii B. Budynek ten w rzucie
ma kształt prostokąta o wymiarach zewnętrznych 23m x 72m i składa się z trzech segmentów
oddzielonych dylatacjami. Wysokość kondygnacji budynku wynosi 3,2m. Konstrukcja zostanie
wykonana z betonu klasy C20/25. Zarówno płyty, jak i żebra oraz podciągi są zbrojone stalą
klasy A-III N.

Warunki eksploatacji

Budynek przeznaczony jest na sąd, w którym dopuszczalna wartość obciążenia na

strop wynosi 3 kN/m2. Klasa ekspozycji została określona jako XC1.

2. Przyjęte rozstawy poszczególnych elementów konstrukcji.

Płyta: 300cm

Żebra: 575cm

Podciągi : 600cm

3.Określenie wysokości h i wysokości użytkowej d płyty.

Klasa konstrukcji S4

leff

d

40



Klasa środowiska XC1

d

7.5cm



h

d

cnom



ϕ

2



=

ϕ

8mm



cnom cmin Δcdev



=

cmin max cmin.b cmin.dur



10mm







=

cnom 10mm 10mm



20 mm







cmin max 8mm 10mm



10mm



(

)

10 mm





h

d

cnom



ϕ

2



99 mm







h

100mm



d

76mm



1

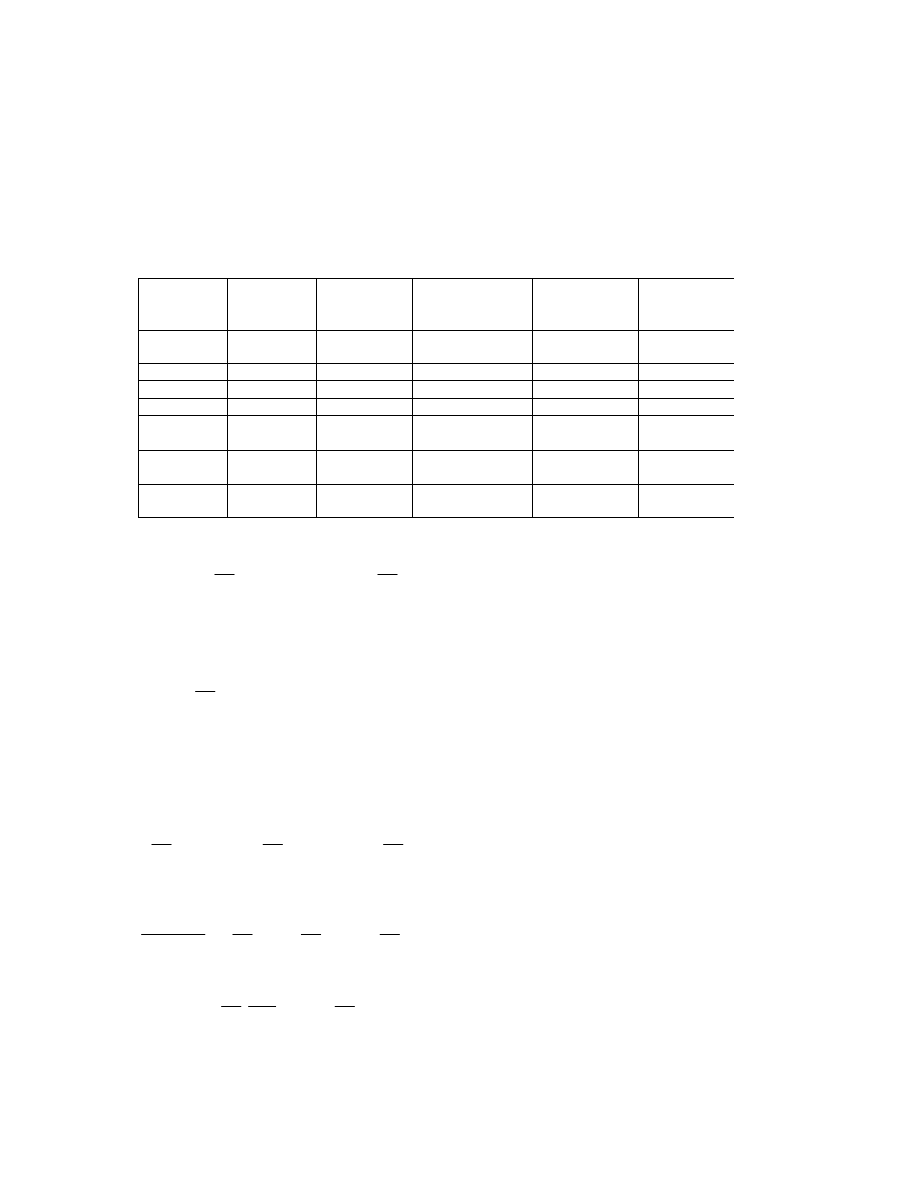
4. Zestawienie obciążeń.

Zestawienie obciążeń stałych 

Projektowany obiekt: biurowiec (kategoria użytkowania B) 

Materiał 

Wysokość 

warstwy h 

[m] 

Ciężar 

objętościowy 

γ [kN/m

3

] 

Obciążenie 

charakterystyczne 

[kN/m

2

] 

Współczynnik 

bezpieczeństwa 

Obciążenie 

obliczeniowe 

[kN/m

2

] 

Płyta 

żelbetowa 

0,1 

25

2,5

1,35

3,375 

Folia PE 

‐ 

‐ 

0,02

1,35

0,027 

Styropian 

0,04 

0,45

0,018

1,35

0,024 

Folia PW 

‐ 

‐ 

0,02

1,35

0,027 

Gładź 

cementowa 

0,05 

20

1

1,35

1,35 

Płytki 

ceramiczne 

0,02 

21

0,42

1,35

0,567 

Obciążenia 

stałe 

0,21 

‐ 

3,978

‐

5,37 

 

gk

3.978

kN

m

2



gd

5.37

kN

m

2



Obciążenia użytkowe

Kategoria obciążonych powierzchni B

qk1 3

kN

m

2



Obciążenie zmienne od przestawnych ścian działowych:

Ściany działowe wykonane z betonu komórkowego (5kN/m

3

) i dwóch warstw zaprawy gipsowej

(15kN/m

3

)

5

kN

m

3

0.12



m

2 15



kN

m

3

0.015



m



1.05

kN

m

2





Według tablicy 3. PN-82 B-02003 obciążenie zastępcze na strop:

1.05

0.5



1.5

0.5



0.5



kN

m

2

0.25

kN

m

2



0.525

kN

m

2





qk2 0.525

kN

m

2

3.2

2.65



0.634

kN

m

2







2

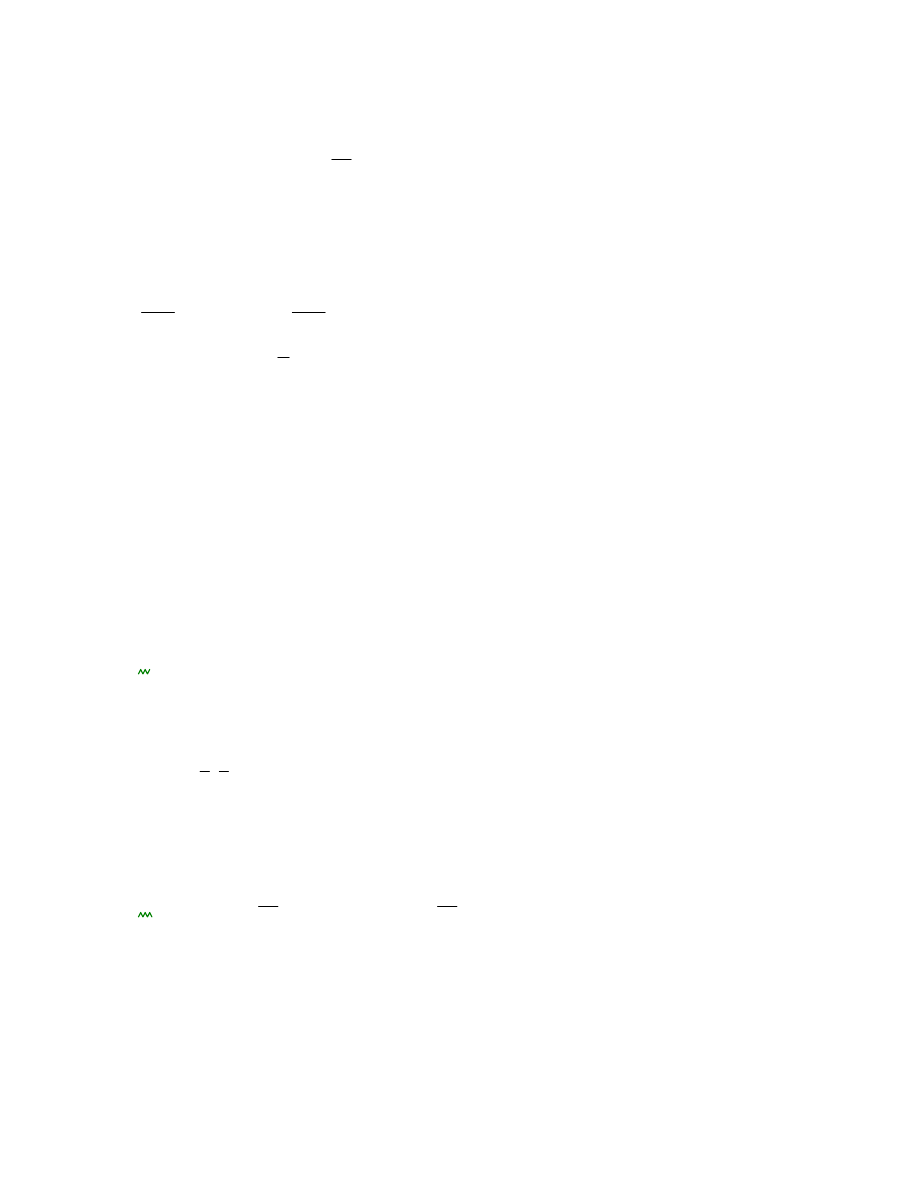
qd

1.5 qk1 qk2









5.451

kN

m

2







5.Wyznaczenie rozpiętości efektywnej płyty.

h

0.1 m



leff.ż

5.75m



leff.ż

d

15



dmin

leff.ż

15

0.383 m





h1

dmin cnom



ϕ

2



40.733 cm







bmin 0.3 h1



12.22 cm







bmax 0.5 h1



20.367 cm







Przyjęto wysokość żebra:

hl 45cm



Przyjęto szerokość żebra:

b

20cm



Rozpiętość pomiędzy osiami żeber

l

3m



Rozpiętość w świetle podpór:

ln

l

b



2.8 m







a

min

h
2

b
2











5 cm







Rozpiętość efektywna pomiędzy żebrami:

leff

ln 2 a





2.9 m





g

gd 1

 m 5.37

kN

m







q

qd 1

 m 5.451

kN

m







leff 2.9m



3

6.Wartości momentów na podstawie tablic Winklera dla belki
pięcioprzęsłowej.

dla M

1

:

dla M

B

:

dla M

2

:

dla M

C

:

dla M

3

:

kg1 0.0781



kgB

0.105





kg2 0.0331



kgC

0.079





kg3 0.0462



kpmin1

0.0263





kpminB

0.119





kpmin2

0.0461





kpminC

0.111





kpmin3

0.0395





kpmax1 0.100



kpmaxB

0.013



kpmax2 0.0787



kpmaxC

0.018



kpmax3 0.0855



MAmin 0



M1min

g kg1



q kpmin1









leff

2



2.321 kN m









MBmin

g kgB



q kpminB









leff

2



10.197



kN m









M2min

g kg2



q kpmin2









leff

2



0.618



kN m









MCmin

g kgC



q kpminC









leff

2



8.656



kN m









M3min

g kg3



q kpmin3









leff

2



0.276 kN m









MAmax 0



M1max

g kg1



q kpmax1









leff

2



8.111 kN m









MBmax

g kgB



q kpmaxB









leff

2



4.146



kN m









M2max

g kg2



q kpmax2









leff

2



5.103 kN m









MCmax

g kgC



q kpmaxC









leff

2



2.743



kN m









M3max

g kg3



q kpmax3









leff

2



6.006 kN m









4

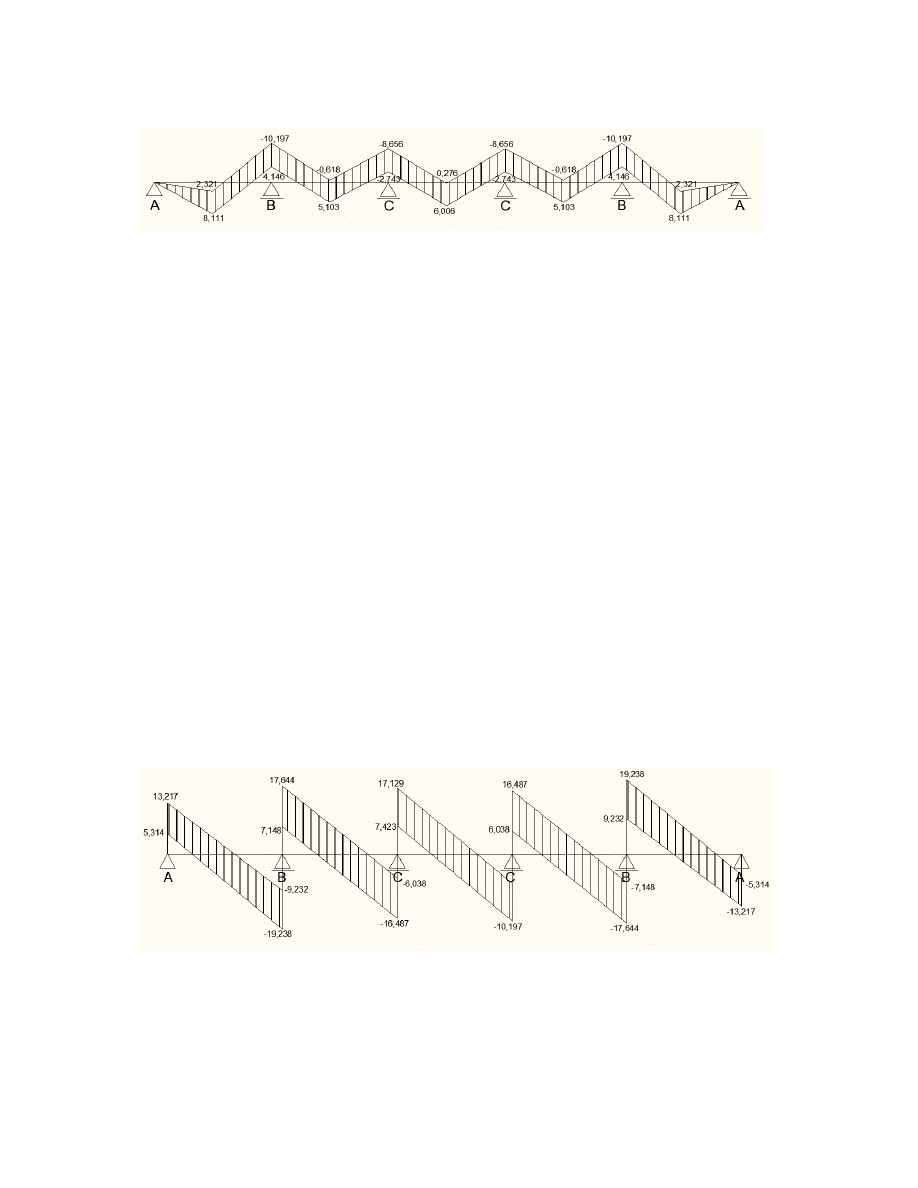
7.Wartości sił poprzecznych na podstawie tablic Winklera dla belki
pięcioprzęsłowej.

dla V

A

:

dla V

Bl

:

dla V

Bp

:

dla V

Cl

:

dla V

Cp

:

kgA 0.395



kgBl

0.606





kgBp 0.526



kgCl

0.474





kgCp 0.500



kpminA

0.053





kpminBl

0.620





kpminBp

0.066





kpminCl

0.576





kpminCp

0.023





kpmaxA 0.447



kpmaxBl 0.013



kpmaxBp 0.598



kpmaxCl 0.085



kpmaxCp 0.591



VAmin

g kgA



q kpminA









leff



5.314 kN







VAmax

g kgA



q kpmaxA









leff



13.217 kN







VBlmin

g kgBl



q kpminBl









leff



19.238



kN







VBlmax

g kgBl



q kpmaxBl









leff



9.232



kN







VBpmin

g kgBp



q kpminBp









leff



7.148 kN







VBpmax

g kgBp



q kpmaxBp









leff



17.644 k







VClmin

g kgCl



q kpminCl









leff



16.487



kN







VClmax

g kgCl



q kpmaxCl









leff



6.038



kN







VCpmin

g kgCp



q kpminCp









leff



7.423 kN







VCpmax

g kgCp



q kpmaxCp









leff



17.129 k







5

8.Obliczenie pola zbrojenia.

Dane:

fyk 500MPa



fyd

fyk

1.15

434.783 MPa







klasa stali A-III N , gatunek stali RB500W

beton C20/25

fck 20MPa



fcd

fck
1.4

14.286 MPa







fctm 2.2MPa



η

1



ξef.lim

0.493



b

1m



bt

b

1 m





d

7.6 cm





Rozstaw głównych prętów zbrojeniowych

Smax min 2 h

 250mm



(

)



Smax 0.2m



Rozstaw zbrojenia rozdzielczego

Sroz.max min 3 h

 400mm



(

)



Sroz.max 0.3m



Podpora A

MEdA M1max 30

 %

2.433 kN m









μA

MEdA

b d

2



η

 fcd



0.029





ξefA

1

1

2 μA







0.03





Zbrojenie ściskane nie jest konieczne w podporze A

zcA

1

0.5 ξefA









d



7.486 cm







Asmin 0.26

fctm

fyd



b

 d



1 cm

2







> 0.0013 bt

 d



0.988 cm

2





AsA

MEdA

zcA fyd



0.748 cm

2







Asmax 0.04 b

 d



30.4 cm

2







Pole zbrojenia na metr bieżący przy maksymalnym rozstawie 20 cm

A'sA

1m

Smax

π ϕ

2



4



2.513 cm

2







Spełnia warunki maksymalnego i minimalnego zbrojenia

6

Przęsło 1

MEd1 M1max 8.111 kN m









μ1

MEd1

b d

2



η

 fcd



0.098





ξef1

1

1

2 μ1







0.104





Zbrojenie ściskane nie jest konieczne w przęśle 1

zc1

1

0.5 ξef1









d



7.206 cm







Asmin 0.26

fctm

fyd



b

 d



1 cm

2







> 0.0013 bt

 d



0.988 cm

2





As1

MEd1

zc1 fyd



2.589 cm

2







Asmax 0.04 b

 d



30.4 cm

2







Pole zbrojenia na metr bieżący przy rozstawie 16 cm

A's1

1m

16cm

π ϕ

2



4



3.142 cm

2







Spełnia warunki maksymalnego i minimalnego zbrojenia

Podpora B

MEdB

MBmin

10.197 kN m









μB

MEdB

b d

2



η

 fcd



0.124





ξefB

1

1

2 μB







0.132





Zbrojenie ściskane nie jest konieczne w podporze B

zcB

1

0.5 ξefB









d



7.097 cm







Asmin 0.26

fctm

fyd



b

 d



1 cm

2







> 0.0013 bt

 d



0.988 cm

2





AsB

MEdB

zcB fyd



3.305 cm

2







Asmax 0.04 b

 d



30.4 cm

2







Pole zbrojenia na metr bieżący przy rozstawie 14 cm

A'sB

1m

14cm

π ϕ

2



4



3.59 cm

2







Spełnia warunki maksymalnego i minimalnego zbrojenia

7

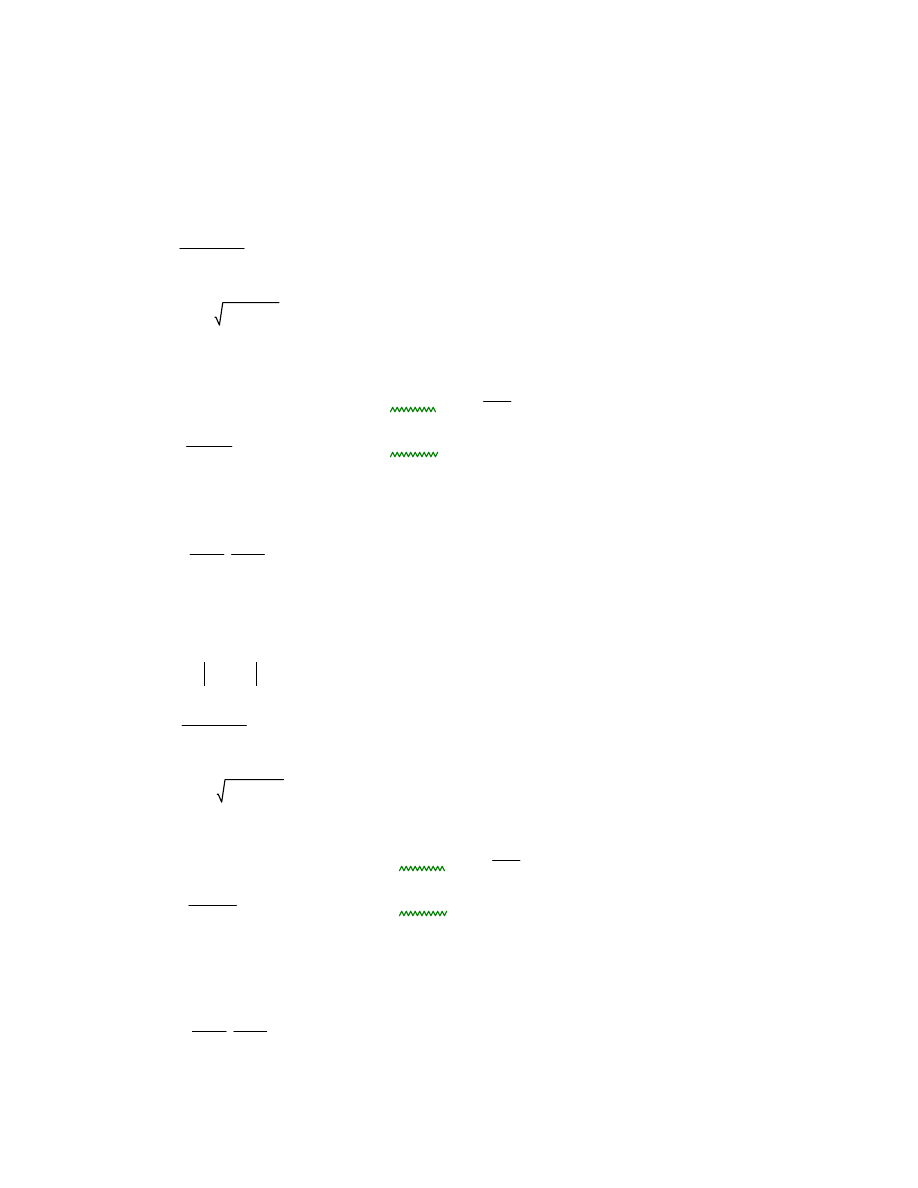
Przęsło 2

MEd2 M2max 5.103 kN m









μ2

MEd2

b d

2



η

 fcd



0.062





ξef2

1

1

2 μ2







0.064





Zbrojenie ściskane nie jest konieczne w przęśle 2

zc2

1

0.5 ξef2









d



7.357 cm







Asmin 0.26

fctm

fyd



b

 d



1 cm

2







> 0.0013 bt

 d



0.988 cm

2





As2

MEd2

zc2 fyd



1.595 cm

2







Asmax 0.04 b

 d



30.4 cm

2







Pole zbrojenia na metr bieżący przy maksymalnym rozstawie 20 cm

A's2

1m

Smax

π ϕ

2



4



2.513 cm

2







Spełnia warunki maksymalnego i minimalnego zbrojenia

Podpora C

MEdC

MCmin

8.656 kN m









μC

MEdC

b d

2



η

 fcd



0.105





ξefC

1

1

2 μC







0.111





Zbrojenie ściskane nie jest konieczne w podporze C

zcC

1

0.5 ξefC









d



7.178 cm







Asmin 0.26

fctm

fyd



b

 d



1 cm

2







> 0.0013 bt

 d



0.988 cm

2





AsC

MEdC

zcC fyd



2.774 cm

2







Asmax 0.04 b

 d



30.4 cm

2







Pole zbrojenia na metr bieżący przy rozstawie 16 cm

A'sC

1m

16cm

π ϕ

2



4



3.142 cm

2







8

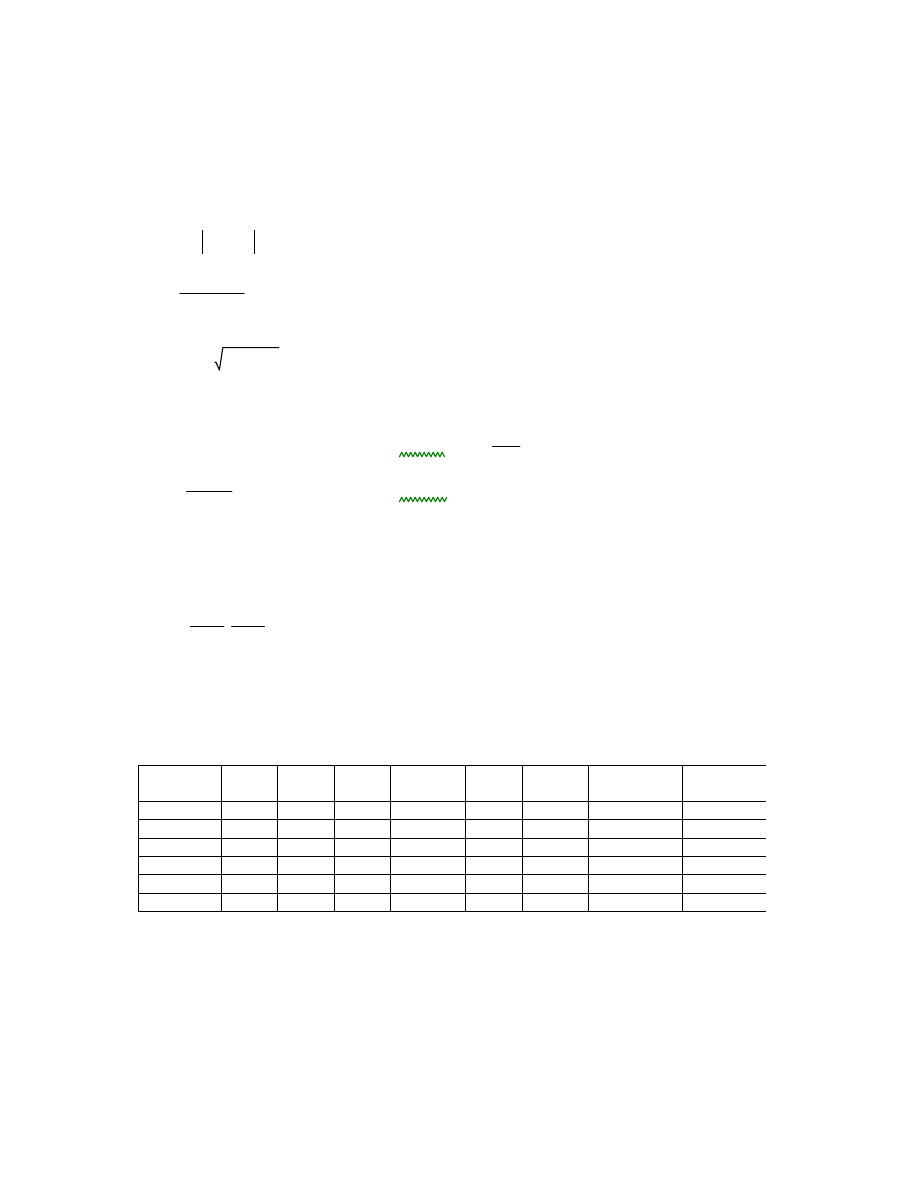
Spełnia warunki maksymalnego i minimalnego zbrojenia

Przęsło 3

MEd3

M3max

6.006 kN m









μ3

MEd3

b d

2



η

 fcd



0.073





ξef3

1

1

2 μ3







0.076





Zbrojenie ściskane nie jest konieczne w przęśle 3

zc3

1

0.5 ξef3









d



7.313 cm







Asmin 0.26

fctm

fyd



b

 d



1 cm

2







> 0.0013 bt

 d



0.988 cm

2





As3

MEd3

zc3 fyd



1.889 cm

2







Asmax 0.04 b

 d



30.4 cm

2







Pole zbrojenia na metr bieżący przy maksymalnym rozstawie 20 cm

A's3

1m

Smax

π ϕ

2



4



2.513 cm

2







Spełnia warunki maksymalnego i minimalnego zbrojenia

9.Zestawienie zbrojenia głównego.

Lokalizacja 

M

Ed 

[kNm]

 

μ 

ξ

ef

Zbrojenie 

ściskane 

z

c

[cm]

A

s

[cm

2

]

Dobrane 

zbrojenie 

A

s

 [cm

2

] 

rzeczywiste 

M

A

 

2,433 

0,029 

0,03

Nie

7,486

0,748

φ8 co 20cm 

2,513

M

1

 

8,111 

0,098 

0,104

Nie

7,206

2,589

φ8 co 16cm 

3,142

M

B 

10,197 

0,124 

0,132

Nie

7,097

3,305

φ8 co 14cm 

3,59 

M

2 

5,103 

0,062 

0,064

Nie

7,357

1,595

φ8 co 20cm 

2,513

M

C 

8,656 

0,105 

0,111

Nie

7,178

2,774

φ8 co 16cm 

3,142

M

3

 

6,006 

0,073 

0,076

Nie

7,313

1,889

φ8 co 20cm 

2,513

 

10.Obliczenie wymaganego zbrojenia rozdzielczego.

MEd

20% MBmin



2.039



kN m









9

Współczynnik pomocniczy:

μ

MEd

b d

2



fcd



0.025





Zasięg strefy ściskanej:

ξef

1

1

2 μ







0.025





ξef

ξef.lim



- zbrojenie ściskane nie jest konieczne

ramię sił wewnętrznych z

c

:

zc

1

0.5 ξef









d



7.505 cm







przekrój zbrojenia rozciąganego A

sr:

Asr

MEd

zc fyd



0.625 cm

2







Dobrane pole zbrojenia rozdzielczego:

A'sr

1m

Sroz.max

π

6

2

 mm

2

4



0.942 cm

2







Przyjęto zbrojenie rozdzielcze ϕ6 co 30 cm.

11. Wyznaczenie długości zakotwienia prętów zbrojeniowych.

Podpora A:

fbd 2.25 η1



η2



fctd



=

wartość obliczeniowa granicznego naprężenia przyczepności
dla prętów żebrowanych

fctd 1.07MPa



obliczeniowa wytrzymałość betonu klasy C20/25 na rozciąganie

współczynnik zależny od jakości warunków przyczepności i ułożenia pręta
zbrojenia w betonie; dla grubości płyty h<250mm, warunki przyczepności
wszystkich prętów są uznawane za dobre i współczynnik ten przyjmuje
wartość równą 1

η1

1.0



η2

1.0



współczynnik zależny od średnicy pręta; dla prętów ϕ<32mm przyjmuje
wartość równą 1

fbd 2.25 η1



η2



fctd



2.408 MPa







podstawowa długość zakotwienia

lb.rqd

ϕ σsd



4 fbd



=

σsG

fyd 434.783 MPa







naprężenie obliczeniowe przekroju, od którego odmierza się
długość zakotwienia, przyjęto równe obliczeniowej wartości
granicy plastyczności stali

lb.rqdA

ϕ σsG



4 fbd



36.119 cm







10

lbd α1 α2



α3



α4



α5



lb.rqd





obliczeniowa długość zakotwienia

α1

1



współczynnik zależny od kształtu prętów, przy założeniu, że otulenie jest odpowiednie

α2

1



współczynnik zależny od najmniejszego otulenia betonem

α3

1



współczynnik zależny od wpływu skrępowania betonu przez zbrojenie poprzeczne

α4

0.7



współczynnik uwzględniający wpływ jednego lub większej liczby prętów poprzecznych
przyspojonych na obliczeniowej długości zakotwienia

α5

1



współczynnik uwzględniający wpływ nacisku poprzecznego do płaszczyzny
rozłupywania wzdłuż obliczeniowej długości zakotwienia

lbdA

α1 α2



α3



α4



α5



lb.rqdA



25.283 cm







dla prętów rozciąganych

lbmin max 0.3 lb.rqdA



10ϕ



100mm







10.836 cm







lbd lbmin



lbdA 25.283 cm





20% ln



56 cm





Pręt zbrojeniowy na górze, jego wymiar w prawą stronę licząc od lica wewnętrznego
ściany wynosi co najmniej 20%l

n

, w związku z czym ustalam długość tę na 56cm,

natomiast w lewą stronę obliczony wymiar wyniósł w zaokrągleniu 26cm. Jako że ściana
ma grubość 20cm, a wyliczona otulina wynosi 2cm, pozostaje 8cm pręta do zagięcia.

Przęsło 1:

10ϕ

8 cm





σsd

0.25fyd 108.696 MPa







lb.rqd1

ϕ σsd



4 fbd



9.03 cm







lbd1

α1 α2



α3



α4



α5



lb.rqd1



6.321 cm







dla prętów rozciąganych

lbmin max 0.3 lb.rqd1



10ϕ



100mm







10 cm







lbd lbmin



lbd1

lbmin 10 cm







Pręt zbrojeniowy na dole, jego wydłużenie w prawą stronę wynosi co najmniej 10ϕ, w
związku z czym ustalam długość tę na 8cm, natomiast wydłużenie w lewą stronę wynosi
10cm.

11

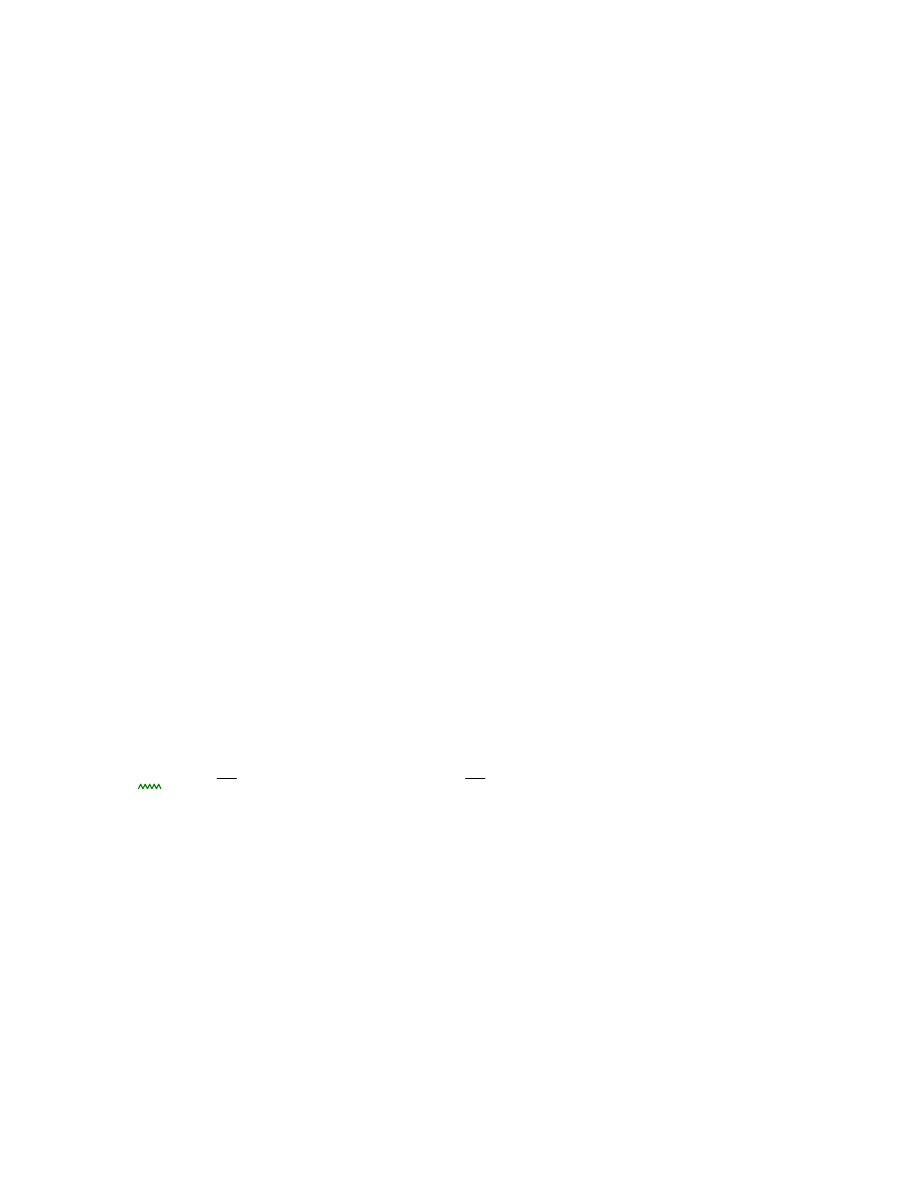
Podpora B:

25% ln



70 cm





Pręt zbrojeniowy na górze, jego wymiar i w lewą, i w prawą stronę licząc od lica wewnętrznego
ściany wynosi co najmniej 25%l

n

, w związku z czym ustalam długość tę na 70cm

Przęsło 2:

10ϕ

8 cm





Pręt zbrojeniowy na dole, jego wydłużenie wynosi co najmniej 10ϕ, w związku z czym
ustalam długość tę na 8cm

Podpora C:

25% ln



70 cm





Pręt zbrojeniowy na górze, jego wymiar i w lewą, i w prawą stronę licząc od lica wewnętrznego
ściany wynosi co najmniej 25%l

n

, w związku z czym ustalam długość tę na 70cm

Przęsło 3:

10ϕ

8 cm





Pręt zbrojeniowy na dole, jego wydłużenie wynosi co najmniej 10ϕ, w związku z czym
ustalam długość tę na 8cm

12.Wartości momentów w stanie granicznym użytkowania.

Obciążenia charakterystyczne na metr bieżący płyty:

gk

3.978

kN

m



qk

b qk1 qk2









3.634

kN

m







Wyznaczenie obwiedni momentów

leff 2.9m



Momenty maksymalne:

M1.max

gk 0.078



qk 0.1









leff

2



5.666 kN m









MA.max 0.2 M1.max



1.133 m kN







MB.max

gk 0.105



(

)



qk 0.013

(

)









leff

2



3.115



kN m









12

M2.max

gk 0.033



qk 0.079









leff

2



3.518 kN m









MC.max

gk 0.079



(

)



qk 0.018

(

)









leff

2



2.093



kN m









M3.max

gk 0.046



qk 0.086









leff

2



4.167 kN m









Momenty minimalne:

M1.min

gk 0.078



qk 0.026



(

)









leff

2



1.815 kN m









MA.min 0.2M1.min 0.363 kN m









MB.min

gk 0.105



(

)



qk 0.119



(

)









leff

2



7.15



kN m









M2.min

gk 0.033



qk 0.046



(

)









leff

2



0.302



kN m









MC.min

gk 0.079



(

)



qk 0.111



(

)









leff

2



6.035



kN m









M3.min

gk 0.046



qk 0.040



(

)









leff

2



0.316 kN m









13.Sprawdzenie stanu zarysowania metodą uproszczoną.

wmax 0.4mm



- graniczna szerokość rys wg tab 7.1 normy dla klasy ekspozycji XC1

b

1 m



h

0.1 m



d

7.6 cm





Ac b h



0.1 m

2





Przęsło 1:

Msd.1 M1.max 5.666 kN m









A's1 3.142 cm

2





ρ1

A's1

Ac

100



%

0.314 %







ζ

0.90



σs1

Msd.1

ζ

d

 A's1



263.66 MPa







Maksymalny rozstaw prętów wynosi 220 mm. Przyjęto 160mm. Warunek spełniony.

13

Przęsło 2:

Msd2 M2.max 3.518 kN m









A's2 2.513 cm

2





ρD2

A's2

Ac

100



%

0.251 %







ζ

0.90



σsd2

Msd2

ζ

d

 A's2



204.667 MPa







Maksymalny rozstaw prętów wynosi 280 mm. Przyjęto 200mm.Warunek spełniony.

Przęsło 3:

Msd3 M3.max 4.167 kN m









A's3 2.513 cm

2





ρD3

A's3

Ac

100



%

0.251 %







ζ

0.90



σsd3

Msd3

ζ

d

 A's3



242.41 MPa







Maksymalny rozstaw prętów wynosi 250 mm. Przyjęto 200mm. Warunek spełniony

Podpora A:

MsdA MA.max 1.133 kN m









A'sA 2.513 cm

2





ρA

A'sA

Ac

100



%

0.251 %







ζ

0.90



σsA

MsdA

ζ

d

 A'sA



65.915 MPa







Brak zagrożenia zarysowaniem.

14

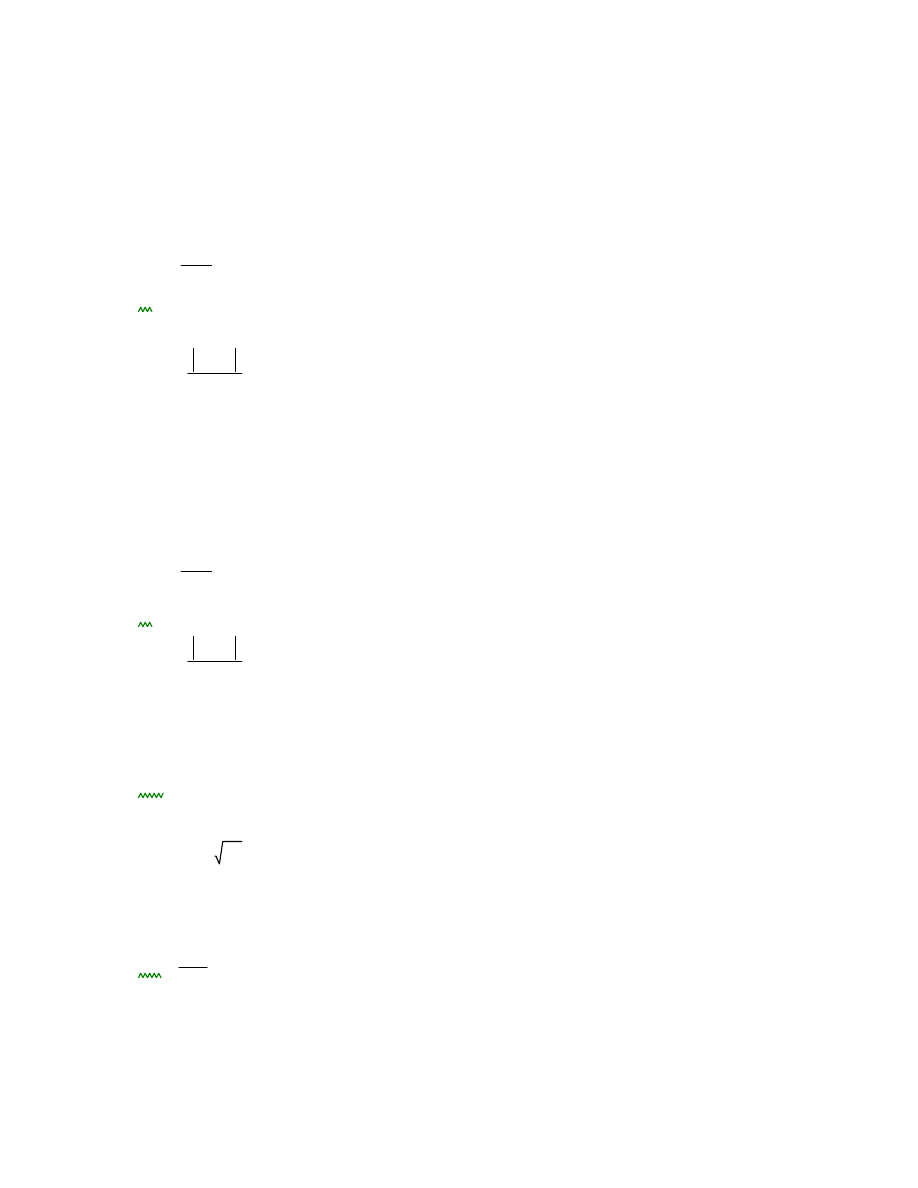
Podpora B:

MsdB MB.min

7.15



kN m









A'sB 3.59 cm

2





ρB

A'sB

Ac

100



%

0.359 %







ζ

0.90



σsB

MsdB

ζ

d

 A'sB



291.128 MPa







Maksymalny rozstaw prętów wynosi 180 mm. Przyjęto 140mm. Warunek spełniony.

Podpora C:

MsdC MC.min

6.035



m kN







A'sC 3.142 cm

2





ρC

A'sC

Ac

100



%

0.314 %







ζ

0.90



σsC

MsdC

ζ

d

 A'sC



280.861 MPa







Maksymalny rozstaw prętów wynosi 200 mm. Przyjęto 160mm. Warunek spełniony.

14.Sprawdzenie stanu ugięcia metodą uproszczoną.

fck 20



ρ0

10

3



fck



0.447 %







- porównawczy stopień zbrojenia

Obliczam wymagane ze względu na nośność stopnie zbrojenia rozciąganego:

ρ1

A's1

b h



0.314 %







<

ρ0 0.447 %





15

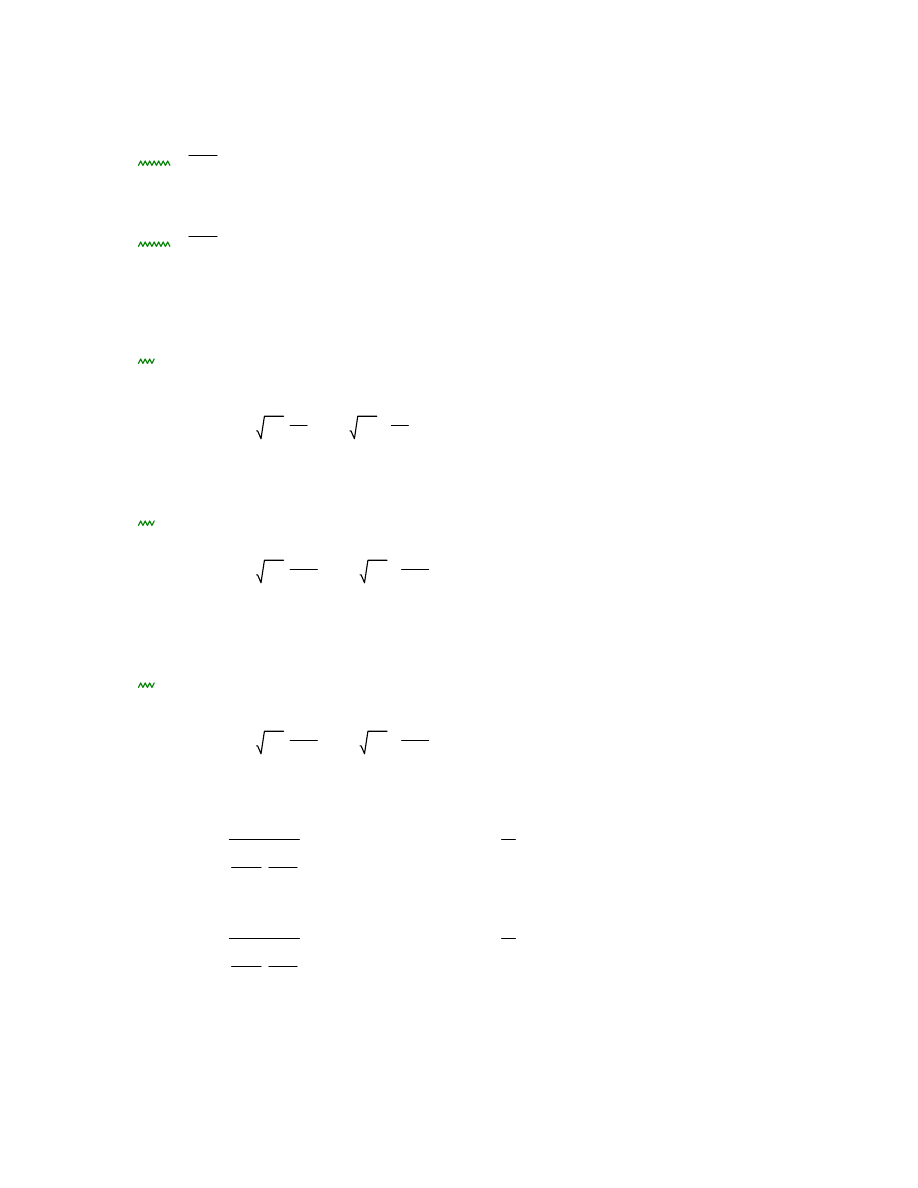
ρD2

A's2

b h



0.251 %







<

ρ0 0.447 %





ρD3

A's3

b h



0.251 %







<

ρ0 0.447 %





Wyznaczam podstawową graniczną wartość ilorazu rozpiętości do wysokość przekroju:

Przęsło 1

K

1.3



- współczynnik zależny od rodzaju konstrukcji

ld1 K 11 1.5 fck



ρ0
ρ1





3.2 fck



ρ0
ρ1

1















1.5























31.842





Przęsło 2

K

1.5



- współczynnik zależny od rodzaju konstrukcji

ld2 K 11 1.5 fck



ρ0

ρD2





3.2 fck



ρ0

ρD2

1















1.5























49.176





Przęsło 3

K

1.5



- współczynnik zależny od rodzaju konstrukcji

ld3 K 11 1.5 fck



ρ0

ρD3





3.2 fck



ρ0

ρD3

1















1.5























49.176





Przeliczam na wartość dla naprężeń rzeczywistych:

ld1.lim ld1

500

fyk

MPa

As1

A's1





38.639





>

ln

d

36.842



ld2.lim ld2

500

fyk

MPa

As2

A's2





77.479





>

ln

d

36.842



16

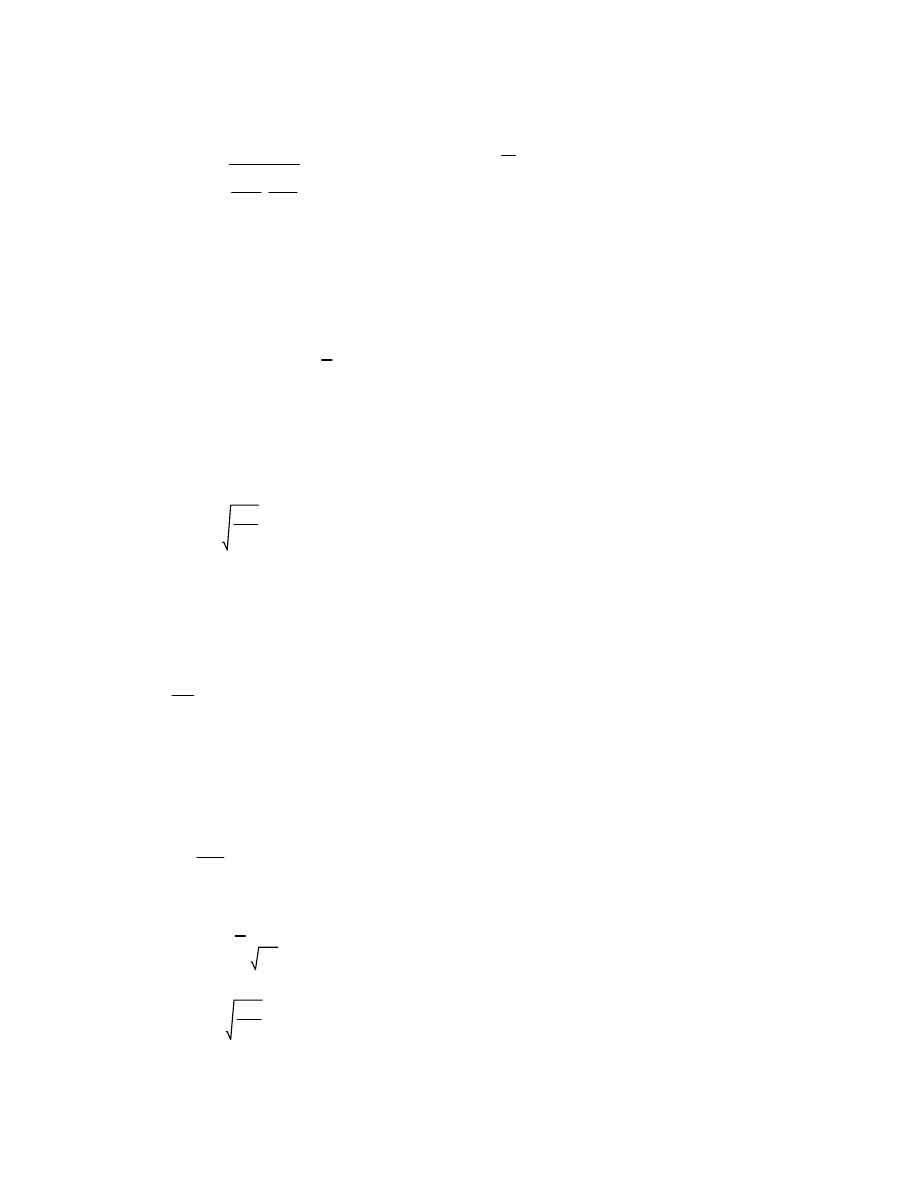
ln

d

36.842



ld3.lim ld3

500

fyk

MPa

As3

A's3





65.425





>

Warunek ugięć jest spełniony.

15. Nośność na ścinanie elementu.

VRdc

CRdc k



100 ρl

 fck







1

3











b

 d



vmin b

 d





=

gdzie :

k - współczynnik zapisany wzorem:

k

min 1

200

d



2.0















=

f

ck

- wytrzymałość charakterystyczna betonu na rozciąganie

d - wysokość użyteczna - 120 mm

ρ

l

- stopień zbrojenia na zginanie wyrażony wzorem:

ρl

Asl
b d



=

A

sl

- pole przekroju zbrojenia rozciąganego

b - najmniejsza szerokość strefy rozciąganej przekroju - 100 mm

C

Rdc

- współczynnik ujmujący zależność pomiędzy f

ctd

i f

ck

w postaci:

CRdc

0.18

1.4

0.129





v

min

- współczynnik określany ze wzoru:

vmin 0.035 k

3

2



fck



=

k

min 1

200

76



2.0















2





17

vmin 0.035 k

3

2



fck



0.443





Podpora A

ρA

A's1

b h



3.142

10

3









VRdcA

CRdc k



100 ρA



20







1

3











1000



76



3.606

10

4







vmin 1000



76



3.365

10

4





36.06kN

33.65kN



VA 5.314kN



<

36.06kN

Podpora B

ρ2

A's2

b h



2.513

10

3









VRdcB

CRdc k



100 ρ2



fck







1

3











1000



76



3.348

10

4







vmin 1000.



76



3.365

10

4





33.65kN

33.48kN



VB 19.238kN



<

33.65kN

Zbrojenie na ścinanie nie jest wymagane.

Podpora C

ρD3

A's3

b h



2.513

10

3









18

VRdcC

CRdc k



100 ρD3



fck







1

3











1000.



76



3.348

10

4







vmin 1000



76



3.365

10

4





VC 15.457kN



<

33.65kN

Zbrojenie na ścinanie nie jest wymagane.

19