
Politechnika Śląska
Gliwice, 2006/2007
Wydział: Automatyki, Elektroniki i Informatyki
Semestr: 6 (letni)
Kierunek: Automatyka i robotyka
Podstawy Automatyki
– laboratorium
Ćw 4. Metoda linii pierwiastkowych.
Data ćwiczeń laboratoryjnych:
14.03.2007
Grupa: 1
Sekcja: 3
Skład osobowy sekcji:
Zięba Andrzej
Bojko Marcin
1. Cel ćwiczenia:
Celem ćwiczenia było przyswojenie analizy układów regulacji przy użyciu metody linii
pierwiastkowych, oraz zbadanie wpływu wartości parametrów transmitancji na charakter układu
regulacji. W ramach laboratorium należało również zbadać wpływ stosowania korektora PD na
układ regulacji.
2. Program ćwiczenia:
1. Analiza układów regulacji z wykorzystaniem metody linii pierwiastkowych.
1.1.
Wpływ położenia biegunów.
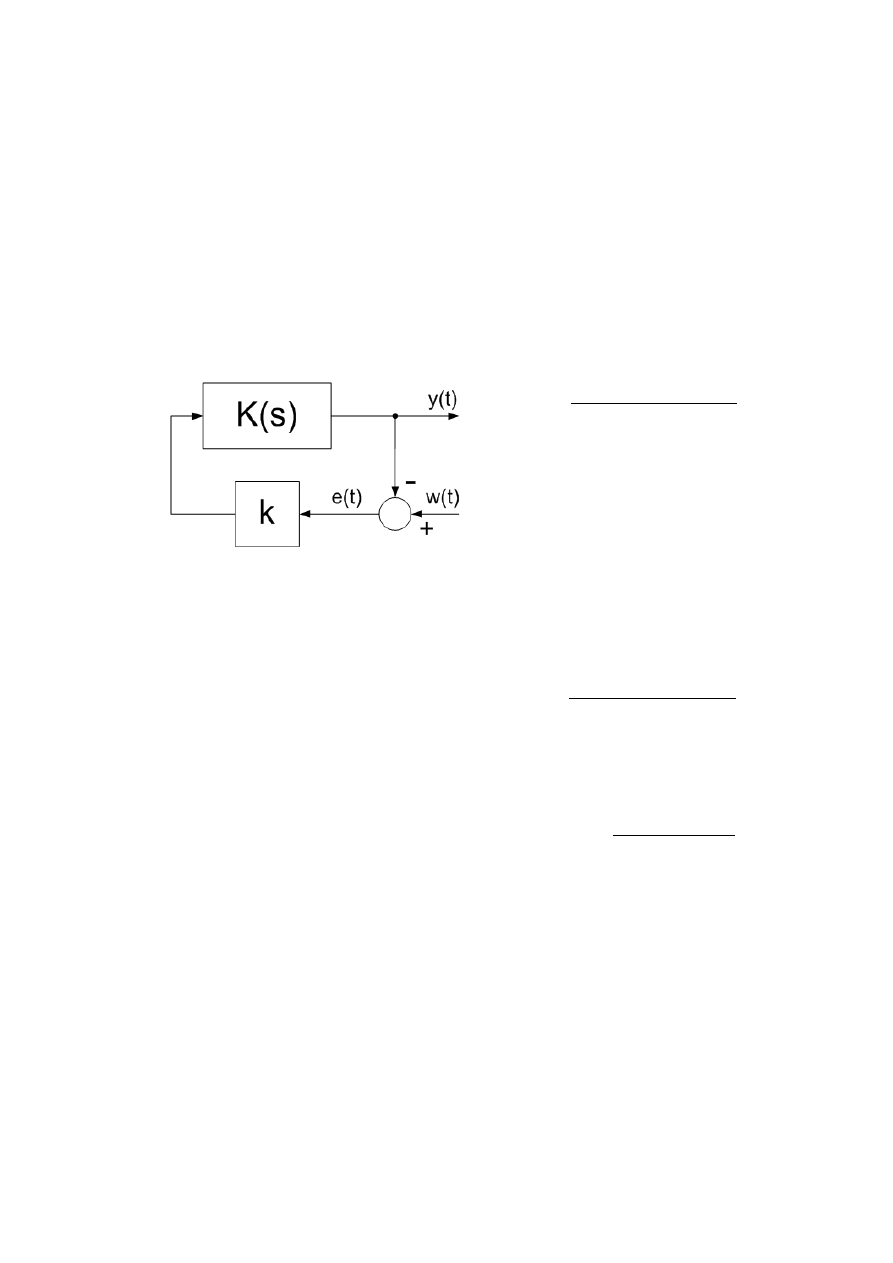
Dla układu regulacji przedstawionego na rys.1 składającego się z elementu III-go rzędu:
K s=
1
s− p
1
s− p
2
s− p
3
1
Rysunek 1. Schemat blokowy UR.
przebadaj zależność przebiegu linii pierwiastkowych od charakteru biegunów układu
otwartego (zespolone, rzeczywiste, wielokrotne). Zaznacz kąt nachylenia asymptot oraz
centroid. Obiekt (1) powinien być stabilny.
1.2.
Wpływ położenia zera.
Wprowadź do obiektu (1) zero „z
1
”:
K s=
s−z
1
s− p
1
s− p
2
s− p
3
2
a następnie przeanalizuj wpływ położenia zera transmitancji układu otwartego na
przebieg linii pierwiastkowych.
1.3.
Wpływ wzmocnienia w pętli sprzężenia zwrotnego.
W układzie z rys. 1 przyjmij transmitancję układu otwartego (stabilnego) w postaci:
K s=
1
s s− p
1
s− p
2
3
Wyrysuj linie pierwiastkowe układu zamkniętego oraz dobierz wzmocnienie k tak aby:
a) odpowiedź stabilnego układu zamkniętego na skok jednostkowy była aperiodyczna,
b) odpowiedź układu zamkniętego na skok jednostkowy była oscylacyjna,
c) układ zamknięty znalazł się na granicy stabilności (k = k
gr
),
d) układ zamknięty był niestabilny (k > k
gr
).
Znajdź wszystkie pierwiastki równania charakterystycznego przy wybranym
wzmocnieniu. Narysuj charakterystykę amplitudowo-fazową układu oraz odpowiedź
układu zamkniętego na skokową zmianę wartości zadanej w(t).
2. Korekcja układów regulacji automatycznej.
2.1.
Układ bez korekcji.
Dla układu regulacji z rys.1 o transmitancji obiektu takiej jak w punkcie 1.3 wykreśl
przebieg linii pierwiastkowych. Wybierz wzmocnienie:
k
1
< k
gr
– takie, że układ zamknięty nie spełnia wymagań przed nim stawianych, takich
jak: stopień stabilności, stopień oscylacyjności;
k
2
< k
gr
– takie, że układ zamknięty spełnia powyższe wymagania.
Znajdź wszystkie pierwiastki odpowiadające danemu wzmocnieniu oraz zaznacz
„obszar niedozwolony”. Wprowadź wyznaczone wzmocnienia do układu, a następnie
wykreśl odpowiedź skokową układu zamkniętego.
2.2.
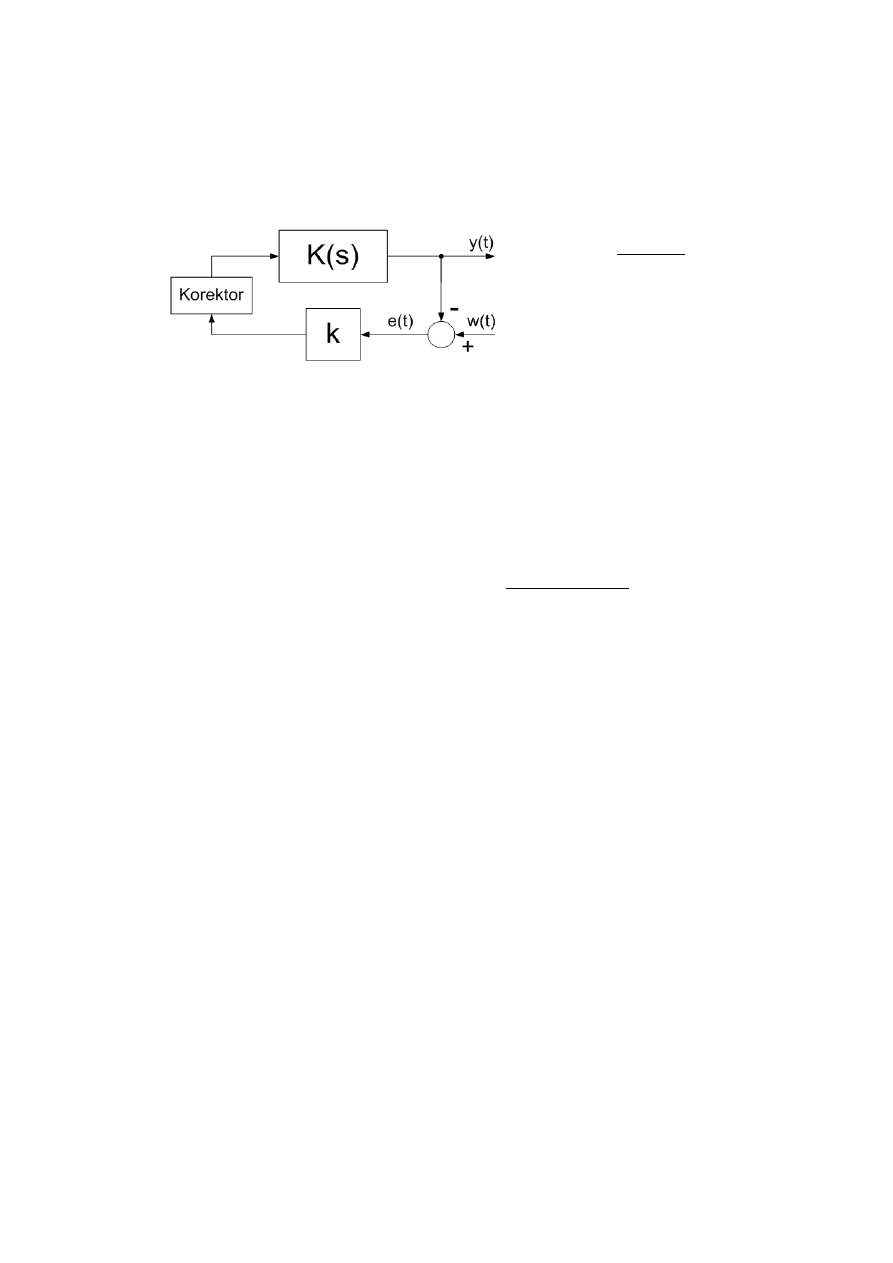
Układ z korekcją.
Dobierz szeregowo dołączony człon korekcyjny typu PD (rys. 2) o transmitancji:
K
k
s=
1s T
k
1s T
k
, 1
4
Rysunek 2. Schemat UR po korekcji.
poprawiający działanie układu. Dobierz jego parametry wykorzystując metodę
„skreślania zer i biegunów”. Wyrysuj linie pierwiastkowe układu zamkniętego i wybierz
wzmocnienie k tak aby układ spełniał wymagania z pkt.2.1. Zaznacz pierwiastki
równania charakterystycznego układu zamkniętego dla tego wzmocnienia. Wykreśl
odpowiedź skokową zamkniętego układu regulacji po korekcji i porównaj ją z
odpowiedziami układu bez korektora (pkt.2.1).
3.
Wpływ stałej czasowej.
W układzie przedstawionym na rys. 1 przyjmij obiekt regulacji w postaci:
K s=
1sT
s s1s T
o
1
; k , T
o
−
dane
5
Przeprowadź analizę wpływu stałej czasowej T na własności układu zamkniętego.
Wykorzystując metodę linii pierwiastkowych przedstaw rozkład pierwiastków równania
charakterystycznego układu zamkniętego w zależności od wartości parametru T.
3. Realizacja zadań:
Ad 1.
Analiza układów regulacji z wykorzystaniem metody linii pierwiastkowych.
Kod źródłowy programu:
close all;
clear all;
clc;
% Wprowadzenie transmitancji:
s=tf('s');
disp('Wprowadz transmitancje obiektu:');
Ko=minreal(input('K(s) = '))
% Wyrysowanie przebiegow linii pierwiastkowych:
figure;
rlocus(Ko,'k');
hold on;
xl=xlim;
yl=ylim;
xlim(xl);
ylim(yl);
% Wyznaczenie i wyrysowanie asymptot:
[Zera,Bieguny]=zpkdata(Ko,'v');
[L_Z]=size(Zera);
[L_B]=size(Bieguny);
L_Z=L_Z(1);
L_B=L_B(1);
sum_B=0;
sum_Z=0;
if L_B>0
v=0;
v(1: size(Bieguny))=1;
sum_B=Bieguny'*v';
end
if L_Z>0
v=0;
v(1: size(Zera))=1;
sum_Z=Zera'*v';
end
if L_B-L_Z>0

h=(sum_B-sum_Z)/(L_B-L_Z);
disp(['Punkt przeciecia asymptot: (',num2str(h),',0i)']);
disp(' ');
disp('Katy nachylenia asymptot:');
v=0;
for i=1: 2: L_B-L_Z
v((i+1)/2)=180*i/(L_B-L_Z);
disp(['+- ',num2str(v((i+1)/2)),' stopni']);
if v((i+1)/2)<90
plot([h xl(2)],[0 xl(2)-h]*tan(v((i+1)/2)*pi/180),':k');
plot([h xl(2)],[0 xl(2)-h]*tan(v((i+1)/2)*pi/180)*(-1),':k');
end
if v((i+1)/2)>90 && v((i+1)/2)~=180
plot([h xl(1)],[0 xl(1)-h]*tan(v((i+1)/2)*pi/180),':k');
plot([h xl(1)],[0 xl(1)-h]*tan(v((i+1)/2)*pi/180)*(-1),':k');
end
if v((i+1)/2)==90
plot([h h],yl,':k');
end
if v((i+1)/2)==180
plot([xl(1) h],[0 0],':k');
end
end
plot(h,0,'dk');
else
disp('Brak asymptot.');
end
title('Root Locus','Fontsize',14);
xlabel('Real Axis','Fontsize',12);
ylabel('Imaginary Axis','Fontsize',12);
% Wprowadzenie wzmocnienia do ukladu i zaznaczenie pierwiastkow dla danego wzm.:
disp(' ');
k=input('Podaj wzmocnienie: k = ');
rlocus(Ko,'pk',k);
% Wyznaczenie pierwiastkow rownania charakterystycznego ukladu zamknietego:
K=minreal(k*Ko/(1+k*Ko));
[ZERA,BIEGUNY]=zpkdata(K,'v');
disp(' ');
disp('Pierwiastki rownania charakterystycznego ukladu zamknietego:');
disp(num2str(BIEGUNY'));
% Wyrysowanie charakterystyki ampli.-faz. i odpowiedzi skokowej:
figure;
nyquist(k*Ko,'k');
title('Nyquist Diagram','Fontsize',14);
xlabel('Real Axis','Fontsize',12);
ylabel('Imaginary Axis','Fontsize',12);
figure;
step(K,'k');
hold on;
title('Step Response','Fontsize',14);
xlabel('Time','Fontsize',12);
ylabel('Amplitude','Fontsize',12);
Oznaczenia:
✗
pierwiastek równania charakterystycznego obiektu
centroida (punkt przecięcia asymptot)
pierwiastek równania charakterystycznego UR dla wzmocnienia k
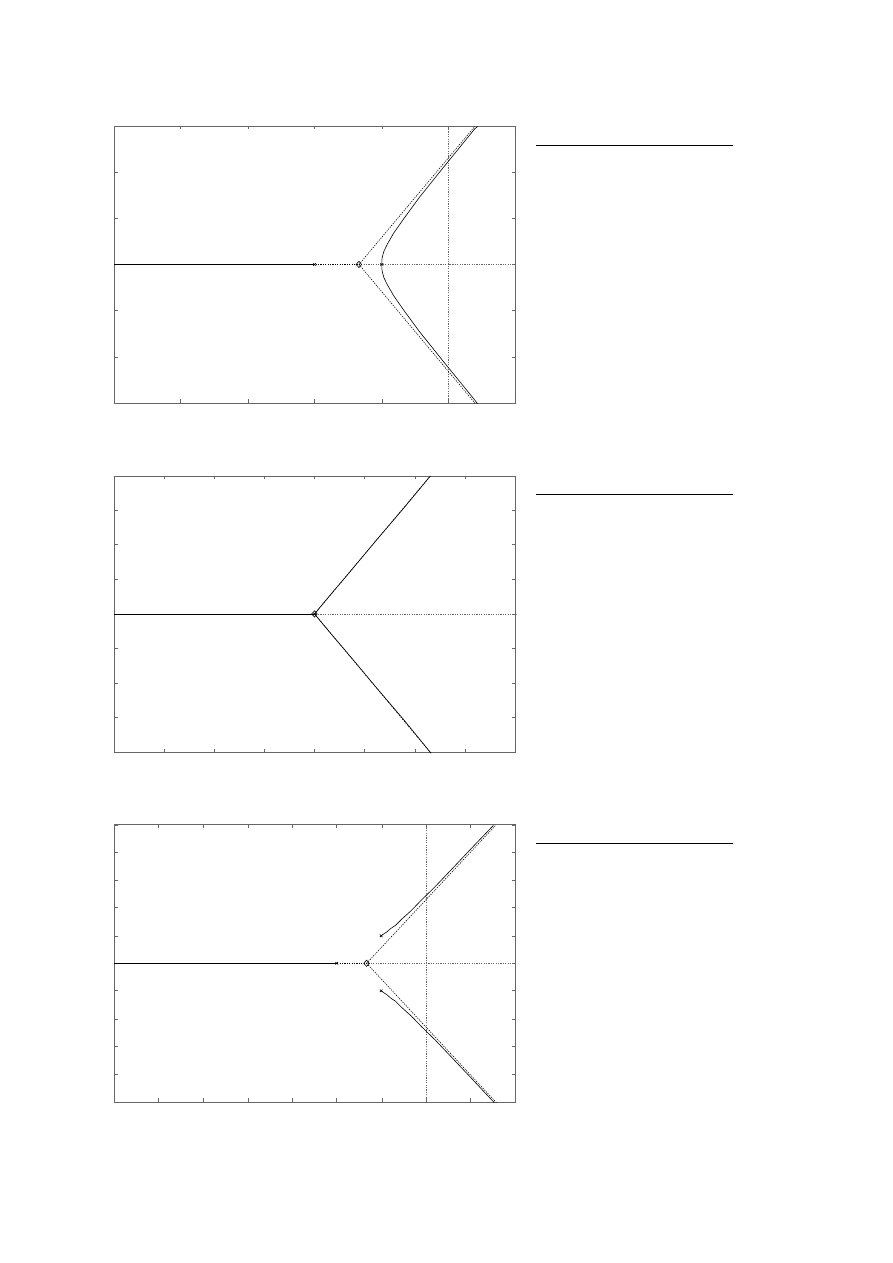
Ad 1.1.
a) p
1
= -1, p
2
= -2, p
3
= -4.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/(s+1)/(s+2)/(s+4)
Transfer function:
1
----------------------
s^3 + 7 s^2 + 14 s + 8
Punkt przeciecia asymptot: (-2.3333,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
- 1 0
- 8
- 6
- 4
- 2
0
2
- 8
- 6
- 4
- 2
0
2
4
6
8
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
b) p
1
= -2, p
2
= -2, p
3
= -4.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/(s+2)/(s+2)/(s+4)
Transfer function:
1
-----------------------
s^3 + 8 s^2 + 20 s + 16
Punkt przeciecia asymptot: (-2.6667,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
c) p
1
= -2, p
2
= -2, p
3
= -2.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/(s+2)/(s+2)/(s+2)
Transfer function:
1
----------------------
s^3 + 6 s^2 + 12 s + 8
Punkt przeciecia asymptot: (-2,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
d) p
1
= -2, p
2
= -1 + 1i, p
3
= -1 - 1i.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/(s+2)/(s^2+2*s+2)
Transfer function:
1
---------------------
s^3 + 4 s^2 + 6 s + 4
Punkt przeciecia asymptot: (-1.3333,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
- 1 0
- 8
- 6
- 4
- 2
0
2
- 6
- 4
- 2
0
2
4
6
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 4
- 3 . 5
- 3
- 2 . 5
- 2
- 1 . 5
- 1
- 0 . 5
0
- 2
- 1 . 5
- 1
- 0 . 5
0
0 . 5
1
1 . 5
2
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
1
2
- 5
- 4
- 3
- 2
- 1
0
1
2
3
4
5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is

Wnioski:
●
Dla transmitancji obiektu określonej wzorem (1) kąty nachylenia asymptot są stałe i nie
zależą od wartości przyjętych pierwiastków.
●
Dla transmitancji obiektu określonej wzorem (1) położenie centroidy na osi liczb
rzeczywistych jest uwarunkowane przez średnią arytmetyczną pierwiastków równania
charakterystycznego obiektu.
●
Tylko w przypadku kiedy pierwiastki równania charakterystycznego omawianej
transmitancji obiektu są rzeczywiste możliwe jest dobranie wartości wzmocnienia k (dla k
mniejszego od pewnej wartości zależnej od rozkładu tych pierwiastków), w taki sposób aby
układ zamknięty był aperiodyczny. W pozostałych przypadkach układ zamknięty jest
periodyczny.
●
Dla tak przyjętej transmitancji obiektu zawsze istnieje pewna wartość graniczna
wzmocnienia k
gr
dla której układ zamknięty przestaje być stabilny.
Ad 1.2.
a) p
1
= -2, p
2
= -4, p
3
= -6, z
1
= -1.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = (s+1)/(s+2)/(s+4)/(s+6)
Transfer function:
s + 1
------------------------
s^3 + 12 s^2 + 44 s + 48
Punkt przeciecia asymptot: (-5.5,0i)
Katy nachylenia asymptot:
+- 90 stopni
b) p
1
= -2, p
2
= -4, p
3
= -6, z
1
= -3.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = (s+3)/(s+2)/(s+4)/(s+6)
Transfer function:
s + 3
------------------------
s^3 + 12 s^2 + 44 s + 48
Punkt przeciecia asymptot: (-4.5,0i)
Katy nachylenia asymptot:
+- 90 stopni
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
- 1 0
- 8
- 6
- 4
- 2
0
2
4
6
8
1 0
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
- 8
- 6
- 4
- 2
0
2
4
6
8
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
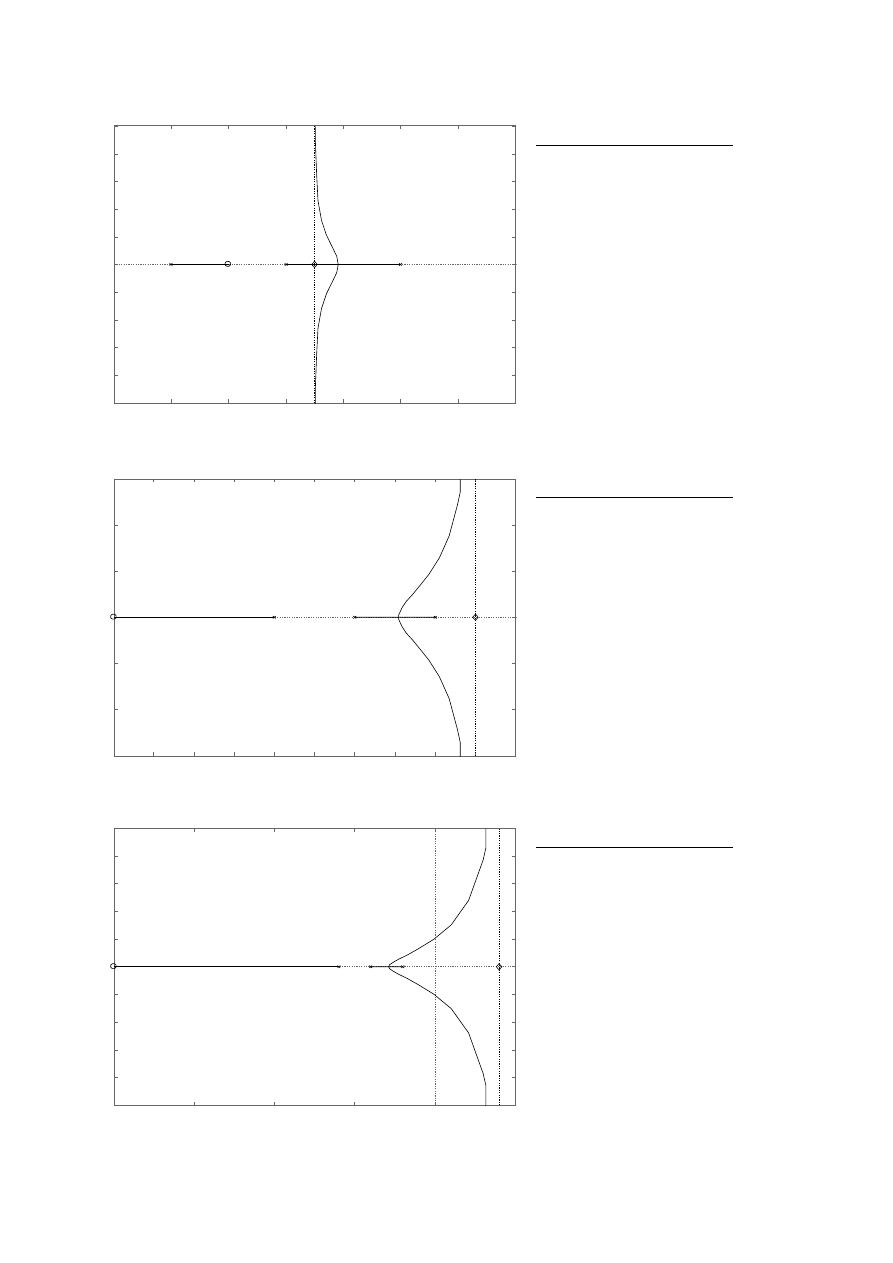
c) p
1
= -2, p
2
= -4, p
3
= -6, z
1
= -5.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = (s+5)/(s+2)/(s+4)/(s+6)
Transfer function:
s + 5
------------------------
s^3 + 12 s^2 + 44 s + 48
Punkt przeciecia asymptot: (-3.5,0i)
Katy nachylenia asymptot:
+- 90 stopni
d) p
1
= -2, p
2
= -4, p
3
= -6, z
1
= -10.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = (s+10)/(s+2)/(s+4)/(s+6)
Transfer function:
s + 10
------------------------
s^3 + 12 s^2 + 44 s + 48
Punkt przeciecia asymptot: (-1,0i)
Katy nachylenia asymptot:
+- 90 stopni
e) p
1
= -2, p
2
= -4, p
3
= -6, z
1
= -20.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = (s+20)/(s+2)/(s+4)/(s+6)
Transfer function:
s + 20
------------------------
s^3 + 12 s^2 + 44 s + 48
Punkt przeciecia asymptot: (4,0i)
Katy nachylenia asymptot:
+- 90 stopni
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
- 1 0
- 8
- 6
- 4
- 2
0
2
4
6
8
1 0
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 1 0
- 9
- 8
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
- 1 5
- 1 0
- 5
0
5
1 0
1 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 2 0
- 1 5
- 1 0
- 5
0
5
- 5 0
- 4 0
- 3 0
- 2 0
- 1 0
0
1 0
2 0
3 0
4 0
5 0
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is

f) p
1
= -2, p
2
= -4, p
3
= -6, z
1
= +1.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = (s-1)/(s+2)/(s+4)/(s+6)
Transfer function:
s - 1
------------------------
s^3 + 12 s^2 + 44 s + 48
Punkt przeciecia asymptot: (-6.5,0i)
Katy nachylenia asymptot:
+- 90 stopni
g) p
1
= -1 + 1i, p
2
= -1 - 1i, p
3
= -2, z
1
= -0.5.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = (s+0.5)/(s^2+2*s+2)/(s+2)
Transfer function:
s + 0.5
---------------------
s^3 + 4 s^2 + 6 s + 4
Punkt przeciecia asymptot: (-1.75,0i)
Katy nachylenia asymptot:
+- 90 stopni
Wnioski:
●
Dla transmitancji obiektu określonej wzorem (1) kąty nachylenia asymptot są stałe i nie
zależą od wartości przyjętych pierwiastków ani zera.
●
Jeżeli wprowadzone do układu otwartego zero zawiera się w przedziale
∑
i =1
i=3
p
i
0
to
zamknięty układ regulacji jest stabilny dla dowolnego wzmocnienia. W przeciwnym razie
istnieje pewne wzmocnienie graniczne k
gr
poniżej którego układ jest stabilny.
●
Powyżej pewnej wartości wzmocnienia dla której występuje para sprzężonych pierwiastków
równania charakterystycznego dla układu zamkniętego ze wzrostem wzmocnienia można
wyróżnić dwie sytuacje. Gdy pierwiastek rzeczywisty przesuwa się w lewo to zespolone w
prawo, a gdy pierwiastek rzeczywisty przesuwa się w prawo to zespolone w lewo.
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
1
- 2 5
- 2 0
- 1 5
- 1 0
- 5
0
5
1 0
1 5
2 0
2 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 2 . 5
- 2
- 1 . 5
- 1
- 0 . 5
0
- 8
- 6
- 4
- 2
0
2
4
6
8
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
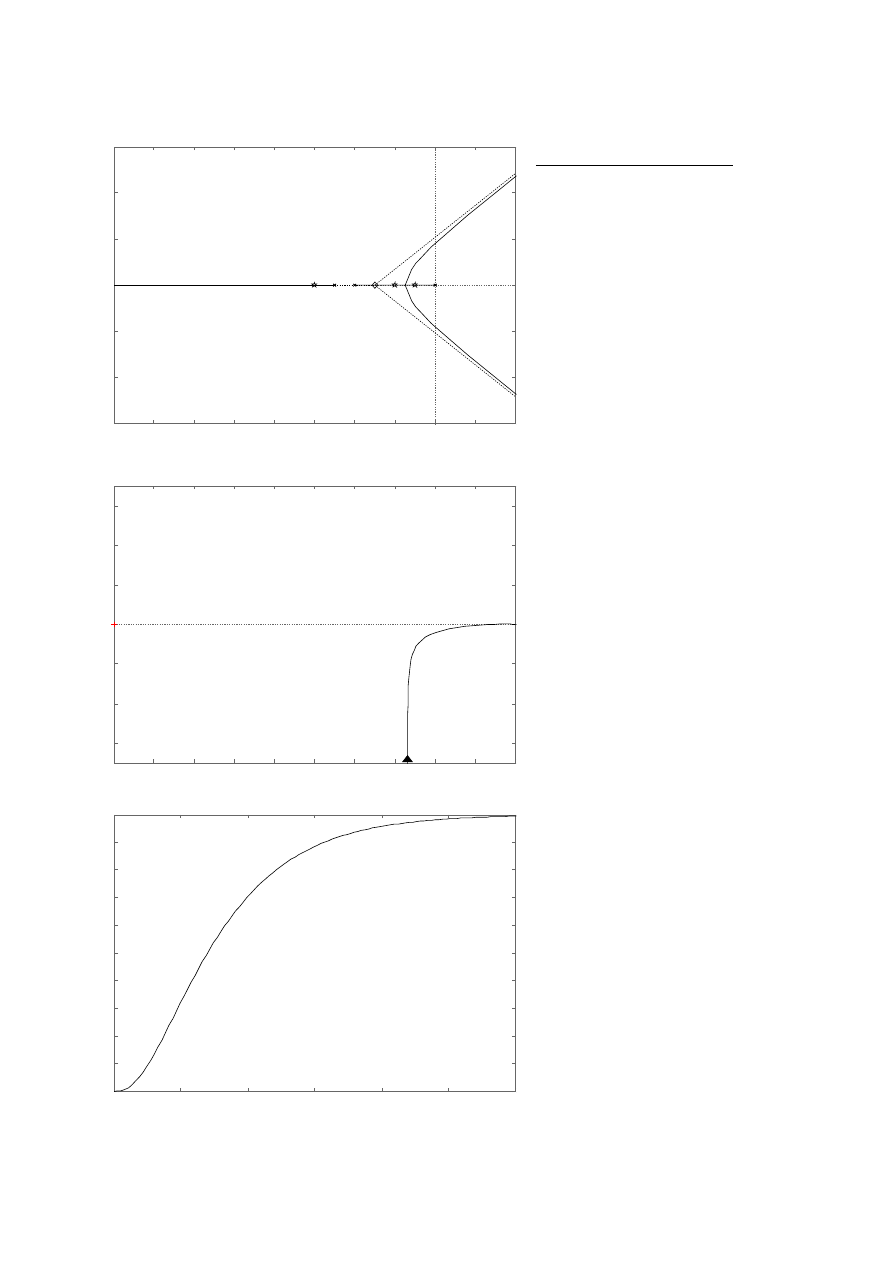
Ad 1.3.
a) p
1
= -4, p
2
= -5, k = 12.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/s/(s+4)/(s+5)
Transfer function:
1
------------------
s^3 + 9 s^2 + 20 s
Punkt przeciecia asymptot: (-3,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
Podaj wzmocnienie: k = 12
Pierwiastki rownania charakterystycznego
ukladu zamknietego:
-6
-2
-1
- 1 6
- 1 4
- 1 2
- 1 0
- 8
- 6
- 4
- 2
0
2
4
- 1 5
- 1 0
- 5
0
5
1 0
1 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 1
- 0 . 9
- 0 . 8
- 0 . 7
- 0 . 6
- 0 . 5
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0
- 3
- 2
- 1
0
1
2
3
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
1
2
3
4
5
6
0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 7
0 . 8
0 . 9
1
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e

b) p
1
= -4, p
2
= -5, k = 100.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/s/(s+4)/(s+5)
Transfer function:
1
------------------
s^3 + 9 s^2 + 20 s
Punkt przeciecia asymptot: (-3,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
Podaj wzmocnienie: k = 100
Pierwiastki rownania charakterystycznego
ukladu zamknietego:
-8.0581
-0.47096-3.4911i
-0.47096+3.4911i
- 1 6
- 1 4
- 1 2
- 1 0
- 8
- 6
- 4
- 2
0
2
4
- 1 5
- 1 0
- 5
0
5
1 0
1 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 2 . 5
- 2
- 1 . 5
- 1
- 0 . 5
0
- 3 0
- 2 0
- 1 0
0
1 0
2 0
3 0
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
2
4
6
8
1 0
1 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e
c) p
1
= -4, p
2
= -5, k = 180.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/s/(s+4)/(s+5)
Transfer function:
1
------------------
s^3 + 9 s^2 + 20 s
Punkt przeciecia asymptot: (-3,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
Podaj wzmocnienie: k = 180
Pierwiastki rownania charakterystycznego
ukladu zamknietego:
-9
-5.218e-015-4.4721i
-5.218e-015+4.4721i
- 1 6
- 1 4
- 1 2
- 1 0
- 8
- 6
- 4
- 2
0
2
4
- 1 5
- 1 0
- 5
0
5
1 0
1 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 4 . 5
- 4
- 3 . 5
- 3
- 2 . 5
- 2
- 1 . 5
- 1
- 0 . 5
0
- 6 0
- 4 0
- 2 0
0
2 0
4 0
6 0
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
5
1 0
1 5
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
1 . 8
2
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e
d) p
1
= -4, p
2
= -5, k = 500.
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/s/(s+4)/(s+5)
Transfer function:
1
------------------
s^3 + 9 s^2 + 20 s
Punkt przeciecia asymptot: (-3,0i)
Katy nachylenia asymptot:
+- 60 stopni
+- 180 stopni
Podaj wzmocnienie: k = 500
Pierwiastki rownania charakterystycznego
ukladu zamknietego:
-11.2002
1.10008-6.5903i
1.10008+6.5903i
Wnioski:
●
Ze wzrostem wzmocnienia do pewnej granicy polepsza się jakość regulacji następnie w
momencie pojawienia się oscylacji maleje, aż do utraty stabilności układu.
- 1 6
- 1 4
- 1 2
- 1 0
- 8
- 6
- 4
- 2
0
2
4
- 1 5
- 1 0
- 5
0
5
1 0
1 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 1 2
- 1 0
- 8
- 6
- 4
- 2
0
- 1 5 0
- 1 0 0
- 5 0
0
5 0
1 0 0
1 5 0
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
0 . 5
1
1 . 5
2
2 . 5
- 1 0
- 5
0
5
1 0
1 5
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e

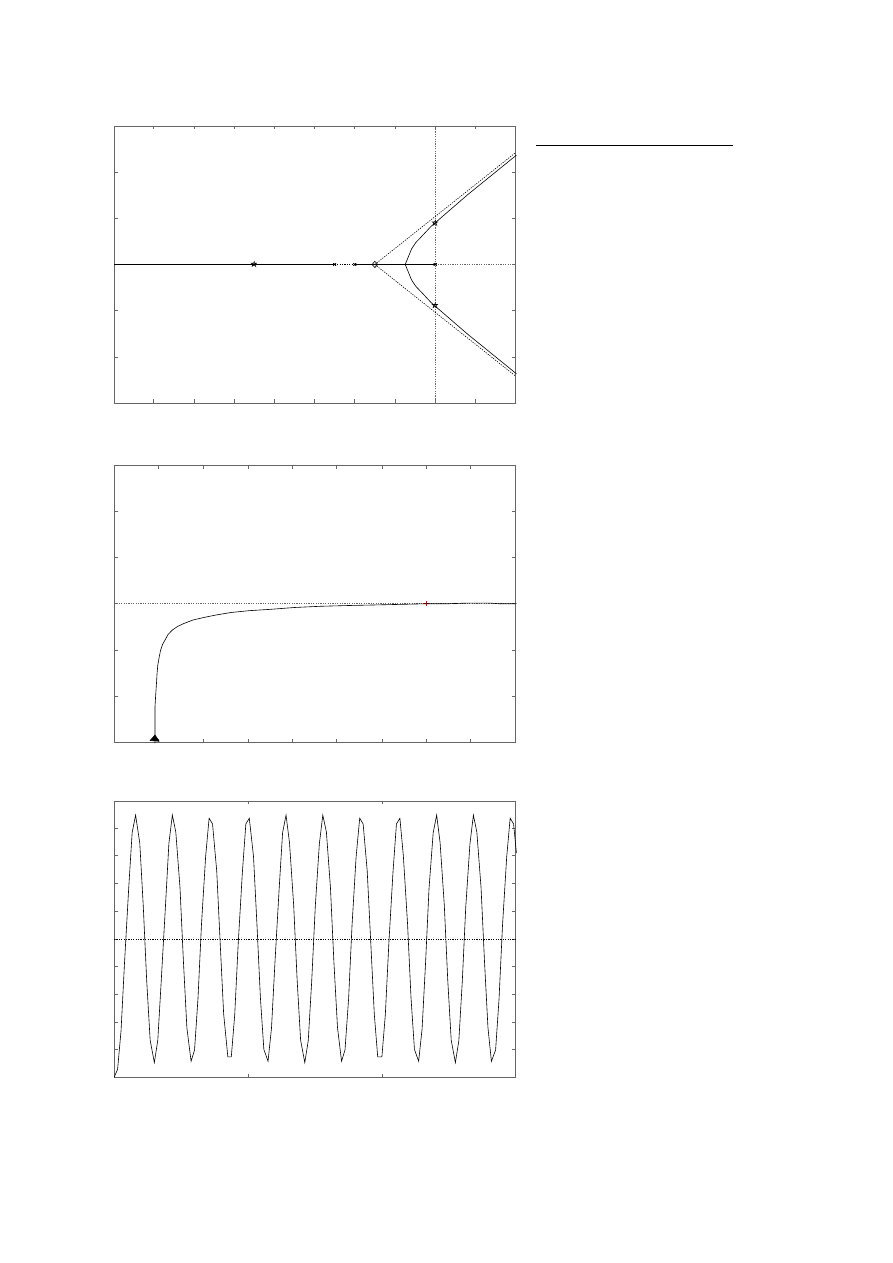
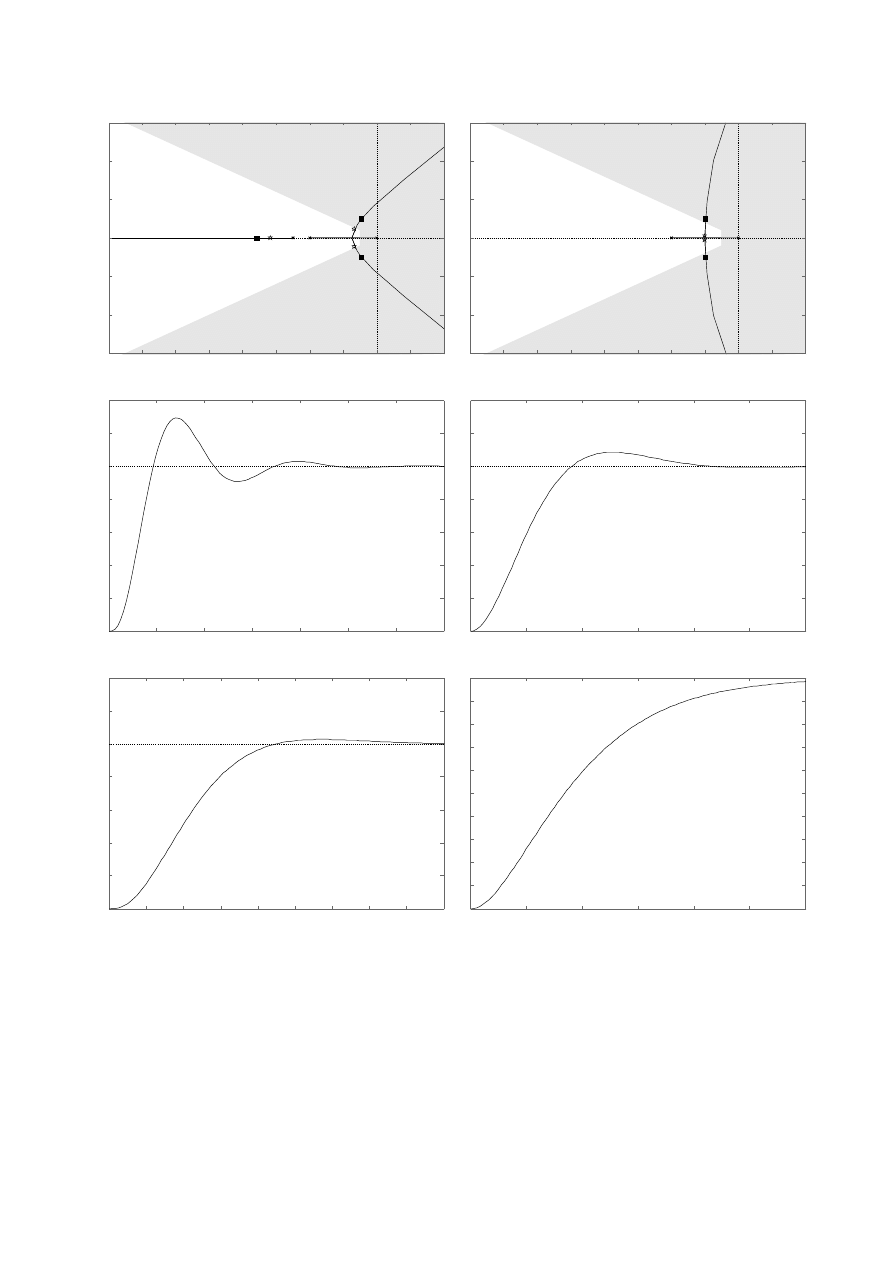
Ad 2.
Korekcja układów regulacji automatycznej.
Kod źródłowy programu:
close all;
clear all;
clc;
% Wprowadzenie transmitancji:
s=tf('s');
disp('Wprowadz transmitancje obiektu:');
Ko=minreal(input('K(s) = '))
% Wyrysowanie przebiegow linii pierwiastkowych:
rlocus(Ko,'k');
hold on;
xl=xlim;
yl=ylim;
xlim(xl);
ylim(yl);
title('Root Locus','Fontsize',14);
xlabel('Real Axis','Fontsize',12);
ylabel('Imaginary Axis','Fontsize',12);
% Wprowadzenie wymagan:
disp('Wprowadz wymagania:');
st_stab=input('Stopien stabilnosci: ');
st_oscy=input('Stopien oscylacyjnosci: ');
% Zaznaczenie obszaru niespelniajacego wymagan:
fill([xl(1) -st_stab -st_stab xl(1) xl(2) xl(2)],...
[-xl(1)*st_oscy st_stab*st_oscy -st_stab*st_oscy xl(1)*st_oscy yl(1) yl(2)],'k',...
'EdgeColor',[0.9 0.9 0.9],'FaceColor',[0.9 0.9 0.9]);
plot(xl,[0 0],':k',[0 0],yl,':k');
rlocus(Ko,'k');
set(gca,'Layer','top');
% Wprowadzenie wzmocnien do ukladu:
disp(' ');
disp('Wprowadz wzmocnienia:');
k1=input('Wprowadz wzmocnienie niespelniajace wymagan: k1 = ');
k2=input('Wprowadz wzmocnienie spelniajace wymagania: k2 = ');
% Wyrysowanie rozkladu pierwiastkow dla wprowadzonych wzmocnien:
rlocus(Ko,'sk',k1);
rlocus(Ko,'pk',k2);
% Wyznaczenie pierwiastkow r. char. ukl. zamknietego i wyrysowanie
% przebiegow odpowiedzi skokowej dla danych wzmocnien:
K1=minreal(k1*Ko/(1+k1*Ko));
K2=minreal(k2*Ko/(1+k2*Ko));
[ZERA1,BIEGUNY1]=zpkdata(K1,'v');
[ZERA2,BIEGUNY2]=zpkdata(K2,'v');
disp(' ');
disp('Pierwiastki row. char. dla k1:');
disp(num2str(BIEGUNY1));
disp('Pierwiastki row. char. dla k2:');
disp(num2str(BIEGUNY2));
figure;
step(K1);
title('Step Response for k1','Fontsize',14);
xlabel('Time','Fontsize',12);
ylabel('Amplitude','Fontsize',12);
figure;
step(K2);
title('Step Response for k2','Fontsize',14);
xlabel('Time','Fontsize',12);
ylabel('Amplitude','Fontsize',12);
% Wprowadzenie transmitancji korektora:
disp(' ');
disp('Wprowadz transmitancje korektora:');
Kk=minreal(input('Kk(s) = '))
Kok=minreal(Kk*Ko);
% Wyrysowanie rozkladu pierwiastkow po korekcji:
figure;
rlocus(Kok,'k');
title('Root Locus','Fontsize',14);
xlabel('Real Axis','Fontsize',12);
ylabel('Imaginary Axis','Fontsize',12);
hold on;
fill([xl(1) -st_stab -st_stab xl(1) xl(2) xl(2)],...
[-xl(1)*st_oscy st_stab*st_oscy -st_stab*st_oscy xl(1)*st_oscy yl(1) yl(2)],'k',...
'EdgeColor',[0.9 0.9 0.9],'FaceColor',[0.9 0.9 0.9]);
xlim(xl);
ylim(yl);
plot(xl,[0 0],':k',[0 0],yl,':k');
rlocus(Kok,'k');
set(gca,'Layer','top');
% Wyrysowanie rozkladu pierwiastkow dla wprowadzonych wzmocnien:
rlocus(Kok,'sk',k1);
rlocus(Kok,'pk',k2);
% Wyznaczenie pierwiastkow r. char. ukl. zamknietego i wyrysowanie
% przebiegow odpowiedzi skokowej dla danych wzmocnien:
K1k=minreal(k1*Kok/(1+k1*Kok));
K2k=minreal(k2*Kok/(1+k2*Kok));
[ZERA1k,BIEGUNY1k]=zpkdata(K1k,'v');
[ZERA2k,BIEGUNY2k]=zpkdata(K2k,'v');
disp(' ');

disp('Pierwiastki row. char. dla k1:');
disp(num2str(BIEGUNY1k));
disp('Pierwiastki row. char. dla k2:');
disp(num2str(BIEGUNY2k));
figure;
step(K1k);
title('Step Response for k1','Fontsize',14);
xlabel('Time','Fontsize',12);
ylabel('Amplitude','Fontsize',12);
figure;
step(K2k);
title('Step Response for k2','Fontsize',14);
xlabel('Time','Fontsize',12);
ylabel('Amplitude','Fontsize',12);
W przykładzie tym korektorem poprawiono jakość regulacji dla obu wartości
wzmocnień z punktu 2.1. czyli dla wzmocnienia przy którym spełnione są narzucone wymagania
oraz dla wzmocnienia przy którym te wymagania nie są spełnione.
Parametry obiektu:
p
1
= -4, p
2
= -5.
Parametry korektora:
T
k
= 0.2, α = 0.05.
Wybrane wzmocnienia:
k
1
= 50, k
2
= 20.
Oznaczenia:
✗
pierwiastek równania charakterystycznego obiektu
pierwiastek równania charakterystycznego UR dla wzmocnienia k1
pierwiastek równania charakterystycznego UR dla wzmocnienia k2
Wynik działania programu:
Wprowadz transmitancje obiektu:
K(s) = 1/s/(s+4)/(s+5)
Transfer function:
1
------------------
s^3 + 9 s^2 + 20 s
Wprowadz wymagania:
Stopien stabilnosci: 1
Stopien oscylacyjnosci: 1
Wprowadz wzmocnienia:
Wprowadz wzmocnienie niespelniajace wymagan: k1 = 50
Wprowadz wzmocnienie spelniajace wymagania: k2 = 20
Przed korekcjia:
Pierwiastki row. char. dla k1:
-7.185
-0.90752+2.477i
-0.90752-2.477i
Pierwiastki row. char. dla k2:
-6.3445
-1.3277+1.1787i
-1.3277-1.1787i
Wprowadz transmitancje korektora:
Kk(s) = (0.2*s+1)/(0.2*0.05*s+1)
Transfer function:
20 s + 100
----------
s + 100
Po korekcji:
Pierwiastki row. char. dla k1:
-100.1039
-1.948027+2.488937i
-1.948027-2.488937i
Pierwiastki row. char. dla k2:
-100.0416
-1.979184+0.2848942i
-1.979184-0.2848942i
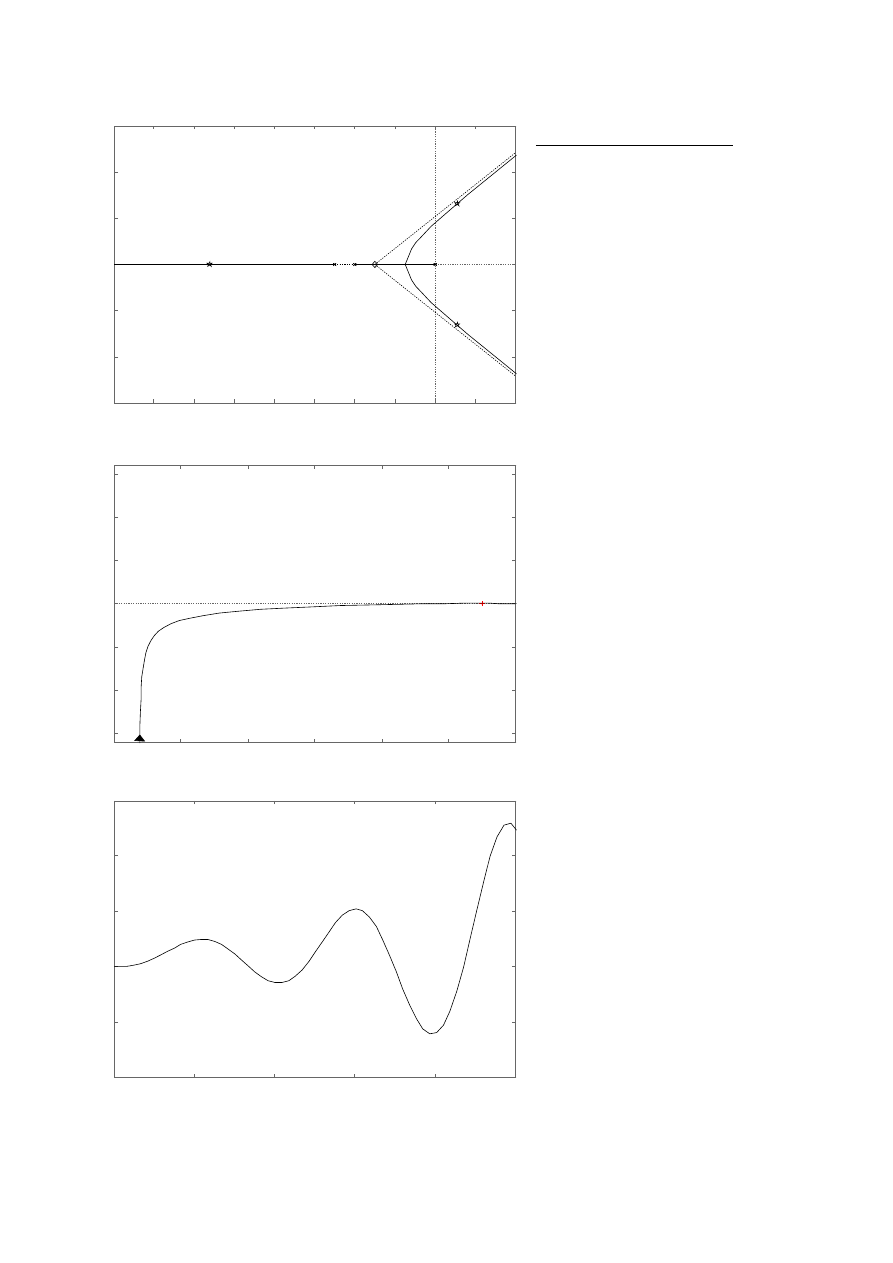
Przed korekcją:
Po korekcji:
Wnioski:
●
Jak widać na załączonych wyżej wykresach zastosowanie filtra korekcyjnego PD o
odpowiednio dobranych parametrach w znacznym stopniu poprawia jakość regulacji.
●
Czas ustalania się przebiegów odpowiedzi skokowych (dla zadanego otoczenia) jest krótszy
w układzie regulacji z korektorem o odpowiednio dobranych parametrach.
●
Oscylacje w układzie regulacji z korektorem znacznie szybciej zanikają.
●
Wzmocnienie k
gr
powyżej którego układ zamknięty przestaje być stabilny jest znacznie
wyższe po zastosowaniu korektora.
●
W niektórych warunkach możliwe jest dobranie korektora w taki sposób, że dla danego
wzmocnienia k, układ regulacji niespełniający wymagań przed nim stawianych w
połączeniu z korektorem będzie je spełniał.
- 1 6
- 1 4
- 1 2
- 1 0
- 8
- 6
- 4
- 2
0
2
4
- 1 5
- 1 0
- 5
0
5
1 0
1 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
- 1 6
- 1 4
- 1 2
- 1 0
- 8
- 6
- 4
- 2
0
2
4
- 1 5
- 1 0
- 5
0
5
1 0
1 5
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
1
2
3
4
5
6
7
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
S t e p R e s p o n s e f o r k 1
T i m e ( s e c )
A
m
p
li
tu
d
e
0
0 . 5
1
1 . 5
2
2 . 5
3
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
S t e p R e s p o n s e f o r k 1
T i m e ( s e c )
A
m
p
li
tu
d
e
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
4 . 5
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
S t e p R e s p o n s e f o r k 2
T i m e ( s e c )
A
m
p
li
tu
d
e
0
0 . 5
1
1 . 5
2
2 . 5
3
0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 7
0 . 8
0 . 9
1
S t e p R e s p o n s e f o r k 2
T i m e ( s e c )
A
m
p
li
tu
d
e
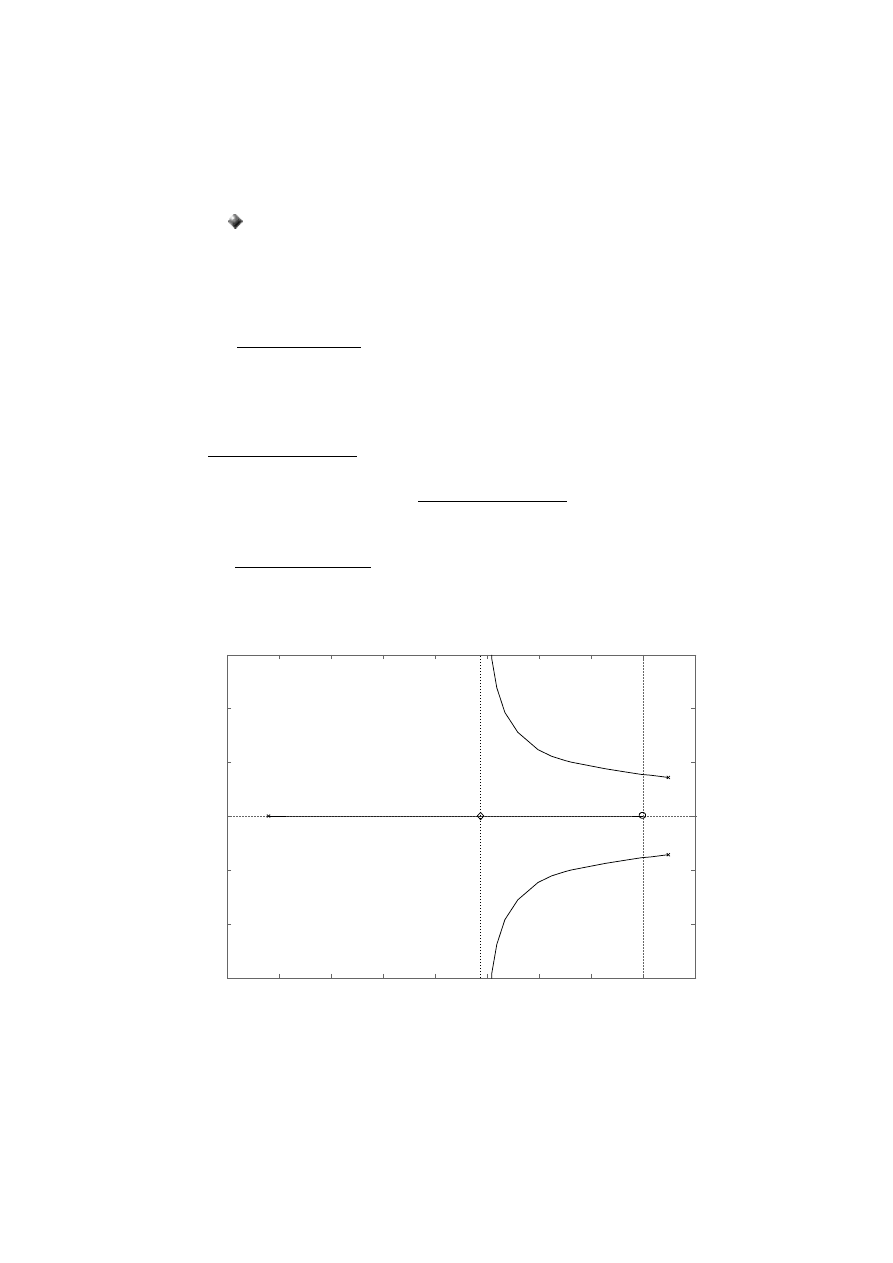
Ad 3.
Wpływ stałej czasowej.
Wykorzystano kod źródłowy użyty w punkcie 1.
Oznaczenia:
✗
biegun równania charakterystycznego obiektu
centroida (punkt przecięcia asymptot)
○
zero równania charakterystycznego obiektu
Analityczne wyznaczenie transmitancji G(s) w celu zaobserwowania za pomocą linii
pierwiastkowych wpływu stałej czasowej na rozkład pierwiastków:
K s=
1sT
s s1 s T
o
1
; k =3 , T
o
=
4
Równanie charakterystyczne:
1k⋅K s =0
s s1T
o
s1k sTk =0
1
sTk
s s1T
o
s1k
=
0
1T⋅G s=0 ; gdzie :G s =
sk
s s1T
o
s1k
Po podstawieniu wartości liczbowych:
G s =
3s
s s1 4s13
Wizualizacja wpływu stałej czasowej:
Wnioski:
●
Ze wzrostem stałej czasowej T zespolone pierwiastki równania charakterystycznego
przesuwają się w lewo, natomiast pierwiastek rzeczywisty w prawo.
●
W ogólnym przypadku zbyt mała wartość stałej czasowej T sprawia że układ zamknięty jest
niestabilny, jednakże można dobrać parametry w taki sposób by układ regulacji był stabilny
w całym zakresie zmian T.
- 1 . 6
- 1 . 4
- 1 . 2
- 1
- 0 . 8
- 0 . 6
- 0 . 4
- 0 . 2
0
0 . 2
- 3
- 2
- 1
0
1
2
3
R o o t L o c u s
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
Document Outline
Wyszukiwarka
Podobne podstrony:
Cw 4 Metoda linii pierwiastkow Nieznany
Ćw 4 Metoda linii pierwiastkowych
Metoda linii pierwiastkowych
Metoda projektowania układów regulacji za pomocą linii pierwiastkowych
Metoda projektowania układów regulacji za pomocą linii pierwiastkowych
cw 4 metoda ABC
OBLICZENIE PŁYT METODĄ LINII ZAŁOMU 3, Obliczyć obciążenie graniczne płyty metodą lini załomów stosu
Ćwiczenie 1 - Brudnopis, Politechnika Poznańska, Elektrotechnika, Teoria pola elektromagnetycznego,
Reguły konstrukcji linii pierwiastkowych
wykresy z moich linii pierwiastkowych
cw metoda algebraiczna
Cw 5 Metoda Zapasu jednookresowego
Reguły konstrukcji linii pierwiastkowych, Automatyka Robotyka Pomiary
po stresach-cw, Metoda indygokarminowa - barwnik indygokarminowy barwi martwe tkanki na niebiesko, n
Metoda przybliżania pierwiastków funkcji f
Cw 6 Metoda Wagnera Withina szczegolny przypadek
Ćw 4 Metoda średniej szerokości Gaussa oraz metoda Clarke’a
Cw 5 Metoda Zapasu jednookresowego
więcej podobnych podstron