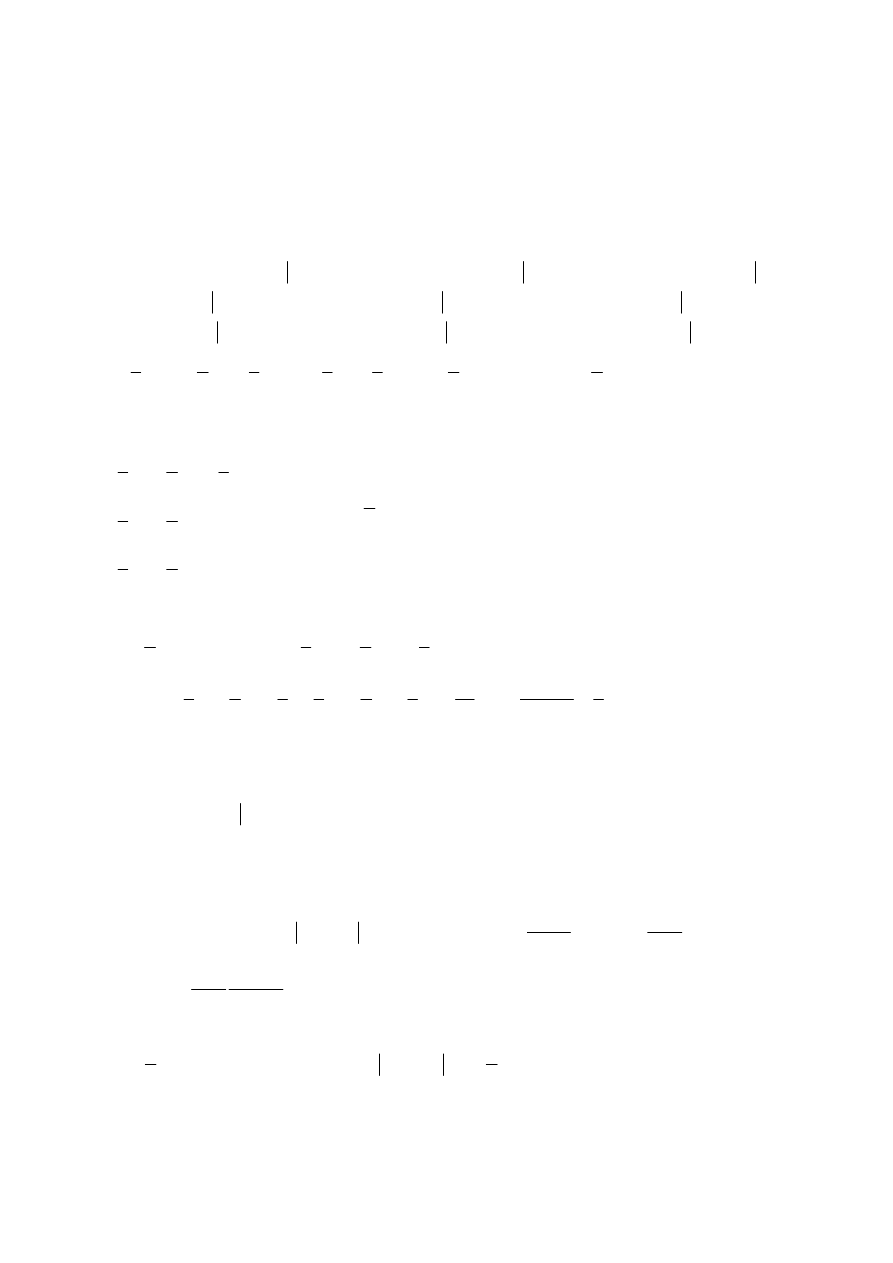
Egzamin dla Aktuariuszy z 9 października 2006 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
(
)
1
1
+
+
−
=
n
n
n
n
EX
EX
X
X
E
ODP
(
)
(
)
(
)
(
)
(
)
(
)
(
)
[
]
1
1
2
2
2
1
2
1
1
1
1
1
1
1
=
=
=
+
=
=
=
+
=
=
=
=
+
+
+
+
n
n
n
n
n
n
n
n
n
n
n
X
P
X
X
P
X
P
X
X
P
X
P
X
X
P
X
X
E
(
)
(
)
(
)
(
)
[
]
(
)
(
)
+
=
=
=
+
=
=
=
+
=
=
=
+
+
+
+
2
2
2
4
1
1
3
3
3
1
3
1
1
1
n
n
n
n
n
n
n
n
n
X
P
X
X
P
X
P
X
X
P
X
P
X
X
P
(
)
(
)
(
)
(
)
[
]
(
)
(
)
3
3
3
9
2
2
3
3
3
2
6
1
1
1
=
=
=
+
=
=
=
+
=
=
=
+
+
+
+
n
n
n
n
n
n
n
n
n
X
P
X
X
P
X
P
X
X
P
X
P
X
X
P
3
2
1
3
2
1
3
1
2
1
7
3
2
3
2
9
)
0
0
(
6
2
1
4
3
1
3
1
3
3
1
2
1
2
3
1
p
p
p
p
p
p
p
p
p
p
+
+
=
⋅
+
+
+
⋅
+
+
+
+
+
→
3
2
1
1
3
2
,
p
p
p
EX
EX
n
n
+
+
→
+
ROZKŁAD STACJONARNY:
=
=
→
=
+
=
+
=
+
+
1
3
1
2
3
3
1
2
2
1
1
3
2
1
3
2
3
2
3
1
2
1
3
1
3
1
2
1
3
1
p
p
p
p
p
p
p
p
p
p
p
p
p
p
1
3
2
1
=
+
+
p
p
p
8
3
,
4
1
,
8
3
1
3
2
3
2
1
1
1
1
=
=
=
→
=
+
+
p
p
p
p
p
p
125
,
0
8
1
8
32
33
4
8
33
8
3
3
4
1
2
8
3
8
3
7
4
1
3
8
3
2
2
=
=
−
=
−
=
⋅
+
⋅
+
−
⋅
+
⋅
+
⋅
=
ODP
Zadanie 2
(
)
∑
∞
=
=
=
=
1
)
(
k
N
N
k
N
P
k
N
M
E
EM
)
2
,
1
(
)
1
(
)
(
)
(max
∈
−
=
<
=
<
t
t
t
X
P
t
P
k
k
1
max
)
1
(
−
−
=
k
t
k
f
∫
∫
+
+
=
+
+
=
+
=
=
−
=
−
=
+
−
−
2
1
1
0
1
0
1
1
1
1
1
1
)
1
(
1
)
1
(
max
k
k
w
k
kw
dw
w
w
k
w
t
dt
t
kt
E
k
k
k
k
∑
∑
∞
=
∞
=
=
−
+
+
−
⋅
+
+
=
1
1
3
3
)
1
(
2
)
1
(
2
!
)!
2
(
1
k
k
k
k
N
p
p
k
k
p
p
k
k
k
k
EM
∑
∑
∞
=
∞
=
=
−
=
−
+
−
+
−
=
=
+
=
−
+
−
+
+
=
1
2
3
2
1
3
3
3
1
)
1
(
1
)
1
(
2
1
1
1
)
1
(
1
2
2
1
k
n
r
n
k
p
p
p
n
n
n
n
k
p
p
p
k
k
k
4
4
4
4
4
8
4
4
4
4
4
7
6
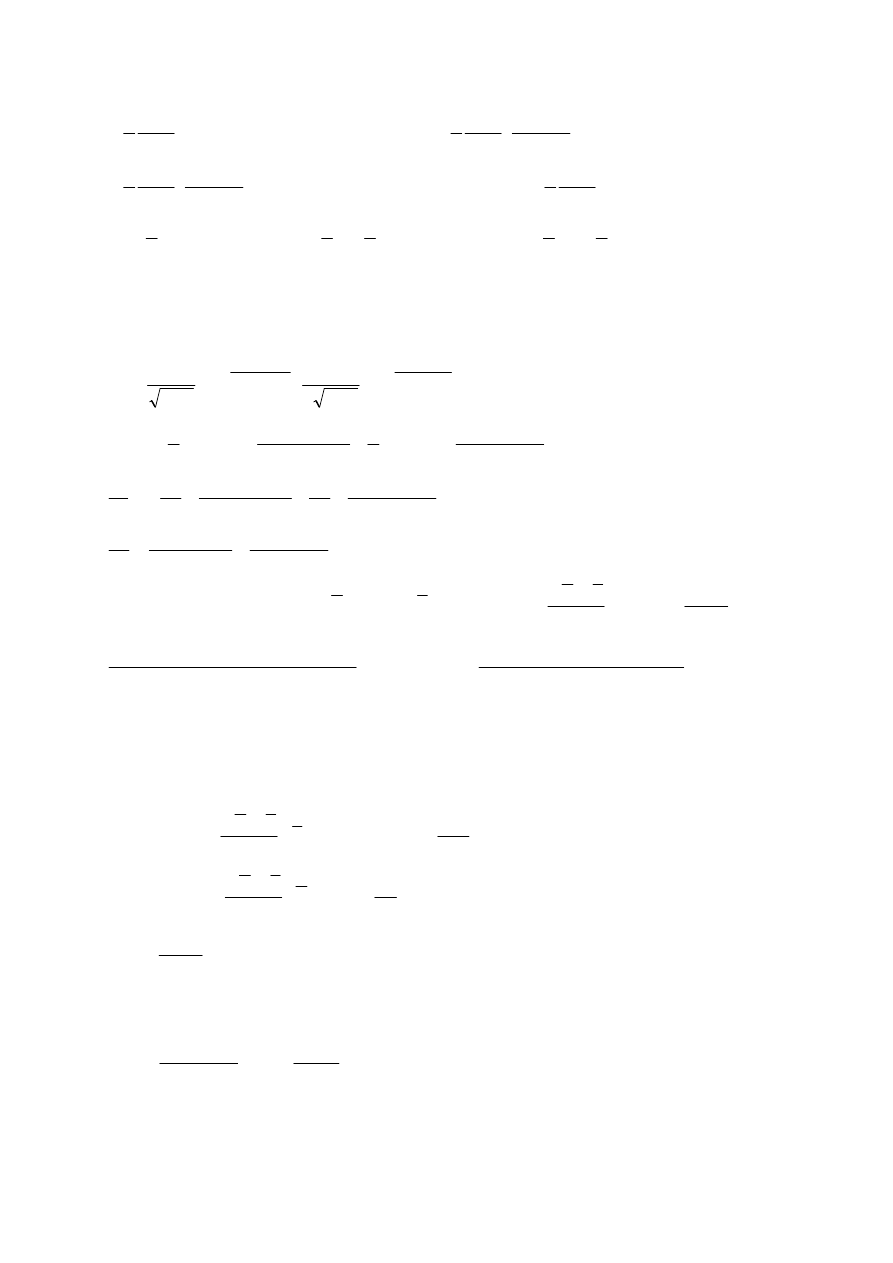
(
)
∑
∞
=
=
−
−
−
−
−
−
−
−
=
−
+
−
+
−
−
=
2
2
2
2
3
2
2
)
1
(
1
2
)
1
(
)
1
(
2
1
2
1
1
)
1
(
1
)
1
(
1
2
1
n
n
p
p
p
p
p
p
p
p
p
p
p
p
n
n
n
p
p
=
−
+
+
−
−
−
=
+
−
+
−
+
−
−
−
=
3
2
3
2
3
2
1
)
1
)(
1
(
1
2
1
1
2
2
1
2
2
)
1
(
2
1
2
1
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
2
1
2
1
2
1
2
1
2
1
1
1
)
1
(
2
1
1
2
3
3
2
3
−
−
−
=
−
+
−
−
=
−
+
+
−
=
Zadanie 3
2
: σ
x
=
(
)
(
)
x
µ
y
n
x
µ
X
n
i
i
e
x
e
x
L
8
2
2
2
2
2
1
2
1
∑
∑
−
−
−
−
Π
Π
=
(
)
(
)
x
µ
y
x
n
x
µ
X
x
n
L
i
i
8
)
8
ln(
2
2
)
2
ln(
2
ln
2
2
∑
∑
−
−
Π
−
−
−
Π
−
=
(
)
(
)
0
8
2
2
2
2
2
2
2
=
−
+
−
−
+
−
=
∂
∂
∑
∑
x
µ
y
x
n
x
µ
X
x
n
x
i
i
(
)
(
)
0
4
=
−
+
−
=
∂
∂
∑
∑
x
µ
y
x
µ
X
µ
i
i
(
)
(
)
∑
∑
≅
+
=
→
=
−
+
−
=
−
+
−
n
σ
µ
N
µ
Y
X
µ
µ
n
Y
n
µ
n
X
n
µ
y
µ
X
i
i
2
8
,
0
;
ˆ
,
5
4
ˆ
0
4
4
4
(
)
(
)
(
)
(
)
n
µ
y
µ
X
x
σ
x
nx
µ
X
µ
y
i
i
i
i
8
4
ˆ
ˆ
0
8
8
4
2
2
2
2
2
2
∑
∑
∑
∑
−
+
−
=
=
→
=
−
−
+
−
można pokazać, że to jest maximum
(
)
(
)
∑
∑
∑
∑
+
−
+
+
−
=
2
2
2
2
4
8
4
2
)
(
µ
nE
X
µ
E
X
E
µ
nE
y
µ
E
y
E
LICZ
E
i
i
i
i
(
)
∑
+
=
2
2
2
4
µ
σ
n
y
E
i
(
)
∑
+
=
2
2
2
µ
σ
n
X
E
i
(
)
2
2
2
2
2
8
,
0
4
2
,
0
8
,
0
5
4
σ
µ
n
µ
n
σ
n
µ
n
Y
n
Y
X
E
y
µ
E
i
+
=
+
+
=
+
=
∑
(
)
2
2
2
2
2
8
,
0
2
,
0
8
,
0
5
4
σ
µ
n
µ
n
µ
n
σ
n
X
n
Y
X
E
X
µ
E
i
+
=
+
+
=
+
=
∑
2
2
2
8
,
0
µ
n
σ
µ
E
+
=
(
)
(
)
=
+
+
+
−
+
+
+
+
+
−
+
=
2
2
2
2
2
2
2
2
2
2
2
2
4
2
,
3
8
,
0
8
4
4
8
,
0
8
,
0
2
4
)
(
µ
n
σ
σ
µ
n
µ
n
σ
n
µ
n
σ
σ
µ
n
µ
n
σ
n
LICZ
E
(
)
(
)
)
4
8
(
4
8
4
2
2
,
3
4
,
6
4
8
,
0
6
,
1
4
2
2
2
−
=
+
−
+
+
−
+
+
−
+
+
−
=
n
σ
n
n
n
n
n
n
µ
n
n
σ
4
8
8
8
)
4
8
(
ˆ
2
2
−
=
→
−
=
n
n
a
n
n
σ
σ
E
Zadanie 4
a – liczba białych
76-a – czarne
max
10
76
4
76
6
)
6
(
→
−
=
a
a
b
P
sprawdzamy i wychodzi max dla a=46
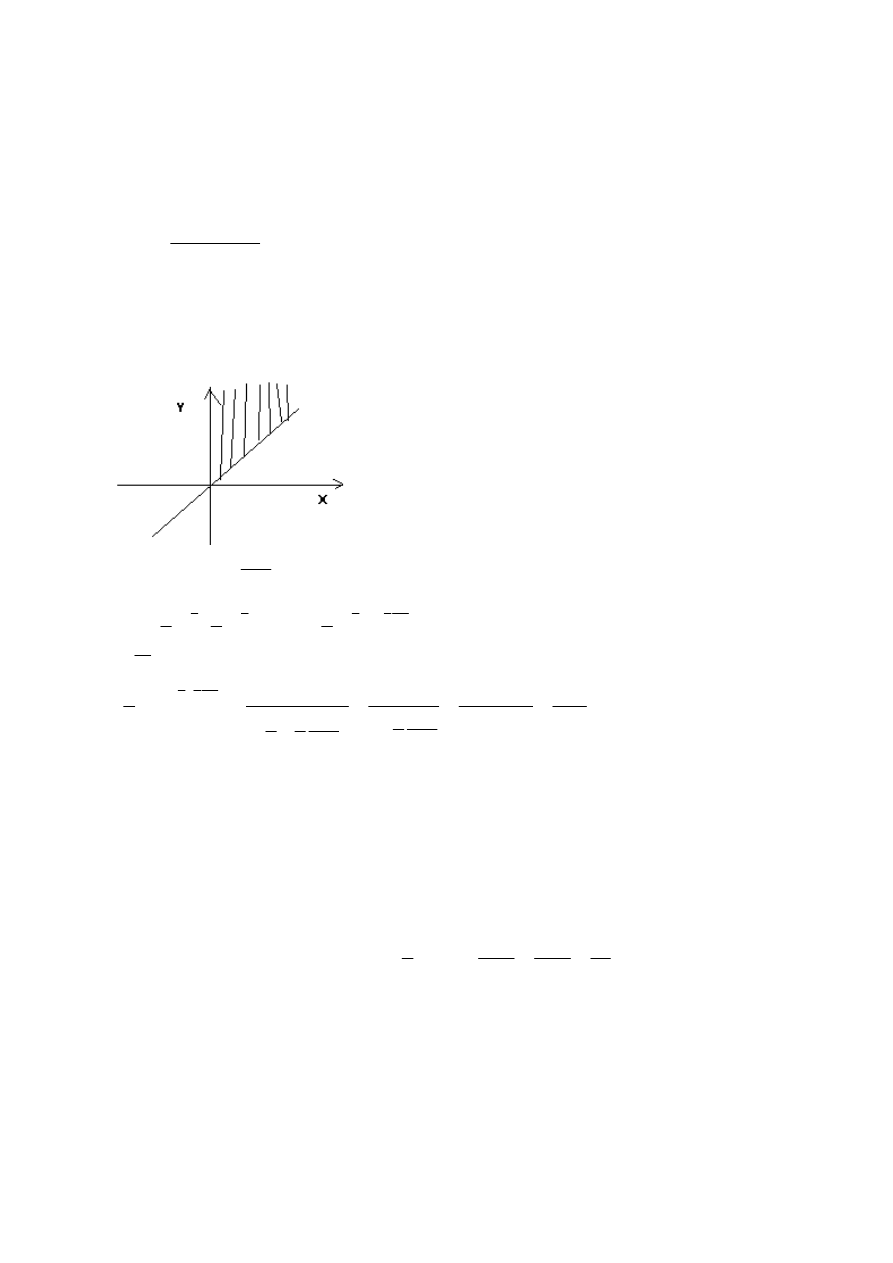
Zadanie 5
)
1
,
0
(
1
)
(
∈
−
>
=
<
t
X
t
t
Y
P
t
Z
P
∫
∫
∫
∞
∞
−
−
−
∞
−
−
−
=
=
=
0
0
1
6
1
4
1
1
4
1
6
1
4
1
4
1
6
1
dx
e
e
dydx
e
e
x
t
t
x
x
t
t
x
y
5
,
0
2
3
2
2
3
3
1
3
2
1
1
1
6
1
4
1
4
1
4
1
0
1
6
1
4
1
=
+
=
−
+
=
−
+
=
−
+
=
=
∫
∞
−
+
−
t
t
t
t
t
t
t
t
t
e
t
t
x
6t=t+2
5t=2
t=0,4 czyli odpowiedź C prawidłowa
Zadanie 6
Przy założeniu symetrii F(0)=0,5
(
)
=
=
−
=
<
>
)
7
,
6
,
5
,
4
,
3
(
1
3
lub
7
0
K
P
K
K
P
64
7
1024
112
1024
912
1
2
1
7
10
6
10
5
10
4
10
3
10
1
10
=
=
−
=
+
+
+
+
−
=
Zadanie 7
(
)
2
10
10
;
10
σ
m
N
S
≅
(
)
2
25
25
;
25
σ
m
N
S
≅
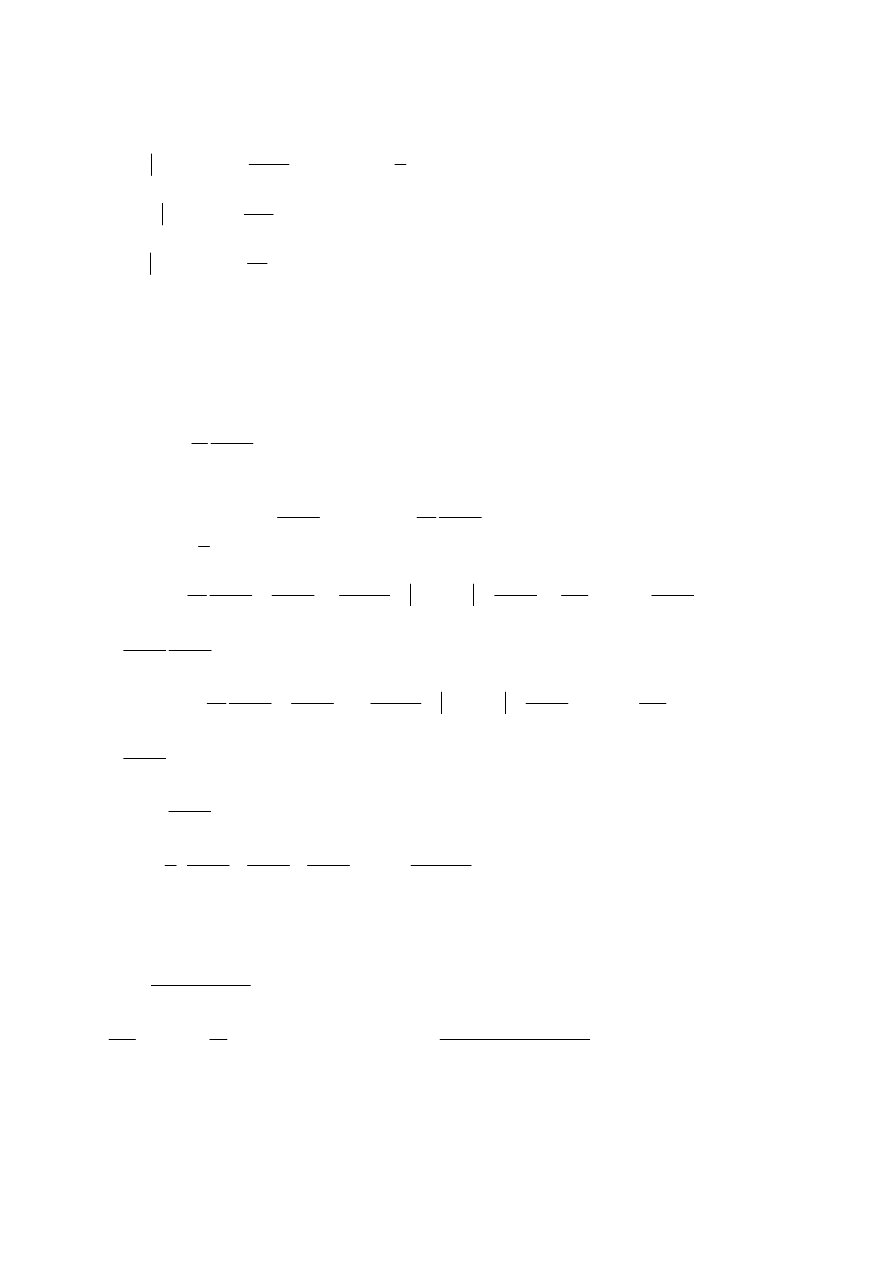
(
)
(
)
2
25
:
11
10
10
25
10
10
;
cov
;
cov
σ
S
S
S
S
S
=
+
=
(
)
(
)
25
25
2
2
25
10
5
2
25
25
10
10
S
m
S
σ
σ
m
S
S
E
=
−
+
=
(
)
2
2
25
10
6
10
250
100
1
var
σ
σ
S
S
=
−
=
(
)
2
25
2
2
25
2
25
2
10
16
,
0
6
25
4
6
S
σ
S
σ
S
S
E
+
=
+
=
Zadanie 8
Można zauważyć, że
λˆ
jest równa średniej z tych które co najmniej 2 są równe
K – wynik dla
P(K=i) – warunkowe bo 0 niezauważalne
1
1
!
)
(
−
=
=
λ
i
e
i
λ
i
K
P
UCIĘTY POISSON
do średniej można zdefiniować X taką , że
1
1
!
)
(
,
1
)
1
(
)
0
(
−
=
=
−
=
=
+
=
λ
k
λ
e
k
λ
k
X
P
e
λ
K
P
X
P
dla k>=2
i wtedy
X
λ
=
ˆ
(
)
∑
∑
∑
∞
=
∞
=
∞
=
−
−
=
−
−
=
−
=
=
−
=
−
−
=
−
=
2
2
1
1
1
!
1
1
1
)!
1
(
1
1
1
1
!
k
k
n
λ
λ
λ
λ
λ
n
λ
k
λ
λ
k
e
e
λ
e
e
e
n
λ
λ
e
n
k
k
λ
e
e
k
λ
k
EX
λ
e
e
e
λ
e
λ
λ
λ
λ
=
−
−
=
1
1
∑
∑
∑
∞
=
∞
=
∞
=
−
=
+
−
=
=
−
=
−
−
=
−
=
2
2
1
2
2
!
)
1
(
1
1
1
)!
1
(
1
1
1
1
!
k
k
n
λ
λ
n
λ
k
λ
λ
k
e
e
n
λ
λ
n
e
n
k
k
λ
k
e
e
k
λ
k
EX
[
]
λ
λ
λ
e
λ
e
λ
e
−
−
+
−
=
1
1
(
)
2
1
1
var
λ
e
λ
e
λ
e
K
λ
λ
λ
−
−
+
−
=
−
( )
[
]
2
2
2
1
1
1
1
1
1
λ
λ
λ
e
e
n
λ
e
λ
e
λ
e
e
λ
e
n
ODP
λ
λ
λ
λ
λ
λ
λ
+
−
−
=
−
−
−
−
+
−
=
Zadanie 9
(
)
(
)
(
)
∑
+
+
−
+
=
+
Π
=
+
i
θ
θ
i
θ
θ
X
θ
θ
θ
L
X
θ
L
2
ln
1
ln
4
2
ln
4
ln
,
2
2
1
1
1
1
4
1
4
1
1
1
1
(
)
(
)
∑
∑
+
−
−
=
→
=
+
−
+
=
∂
∂
i
i
X
θ
X
θ
θ
2
ln
2
ln
4
4
ˆ
0
2
ln
4
2
ln
4
1
1
1
to max (można
sprawdzić)
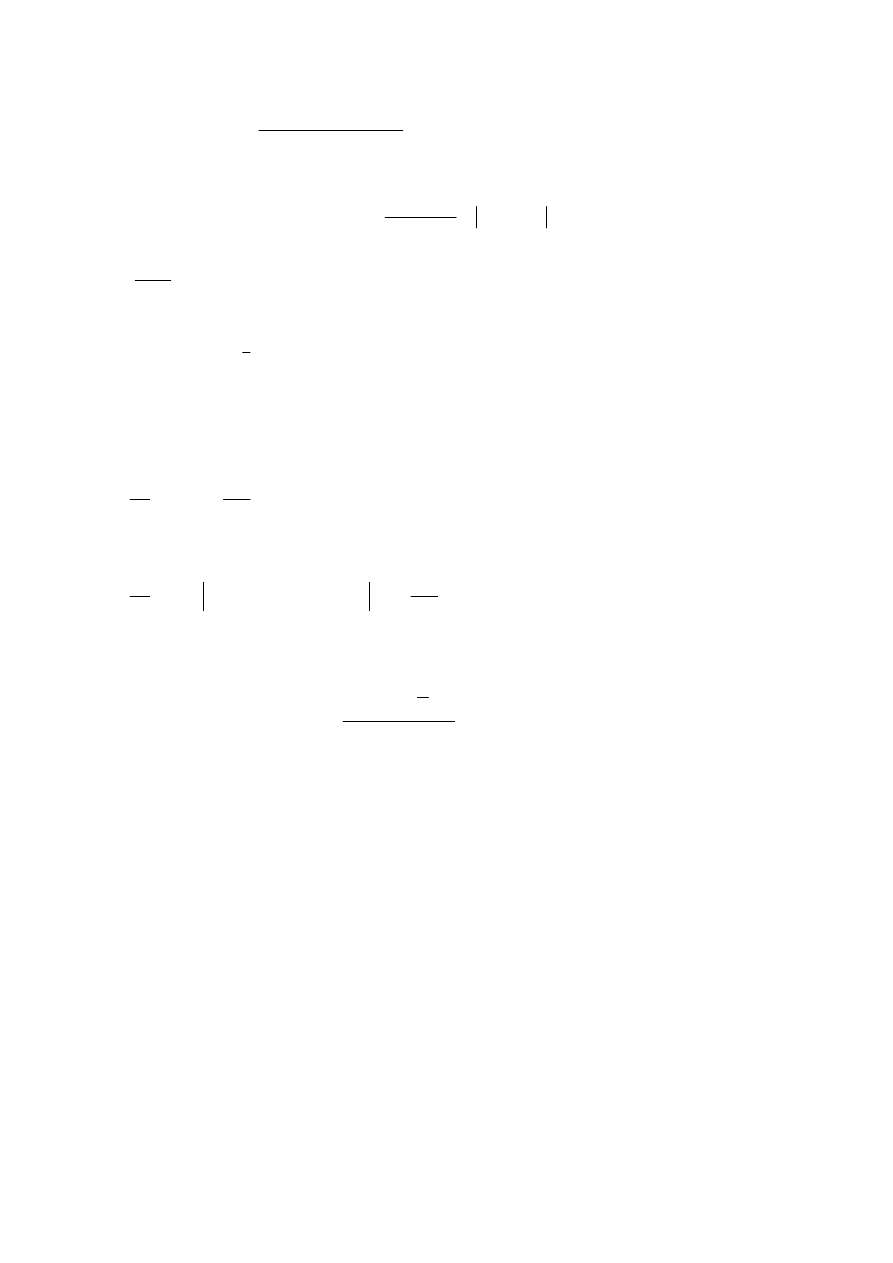
analogicznie:
(
)
∑
+
−
−
=
i
y
θ
2
ln
2
ln
5
5
ˆ
2
założenie:
θ
θ
θ
=
=
2
1
(
)
(
)
∫
−
+
=
=
+
=
+
=
−
<
=
<
+
2
0
1
2
)
2
(
2
2
)
2
ln(
t
e
θ
θ
t
w
x
x
θ
e
X
P
t
X
P
∫
−
+
−
=
=
t
e
θ
t
θ
θ
θ
e
w
θ
2
1
2
1
2
)
2
(ln
.
2
)
2
ln(
WYKL
PRZESUN
e
θ
f
θ
t
θ
x
≅
=
−
+
bo:
θ
t
θ
θ
t
e
θ
e
θ
−
−
−
=
2
)
2
ln
(
∫
≅
−
=
=
<
−
−
≅
θ
t
t
x
θ
θ
wykl
X
wykl
e
e
θ
t
X
θ
P
0
)
(
)
1
(
1
)
(
∑
∑
Γ
≅
+
Γ
≅
+
5ln2
o
y
przesuniet
)
1
,
5
(
)
2
ln(
4ln2
o
y
przesuniet
)
1
,
4
(
)
2
ln(
y
θ
X
θ
→
(
)
∑
∑
Γ
≅
−
+
Γ
≅
−
+
)
1
,
4
(
2
ln
4
2
ln
)
1
,
5
(
2
ln
5
)
2
ln(
θ
X
θ
θ
y
θ
i
i
)
1
,
4
(
),
1
,
5
(
5
4
ˆ
ˆ
2
1
Γ
≅
Γ
≅
>
=
>
Y
X
t
Y
X
P
t
θ
θ
P
(
)
→
<
=
<
Γ
≅
t
χ
P
t
X
P
X
)
8
(
)
2
(
2
)
1
,
4
(
(
)
347
,
3
05
,
0
)
8
,
10
(
5
4
)
8
(
),
10
(
ˆ
ˆ
2
2
2
1
≈
→
=
>
=
>
=
≅
≅
=
>
t
t
F
P
t
Y
X
P
χ
Y
χ
X
t
θ
θ
P
Zadanie 10
Wiemy z zestawu 6.12.2003, że
(
)
)
11
(
2
2
2
χ
σ
X
X
i
w
i
≅
−
∑
(
) (
)
05
,
0
)
11
(
ˆ
2
2
1
2
=
<
=
<
χ
a
P
σ
σ
P
(
)
→
=
>
05
,
0
)
11
(
2
χ
b
P
odpowiedź C jest prawidłowa
Wyszukiwarka
Podobne podstrony:
2006.10.09 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
1998 10 03 prawdopodobie stwo i statystykaid 18585
2000 12 09 prawdopodobie stwo i statystykaid 21582
2002 10 12 prawdopodobie stwo i statystykaid 21648
1996 10 26 prawdopodobie stwo i statystykaid 18572
2010.10.04 prawdopodobie stwo i statystyka
2001.10.13 prawdopodobie stwo i statystyka
2008.10.06 prawdopodobie stwo i statystyka
2007.10.08 prawdopodobie stwo i statystyka
2004.10.11 prawdopodobie stwo i statystyka
2009.10.05 prawdopodobie stwo i statystyka
1999 10 23 prawdopodobie stwo i statystykaid 18598
2006 06 05 prawdopodobie stwo i statystykaid 25461
2009 10 05 prawdopodobie stwo i statystykaid 26670
2000.10.14 prawdopodobie stwo i statystyka
2000.12.09 prawdopodobie stwo i statystyka
1996.10.26 prawdopodobie stwo i statystyka
2003.10.11 prawdopodobie stwo i statystyka
więcej podobnych podstron