1

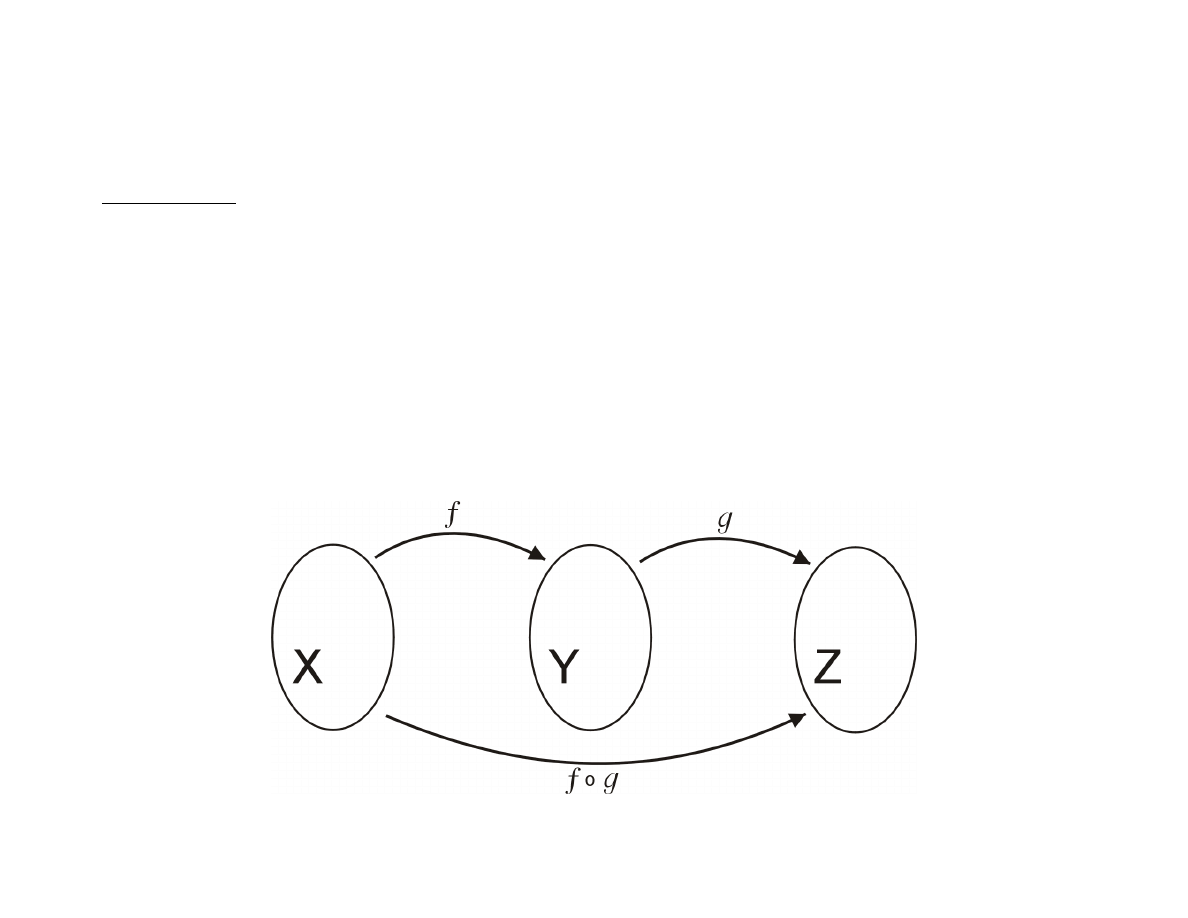
Złożenie funkcji

Definicja

Załóżmy, że

f : X → Y

,

g : Y → Z

są funkcjami.

Złożeniem funkcji

f

i

g

nazywamy funkcję

h : X → Z

daną

wzorem

h(x) = g(f (x))

.

Złożenie

f

i

g

oznaczamy symbolem

f ◦ g

(

h = f ◦ g

),

funkcję

f

nazywamy funkcją wewnętrzną, a funkcję

g

- funkcją

zewnętrzną.

2

Uwaga

•

Złożenie dwóch funkcji rosnących jest funkcją rosnącą.

•

Złożenie dwóch funkcji malejących jest funkcją rosnącą.

• Złożenie funkcji rosnącej i funkcji malejącej jest funkcją malejącą.

Przykład

Określmy funkcje złożone

f ◦ f

,

f ◦ g

,

g ◦ f

,

g ◦ g

, jeżeli

f (x) = x

2 i

g(x) =

√

x

.

3

Funkcja odwrotna

Definicja

Funkcję

f : X → Y

nazywamy funkcją różnowartościową

(injekcją), jeżeli

∀

x

1

,x

2

∈X

( x

1

6= x

2

)

=⇒

f (x

1

) 6= f (x

2

)

!

.

Funkcją różnowartościową będziemy oznaczać:

f : X

1−1

−→ Y

.

Definicja

Funkcję

f : X → Y

nazywamy funkcją ”na”

(surjekcją), jeżeli

W

f

= Y

, tzn.

∀

y∈Y

∃

x∈X

y = f (x).

Funkcją ”na” będziemy oznaczać:

f : X

na

−→ Y

.

4

Definicja

Funkcję, która jest jednocześnie ”1-1” i ”na” nazywamy

funkcją

wzajemnie

jednoznaczną

(bijekcją)

i

oznaczamy

f : X

1−1

−→

na

Y

.

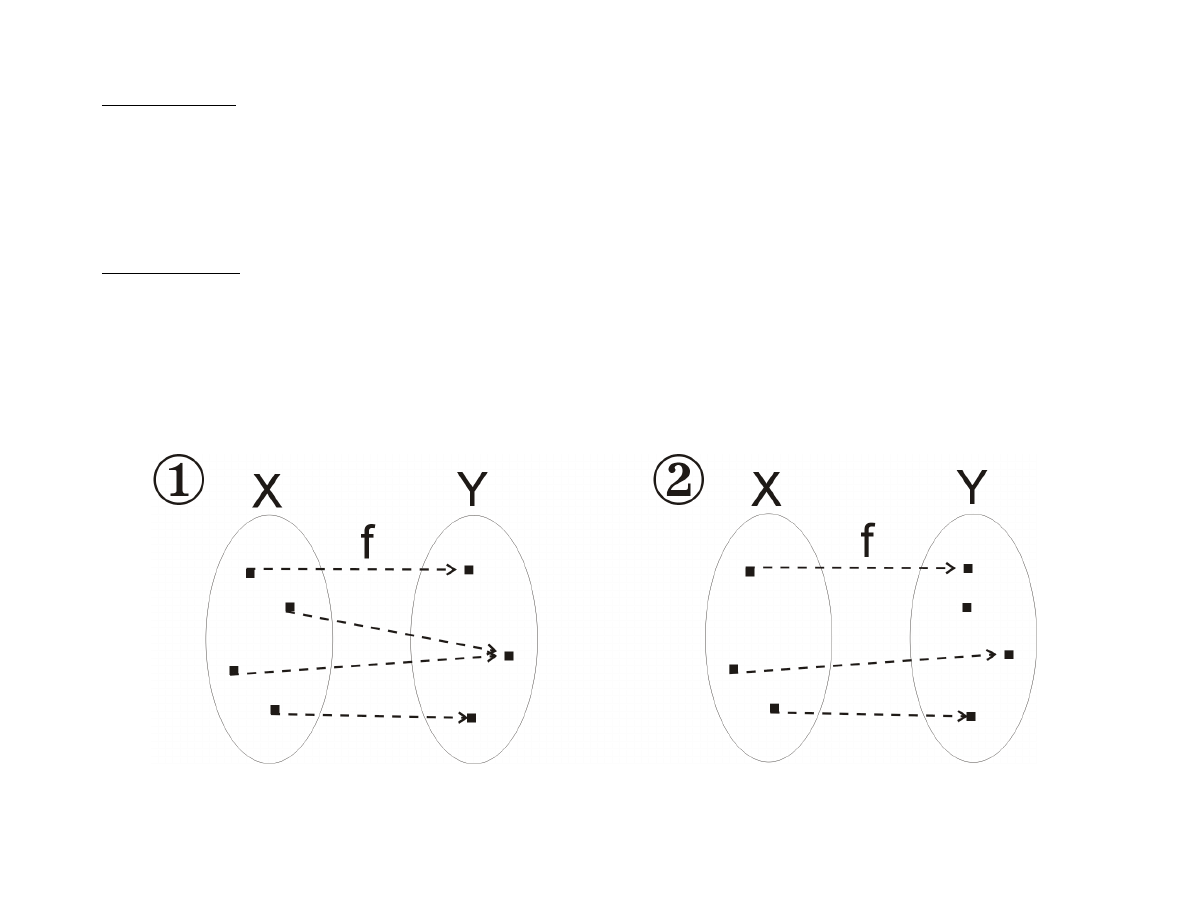
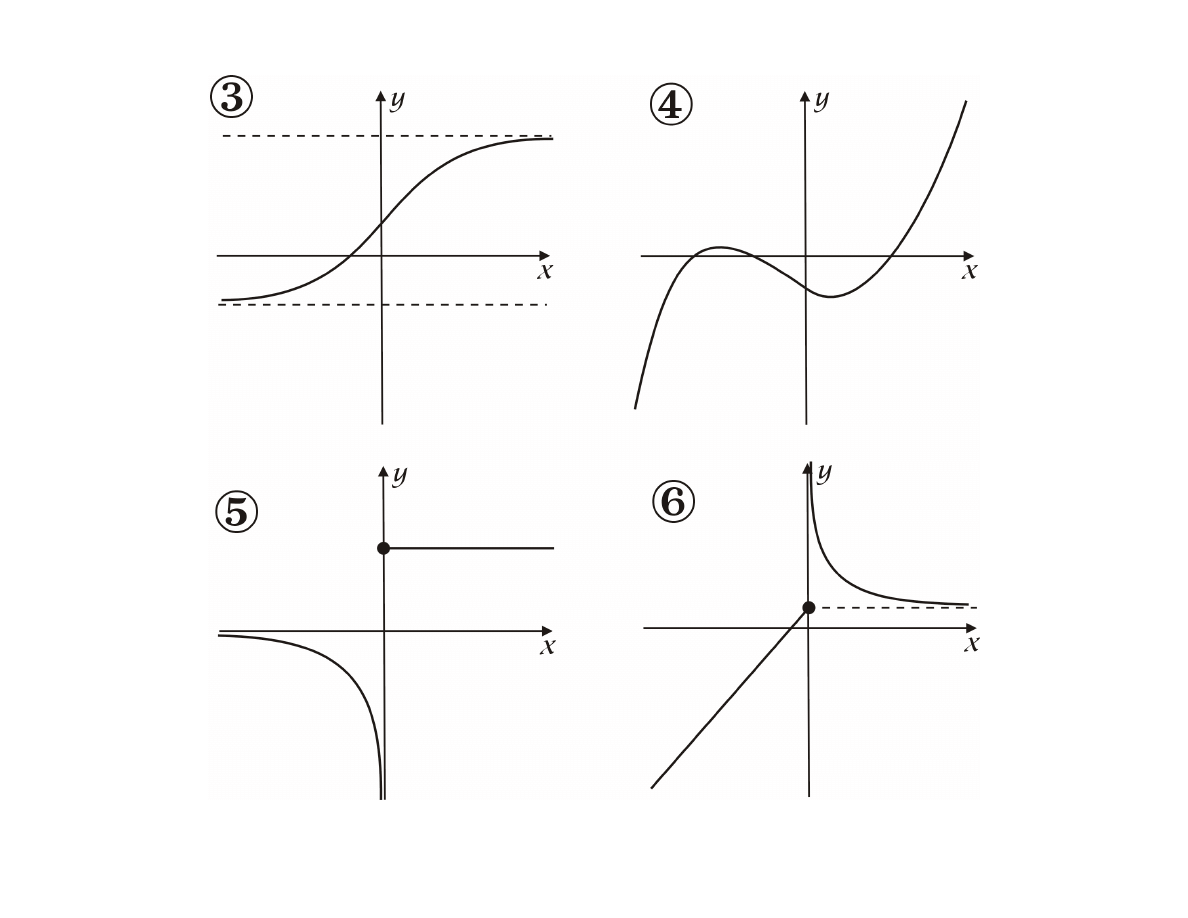
Przykład

Czy funkcje zilustrowane grafami lub wykresami są

różnowartościowe i ”na” ?

5

6

Uwaga

• Złożenie dwóch funkcji różnowartościowych jest funkcją różnowartościową.

•

Funkcja ściśle monotoniczna jest funkcją różnowartościową.

Przykład

Sprawdźmy, czy funkcja

f (x) =

2x − 3

x + 1

jest różnowartościowa w swojej dziedzinie.

7

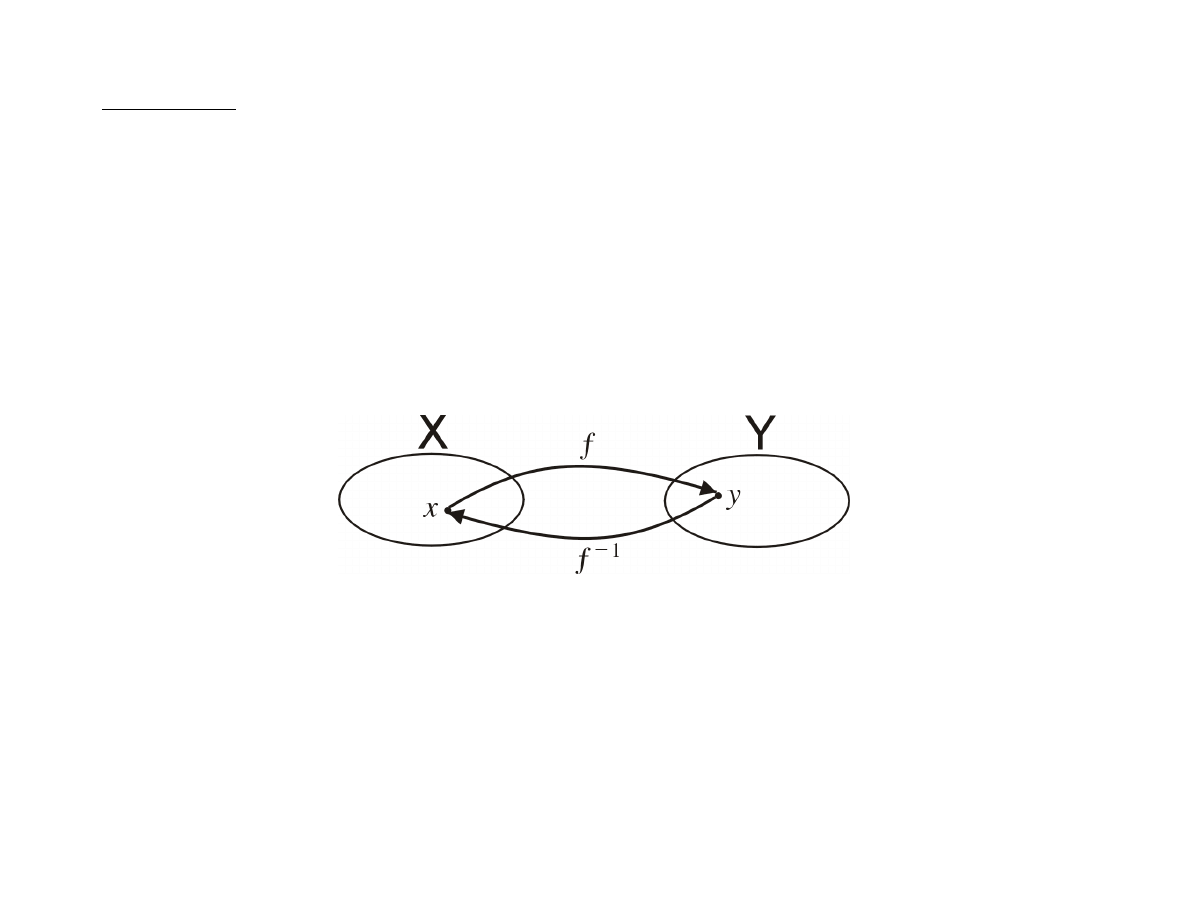
Definicja

Niech

f : X → Y

będzie funkcja wzajemnie jednoznaczną.

Funkcję

f

−1

: Y → X

nazywamy funkcją odwrotną do funkcji

f

,

jeżeli dla każdego

x ∈ X

i

y ∈ Y

f

−1

(y) = x

⇐⇒

y = f (x).

f ◦ f

−1

= Id

X

(f ◦ f

−1

)(x) = f

−1

(f (x)) = f

−1

(y) = x

f

−1

◦ f = Id

Y

(f

−1

◦ f )(y) = f (f

−1

(y)) = f (x) = y

8

Uwaga

Wykres funkcji odwrotnej otrzymujemy z wykresu funkcji

danej, odbijając go symetrycznie względem prostej

y = x

.

Przykład

Wyznaczmy funkcję odwrotną do funkcji:

•

y = x

3

x ∈ R

•

y = x

2

− x

x ∈ [1, +∞)

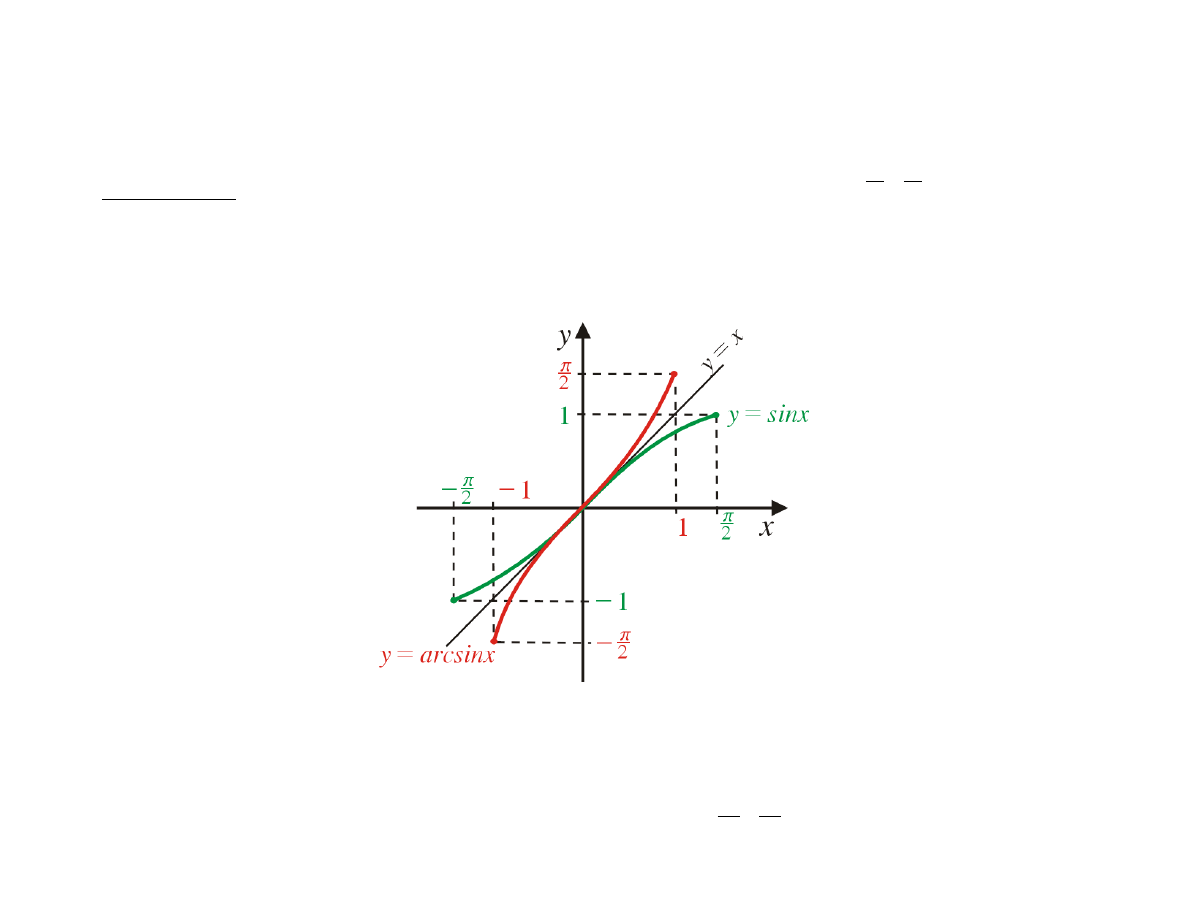
9

Funkcje cyklometryczne

Definicja

Funkcję odwrotną do funkcji

f :

"

−

π

2

,

π

2

#

→ [−1, 1]

danej wzorem

f (x) = sin x

nazywamy funkcją arcsin (czyt. arkus

sinus).

arcsin : [−1, 1] →






−

π

2

,

π

2






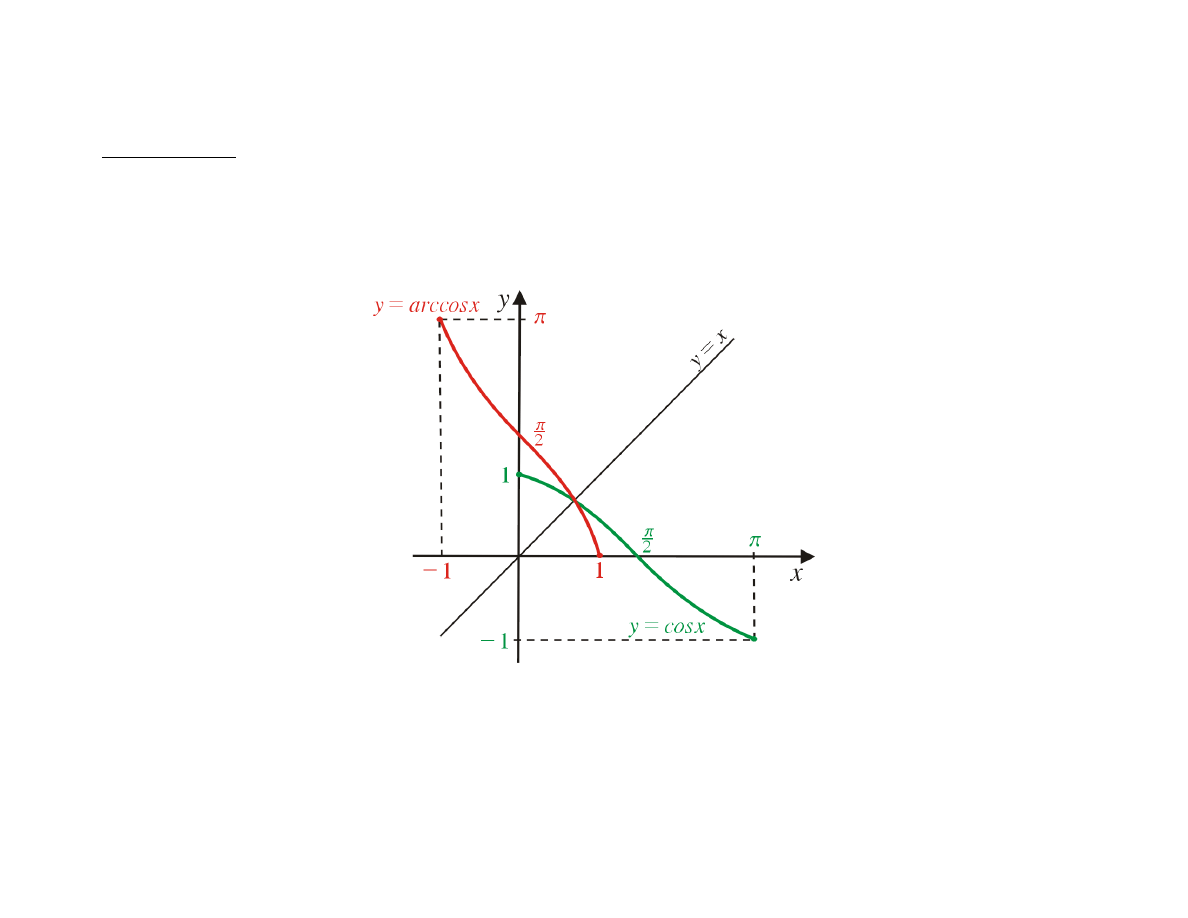
10

Definicja

Funkcję odwrotną do funkcji

f : [0, π] → [−1, 1]

danej wzorem

f (x) = cos x

nazywamy funkcją arccos (czyt. arkus

cosinus).

arccos : [−1, 1] → [0, π]

11

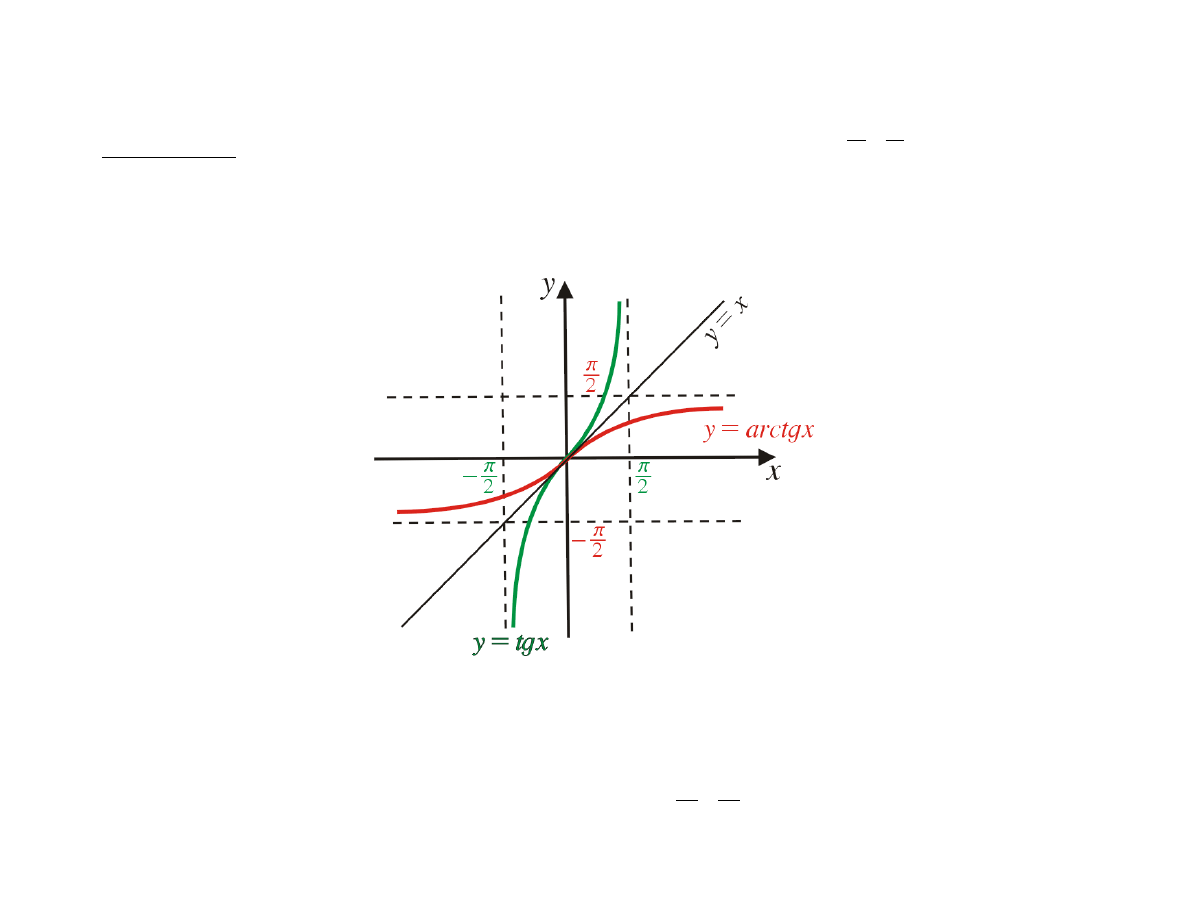
Definicja

Funkcję odwrotną do funkcji

f :

−

π

2

,

π

2

!

→ R

danej

wzorem

f (x) = tg x

nazywamy funkcją arctg (czyt. arkus tangens).

arctg : R →






−

π

2

,

π

2






12

Ćwiczenie

Napisz definicję funkcji arcctg (czyt. arkus kotangens),

jako funkcji odwrotnej do funkcji

f : [0, π] → R

danej wzorem

f (x) = ctg x

.

Przykład

Oblicz:

• arcsin (−

1
2

)

• arccos

√

2

2

• arctg (−

√

3)

13

Podstawowe związki między funkcjami cyklometrycznymi

Dla każdego

x ∈ [−1, 1]

zachodzi:

arcsin x = − arcsin (−x) =

π

2

− arccos x

Dla każdego

x ∈ R

zachodzi:

arctg x = − arctg (−x) =

π

2

− arcctg x

14

Funkcje elementarne

Definicja

Podstawową funkcją elementarną nazywamy funkcję

stałą, potęgową, wykładniczą, logarytmiczną, trygonometryczną lub

cyklometryczną. Funkcję, którą można otrzymać z podstawowych

funkcji elementarnych za pomocą skończonej liczby działań arytmetycznych

oraz operacji złożenia funkcji, nazywamy funkcją elementarną.

Przykład

Następujące funkcje są funkcjami elementarnymi:

• f (x) = a

n

x

n

+ a

n−1

x

n−1

+ . . . + a

2

x

2

+ a

1

x + a

0

• f (x) =

a

n

x

n

+ a

n−1

x

n−1

+ ... + a

2

x

2

+ a

1

x + a

0

b

m

x

m

+ b

m−1

x

m−1

+ ... + b

2

x

2

+ b

1

x + b

0

• f (x) =

3

√

3x

2

+ 1,

f (x) = log

2

(x + 3),

f (x) = sin(arctg x + 1)

• sh x =

e

x

−e

−x

2

,

ch x =

e

x

+e

−x

2

Przykład

Uzasadnić, że funkcja

f : R → [0, +∞]

dana wzorem

15

f (x) = |x|

jest funkcją elementarną.

Przykład

Przykłady funkcji nieelementarnych:

• Funkcja ”signum”:

sgn x =







































































1

x > 0

0

x = 0

−1

x < 0

• Funkcja ”część całkowita”:

z(x) = k

jeżeli

x ∈ [k, k + 1),

k ∈ Z

• Funkcja Dirichleta:

D(x) =











































1

x ∈ Q

0

x ∈ R r Q