POLITECHNIKA ŚLĄSKA

GLIWICE

WYDZIAŁ MECHANICZNY TECHNOLOGICZNY

Katedra Budowy Maszyn

MODELOWANIE UKŁADÓW MECHANICZNYCH

Krzysztof Pisarski

AiR_AB4_2012/2013

Semestr III zaoczny

Systemy mechaniczne są na ogół budowane ze sztywnych elementów,

połączonych za pomocą par kinematycznych, które zapewniają odpowiednią

ruchliwość mechanizmów tworzących system i w konsekwencji jego skoordynowane

działanie. Ze względu na "ziarnistą" strukturę, takie systemy są najczęściej

odzwierciedlane przez modele fizyczne o

parametrach rozłożonych w przestrzeni, w

postaci układu ciał materialnych, poddanych działaniu więzów i sił zewnętrznych.

Sposobów wyznaczania równań równowagi dynamicznej badanych układów

jest przynajmniej kilka. Centralnym zagadnieniem

wyprowadzenia równań ruchu

dla danego

modelu układu fizycznego, jak już wcześniej podano, jest sformułowanie

zależności wyrażających równowagę sił, wydatków przepływów lub zmian energii dla

badanego układu, albo napisanie równań spójności opisujących zależności

występujące między ruchami elementów, ze względu na sposób ich połączenia.

Przy układaniu równań ruchu należy rozważyć niezależnie:

-

zmienne przepływu i spadku;

-

równania równowagi lub spójności;

- zale

żności fizyczne dla każdego elementu;

- przedstawi

ć te zależności w postaci równań

Przedstawiona procedura dla układów mechanicznych obejmuje:

- zale

żności geometryczne;

-

równowagę sił;

- zwi

ązki między geometrią układu i siłami.

W przypadku prostych

układów o niewielkiej liczbie stopni swobody można

przy

układaniu równań ruchu wykorzystać wprost II prawo Newtona lub zasadę

d’Alemberta (metoda sił). Dla układów złożonych o większej liczbie stopni swobody

wygodnie jest zastosowa

ć równania Lagrange’a II rodzaju (metoda energetyczna)

wyprowadzane w mechanice analitycznej.

Założenia przyjmowane przy układaniu równań ruchu:

- rozwa

żane układy mają więzy holonomiczne, czyli więzy niezależne od pochodnych

współrzędnych uogólnionych (prędkości uogólnionych);

- model obliczeniowy rozwa

żanego układu rzeczywistego jest modelem dyskretnym,

jego

położenie opisuje skończona liczba współrzędnych uogólnionych;

-

do zdefiniowania sił uogólnionych wykorzystuje się zasadę prac przygotowanych.

Zasady i etapy modelowania

W procesie opisu systemu wykorzystuje się kolejno kilka rodzajów modeli.

a)

lingwistyczne (opis słowny),

b) graficzne (np. schemat obwodu, wykresy charakterystyk),

c) matematyczne.

Ostatecznym celem jest model matematyczny. Ten możemy uzyskać poprzez

wykorzystanie podstawowych praw/zasad techniki (np. Ohma, Newtona, Hooka,

zachowania energii) do opisu systemu (modelowanie fizykalne) lub przez zapis

matematyczny funkcji systemu bez analizy na poziomie fizycznym (modelowanie

funkcjonalne).

Proces tw

orzenia modelu przebiega następująco:

1) analiza budowy elementu

2) o

bserwacja zachowania się elementu

3) z

astosowanie praw/zasad do określenia postaci modelu fizykalnego i wartości

jego parametrów (patrz przykład filtra) lub oddanie funkcji wykonywanej przez

element w modelu funkcjonalnym (przykład oczu ludzkich)

4) i

dentyfikacja brakujących elementów modelu (np. wyznaczenie stałej czasowej )

5) w

eryfikacja utworzonego modelu przez porównanie jego odpowiedzi z

odpowiedzią elementu

Modelowanie w diagnostyce maszyn

Poznanie stanu dynamicznego obiektu wymaga w ujęciu eksperymentalnym

jednoznacznego skojarzenia cech stanu obiektu ze zbiorem miar i ocen

generowanych

procesów

wyjściowych

-

czyli

symptomów.

Algorytmy

przyporządkowujące sobie oba zbiory cech - konstrukcji i symptomów - są podstawą

tworzenia modeli obiektów.

W ogóle modele stosowane w badaniach mogą być: symptomowe i

holistyczne.

Modele symptomowe opisuj

ą stan techniczny obiektu w kategoriach obserwowanych

symptomów, nie zawierających czasu dynamicznego "t" lecz tylko czas życia "q".

Natomiast

modele holistyczne ujmuj

ą dynamikę systemu i jego procesy zużyciowe łącznie.

W technice mo

żna wyróżnić następujące cele tworzenia modeli:

- dla potrzeb projektowania

, gdzie model służy do optymalizacji struktury i

parametrów konstruowanego obiektu i jest narzędziem oceny "jakości" konstrukcji,

eliminacji słabych ogniw, projektowania układów nadzoru, (modele funkcjonalne i

niezawodno

ściowe);

- dla potrzeb diagnozowania, gdzie model jest podstaw

ą ustalenia algorytmu

diagnozowania, który prowadzi do określenia stanu aktualnego i przyszłego obiektu;

- dla potrzeb u

żytkowania i sterowania, wykorzystujących model do podejmowania

decyzji

z działającym obiektem (zakres działać obsługowych, decyzje

eksploatacyjne).

Aktualny

stan

dynamiczny

maszyny

mo

żna określać obserwując

funkcjonowanie obiektu, tzn. jego wyj

ście główne przekształconej energii (lub

produktu), oraz wyj

ście dyssypacyjne - gdzie obserwuje się procesy resztkowe, np.

termiczne, wibracyjne, akustyczne, elektromagnetyczne.

Zale

żnie od modelu można to zobrazować odpowiednio – dla modelu

symptomowego i holistycznego w uj

ęciu mechanicznym, jak na rysunku poniżej.

W przypadku modelu tradycyjnego (rys.1) stan obiektu jest definiowany w

kategoriach symptomowych, jako

ści i bezpieczeństwa, poprzez wektor miar

bezpo

średnich lub pośrednich. Obserwacja tych wyjść daje całą gamę możliwości

diagnozowania stanu poprzez: obserwacj

ę procesów roboczych, badania jakości

wytworów lub obserwację procesów resztkowych.

Modelowanie symptomowe

Najbardziej ogólny model obiektu dla potrzeb oceny stanu w ujęciu

symptomowym przedstawiono na rys.1. Stan obiektu mo

żna tu określać obserwując

funkcjonowanie obiektu, tzn. jego wyj

ście główne przekształconej energii (lub

produktu) oraz wyj

ście dyssypacyjne, gdzie obserwujemy różnego typu procesy

resztkowe (termiczne, wibracyjne, akustyczne, elektromagnetyczne).

Przedstawiony model obiektu

opisuje równanie wektorowe :

G ( X, S, E, Z, N ) = 0

Interesuj

ący nas stan obiektu można więc określić z zależności :

X = g ( S, Z, E, N )

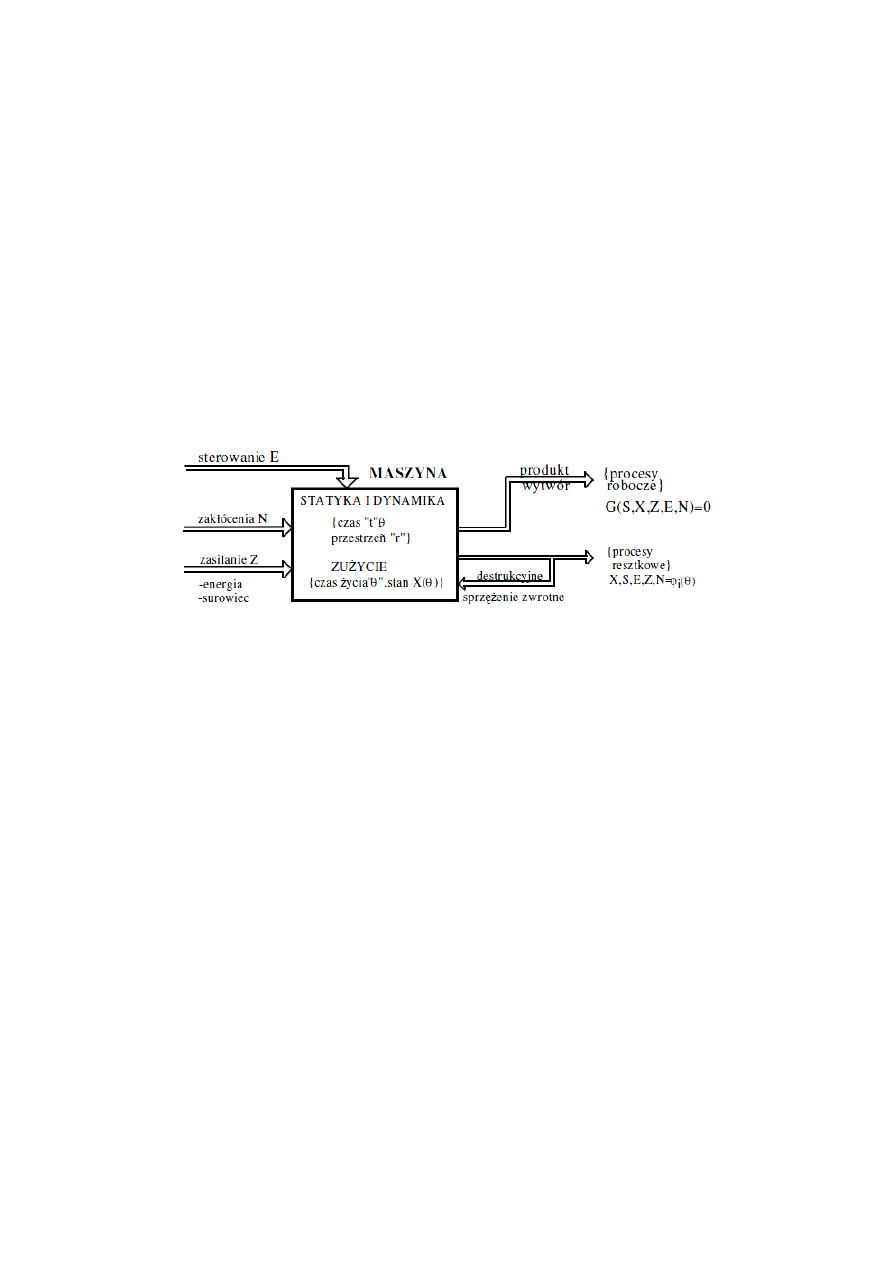
Realizacja eksperymentalna powy

ższej zależności jest możliwa po przyjęciu

uproszcze

ń, zakładających stałość w sensie wartości średnich wektorów E, Z = 0, a

wynikaj

ących z przyjętego modelu obiektu. Mamy zatem :

X = F ( S )

Z,E

=

const

+ N

Uwzgl

ędniając dziedziny określoności poszczególnych wektorów tej relacji,

otrzymujemy podstawowe równanie stanu w postaci :

X (t,q,r) = A (r) S (q, r) + N (q,r)

Wektorowy opis struktury obiektu, jego wej

ść: zasilania, sterowania i zakłóceń oraz

wyj

ść energetycznych (użytecznych i resztkowych) prowadzi bezpośrednio do opisu

mo

żliwych relacji diagnostycznych.

Rys.1. Model obiektu diagnostyki

OGÓLNY MODEL SERWOMECHANIZMU ELEKTROHYDRAULICZNEGO

Uproszczony

model

serwomechanizmu

elektrohydraulicznego

przedstawiony został na rysunku 2. Wykorzystuje się tutaj standardową

reprezentację graficzną stosowaną podczas projektowania układów hydraulicznych

(norma PN-ISO 1219- 1:1994).

Modelowanie serwomechanizmu elektrohydraulicznego polega na rozpatrzeniu

dynamiki ruchu suwaka rozdzielacza, bilansu przepływów w komorach rozdzielacza i

siłownika oraz dynamiki ruchu tłoczyska siłownika pod wpływem sił występujących w

układzie.

Praktycznie wszystkie fizyczne układy przejawiają własności nieliniowe. W

najprostszych przypadkach może to być ograniczenie ruchu, tarcie, histereza,

zużycie mechaniczne lub luzy. Podczas modelowania złożonych układów

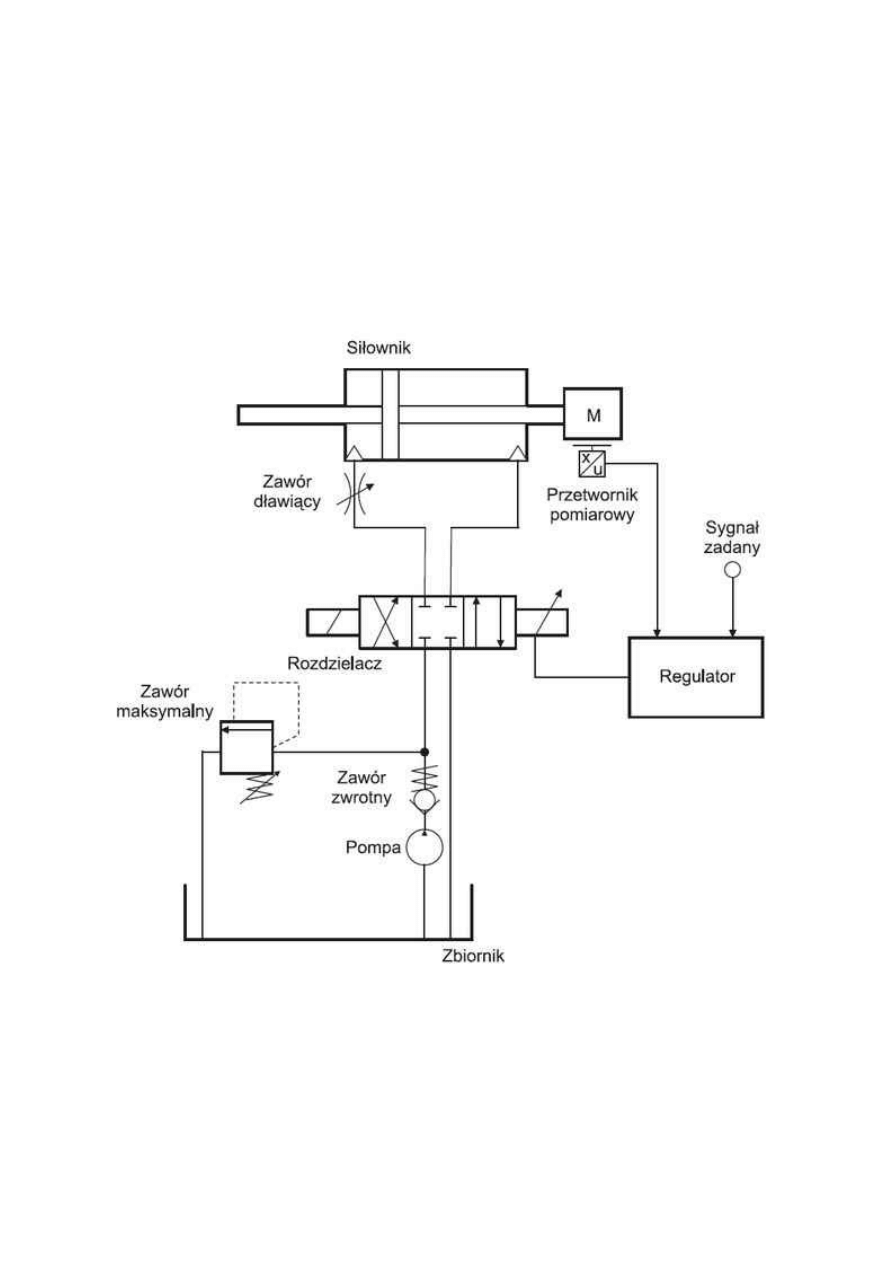
elektrohydraulicznych możliwe jest czasem (poprzez linearyzację w punkcie pracy)

wyprowadzenie m

odelu liniowego, który będzie przybliżał zachowanie rzeczywistego

systemu. Oczywiście model i jego parametry zależą ściśle od budowy elementów

serwomechanizmu

, zastosowanego rozdzielacza i siłownika, układu zasilającego,

cieczy roboczej i warunków otoczenia. Tak więc podczas wyznaczania modelu

często przyjmuje się założenia upraszczające i rozpatruje układ o charakterystycznej

konfiguracji, pracujący w określonych warunkach.

,,

Rys. 2. Schemat poglądowy serwomechanizmu elektrohydraulicznego