Politechnika Świętokrzyska
Wydział Mechatroniki i Budowy Maszyn
Centrum Laserowych Technologii Metali PŚk i PAN
Zakład Informatyki i Robotyki
Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem. II,
Specjalność: SUM - Inżynieria Produkcji, studia uzupełniające, 2002÷2003.
Ćwiczenie nr 3.
Dobór parametrów regulatora - symulacja komputerowa
1. Wstęp
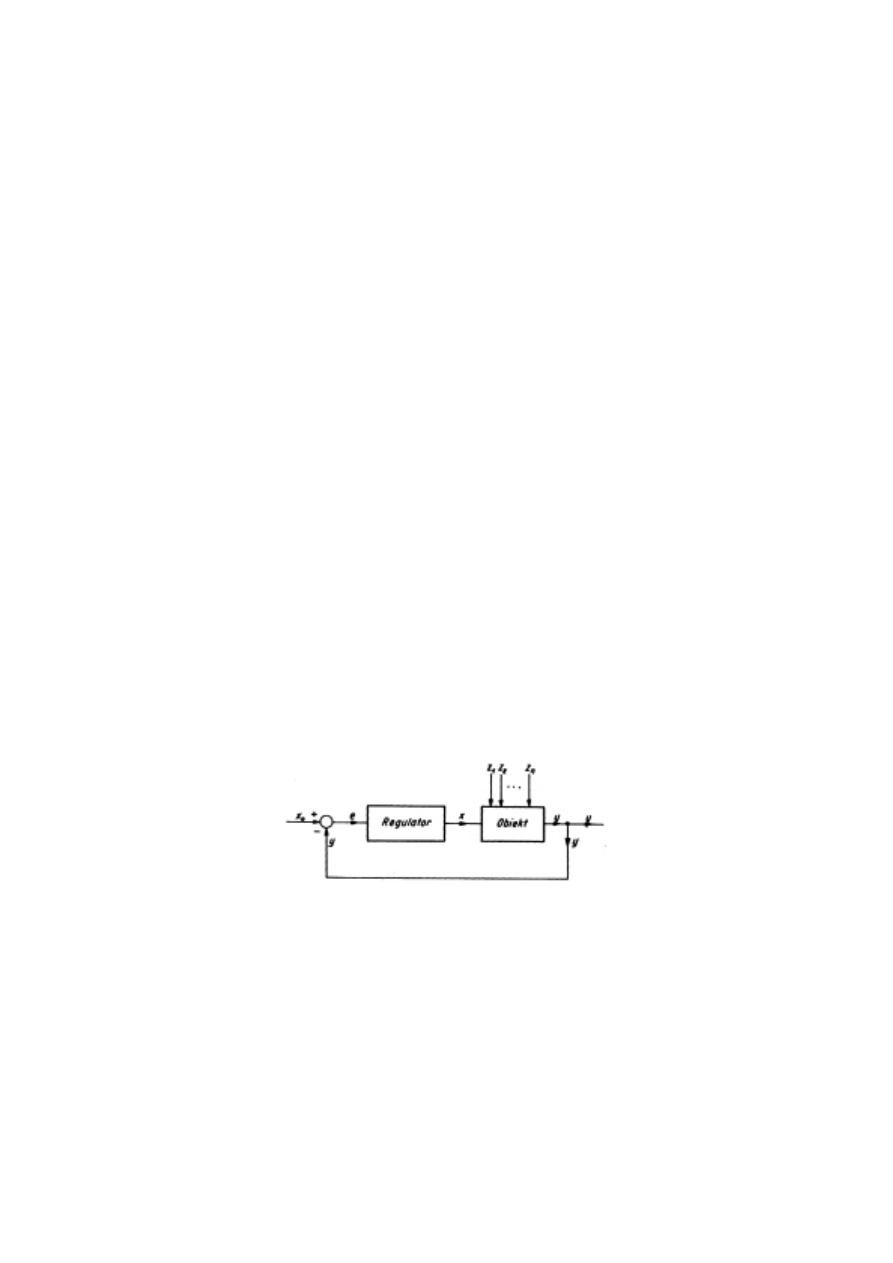
Najprostszy układ automatycznej regulacji można przedstawić za pomocą
schematu blokowego podanego na rys. 1.1 . Na schemacie tym występują dwa bloki
podstawowe, a mianowicie obiekt regulacji i regulator, które są podstawowymi
elementami najprostszego układu regulacji. Pod pojęciem obiektu regulacji rozumiemy tę
część układu automatycznej regulacji, na której własności nie mamy wpływu, gdyż jest
narzucona. Regulatorem zaś jest pozostała część układu automatycznej regulacji o
własnościach tak dobranych, aby zestawiony układ posiadał wymagane własności. W
obiekcie jednowymiarowym wyróżniamy następujące sygnały, sygnał regulowany
y ,
sygnał regulujący x , sygnały zakłócające
z
1,
z
2,
..., z
n
.
Rys 1.1 Schemat blokowy typowego układu automatycznej regulacji
Sygnał regulowany lub sygnał wyjściowy
y jest to ten sygnał, który mimo
zmieniających się warunków pracy obiektu, czyli jak mówimy mimo przychodzących
sygnałów zakłócających ma być utrzymywany stały w czasie lub zmieniać się według
określonej funkcji wyznaczonej sygnałem
x
o
, zwanym sygnałem sterującym lub
sygnałem zadanym. Porównania sygnału regulowanego i sygnału sterującego dokonuje
1
się w tzw. węźle sumacyjnym. Otrzymana w tym węźle różnica
x
o
−y
, czyli tzw. sygnał
błędu lub sygnał uchybu
e , zostaje wprowadzona na wejście elementu zwanego
regulatorem. Zadaniem regulatora jest taka zmiana sygnału regulującego lub sygnału
wyjściowego
x , aby sygnał błędu e był jak najmniejszy, czyli aby sygnał regulowany
y
różnił się jak najmniej od sygnału sterującego
x
o
. Na wyjściu obiektu znajduje się
tzw. węzeł informacyjny umożliwiający pobranie z wyjścia obiektu sygnału regulowanego
y
potrzebnego do doprowadzenia tzw. pętlą sprzężenia zwrotnego do węzła
sumacyjnego.
Układ automatycznej regulacji tworzy więc tzw. układ zamknięty, przy czym
chodzi w tym przypadku o jego zamknięcie wspomnianą pętlą sprzężenia zwrotnego. W
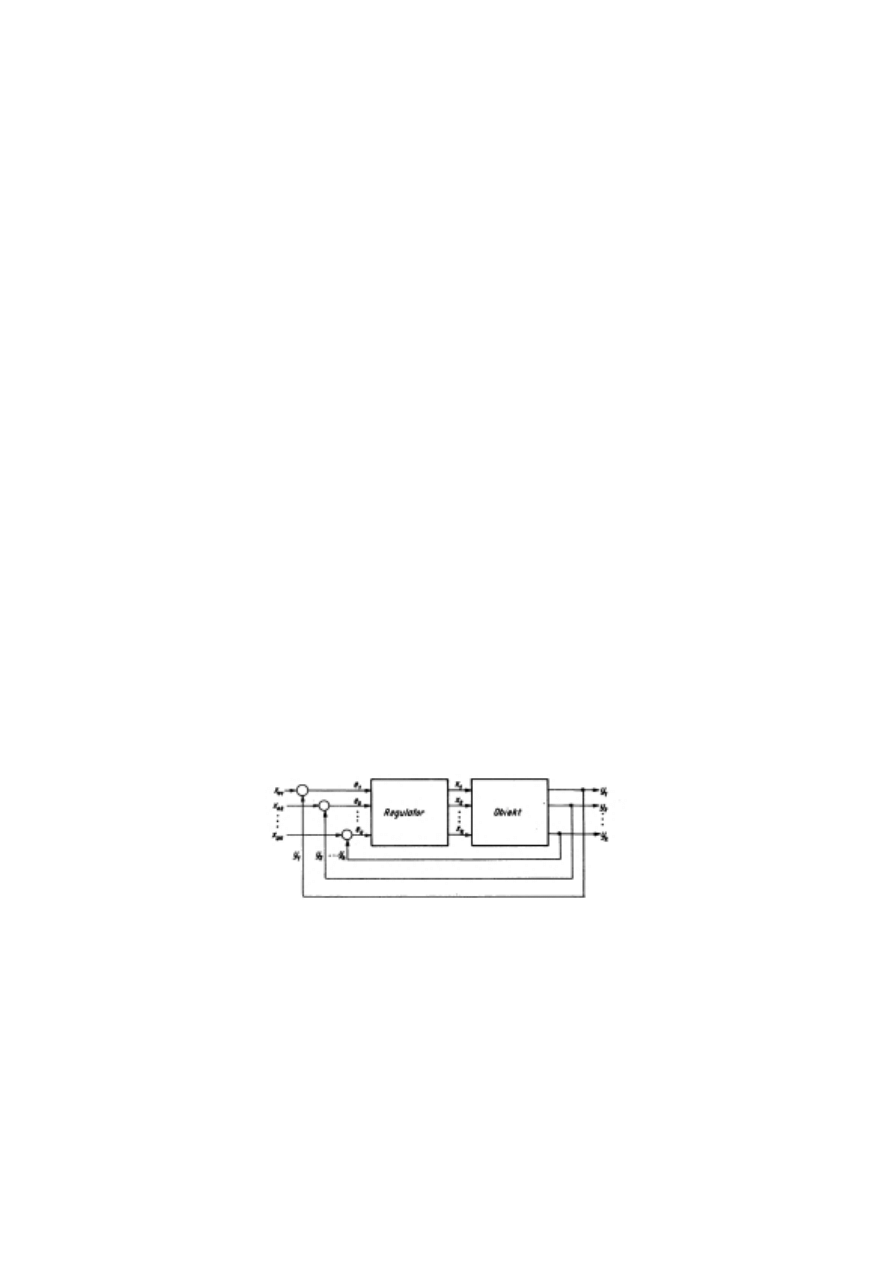
przypadku gdy obiekt jest elementem wielowymiarowym, a więc o wielu sygnałach
wejściowych i wyjściowych, regulator musi być również wielowymiarowy. Schemat
blokowy układu automatycznej regulacji dla tego przypadku jest pokazany na rys 1.2.
Klasyfikację układów automatycznej regulacji można przeprowadzić biorąc pod
uwagę różne kryteria. Najczęściej spotyka się podziały dokonane ze względu na:
–
zadanie, jakie spełnia dany układ,
–
rodzaj występujących w nich elementów,
–
sposób pomiaru wielkości regulowanej.
Rys 1.2 Schemat blokowy wielowymiarowego układu automatycznej regulacji
Podział układów regulacji automatycznej, ze względu na zadania jakie spełniają,
można przeprowadzić rozpatrując charakter sygnału sterującego. W tej grupie można
wyróżnić następujące typy układów:
- układy stabilizacji automatycznej,
W układach stabilizacji automatycznej sygnał sterujący ma stałą, raz nastawioną
2

wartość
x
o
=const
. W procesie regulacji układ ma za zadanie utrzymywać stałą wartość
sygnału regulowanego
y równą
x
o
. Przykładami takich układów mogą być: układ
regulacji automatycznej prędkości obrotowej turbiny, napięcia generatora, temperatury
pary i inne.
- układy nadążne,
W układach nadążnych sygnał sterujący
x
o
jest nieznaną funkcją czasu. Zmiany
sygnału sterującego
x
o
nie zależą od procesu zachodzącego wewnątrz układu
automatycznej regulacji, ale są wywołane zjawiskami występującymi poza układem
regulacji. Przykładem takiego układu może być radarowy układ nadążny, układ
wspomagający ruch kierownicy w samochodzie i inne.
- układy regulacji programowej,
Układ regulacji programowej jest szczególnym przypadkiem układu nadążnego. Z
regulacją programową mamy do czynienia wtedy, gdy sygnał sterujący zmienia się
według pewnego programu, określonego zadaną z góry funkcją czasu.
- układy regulacji ekstremalnej,
Regulację ekstremalną stosuje się wtedy, gdy przy zmianie wielkości regulującej w
pewnym momencie wielkość regulowana osiąga ekstremum. Zazwyczaj położenie tego
ekstremum nie jest stałe, lecz ulega przesuwaniu, spowodowanemu obecnością sygnałów
zakłócających. Zadaniem układów regulacji ekstremalnej jest w takim przypadku
utrzymywanie wielkości regulowanej możliwie blisko wartości ekstremalnej.
2. Regulator liniowy PID
Regulator, to urządzenie w układzie automatycznej regulacji, które na podstawie
wejściowego sygnału błędu
e
t (rys. 1.1) kształtuje sygnał wejściowy układu xt ,
by osiągnąć żądany efekt regulacji. Sygnał błędu nazywamy również uchybem regulacji.
Jest on wyznaczany poprzez porównanie wartości zadanej
x
o
t
z sygnałem
wyjściowym y t .
Praktyczne zastosowanie w przemysłowych systemach regulacji znalazł regulator
PID. Posiada on ciągłe wyjście i składa się z trzech różnych funkcjonalnie bloków:
3

‒
proporcjonalnego (P),
‒
całkującego (I),
‒
różniczkującego (D).
Poniżej przedstawiono transmitancję operatorową regulatora PID idealnego (2.1) i
rzeczywistego (2.2):
K
PID
s=k
p
1
T
i
∗s
T
d
∗s (2.1)
K
PID
s=k
p
1
T
i
∗s
T
d
∗s
s
∗T 1
(2.2)
gdzie:
k
p
- wzmocnienie,
T
i
- czas zdwojenia (stała czasowa akcji całkującej),
T
d
- czas wyprzedzenia (stała czasowa akcji różniczkującej),
T - stała czasowa.
Regulator PID cechuje prosta konstrukcja oraz duża uniwersalność zastosowań.
Przez lata dopracowano się również dużej niezawodności układu. Znajduje on
zastosowanie głownie do stałowartościowej regulacji przepływu, temperatury, położenia,
prędkości, ciśnienia, napięcia i innych. Podczas pracy regulator PID dąży do utrzymania
zadanej wartości sygnału regulowanego, zależnie od wartości nastaw parametrów trzech
bloków funkcjonalnych. Każdy z tych bloków kształtuje sygnał wyjściowy przy użyciu
ściśle określonej funkcji – mówimy, że regulator ma określoną akcję. Parametry regulatora
nazywamy również nastawami.
3. Dobór nastaw regulatora liniowego PID
Optymalizacja nastaw regulatora dla określonego układu regulacji bywa trudna i
uciążliwa. Dużym ułatwieniem jest posługiwanie się charakterystykami logarytmicznymi
obiektu oraz regulatora. Właściwy dobór nastaw pozwala otrzymać żądane wartości:
‒
statycznego błędu regulacji
C
ur
,
‒
przeregulowania
C
mr
,
‒
czasu regulacji
t
rr
.
4
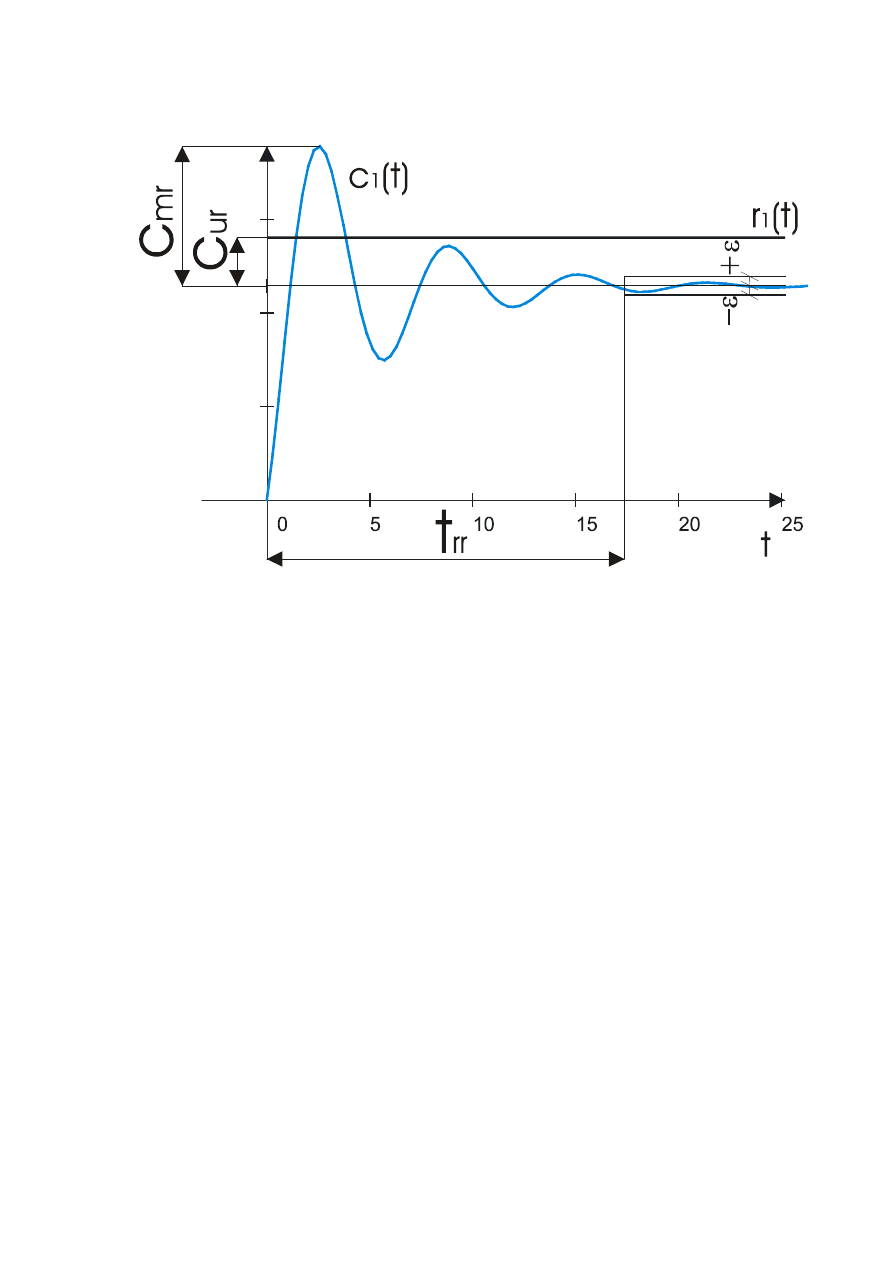
Rys.3.1 Sygnał wymuszający i odpowiedzi układu
r
1
t
- sygnał zadany,
c
1
t
- odpowiedź układu, ± - dopuszczalne odchylenie
regulacji.
W
wyniku
zastosowania
w
regulatorze
wyłącznie
akcji
proporcjonalnej
otrzymujemy regulator P. Wykorzystanie go nie eliminuje błędu statycznego, który zależy
od wielkości wzmocnienia. Wielkość wzmocnienia wpływa również na szybkość działania
oraz amplitudę sygnału wyjściowego. Większy parametr
k
p
oznacza skrócenie czasu
regulacji i wzrost amplitudy przebiegu wyjściowego.
Regulator I otrzymujemy stosując wyłącznie akcję całkującą. Regulator ten reaguje
na wszelkie odchyłki wolnozmiennego sygnału regulowanego. Likwiduje do zera błąd
statyczny regulacji. Czas regulacji ulega wydłużeniu. Zwiększenie wzmocnienia z
jednoczesnym zmniejszeniem wartości stałej zdwojenia powoduje wzrost akcji całkującej
regulatora.
Regulator D reaguje na każdą zmianę sygnału regulowanego. Skraca czas regulacji.
Zmniejsza przeregulowanie.
5

Jak wcześniej wspomniano do doboru nastaw potrzebna jest znajomość
charakterystyk obiektu i regulatora. Niestety w wielu przypadkach może stanowić to
dużą trudność. W związku z tym opracowano metody przybliżone, które nie wymagają
znajomości charakterystyk, a jedynie przeprowadzenia prostego doświadczenia. Sposób
ten zwany jest metodą Zieglera-Nicholsa lub metodą inżynierską. Polega on na
podłączeniu do obiektu regulatora nastawionego wyłącznie na akcję proporcjonalną z
minimalną wartością
wzmocnienia
k
p
(
T
i
∞
i
T
d
0
).
Następnie należy
stopniowo zwiększać współczynnik wzmocnienia do wystąpienia w układzie oscylacji
niegasnących. Współczynnik wzmocnienia dla oscylacji niegasnących określa się
współczynnikiem wzmocnienia krytycznego
k
pkr
, a okres oscylacji niegasnących
okresem drgań niegasnących
T
osc
. Po dokonaniu pomiaru współczynnika
k
pkr
i
okresu
T
osc
można wyznaczyć wartości nastaw dla poszczególnych regulatorów:
‒
regulator P:
k
p
=0.5∗k
pkr
;
‒
regulator PI:
k
p
=0.45∗k
pkr
,
T
i
=0.85∗T
osc
;
‒
regulator PID:
k
p
=0.6∗k
pkr
,
T
i
=0.5∗T
osc
,
T
d
=0.12∗T
osc
;
Reguła Zieglera-Nicholsa ma znaczenie pomocnicze. Może stanowić bazę do
wyprowadzenia
doświadczalnego
właściwych
nastaw
regulatora
w
układzie
rzeczywistego obiektu.
4. Wyznaczanie odpowiedzi układu: obiekt - regulator PID na wymuszenie
jednostkowe
Przykład 4.1
-->s=poly(0,'s');
-->dom='c';
-->s=poly(0,'s');
-->str='[(s-1)/(s^2+5*s+1)]';
-->rep=x_dialog('Obiekt regulowany',str);
-->if rep==[] then return,end
-->Plant=evstr(rep);
-->Plant=syslin('c',Plant);
-->P22=tf2ss(Plant);
6

-->[ny,nu,nx]=size(P22);
-->defv=['-1.2','1','0.1'];
-->while %t
-->mode(1)
-->if dom=='c' then
-->title='Parametry regulatora PID K(s)=Kp*(1+Ti/s+Ts*s)';
-->end
-->defv=x_mdialog(title,['Kp=';'Ti=';'Ts='],defv);
-->if
defv==[]
then
warning('Symulacja
zatrzymana!');return;
end
-->Kp=evstr(defv(1));T0=evstr(defv(2));T1=evstr(defv(3));
-->if dom=='c' then
-->Kpid=tf2ss(Kp*(1+T0/s+T1*s));
-->end
-->W=[1, -P22; Kpid,1];
-->Winv=inv(W);
-->disp(spec(Winv(2)),'p
ę
tla sprz
ęż
enia zwrotnego');
-->if maxi(real(spec(Winv(2)))) > 0 then
-->x_message('Układ niestabilny!!!');
-->else
-->x_message('Układ stabilny!!!');
-->break;
-->end
-->mode(-1)
-->end
-->[Spid,Rpid,Tpid]=sensi(P22,Kpid);
-->Tpid(5)=clean(Tpid(5));
-->disp(clean(ss2tf(Spid)),'Funkcja wra
ż
liwo
ś
ci');
-->disp(clean(ss2tf(Tpid)),'Dopełnieniowa funkcja
wra
ż
liwo
ś
ci');
-->resp=['Charakterystyka cz
ę
stotliwo
ś
ciowa';
'Charakterystyka czasowa'];
-->while %t do
-->n=x_choose(resp,'Wybierz charakterystyk
ę
');
-->if degree(Tpid(5))>0 then
-->warning('Niepoprawna funkcja przej
ś
cia!')
7

-->Tpid(5)=coeff(Tpid(5),0);
-->end
-->Tpid(5)=coeff(Tpid(5));
-->select n;
-->case 0
-->break
-->case 1
-->mode(1)
-->xbasc(1);xset("window",1);xselect();bode(Tpid);
-->mode(-1)
-->case 2
-->if Plant(4)=='c' then
-->mode(1)
-->defv=['0.1','50'];
-->title='Wprowad
ź
okres próbkowania i czas symulacji';
-->rep=x_mdialog(title,['Okres
próbkowania?';'Czas
symulacji?
'],defv);
-->if rep==[] then break,end
-->dttmax=evstr(rep);
-->dt=evstr(dttmax(1));tmax=evstr(dttmax(2));
-->t=0:dt/5:tmax;
-->n1=x_choose(['Charakterystyka skokowa?';'Charakterystyka
impulsowa?'],'Symulacja:');
-->if n1==0 then
-->warning('Zatrzymano program!');return;
-->end
-->if n1==1 then
-->xbasc(1);xset("window",1);xselect();
-->plot2d([t',t'],[(csim('step',t,Tpid))',ones(t')])
-->break
-->end
-->if n1==2 then
-->xbasc(1);xset("window",1);xselect();
-->plot2d([t',t'],[(csim('impul',t,Tpid))',0*t'])
-->break
-->end
8

-->mode(-1)
-->end
-->end
-->end
5.Przebieg ćwiczenia.
Wyznacz odpowiedzi dowolnych układów na wymuszenie jednostkowe. Podaj
wpływ parametrów
k
p
,
T
i
,
T
d
na przeregulowanie, błąd statyczny i czas regulacji.
9
Wyszukiwarka
Podobne podstrony:
Dobór parametrów regulatora PID – symulacja komputerowa
Dobor parametrow regulatora id Nieznany
Dobór parametrów regulatora PID – symulacja komputerowa
dobór parametru klotoidy
Banas Chrabaszcz zaoczne Dobor nastaw regulatorów
DOBÓR NASTAW REGULATORA PID
05 Dobor nastaw regulatora w ko Nieznany (2)
DOBÓR NASTAW REGULATORÓW TYPU PID METODĄ CHARAKTERYSTYK SKOKOWYCH
B1 Wyznaczanie parametrów regulatorów metod reduktów
krzywa przejsciowa, 1 dobor parametru klotoidy
DOBÓR NASTAW REGULATORÓW W MODELOWYM UKŁADZIE AUTOMATYCZNEJ REGULACJI, SGGW Technika Rolnicza i Leśn
krzywa przejsciowa 1. dobor parametru klotoidy
dobór parametrów
Dobór nastaw regulatorów
Dobór nastaw regulatorów
Dobór nastaw regulatora
syposz,podstawy automatyki, DOBÓR NASTAW REGULATORÓW
15 dobor nastaw regulatoraid 16127 ppt
więcej podobnych podstron