Łukasz Czech

25 lutego 2013 r.

Algebra liniowa z geometrią – zestaw nr 16

Zadanie 1 Napisz równanie normalne, ogólne, parametryczne i odcinkowe płaszczyzn
spełniających warunki:

a) przechodzącej przez punkty P

1

= (1, 1, 1), P

2

= (−1, 0, 1), P

3

= (5, 6, 7);

b) przechodzącej przez punkt P = (0, 1, 0) i równoległej do wektorów −

→

a = (−1, 3, 0),

−

→

b = (3, 1, −5);

c) przechodzącej przez punkt P = (−1, 4, 1) i równoległej do płaszczyzny π

1

: x − y +

6z − 12 = 0;

d) przechodzącej przez punkt P = (2, 3, −6) i prostopadłej do płaszczyzn π

1

: x + y +

z − 5 = 0 oraz π

2

: x − y + 2 = 0.

Zadanie 2 Napisz równanie parametryczne i kierunkowe prostych spełniających wa-
runki:

a) przechodzącej przez punkty P

1

= (1, 0, 6), P

2

= (−2, 2, 4);

b) przechodzącej przez punkt P = (0, −2, 3) i prostopadłej do płaszczyzny π : 3x −

y + 2z − 6 = 0;

c) przechodzącej przez punkt P = (7, 2, 0) i prostopadłej do wektorów −

→

v

1

= (2, 0, −3),

−

→

v

2

= (−1, 2, 0);

d) będącej dwusieczną kąta utworzonego przez proste l

1

:

x+2

3

=

y−4

−1

=

z
5

oraz l

2

:

x−2

−1

=

y+1

2

=

z−3

4

.

Zadanie 3 Zbadaj czy:

a) prosta m :







2x + y − z + 3 = 0
x − 2y + z − 5 = 0

jest zawarta w płaszczyźnie π : 5y −3z +13 = 0;

b) punkty A = (0, 1, 5), B = (1, 2, 3) należą do płaszczyzny π :



















x = −1 + s + t

y = 2 + 3s − t
z = 3 − s + 2t

gdzie s, t ∈ R;

c) proste l

1

:

x+1

−2

=

y−3

1

=

z+4

−8

, l

2

:

x

1

=

y−1

1

=

z−2

2

mają punkt wspólny.

Zadanie 4 Znajdź punkt, w którym przecinają się proste l

1

:







x + 2y − z + 4 = 0

y + z − 3 = 0

oraz l

2

:







2x − y − 2z + 8 = 0
x + 2y + 2z − 5 = 0

.

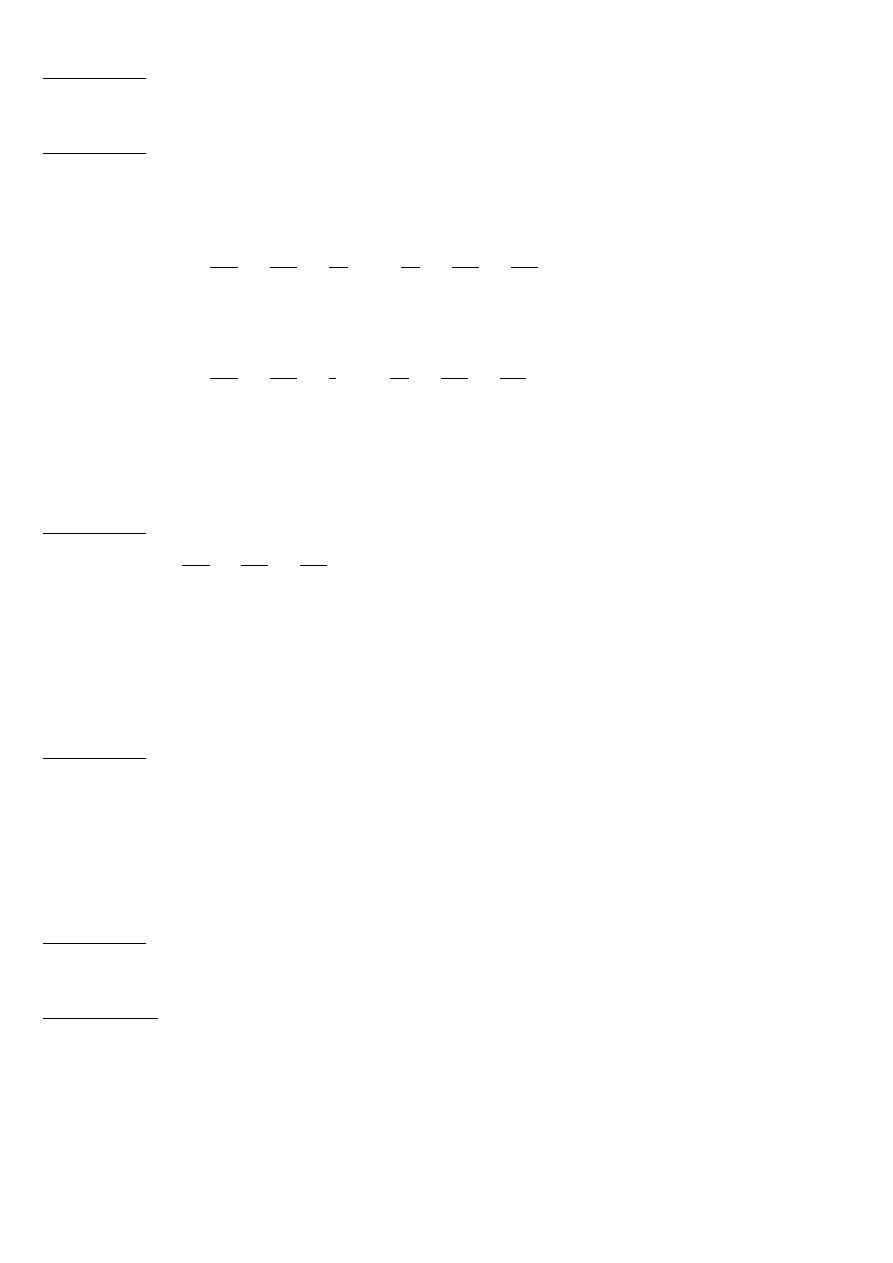
Zadanie 5 Znajdź punkt przecięcia się płaszczyzn π

1

: 3x+y+z +1 = 0, π

2

: x+2z +6 =

0, π

3

: 3y + 2z = 0.

Zadanie 6 Oblicz odległość:

a) płaszczyzn π

1

: 2x + y − 2z = 0, π

2

: x + y − 3z + 5 = 0;

b) płaszczyzn π

1

: x − 2y + 2z + 5 = 0, π

2

: 3x − 6y + 6z − 3 = 0;

c) prostych l

1

:

x−1

1

=

y+1

2

=

z

−1

, l

2

:

x

−2

=

y−1

−4

=

z−3

2

;

d) prostych l

1

:







x = 0

y = 0

oraz l

2

:







x = 1

z = 1

;

e) prostych l

1

:

x−9

4

=

y−2

−3

=

z
1

, l

2

:

x

−2

=

y+7

9

=

z−2

2

;

f) prostej l :



















x = 2 + t

y = −3 + 2t
z = 2 − t

, gdzie t ∈ R, od płaszczyzny π : 2x + y + 4z = 0.

Zadanie 7 Oblicz miarę kąta między:

a) prostą l :

x−3

2

=

y−1

0

=

z+2

−3

i płaszczyzną π : x − z = 0;

b) płaszczyznami π

1

: x − 2y + 3z − 5 = 0, π

2

: 2x + y − z + 3 = 0;

c) prostymi l

1

:



















x = 1 − t

y = −2 + t
z = 3t

gdzie t ∈ R oraz l

2

:



















x = 3 − 2s

y = 4 − s
z = 1 + 3s

gdzie s ∈ R.

Zadanie 8 Znajdź punkt symetryczny do punktu P = (2, 3, −1) względem:

a) prostej l :



















x = 1 + 2t

y = 2 + 4t
z = −3 − t

, gdzie t ∈ R;

b) płaszczyzny π : 2x − y + z − 6 = 0.

Zadanie 9 Oblicz objętość i pole powierzchni bryły ograniczonej płaszczyznami x − y =
1, x − y = 5, x + 2z = 0, x + 2z = 3, z = −1, z = 4.

Zadanie 10 Oblicz pole trójkąta utworzonego przez parami przecinające się proste:

l

1

:



















x = −2 + 2t

y = 0
z = 4t

,

l

2

:



















x = 0

y = 3 + 3s
z = −4s

,

l

3

:



















x = −2k

y = 3 − 3k
z = 0

, gdzie t, s, k ∈ R.