MO
Z2/13. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 13
1
Z2/13. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 13
Z2/13.1. Zadanie 13
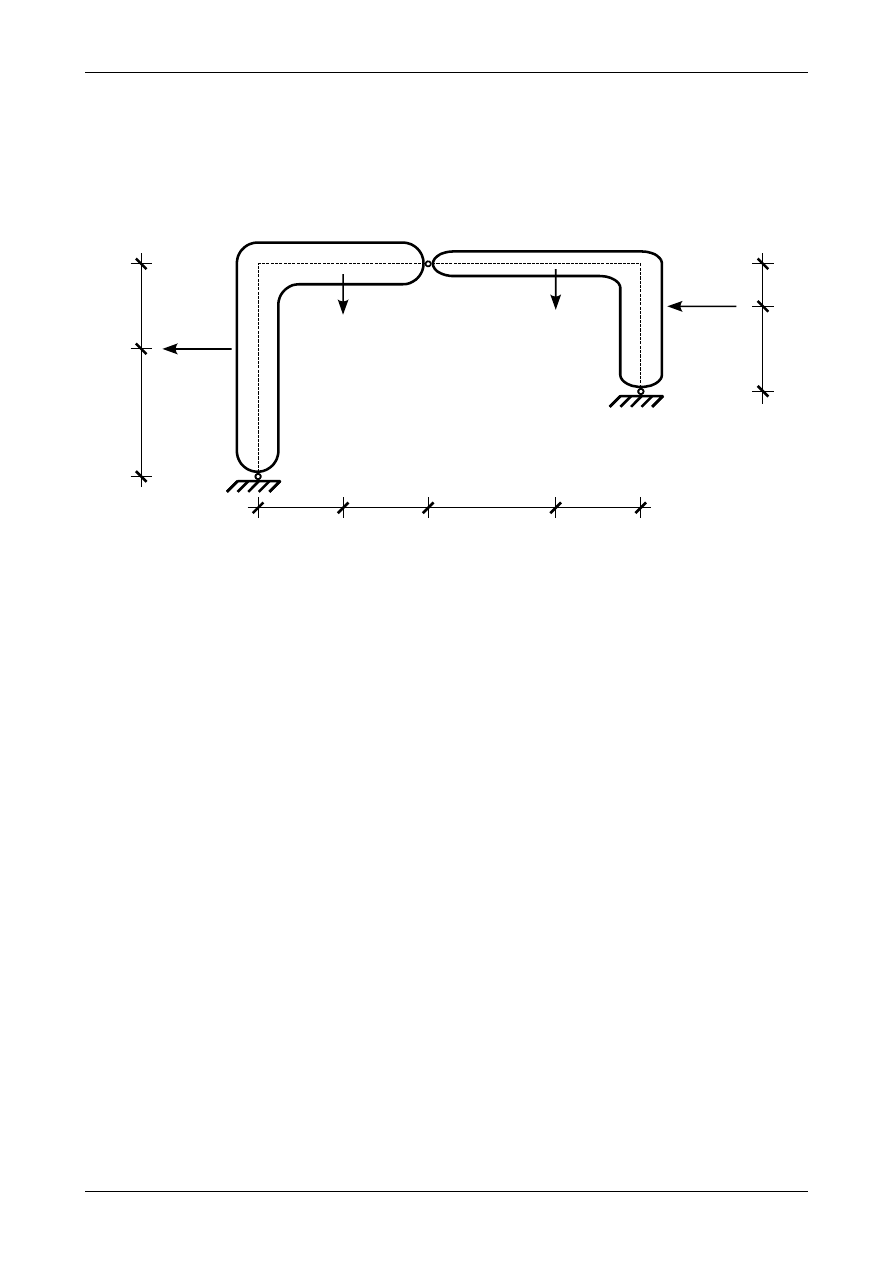
Wyznaczyć analitycznie reakcje we wszystkich przegubach rzeczywistych A, B i C układu trójprzegu-
bowego przedstawionego na rysunku Z2/13.1.
A
B
C
2,0
2,0
3,0
2,0
1,
0
2,
0
2,
0
3,
0
8,0 kN
12,0 kN
16,0 kN
24,0 kN
[m]
I
II
Rys. Z2/13.1. Układ trójprzegubowy
Z2/13.2. Analiza kinematyczna układu trójprzegubowego
Układ trójprzegubowy składa się z dwóch tarcz sztywnych mających razem sześć stopni swobody.
Wszystkie trzy przeguby rzeczywiste A, B i C odbierają razem także sześć stopni swobody. Został więc
spełniony warunek konieczny geometrycznej niezmienności (1.4).
Wszystkie trzy przeguby rzeczywiste A, B i C nie leżą na jednej prostej. Został tym samym spełniony
warunek dostateczny geometrycznej niezmienności.
Ponieważ układ trójprzegubowy przedstawiony na rysunku Z2/13.1 spełnia warunek konieczny i
dostateczny geometrycznej niezmienności jest więc on układem geometrycznie niezmiennym i statycznie
wyznaczalnym.
Z2/13.3. Analiza statyczna układu trójprzegubowego
W przegubie rzeczywistym jak wiadomo działa jedna reakcja. Wiemy o niej tylko to, że kierunek jej
musi przejść przez przegub rzeczywisty. W takim przypadku rozkładamy reakcję w przegubie rzeczywistym
na dwie składowe: poziomą i pionową. Założone zwroty składowych reakcji w przegubach A i C
przedstawia rysunek Z2/13.2. Rysunek Z2/13.3 przedstawia założone zwroty reakcji działających na tarczę
sztywną numer I. Rysunek Z2/13.4 przedstawia założone zwroty reakcji działających na tarczę sztywną
numer II. Rysunek Z2/13.5 przedstawia założone zwroty reakcji działających w przegubie rzeczywistym B.
Pierwszym równaniem służącym do wyznaczenia składowych reakcji w przegubie rzeczywistym A
będzie równanie sumy momentów wszystkich sił działających na cały układ trójprzegubowy względem
punktu C. Dodatni moment będzie jak wiadomo kręcił zgodnie z ruchem wskazówek zegara. Zgodnie z
rysunkiem Z2/13.2 równanie to będzie miało postać
M
C
=V
A
⋅9,0−H
A
⋅2,0−16,0⋅1,0−24,0⋅7,0−12,0⋅2,0−8,0⋅2,0=0
V
A
⋅9,0−H
A
⋅2,0=224,0
.
(Z2/13.1)
Dr inż. Janusz Dębiński
Zaoczni
MO
Z2/13. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 13
2
A
B
C
2,0
2,0
3,0
2,0
1,
0
2,
0
2,
0
3,
0
8,0 kN
12,0 kN
16,0 kN
24,0 kN
[m]
I
II
V
A
H
A
V
C
H
C
2,
0
1,
0
X
Y
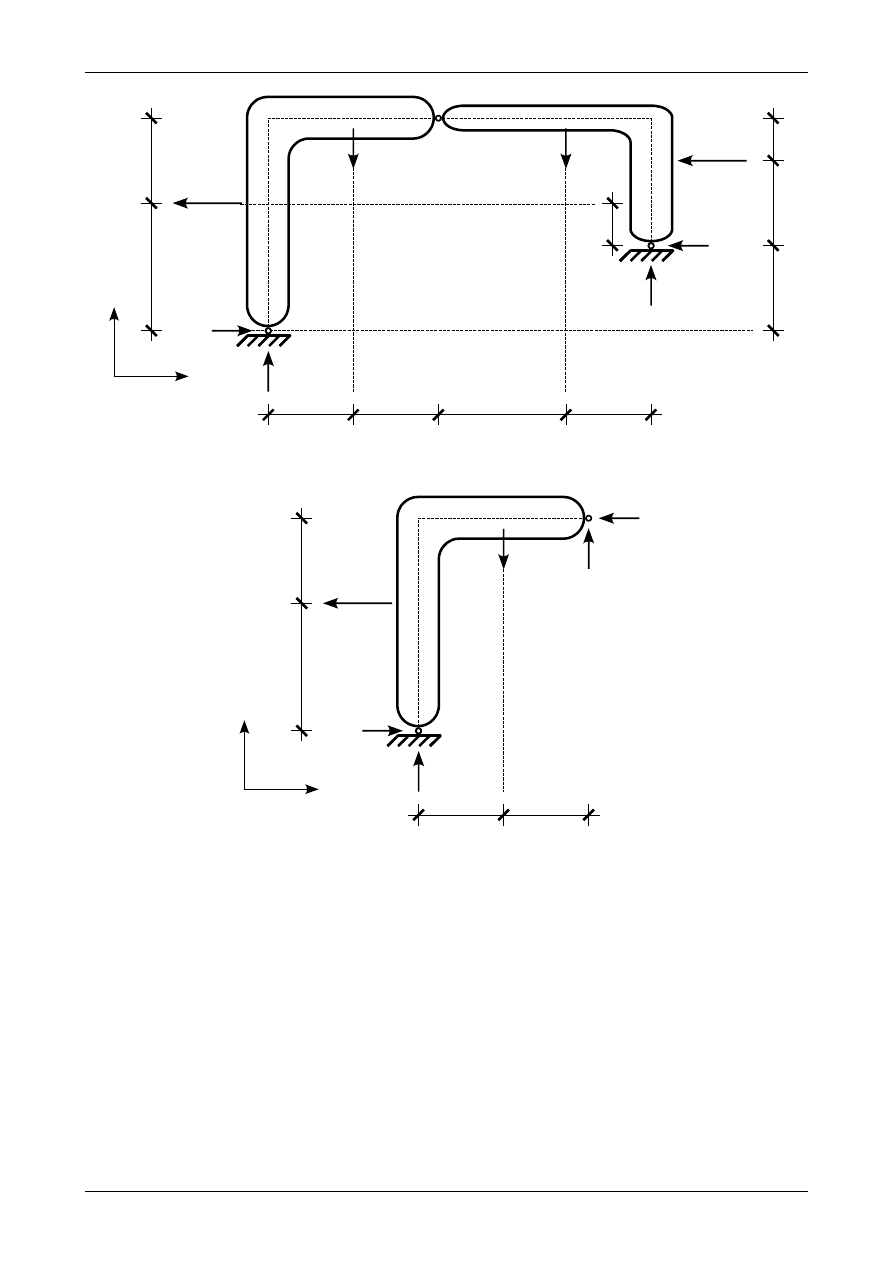
Rys. Z2/13.2. Założone zwroty składowych reakcji w przegubach A i C
A
B
2,0
2,0
2,
0
3,
0
16,0 kN
24,0 kN
[m]
I
V
A
H
A
V
B
(I)
H
B
(I)
X
Y
Rys. Z2/13.3. Założone zwroty składowych reakcji w przegubach A i B działające na tarczę sztywną numer I
Drugim równaniem służącym do wyznaczenia składowych reakcji w przegubie rzeczywistym A
będzie równanie sumy momentów wszystkich sił działających na tarczę sztywną numer I względem punktu
B. Dodatni moment będzie jak wiadomo kręcił zgodnie z ruchem wskazówek zegara. Zgodnie z rysunkiem
Z2/11.3 równanie to będzie miało postać
M
B
I
=V
A
⋅4,0−H
A
⋅5,016,0⋅2,0−24,0⋅2,0=0
V
A
⋅4,0−H
A
⋅5,0=16,0
.
(Z2/13.2)
Równania równowagi (Z2/13.1) i (Z2/13.2) będą tworzyły układ dwóch równań z dwiema
niewiadomymi, którymi będą składowe reakcji w przegubie rzeczywistym A, w postaci
Dr inż. Janusz Dębiński
Zaoczni
MO
Z2/13. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 13
3
B
C
3,0
2,0
1,
0
2,
0
8,0 kN
12,0 kN
[m]
II
V
C
H
C
V
B
(II)
H
B
(II)
X
Y
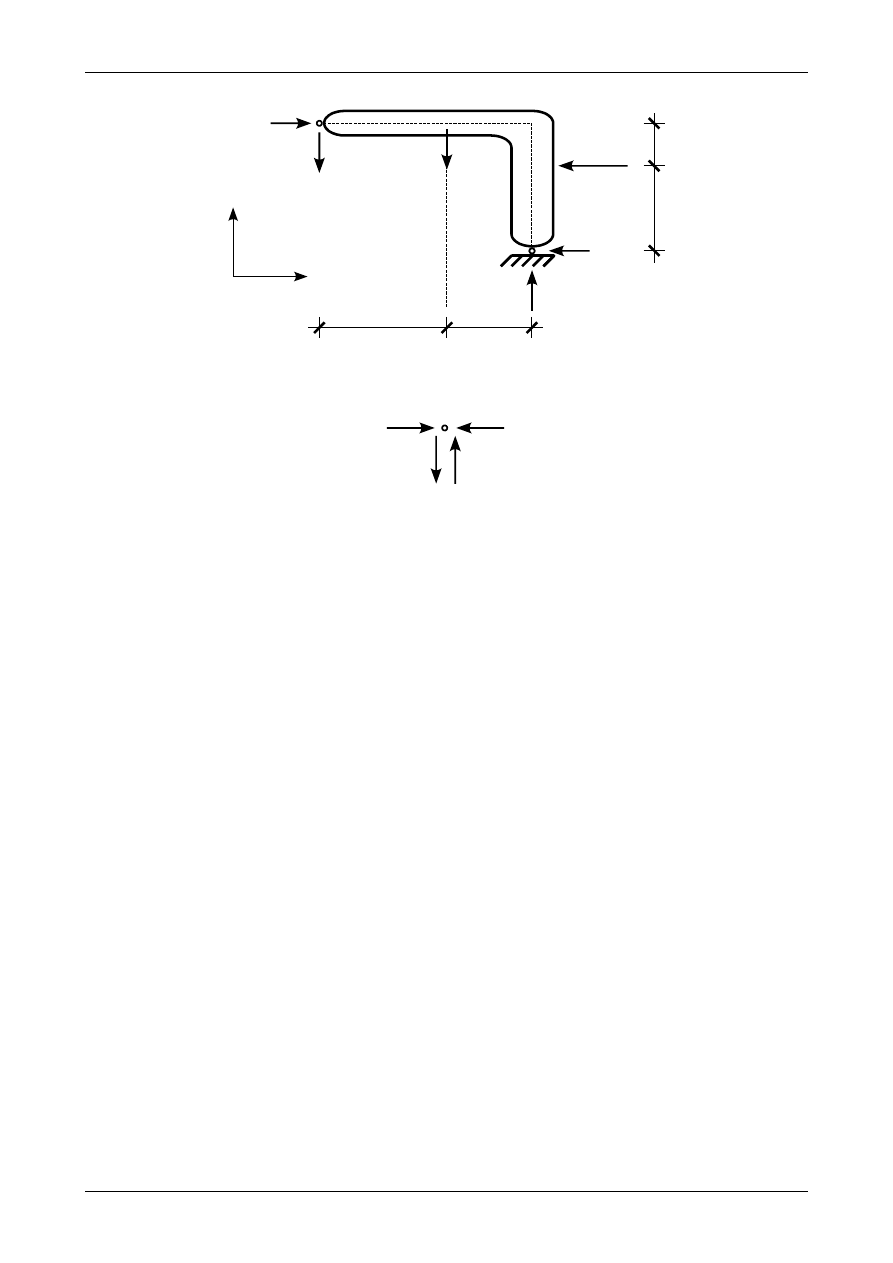
Rys. Z2/13.4. Założone zwroty składowych reakcji w przegubach B i C działające na tarczę sztywną numer II
B
V
B
(I)
H
B
(I)
V
B
(II)
H
B
(II)
Rys. Z2/13.5. Założone zwroty reakcji w przegubie rzeczywistym B
{
V
A
⋅
9,0
−
H
A
⋅
2,0
=
224,0
V
A
⋅
4,0
−
H
A
⋅
5,0
=
16,0
.
(Z2/13.3)
Rozwiązaniem układu są składowe reakcji w przegubie rzeczywistym A o wartościach
V
A
=
29,41 kN
,
(Z2/13.4)
H
A
=20,32 kN
,
(Z2/13.5)
Obie składowe mają więc zwroty zgodne z przyjętymi na początku obliczeń.
Pierwszym równaniem służącym do wyznaczenia składowych reakcji w przegubie rzeczywistym C
będzie równanie sumy momentów wszystkich sił działających na cały układ trójprzegubowy względem
punktu A. Dodatni moment będzie jak wiadomo kręcił zgodnie z ruchem wskazówek zegara. Zgodnie z
rysunkiem Z2/13.2 równanie to będzie miało postać
M
A
=−V
C
⋅9,0−H
C
⋅2,0−16,0⋅3,024,0⋅2,012,0⋅7,0−8,0⋅4,0=0
V
C
⋅9,0H
C
⋅2,0=52,0
.
(Z2/13.6)
Drugim równaniem służącym do wyznaczenia składowych reakcji w przegubie rzeczywistym C
będzie równanie sumy momentów wszystkich sił działających na tarczę sztywną numer II względem punktu
B. Dodatni moment będzie jak wiadomo kręcił zgodnie z ruchem wskazówek zegara. Zgodnie z rysunkiem
Z2/11.4 równanie to będzie miało postać
Dr inż. Janusz Dębiński
Zaoczni

MO
Z2/13. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 13
4
M
B
II
=−V
C
⋅5,0H
C
⋅3,012,0⋅3,08,0⋅1,0=0
V
C
⋅5,0−H
C
⋅3,0=44,0
.
(Z2/13.7)
Równania równowagi (Z2/13.6) i (Z2/13.7) będą tworzyły układ dwóch równań z dwiema
niewiadomymi, którymi będą składowe reakcji w przegubie rzeczywistym C w postaci
{
V
C
⋅
9,0
H
C
⋅
2,0
=
52,0
V
C
⋅
5,0
−
H
C
⋅
3,0
=
44,0
.
(Z2/13.8)
Rozwiązaniem układu są składowe reakcji w przegubie rzeczywistym C o wartościach
V
C
=6,595 kN
,
(Z2/13.9)
H
C
=−3,675 kN
,
(Z2/13.10)
Składowa pionowa reakcji w przegubie rzeczywistym C ma zwrot zgodny z przyjętym na początku obliczeń
natomiast składowa pozioma reakcji ma zwrot przeciwny do przyjętego.
W celu sprawdzenia obliczeń zastosujemy równania sumy rzutów wszystkich sił działających na cały
układ trójprzegubowy na osie poziomą X i pionową Y. Jako dodatni przyjmiemy kierunek zgodny ze
zwrotem osi X lub Y. Równania te, zgodnie z rysunkiem Z2/13.2, mają postać
X =H
A
−H
C
−16,0−8,0=20,32−
−3,675
−24,0=−0,005≈0
,
(Z2/13.11)
Y =V
A
V
C
−24,0−12,0=29,416,595−36,0=0,005≈0
.
(Z2/13.12)
Równania równowagi (Z2/13.11) i (Z2/13.12) zostały spełnione możemy więc stwierdzić, że składowe
reakcji w przegubach A i C zostały wyznaczone poprawnie.
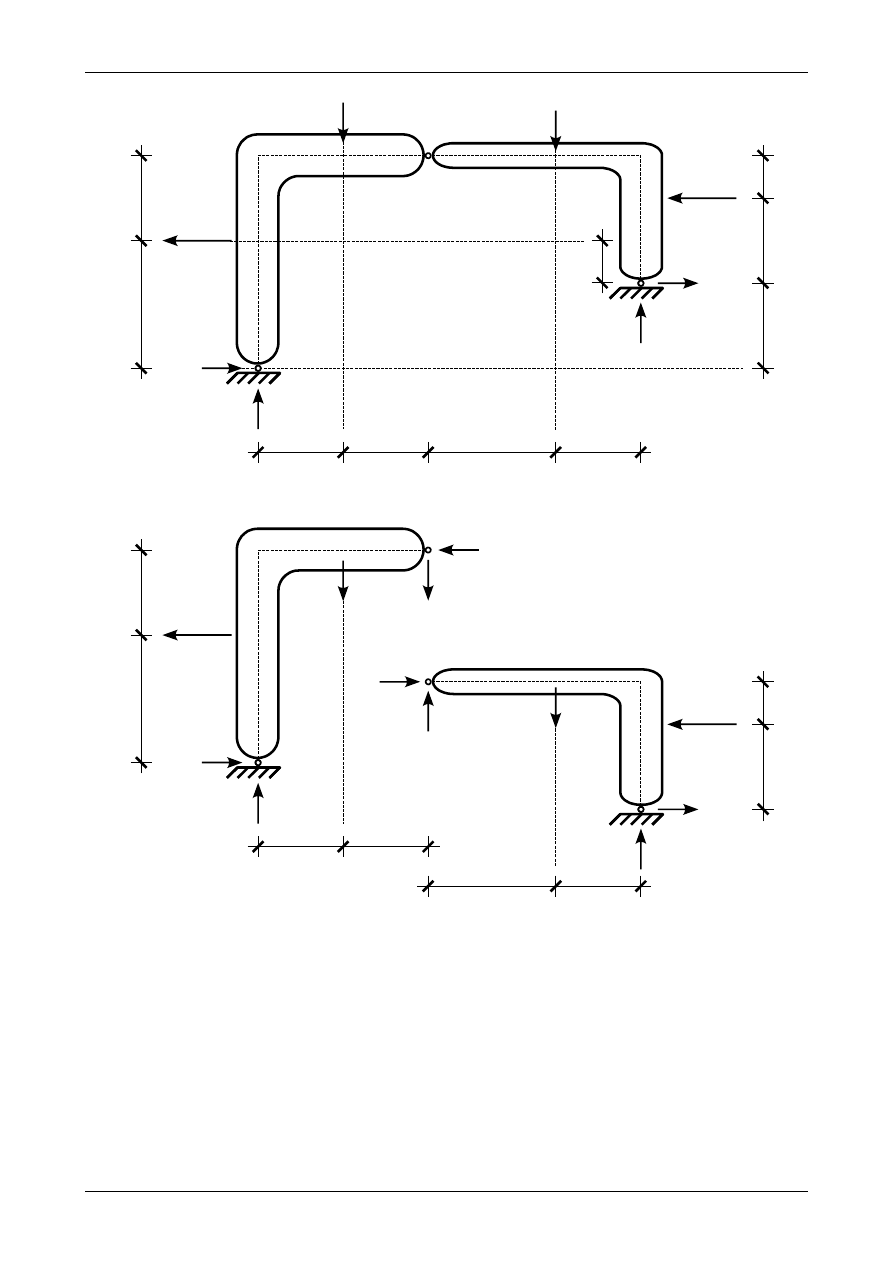
Rysunek Z2/13.6 przedstawia prawidłowe wartości i zwroty składowych reakcji w przegubach
rzeczywistych A i C. Składowe tych reakcji oraz siły czynne działające na obie tarcze sztywne znajdują się
w równowadze.
Aby wyznaczyć poziomą składową reakcji w przegubie B działającą na tarczę sztywną numer I
zastosujemy równanie sumy rzutów wszystkich sił działających na tę tarczę na oś X. Jako dodatni
przyjmiemy kierunek zgodny ze zwrotem osi X. Zgodnie z rysunkiem Z2/13.3 składowa ta ma wartość
X
I
=−H
B
I
H
A
−16,0=0
−H
B
I
20,32−16,0=0
H
B
I
=4,32kN
.
(Z2/13.13)
Aby wyznaczyć pionową składową reakcji w przegubie B działającą na tarczę sztywną numer I
zastosujemy równanie sumy rzutów wszystkich sił działających na tę tarczę na oś Y. Jako dodatni
przyjmiemy kierunek zgodny ze zwrotem osi Y. Zgodnie z rysunkiem Z2/13.3 składowa ta ma wartość
Dr inż. Janusz Dębiński
Zaoczni
MO
Z2/13. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 13
5
A
B
C
2,0
2,0
3,0
2,0
1,
0
2,
0
2,
0
3,
0
8,0 kN
12,0 kN
16,0 kN
24,0 kN
[m]
I
II
2,
0
1,
0
29,41 kN
20,32 kN
6,595 kN
3,675 kN
Rys. Z2/13.6. Prawidłowe wartości i zwroty składowych reakcji w przegubach rzeczywistych A i C
A
B
2,0
2,0
2,
0
3,
0
16,0 kN
24,0 kN
I
29,41 kN
20,32 kN
5,41 kN
4,32 kN
B
C
3,0
2,0
1,
0
2,
0
8,0 kN
12,0 kN
[m]
II
6,595 kN
3,675 kN
5,41 kN
4,32 kN
Rys. Z2/13.7. Prawidłowe wartości i zwroty składowych reakcji w przegubach rzeczywistych A, B i C
Y
I
=V
B
I
V
A
−24,0=0
V
B
I
29,41−24,0=0
V
B
I
=−5,41 kN
.
(Z2/13.14)
Pozioma składowa reakcji w przegubie B ma zwrot zgodny z założonym natomiast pionowa składowa
reakcji w przegubie B ma zwrot przeciwny do założonego. Rysunek Z2/13.7 przedstawia prawidłowe zwroty
składowych reakcji w przegubie rzeczywistym B działające na tarczę sztywną numer I.
Dr inż. Janusz Dębiński
Zaoczni

MO
Z2/13. PODSTAWY STATYKI NA PŁASZCZYŹNIE – ZADANIE 13
6
Składowe reakcji w przegubie B działające na tarczę sztywną numer II mają takie same wartości ale
przeciwne zwroty jak te same składowe działające na tarczę sztywną numer I. Wynika to bezpośrednio z
równowagi założonych zwrotów składowych reakcji w przegubie rzeczywistym B przedstawionych na
rysunku Z2/13.5. Możemy więc napisać, że
H
B
II
=H
B
I
=4,32 kN
,
(Z2/13.15)
V
B
II
=V
B
I
=−5,41 kN
.
(Z2/13.16)
W celu sprawdzenia obliczeń składowych reakcji w przegubie B zastosujemy równania sumy rzutów
wszystkich sił działających na tarczę sztywną numer II na osie: poziomą X i pionową Y. Jako dodatnie
przyjmiemy kierunki zgodne ze zwrotami osi X i Y. Zgodnie z rysunkiem Z2/13.4 równanie sumy rzutów na
oś X ma postać
X
II
=H
B
II
−H
C
−8,0=4,32−
−3,675
−8,0=−0,005≈0
.
(Z2/13.17)
Zgodnie z rysunkiem Z2/13.4 równanie sumy rzutów na oś Y ma postać
Y
II
=−V
B
II
V
C
−12,0=−
−5,41
6,595−12,0=0,005≈0
.
(Z2/13.18)
Równania równowagi (Z2/13.17) i (Z2/13.18) zostały spełnione, możemy więc stwierdzić, że poziome i
pionowe składowe reakcji w przegubie B zostały wyznaczone poprawnie.
Rysunek Z2/13.7 przedstawia prawidłowe wartości i zwroty składowych reakcji w przegubach
rzeczywistych A, B i C. Składowe tych reakcji oraz siły czynne działające na każdą z tarcz sztywnych
znajdują się w równowadze.
Rysunek Z2/13.8 przedstawia prawidłowe wartości i zwroty składowych reakcji działających w
przegubie rzeczywistym B.
B
5,41 kN
4,32 kN
5,41 kN
4,32 kN
Rys. Z2/13.8. Składowe reakcji działających w przegubie rzeczywistym B
Dr inż. Janusz Dębiński
Zaoczni
Document Outline
- Z2/13.1. Zadanie 13
- Z2/13.2. Analiza kinematyczna układu trójprzegubowego
- Z2/13.3. Analiza statyczna układu trójprzegubowego
Wyszukiwarka
Podobne podstrony:
02 04 podstawy statyki zadanie Nieznany (2)
02 11 podstawy statyki zadanie Nieznany (2)
02 06 podstawy statyki zadanie Nieznany (2)
02 09 podstawy statyki zadanie Nieznany (2)
02 03 podstawy statyki zadanie Nieznany (2)
02 12 podstawy statyki zadanie Nieznany (2)
02 08 podstawy statyki zadanie Nieznany (2)
02 07 podstawy statyki zadanie Nieznany (2)
02 05 podstawy statyki zadanie 05id 3503
02 10 podstawy statyki zadanie 10
02 01 podstawy statyki zadanie 01
02 05 podstawy statyki zadanie 05
02 01 podstawy statyki zadanie 01id 3499
02 14 podstawy statyki zadanie 14
02 16 podstawy statyki zadanie 16
więcej podobnych podstron