1

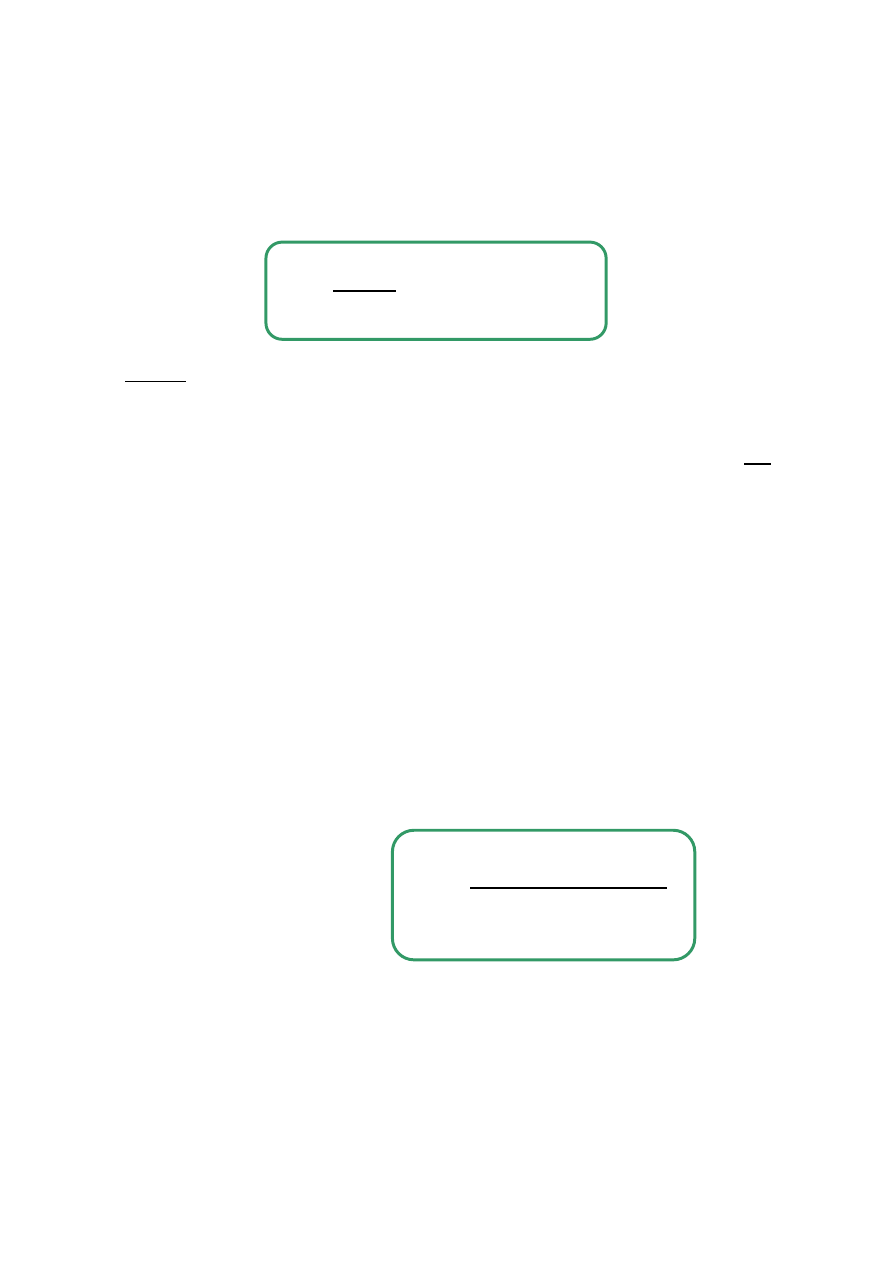
DRGANIA WYMUSZONE

Układ oscylacyjny na który działa siła wymuszająca.

)

(

2

2

t

F

kx

dt

x

d

m

+

−

=

m

t

F

x

dt

x

d

/

)

(

2

0

2

2

=

+

ω

- równanie niejednorodne

Podstawmy

)

cos(

)

(

0

t

F

t

F

ω

⋅

=

m

k

=

2

0

ω

)

cos(

)

sin(

)

cos(

2

t

C

a

t

C

v

t

C

x

ω

ω

ω

ω

ω

⋅

−

=

⋅

−

=

⋅

=

)

cos(

)

cos(

)

cos(

0

2

0

2

t

F

t

C

m

t

C

m

ω

ω

ω

ω

ω

⋅

+

⋅

⋅

−

=

⋅

−

)

(

2

2

0

0

ω

ω

−

=

m

F

C

•

Je

żeli

0

ω ω

<

to

0

>

C

•

Je

żeli

0

ω ω

>

to

0

<

C

•

przy du

żych wartościach

2

0

2

ω

ω

−

amplituda maleje.

•

Je

żeli

0

ω

ω

≈

to

∞

→

C

- drgania rezonansowe

)

cos(

)

(

t

C

t

x

ω

⋅

=

2

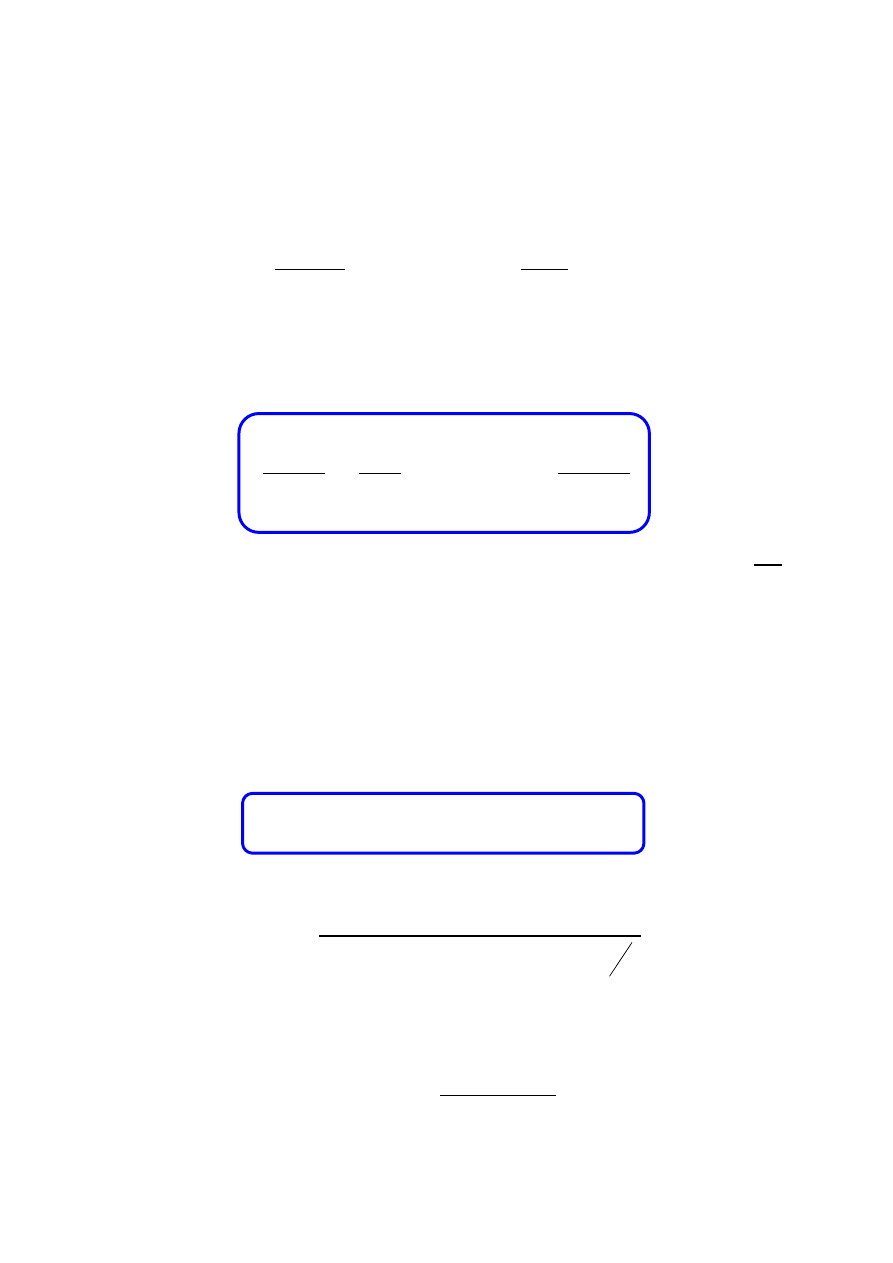
DRGANIA WYMUSZONE z TŁUMIENIEM

Równanie ruchu:

2

2

( )

d x

dx

m

kx

C

F t

dt

dt

= −

−

+

po uporz

ądkowaniu:

2

2

0

2

( )

d x

dx

F t

x

dt

m

dt

γ ω

+

+

=

gdzie

m

C

=

γ

Dla harmonicznej siły wymuszaj

ącej:

)

cos(

)

(

0

t

F

t

F

ω

⋅

=

rozwi

ązaniem równania jest:

)

cos(

)

(

0

θ

ω

+

⋅

=

t

x

t

x

(

)

[

]

2

1

2

2

2

2

2

0

0

0

/

ω

γ

ω

ω

+

−

=

m

F

x

2

2

0

tg

ω

ω

γω

θ

−

−

=

3

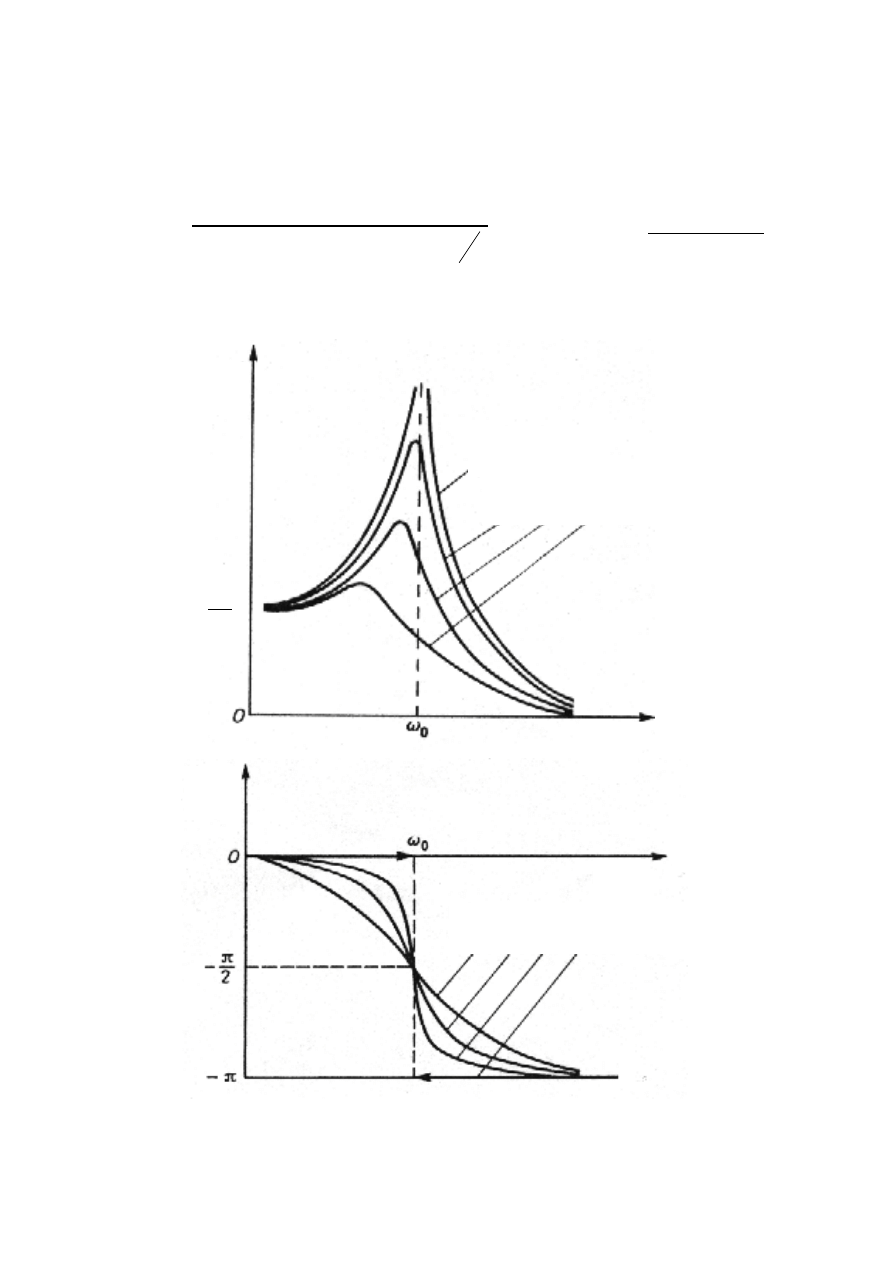
AMPLITUDA I FAZA DRGAŃ WYMUSZONYCH

(

)

[

]

2

1

2

2

2

2

2

0

0

0

/

ω

γ

ω

ω

+

−

=

m

F

x

2

2

0

tg

ω

ω

γω

θ

−

−

=

x

0

θ

ω

ω

0

F

k

γ

0

= 0

γ

1

<

γ

2

<

γ

3

γ

3

>

γ

2

>

γ

1

>

γ

0

=

0

4

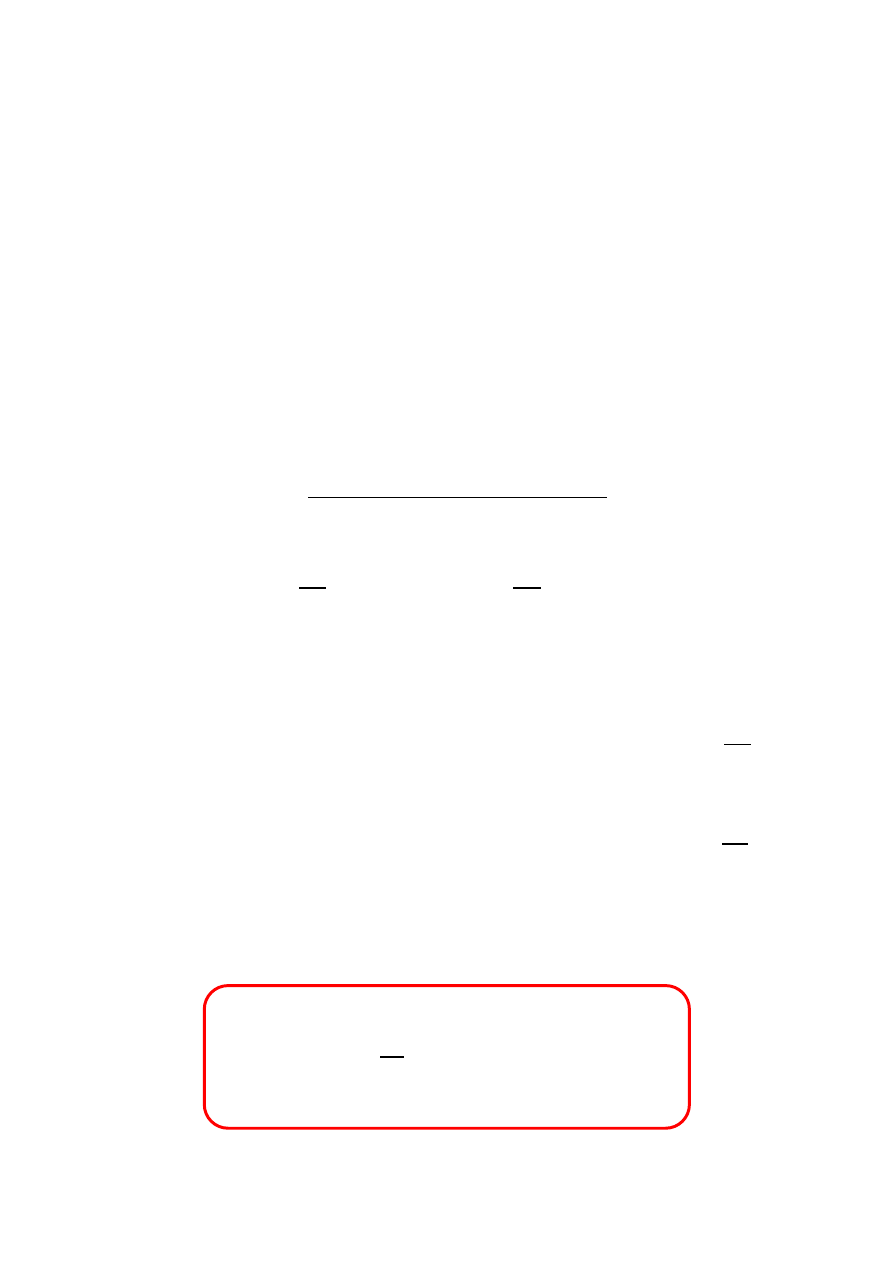
ENERGIA ZMAGAZYNOWANA

Stan ustalony

0

cos(

)

x

x

t

ω θ

=

+

Średnia energia drgań w stanie ustalonym jest stała,
równa sumie

średniej energii kinetycznej i średniej

energii potencjalnej.

Warto

ść średnia zmagazynowanej energii

>

<

+

>

<

>=

<

2

2

0

2

2

1

2

1

x

m

v

m

E

m

ω

( m

ω

0

2

= k )

(

)

(

)

2

2

0

0

2

2

2

0

0

1

cos

2

1

sin

2

x

x

t

x

x

v

x

t

v

x

ω θ

ω

ω θ

ω

=

+

<

>=

= −

+

<

>=

(

)

2

0

2

0

2

4

1

x

m

E

m

⋅

+

>=

<

ω

ω

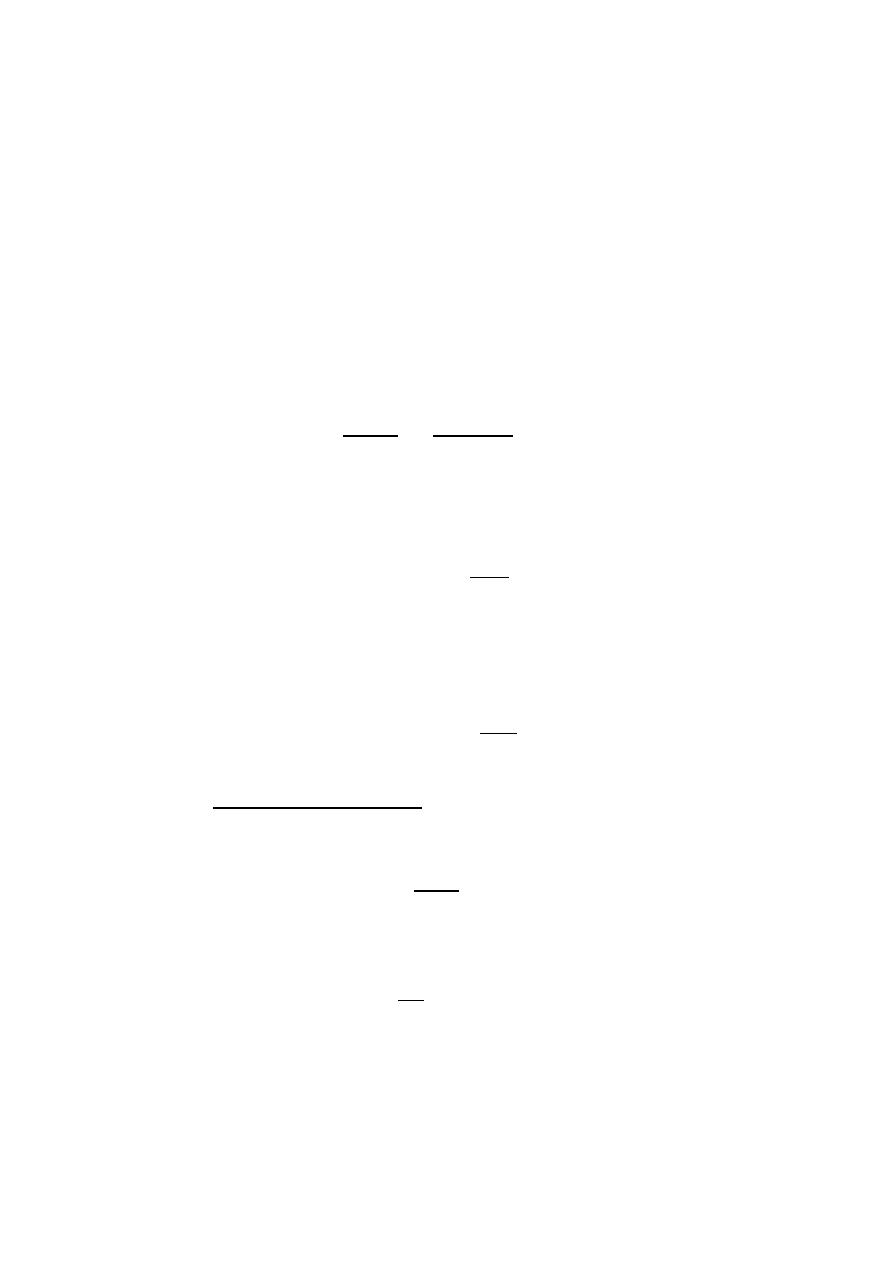
5

MOC DOSTARCZANA

Żeby utrzymać stałą amplitudę drgań trzeba dostarczać
energii z zewn

ątrz. Energia dostarczana równa jest pracy

wykonywanej przez sił

ę zewnętrzną przeciwko sile oporu.

Moc jest równa pracy wykonanej w jednostce czasu.
Jednostk

ą mocy jest 1 wat [1W=1 J/s]:

dW

F ds

P

F v

dt

dt

⋅

=

=

= ⋅

w przypadku ruchu jednowymiarowego, kiedy

F = F

x

dx

P

F

dt

=

W ruchu drgaj

ącym pracę wykonuje siła

dx

F

m

dt

γ

=

Średnia moc dostarczana:

2

2

dx

P

m

mv

dt

γ

γ





= ⋅

= ⋅









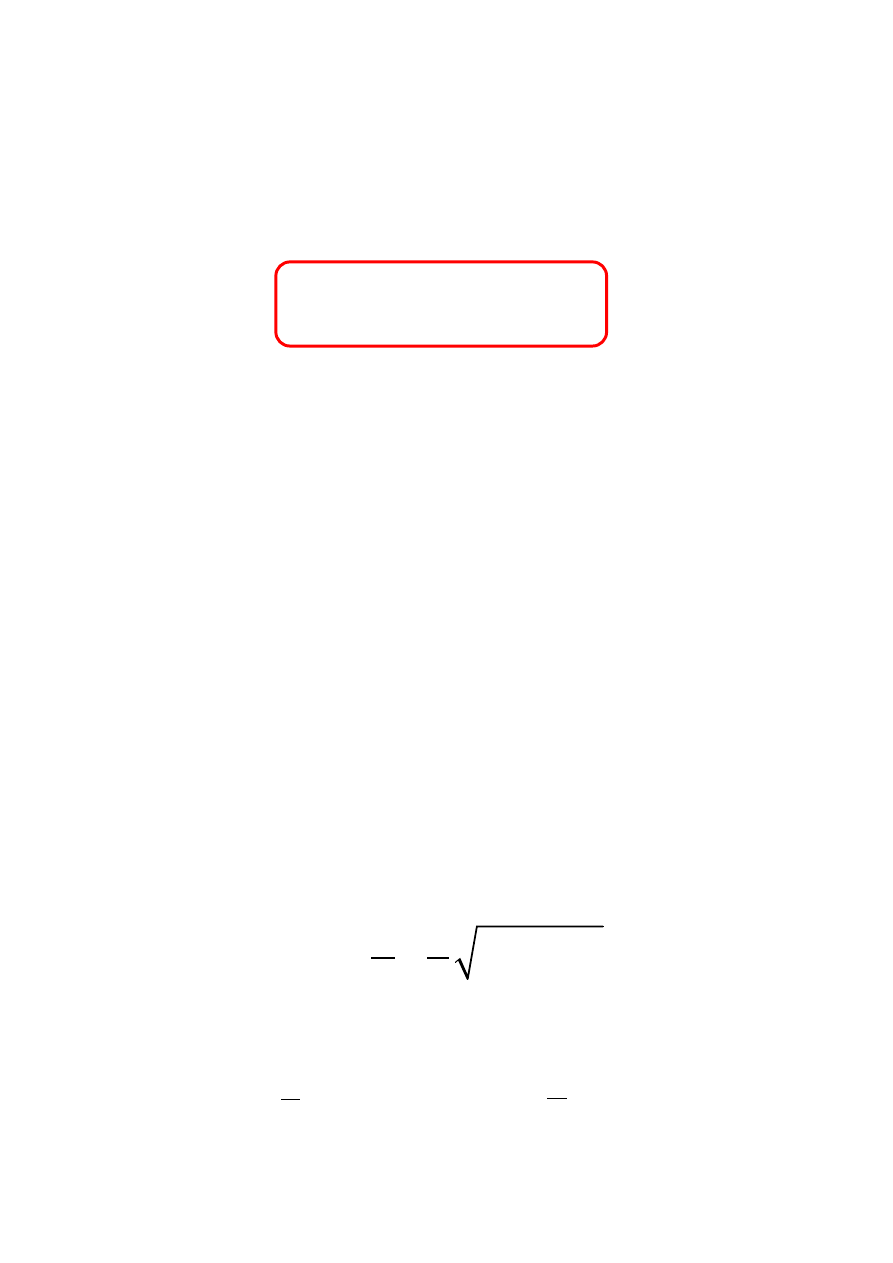
2

0

2

2

1

x

m

P

ω

γ

⋅

⋅

>=

<

•

po wł

ączeniu siły wymuszającej gromadzenie energii

•

w stanie ustalonym pokrycie strat cieplnych.

6

DRGANIA TŁUMIONE

Równanie ruchu po wy ł

ączeniu siły F(t)

0

2

0

=

+

+

x

x

x

ω

γ

rozwi

ązanie w postaci

t

x

A e

α

=

Sprawdzenie:

2

2

0

0

x

x

x

α

αγ

ω

+

+

=

2

2

0

(

)

0

x

α

αγ ω

+

+

=

po podzieleniu przez

x

otrzymuje si

ę

równanie kwadratowe na

α

:

2

2

0

0

α αγ ω

+

+

=

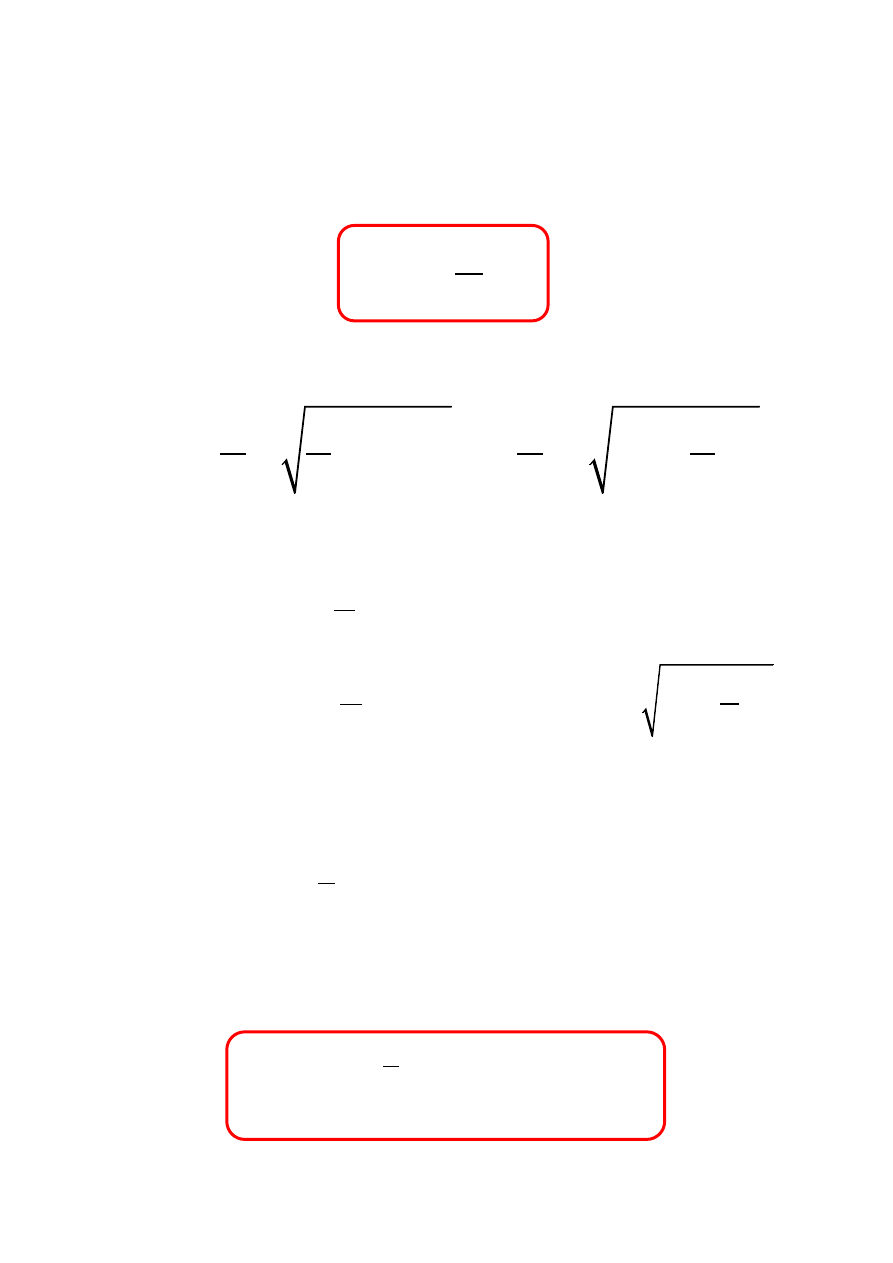
którego rozwi

ązanie jest postaci:

2

2

0

1

4

2

2

γ

α

γ

ω

= − ±

−

Mo

żliwe są dwa przypadki:

2

2

0

1

4

ω

γ

>

lub

2

2

0

1

4

ω

γ

≤

7

DRGANIA TŁUMIONE

Przypadek 1

2

2

0

1

4

ω

γ

>

α

jest liczb

ą zespoloną

2

2

2

2

0

0

1

1

2

4

2

4

i

γ

γ

α

γ

ω

ω

γ

= − ±

−

= − ±

−

Dwa rozwi

ązania

1

2

1

1

1

2

2

2

t

i

t

t

i

t

x

A e

x

A e

γ

γ

γ

ω

γ

ω

−

+

−

−



=







=



2

2

0

1

4

γ

ω

ω

γ

=

−

Ogólne rozwi

ązanie

1

2

1

2

(

)

t

i

t

i

t

x

e

A e

A e

γ

γ

γ

ω

ω

−

⋅

−

=

+

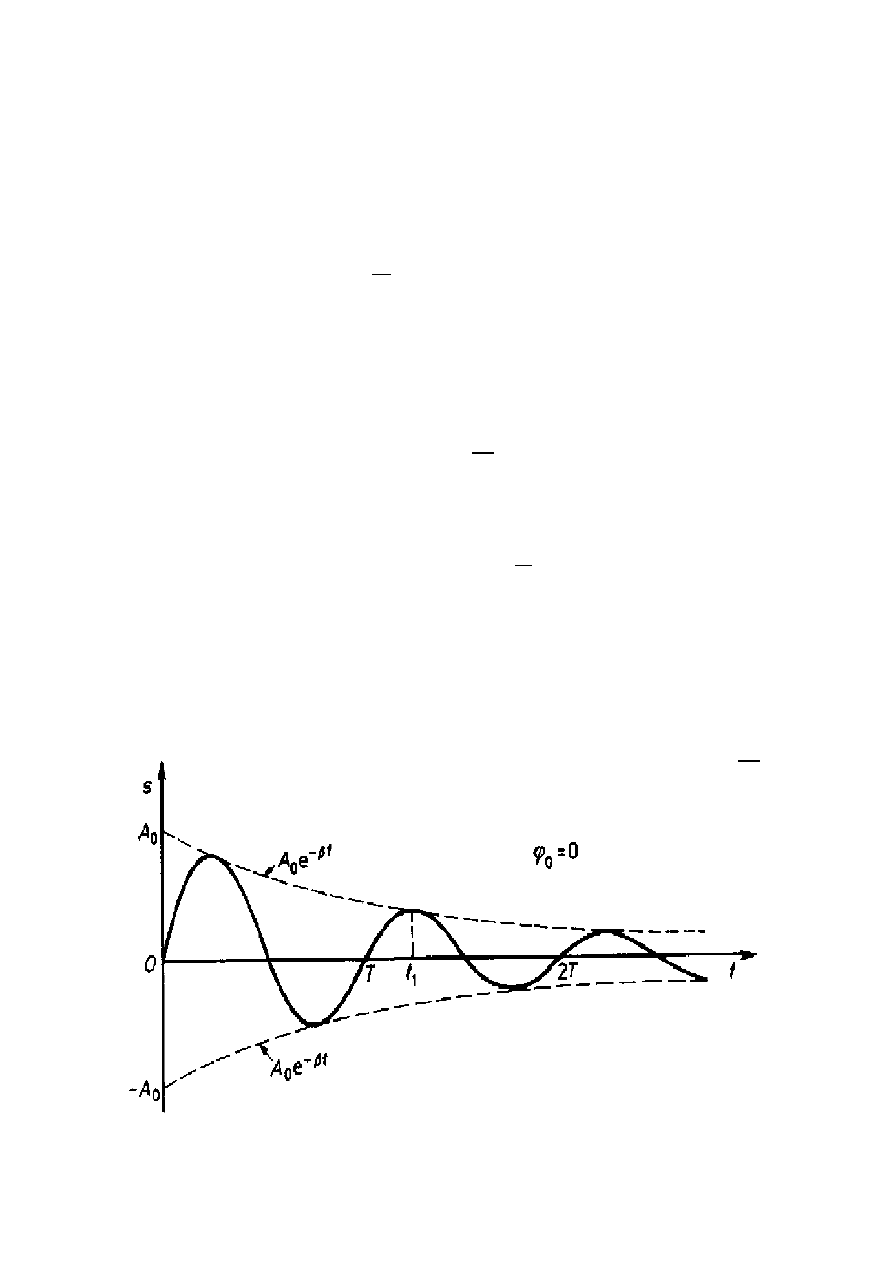
Rozwi

ązanie rzeczywiste

1

2

0

0

cos(

)

t

x

A e

t

γ

γ

ω

ϕ

−

⋅

=

+

8

DRGANIA TŁUMIONE

Rozwi

ązanie:

1

2

0

0

cos(

)

t

x

A e

t

γ

γ

ω

ϕ

−

⋅

=

+

opisuje oscylacje o cz

ęstości

2

/

1

2

2

0

)

4

1

(

γ

ω

ω

γ

−

=

i amplitudzie

1

2

0

( )

t

A t

A e

γ

−

⋅

=

A

0

i

ϕ

0

wyznacza si

ę

z warunków pocz

ątkowych

2

/

1

2

2

0

)

4

1

(

γ

ω

ω

γ

−

=

9

RUCH APERIODYCZNY

Przypadek 2

2

2

0

1

4

ω

γ

≤

2

2

0

1

1

2

4

α

γ

γ

ω

= −

±

−

jest liczb

ą rzeczywistą

1

2

1

2

t

t

x

A e

A e

α

α

=

+

2

2

1

0

1

1

2

4

α

γ

γ

ω

= −

+

−

2

2

2

0

1

1

2

4

α

γ

γ

ω

= −

−

−

Rozwi

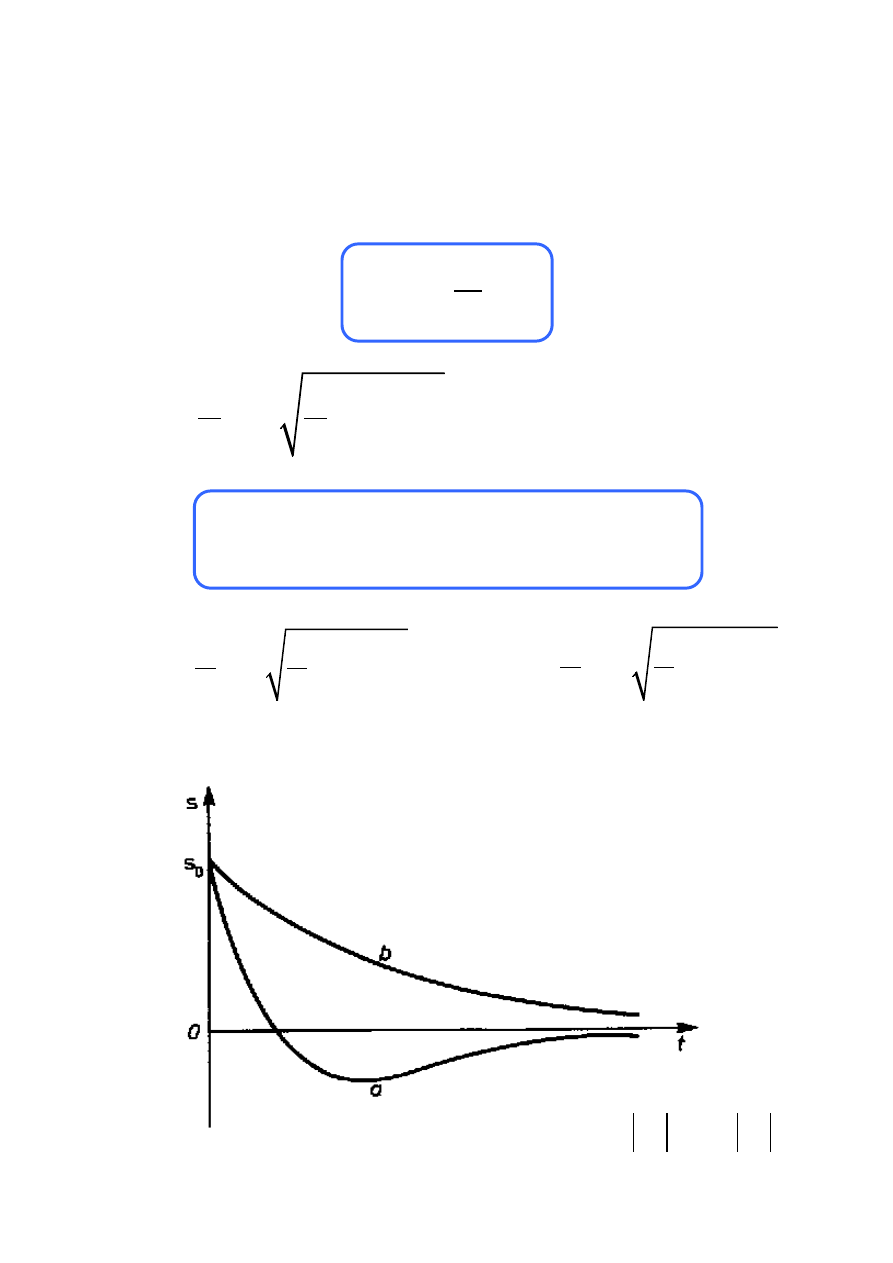
ązanie jest rzeczywiste i aperiodyczne.

typ (a) gdy v

0

║

−

s

0

oraz

0

1

0

s

v

α

>

10

ROZWIĄZANIE OGÓLNE

I ROZWIĄZANIE SZCZEGÓLNE

Równanie niejednorodne:

m

F

x

x

x

/

2

0

=

+

+

ω

γ

Rozwiązanie szczególne tego równania dla F=F

0

cos

ω

t:

( )

0

( )

cos(

)

s

x

t

x

t

ω θ

=

+

Je

żeli do

x

(s)

dodamy funkcj

ę będącą rozwiązaniem

równania jednorodnego:

0

2

0

=

+

+

x

x

x

ω

γ

czyli:

1

( )

2

0

0

( )

c o s(

)

t

o

x

t

A e

t

γ

γ

ω

ϕ

−

⋅

=

+

lub

1

2

( )

1

2

( )

a t

a t

o

x

t

A e

A e

=

+

nazywan

ą rozwiązaniem ogólnym równania

niejednorodnego, to suma tych rozwi

ązań też będzie

rozwi

ązaniem równania niejednorodnego.

)

(

)

(

)

(

)

(

)

(

t

x

t

x

t

x

s

o

+

=