Układ oscylacyjny na który działa siła wymuszająca.
2
d x
m
= − kx + F ( t)
2
dt
d 2 x
2
+ ω x = F ( t) / m dt 2
0
- równanie niejednorodne
2
k
ω0 =
Podstawmy F ( t ) = F ⋅ cos(ω t ) 0
m
x = C ⋅ cos(ω t) v = − Cω ⋅ sin(ω t) 2
a = − Cω ⋅ cos(ω t) 2
− mω C ⋅ cos( t
ω )
2
= − mω ⋅ C ⋅ cos( t
ω ) + F ⋅ cos( t
ω )
0
0
x( t) = C ⋅ cos(ω t) F 0
C =
m(
2
2
ω − ω )
0
• Jeżeli ω << ω
C >
0 to
0
• Jeżeli ω >>ω to C < 0
0
• przy dużych wartościach 2
2
ω − ω amplituda maleje.
0
• Jeżeli ω ≈ ω
C →
0 to
∞ - drgania rezonansowe
1
DRGANIA WYMUSZONE z TŁUMIENIEM
d 2 x
dx
m
+ C
+ kx = F
dt 2
dt
d 2 x
dx
2
F
+
γ + ω x
0
=
dt 2
dt
m
C
gdzie γ = m
Dla harmonicznej siły wymuszającej:
F ( t ) = F ⋅ cos(ω t) 0
Rozwiązaniem równania jest:
x( t ) = x ⋅ cos( ω t + θ ) 0
F /
0
x =
m
0
([ 2ω −ω +γ ω
0
)22 2 ]122
γω
tgθ = − 2
2
ω −ω
0
2
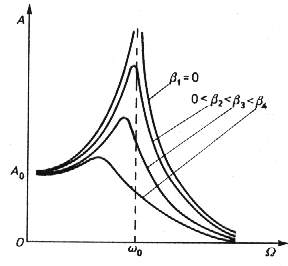
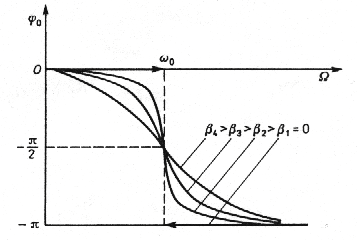
AMPLITUDA I FAZA DRGAŃ WYMUSZONYCH
F /
0
γω
x =
m
θ
0
([
tg = − 2
2
ω −ω
+ γ ω
2
ω −ω
0
0
)22 2 ]122
3
Średnia energia drgań w stanie ustalonym jest stała, równa sumie średniej energii kinetycznej i średniej energii potencjalnej.
Wartość średnia zmagazynowanej energii
< E
ω
m >= 1 m <
1
2
v > +
2
m
x
0 <
2 >
2
2
1
2
2
x = x cos ω t < x >=
x
0
0
2
1
2
2
2
v = − x ω sin ω t < v >=
x ω
0
0
2
1
< E >=
ω +ω ⋅
m
( 2 2
m
x
0 )
2
0
4
4
Żeby utrzymać stałą amplitudę drgań trzeba dostarczać energii z zewnątrz. Energia dostarczana równa jest pracy wykonywanej przez siłę zewnętrzną przeciwko sile oporu.
Moc jest równa pracy wykonanej w jednostce czasu.
Jednostką mocy jest 1 wat [1W=1 J/s]:
dW
F ⋅ ds
P =
=
= F ⋅ v
dt
dt
w przypadku ruchu jednowymiarowego, kiedy F = Fx dx
P = F dt
W ruchu drgającym moc dostarczana jest przez siłę dx
F = mγ dt
Średnia moc dostarczona:
2
dx
2
< P >=< γ ⋅ m
>=< γ ⋅ mv >
dt
1
2
2
< P >= γ ⋅ m ⋅ω x 0
2
• po włączeniu siły wymuszającej gromadzenie energii
• w stanie ustalonym pokrycie strat cieplnych.
5
2
x
+ x
γ + ω x = 0
0
~
~
iα t
rozwiązanie x = A e
Sprawdzenie:
( iα ) 2
2
x + iαγ x + ω x = 0
0
2
~
(
2
−α + iαγ + ω ) iα t
Ae
= 0
0
2
2
α − α
i γ − ω = 0
0
( równanie kwadratowe na α)
γ 1
2
2
α = i ±
− γ + 4ω0
2
2
1
1
2
2
α = γ i ± ω − γ
0
2
4
Możliwe są dwa przypadki:
2
1
2
1 2
ω − γ > 0
2
ω − γ ≤
0
0
4
lub
0
4
6
Przypadek 1
2
1 2
ω − γ > 0
0
4
Dwa rozwiązania
− 1
~
γ
ω
x
~
1 =
t
i
t
A e 2 e
γ
1
1
−
~
γ
1
t
−
2
2
i ω t
ω0 − γ =
x~
ω
4
2
= A e 2 e
γ
2
Ogólne rozwiązanie
~
−γ / 2
ˆ iω t
γ
ˆ
− ω
x = e
(
i
t
A e
+ A e γ )
1
2
Rozwiązanie rzeczywiste
γ t / 2
x =
−
A e
cos(ωγ t + ϕ )
0
0
Otrzymaliśmy oscylacje o częstości
1
2
2
1 / 2
ω = (
γ
ω − γ )
0
4
i amplitudzie
−γ t / 2
A( t ) = A e
0
A0 i ϕ0 wyznacza się z warunków początkowych 7
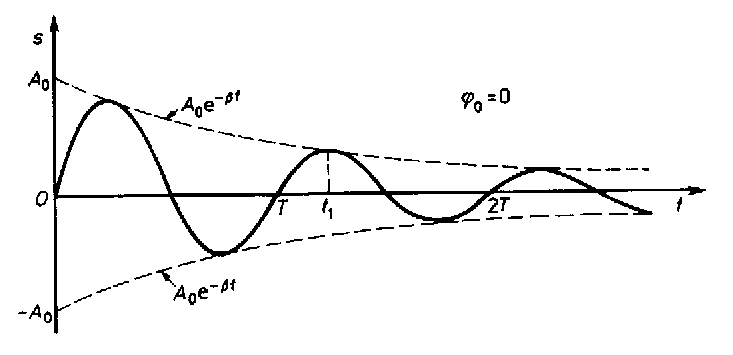
DRGANIA TŁUMIONE
γ t / 2
x =
−
A e
cos(ωγ t + ϕ )
0
0
A t
δ
( )
= ln
= /
1
(
)
2 T
γ
A t
( + T)
logartymiczny dekrement tłumienia.
8
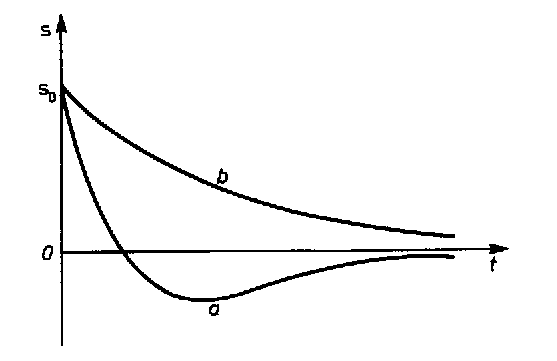
RUCH APERIODYCZNY
Przypadek 2
2
1 2
ω − γ ≤ 0
0
4
1
1
2
2
α ± = iγ ± i
γ − ω 0
2
4
jest liczbą urojoną
− a t
− a t
x = A e 1 + A e 2
1
2
gdzie a1 = ia+ oraz a2 = ia−
Rozwiązanie jest rzeczywiste i aperiodyczne.
>
typ (a) gdy v
v
α s
0 -s0 oraz
0
1
0
9
I ROZWIĄZANIE SZCZEGÓLNE
Równanie niejednorodne:
x
+ γ x
2
+ ω x = F / m
0
Rozwiązanie szczególne równania niejednorodnego: ( )
x s ( t ) = x cos( ω t + ϕ + θ ) 0
0
Jeżeli do x(s) dodamy funkcję będącą rozwiązaniem równania jednorodnego:
2
x
+ γ x + ω x = 0
0
czyli:
( o )
γ t / 2
x
t =
−
A e
ω γ t + ϕ
( )
cos(
)
0
0
lub
( o )
− a t
− a t
x
( t ) = A e 1 + A e 2
1
2
nazywaną rozwiązaniem ogólnym równania niejednorodnego, to suma tych rozwiązań też będzie rozwiązaniem równania niejednorodnego.
x( t)
( o)
= x ( t)
( s)
+ x ( t)
10
Wyszukiwarka
Podobne podstrony:
F13 drgania wymuszone
5 drgania wymuszone, Politechnika Łódzka, Do Wojciechowskiego
MF10 drgania wymuszone
Wykład 14 Drgania wymuszone oscylatora harmonicznego ppt
MF13 drgania wymuszone
MF10 drgania wymuszone
DRGANIA WYMUSZONE1a
drgania wymuszone nietlumione prezentacja new
drgania wymuszone, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane,
Drgania wymuszone z tłumieniem układu o jednym stopniu swobody, wip, Drgania
10 Rezonans w obwodzie szeregowym RLC Elektromagnetyczne drgania wymuszone w obwodzie RLC
Losowe drgania wymuszone fundamentu skrzyniowego
Drgania wymuszone układów o 1 st swobody
MF13 drgania wymuszone
Drgania wymuszone oscylatora tłumionego
Drgania wymuszone nietłumione układu o jednym stswobody, wip, Drgania
fiztomi10, MIBM WIP PW, fizyka 2, laborki fiza(2), 10-Rezonans w obwodzie szeregowym RLC. Elektromag
drgania wymuszone, mechanika 1
więcej podobnych podstron