11/ 1

11. DRGANIA TŁUMIONE I WYMUSZONE

(4 strony)

DRGANIA TŁUMIONE

Drgania układu na który działa siła tłumiąca proporcjonalna do wartości prędkości, ale

przeciwnie skierowana

dt

dx

F

r

β

−

=

(tak jak na przykład siła lepkości) opisuje równanie:

2

2

d x

dx

m

kx

dt

dt

β

= − −

po uporządkowaniu przyjmuje postać:

2

2

0

2

0

d x

dx

x

dt

dt

γ ω

+

+

=

gdzie

m

/

β

γ

=

.

Równanie to ma dwa rodzaje rozwiązań, inne dla

ω

0

> γ/2

ι

inne dla

ω

0

> γ/2.

•

W przypadku, gdy

ω

0

> γ/2

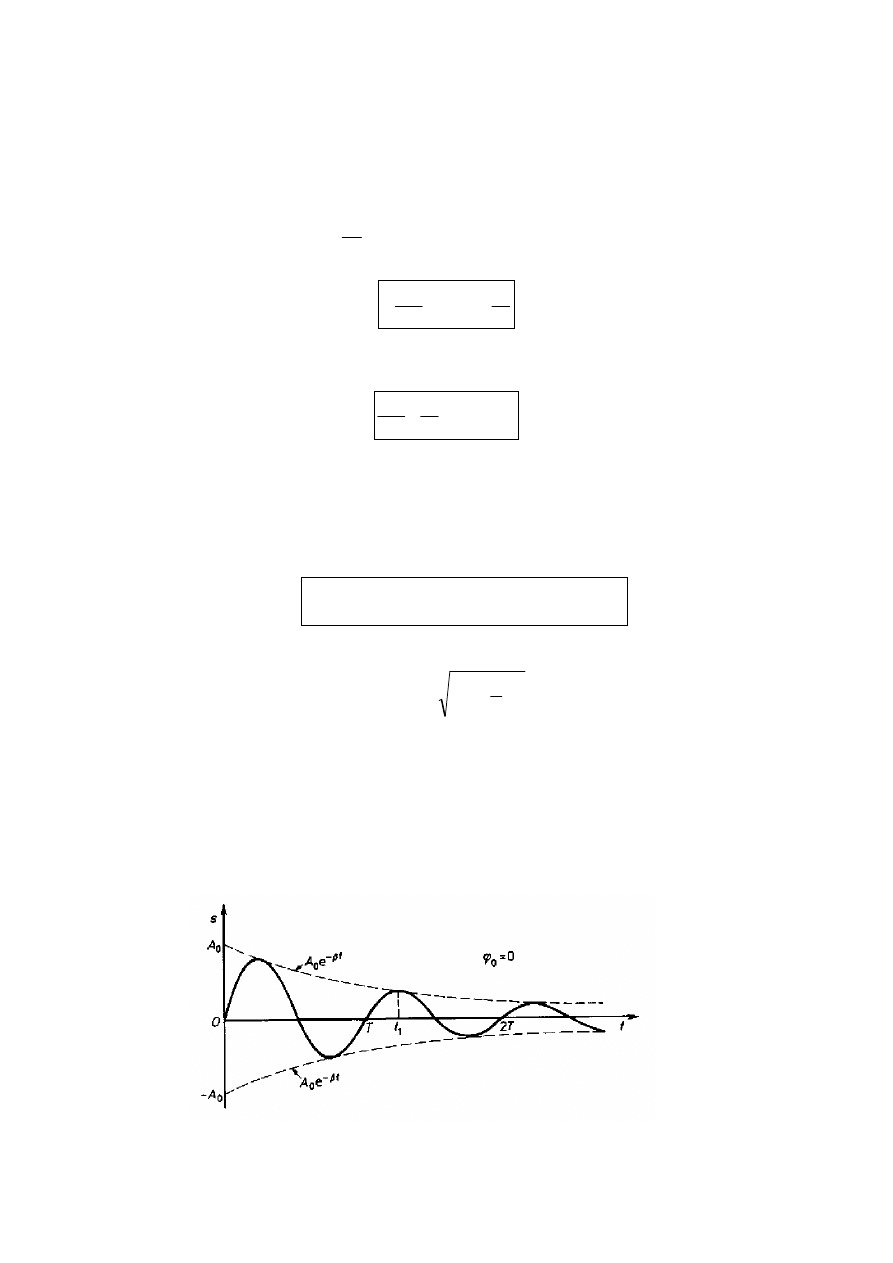
rozwiązanie jest postaci

)

cos(

0

2

/

0

ϕ

ω

γ

γ

+

=

−

t

e

A

x

t

opisujące drgania o częstości

2

2

0

4

1

γ

ω

ω

γ

−

=

,

malejącej z czasem amplitudzie

/ 2

0

( )

t

A t

A e

γ

−

=

i przesunięciu fazowym

ϕ

0

.

Wartości A

0

i

ϕ

0

można wyznaczyć z wartości początkowych wychylenia z położenia

równowagi x

0

= x(0) oraz prędkości v

0

= v(0)

drgania tłumione

11/ 2

•

W przypadku gdy

ω

0

< γ/2

rozwiązanie jest sumą dwóch funkcji wykładniczych

t

a

t

a

e

A

e

A

x

2

1

2

1

−

−

+

=

gdzie

2

0

2

1

4

1

2

1

ω

γ

γ

α

−

−

−

=

oraz

2

0

2

2

4

1

2

1

ω

γ

γ

α

−

+

−

=

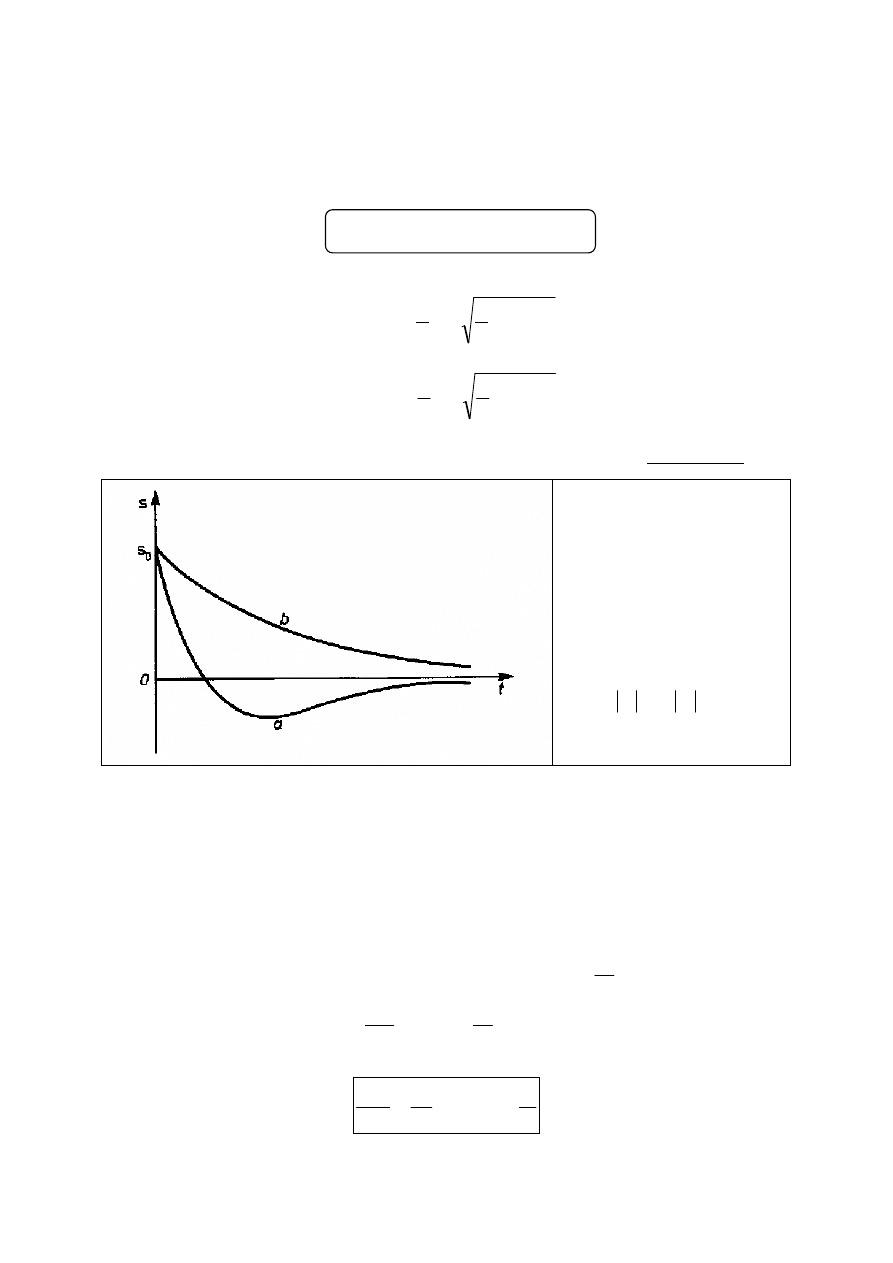
Ruch ciała w tym przypadku nie jest okresowy, mówimy, że jest to ruch aperiodyczny

Rozwiązanie typu (a)
występuje gdy v

0

jest

przeciwnie skierowane
do x

0

oraz

0

1

0

x

v

α

>

DRGANIA WYMUSZONE

Drgania wymuszone powstają w układzie pod wpływem zewnętrznego źródła energii o
zmieniającym się w czasie natężeniu np. drganie membrany głośnika pod wpływem
zmiennego pola elektromagnetycznego, drgania obiektu wywołane ruchem podłoża, drgania
w obwodzie elektrycznym wywołane zmiennym napięciem, drgania ładunków w atomach i
cząsteczkach pod wpływem zmiennego pola elektrycznego fali świetlnej.

Równanie drgań wymuszonych siłą F(t) i tłumionych siłą

dt

dx

F

r

β

−

=

jest postaci

)

(

2

2

t

F

dt

dx

kx

dt

x

d

m

+

−

−

=

β

lub w wygodniejszej postaci

m

F

x

dt

dx

dt

x

d

=

+

+

2

0

2

2

ω

γ

11/ 3

gdzie

m

/

β

γ

=

. Podstawiając siłę wymuszającą

)

cos(

0

0

ϕ

ω

+

=

t

F

F

otrzymuje się

rozwiązanie w postaci drgań o tej samej częstości co siła wymuszająca. Wychylenie ciała z
położenia równowagi opisywane jest przez funkcję

)

cos(

0

0

ϕ

θ

ω

+

+

=

t

x

x

o

amplitudzie

(

)

[

]

2

1

2

2

2

2

2

0

0

0

/

ω

γ

ω

ω

+

−

=

m

F

x

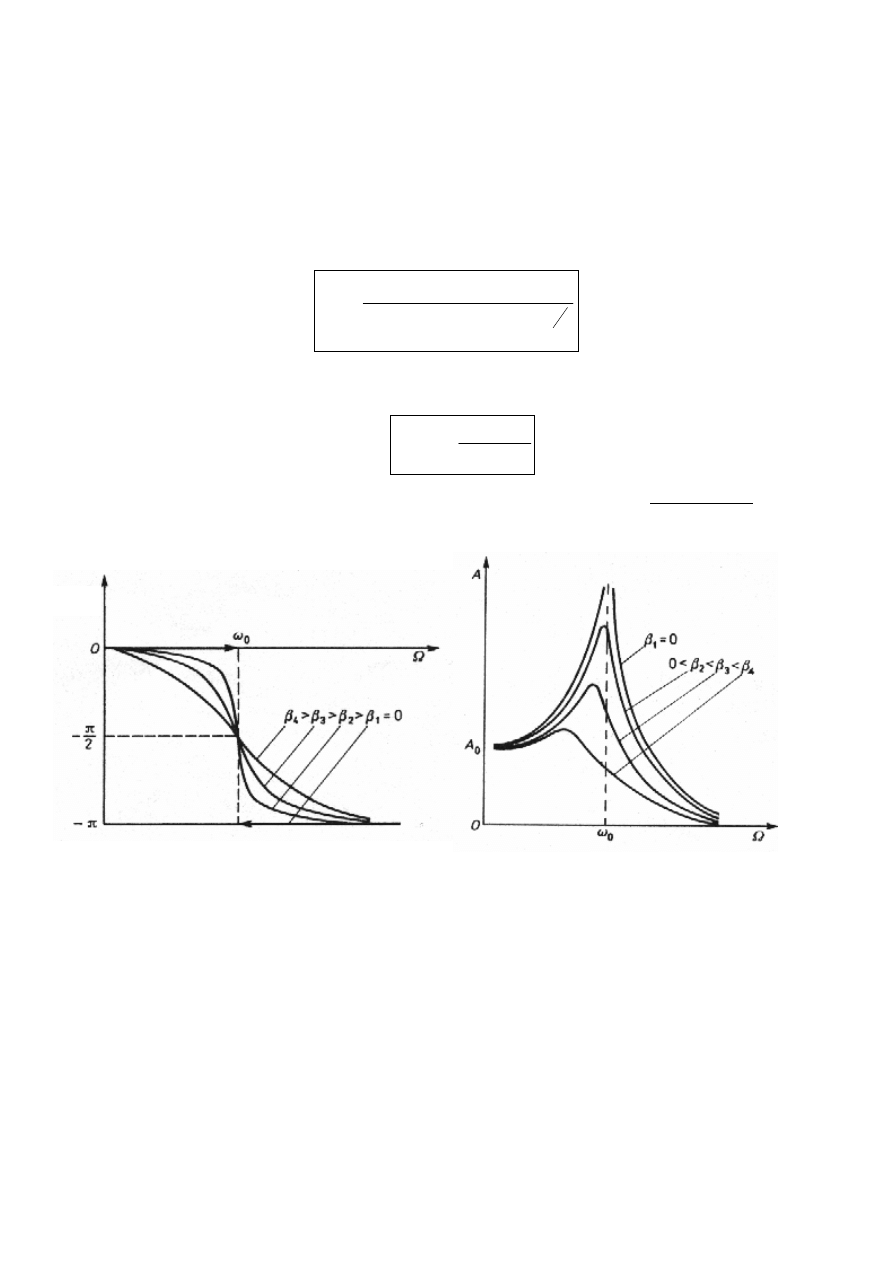
i przesunięciu fazowym

θ

danym równaniem

2

2

0

tg

ω

ω

γω

θ

−

−

=

Kąt

θ

ma wartość ujemną dla wszystkich

ω

, co odpowiada wychyleniu

x

opóźnionemu w

fazie w stosunku do siły F .

dla

β

= 0

amplituda x

0

= C

a różnica faz ,

θ,

jest

równa 0 lub

−π

θ