11. DRGANIA WYMUSZONE (4 strony) Drgania wymuszone powstają w układzie pod wpływem zewnętrznego źródła energii o zmieniającym się w czasie natężeniu np. drganie membrany głośnika pod wpływem zmiennego pola elektromagnetycznego, drgania obiektu wywołane ruchem podłoża, drgania w obwodzie elektrycznym wywołane zmiennym napięciem, drgania ładunków w atomach i cząsteczkach pod wpływem zmiennego pola elektrycznego fali świetlnej.

Równanie ruchu oscylatora z siłą wymuszającą

2

d x

(*) m

= − kx + F( t) - jest równaniem niejednorodnym 2

dt

Funkcja F ( t) może być różnej postaci. Ponieważ dowolną funkcję okresową można przedstawić w postaci szeregu Fouriera a funkcję nieokresową w postaci całki Fouriera przeanalizujmy przypadek

F ( t ) = F ⋅ cos( ω t ) 0

Sprawdźmy czy x = C ⋅ cos( ω t ) jest rozwiązaniem równania ruchu (*), czyli czy układ porusza się w zgodnym rytmie z siłą wymuszającą:

x = C ⋅ cos( ω t )

v = − C ω ⋅ sin( ω t )

2

a = − C ω

⋅ cos( ω t)

podstawiając to do równania (*) otrzymujemy:

2

− mω C ⋅ cos(ω t)

2

= − mω ⋅ C ⋅ cos(ω t) + F ⋅ cos(ω t) 0

0

gdzie

2

ω = k / m jest częstością kątową drgań swobodnych. Po podzieleniu przez cosω t 0

otrzymujemy warunek na C.

F 0

C = m( 2

2

ω − ω )

0

Funkcja x = C ⋅ cos(ω t) jest więc rozwiązaniem równania tylko dla wyznaczonej wartości C.

Masa m drga z częstością siły wymuszającej, a amplituda tych drgań zależy od F , ω i ω : 0

0

a) Jeżeli ω < ω to C > 0 , przesunięcie jest tak samo skierowane jak siła.

0

b) Jeżeli ω > ω to C < 0 , przesunięcie jest odwrotnie skierowane niż siła - przeciwna faza 0

Ponadto przy dużych wartościach

2

2

ω − ω amplituda drgań maleje.

0

c) Jeżeli ω ≈ ω to C → ∞ . Jeżeli częstość siły dobierzemy tak, aby była zgodna z 0

częstością drgań własnych to otrzymujemy bardzo duże amplitudy. Oczywiście nie można osiągnąć C → ∞ ponieważ w rzeczywistym świecie istnieją siły oporu, których dotąd nie uwzględniliśmy.

Drgania wymuszone z tłumieniem

Dodajmy teraz do równań siłę tarcia. Istnieje wiele sytuacji (siła lepkości w płynach, spadek napięcia na oporze U=IR), gdy siła tarcia jest proporcjonalna do szybkości.

dx

2

d x

dx

Równanie ruchu z siłą tłumiącą F = −β

jest postaci m

= − kx − β

+ F( t) ;

r

dt

2

dt

dt

Sprowadźmy to równanie do wygodniejszej postaci

11/ 1

d 2 x

dx

2

F

+

γ + ω x

0

=

dt 2

dt

m

gdzie γ = β / m . Podstawiając siłę F = F cos(ω t + ϕ ) otrzymuje się rozwiązanie w postaci 0

0

drgań o tej samej częstości co siła wymuszająca. Wychylenie ciała z położenia równowagi opisywane jest przez funkcję

x = x cos(ω t + θ + ϕ )

0

0

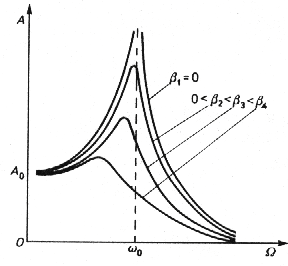
o amplitudzie

F /

0

x =

m

0

([ 2

ω − ω

+ γ ω

0

)2

2

2

]122

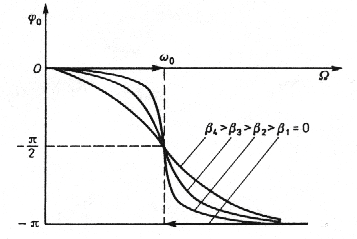
i przesunięciu fazowym θ danym równaniem

γω

tgθ = −

2

2

ω − ω

0

Kąt θ ma wartość ujemną dla wszystkich ω, co odpowiada wychyleniu x opóźnionemu w fazie w stosunku do siły F .

θ

dla β = 0 amplituda x0 = C a różnica faz , θ, jest równa 0 lub −π

ENERGIA

Sumę energii kinetycznej i potencjalnej oscylatora nazwa się energią zmagazynowaną. Jej wartość średnia w stanie ustalonym, kiedy amplituda się nie zmienia, jest stała.

< E

ω

m >= 1 m <

1

2

v > +

2

m

x

0 <

2 >

2

2

1

2

2

x = x cosω t

,

< x >=

x

0

0

2

podstawiając

1

2

2

2

v = − x ω sin ω t

,

< v >=

x ω

0

0

2

11/ 2

Otrzymujemy

1

< E >= m ω + ω ⋅

m

( 2 2 x

0 )

2

0

4

Na początku, po włączeniu siły F zachodzi gromadzenie energii i związany z tym wzrost amplitudy drgań a następnie w stanie ustalonym układ pobiera energię tylko na pokrycie występujących strat cieplnych. Siła wykonuje dużą pracę wprowadzając oscylator w ruch.

Aby go utrzymać w ruchu musi jedynie pokonywać tarcie. Jeżeli tarcie jest małe oscylator może uzyskiwać bardzo duże energie.

Otrzymane rozwiązanie x = x cos(ω t + θ + ϕ ) 0

0

opisuje drgania w stanie ustalonym.

DRGANIA TŁUMIONE

Po wyłączeniu siły wymuszającej straty energii, które do tej pory były uzupełniane przez pracę wykonywaną przez siłę wymuszającą F spowodują malenie energii zmagazynowanej.

Równanie będzie teraz :

2

x

+ γ x + ω

x = 0

0

• W przypadku, gdy ω0 > γ/2

rozwiązanie jest postaci

γ t / 2

x =

−

A e

cos( ω γ t + ϕ )

0

0

i opisuje oscylacje o częstości

1

2

2

ωγ = ω − γ ,

0

4

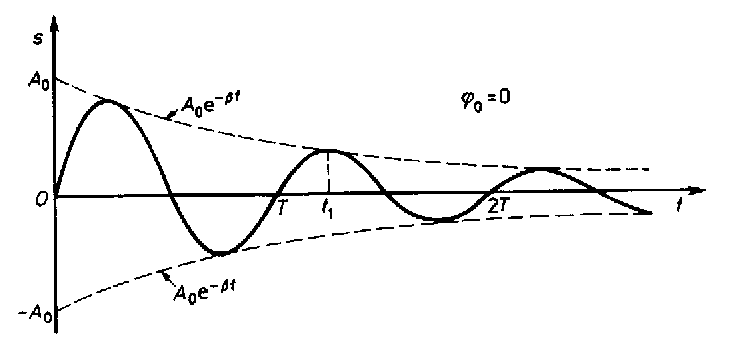
malejącej z czasem amplitudzie

−γ t / 2

A( t ) = A e

o

i przesunięciu fazowym ϕ0.

Wartości A0 i ϕ0 można wyznaczyć z wartości początkowych wychylenia z położenia równowagi x0 = x(0) oraz prędkości v0 = v(0) Wielkość

A t

δ

( )

= ln

= 1

( / )

2 T

γ

A t

( + T)

nazywamy logartymicznym

dekrementem tłumienia.

drgania tłumione

11/ 3

• W przypadku gdy ω0 < γ/2

rozwiązanie jest sumą dwóch funkcji wykładniczych

− a t

− a t

x = A e 1 + A e

2

1

2

gdzie

1

1

2

2

α = − γ −

γ − ω

1

0

2

4

oraz

1

1

2

2

α = − γ +

γ − ω

2

0

2

4

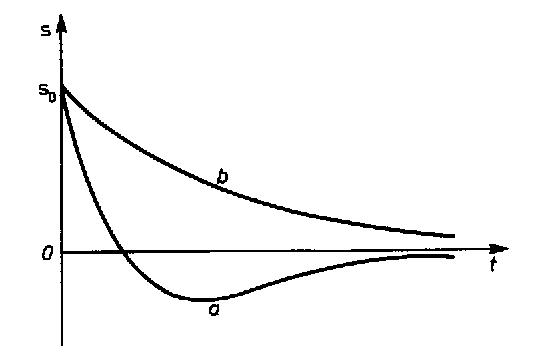
Ruch ciała w tym przypadku nie jest okresowy, mówimy, że jest to ruch aperiodyczny Rozwiązanie typu (a)

występuje gdy v0 jest

przeciwnie skierowane

do x0

oraz v > α x

0

1

0

11/ 4