Metoda Maxwella – Mohra
Układy statycznie niewyznaczalne
Metoda sił
Zasada minimum energii

Metody energetyczne

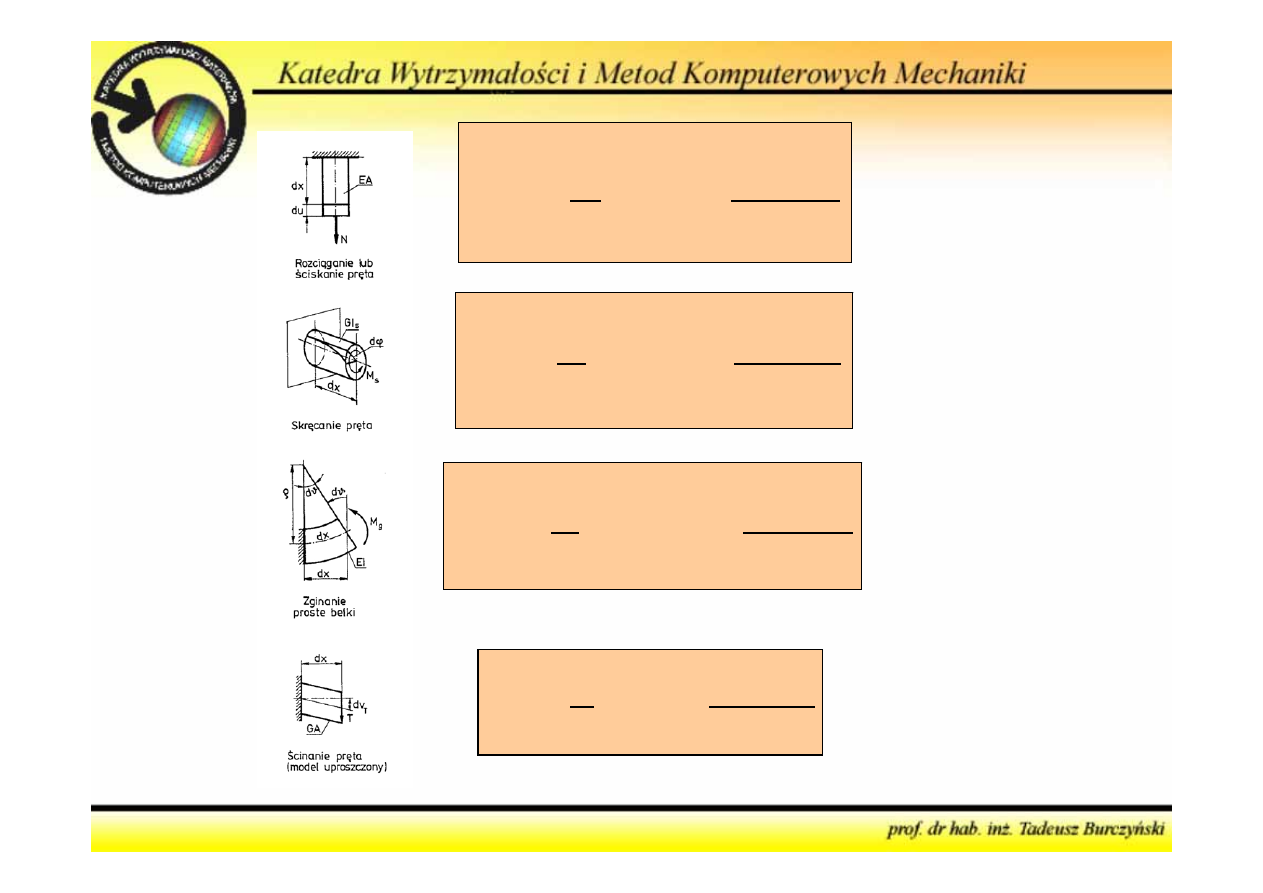
2

1

2

2

N dx

dV

Ndu

EA

=

=

2

1

2

2

S

s

S

M dx

dV

M d

GI

ϕ

=

=

2

1

2

2

g

g

M dx

dV

M d

EI

ϑ

=

=

2

1

2

2

T

T dx

dV

Tdv

GA

β

=

=

Energia

sprężysta

układu

prętowego

(

)

(

)

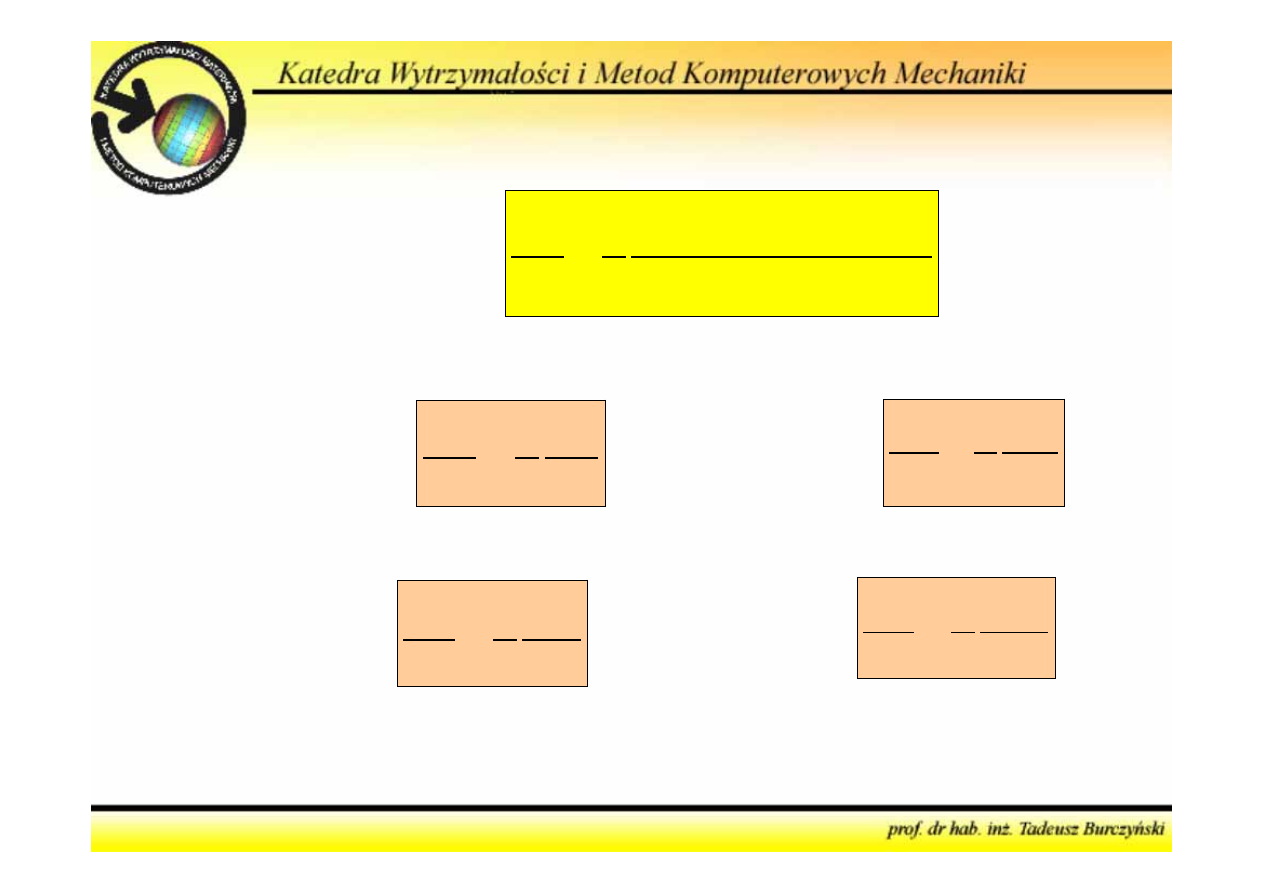
2

1

2

Sila wewnętrzna

dV

dx

Sztywnosc

=

2

1

2

dV

N

dx

EA

=

Rozciąganie:

2

1

2

g

M

dV

dx

EI

=

Zginanie:

2

1

2

s

s

M

dV

dx

GI

=

Skręcanie:

2

1

2

dV

T

dx

GA

β

=

Ścinanie:

(

)

(

)

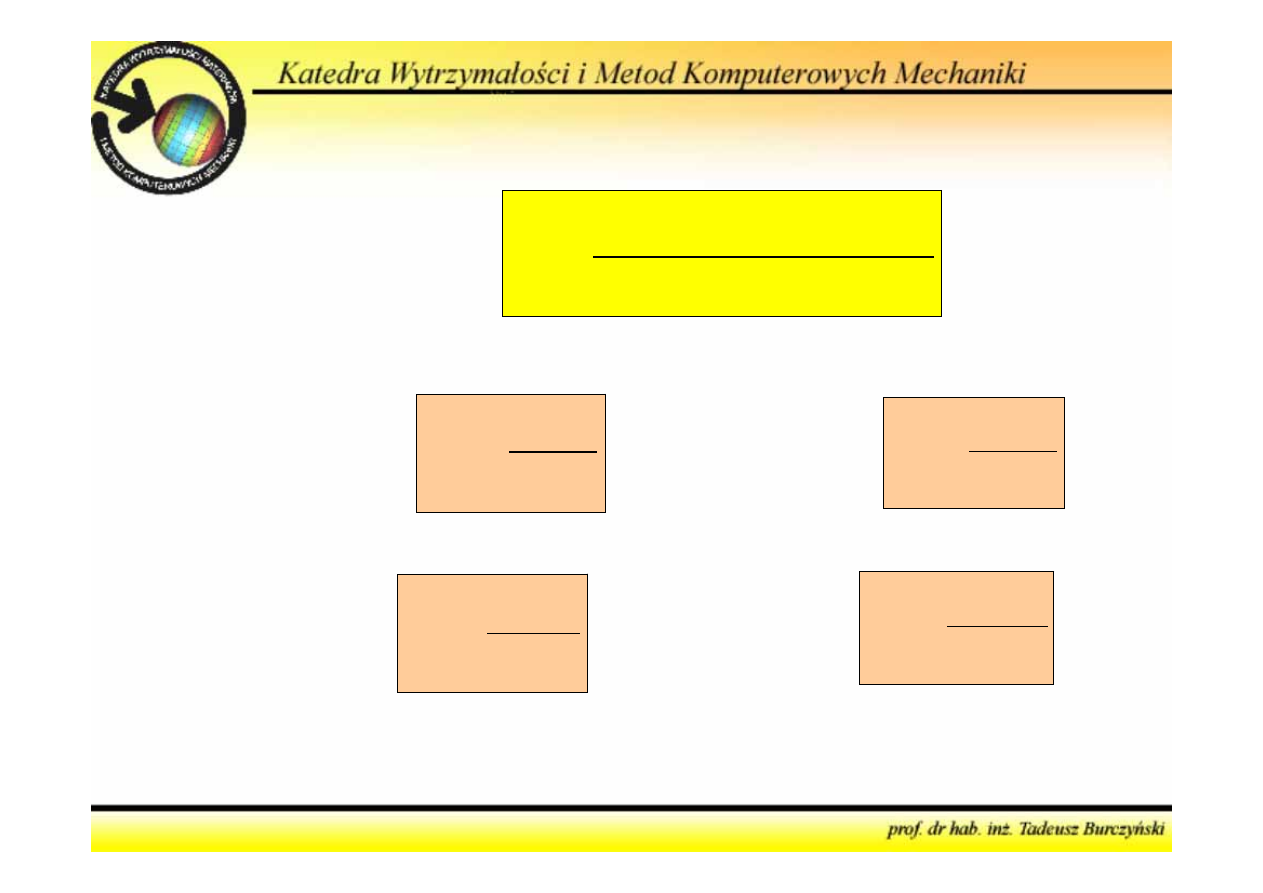
2

0

2

l

Sila wewnętrzna dx

V

Sztywnosc

=

∫

2

0

2

l

N dx

V

EA

=

∫

Rozciąganie:

2

0

2

l

g

M dx

V

EI

=

∫

Zginanie:

2

0

2

l

s

s

M dx

V

GI

=

∫

Skręcanie:

2

0

2

l

T dx

V

GA

β

=

∫

Ścinanie:

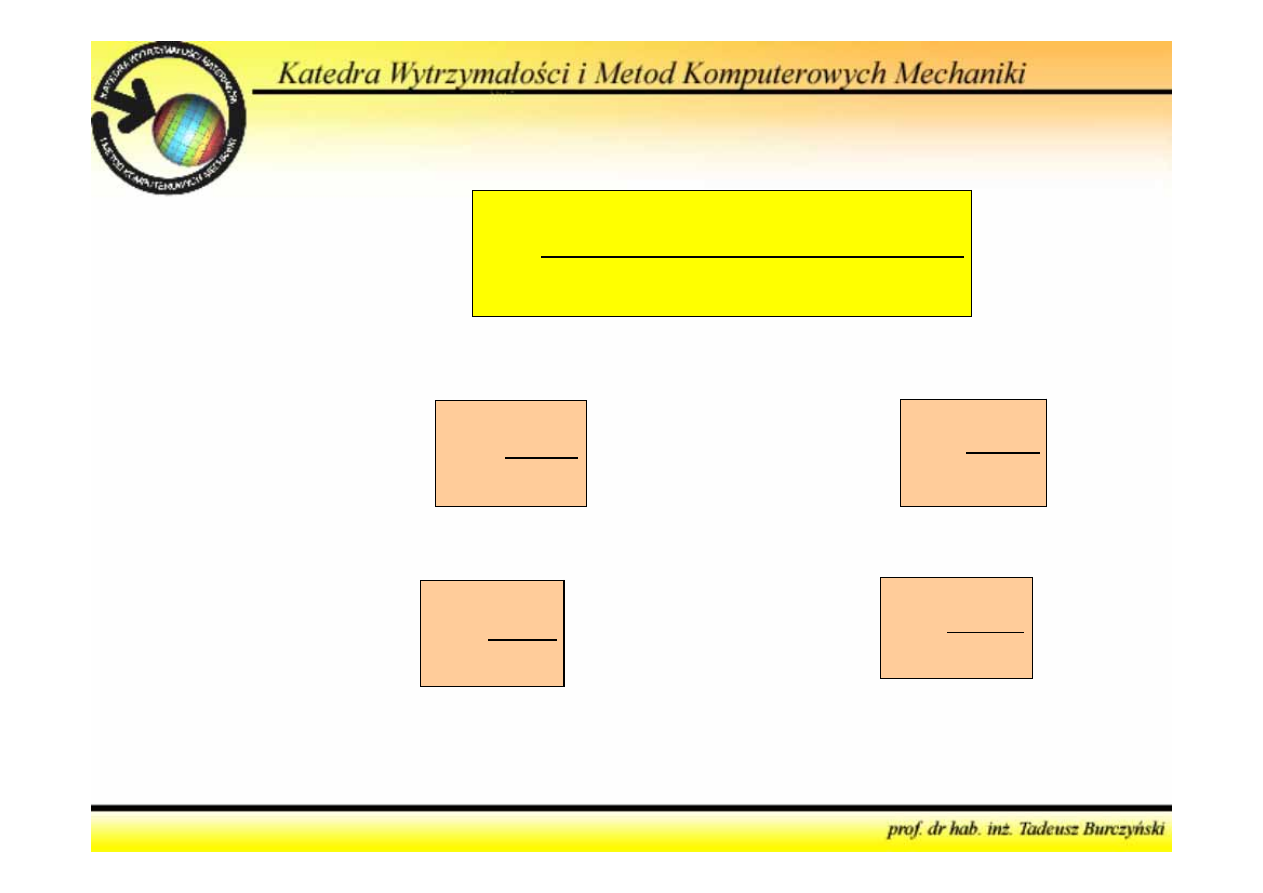
2

2

N l

V

EA

=

Rozciąganie:

Jeśli

N

oraz

EA

nie zależą od

x

2

2

s

s

M l

V

GI

=

Skręcanie:

Jeśli

M

s

oraz

GI

s

nie zależą od

x

2

2

g

M l

V

EI

=

Zginanie:

Jeśli

M

g

oraz

EI

nie zależą od

x

2

2

T l

V

GA

β

=

Ścinanie:

Jeśli

T

oraz

GA

nie zależą od

x

(

)

(

)

2

2

Sila wewnętrzna dlugosc

V

Sztywnosc

=

Jeśli

siła wewnętrzna

oraz

sztywność

nie zależą od

x

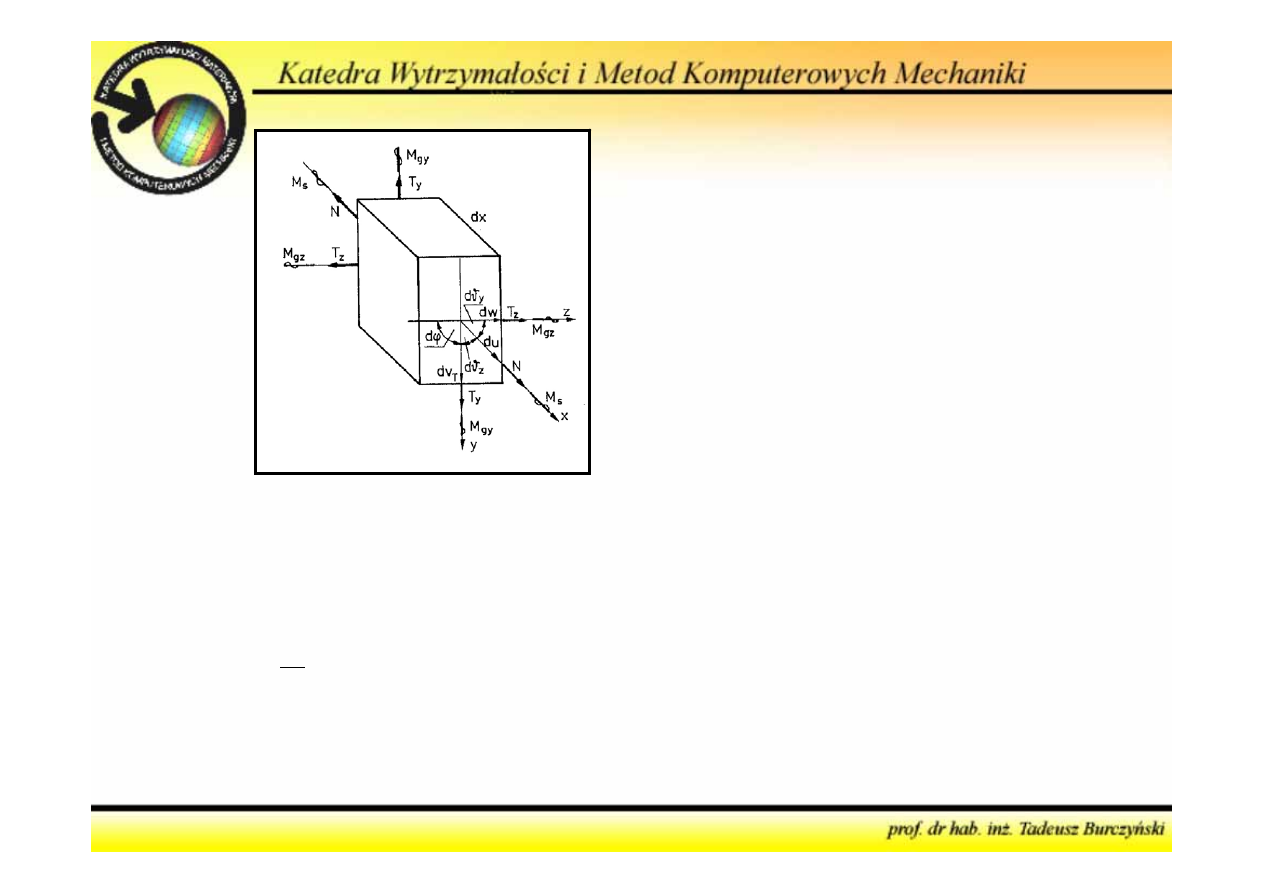
W przypadku ogólnym energia
sprężysta odkształcenia odcinka
pręta o długości dx będzie równa
sumie prac składowych sił
wewnętrznych

N, M

s

, M

gy

, M

gz

, T

y

, T

z

na odpowiadających im
przemieszczeniach

du, d

ϕ

, d

θ

y

, d

θ

z

,

d

υ

T

, dw

T

.

Jeśli odcinek pręta o długości dx uznać za odrębny układ, to

N, M

s

,

M

gy

, M

gz

, T

y

, T

z

należy traktować jako siły zewnętrzne

(

)

1

2

s

gy

y

gz

z

y

T

z

T

dV

Ndu M d

M d

M d

T d

T dw

ϕ

ϑ

ϑ

υ

=

+

+

+

+

+

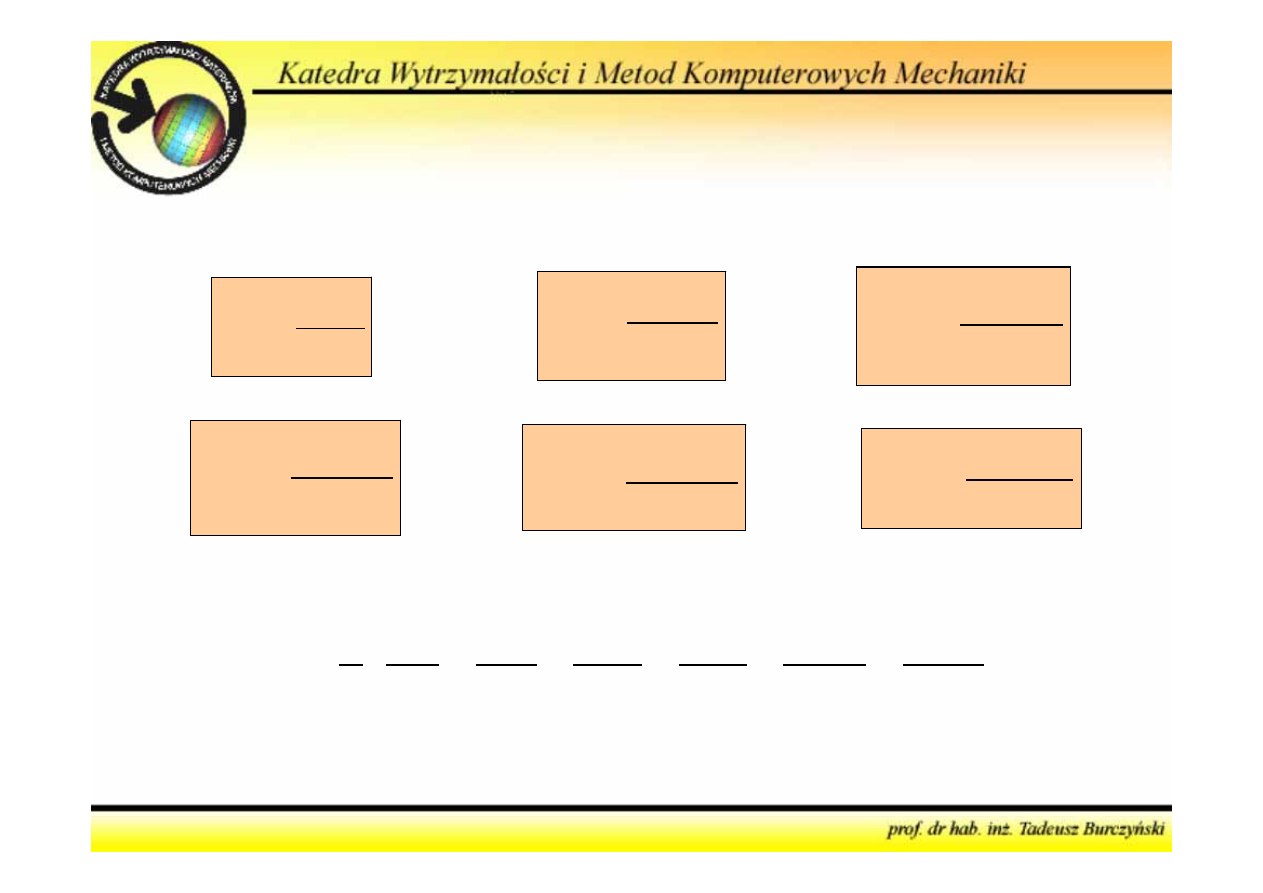
Po uwzględnieniu, że przemieszczenia są następującymi
funkcjami składowych sił wewnętrznych

Ndx

du

EA

=

s

s

M dx

d

GI

ϕ

=

gy

y

y

M dx

d

EI

ϑ

=

gz

z

z

M dx

d

EI

ϑ

=

y y

T

T dx

d

GA

β

υ

=

z z

T

T dx

dw

GA

β

=

Otrzymamy zależność

2

2

2

2

2

2

1

2

gy

gz

y y

s

z z

s

y

z

M

M

T

N

M

T

dV

dx

EA GI

EI

EI

GA

GA

β

β

⎛

⎞

=

+

+

+

+

+

⎜

⎟

⎜

⎟

⎝

⎠

Energia sprężysta w pręcie prostym w

przypadku ogólnym

2

2

2

2

2

2

0

1

2

l

gy

gz

y y

s

z z

s

y

z

M

M

T

N

M

T

V

dx

EA GI

EI

EI

GA

GA

β

β

⎛

⎞

=

+

+

+

+

+

⎜

⎟

⎜

⎟

⎝

⎠

∫

Metody energetyczne wyznaczania

przemieszczeń

• Castigliana

•

Maxwella-Mohra

Metoda Maxwella-Mohra

W celu określenia dowolnego uogólnionego przemieszczenia

u

w

prętowym układzie liniowosprężystym metodą Maxwell-Mohra
wykonamy następujące operacje:

• Wyznaczymy siły

N, M

s

, M

gy

, M

gz

, T

y

, T

z

w prętach układu, wywołane

obciążeniem rzeczywistym

• Obciążamy układ siłą jednostkową odpowiadającą
poszukiwanemu przemieszczeniu

u

i wyznaczamy

N’, M

s

’, M’

gy

, M’

gz

,

T’

y

, T’

z

, które wywołuje ona w prętach

1

W miejsce jednostkowej siły wprowadźmy siłę
uogólnioną o wartości P (P=0), która wywoła dodatkowo
siły wewnętrzne:

'

2

' 2

'

2

'

2

' 2

' 2

0

(

)

(

)

(

)

1

2

(

)

(

)

(

)

gy

gy

s

s

l

s

y

gz

gz

y

y

y

z

z

y

z

M

PM

N PN

M

PM

EA

GI

EI

V

dx

M

PM

T

PT

T

PT

EI

GA

GA

β

β

⎛

⎞

+

+

+

+

+

+

⎜

⎟

⎜

⎟

=

⎜

⎟

+

+

+

⎜

⎟

+

+

⎜

⎟

⎝

⎠

∫

'

'

'

'

'

',

,

,

,

,

s

gy

gz

y

z

PN PM PM

PM

PT PT

0

P

V

u

P

=

∂

⎛

⎞

= ⎜

⎟

∂

⎝

⎠

1

1

Metoda Maxwella-Mohra

'

'

'

'

'

'

0

l

gy

gy

gz

gz

y y

y

s

s

z z

z

s

y

z

M M

M M

T T

NN

M M

T T

u

dx

EA

GI

EI

EI

GA

GA

β

β

⎛

⎞

=

+

+

+

+

+

⎜

⎟

⎜

⎟

⎝

⎠

∫

W celu określenia przemieszczenia

u

metodą Maxwella-Mohra dla

dowolnego liniowosprężystego układu prętowego należy dokonać
sumowania całek, obliczonych dla poszczególnych przedziałów
(prętów).

Statycznie niewyznaczalne układy

prętowe

Układ prętowy jest

statycznie niewyznaczalny

, jeśli nie można określić

reakcji w podporach czy sił wewnętrznych w przekrojach prętów,
posługując się wyłącznie równaniami równowagi.

Liczba sił statycznie niewyznaczalnych, czyli

hiperstatycznych

, równa

różnicy między liczbą wszystkich sił niewiadomych, a liczbą równań
równowagi, określa stopień statycznej niewyznaczalności układu
prętowego.

Statycznie niewyznaczalne układy

prętowe

Rozwiązanie każdego zadania statycznie niewyznaczalnego oprócz
wykorzystania warunków równowagi wymaga uwzględnienia
geometrycznych i fizycznych aspektów odkształcalności ciała.

Formułuje się w tym celu trzy grupy zależności:

A. Równania równowagi,

B. Warunki geometryczne

C. Związki fizyczne

Wyróżnić można dwie podstawowe metody rozwiązywania zadań

statycznie niewyznaczalnych:

- metodę sił - metodę przemieszczeń

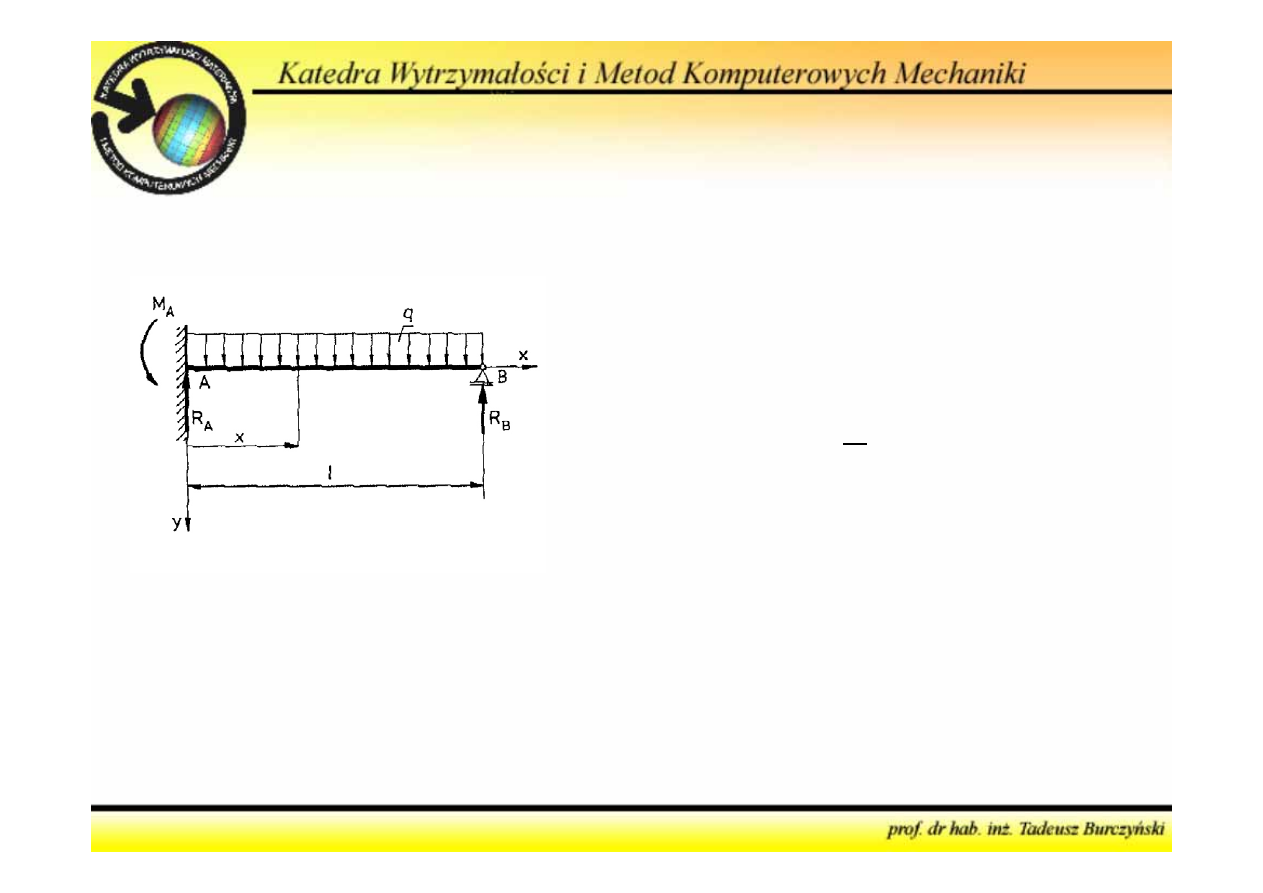
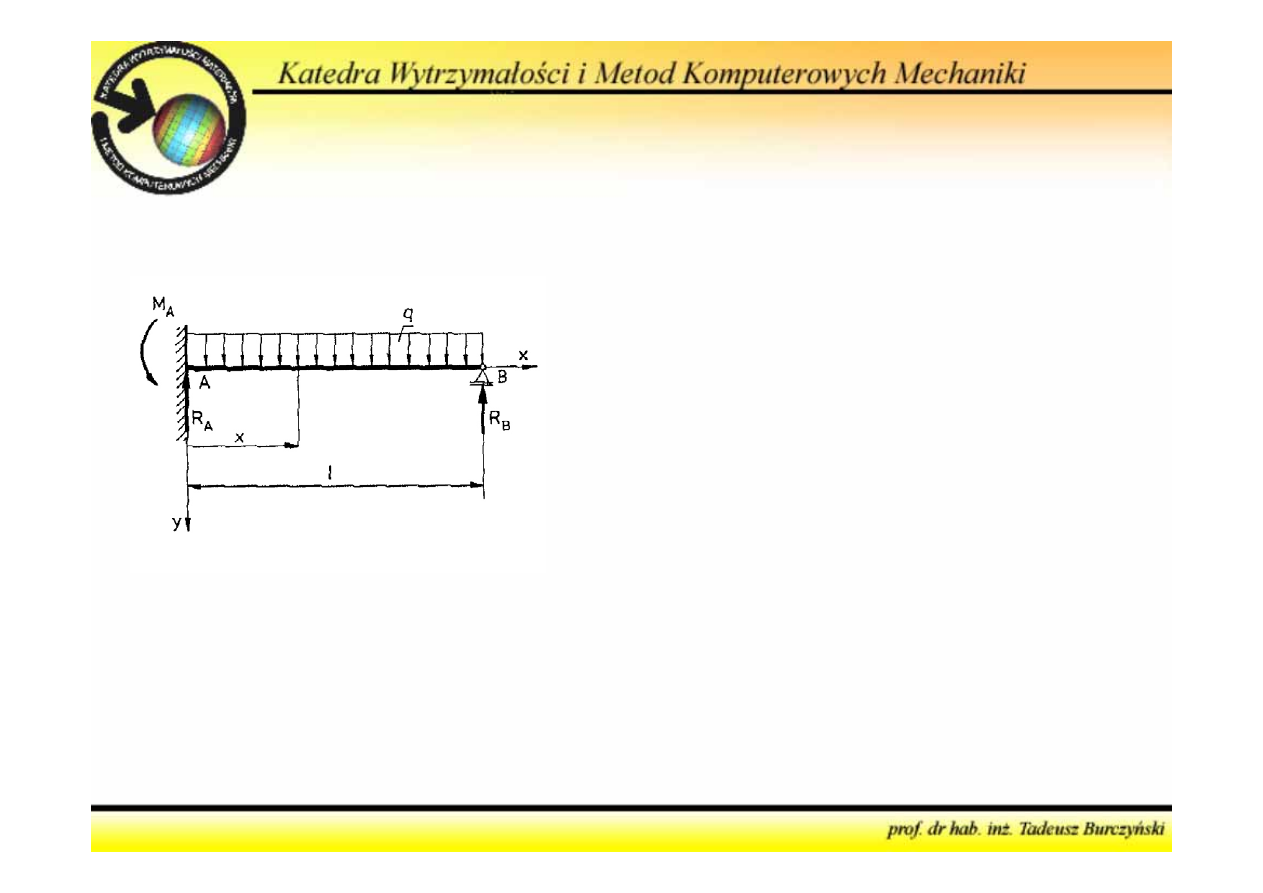
Równania równowagi

2

0

1

0

2

A

B

A

A

ql R

R

M

R l

ql

−

−

=

−

+

−

=

Równania:

2

Niewiadome:

3

Zadanie jednokrotnie (

3-2

) statycznie niewyznaczalne

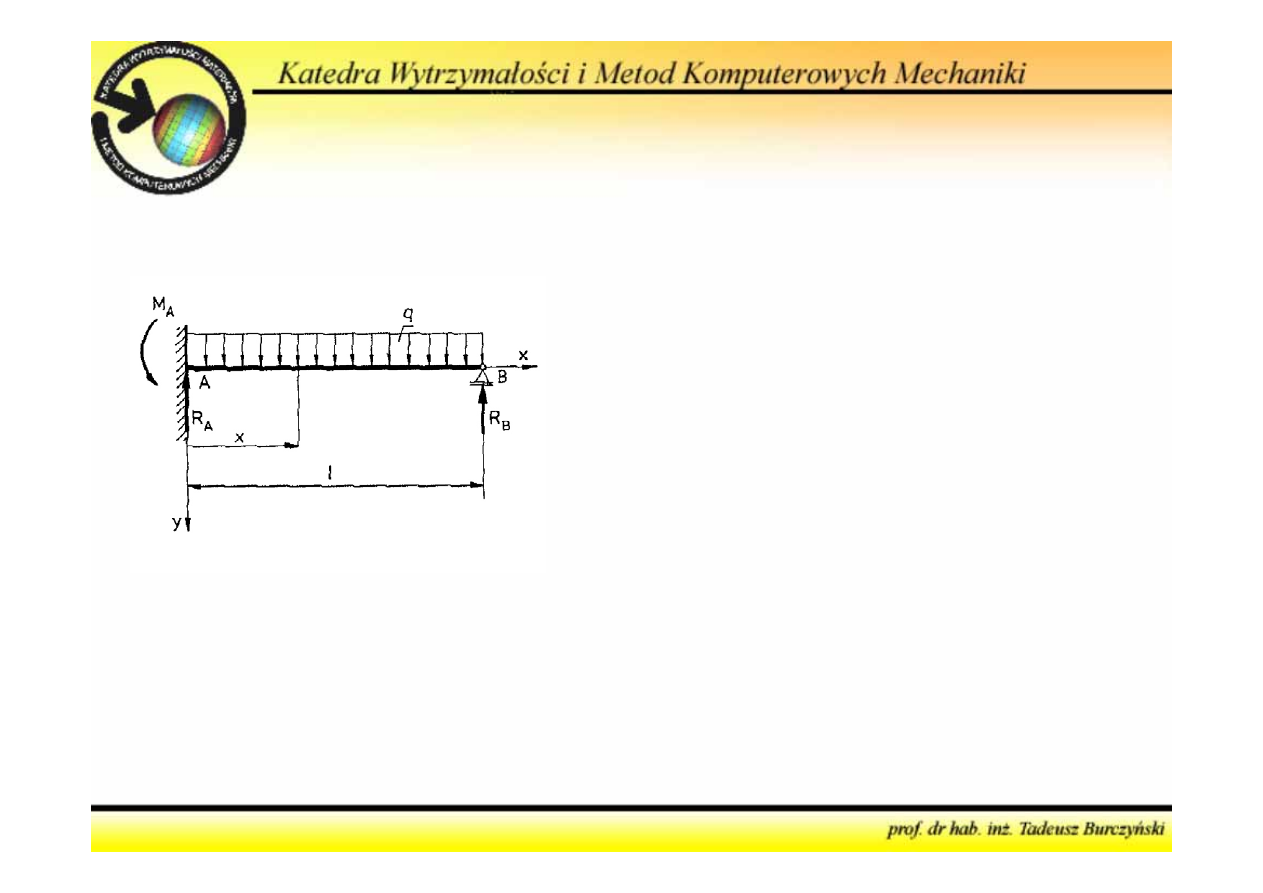
Warunki geometryczne

0

B

υ

=

Reakcja R

B

(traktowana jako wielkość

hiperstatyczna) jest spowodowana

podparciem belki w punkcie B, co odpowiada

następującemu warunkowi geometrycznemu

Związki fizyczne

Związek fizyczny powinien uzależniać

υ

B

od

sił działających na belkę oraz jej własności

sprężystych.

Okazuje się, że warunek geometryczny

υ

B

=0 jest po prostu dodatkowym warunkiem

brzegowym.

Metoda sił

1. Określić rodzaj i liczbę wielkości podporowych i sformułować

równania równowagi

Algorytm postępowania

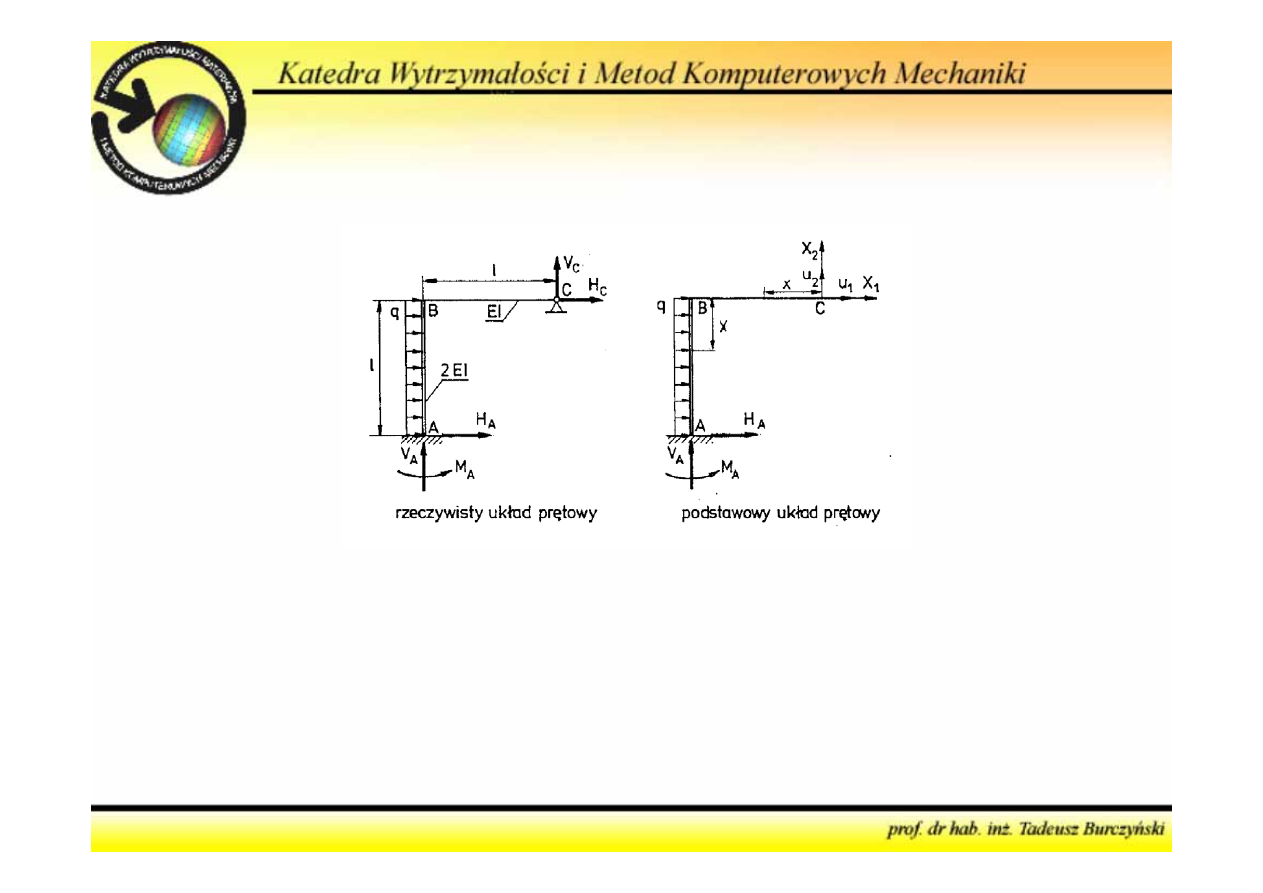
Metoda sił

- Punkt C – podpora przegubowa stała –

dwie reakcje

(pozioma i pionowa)

- Punkt A – utwierdzenie –

trzy reakcje

(pozioma, pionowa i moment)

równania

równowagi

2

0

0

1

0

2

A

C

A

C

C

C

A

H

H

ql

V

V

V l H l

ql

M

+

+

=

+

=

−

−

+

=

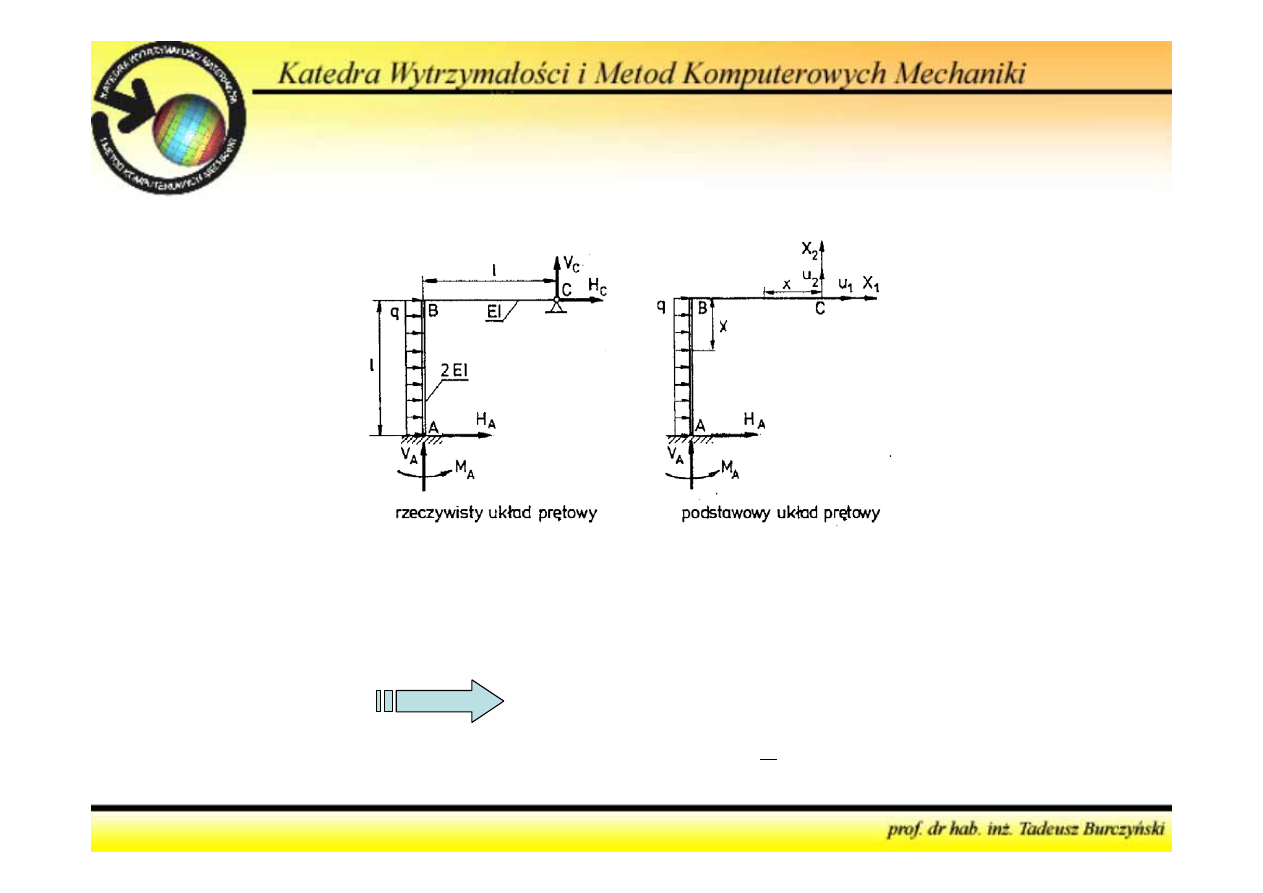
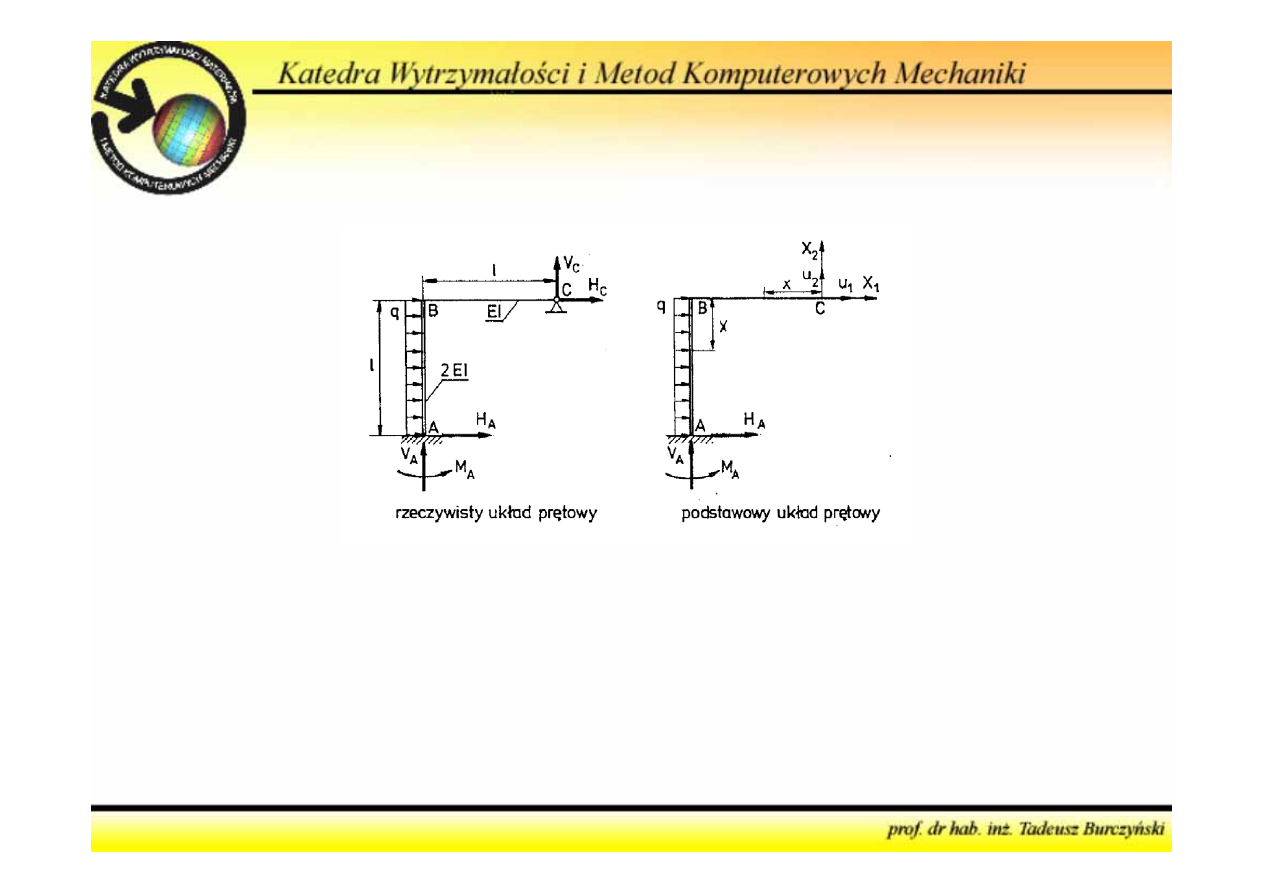
Metoda sił

2. Obliczyć stopień statycznej niewyznaczalności i utworzyć

podstawowy układ prętowy

Algorytm postępowania

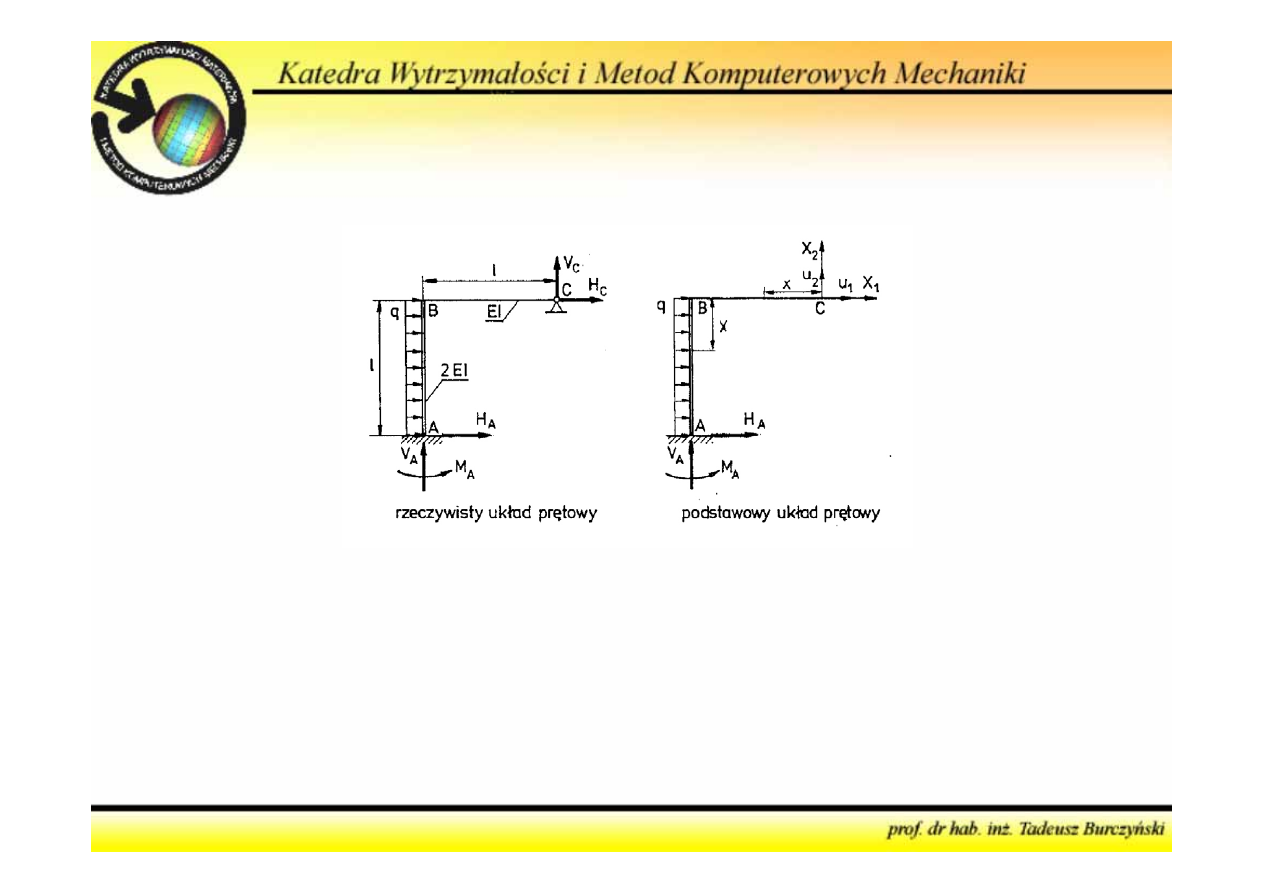
Metoda sił

- Liczba niewiadomych

5

(reakcje)

- Liczba równań

3

5 – 3 = 2

- rama jest dwukrotnie

statycznie niewyznaczalna

Wielkości hiperstatyczne:

X

1

=

H

c

X

2

=

V

c

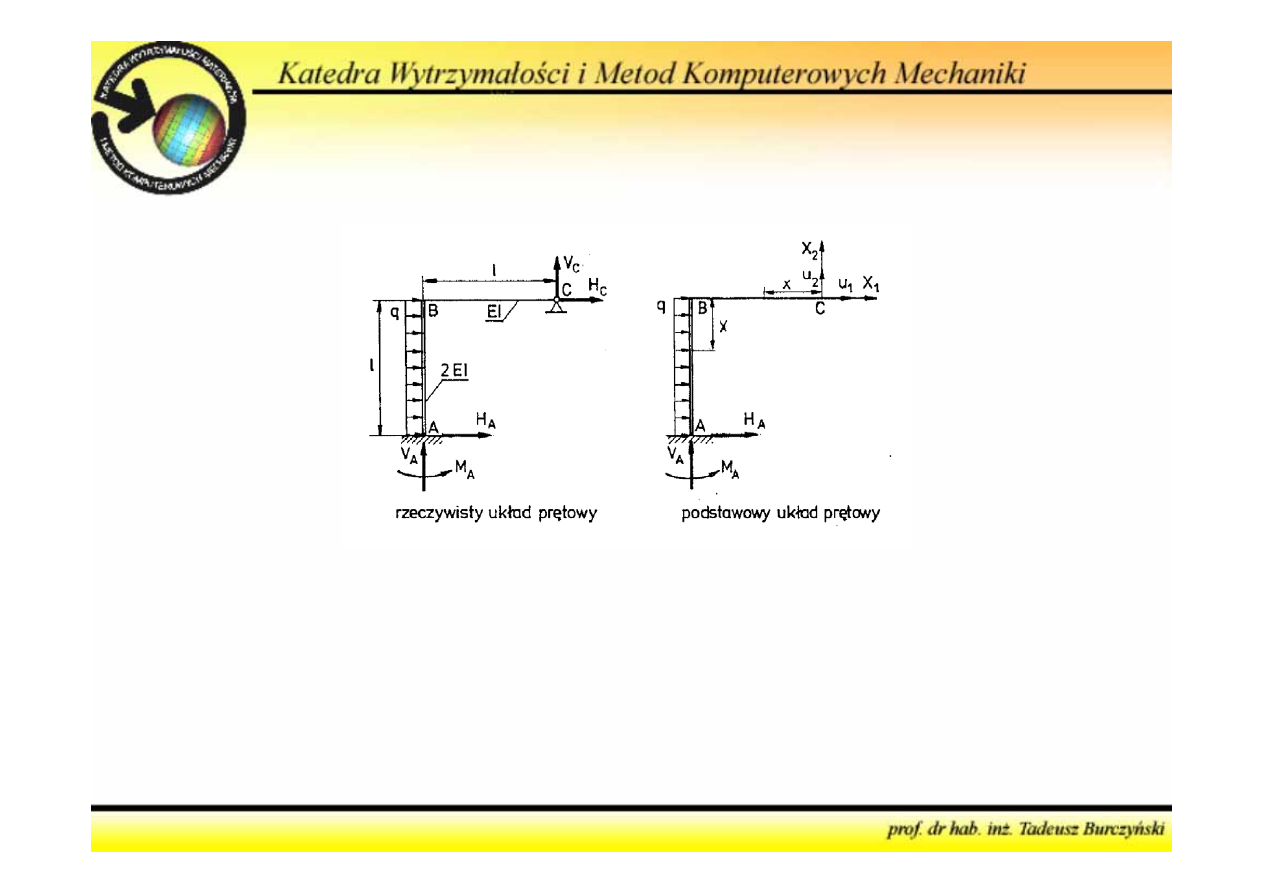
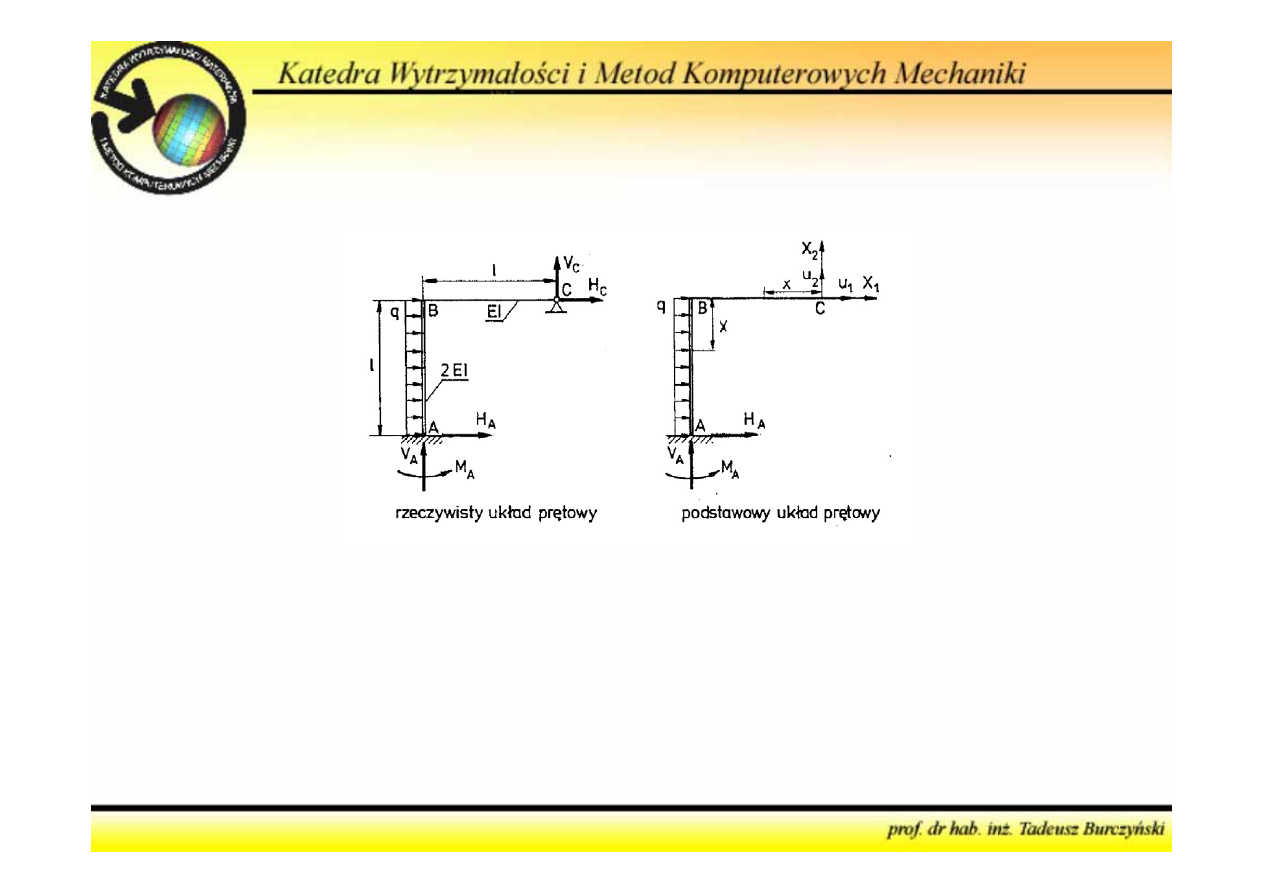
Metoda sił

3. Określić warunki geometryczne oraz związki fizyczne i

sformułować na ich podstawie równania kanoniczne metody sił

Algorytm postępowania

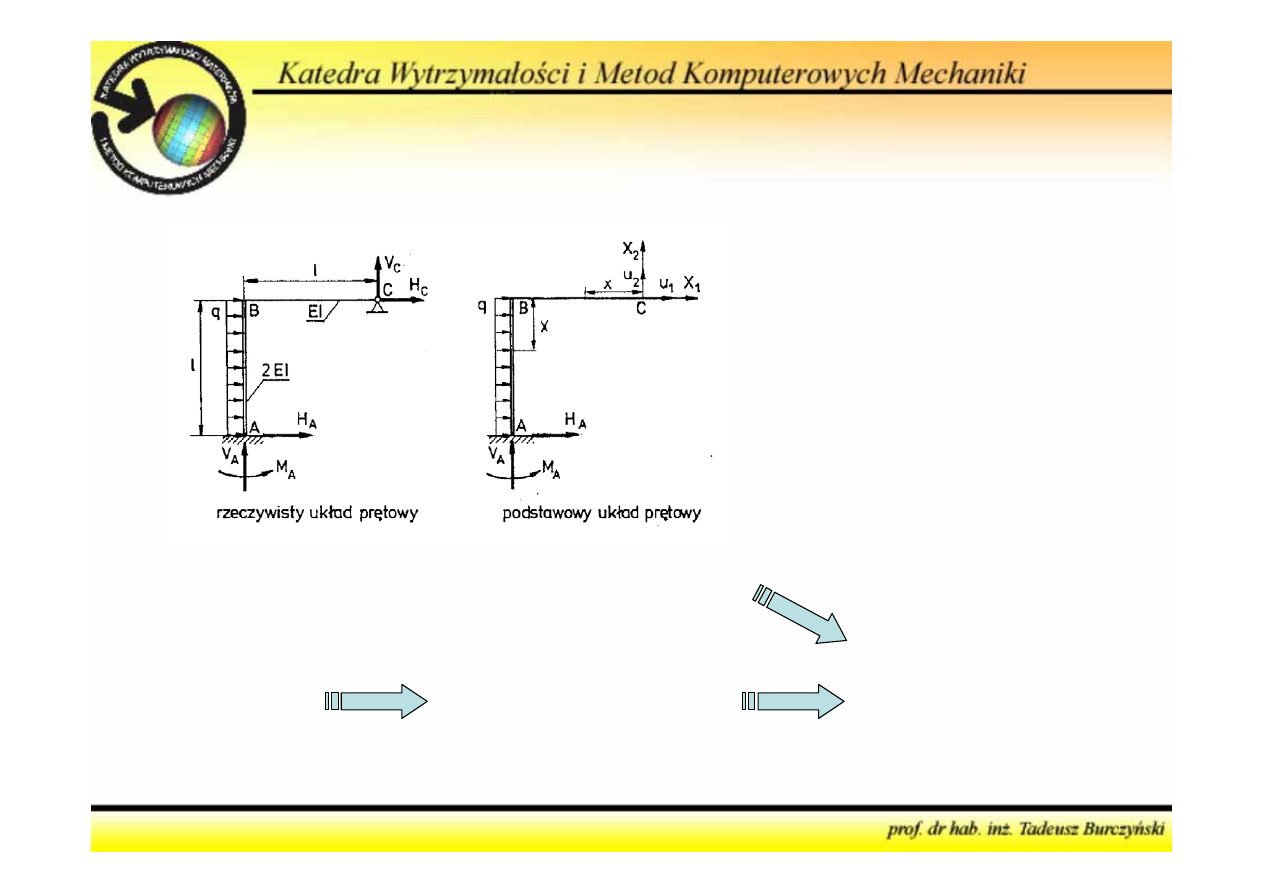
Metoda sił

u

1

= 0, u

2

= 0

Związki

fizyczne

1

11

1

12

2

1

2

21

1

22

2

2

P

P

u

f X

f X

u

f X

f X

=

+

+ Δ

=

+

+ Δ

11

1

12

2

1

21

1

22

2

2

0

0

P

P

f X

f X

f X

f X

+

+ Δ =

+

+ Δ =

1

2

,

P

P

Δ Δ

- część przemieszczeń

u

1

i u

2

spowodowana

działaniem obciążenia q.

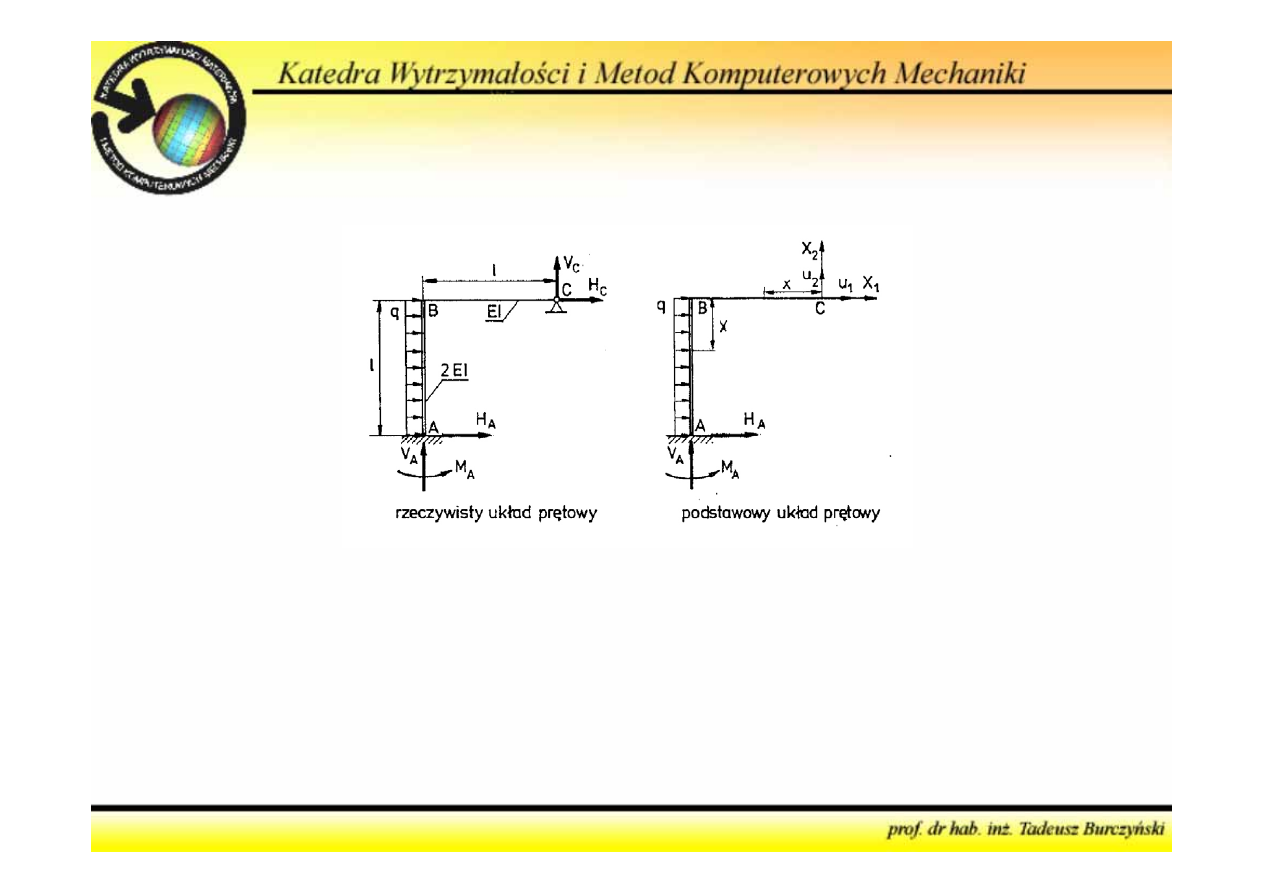
Metoda sił

4. Obliczyć współczynniki równań kanonicznych metody sił

Algorytm postępowania

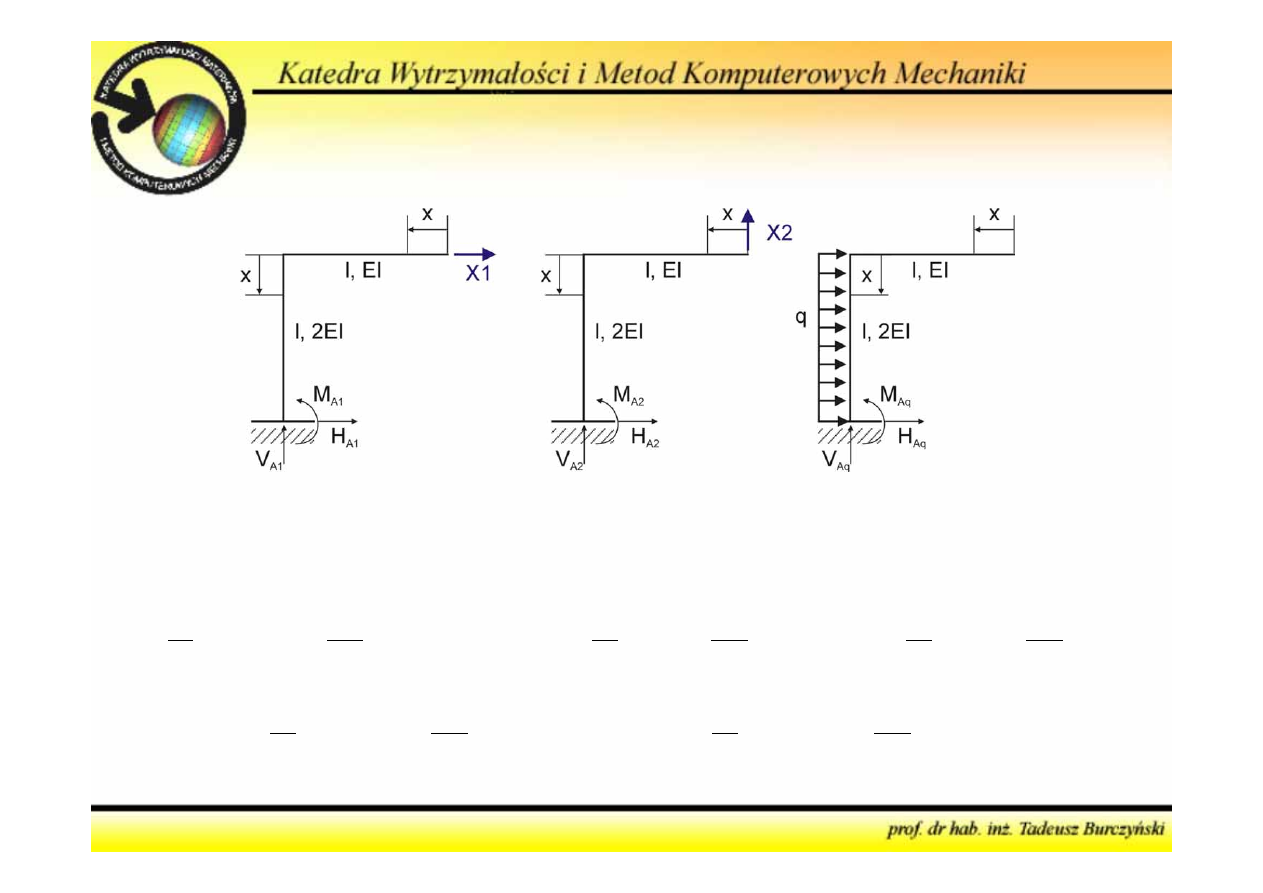
Metoda sił

Algorytm postępowania

12

12

11

22

21

21

0

0

1

1

2

l

l

g

g

g

g

f

M M dx

M

M dx

f

EI

EI

=

+

=

∫

∫

2

2

11

11

21

0

0

1

1

2

l

l

g

g

f

M dx

M dx

EI

EI

=

+

∫

∫

1

1

11

2

21

0

0

1

1

2

l

l

P

g P

g

g P

g

M

M dx

M

M dx

EI

EI

Δ =

+

∫

∫

2

2

22

12

22

0

0

1

1

2

l

l

g

g

f

M dx

M

dx

EI

EI

=

+

∫

∫

2

1

12

2

22

0

0

1

1

2

l

l

P

g P

g

g P

g

M

M dx

M

M

dx

EI

EI

Δ =

+

∫

∫

M

g11

, M

g21

M

g12

, M

g22

M

g1P

, M

g2P

1

2

1

1

X
X

=

=

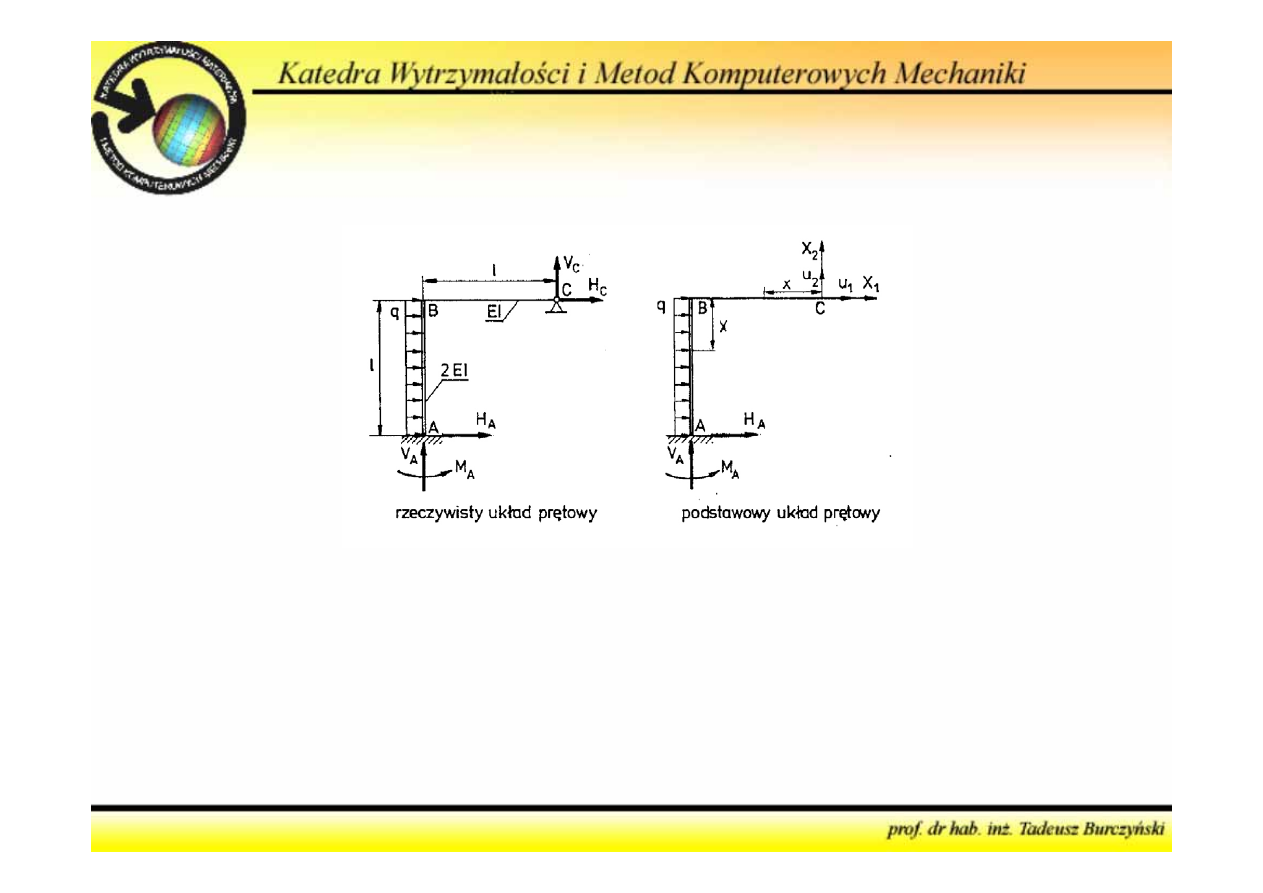
Metoda sił

5. Wyznaczyć z równań kanonicznych metody sił wielkości

hiperstatyczne

Algorytm postępowania

1

2

X

X

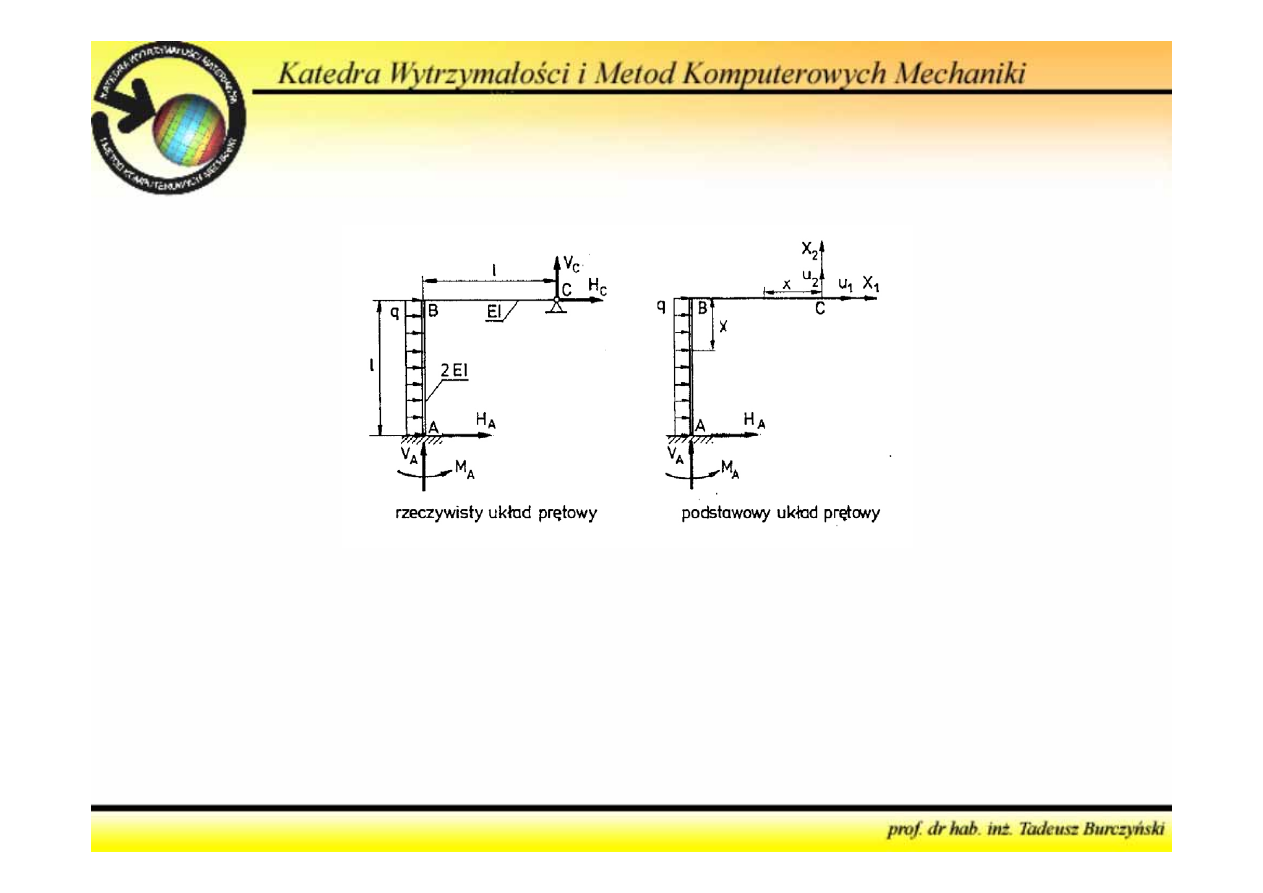
Metoda sił

6. Wykorzystując równania równowagi, znaleźć pozostałe

niewiadome

Algorytm postępowania

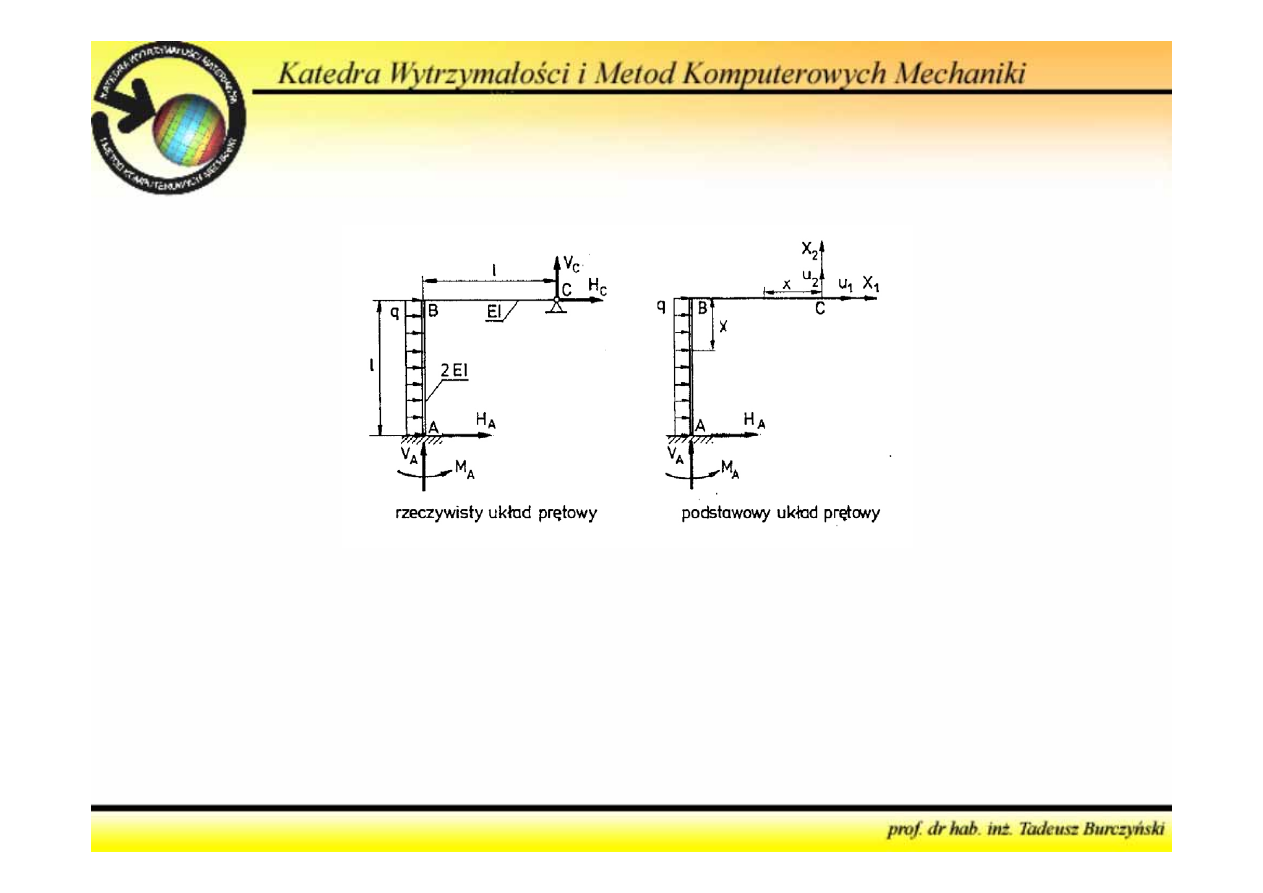
Metoda sił

7. Sformułować równania i narysować wykresy sił wewnętrznych

Algorytm postępowania

Metoda sił

8. Wyznaczyć poszukiwane przemieszczenia

Algorytm postępowania

Zasada minimum energii sprężystej

Menabrei-Castigliana

Energia sprężysta układu statycznie niewyznaczalnego V jest wyrażona
przez znane siły zewnętrzne (obciążenia) i niewiadome wielkości
hiperstatyczne X

1

, ..., X

n

oraz niehiperstatyczne.

Jeżeli wykorzystując równania równowagi, uzależni się niewiadome
niehiperstayczne od wielkości hiperstatycznych oraz obciążeń, energia
V stanie się funkcją X

1

, ..., X

n

, jako zmiennych niezależnych.

Warunki geometryczne, jakie muszą spełniać przemieszczenia u

1

, ...,

u

n

, odpowiadające wielkościom hiperstatycznym X

1

, ...,X

n

, można

zapisać nastepująco

u

1

= 0, ..., u

n

= 0

Zasada minimum energii sprężystej

Menabrei-Castigliana

Stosując metodę Castigliana, można określić przemieszczenia z
wykorzystaniem do tego celu energii sprężystej V(X

1

, ..., X

n

)

1

1

, ... ,

n

n

V

V

u

u

X

X

∂

∂

=

=

∂

∂

związki

fizyczne

Po podstawieniu do związków geometrycznych:

1

0, ... ,

0

n

V

V

X

X

∂

∂

=

=

∂

∂

Zasada minimum energii sprężystej

Menabrei-Castigliana

Spośród wszystkich możliwych zbiorów

wielkości X

1

, ..., X

n

zbiorem rzeczywistych

wielkości hiperstatycznych jest ten, dla

którego energia sprężysta całego układu

prętowego V osiąga wartość minimalną.