METODY ENERGETYCZNE

Wykorzystuje się je m.in. do wyznaczania niewiadomych w układach hiperstatycznych w
zakresie stosowalności prawa Hooke’a. Stosowanie tych metod wymaga określenia energii
sprężystej (potencjalnej) zgromadzonej w ciałach odkształconych.

Odkształcenia sprężyste wywołują prace na przemieszczeniach poszczególnych punktów
ciała. Praca ta jest miara energii która zmienia swoją postać. Podczas odkształcenia następuje
zamiana energii jakiegoś układu zewnętrznego na energię potencjalną ciała odkształconego.

V = L

L

– praca układu zewnętrznego

V

– energia sprężysta ciała odkształconego

Przypomnienie wyrażeń na energię sprężystą dla:

Rozciąganie

A

E

l

P

V

A

E

l

P

V

P

L



















2

2

2





Skręcanie

0

2

0

2

2

J

G

l

M

V

J

G

l

M

V

M

L

S

S

S

























Zginanie

J

E

l

M

V

g









2

2

Ścinanie

A

G

l

T

V









2

2



Dla pręta obciążonego obciążeniem złożonym zmiennym na długości l całkowitą energię
sprężystą wyznaczymy z zależności:

















l

l

g

l

S

l

GA

dx

T

EJ

dx

M

GJ

dx

M

EA

dx

P

V

2

2

2

2

2

2

0

2

2



UKŁADY LINIOWO-SPRĘŻYSTE (UKŁADY CLAPEYRONA)

Układy liniowo sprężyste są to takie układy materialne, w których przemieszczenia uogólnione
dowolnego punktu wywołane działaniem na ten układ obciążeń uogólnionych, są jednorodnymi
liniowymi funkcjami tych obciążeń.



=



1

P

1

+



2

P

2

+ ......... +



n

P

n



1

,



2

......

– liczby wpływowe

Obciążenia uogólnione – dowolne obciążenia takie jak: siła skupiona, moment, obciążenie ciągłe
Przemieszczenie uogólnione – takie przemieszczenie na którym obciążenie uogólnione

wykonuje pracę.

Układ Clapeyrona powinien spełniać następujące warunki:

1.

Materiał liniowo-sprężysty.

2.

Układ powinien mieć wystarczającą liczbę więzów do zapewnienia równowagi.

3.

Działanie jednego z obciążeń nie może zmieniać działania innych obciążeń.

4.

Praca ewentualnych sił tarcia powinna być na tyle mała, aby można było ją pominąć.

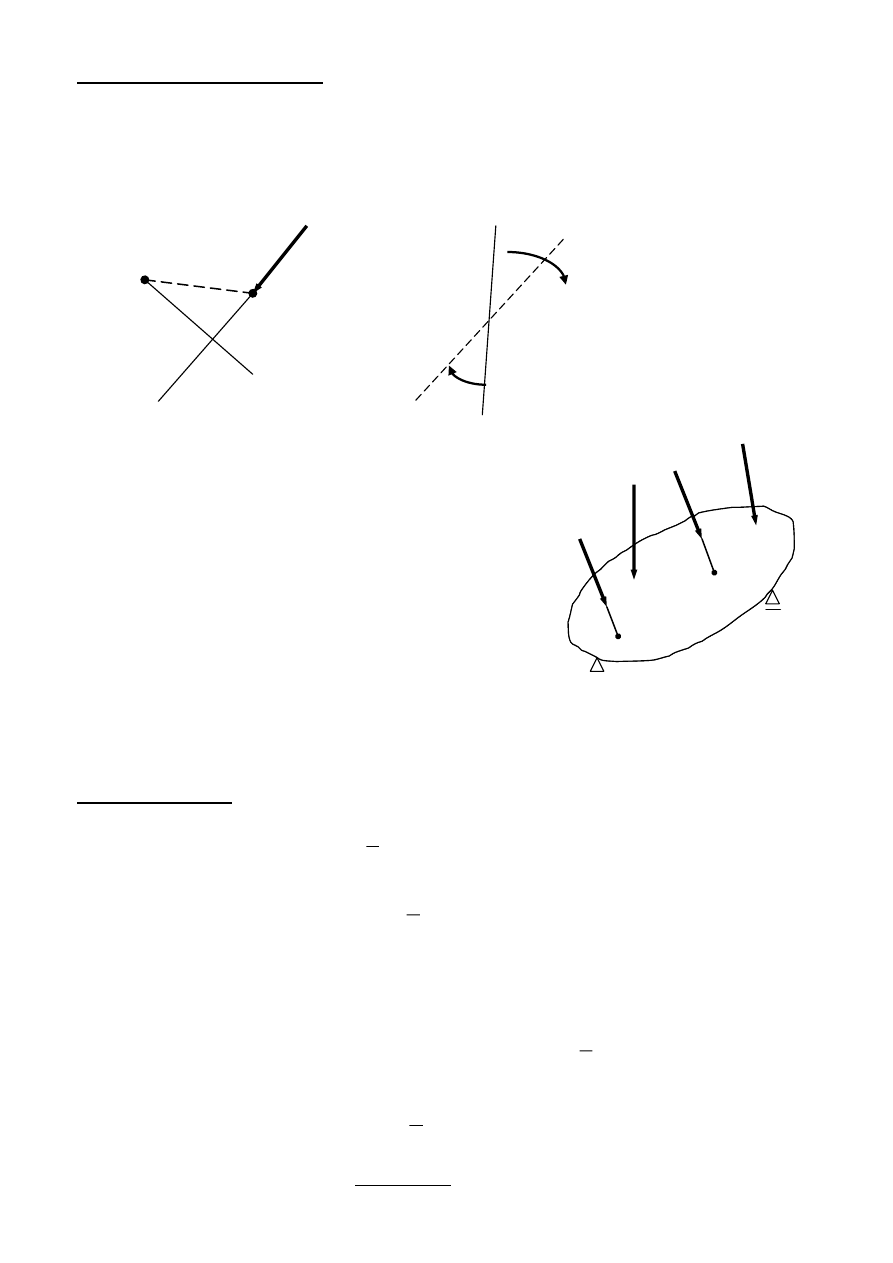
Przemieszczenia uogólnione

Jeżeli punkt A przyłożenia siły P przesunął się w nowe położenie A’ to do obliczenia pracy tej
siły mnożymy jej wartość przez rzut u, całkowitego przemieszczenia na kierunek działania siły.

u

– przemieszczenie odpowiadające sile skupionej P



- przemieszczenie

uogólnione
odpowiadające
momentowi M

Układ sił uogólnionych P

K

(k=1, 2, ......n)

działający

na ustrój liniowo-sprężysty, powoduje powstanie
przemieszczeń uogólnionych poszczególnych
punktów tego ustroju.

Przemieszczenie u

i

dowolnego punktu i

zależy od

wszystkich sił układu i wyraża się wzorem:

u

i

=



i1

P

1

+



i2

P

2

+ ....... +



ik

P

k

+ .... +



in

P

n

lub

k

n

k

ik

i

P

u







1



gdzie



i

k

– liczba wpływowa (przemieszczenie jednostkowe), określa w jakim stopniu dane

obciążenie uogólnione wpływa na przemieszczenie punktu i.

Energia sprężysta

Praca sił uogólnionych

k

n

k

ik

i

n

i

i

i

P

u

ale

u

P

L













1

1

2

1



więc

i

k

n

i

n

k

ik

P

P

L

V











1

1

2

1



Energia sprężysta ustroju liniowo-sprężystego jest jednorodną kwadratową funkcją obciążeń.

(Tw. Clapeyrona)

Jeżeli siły P

i

wyrazimy przez odpowiadające im przemieszczenia u

i

to:

k

n

k

ik

i

u

a

P







1

oraz







n

i

i

i

u

P

L

1

2

1

więc

i

k

n

i

n

k

ik

u

u

a

L

V











1

1

2

1

Energia sprężysta jest jednorodną kwadratową funkcją przemieszczeń.

u

A’

P

A

P

1

P

2

P

i

P

n

u

1

u

i

l

l’



M

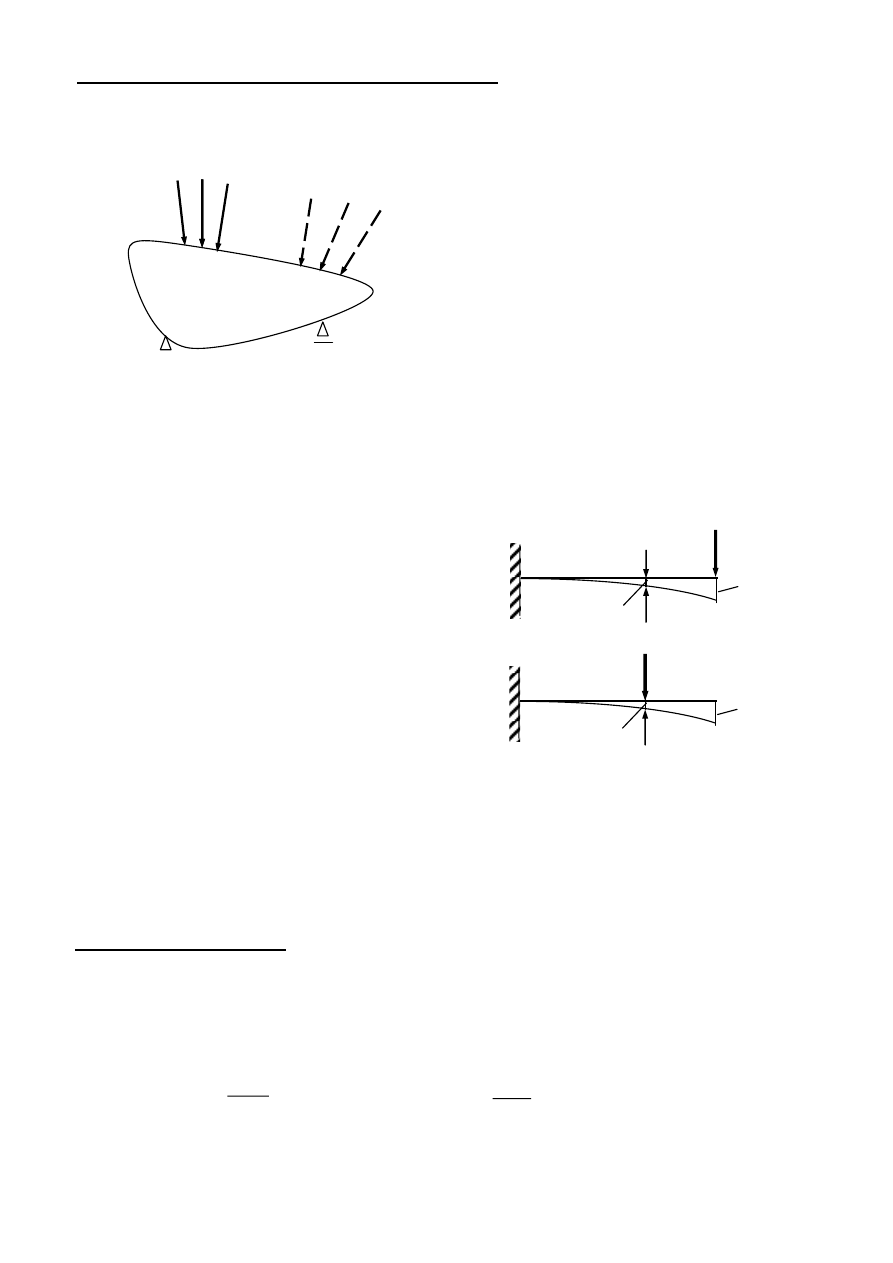
Twierdzenie o wzajemności prac i przemieszczeń

Układ liniowo sprężysty obciążony układem sił 1, obciąża się dodatkowo układem sił 2.

Suma prac wykonanych przez siły:

L

11

+ L

22

+ L

12

= V

Przy zmianie kolejności obciążeń:

L

22

+ L

11

+ L

21

= V

Po przyrównaniu:

L

12

= L

21

(



)

Twierdzenie Bettiego:

Suma prac sił układu pierwszego na odpowiadających im przemieszczeniach
wywołanych siłami układu drugiego, jest równa sumie prac układu drugiego na
odpowiadających im przemieszczeniach wywołanych siłami układu pierwszego

Gdy obciążeniem są tylko dwie pojedyncze

siły P

1

i P

2

wówczas zgodnie z (



):

P

1

u

12

= P

2

u

21

gdy P

1

= P

2

to:

u

12

= u

21

(



)

Równanie (



) wyraża twierdzenie Maxwella:

Jeżeli na układ liniowosprężysty działają dwie równe co do modułu uogólnione
siły, to przemieszczenie odpowiadające pierwszej lecz wywołane przez drugą,
jest równe przemieszczeniu odpowiadającemu drugiej, lecz spowodowanemu
pierwszą siłą.

Twierdzenie Castigliano:

Pochodna cząstkowa energii sprężystej całego układu liniowosprężystego
względem jednej z niezależnie działających sił obciążających jest równa
odpowiadającemu tej sile przemieszczeniu.

i

i

u

P

V







lub

i

i

P

u

V







Poch

odna cząstkowa energii sprężystej względem przemieszczenia równa się

odpowiadającej mu sile.

P

i

P

j

1

2

P

1

u

11

u

21

P

2

u

12

u

22

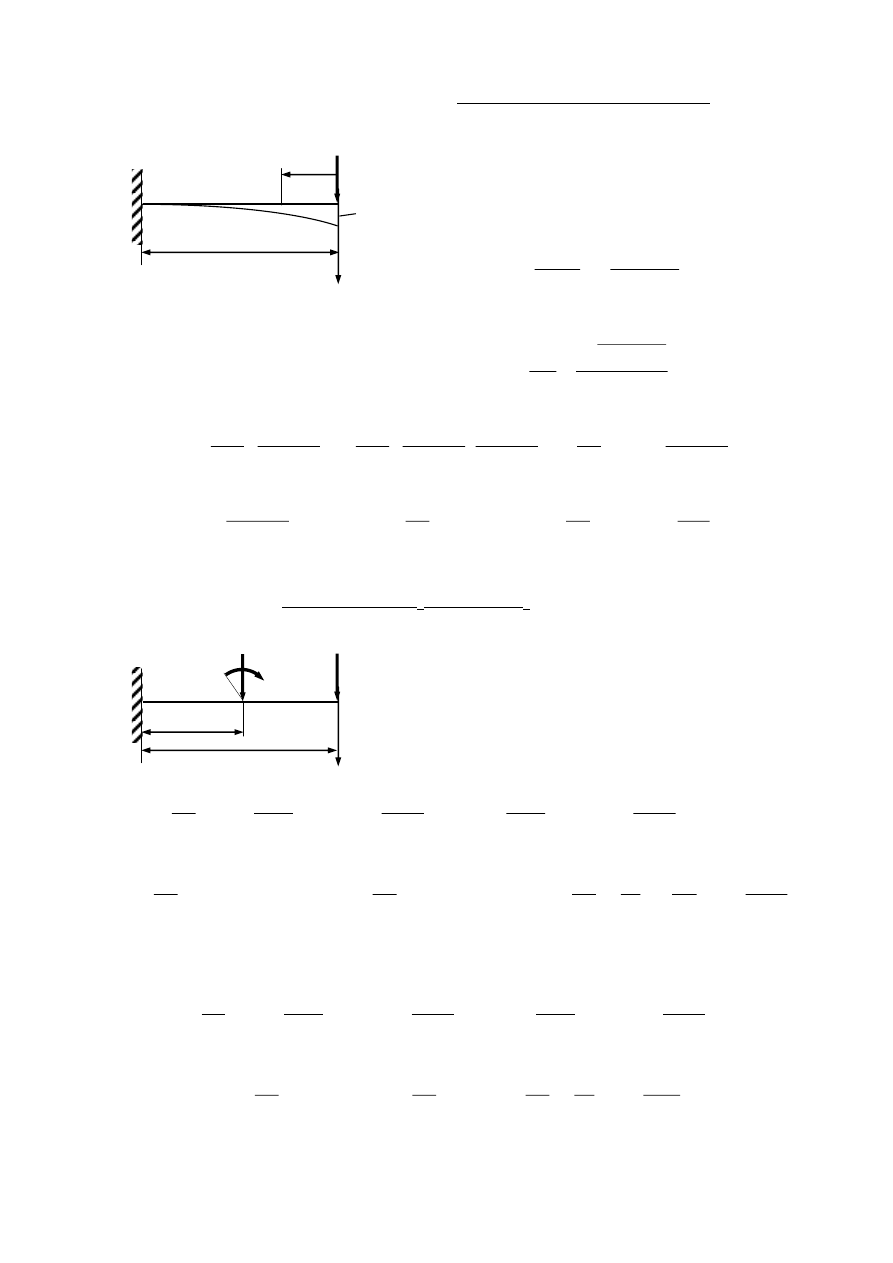
Zastosowanie twierdzenia Castigliano prześledzimy na prostym przykładzie.

Wyznaczymy ugięcie pod siłą P.

Moment gnący w przekroju x:

M

g

(x)= -

P·x

Energia sprężysta belki:









l

g

l

g

EJ

dx

x

M

EJ

dx

M

U

0

2

0

2

2

)

(

2

Przemieszczenie u

P

zgodnie z tw. Castigliano:

P

EJ

dx

x

M

P

U

u

l

g

P















0

2

2

)

(

przy EJ = const

dx

P

x

M

x

M

EJ

dx

P

x

M

x

M

x

M

EJ

dx

P

x

M

EJ

u

l

g

g

g

l

g

g

l

g

P































0

0

2

0

2

)

(

)

(

1

)

(

)

(

)

(

2

1

)

(

2

1

u nas

EJ

Pl

dx

x

P

EJ

dx

x

x

P

EJ

u

i

x

P

x

M

l

l

P

g

3

1

)

)(

(

1

)

(

3

0

2

0



























Załóżmy, że chcielibyśmy dodatkowo określić ugięcie i kąt obrotu dla x=0,5l. Zakładamy, że
w tym przekroju działają dodatkowo siła F

0

i moment M

0

. (W rzeczywistości są to siły zerowe)

Momenty gnące

M

I

= - Px

M

II

= - Px

– F

0

(x

– 0,5l) – M

0

ugięcie dla x = 0,5 l

)

5

,

0

(

;

0

1

0

0

5

,

0

0

5

,

0

0

0

l

x

F

M

F

M

dx

F

M

M

dx

F

M

M

EJ

u

II

I

l

l

l

II

II

I

I

















































EJ

Pl

l

x

P

x

P

EJ

dx

l

Px

Px

EJ

dx

l

x

Px

EJ

u

l

l

l

l

l

l

48

5

4

3

1

)

5

,

0

(

1

))

5

,

0

(

(

(

1

3

5

,

0

2

3

5

,

0

2

5

,

0



































































natomiast kąt obrotu

1

;

0

1

0

0

5

,

0

0

5

,

0

0

0















































M

M

M

M

dx

M

M

M

dx

M

M

M

EJ

II

I

l

l

l

II

II

I

I



zatem

EJ

Pl

x

P

EJ

Pxdx

EJ

dx

Px

EJ

l

l

l

l

l

l

8

3

2

1

1

)

1

(

1

2

5

,

0

2

5

,

0

5

,

0































































Jak widać z powyższego przykładu, zastosowanie sił zerowych umożliwiło określenie
przemieszczeń w dowolnym przekroju belki.

P

y

l

u

P

x

P

y

l

I

II

F

0

l/2

M

0

Metoda Maxwella

– Mohra

Rozważmy dowolny płaski układ sił obciążony siłami w swej płaszczyźnie. W prętach siłami
wewnętrznymi będą: N

i

, T

i

i M

gi

.

Energię każdego pręta (ściślej każdego przedziału) wyrazimy:

i

l

i

i

gi

l

i

i

i

i

i

i

l

i

i

i

ds

J

E

M

ds

A

G

T

ds

A

E

N

V

i

i

i













2

2

2

2

2

2





i

– wsp. zależny od kształtu przekroju

Energia całego układu będzie suma:

V =



V

i

Chcąc wyznaczyć przemieszczenie w określonym miejscu i kierunku, przykładamy tam siłę
jednostkową F = 1 wywołującą siły wewnętrzne M’

g

, N’ i T’.

przemieszczenie

i

n

i

l

i

i

ig

gi

i

n

i

l

i

i

i

i

i

n

i

l

i

i

i

i

ds

J

E

M

M

ds

A

G

T

T

ds

A

E

N

N

F

V

f

i

i

i

























1

'

1

'

1

'



W przypadku belek najczęściej U jest funkcją tylko M

g

, a w przypadku np. kratownic tylko N.

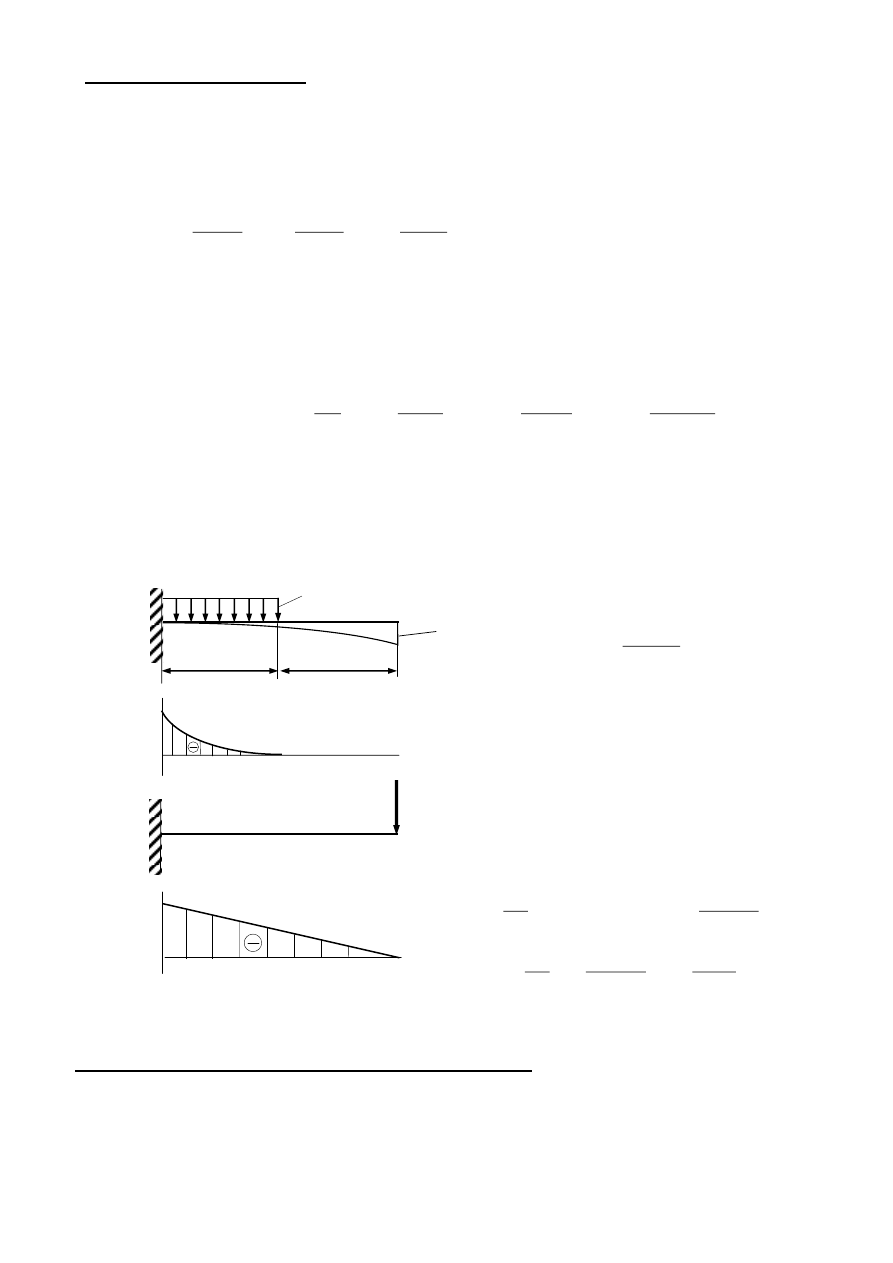
Przykład. Wyznaczyć ugięcie f swobodnego końca belki metodą Maxwella-Mohra. EJ=const.

Przedział I

0 ≤ x ≤ b

M

g I

=0

Przedział II

b ≤ x ≤ a+b

2

)

(

2

b

x

q

M

II

g







Obciążamy belkę na jej końcu siłą P=1
i wyznaczamy momenty n

ią wywołane

x

x

P

M

I

g











'

x

x

P

M

II

g











'

Ugięcie





























b

b

a

b

I

g

I

g

dx

x

b

x

q

dx

M

M

EJ

f

0

2

'

)

(

2

)

(

1

)

4

3

(

24

2

)

(

1

3

2

b

a

EJ

qa

xdx

b

x

q

EJ

f

b

a

b













Całkowanie graficzne sposobem Wereszczagina 1924 – (chociaż znane od 1884)

Całkę typu

dx

x

f

x

f

b

a

)

(

)

(

2

1



(jeżeli jedna z tych funkcji np. f

2

(x) jest funkcją liniową),

możemy przedstawić jako iloczyn pola pod krzywą f

1

(x) i rzędnej funkcji f

2

(x) odpowiadającą

położeniu środka ciężkości pola pod f

1

(x).

f

a

II

I

b

q

M

g

P=1

M’

g

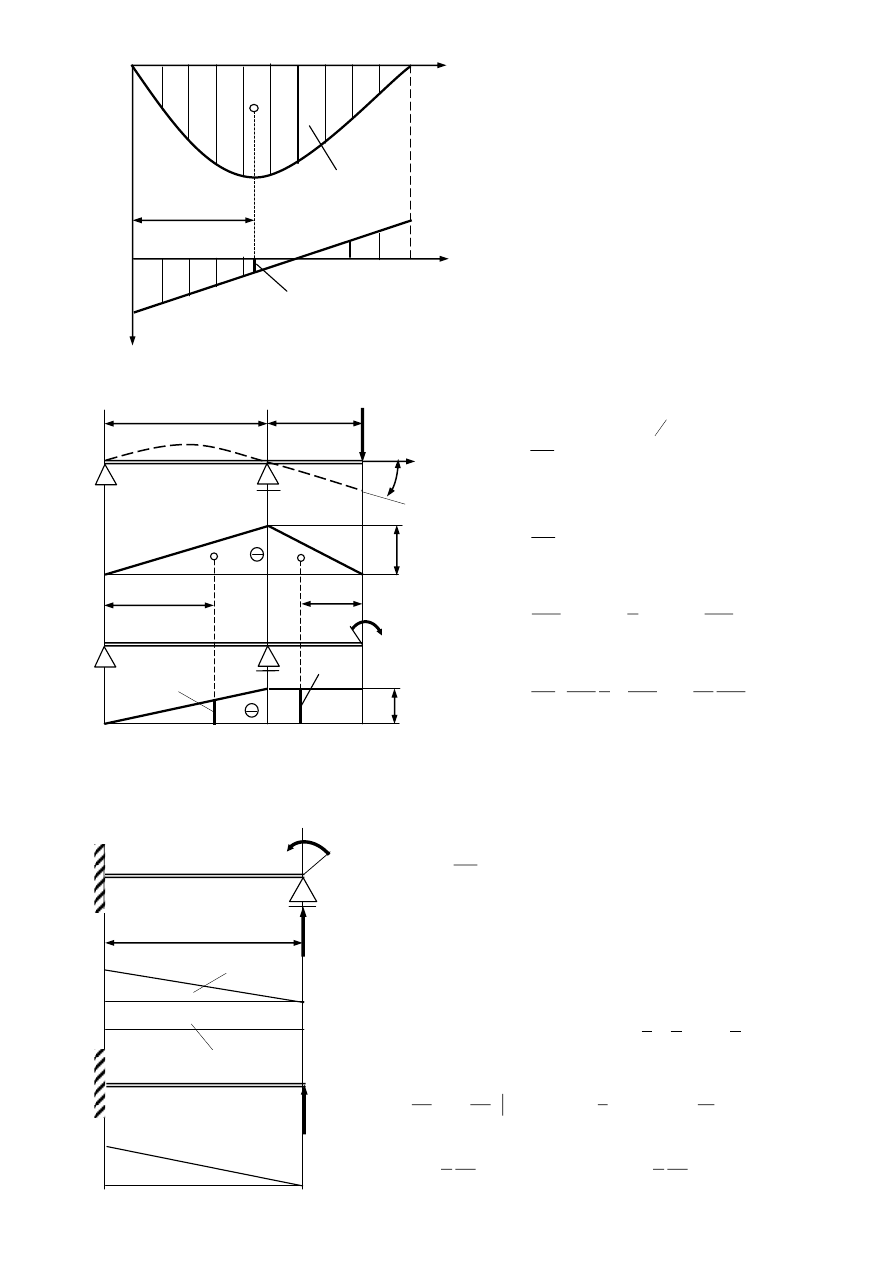
W naszym przypadku mamy np.

'

'

0

g

g

l

g

M

M

M







Przykład Wyznaczyć kąt ugięcia belki w punkcie C.























l

l

C

dx

M

M

dx

M

M

EJ

0

2

0

'

2

2

'

1

1

1







'

2

2

'

1

1

1

S

S

C

y

y

EJ











1

;

8

;

3

2

;

4

'

2

2

2

'

1

2

1













S

S

y

Pl

y

Pl

EJ

Pl

Pl

Pl

EJ

C

2

2

2

24

7

1

8

3

2

4

1





















Metodę Maxwella-Mohra można wykorzystać do rozw. układów statycznie niewyznaczalnych
Przykład

rozw

iązanie:

analityczne,

wykreślne

R

H

– reakcja hiperstatyczna

dx

M

M

EJ

f

g

l

g

H

'

0

1

0







'

'

0

S

g

l

g

y

M

M







M

g

= R

H

x



1

=M l;



2

=½R

H

l

2

M

g

= 1 x

y

S1

=l/2;

y

S2

=⅔l







l

H

dx

x

M

x

R

0

0

)

)(

(

0

3

2

2

1

2

2

2









l

l

R

l

l

M

H

0

2

3

0

2

3





l

H

x

M

x

R

2

3

1

2

3

l

M

l

R

H





l

M

R

H

2

3





l

M

R

H

2

3





M

g

M’

g

x

x

y





M’

g

x

S

S

x

P

l

l/2

A

B

C



M

g

S

1



2

½Pl

x

s1

=⅔l

x

s1

=⅔½l

K=1

M’

g

M’

gS1

M’

gS2

1

S

2

R

H

M

l

P=1

R

H

l

M

l



2



1

l