
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Elementy przynależne
O elementach przynależnych mówi się wówczas, gdy tworzą one zbiór zawierający
wspólny punkt lub prostą. Można wyróżnić przynależność:
punktu i prostej,
prostej i płaszczyzny,
punktu i płaszczyzny.
Punkt i prosta przynależne do siebie
Zgodnie z tym punkt A leżący na prostej m lub prosta m przechodząca przez punkt A
tworzą parę elementów przynależnych do siebie.
Oznacza to, że ich jednoimienne rzuty także przynależą do siebie.
Zadanie 1
Dane są rzuty prostej m oraz punktów A,B,C (rys.1). Określić, pomiędzy którymi
elementami zachodzi związek przynależności?
x
A''
B''
C''
A'
B'
C'
m''
m'
Rys.1
Odpowiedź:
Przynależne elementy to pary: m, A oraz m, C.
Nie przynależą do siebie m oraz B.

Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Prosta i płaszczyzna przynależne do siebie
Zw
iązek przynależności ma miejsce w dwóch przypadkach:
dwa różne punkty prostej leżą na tej płaszczyźnie;
prosta przechodzi przez punkt leżący na tej płaszczyźnie i jest równoległa do
prostej leżącej na tej płaszczyźnie.
Zadanie 2
Płaszczyzna
opisana jes
t punktami A, B, C stanowiącymi wierzchołki trójkąta
(
=ABC) (rys.2). Wykreślić rzuty prostej dowolnej l, leżącej na tej płaszczyźnie, ale
nie przechodzącej przez żaden z danych wierzchołków.
x
A''
B''
C''
A'
B'
C'
Rys.2

Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Znaleźć należy dwa inne niż A,B,C punkty. Pierwszy z nich (1) leżeć będzie na
prostej a przechodzącej przez punkty A i B (rys.3).
x
A''
B''
C''
A'
B'
C'
a''
a'
1'
1''
Rys.3

Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Drugi punkt (2) obrać należy na prostej b, wyznaczonej przez punkty B i C (rys.4).
x
A''
B''
C''
A'
B'
C'
a''
a'
1'
1''
b''
b'
2''
2'
Rys.4
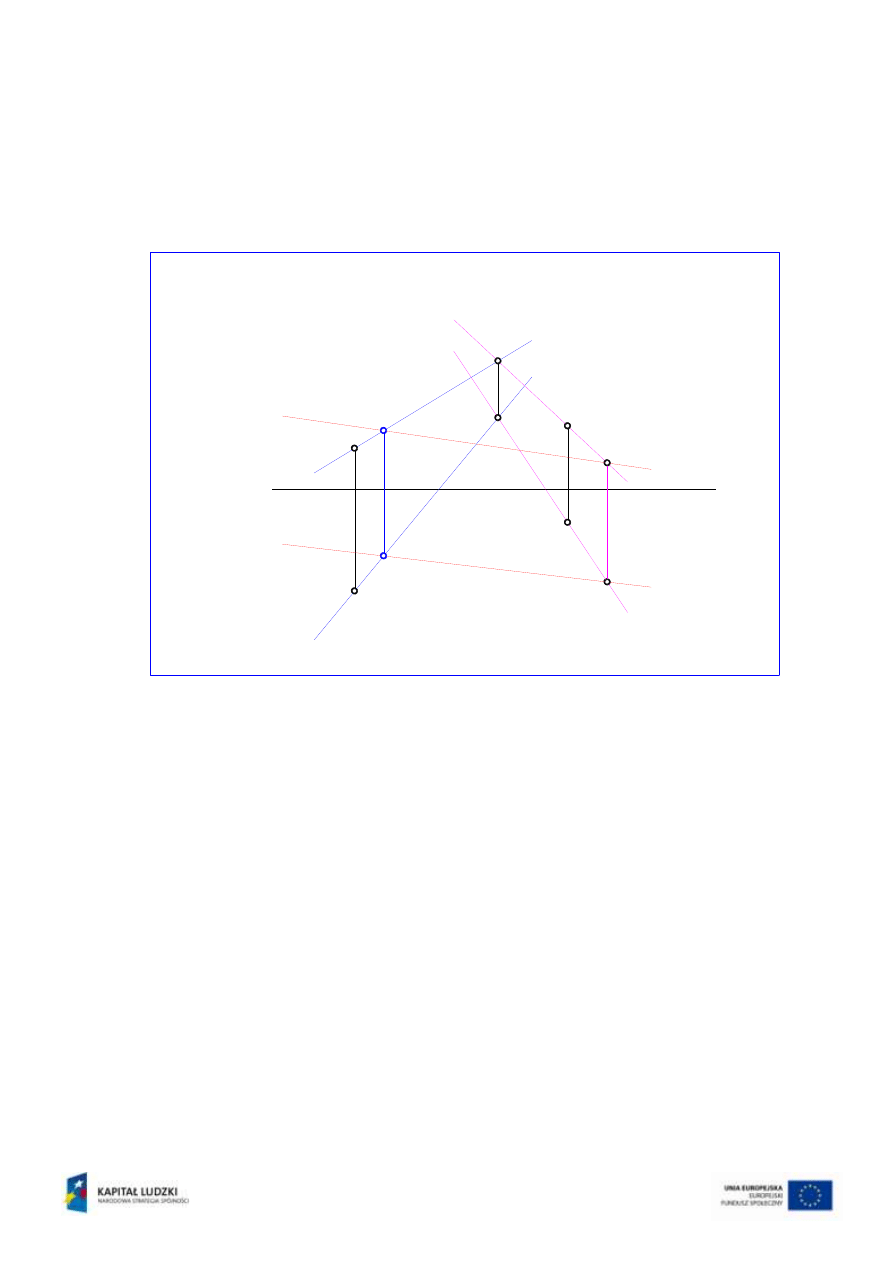
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Punkty 1 i 2 leżą na płaszczyźnie, zatem poprowadzona przez nie prosta l także leży
na płaszczyźnie, co rozwiązuje zadanie (rys.5).
x
A''
B''
C''
A'
B'
C'
a''
a'
1'
1''
b''
b'
2''
2'
l''
l'
Rys.5

Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
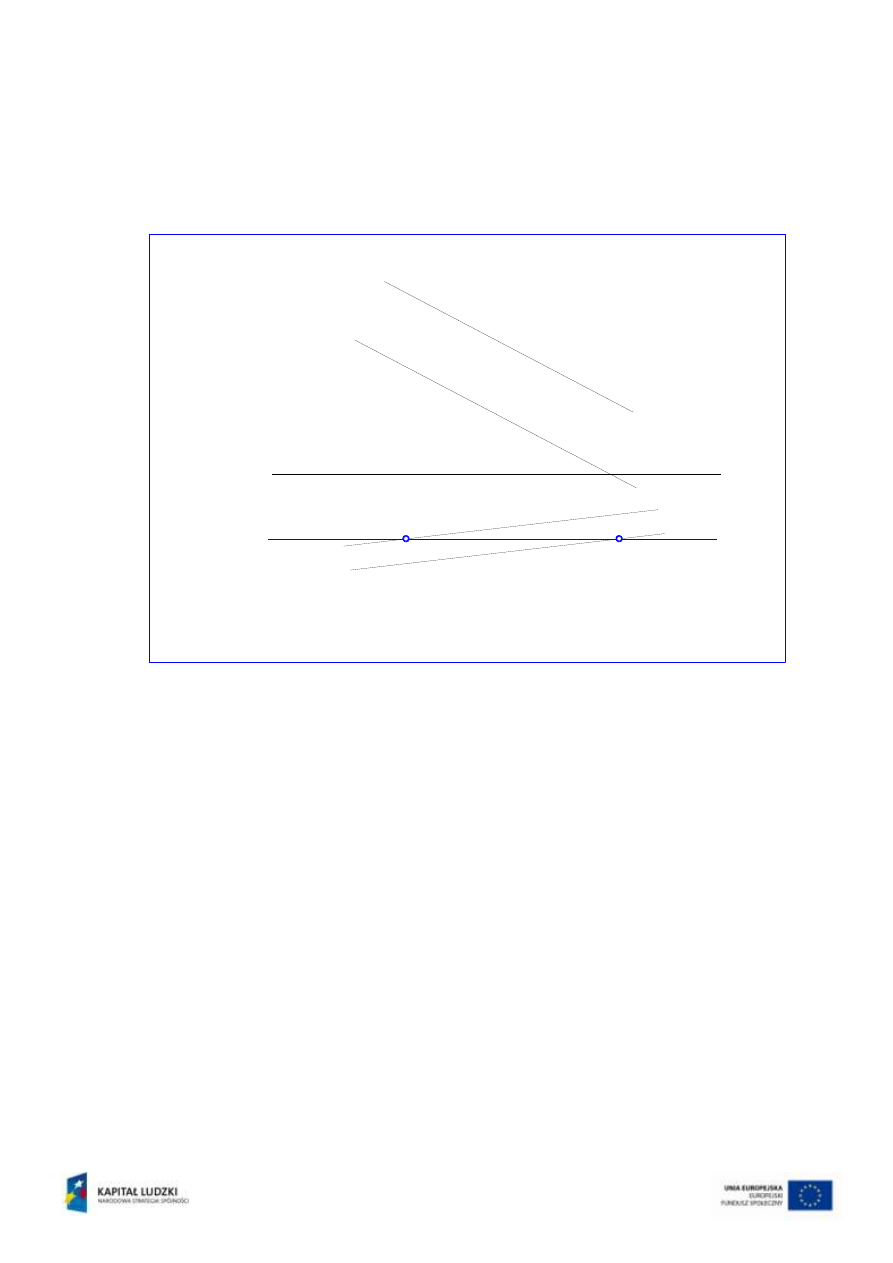
Zadanie 3
Płaszczyzna
opisana jest dwiema prostymi równoległymi m oraz n (
=mn) (rys.6).
Wykreślić rzuty prostej czołowej c, leżącej na tej płaszczyźnie.
x
m''
m'
n''
n'
Rys.6
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
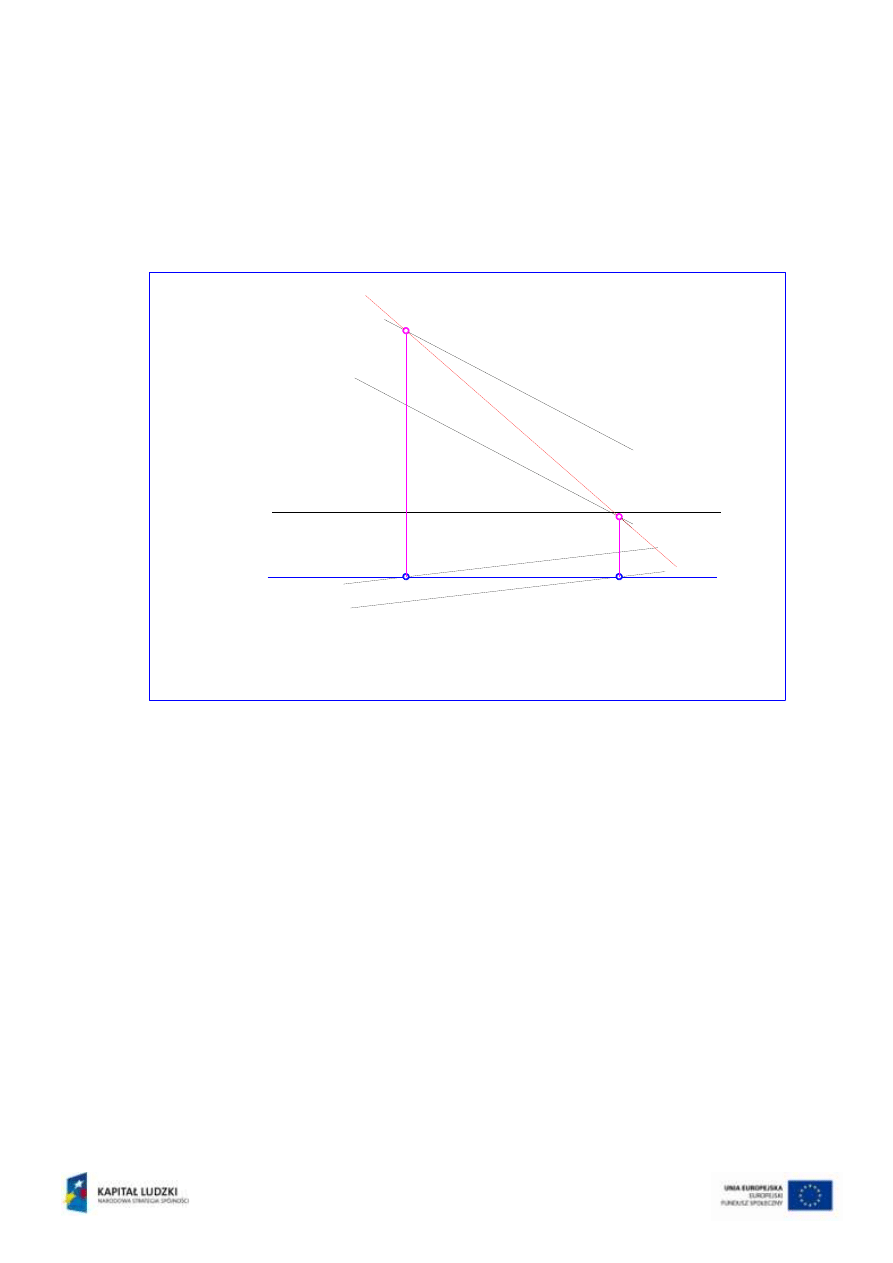
Można wykreślić rzut poziomy c’ prostej czołowej c, jako równoległy do osi rzutów x.
Przecina się on z rzutami m’ oraz n’ określając rzuty 1’ i 2’ punktów 1 i 2. (rys.7).
x
m''
m'
n''
n'
c'
1'
2'
Rys.7
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
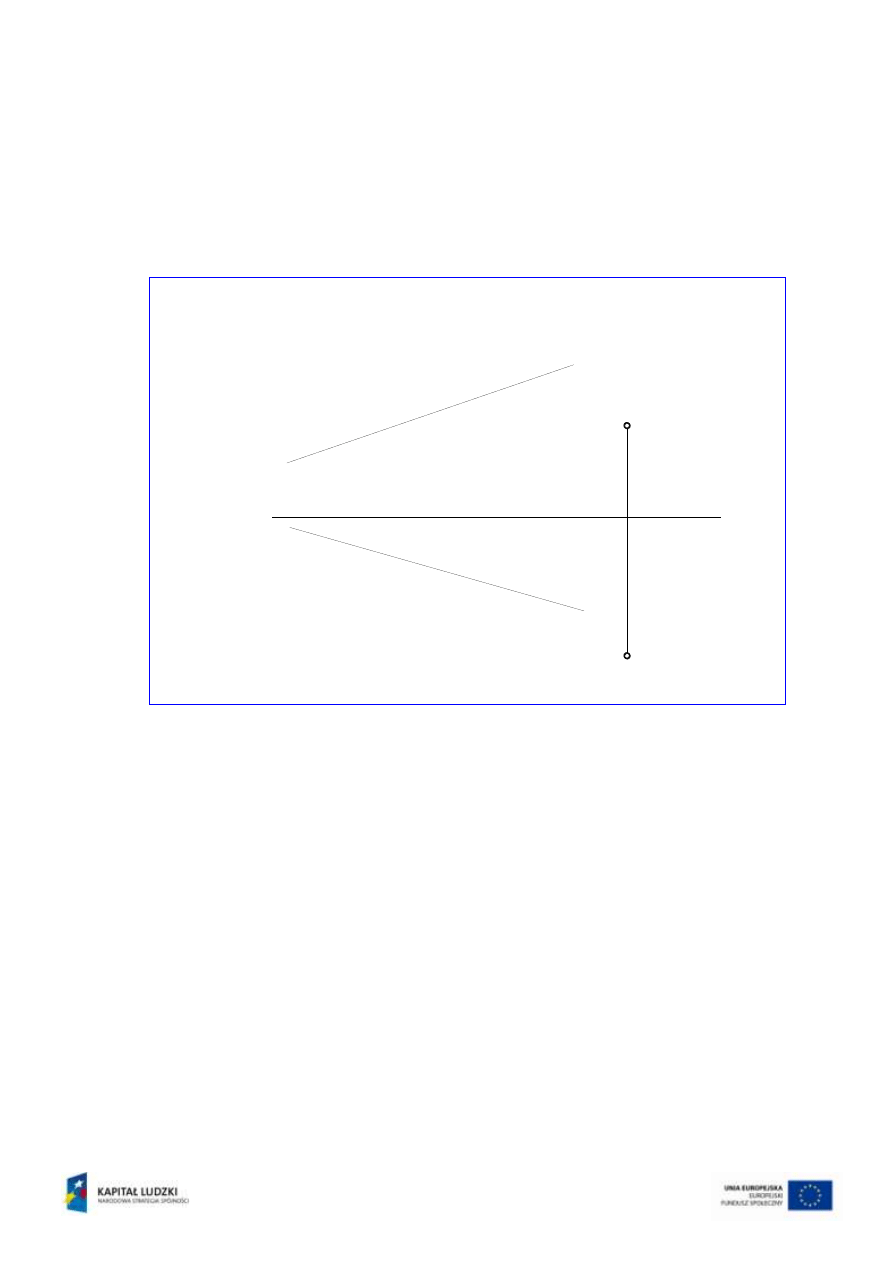
Wykorzystując proste odnoszące, znajduje się rzuty pionowe 1’’ i 2’’ punktów na
przecięciu z rzutami pionowymi m’’ i n’’ prostych, a także przeprowadzony przez nie
rzu
t pionowy c’’ prostej czołowej (rys.8).
x
m''
m'
n''
n'
c'
1'
2'
1''
2''
c''
Rys.8
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
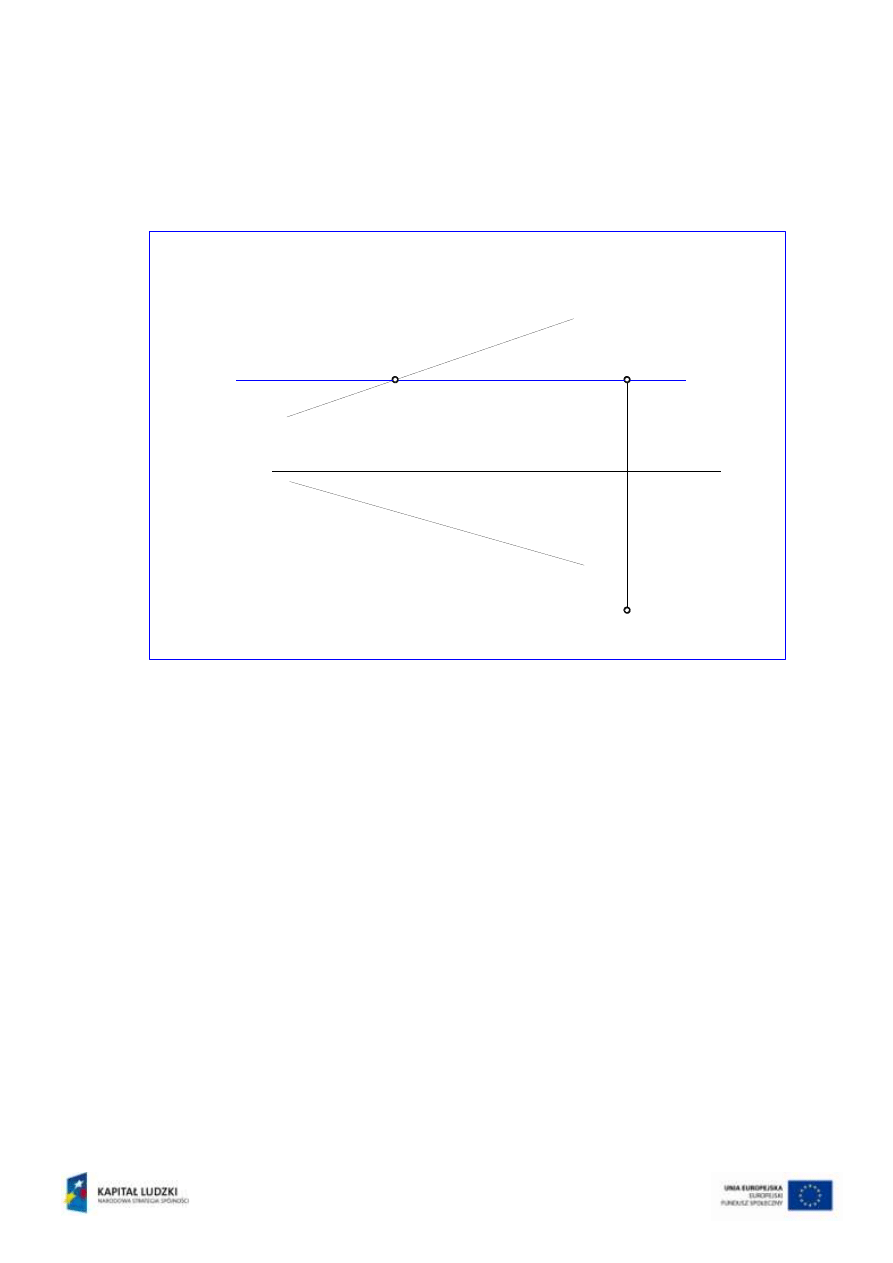
Zadanie 4
Płaszczyzna
opisana jest przez rzuty prostej m i punktu A (
=mA). Należy
wykreślić rzuty prostej poziomej p, leżącej na płaszczyźnie.
x
m''
m'
A'
A''
Rys.9
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Rzut pionowy p’’ prostej p wykreślić można wprost, jako równoległy do osi rzutów x,
przechodzący przez rzut A’’ i przecinający rzut m’’ w punkcie 1’’ (rys.10).
x
m''
m'
A'
A''
1''
p''
Rys.10

Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
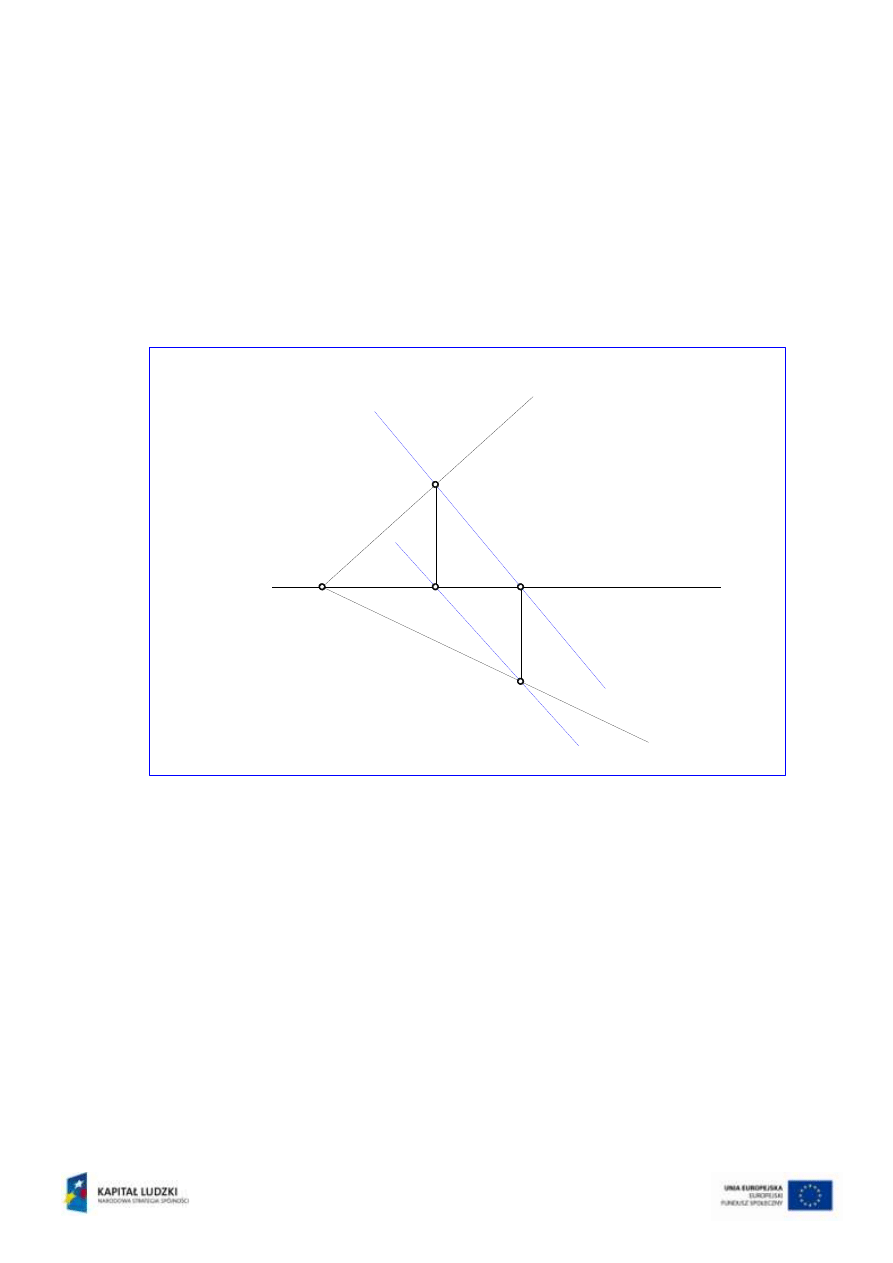
Za pomocą prostej odnoszącej wyprowadzonej z rzutu 1’’ punktu 1 znajduje się 1’ na
przecięciu z m’. Poszukiwany drugi rzut p’ przechodzi przez A’ oraz 1’. (rys.11).
x
m''
m'
A'
A''
1''
p''
1'
p'
Rys.11
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Przynależność prostej i płaszczyzny, gdy dane są ślady prostej i
płaszczyzny
Je
śli prosta m i płaszczyzna
przynależą do siebie w przestrzeni, to na
płaszczyźnie rysunku
=
1
=
2
ich jednoimienne ślady także przynależą
do siebie (rys.12). Oznacza to, że ślad poziomy H
m
prostej m
leży na
śladzie h
płaszczyzny
, a ślad pionowy prostej V
m
leży na śladzie
pionowym v
płaszczyzny.
x
v
X
h
V
m
m''
m'
V'
m
H''
m
H
m
Rys.12
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
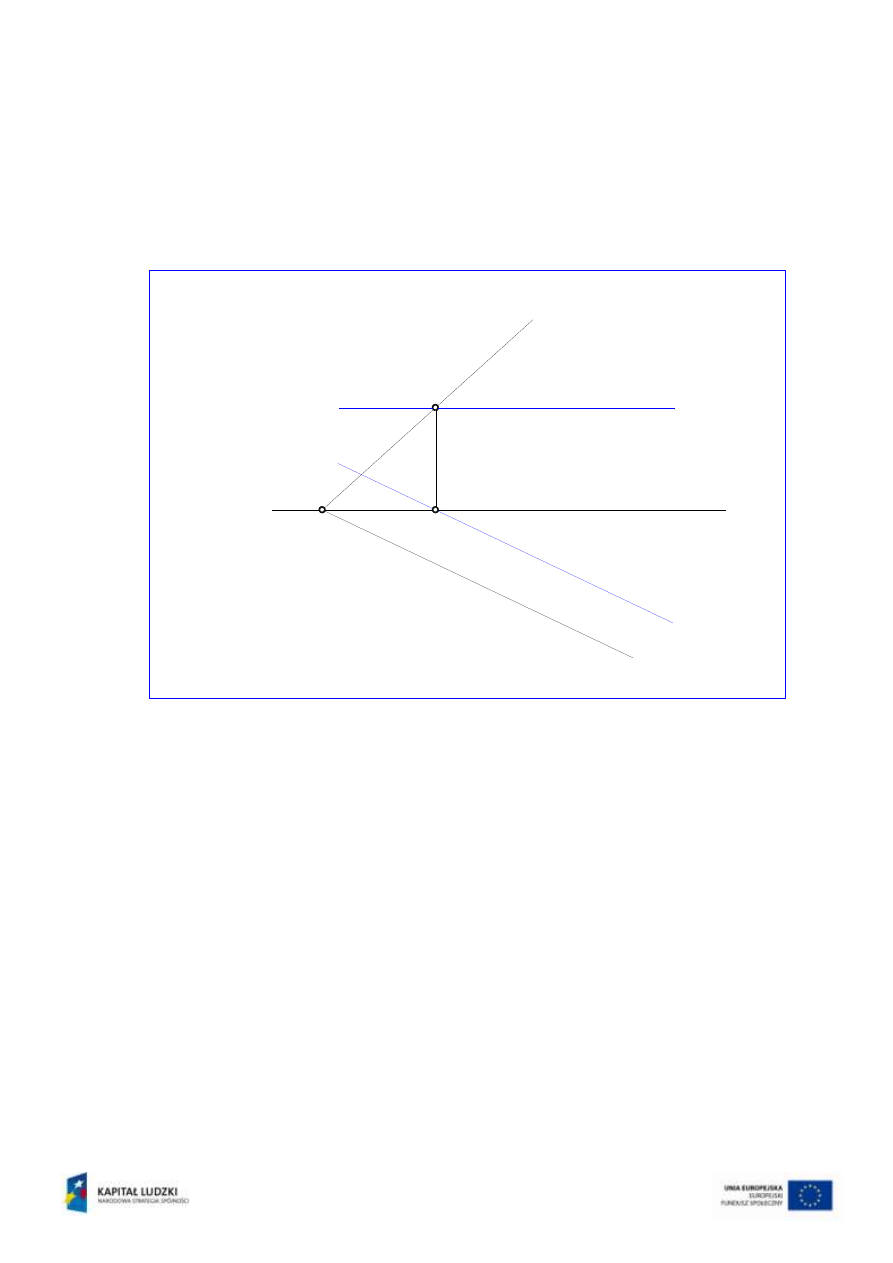
Na szczególną uwagę zasługują dwie proste charakterystyczne,
spełniające warunki przynależności do płaszczyzny. Są to:
Prosta pozioma m przynależna do płaszczyzny
(rys.13).
x
v
X
h
V
m
m''
m'
V'
m
Rys.13
Prosta taka nie posiada śladu poziomego Hm, bo z definicji nie przecina rzutni
poziomej. Zamiast tego jej rzut poziomy
m’ zachowuje równoległość do śladu
poziomego płaszczyzny h
.
Istniejący ślad pionowy Vm prostej m zgodnie z definicją
leży na śladzie pionowym v
płaszczyzny
.
Dla wygody można taką prostą
oznaczyć jako p.
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
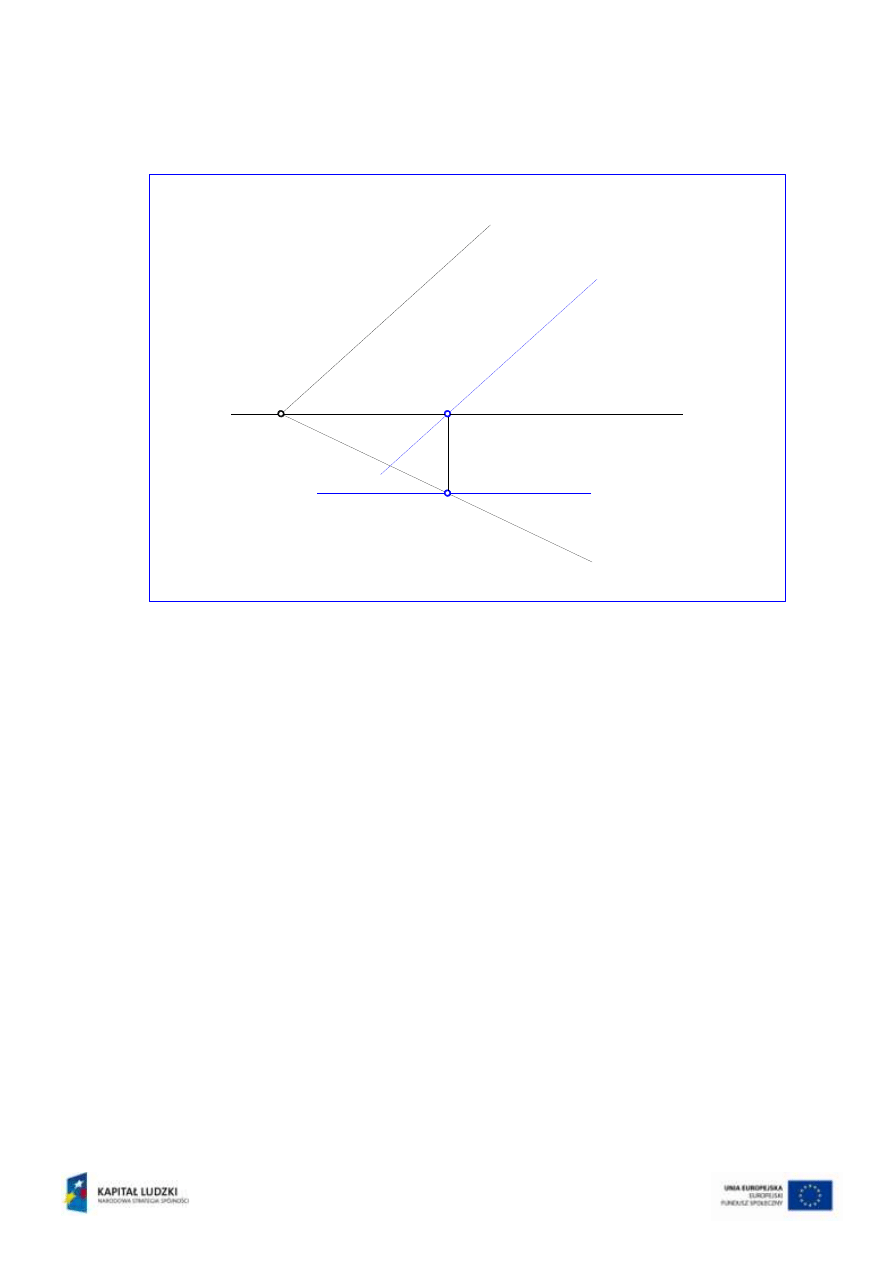
Prosta czołowa m przynależna do płaszczyzny
(rys.14)
x
v
X
h
H
m
m''
m'
H''
m
Rys.14
Prosta taka nie posiada śladu pionowego Vm, bo z definicji nie przecina rzutni
pionowej. Zamiast tego jej rzut pionowy
m’’ zachowuje równoległość do śladu
pionowego płaszczyzny v
.
Istniejący ślad poziomy Hm prostej m zgodnie z definicją
leży na śladzie poziomym h
płaszczyzny
.
Dla wygody można taką prostą
oznaczyć jako c.
Wyszukiwarka
Podobne podstrony:
1 elementy przynalezne
Elementy przynależne
Konstrukcja elementów przynaleznych wielokąt z otworem
1 pr kontr elementy przynalezne Nieznany (2)
1 pr kontr elementy przynalezne
Wyk 02 Pneumatyczne elementy
Elementy prawa prawo administracyjne
7 Mikro i makro elementy naszej diety
Wykład 4 Elementarne zagadnienia kwantowe
Elementy klimatu
7 Sposób montażu charakterystycznych elementów
Elementy fizyki jądrowej
Doradztwo i jego prawny element procesu decyzyjnego
Podział chorób nerek z elementami patofizjologii
Praca zespolowa z elementami komunikacji interpersonalnej ed wczesn
więcej podobnych podstron