Całki niewłaściwe
I. Całki niewłaściwe w przedziale nieskończonym.
Niech funkcja f będzie określona w przedziale < a,∞) i całkowalna w każdej skończonej części T
< a, T > tego przedziału. Granicę lim f ( x) dx nazywamy całką funkcji f w granicach od a do T →∞ ∫
a
∞
nieskończoności i oznaczamy symbolem ∫ f ( x) dx . W przypadku, gdy granica ta jest skończona, a
mówimy, że całka jest zbieżna. Jeżeli granica jest nieskończona lub nie istnieje, to mówimy, że całka jest rozbieżna.
Poniżej podamy kilka przykładów badania zbieżności całek niewłaściwych.
Rachunki wykonamy za pomocą kalkulatora ClassPad 300 Plus.
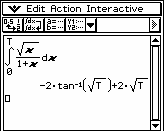
Przykład 1. Zbadać zbieżność całki
∞
∫ x dx
1 + x
0
Zgodnie z definicją, liczymy całkę T
∫ x dx
1 + x
0
oraz granicę
Zatem całka jest rozbieżna.
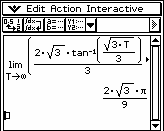
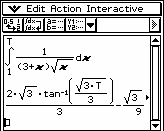
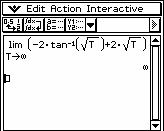
Przykład 2. Zbadać zbieżność całki
∞
∫ dx
(3
x) x
1
+
Zgodnie z definicją, liczymy całkę T
∫ dx
(3
)
1
+ x x
oraz granicę
Zatem całka jest zbieżna.
II. Całki funkcji nieograniczonych.
Jeżeli przedział < a, b > zawiera punkt c ∈ ( a, b) , w którego otoczeniu funkcja f jest nieograniczona, to całkę niewłaściwą funkcji f w przedziale < a, b > określamy jako b
c− ε
b
∫ f ( x) dx = lim f ( x) dx +lim f ( x) dx ε →0 ∫
δ →0 ∫
a
a
c+ δ
W przypadku, gdy c = a lub c = b , znika jeden ze składników.
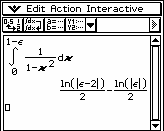
Przykład 3. Zbadać zbieżność całki 1
∫ dx
− 2
1 x
0
W tym przypadku
1
−
1 ε
∫ dx =
dx
lim
2
ε → ∫
1− x
1 − 2
0
x
0
0
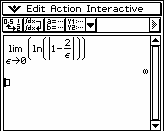
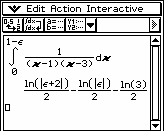
Ponieważ
ln ε − 2
ln ε
1
ε − 2 1
2
−
= ln
= ln1−
2
2
2
ε
2
ε
oraz
więc całka jest rozbieżna.
Przykład 4. Zbadać zbieżność całki 2
∫ dx
2
x − 4 x + 3
0
Ponieważ 2
x − 4 x + 3 = ( x − )(
1 x − )
3 , więc
2
2
1
2
∫ dx
=
dx
dx
dx
2
∫
= ∫
+ ∫
x − 4 x + 3
( x − )(
1 x − )
3
( x − )(
1 x − )
3
( x − )(
1 x − )
3
0
0
0
1
Zbadajmy zbieżność pierwszej całki: 1
−
1 ε
∫
dx
=
dx
lim
ε →0 ∫
( x − )(
1 x − )
3
( x − )(
1 x − )
3
0
0
Rozumując jak w Przykładzie 3 stwierdzamy, że pierwsza całka jest rozbieżna.
Nie ma więc potrzeby badania zbieżności drugiej całki.
Ostatecznie, dana całka jest rozbieżna.
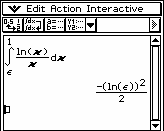
Przykład 5. Zbadać zbieżność całki 1
∫ ln x dx
x
0
Zgodnie z definicją mamy
1
1
∫ ln x =
ln x
dx
lim
dx
ε →0 ∫
x
x
0
0+ ε
Ponieważ
oraz
lim(ln ε )2 = ∞
ε →0
więc nasza całka jest rozbieżna.
Wyszukiwarka
Podobne podstrony:
AM23 w01 Całki niewłaściwe pierwszego rodzaju
Calki niewlasciwe
090 Całki niewlaściwe
CALKI NIEWLASCIWE2008 id 107240 Nieznany
FiR Całki niewłaściwe
calki niewlasciwe
5 6 Całki niewłaściwe
calki niewlasciwe
AM23 w01 Całki niewłaściwe pierwszego rodzaju
w 11 całki niewłasciwe
am1 0708 cz 11 calki niewlasciwe
Sciaga17 Calki niewlasciwe
Całki oznaczone i niewłaściwe
Całki oznaczone i niewłaściwe
Calki oznaczone i niewlasciwe grupa 3
więcej podobnych podstron