1

D. Ciołek

EKONOMETRIA – wykład 3

EKONOMETRIA

Wykład 3: Weryfikacja modelu ekonometrycznego.

dr Dorota Ciołek

Katedra Ekonometrii

Wydział Zarządzania UG

http://wzr.pl/dci

[e-mail]

2

D. Ciołek

EKONOMETRIA – wykład 3

Etapy procesu weryfikacji

Weryfikacja ekonomiczna („zdrowo rozsądkowa” ):

-

Sprawdzenie zgodności wyników oszacowania z teorią
ekonomiczną i doświadczeniem.

Weryfikacja stochastyczna:

-

Sprawdzenie prawdziwości założeń dotyczących składnika
losowego – badanie własności estymatora MNK w tym modelu.

Weryfikacja ilościowa:

-

Sprawdzenie istotności zależności między zmienną endogeniczną
a zmiennymi objaśniającymi,

-

Sprawdzenie dobroci dopasowania modelu do danych
rzeczywistych,

-

Sprawdzenie poprawności doboru postaci analitycznej modelu.

3

D. Ciołek

EKONOMETRIA – wykład 3

Weryfikacja stochastyczna:

-

Weryfikacja hipotezy o normalności rozkładu
składnika losowego.

-

Weryfikacja hipotezy o braku autokorelacji
składników losowych.

-

Weryfikacja hipotezy o stałości wariancji składników
losowych.

Jeżeli powyższe hipotezy są prawdziwe wówczas:

estymator MNK parametrów strukturalnych liniowego
modelu ekonometrycznego jest estymatorem
nieobciążonym, zgodnym i najbardziej efektywnym w klasie
estymatorów nieobciążonych – BLUE.

4

D. Ciołek

EKONOMETRIA – wykład 3

I Normalność rozkładu składnika losowego

Stosując większość testów statystycznych zakładamy, że badana

zmienna ma rozkład normalny.

Testowanie normalności rozkładu

np. Test Jarque,a-Bery

W rozkładzie normalnym: miara skośności

S=0

miara kurtozy

K=3

gdzie - drugi, trzeci i czwarty moment centralny

rozkładu.

t



3

2

2

3







S

2

2

4







K

4

3

2

,

,







5

D. Ciołek

EKONOMETRIA – wykład 3

I Normalność rozkładu składnika losowego

Hipotezy testu:

Statystyka z próby:

Statystyka ma asymptotycznie rozkład .

Prawostronny obszar krytyczny określony przez .

Test ma zastosowanie tylko dla dużych prób.

N

ma

nie

H

N

H

t

A

t





:

~

:

0



























24

3

6

2

2

K

S

T

JB

)

2

(

2



)

2

(

2





6

D. Ciołek

EKONOMETRIA – wykład 3

I Normalność rozkładu składnika losowego

W przypadku niespełniania założenia o normalności:

-

Zmodyfikować metody uwzględniając inny, lepszy w danym
przypadku rozkład: gamma, log-normalny, itd.

-

Dokonać transformacji zmiennych (np. zlogarytmować,
podnieść do potęgi) tak, aby uzyskać rozkład normalny.

Przykładem takiej transformacji jest transformacja Boxa-Coxa.

7

D. Ciołek

EKONOMETRIA – wykład 3

II Autokorelacja składników losowych

Jeżeli składniki losowe z okresu t nie przenoszą swego

oddziaływania na okres następne – brak autokorelacji:

Występuje autokorelacja składników losowych, wówczas gdy:

Jeżeli w modelu występuje autokorelacja rzędy 1, możemy

zapisać:

gdzie: to współczynnik autokorelacji rzędu 1,

to błąd czysto losowy.

)

(

;

0

)

(

s

t

E

s

t









)

(

;

0

)

(

s

t

E

s

t









)

,...,

2

(

;

1

1

T

t

t

t

t

















1



1

|

|

1





t



8

D. Ciołek

EKONOMETRIA – wykład 3

II Autokorelacja składników losowych

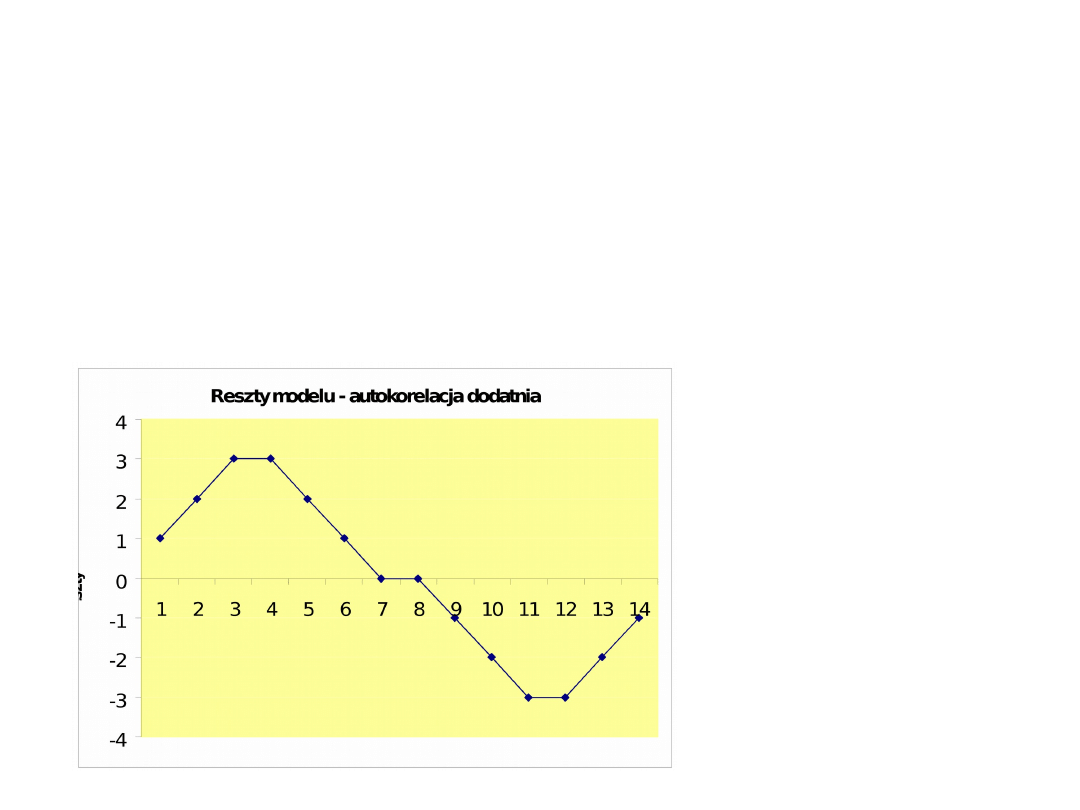
Autokorelacja w modelu może być autokorelacją dodatnią:

Wtedy, gdy obok siebie występować będą seriami składniki

losowe takich samych znaków

1

ˆ

0

1







909

,

0

ˆ

1





9

D. Ciołek

EKONOMETRIA – wykład 3

II Autokorelacja składników losowych

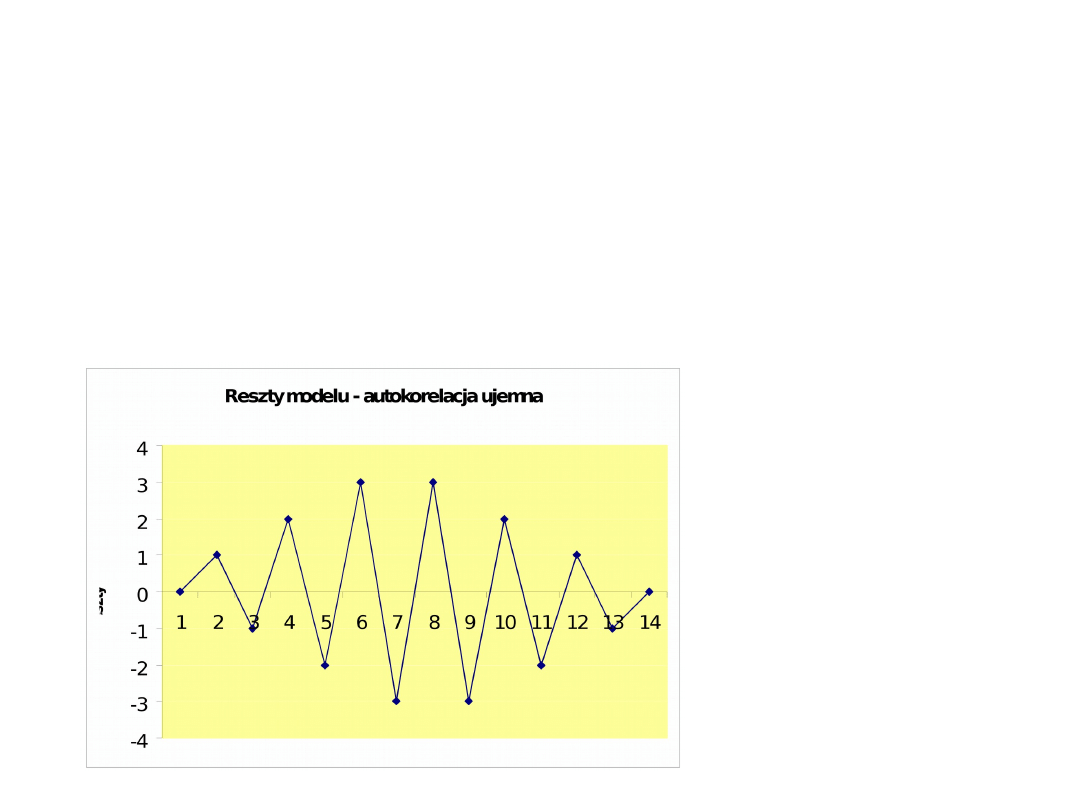
Autokorelacja w modelu może być autokorelacją ujemną:

Wtedy, gdy obok siebie występują składniki losowe o różnych

znakach.

0

ˆ

1

1









964

,

0

ˆ

1







10

D. Ciołek

EKONOMETRIA – wykład 3

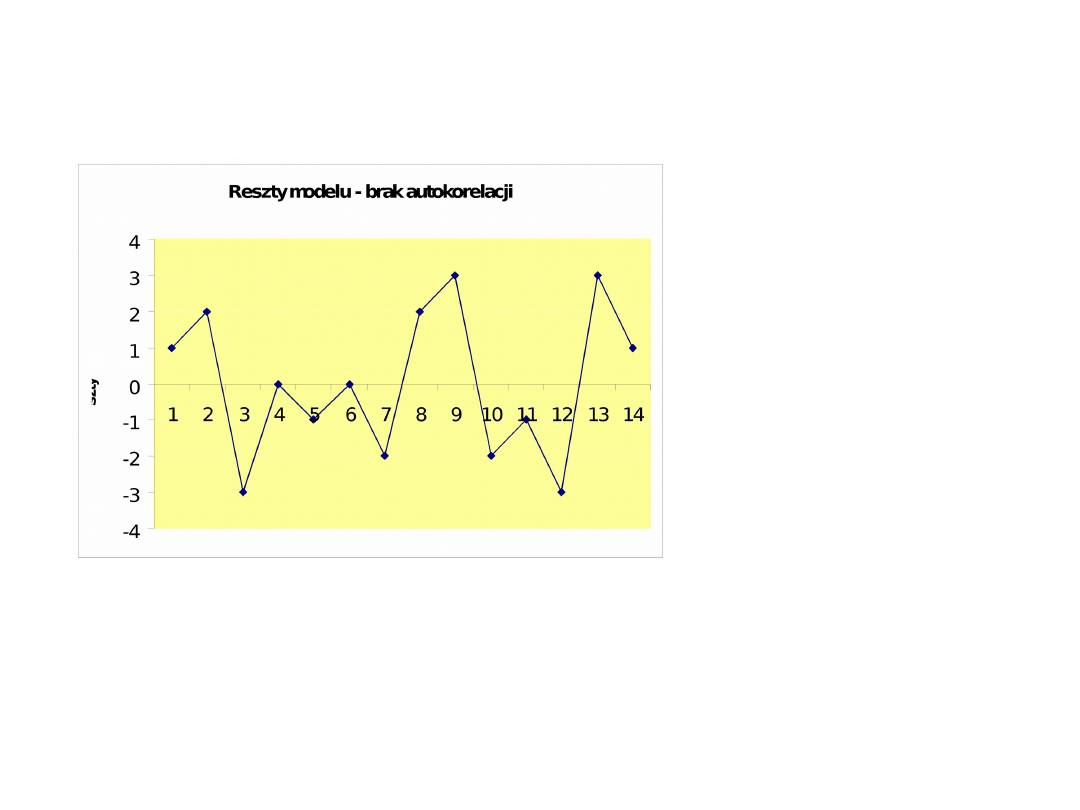
II Autokorelacja składników losowych

W praktyce jednak badanie autokorelacji składników

losowych nie jest takie proste.

164

,

0

ˆ

1







11

D. Ciołek

EKONOMETRIA – wykład 3

II Autokorelacja składników losowych

W modelach dla danych przekrojowych występowanie autokorelacji

należy rozważać w inny sposób.

-

Jeżeli kolejność ustawienia badanych jednostek jest dowolna
wówczas nie można ustalić wiarygodnej wartości współczynnika
autokorelacji.

-

Jeżeli kolejność ustawienia jednostek jest określona: sąsiednie
regiony lub państwa, sąsiadki na osiedlu, itp. wówczas
występowanie autokorelacji składników losowych możemy
interpretować jako efekt naśladowanictwa.

W modelach przekrojowych nie badamy autokorelacji w

czasie.

(Możemy mieć ewentualnie do czynienia z autokorelacją

przestrzenną*).

12

D. Ciołek

EKONOMETRIA – wykład 3

II Przyczyny autokorelacja składników

losowych

-

Pominięcie w modelu ważnej zmiennej egzogenicznej.

-

Niewłaściwy dobór opóźnień zmiennych objaśniających.

-

Efekt „wygasającego echa” – czynnik przypadkowy, który w
pewnym momencie zadziałał ze znaczną siłą i jego
działanie ma swoje skutki w następnych okresach –
autokorelacja dodatnia.

-

Wybór niewłaściwej postaci analitycznej modelu.

-

Uwzględnienie w modelu zbyt dużej liczby zmiennych
objaśniających przypadkowo dobranych.

-

Pominięcie efektu sezonowości analizowanej zmiennej
endogenicznej.

13

D. Ciołek

EKONOMETRIA – wykład 3

II Skutki autokorelacja składników losowych

-

MNK przestaje być BLUE – nadal jest estymatorem
nieobciążonym, ale przestaje być najefektywniejszy.

-

Wariancja resztowa staje się obciążonym estymatorem
wariancji składników losowych.

Obciążone i nieefektywne stają się estymatory błędów

szacunku parametrów strukturalnych.

Błędne są wyniki testów istotności.

-

Niewiarygodne syntetyczne miary dopasowania.

14

D. Ciołek

EKONOMETRIA – wykład 3

II Testowanie występowania autokorelacji

Testowanie zachowania składników losowych przeprowadzamy

na szeregu reszt uzyskanych z modelu oszacowanego MNK.

1) Test Durbina-Watsona

- Służy do badania autokorelacji rzędu pierwszego

Statystyka z próby:

Jeżeli w modelu podejrzewamy występowanie

autokorelacji dodatniej, wówczas hipotezy testu:















T

t

t

T

t

t

t

DW

1

2

2

2

1

ˆ

)

ˆ

ˆ

(







4

,

0



DW

2

,

0



DW











0

:

0

:

1

1

0





A

H

H

15

D. Ciołek

EKONOMETRIA – wykład 3

II Testowanie występowania autokorelacji

Jeżeli w modelu podejrzewamy występowanie

autokorelacji ujemnej, wówczas hipotezy testu:

W takim przypadku wyliczamy nową wartość statystyki:

W obu przypadkach z tablic testu Durbina-Watsona

odczytujemy dwie wartości krytyczne (dla liczby obserwacji
T i liczby zmiennych objaśniających k):











0

:

0

:

1

1

0





A

H

H



4

,

2



DW

DW

DW



4

*

u

l

d

d

16

D. Ciołek

EKONOMETRIA – wykład 3

II Testowanie występowania autokorelacji

Reguła decyzyjna:

-

Jeżeli , to odrzucamy hipotezę zerową.

-

Jeżeli , brak podstaw do odrzucenia
hipotezy zerowej.

-

Jeżeli , to wartość statystyki znajduje
się w tzw. obszarze niekonkluzywności testu, test DW nie
daje odpowiedzi, czy w modelu występuje autokorelacja
składników losowych.

Relacja między statystyką DW a współczynnikiem

autokorelacji:

l

d

DW

DW



)

lub

(

*

u

d

DW

DW



)

lub

(

*

u

l

d

DW

DW

d





)

lub

(

*

)

ˆ

1

(

2

1







DW

-1

0

1

D
W

4

2

0

1

ˆ











17

D. Ciołek

EKONOMETRIA – wykład 3

II Testowanie występowania autokorelacji

Warunki stosowania testu Durbina-Watsona:

-

W modelu musi występować wyraz wolny.

-

Zmienne objaśniające muszą być nielosowe.

-

Wśród zmiennych objaśniających nie może znajdować się
zmienna endogeniczna opóźniona w czasie.

-

Liczba obserwacji powinna być wystarczająco duża: im
mniejsza liczba obserwacji tym szerszy przedział
niekonkluzywności testu.

Należy pamiętać, że test DW bada tylko autokorelację rzędu

pierwszego (pomiędzy sąsiednimi obserwacjami).

18

D. Ciołek

EKONOMETRIA – wykład 3

II Testowanie występowania autokorelacji

Dla modeli, w których zmiennymi objaśniającymi są zmienne

endogeniczne opóźnione w czasie:

2) Test h Durbina

Hipotezy testu:

Statystyka z próby:

gdzie jest empiryczną wariancją błędu estymacji

parametru , T oznacza liczebność próby,

zaś oznacza współczynnik autokorelacji reszt MNK.











0

:

0

:

1

1

0





A

H

H

)

ˆ

(

ˆ

ˆ

1

2

1

1







T

T

h





)

ˆ

(

ˆ

1

2





1



t

t

tK

K

t

t

y

x

x

y























 1

1

1

1

0

...

1



ˆ

19

D. Ciołek

EKONOMETRIA – wykład 3

II Testowanie występowania autokorelacji

Statystyka

h

ma asymptotycznie rozkład normalny

standaryzowany:

Wartości krytyczne dla testu

h

:

Hipoteza zerowa jest odrzucana wówczas, gdy:

Testu nie można zastosować, gdy:

)

1

;

0

(

~N

h

9

,

0

)

645

,

1

|

(|

1

,

0





z

z

P

95

,

0

)

96

,

1

|

(|

05

,

0





z

z

P

99

,

0

)

576

,

2

|

(|

01

,

0





z

z

P



z

h 

|

|

1

)

ˆ

(

ˆ

1

2







T

20

D. Ciołek

EKONOMETRIA – wykład 3

II Sposoby eliminacji autokorelacji z modelu

1) Rozpoznanie przyczyn występowania autokorelacji i

odpowiednia zmiana konstrukcji modelu:

- dołączenie nowej zmiennej objaśniającej,

- zdynamizowanie modelu, bądź zmiana opóźnień,

- dołączenie zmiennej lub funkcji tej zmiennej, by

wyodrębnić nadzwyczajny efekt czynnika

losowego,

- zmianie postaci analitycznej modelu,

- redukcji liczby zmiennych objaśniających

(zmniejszenie efektów pozornego wyjaśnienia),

- dołączeniu zmiennej cyklicznej dwuokresowej.

21

D. Ciołek

EKONOMETRIA – wykład 3

II Sposoby eliminacji autokorelacji z modelu

2) Zastosowanie innej niż MNK metody szacowania parametrów

strukturalnych – Uogólnione Metody Najmniejszych
Kwadratów.

Metody te polegają na odpowiednim przekształceniu
pierwotnych obserwacji zmiennych modelu, tak by
wyeliminować z nich autokorelację i następnie na
oszacowaniu modelu MNK.

22

D. Ciołek

EKONOMETRIA – wykład 3

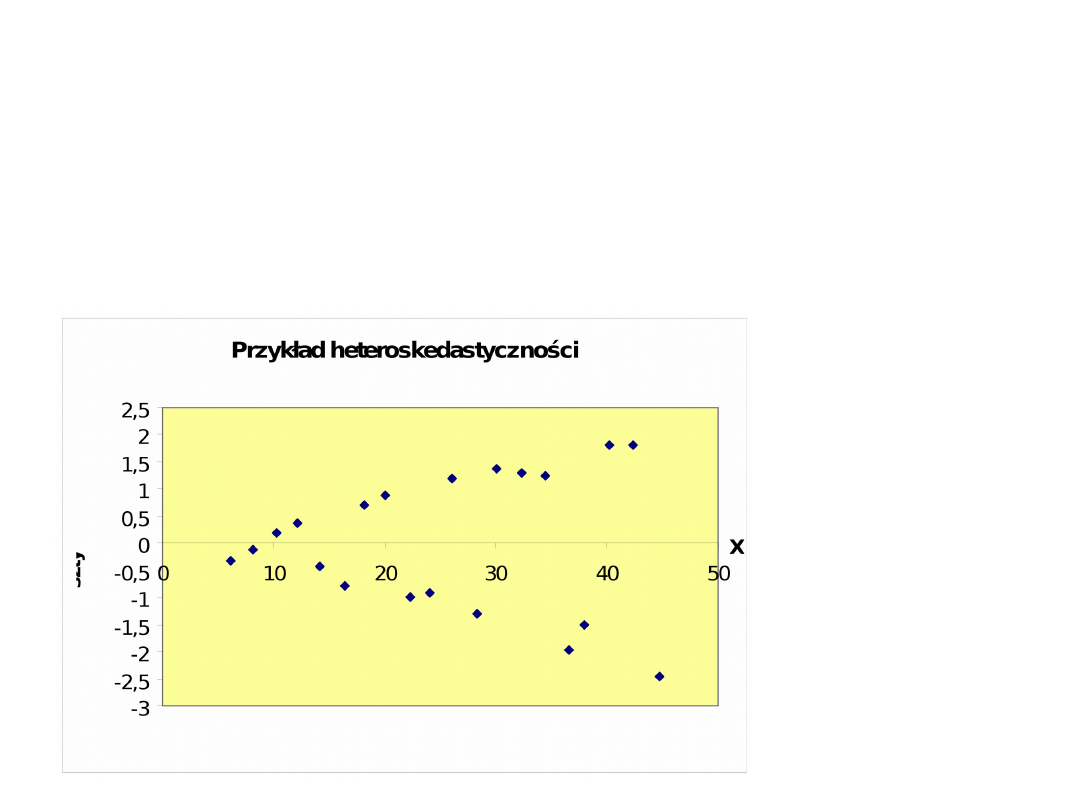
III Stałość wariancji składników losowych

Homoskedastyczność – składniki losowe w modelu mają stałą

wariancję.

Heteroskedastyczność – składniki losowe w modelu nie mają stałej

wariancji.

Reszty są większe,
im większe są
wartości zmiennej
objaśniającej.

tzn. Wariancja reszt
jest zmienna.

23

D. Ciołek

EKONOMETRIA – wykład 3

III Testowanie heteroskedastyczności

Z własności numerycznych MNK wynika, że reszty są

nieskorelowane ze zmiennymi objaśniającymi.

Dlatego bada się np. zależność reszt od wartości zmiennych

podniesionych do kwadratów, do potęgi trzeciej itd. –
różne testy.

Test White’a

W jednej z wersji wykorzystuje regresję kwadratów reszt ze

względu na stałą i kwadraty wartości teoretycznej zmiennej
endogenicznej:

Badamy, czy parametr

α

1

jest statystycznie istotny.

t

t

t

u

y 





2

1

0

2

ˆ

ˆ







24

D. Ciołek

EKONOMETRIA – wykład 3

III Testowanie heteroskedastyczności

Hipotezy testu:

H

o

odrzucamy, gdy parametr

α

1

okaże się statystycznie

istotny, tzn. że wartości reszt wzrastają lub zmniejszają się
wraz ze wzrostem wartości wszystkich zmiennych
objaśniających w modelu – wariancja reszt nie jest stała.

Statystyka testu W wyliczana w pakietach komputerowych ma

dwie wersje:

Dla dużych prób:

Dla małych prób:

s

t

H

T

t

H

s

t

t

A

o









2

2

2

2

:

,...,

2

,

1

:

















 

1

~

2

2







)

2

,

1

(

~



T

F

F



25

D. Ciołek

EKONOMETRIA – wykład 3

III Skutki heteroskedastyczności

-

Estymator MNK parametrów strukturalnych nadal jest
estymatorem nieobciążonym, ale staje się nieefektywny.

-

Obciążone oceny błędów szacunku parametrów
strukturalnych.

-

Niewiarygodne wyniki testów istotności.

Sposoby rozwiązania problemu

-

Stosujemy Ważoną Metodę Najmniejszych Kwadratów
(WMNK).

-

Wykorzystujemy tzw., deflatory, które zmieniają poziom
wartości zmiennych.

-

Transformujemy dane do postaci logarytmicznej.

26

D. Ciołek

EKONOMETRIA – wykład 3

IV Testowanie poprawności wyboru postaci

analitycznej

Test Ramseya (RESET - test)

Testuje, czy postać liniowa jest poprawna, czy też należałoby

wybrać wielomian wyższego stopnia.

W jednej z wersji testu sprawdzane jest, czy podniesione do

kolejnych potęg wartości teoretyczne zmiennej
endogenicznej nie są pominiętymi zmiennymi w modelu.

Hipotezy testu:

t

p

t

p

t

t

tk

k

t

t

y

y

y

x

x

y

































)

ˆ

(

....

)

ˆ

(

)

ˆ

(

...

3

3

2

2

1

1

0





















0

0

3

2

0

i

i

A

p

H

H









:

...

:

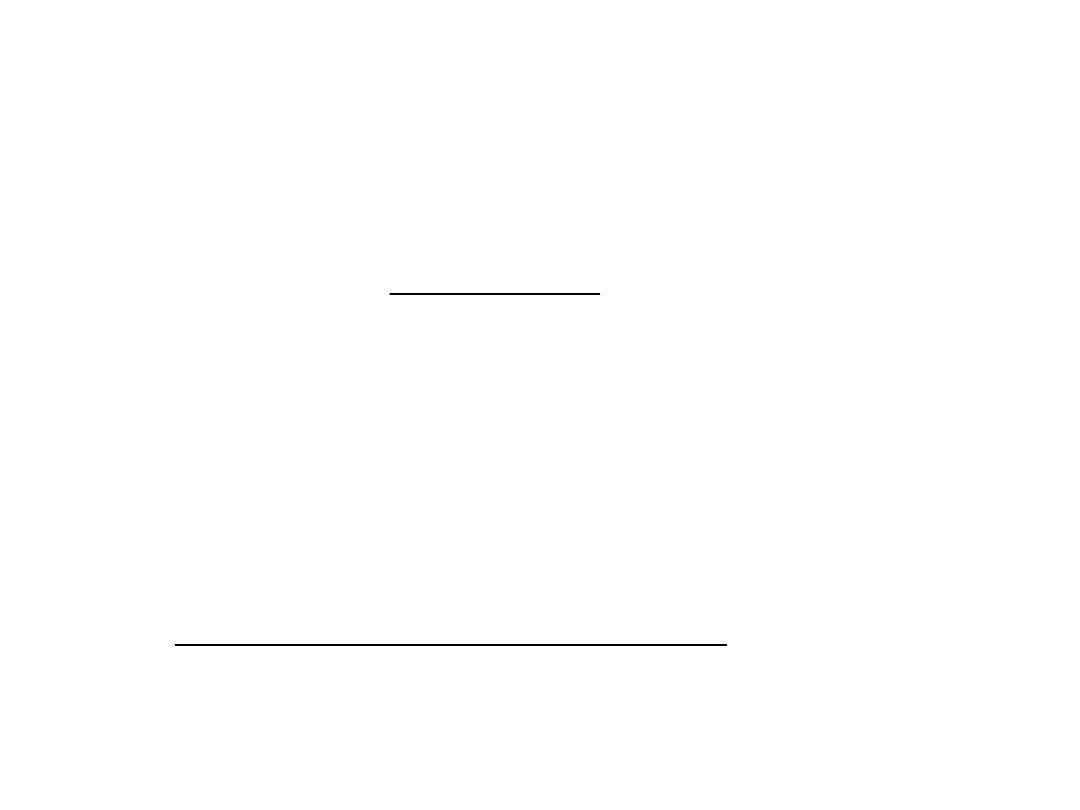
27

D. Ciołek

EKONOMETRIA – wykład 3

IV Testowanie poprawności wyboru postaci

analitycznej

Statystyka dla dużych prób:

gdzie: - suma kwadratów reszt z modelu bez wartości

teoretycznych

y

.

- suma kwadratów reszt z modelu poszerzonego.

Statystyka dla małych prób:

2

1

.

)

(

)

1

(

)

(

2

1

~

/

)

(













p

asymp

k

p

k

k

p

T

S

S

S







)

(

)

(k

S

)

(

)

1

(



 p

k

S

1

2

.

)

1

(

)

1

(

)

(

~

)

2

/(

)

1

/(

}

{

































p

p

k

T

asymp

p

k

p

k

k

F

p

k

T

S

k

p

k

S

S

F



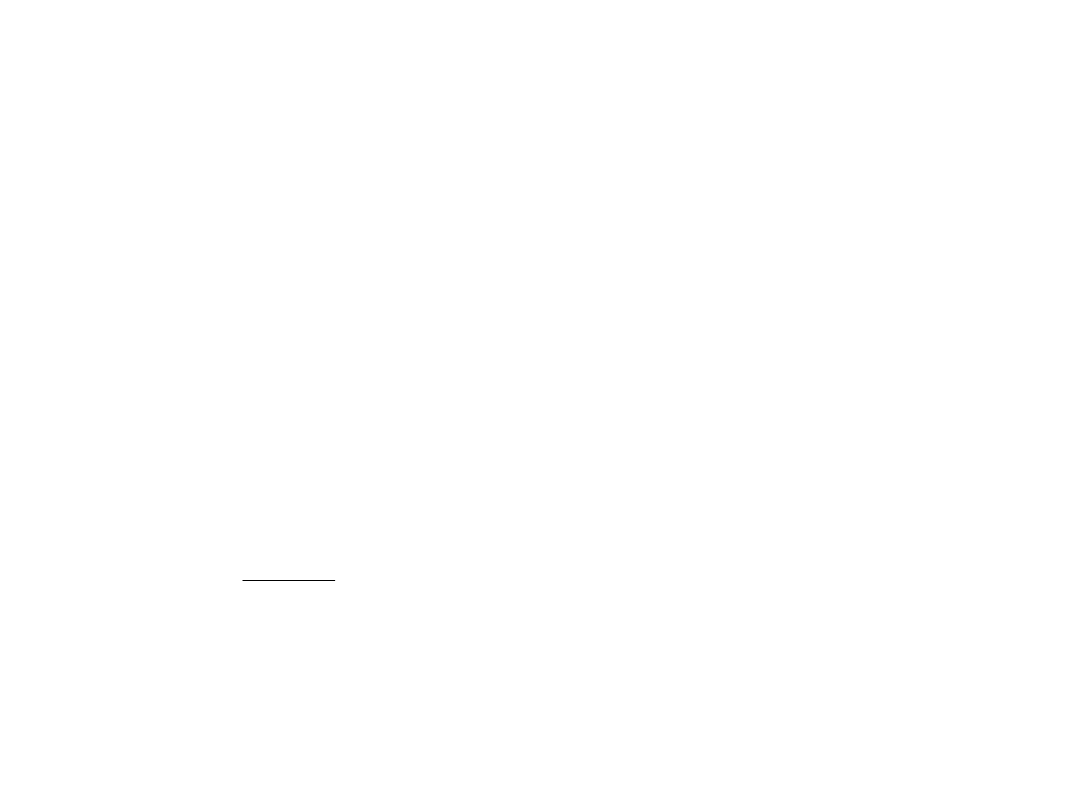
28

D. Ciołek

EKONOMETRIA – wykład 3

V Istotność parametrów strukturalnych

1) Test t-Studenta

indywidualnej istotności parametru strukturalnego

Hipotezy:

Statystyka z próby:

Iloraz ten na rozkład:

)

,...,

1

,

0

(

0

:

0

:

0

k

i

H

H

i

A

i

















)

,...,

1

,

0

(

)

ˆ

(

ˆ

ˆ

k

i

t

i

i

i











1

~



 k

T

i

t

t

29

D. Ciołek

EKONOMETRIA – wykład 3

V Istotność parametrów strukturalnych

W hipotezie zerowej mamy równość stąd:

obszar krytyczny jest obszarem dwustronnym

Pole obszaru krytycznego w każdym teście jest równe poziomowi

istotności (stąd konieczność podzielenia na 2).

W teście t-Studenta H

0

odrzucamy gdy:

Mówimy wówczas, że:

Parametr statystycznie różni się od zera, jest statystycznie istotny.

Zmienna objaśniająca stojąca przy tym parametrze ma
statystycznie istotny wpływ na zmienną endogeniczną.



2

/

|

|



t

t

i





30

D. Ciołek

EKONOMETRIA – wykład 3

V Istotność parametrów strukturalnych

2) Test F

łącznej istotności parametru strukturalnego

Hipotezy:

Statystyka z próby:

Statystyka na rozkład:



















0

:

0

...

:

*

2

1

*

0











A

k

H

H

2

2

1

*





R

k

k

T

F







k

k

T

F

F

1

~

*







31

D. Ciołek

EKONOMETRIA – wykład 3

Do wszystkich testów statystycznych

Prawdopodobieństwo empiryczne – wartość-p, prob, p-value,

jest to prawdopodobieństwo przyjęcia przez statystykę wartości

nie mniejszej od uzyskanej wartości statystyki z próby, przy
założeniu, że hipoteza zerowa jest prawdziwa – tzw.
prawdopodobieństwo empiryczne.

Reguła decyzyjna:

wartość p >



- brak podstaw do odrzucenia

H

0

.

wartość p 



- odrzucamy

H

0

.

Inaczej

wartość p

oznacza poziom istotności, powyżej

którego należy odrzucić hipotezę zerową.

32

D. Ciołek

EKONOMETRIA – wykład 3

Estymacja przedziałowa

Iloraz różnicy między oceną parametru a jego rzeczywistą

wartością ma rozkład t-Studenta:

Wartości pochodzące z rozkładu t-Studenta są skoncentrowane

wokół zera, a prawdopodobieństwo pojawienie się wartości
dużych jest bliskie 0.

Zatem można zapisać:

1

~

)

ˆ

(

ˆ

ˆ









k

t

i

i

i

i

t

t













































1

|

)

ˆ

(

ˆ

ˆ

|

2

/

t

P

i

i

i

33

D. Ciołek

EKONOMETRIA – wykład 3

Estymacja przedziałowa

Otrzymujemy:

Jest to przedział ufności dla parametru strukturalnego.
Z prawdopodobieństwem równym współczynnikowi ufności, powyższy

przedział zawiera nieznany parametr strukturalny











































1

)

ˆ

(

ˆ

ˆ

2

/

2

/

t

t

P

i

i

i



































1

)

ˆ

(

ˆ

ˆ

)

ˆ

(

ˆ

2

/

2

/

i

i

i

i

t

t

P





































1

)

ˆ

(

ˆ

ˆ

)

ˆ

(

ˆ

ˆ

2

/

2

/

i

i

i

i

i

t

t

P

i



34

D. Ciołek

EKONOMETRIA – wykład 3

Macierz wariancji i kowariancji błędów estymacji

parametrów strukturalnych

Błędy estymacji parametrów strukturalnych:

Relacje między błędami zapisać można w postaci wariancji i

kowariancji, które tworzą tzw. macierz wariancji i kowariancji
błędów:







































k

k

















ˆ

ˆ

ˆ

ˆ

1

1

0

0









T

E

E

E

)

ˆ

(

ˆ

)

ˆ

(

ˆ

ˆ



















35

D. Ciołek

EKONOMETRIA – wykład 3

Macierz wariancji i kowariancji błędów estymacji

parametrów strukturalnych

Na głównej przekątnej macierzy znajdują się wariancje błędów,
poza główną przekątną – kowariancje.

Macierz jest macierzą symetryczną.

  











 







 



 

































k

k

k

k

k



















































ˆ

ˆ

,

ˆ

ˆ

,

ˆ

ˆ

,

ˆ

ˆ

ˆ

,

ˆ

ˆ

,

ˆ

ˆ

,

ˆ

ˆ

2

1

0

1

1

2

0

1

0

1

0

0

2

ˆ



















ˆ

36

D. Ciołek

EKONOMETRIA – wykład 3

Macierz wariancji i kowariancji błędów estymacji

parametrów strukturalnych

Macierz ta przyjmuje następującą postać:

gdzie oznacza wariancję składników losowych.

Nieznaną wariancję zastępujemy wariancją reszt modelu:

Otrzymamy wówczas próbkową macierz .

Pierwiastki z elementów na głównej przekątnej są

błędami szacunku parametrów strukturalnych.





1

2

ˆ







X

X

T







2







ˆ

1

ˆ

ˆ

1

2

2











k

T

T

t

t







37

D. Ciołek

EKONOMETRIA – wykład 3

Błędy szacunku parametrów strukturalnych

Oszacowany model regresji wielorakiej można zapisać:

Interpretacja:

Szacując parametr mylimy się średnio in plus, in minus .

lub

uwzględniamy błąd szacunku w interpretacji parametru

strukturalnego.

i



 





 





 





tk

k

t

t

x

x

y

k



















ˆ

ˆ

1

ˆ

ˆ

1

ˆ

ˆ

0

ˆ

...

ˆ

ˆ

ˆ

1

0















 

i





ˆ

ˆ

38

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

1) Średni błąd resztowy (odchylenie standardowe reszt)

określa, o ile jednostek (in plus; in minus), przeciętnie rzecz

biorąc, zaobserwowane wartości zmiennej endogenicznej
odchylają się od wartości teoretycznych (wyznaczonych na
podstawie oszacowanego modelu) tej zmiennej.

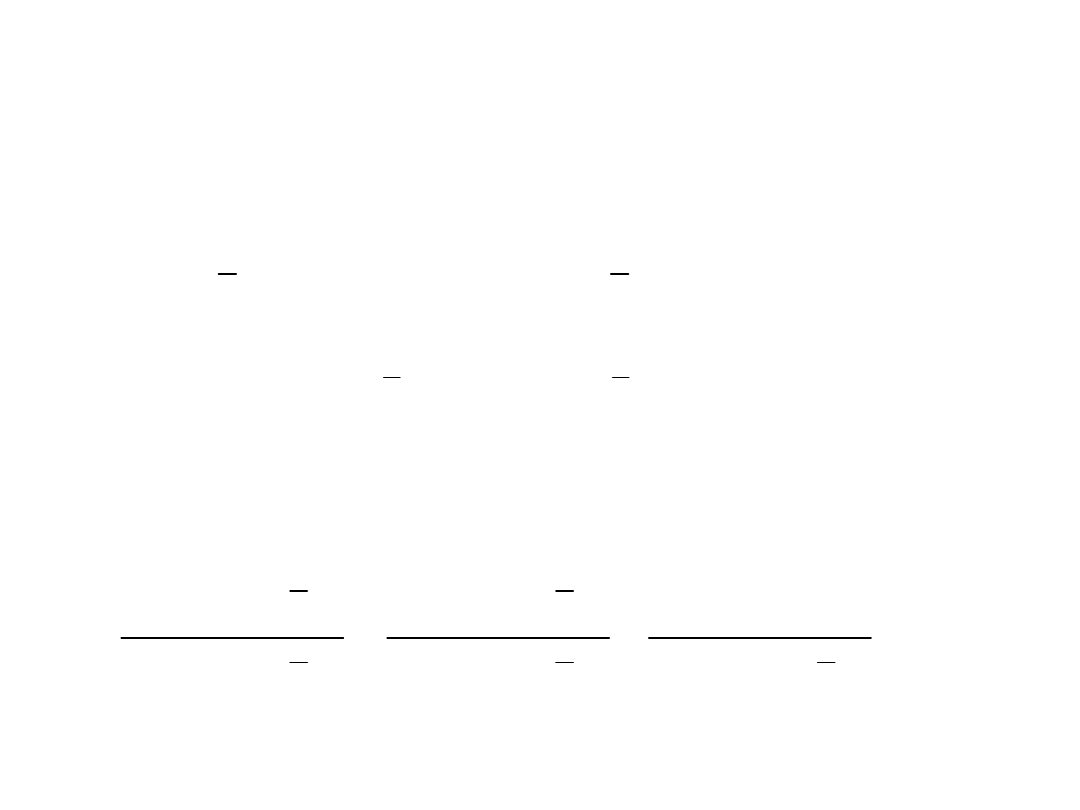
2) Współczynnik zmienności losowej

Informuje o tym, jaki jest procentowy udział średniego błędu reszt

w średniej wartości zmiennej endogenicznej.

2









ˆ

ˆ 

100

y

V







ˆ



39

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

Zmienność zmiennej endogenicznej można podzielić:

zmienność rzeczywista = zmienność teoretyczna +

zmienność reszt.

Dzieląc obie strony równości przez zmienność rzeczywistą

otrzymujemy:









t

t

t

y

y

y

y



ˆ

ˆ 











2

1

2

1

2

1

ˆ

ˆ

t

T

t

t

T

t

t

T

t

y

y

y

y























1

1

2

1

2

1

2

1

2

1

2

1

2









































T

t

t

T

t

t

T

t

t

T

t

t

T

t

t

T

t

t

y

y

y

y

y

y

y

y

y

y

)

(

ˆ

)

(

)

ˆ

(

)

(

)

(



40

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

3) Współczynnik determinacji

Informuje, jaka część całkowitej zmienności zmiennej

endogenicznej została ,,wyjaśniona'' przez model empiryczny.

4) Współczynnik zbieżności (indeterminacji)

Informuje, jaka część rzeczywistej zmienności zmiennej

endogenicznej nie została ,,wyjaśniona'' przez model
empiryczny, tj. kształtuje się pod wpływem czynników
nieuwzględnionych w modelu empirycznym.















T

t

t

T

t

t

y

y

y

y

R

1

2

1

2

2

)

(

)

ˆ

(













T

t

t

T

t

t

y

y

1

2

1

2

2

)

(

ˆ





41

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

Jeżeli w modelu występuje wyraz wolny, to:
oraz

W każdym przypadku suma obu współczynników:

Należy pamiętać, że:

W przypadku szacowania modelu dla niestacjonarnych szeregów

czasowych, wraz ze wzrostem liczebności próby, obie miary
stają się obciążone i oceniają dopasowanie zbyt optymistyczne.

1

0

2



R

1

0

2







1

2

2







R

42

D. Ciołek

EKONOMETRIA – wykład 3

Efekt pozornego wyjaśniania

Suma kwadratów reszt zależy od liczby zmiennych

objaśniających w modelu – im większa liczba zmiennych tym
mniejsza suma kwadratów reszt.

W modelu z bardzo dużą ilością zmiennych objaśniających

możemy uzyskać sumę kwadratów reszt = 0.

Wartość współczynnik determinacji wzrasta wraz z dodawaniem

nowych zmiennych objaśniających, niezależnie od tego czy
nowe zmienne mają istotny wpływ na zmiany zmiennej
endogenicznej.

Oba współczynniki należy skorygować uwzględniając liczbę

zmiennych objaśniających w modelu.

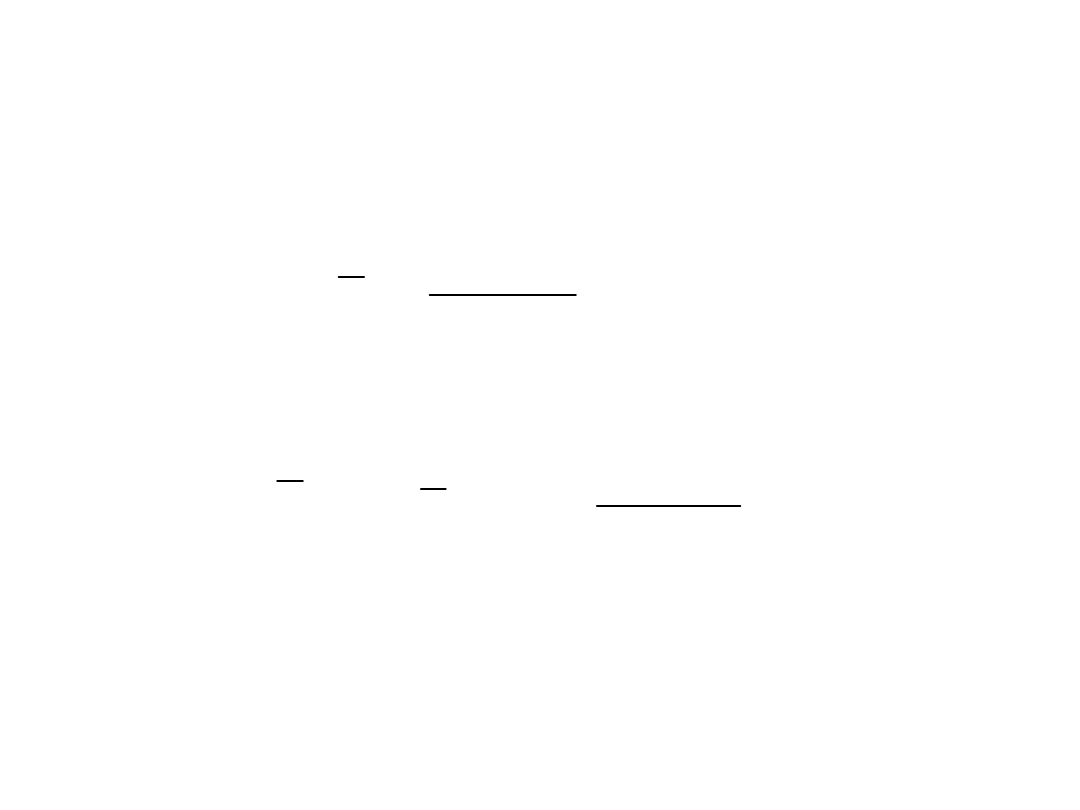
43

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

Korekta o liczbę stopni swobody:
5) Skorygowany współczynnik zbieżności (indeterminacji)

6) Skorygowany współczynnik determinacji

Po uwzględnieniu liczby stopni swobody w modelu, informuje, jaka

część całkowitej zmienności zmiennej endogenicznej została
,,wyjaśniona'' przez model empiryczny.

2

2

1

1













k

T

T

2

2

2

2

1

1

















k

T

k

R

R

44

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

Skorygowany współczynnik zbieżności:

gdzie - wariancja resztowa,

- wariancja zmiennej endogenicznej.

W modelu z więcej niż jedną zmienną objaśniającą:

2

2

2

ˆ

ˆ

y











2





ˆ











T

t

t

y

y

y

T

1

2

2

1

1

)

(

ˆ



2

2







2

2

R

R 

45

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

Wartość zwykłego współczynnika determinacji wzrasta wraz z

dodawaniem do modelu nowej zmiennej objaśniającej.

Wartość skorygowanego współczynnika wzrasta tylko wówczas,

gdy dołączane zmienne mają istotny wpływ na zmienność
zmiennej endogenicznej.

Miary skorygowane:

wykorzystuje się do porównywania różnych modeli, z różną
liczbą zmiennych objaśniających.

Niewielka różnica miedzy i świadczy o braku efektu

,,pozornego wyjaśnienia’’.

2

R

2

R

46

D. Ciołek

EKONOMETRIA – wykład 3

Syntetyczne miary dopasowania

7) Współczynnik korelacji wielorakiej

W modelu z wyrazem wolnym, jest to współczynnik korelacji

liniowej Pearsona między wartościami rzeczywistymi a
teoretycznymi zmiennej endogenicznej.

8) Skorygowany współczynnik korelacji wielorakiej

2

R

R 

)

ˆ

,

(

ˆ

y

y

R





2

R

R 

47

D. Ciołek

EKONOMETRIA – wykład 3

Model regresji bez wyrazu wolnego

Regresja przez początek układu współrzędnych:

- gdy wymaga tego teoria ekonomiczna,

- gdy wyraz wolny znika w wyniku przekształceń zmiennych.

Konsekwencje:

•

Współczynnik determinacji może przyjmować wartości mniejsze
niż 0 i wartości większe niż 100%.

•

Uzyskujemy niedoszacowane błędy szacunku parametrów
strukturalnych.

•

Nie możemy korzystać z niektórych testów statystycznych.

Współczynnik determinacji powinno się liczyć jako kwadrat

współczynnika korelacji miedzy wartościami rzeczywistymi i
teoretycznymi zmiennej endogenicznej.

48

D. Ciołek

EKONOMETRIA – wykład 3

Na co należy zwrócić szczególną uwagę (podsumowanie):



Na czym polega weryfikacja model ekonometrycznego?



Z jakich etapów składa się weryfikacja?



Dlaczego ważna jest normalność rozkładu składnika losowego?



Hipotezy testu badającego normalność.



Dlaczego ważne jest założenie o braku autokorelacji i stałości

wariancji?



Hipotezy testu na brak autokorelacji.



Hipotezy testu na stałość wariancji (homoscedastyczność).



Test na postać analityczną modelu.



Co bada test istotności – jakie ma hipotezy (test t-Studenta i test

F)?



Jak interpretujemy wartość p dla każdego testu?



Przedziały ufności dla parametrów strukturalnych.



Miary dopasowania i ich interpretacja.



Na czym polega efekt pozornego wyjaśniania?