D. Ciołek

EKONOMETRIA – wykład 6

EKONOMETRIA

Wykład 6: Prognozowanie na podstawie modelu ekonometrycznego.

dr Dorota Ciołek

Katedra Ekonometrii

Wydział Zarządzania UG

http://wzr.pl/dc

[e-mail]

D. Ciołek

EKONOMETRIA – wykład 6

Podstawowe pojęcia

Prognozowanie – predykcja ekonometryczna – wnioskowanie

o przyszłości na podstawie znajomości przeszłości np. modelu

ekonometrycznego.

Prognoza - jest to sąd dotyczący przyszłości, wydany na

podstawie wiedzy posiadanej przez prognostyka, za pomocą

konkretnej metody prognozowania.

Zmienna prognozowana – zmienna, której wartości w

przyszłości przewidujemy.

Zmienne prognozujące – zmienne egzogeniczne w modelu

ekonometrycznych, których przyszłe wartości pozwolą na

wyznaczenie prognozy zmiennej prognozowanej.

Okres prognozowany – okres czasu, którego dotyczy prognoza.

D. Ciołek

EKONOMETRIA – wykład 6

Założenia procesu predykcji



Znany jest model ekonometryczny, w którym zmienna
prognozowana odgrywa rolę zmiennej objaśnianej.



Znane są wartości zmiennych objaśniających w okresie
prognozowanym.



Rozkład składnika losowego spełnia zestaw klasycznych
założeń.



Parametry modelu są stabilne, a jeżeli ulegają zmianie to
charakter tych zmian daje się z odpowiednią dokładnością
przewidzieć.



Dopuszczalna jest ekstrapolacja zmiennych poza próbę
statystyczną.

D. Ciołek

EKONOMETRIA – wykład 6

Zasady predykcji



Zasada predykcji nieobciążonej – prognoza ustalana jest na
poziomie wartości oczekiwanej zmiennej prognozowanej w
okresie prognozowanym.



Zasada predykcji według największego
prawdopodobieństwa – prognoza ustalana jest na poziomie
dominanty rozkładu zmiennej prognozowanej w okresie
prognozowanym.

D. Ciołek

EKONOMETRIA – wykład 6

Testowanie stabilności modelu

Model ekonometryczny może być wykorzystany do

prognozowania w przyszłość, jeżeli oszacowana relacja była
stabilna w przeszłości, co pozwala założyć, że również w
najbliższej przyszłości nie powinna ulec radykalnej zmianie.

1) Test Chowa – test stabilności parametrów strukturalnych

modelu (dla modelu z homoscedastycznością zakłóceń)

- Dostępne obserwacje dzielone są na dwie podpróby:

T= t

1

+ t

2

- Szacujemy dwa oddzielne modele:

)

1

(

)

1

(

)

1

(

)

1

(

1

)

1

(

1

)

1

(

0

)

1

(

...

t

tk

k

t

t

x

x

y



















)

2

(

)

2

(

)

2

(

)

2

(

1

)

2

(

1

)

2

(

0

)

2

(

...

t

tk

k

t

t

x

x

y



















D. Ciołek

EKONOMETRIA – wykład 6

Testowanie stabilności modelu

Zakładamy, że składniki losowe w obu podpróbach mają

jednakowe rozkłady.

Hipotezy:

Statystyka z próby (dla małych prób):

gdzie

S

- jest sumą kwadratów reszt dla całej prób,

S

1

- suma

kwadratów reszt dla pierwszej podpróby,

S

2

- suma kwadratów

reszt dla drugiej podpróby.













)

2

(

)

1

(

1

)

2

(

)

1

(

0

:

:









H

H

)}

1

(

2

/{

)

(

)

1

/(

)

(

2

1

2

1















k

T

S

S

k

S

S

S

F

Chow

D. Ciołek

EKONOMETRIA – wykład 6

Testowanie stabilności modelu

Statystyka z próby ma rozkład:

Reguła decyzyjna:

- odrzucamy hipotezę zerową,

- brak podstaw do odrzucenia

H

0

Statystyka z próby (dla dużych prób):

Hipotezę zerową odrzucamy, gdy:

)

1

(

)}

1

(

2

{









k

k

T

Chow

F

F



)

1

(

)}

1

(

2

{









k

k

T

Chow

F

F



2

)

1

(

.

2

~

)

1

(







k

asymp

Chow

Chow

F

k





)

1

(

2

2





k

Chow







)

1

(

)}

1

(

2

{

~







k

k

T

asymp

Chow

F

F

D. Ciołek

EKONOMETRIA – wykład 6

Testowanie stabilności modelu

2) Test PF – predictive failure test (inna wersja testu Chowa)

Tak jak poprzednio, szacujemy dwa modele dla różnych podprób.

Zapisujemy parametry modelu drugiego jako:

Hipotezy:

Statystyka z próby (dla małych prób):

Statystyka z próby (dla dużych prób):











)

1

(

)

2

(











0

:

0

:

1

0





H

H

)}

1

(

;

{

~

)

1

/(

/

)

(

1

2

.

1

1

2

1













k

t

t

F

k

t

S

t

S

S

F

asymp

PF

)

(

~

2

2

.

2

2

t

F

t

asympt

PF

PF









D. Ciołek

EKONOMETRIA – wykład 6

Testowanie stabilności modelu

3) Test QLR – test na występowanie załamania strukturalnego w

nieokreślonym momencie.

H0: brak zmian strukturalnych w szeregu historycznym,

H1: wystąpiły istotne zmiany strukturalne w szeregu.

Test wskazuje również obserwację, dla której prawdopodobieństwo

wystąpienia znaczącej zmiany strukturalnej jest największe.

Wskazaną obserwację można wykorzystać w omawianym powyżej

teście Chowa jako punkt podziału całego szeregu na dwie
podpróby.

4) Testy Cusum (CUmulated SUM of residual) – testy na stabilność

parametrów.

- Wynik odczytywany z wykresu – skumulowane reszty powinny

mieścić się w określonym przedziale.

D. Ciołek

EKONOMETRIA – wykład 6

Rodzaje prognoz

Prognozy bezwarunkowe – do ich wyznaczenia nie ma

potrzeby przyjęcia założenia, że zajdą konkretne okoliczności,
tzn. nie zakłada się, że zmienne prognozujące przyjmą w
okresie prognozowanym określone wartości.

Prognozowanie na podstawie:

-

modelu tendencji rozwojowej;

-

modelu autoregresyjnego.

Prognozy warunkowe – należy założyć lub wyprognozować

jakie wartości przyjmą zmienne prognozujące w okresie
prognozowanym.

Prognozowanie na podstawie:

-

na podstawie modelu statycznego;

- na

podstawie modelu ADL.

D. Ciołek

EKONOMETRIA – wykład 6

Ocena dokładności prognoz

Ocena ex post – dokonywana wówczas, gdy znana jest już

rzeczywista wartość zmiennej prognozowanej w okresie
prognozowanym. Wykorzystuje odchylenie prognozy od
rzeczywistej wartości zmiennej prognozowanej.

Ocena ex ante – dokonywana w momencie wyznaczania

prognozy, gdy nieznana jest jeszcze rzeczywista wartość
zmiennej prognozowanej w okresie prognozowanym. Ocena
dokładności prognozy w oparciu o dokładność (dopasowanie)
modelu ekonometrycznego.

D. Ciołek

EKONOMETRIA – wykład 6

Błędy prognoz ex post

Ocena jakość prognoz ex post przeprowadzana jest jeszcze przed

okresem realizacji prognozy, czyli ocena przewidywana.

Ocena ex post dokonywana jest na bazie prognoz historycznych –

budujemy prognozy wstecz.

1) Średni kwadratowy błąd prognozy - definiować będziemy,

jako średnie kwadratowe odchylenie zmiennej prognozowanej od
prognozy tej zmiennej:

gdzie: T – ilość dostępnych obserwacji historycznych, j – horyzont

prognozy, y

t+j

– rzeczywista wartość zmiennej w okresie

prognozowanym, y

pt+j

– prognoza zmiennej.

Błąd nie ma interpretacji ekonomicznej.



















j

T

t

p

j

t

j

t

p

j

y

y

j

T

MSE

1

2

)

(

1

1

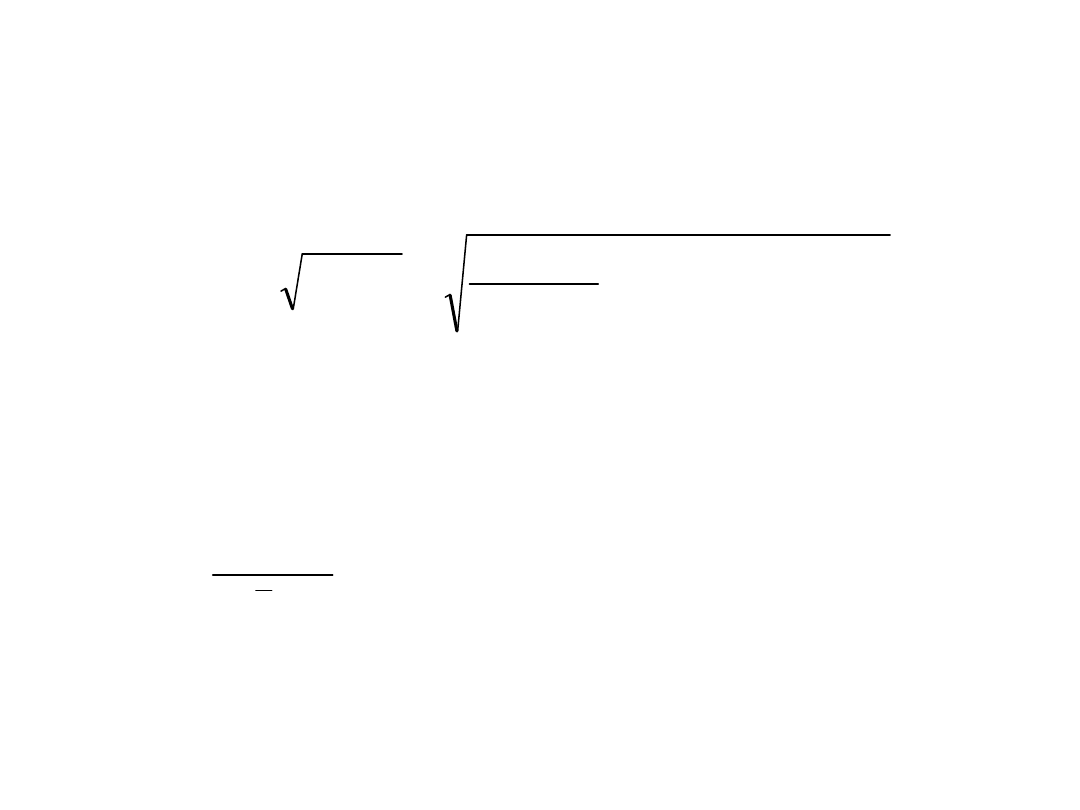
D. Ciołek

EKONOMETRIA – wykład 6

Błędy prognoz ex post cd

2) Średni błąd prognozy - wyznaczać natomiast będziemy jako

pierwiastek kwadratowy ze średniego kwadratowego odchylenia:

Interpretujemy jako przeciętne in plus in minus odchylenie zmiennej

prognozowanej od prognozy tej zmiennej.

3) Przeciętny względny błąd prognozy:

Błąd ten określa procentowy udział średniego błędu prognozy w

średniej wartości prognoz z wyprzedzeniem j okresów. Pozwala
ocenić, czy prognoza jest dopuszczalna – powinien przyjąć wartość
poniżej założonego poziomu dopuszczalności.





















j

T

t

p

j

t

j

t

p

j

p

j

y

y

j

T

MSE

RMSE

1

2

)

(

1

1

100

p

j

p

j

p

j

y

RMSE

V 

D. Ciołek

EKONOMETRIA – wykład 6

Etapy procesu prognozowania na podstawie

modelu ekonometrycznego

1) Oszacowanie modelu ekonometrycznego.

2) Weryfikacja modelu i ocena dobroci dopasowanie – model jest

dobrym narzędziem prognostycznym tylko wtedy, gdy ma
wysoki współczynnik determinacji.

3) Testy własności prognostycznych modelu.

4) Interpretacja błędów prognoz ex post.

5) Wyznaczenie prognozy.

6) Ocena jakości prognozy ex ante (względny błąd prognozy)

7) Interpretacja prognozy punktowej wraz z błędem prognozy ex

ante i prognozy przedziałowej.

D. Ciołek

EKONOMETRIA – wykład 6

Prognozowanie na podstawie modelu statycznego

Wartości zmiennych prognozujących w okresie prognozowanym:

-

są założone jako skutek pewnej decyzji,

-

wyznaczamy na podstawie tendencji rozwojowej tych
zmiennych lub na podstawie innego modelu.

Prognoza punktowa:

Teoretyczna wartość zmiennej prognozowanej w okresie
prognozowanym.

k

j

T

k

j

T

j

T

P

j

T

x

x

x

y

,

2

,

2

1

,

1

0

...

ˆ



























D. Ciołek

EKONOMETRIA – wykład 6

Prognozowanie na podstawie modelu statycznego

Wartości zmiennych prognozujących w okresie prognozowanym:

-

są założone jako skutek pewnej decyzji,

-

wyznaczamy na podstawie tendencji rozwojowej tych
zmiennych lub na podstawie innego modelu.

Prognoza punktowa:

Teoretyczna wartość zmiennej prognozowanej w okresie
prognozowanym.

k

j

T

k

j

T

j

T

P

j

T

x

x

x

y

,

2

,

2

1

,

1

0

...

ˆ



























D. Ciołek

EKONOMETRIA – wykład 6

Prognozowanie na podstawie modelu statycznego

Ocena dokładności prognozy ex ante:

Średni błąd prognozy ex ante:

Informuje, o ile przeciętnie wyznaczona prognoza może odchylać

się od rzeczywistej wartości zmiennej prognozowanej w okresie
prognozowanym.

Względny błąd prognozy ex ante:

Pozwala ocenić

dopuszczalność

prognozy.

2

ˆ

,

ˆ

'

ˆ























j

T

j

t

P

j

T

X

X

%

100

ˆ

ˆ

,
p

j

T

P

j

T

P

j

T

y

V













D. Ciołek

EKONOMETRIA – wykład 6

Prognozowanie na podstawie modelu statycznego

Jeżeli składniki zakłócające modelu mają rozkłady normalne, to:

Zatem:

Prognoza przedziałowa:

)

1

(

,

,

~

ˆ

ˆ

ˆ

ˆ



















k

T

P

j

T

p

j

T

j

T

P

j

T

j

T

t

y

y

















































1

ˆ

ˆ

2

/

,

t

y

y

P

P

j

T

p

j

T

j

T









































1

}

ˆ

ˆ

ˆ

ˆ

{

,

2

/

,

2

/

P

j

T

p

j

T

j

T

P

j

T

p

j

T

t

y

y

t

y

P

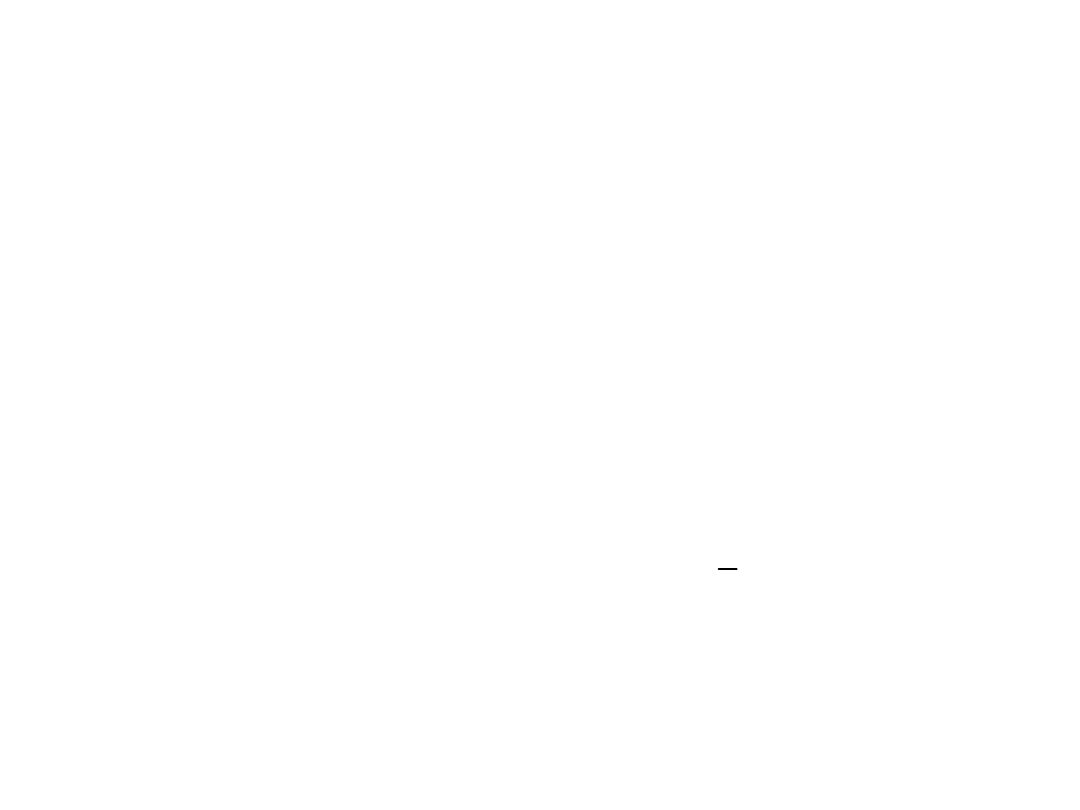
D. Ciołek

EKONOMETRIA – wykład 6

Przykład:

W grupie 2000 rodzin przez 11 miesięcy prowadzono badania

dotyczące miesięcznych wydatków na żywność w setkach zł
(

y

). Przyjęto, ze wydatki te zależą od przeciętnej liczby osób

w rodzinie (

x

1

) oraz miesięcznego dochodu rodziny na

osobę w setkach zł (

x

2

). Oszacowano następujący model

ekonometryczny:

Ponadto wyznaczono:

2

)

019

,

0

(

1

)

284

,

0

(

)

291

,

0

(

1217

,

0

077

,

2

438

,

3

ˆ

t

t

t

x

x

y













835

,

9

001023

,

0

ˆ

984

,

0

2

2







y

R





]

819

,

0

[

052

,

0

]

828

,

0

[

377

,

0

629

,

2







W

JB

DW

]

140

,

0

[

476

,

5



PF

D. Ciołek

EKONOMETRIA – wykład 6

Przykład cd:

Znana jest również:

Należy wyznaczyć prognozę punktową i przedziałową

na okres następny. Jeżeli przypuszcza się, że
przeciętna liczba członków w rodzinie w następnym
okresie wyniesie 2,8, a zmiany miesięcznego
dochodu rodziny są dobrze opisane przez
następujący model tendencji rozwojowej:

Ocenić dopuszczalność tej prognozy w oparciu o ocenę

ex ante.

































034

,

0

049

,

0

008

,

0

049

,

0

081

,

0

042

,

0

008

,

0

042

,

0

085

,

0

ˆ



t

x

t







06

,

0

24

,

6

ˆ

2

D. Ciołek

EKONOMETRIA – wykład 6

Przykład cd:

1) Czy model może być wykorzystany jako narzędzie

prognostyczne?

2) Wektor zmiennych prognozujących w okresie

prognozowanym:

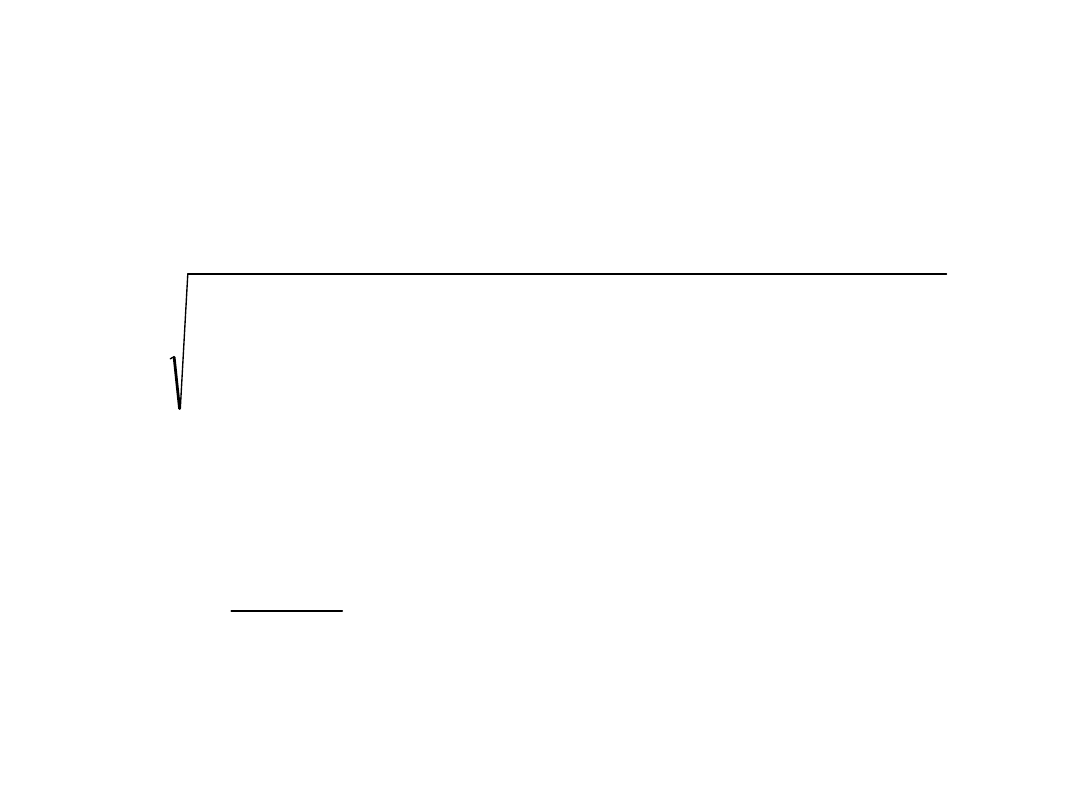
3) Prognoza punktowa:

96

,

6

12

06

,

0

24

,

6

ˆ

8

,

2

2

,

12

1

,

12











x

x





96

,

6

8

,

2

1

12



x

101

,

10

96

,

6

1217

,

0

8

,

2

077

,

2

438

,

3

ˆ

12













P

y

D. Ciołek

EKONOMETRIA – wykład 6

Przykład cd:

4) Dokładność prognozy – ocena ex ante:

Średni błąd prognozy:

Względny błąd prognozy:





0633

,

0

001023

,

0

96

,

6

8

,

2

1

034

,

0

049

,

0

008

,

0

049

,

0

081

,

0

042

,

0

008

,

0

042

,

0

085

,

0

96

,

6

8

,

2

1

ˆ

12

,

























































P





%

627

,

0

%

100

101

,

10

0633

,

0

12







P

V

D. Ciołek

EKONOMETRIA – wykład 6

Przykład cd:

5) Prognoza przedziałowa:

W 95 przypadkach na 100 rzeczywista wartość wydatków na

żywność w okresie 12 znajdzie się w przedziale od 996 do
1024 zł zakładając, że przeciętna liczba osób w rodzinie
wyniesie 2,8, a przeciętny dochód w rodzinie na jedną osobę
wyniesie 396 zł.

05

,

0





0633

,

0

201

,

2

101

,

10

0633

,

0

201

,

2

101

,

10

12













y

24

,

10

96

,

9

12



y

D. Ciołek

EKONOMETRIA – wykład 6

Prognozowanie na podstawie modelu dynamicznego

1) Na podstawie modelu tendencji rozwojowej lub tendencji

rozwojowej z wahaniami sezonowymi.

Za wartości zmiennych prognozujących podstawiane są: t = numer

okresu, na który wyznaczana jest prognoza oraz 1 dla właściwej
zmiennej odpowiadającej danemu kwartałowi lub miesiącowi.

2) Na podstawie modeli z opóźnionymi zmiennymi, np.:

prognozuje się podstawiając do modelu odpowiednio opóźnione

obserwacje na zmiennej objaśniającej.

t

t

dq

dq

dq

t

y

























4

4

3

3

2

2

1

0

t

q

t

q

t

t

t

t

x

x

x

x

y

































...

2

2

1

1

0

0

25

D. Ciołek

EKONOMETRIA – wykład 6

Na co należy zwrócić szczególną uwagę (podsumowanie):



Czym jest predykcja (prognozowanie) ekonometryczne?



Co to jest horyzont prognozy?



Jakie warunki muszą być spełnione, aby możliwe było

wyznaczenie prognozy ekonometrycznej?



Na czym polega zasada predykcji nieobciążonej?



Jak sprawdzić, czy model może być wykorzystany do

prognozowania?



Co to jest prognoza warunkowa, a na czym polega

prognozowanie bezwarunkowe?



Co to znaczy: ocenić prognozę ex ante, a co oznacza ocena ex

post?



Jakie błędy ex post wykorzystuje się do oceny prognoz?



Jak interpretuje się wartość prognozy, błąd ex ante prognozy

oraz przedział ufności dla prognozy?