PROJEKT Z KONSTRUKCJI BETONOWYCH

„BELKA”

Projekt wykonał:

xxxx

xxxx

Strona 1 z 9

1) Schemat obciążeń stałych i zmiennych: q=30 kN/m2

Nq=50 kN

Ng =20 kN

1a – płyta żelbetowa 0,06m

7 – izolacja z papy

25 – płyta z wełny mineralnej twardej 0,04m 14 – gładź wyrównawcza 0,05m

27 – tynk cementowo-wapienny 0,015m

21 – płyty granitowe 0,02m

2) Zestawienie obciążeń charakterystycznych i obliczeniowych: Obciążenie

Współczynnik

Obciążenie

Obciążenie

Warstwa

charakterystyczne

obciążenia γf

obliczeniowe

obliczeniowe

[kN/m2]

(γf>1/γf<1)

(max) [kN/m2]

(min) [kN/m2]

płyta żelbetowa

0,06*25=1,5

1,1/0,9

1,5*1,1=1,65

1,5*0,9=1,35

izolacja z papy

0,02*11=0,22

1,3/0,8

0,22*1,3=0,286

0,22*0,8=0,176

płyta z wełny min.

0,04*2,0=0,08

1,3/0,8

0,08*1,3=0,104

0,08*0,8=0,064

gładź wyr.

0,05*21=1,05

1,3/0,8

1,05*1,3=1,365

1,05*0,8=0,84

tynk cem.-wap.

0,015*19=0,285

1,3/0,8

0,285*0,371

0,285*0,8=0,228

płyty granitowe

0,02*28=0,56

1,2/0,9

0,56*1,2=0,672

0,56*0,9=0,504

SUMA

qk=3,695

-

q01=4,448

q02=3,162

Obciążenie stałe:

N = 20 kN 

g



max

max

min

γ

= 1, 2  N

= 20⋅1, 2 = 24 kN; N

= 20⋅0,8 =16 kN

f

g

g



min

γ

= 0,8 

f



Obciążenie zmienne:

2

max

2

q = 3, 0 kN / m ⇒ q

= 3,0⋅1,3 = 3,9 kN / m

max

N = 50 kN ⇒ N

= 50⋅1,2 = 60 kN

q

q

Strona 2 z 9

Obciążenia przyjęte do obciążenia schematu belki: 2

q

= 3,9 + 4, 448 = 8,348 kN / m

max

2

q

= 3,9 + 3,162 = 7,062 kN / m

min

N

= 60 + 24 = 84 kN

max

N

= 60 +16 = 76 kN

min

3) Wyznaczenie rozpiętości obliczeniowej: l

= l + a

eff

n

n

a = 0,5 t

n

0,5 t = 0, 5 t = 0,125 m

1

2

a = 0,125 m

n

l

=1+ 0,125 =1,125 m

eff 1

l

= 7,5 + 0,125 =

7, 625 m

eff 2

4) Przyjęcie schematu statycznego i wyznaczenie ekstremalnych momentów i sił tnących:

4.1. Schemat statyczny:

4.2. Wyznaczenie ekstremalnego momentu w przęśle: 4.2.1. Schemat obciążenia

4.2.2. Wykres momentów w przęśle:

M

= 216,326⋅2 = 432,652 kNm

max

4.3. Wyznaczenie ekstremalnego momentu na podporach: 4.3.1. Schemat obciążenia

Strona 3 z 9

4.3.2. Wykres momentów na podporach:

M

=190,916⋅2 = 381,832 kNm

max

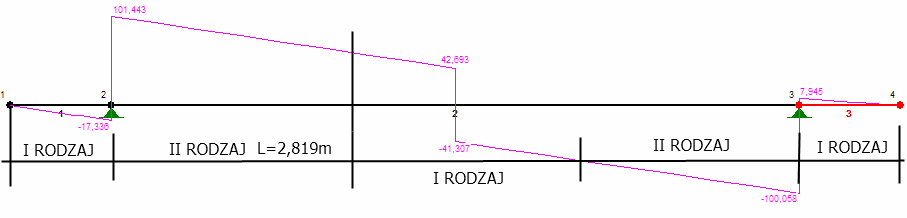
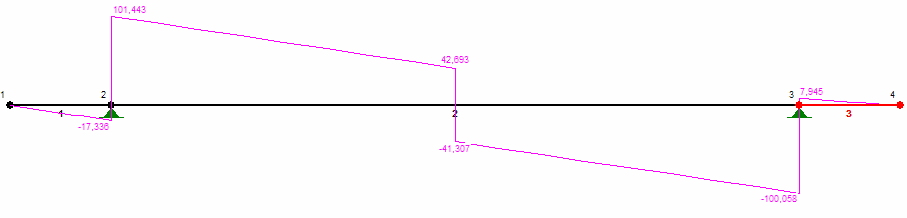
4.4. Wyznaczenie ekstremalnej siły tnącej:

4.4.1. Schemat obciążenia

4.4.2. Wykres sił tnących:

T

=101,443⋅2 = 202,886 kN

max

5) Przyjęcie przekroju belki:

Przyjęty beton i stal: B30, A-II. ρ

= 0,14%; ρ

= 2,96% - z racji, że w belce występują duże min

max

wartości momentów, w dalszych obliczeniach korzystano z ρ = ρ

= 2,96% . Z odpowiednich tablic

max

odczytano także następujące parametry: A = 0, 3988 , f

=16,7 MPa i otulenie c = 0,025 m cd

- wysokość belki:

l

l

eff

eff

7, 625

≤15 → d ≥

=

= 0,51 m

d

15

15

- szerokość belki:

d

Przyjęto:

= 2 ⇒ d = 2 b oraz α =1

w

bw

M

M

M

M

A =

⇒ A =

=

⇒ b =

2

α f b d

α f b (

w

b

α f b

α f A

cd

w

2

)

3

2

3

4

4

cd

w

cd

cd

w

w

3

432, 652 ⋅10−

3

b =

= 0,25 m

w

16, 7 ⋅ 4 ⋅ 0, 3988

Strona 4 z 9

b

=1,13⋅ b = 1,13⋅0,25 = 0,28 m . Wysokość półki h przyjęto równą 10 cm. Ostatecznie eff

w

f

wymiary po zaokrągleniu będą następujące:

b = 0, 25 m

w

b

= 0,50 m

eff

h = 0,1 m

f

h ≈ 51+10 + 2, 5 +1 = 65 cm

przyjęto: h = 10 + 55 = 65 cm

6) Wymiarowanie przekroju teowego na zginanie: Beton: B20; Stal: A-II o f

= 310 MPa ;α f =16,7 MPa ; maksymalny moment wywołany yd

cd

obciążeniem wynosi: M

= 432,652 kNm .

Sd

- sprawdzenie typu przekroju:

Przekrój będzie teowy, jeżeli M

< M

Rd

Sd

M

= α f ⋅ b ⋅ h d −

h

=

⋅

⋅

⋅

−

⋅

=

MNm =

kNm

Rd

cd

eff

f (

0, 5 f ) 16,7 0,5 0,1 (0,51 0,5 0,1) 0,384

384

M

= 384 kNm < M = 432,652 kNm Rd

Sd

Przekrój jest rzeczywiście teowy.

- wymiarowanie:

M = α f ⋅ b − b ⋅ h d − 0, 5 h

= 16,7⋅(0,50 − 0,25)⋅0,1⋅(0,51− 0,5⋅0,1) = 0,192 MNm =192 kNm 1

cd

( eff w) f (

f )

α f ⋅ b − b ⋅ h

⋅

⋅

cd

eff

w

f

16, 7 0, 25 0,1

'

(

)

3

−

2

A =

=

=1,35⋅10 m

1

s

f

310

yd

M = M

− M = 432,652 −192 = 240,652 kNm 2

Sd

1

Strona 5 z 9

M 2

= ξ

−

ξ

eff (1

0, 5 eff )

α f ⋅ b ⋅ d

cd

w

0, 240652

2

−ξ + 0,5ξ = 0

16, 7 ⋅ 0, 25⋅ 0, 51

eff

eff

2

0, 5ξ

−ξ + 0,113 = 0 ⇒ ∆ = 0,774 ⇒ ∆ = 0,88

eff

eff

ξ =1− 0,88 = 0,12 < ξ

= 0,55

eff

eff ,lim

przekrój może być pojedynczo zbrojony:

α f ⋅ b ⋅ d ⋅ξ

⋅

⋅

⋅

cd

w

eff

16, 7 0, 25 0, 51 0,12

"

4

−

2

A =

=

= 8, 24⋅10 m

1

s

f

310

yd

Sumaryczna powierzchnia jest równa:

'

"

3

−

−4

−3

2

2

A = A + A = 1, 35⋅10 + 8, 24 ⋅10 = 2,174 ⋅10 m = 21, 74 cm . Przyjęto zbrojenie w postaci 1

s

1

s

s 1

(7Ø20) o

2

A = 21,99 cm

1

s

7) Wymiarowanie przekroju teowego na ścinanie: Do podpory dochodzą 3 z 7Ø20.

- podpora A z lewej strony i B z prawej strony: V

= 17,336 kN - wartość odczytana z wykresu Sd

k = 1

A

9, 43

sL

ρ =

=

= 0,00739

1

b ⋅ d

25 ⋅ 51

w

V

= 0,35⋅ f ⋅ k(1,2 + 40ρ )⋅ b ⋅ d = 0,35⋅0,87⋅1,00(1,2 + 40⋅0,00739)⋅0,25⋅0,51 =

Rd 1

ctd

1

w

= 0,058 MN = 58 kN

V

> V - odcinek pierwszego rodzaju, więc nie ma potrzeby liczenia ścinania, ale należy zazbroić.

Rd 1

Sd

Ze względów konstrukcyjnych przyjmuję strzemiona ze stali A-0 Ø6 co 30cm.

- podpora A z prawej strony i B z lewej strony: V

= 202,886 kN

Sd

a) Wyznaczenie VRd1:

k = 1, 60 − d = 1, 09

A

9, 43

sL

ρ =

=

= 0,00739

2

b ⋅ d

25 ⋅51

w

V

= 0,35⋅ f ⋅ k(1,2 + 40ρ )⋅ b ⋅ d = 0,35⋅0,87⋅1,09(1,2 + 40⋅0,00739)⋅0,25⋅0,51 =

Rd 1

ctd

2

w

= 0,058 MN = 58 kN

V

< V - konieczne jest obliczeniowe zbrojenie na ścinanie.

Rd 1

Sd

Strona 6 z 9

b) Wyznaczenie VRd2:



f





16

ν



= 0,61

ck

−

 = 0, 61−

 = 0,56



250 



250 

3

V

= 0,5 ν

⋅ ⋅ f ⋅ b ⋅ z = 0,5⋅0,56⋅16,7⋅0,25⋅0,9⋅0,51⋅10 = 536,57 kN

Rd 2

cd

w

c) Wyznaczenie odcinków II rodzaju:

Przyjęto, że belka będzie zbrojona strzemionami prostopadłymi do zbrojenia głównego i nie będzie prętów odgiętych:

V − V

202,886 − 58

Sd

Rd 1

l =

=

=11,32 m

t

g + q

4, 448 + 8,348

l > 1,8 d = 1,8⋅51 = 91,8 cm = 0, 918 m t

ctgΘ = 2

Z racji, że l > 1,8 d odcinek l t

t należy podzielić na mniejsze odcinki. Przyjęto, że lt został podzielony na 3 odcinki l

=

t1, lt2 i lt3, a każdy z nich ma długość 1, 8 d 92 cm . Pozostałą część odcinka lt

( 282 − 3⋅ 92 = 6 cm ) zazbrojono tak samo, jak odcinek lt3.

Ostatecznie przyjęto

- strzemiona

8

∅

- Stal => A0

- fyk = 220 MPa

- fyd = 190 MPa

- ftk = 300 MPa

- Asw1 = 1,00 cm2

d) Rozstaw strzemion dla odcinków II rodzaju: A

f

s 1

w

ywd 1

V

= V

=

z ⋅ ctgΘ

Rd 3

Rd 31

s 1

6

A

f

⋅

⋅

⋅

⋅

⋅

s 1

w

ywd 1

1 190 10 0, 9 0, 51 2

s =

z ⋅ ctgΘ =

= 8,6 cm

1

3

V

202,886 ⋅10

Sd

1⋅190 ⋅ 0,9 ⋅ 0,51⋅ 2

V

=

= 202,81 kN > 0,5 V =101,443

Rd 3

8, 56

Sd

Dla odcinków pierwszego rodzaju przyjęto rozstaw strzemion ze stali A-0 Ø6, co 30cm. Na odcinkach II rodzaju przyjęto rozstaw strzemion ze stali A-0 Ø8, co 10cm.

Strona 7 z 9

8) Zabezpieczenie ścinania: M Sd

F =

+ 0,5⋅ V ⋅ ctgΘ

td

Sd

z

F

= A ⋅ f

td ,max

s 1

yd

F

≥ F

td ,max

td

2

A = 21,99 cm

1

s

f

= 310 MPa

yd

M

= 3

− 81,832 + 202,886⋅0,5⋅7,5 = 378,991 kNm Sd

z = 0, 9 d = 0, 459 m

V

= 202,886 kN

Sd

ctgΘ = 2

6

F

= A ⋅ f = 21,99⋅10− ⋅310000 = 681,69 kN

td ,max

s 1

yd

M Sd

F =

+ 0,5⋅ V ⋅

378, 991

ctgΘ =

+ 0,5⋅202,886⋅2 = 211,146

td

Sd

z

0, 459

9) Ścinanie pomiędzy półką i środnikiem: V

V

Sd

Sd

v

= β

= β

Sd

f

f

z

0, 9 d

dla _ 2 x

∆ = 3,813 m ⇒ M = M

= 381,832 kNm _ i _ V = 85,386 kN

Sd

max

Sd 2

dla _ x

∆ = 1,907 m ⇒ M = 211,32 kNm _ i _ V = V

= 202,886 kN

Sd

Sd 1

max

V

+ V

Sd 1

Sd 2

V

=

=144,136 kN

Sd

2

z = 0, 9 d = 0,9 ⋅ 0,51 = 0, 459 m F

beff 1

0,125

1

c

β =

=

=

= 0,25

f

F

b

0, 5

c

eff

V

144,136

kN

v

Sd

= β

= 0,25

= 78,51

Sd

f 0,9 d

0, 459

m



ctgΘ

V



=ν ⋅ f ⋅ h ⋅

Rd 2

cd

f

2



1+ ctg Θ

v

≤ 

Sd

Asf

V



=

⋅ f ⋅ ctgΘ

Rd 3

yd



s



f



f





16

ν



= 0,61

ck

−

 = 0, 61−

 = 0,56



250 



250 

f

=16,7 MPa

cd

h = 10 cm

f

ctgΘ = 2

Strona 8 z 9

f

= 310 MPa

yd

Asf

−4

2

= 5,03⋅10 m

s f

ctgΘ

kN

V

=ν ⋅ f ⋅ h ⋅

= 0,56⋅16700⋅0,1⋅0,4 = 374,08

Rd 2

cd

f

2

1+ ctg Θ

m

Asf

kN

V

=

⋅ f ⋅ ctgΘ = 5,03⋅31⋅2 = 311,86

Rd 3

yd

s

m

f



kN

V



= 374,08

Rd 2



m

v

≤ 

Sd

kN

V



= 311,86

Rd 3



m

Warunek został spełniony, więc nie będzie ścinania półki.

10)

Stan graniczny ugięcia:

2

2

M

= 0,125⋅ q ⋅ l = 0,125⋅8,348⋅7,625 = 60,67 kNm Sd , lt

lt

eff

B = 30 GPa

∞

2

2

−3

M

⋅ l

⋅

⋅

Sd , lt

eff

5 60, 67 7, 625 10

3

a = α

=

⋅

=12,24⋅10− m = 12,24 mm < a = 30,5 mm k

lim

B

48

30

∞

Belka spełnia warunek ugięcia.

11)

Zarysowanie:

2

2

M

= 0,125⋅ q ⋅ l = 0,125⋅8,348⋅7,625 = 60,67 kNm Sd , lt

lt

eff

ξ = 0,85 ⇒ 0,5% < ρ <1%

l

M Sd, lt

60, 67

kN

σ =

=

= 6,364

= 63,64 MPa

s

2

ξ dA

0,85 ⋅ 0, 51⋅ 21,99

cm

1

s

Belka spełnia warunek zarysowania.

Strona 9 z 9