2.Definicja prędkości średniej i chwilowej punktu

Prędkość średnia w to iloraz drogi i czasu, w którym droga ta została pokonana. Prędkość średnia wyrażona jest wzorem

Prędkość chwilowa jest to jakby prawie prędkość średnia, ale wyznaczana w ciągu bardzo krótkiego przedziału czasu (ściśle rzecz ujmując, powinniśmy wziąć przedział czasu nieskończenie bliski zera).

Postać różniczkowa postać z użyciem granicy

Prędkość chwilowa
postać skalarna

Prędkość chwilowa


postać wektorowa

3. Definicja przyśpieszenia punktu

Przyspieszenie jest miarą zmiany prędkości.

Przyspieszenie chwilowe jest przyspieszeniem jakie obiekt ma w jednej chwili, dokładnie w tym konkretnym ułamku sekundy. 

Postać różniczkowa postać z użyciem granicy

Prędkość chwilowa


postać skalarna

Prędkość chwilowa


postać wektorowa

4.Ruch prostoliniowy jednostajny i zmienny

Ruch prostoliniowy jednostajny - w jednakowych odstępach czasu punkt przebywa jednakowe odcinki drogi .

↑równanie ruchu prostoliniowego jednostajnego

Droga jest liniową funkcją czasu

Wartośc przebytej drogi jest wprosto proporcjonalna do czasu trwania ruchu s=vt , s = f(t)

Wykresem prędkosci w ruchu jednostajnym jest odcinek równoległy do osi czasu .

Pole zawarte pod wykresem prędkości przedstawia przebytą drogę.

Tangens kąta nachylenia lini wykresy s=v(t) jest stosunkiem rzędnej dowolnego punktu tej linii (s) do odciętej tego punktu (t)

Tangensem kąta nachylenia linii wykresu drogi do osi odciętycj przedstawia prędkośc danego ruchu.

Wniosek : im większa prędkośc ruchu tym bardziej stroma linia wykresu drogi s = f(t0

Ruch prostoliniowy :

- zmienny :

przyspieszony i opóźniony ,

Jeśli przyspieszenie jest wielkośćią stałą - ruch jednostajnie zmienny. Jeśli rośnie - przyspieszony , jeśli maleje - opóźniony .

Prędkość jest liniową funkcją czasu v = at v = f(t)

Pole pod wykresem przedstawia przebytądrogę

↑Równanie ruchu jednostajnie zmiennnego

Gdy a > 0 - ruch jednostajnie przyspieszony

a<0 - ruch jednostajnie opóźniony

5. Ruch krzywoliniowy jednostajny i zmienny . Przyspieszeni styczne i normalne

Ruch krzywolniowy jednostajny :

Ruch punktu po torze krzywoliniowym l w którym wektro prędkości jest w każdej chwili styczny do toru oraz stoły co do wartości w czasie ( a zmienia się co do kierunku)

Kierunke wektora przyspieszenia jest w każdej chwili prostopadłu (normalny do wektora prędkości .

Gdy tor punktu jest krzywą płaską , jego kierunkami naturalnymi są styczna i normalna. Na stycznej o wersorze
leży wektor prędkosci
normalna zaś o wersorze
pokrywa się z promieniem krzywizny ρ , którego wartośc w dabym punktcie M można okreslić jako odwrotność krzywizny odpowiadającej danemu punktowi.

Srednią krzywizne łuku MM1 nazywamy stosunek Δφ do długości Δs

Granicę do której zmierza krzywizna średnia , gdy punkt dąży do M ( Δ-> 0 ) nazywamy krzywizną toru w dowlnym punktcie M .

Ruch krzywoliniowy zmiennny :

Ruch punktu po ptrze krzywoliniowym l w którym wektor prędkości jest w każdym punktcie styczny do toru oraz zmienia się co do wartości i co do kierunku

W ruchy krzywoliniiowym zmiennym wektor przyspieszenia punktu jest skierowany pod pewnym kątem α względem wektroa prędkości .

- składowa normalna , rzut wektora przyspieszenia na kierunek normalny do wektora prędkosci

- składowa styczna , rzut wektora pyspieszenia na kierunek wekotra prędkosci .

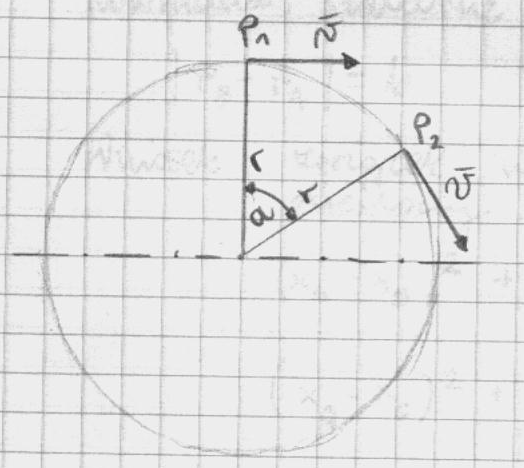
Przyspieszenie styczne - jest składowa przyspieszenai całkowitego w kierunku strycznym do toru i równa się pochodnej względem czasu wartości liczbowej wektora prędkości .

Przyspiesznie normalne
jestr składowa przyspieszenia całkowitego w kierunku normalnym do toru i równe jest kwadratowi prędkości podzielonemu prze promień krzywizny .

Gdy

Prędkośći kątowa ω - jest wektorem leżacym na osi obrotu , mającym wartośc pochodnej względem czasu kąta obrotu

Przyspieszenie kątowa ε - równe co do wartości pochodnej względem czasu prędkości kątowej ω albo drugiej pochodnej względem czasu kąta obrotu φ jest wektorem leżącym na osi obrotu.

6. Ruch jednostajny po okręgu. Droga prędkości przyspieszenie liniowe i kątowe.

Punkt porusza się po okręgu o promieniu r przebywając w równych odstępach czasu t równe odcinki drogi (łuku)

ruch jednost. =stała prędkość dodatkowo wektor v jest styczny do toru

S=p₁p₂=r*alfa p₁p₂-punkty na okręgu s= p₁p₂- łuk i fragment okręgu stanowiący drogę przebytą przez punkt r- promień łuku okręgu alfa-kąt między promieniem prowadzącym do punktów p₁ p₂

gdzie

V=r
Stosunek kąta alfa do czasu t w którym ten kąt został zatoczony nazywamy prędkościa kątową.

przyspieszenie kątowe określa zamianę wektora prędkości kątowej w czasie

7.Pojęcie ciała sztywnego.

Ciało sztywne to zbiór punktów, których wzajemne odległości są stałe. Tzn. że pomijane są odkształcenia zachodzące pod wpływem obciążeń zewnętrznych.

Opis ruchu c. sz. Czyli określenie położenia w dowolnej chwili względem nieruchomego układu współrzędnych (przyjętego za nieruchomy) zprowadza się do wskazania równań ruchu trzech punktów A,B i C nie leżących na jednej prostej.

Niektóre równania ruchu punktów A,B i C:

Pomiędzy dziewięcioma współrzędnymi zachodzą trzy związki stąd jedyne sześc niezależnych współrzędnych określa położenie ciała w przestrzenie

Stad wniosek: ciało sztywne w przestrzeni posiada sześc stopni swobody (l=6)

8. Ruch postępowy ciała sztywnego.

Wszystkie punkty ciała sztywnego doznają tych samych przesunięć.

W ruchu postępowym c. szt. Wszystkie punkty mają takie same prędkości i przyśpieszenie oraz poruszają się po takim samych równoodległych torach.

9. Ruch obrotowy ciała sztywnego.

Ruch, w którym dowolne dwa punkty c. szt. Zostają unieruchomione i wyznaczają prostą zw. Osią obrotu. Wszystkie punkty c. szt. Na tej prostej są unieruchomione. Pozostałe punkty c. szt. Poruszają się po torach będących okręgami o środkach leżących na osi obrotu i leżącymi w płaszczyźnie prostopadłych do osi obrotu.

Tory każdego z punktów c. szt. Są opisane przez promienie o długościach równych odległościom tych punktów od osi Obr.

Równanie drogi: (funkcja kąta)

10. Ruch płaski bryły- pojęcie płaszczyzny kierującej.

Jeśli bryłe k potniemy płaszczyzna B otrzymując przekrój bryły, to ruchem płaskim nazwiemy taki ruch bryły, w którym przekrój S bryły K będzie stale poruszał się w płaszczyźnie B. Wszystkie inne punkty ciała sztywnego będą poruszały się w płaszczyznach równoległych do płaszczyzn B. Płaszczyzna B stałą, nazywamy płaszczyzna kierująca.

Rzuty prędkości dwoch dowolnych punktów ciała sztywnego na prostą łączącą te punkty muszą być sobie równe.

Chwilowy ruch przekroju c. szt. W uchu pł. Jest tuchem obrotowym dookoła chwilowego środka obrotu.

11.Równania ruchu płaskiego - chwilowe położenie, prędkość i przyśpieszenie.

Kinematyczne równania ruchu płask. W postaci wekt.

PRĘDKOŚĆ

Prędkość dowolnego punktu w ruchu płaskim jest sumą geom. Prędkości ruchu postępowego i ruchu obrotowego dookoła obranego obiegu.

Pojęcie ruchu kulistego - określenie położenia bryły

Ruchem kulistym nazywamy ruch, w czasie którego jeden z punktów bryły jest stale nieruchomy. Ruch kulisty jest obrotem dookoła chwilowej osi obrotu (oś ta zmienia swoje polozenie w czasie)

Położenie. Bryła, której jeden punkt jest unieruchomiony ma 3 stopnie swobody. Jej położenie jest opisane w sposób jednoznaczny jedynie za pomocą katów znanych katami Eulera. Dla określenia tych kątów wprowadzamy układ współrzędnych związanych z bryła

Położenie dowolnego punktu A bryły określamy za pomocą wektora r (o stałej długości), którego współrzędne możemy podać w nieruchomym układzie osi x, y, z.

1. Równania ruchu kulistego bryły - prędkość i przyśpieszenie

Ponieważ ruch kulisty jest obrotem wokół chwilowej osi obrotu, wektor prędkości kątowej leży na tej osi.

Przyśpieszenie. Wektor przyśpieszenia kątowego bryły w ruchu kulistym leży na chwilowej osi przyśpieszenia.

Wektor przyśpieszenia kątowego możemy podać tak w nieruchomym układzie osi x, y, z

jaki i w ruchomym układzie osi
- >

Przyśpieszenie liniowe dowolnego punktu A bryły określamy różniczkując względem czasu wyrażenie na prędkość liniową tego punktu.

Gdzie:

- przyspieszenie obrotowe -

- przyspieszenie doosiowe -

Znając położenie chwilowe osi prędkości i przyśpieszenia, wartości przyśpieszenia obrotowego i doosiowego możemy obliczać ze wzoru
i

2. Pojęcie ruchu ogólnego - przemieszczenie bryły, prędkość i przyśpieszenie

Każdy ruch jest zmianą położenia danego ciała lub układu ciał w czasie względem pewnego wybranego układu odniesienia. Układy mogą być dwa:

inercjalny - układ odniesienia względem którego ciało, na które nie działają siły zewnętrzne, pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

Układ nie inercjalny - dowolny układ poruszający się z przyspieszeniem.

Ruch ciała analizuje się przy założeniu, że ciało jest punktem materialnym lub bryłą sztywną. Opis ruchu polega na ustaleniu zależności pomiędzy parametrami ruchu.

3. Zasady dynamiki punktu materialnego

I. Zasada:

Każde ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, dopóki działanie innych ciał nie zmusi go do zmiany tego stanu;

Ciało pozostaje w stanie spoczynku lub stałej prędkości, gdy jest pozostawione samo sobie (działająca na nie siła wypadkowa jest równa zeru);

Inaczej nazywana zasadą bezwładności.

II. Zasada:

Zmiana ruchu jest proporcjonalna do przyłożonej siły i zachodzi w kierunku działającej siły;

Tempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało;

Dla ciał o stałej masie:

a stąd:

Jeżeli na ciało działa stała, niezrównoważona siłą wypadkowa
, to ciało to porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem proporcjonalnym do tej siły a odwrotnie proporcjonalnym do masy - miary bezwładności tego ciała.

III. Zasada:

Działania na siebie dwóch ciał są zawsze równe, lecz przeciwnie skierowane;

Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na drugie ciało;

Te siły oddziaływania między ciałami nazywane są siłami reakcji (albo: siłami oddziaływania).

Uwaga: siły reakcji działają na INNE ciała, więc nie można powiedzieć, że one się równoważą!

4. Siła bezwładności - zasada d'Alamberta

Zasada d^'Alemberta

Równanie ruchu Newtona punktu materialnego i

m_j S_ji S_ij
m_i

P_i

stąd
(a)

jeśli oznaczymy
to (a) ma postać

(36)

B_i siła bezwładności d^'Alemberta

Z przedstawionej zasady d^'Alemberta wynika, że suma sił zewnętrznych i wewnętrznych oraz sił bezwładności danego układu punktów materialnych, jak również suma momentów tych sił względem punktu stałego lub środka masy C równają się zeru. Wynikają stąd następujące dwa równania wektorowe

(37a)

(37b)

ponieważ
i
i uwzględniając ,że równania (37) są równaniami wektorowymi można je zapisać pod postacią równań skalarnych

5. Zasada pędu masy i impulsu siły punktu materialnego

Pęd punktu materialnego

Pęd punktu materialnego jest równy iloczynowi masy m i prędkości v punktu. Pęd jest wielkością wektorową; kierunek i zwrot pędu jest zgodny z kierunkiem i zwrotem prędkości.

W układzie SI jednostka pędu nie ma odrębnej nazwy, a jest określana za pomocą innych jednostek, np. (N·s) lub kilogramometr/sekunda (kg·m/s).

jest to iloczyn który nazywa się impulsem siły. Wywodzi się on ze wzoru:

Przyrost pędu ciała jest równy impulsowi siły działającej na to ciało.

6. Zasada krętu punktu materialnego

Krętem punktu względem osi l nazywamy iloczyn wartości wektora pędu i odległości danego punktu od osi

Wzór:

Krętem bryły względem stałej osi obrotu nazywamy iloczyn masowego momentu bezwładności i brryły względem osi obrotu i prędkości kątowej.

Krętem bryły w ruchu obrotowym jest stały, jeżeli suma momentów sił zewnętrznych względem osi obrotu jest równa zeru wtedy:

gdy

7. Dynamiczne równania ruchu punktu materialnego

Dynamiczne równanie ruchu (różniczkowe równanie ruchu) - równanie różniczkowe, określające szybkość zmian pewnych wielkości fizycznych (np. prędkości, położenia) jako funkcję aktualnego stanu układu. Przez równanie ruchu najczęściej rozumiemy drugą zasadę dynamiki Newtona, zapisaną w postaci równania różniczkowego. W ogólności równanie ruchu dla pojedynczej cząstki można zapisać jako:

gdzie funkcja F jest siłą działającą na ciało w chwili t w punkcie przestrzeni x. Wzór ten redukuje się do prostszej postaci, jeżeli siła dana jest w sposób jawny, np. wynika ze znanego potencjału pola sił.

8. Całkowanie dynamicznych równań ruchu - przykłady

Chyba każdy całkować potrafi. A jak nie to ma pecha!

9. Drgania swobodne i tłumione punktu materialnego

Drgania swobodne (drgania własne) są to drgania ciała wywołane wychyleniem z położenia równowagi trwałej, kiedy na ciało nie działają żadne siły, poza siłami określającymi położenie równowagi i siłami dążącymi do jej przywrócenia. Amplituda drgań zależy od wielkości początkowego wychylenia (energii potencjalnej) lub od prędkości początkowej (energii kinetycznej) nadanej ciału.

Drgania tłumione - to stopniowe zmniejszenie się amplitudy drgań swobodnych wraz z upływem czasu, związane ze stratami energii układu drgającego. Tłumienie obserwowane jest zarówno w układach mechanicznych jak elektrycznych. W przypadku fal biegnących tłumienie prowadzi do zmniejszania się amplitudy fali wraz ze wzrostem odległości od źródła, co wynika z rozpraszania energii w otoczeniu falowodu.

10. Drgania wymuszone punktu materialnego - rezonans mechaniczny

Rezonans mechaniczny to zjawisko polegające na przepływie energii pomiędzy kilkoma (najczęściej dwoma) układami drgającymi. Warunkami koniecznymi do zajścia rezonansu mechanicznego są:

• jednakowa lub zbliżona częstotliwość drgań własnych (lub swobodnych) układów,

• istnienie mechanicznego połączenia między układami.

Przykładem układu, w którym występuje rezonans mechaniczny słabo tłumiony, jest układ wahadeł sprzężonych.

Zjawisko to zachodzi gdy częstotliwość siły wymuszającej zbliża się do częstości drgań własnych. Gdy siła wymuszająca drgania działa na drgające ciało z odpowiednią częstotliwością to amplituda drgań może osiągnąć bardzo dużą wartość nawet przy niewielkiej sile wymuszającej.

Ze zjawiskiem rezonansu spotykamy się jadąc np. autobusem. Przy pewnej prędkości kątowej obrotów silnika, szyby lub niektóre części karoserii zaczynają silnie drgać.

Ruch punktu materialnego po gładkiej równi pochyłej -23

Punkt materialny (masa punktowa) - ciało fizyczne obdarzone masą, ale mające nieskończenie małe rozmiary (będące punktem).

Gładka równia pochyła to taka, że na ciało poruszające się po niej nie dział siła tarcia.

Dwa przypadki:

1. Ruch ciała z góry

2.Ruch ciała pod górę

Ruch wahadła matematycznego - 24

Wahadło matematyczn - Punkt materialny o masie(m) zawieszony na nierozciągliwej i nieważkiej nici w jednorodnym polu grawitacyjnym.

Siłą wprawiająca w ruch wahadło to wypadkowa siły ciężkośći Q=mg i reakcji nici Fn - siła Fz

Wartość wypadkowej siły

Dla małych kątów wychyleń
i

A więc siła wypadkowa przyjmuje postać

Przyrównując Siłę dośrodkową do Fn otrzymujemy wzór na okres Drgań Wahadła.

Takie drgania wahadła matematycznego (bez działania sił zewnętrznych) nazywamy drganiami własnymi wahadła.

Zderzenie proste i ukośne ciał - 25

Zderzenia proste (centralne)

Całkowita energia kinetyczna po zderzeniu jest równa energii kinetycznej ciał przed zderzeniem

Całkowity pęd po zderzeniu jest równy pędowi przed zderzeniem:

Z powyższych równań wynikają prędkości ciał po zderzeniu:

Zderzenia ukośne: (dokończyć)

W zderzeniach niecentralnych przyjmuje się, że zderzające się ciała są w przestrzeni dwuwymiarowej koliste. Założenie, to zapewnia, że w wyniku zderzenia ciała nie są wprawiane w ruch obrotowy.

W takim zderzeniu kulki mogą "odskoczyć" pod pewnymi kątami względem kierunku prędkości kulki uderzającej. Ilustruje to poniższy rysunek.

Zasada zachowania pędu jest spełniona dla każdego kierunku oddzielnie.

Dla składowych poziomych mamy równość:

natomiast dla składowych pionowych obowiązuje równość:

Zasada zachowania energii kinetycznej ma taką samą postać, jak w zderzeniu centralnym.

Dynamiczne równania ruchu układu punktów materialnych - 26 (zrobić )

Najogólniejszy przypadek dynamicznego równania ruchy

Zasada pędu masy i impulsu siły dla układu punktów materialnych - 27

Zasada pędu- pochodna względem czasu wektora ogólnego pędu układu punktów materialnych jest równa wektorowi głównemu sił zewnętrznych działających na dany układ.

Zasada zachowania pędu układu punktów materialnych.

Gdy wektor głowny sił zewnętrznych =0

Pęd układu będzie wektorem stałym

Wniosek: Jeżeli część układu punktów materialnych zmienia w pewnej chwil swój pęd pod wpływem tylko sił wewnętrznych wówczas pęd pozostałej części układu ulega odpowiedniej zmianie, zgodnie z warunkami
, gdyż

Zasade pędu i impulsu siły:

Przyrost wektora pędu ukłądu punktów materialnych w określonym przedziale czasu jest równy sumie impulsów sił zewnętrznych, działających na ten ukłąd.

Kręt układu punktów materialnych - 28

Kręt ogólny układu punktów materialnych względem przyjętego bieguna nazywamy sumę wektorów krętów poszczególnych punktów materialnych.

Kręt poszczególnego punktu materialnego:

W przypadku gdy suma momentów sił zewnętrznych działają na ukłąd jest równy zero

Kręt ogólny jest wektorem stałym:

Natomiast
=const

Jest to zasada zachowania krętu ukłądu punktów materialnych. Warto podkreślić, że ani siły wewnętrzne, ani momenty nie mogą zmienić krętu ogólnego układu.

Ruch układu o zmiennej masie - 29

Siła reakcji cząstki oddzielającej się:

W przypadku, gdy równocześnie oddziela sięlub przyczepia więcej mas dm j równanie

Na siłę reakcji cząsteczek oddzielających się przyjmuje postać:

Zaś:

- wektor prędkości względnej odzielających się lub dołączającej się masy dmj

Uogólnione równanie ruchu i prawo zachowania pędu

Cząstka P o masie m i prędkości v w układzie Inercjalnym.

Do cząstki przyłącza się druga cząstka o Znikomo małej masie dm i prędkości w. Zmiana pędu układu w czasie dt:

Równanie ruchu:

Aby rozwiązać problem takiego ruchu musimy dodatkowo podać zależność masy od czasu m(t) oraz prędkości u od czasu u(t).

Na ogół, technika rozwiązywania r.r ciała o zmiennej masie polega na zastąpieniu różniczkowania po czasie przez różniczkowanie po masie:

Definicja i równania pracy mechanicznej siły stałej 30

Praca - skalarna wielkość fizyczna, miara ilości energii przekazywanej między układami fizycznymi w procesach mechanicznych, elektrycznych, termodynamicznych i innych

Praca jest iloczynem skalarnym działającej siły i wektora przesunięcia stycznego cały czas to toru ruchu (krzywej po jakiej porusza się ciało).

F=const;

= F * r * cosα

Jednostką pracy w układzie SI jest dżul [N*m]=[J]

Praca mechaniczna siły zmiennej 31

W przypadku gdy wektor siły nie jest stały lub przemieszczenie nie jest prostoliniowe to praca jest sumą prac wykonanych na niewielkich odcinkach, na których uznaje się że spełnione są powyższe warunki, co wyrażone w postaci całki przedstawia się następująco:

Całkowanie odbywa się po drodze L jaką przebywa punkt zaczepienia siły.

Gdzie:

W - praca,

F - siła,

S - przesunięcie

α - kąt między wektorem siły i przesunięcia

Jednostką pracy w układzie SI jest dżul [N*m]=[J]

Praca mechaniczna na torze kołowym. 32

W przypadku gdy wektor przemieszczenia nie jest prostoliniowy (jest np. kołowy) wzór na prace definiujemy następująco:

Całka ta jest tzw. całką krzywoliniową. Całość symbolizuje pracę wykonaną po dowolnej krzywej od punktu 1 do punktu 2.

Gdzie:

W - praca,

F - siła,

S - przesunięcie

Praca mechaniczna siły sprężystościn 33

Praca siły sprężystości.

Rozpatrzmy sprężynę AD, której koniec A jest zamocowany nieruchomo (rys.24.6).Przy rozciąganiu sprężyny powstaje w niej siła sprężystości, a na ciało wywołujące rozciąganie działa siła reakcji sprężyny P . Wartość tej siły jest równa

P = kAB

gdzie k jest stałą sprężystości sprężyny. Rzuty siły P na osie Ox, Oy, Oz są równe:

Px=-kx Py=0 Pz=0

A zatem praca elementarna wynosi:

Praca siły sprężystości na przesunięciu AC = h jest równa

Na (rys.24.6) pokazano wykres zmiany siły Px w zależności od przemieszczenia końca sprężyny x.

34 Praca mechaniczna siły ciężkości

• Moc i sprawność układu

Def. P=


=

Moc w ruchu obrotowym

Moc obrotowa

Sprawnością mechaniczna nazywamy stosunek pracy lub mocy uzytej do pracy lub mocy włożonej η=
=

• Zasada pracy i energii kinetycznej

Energia kinetyczna poruszającego się puntku materialnego rosnie lub maleje o wielkość pracy wykonanje przez sily działające na ten punkt

• Praca w polu sił

W polu potencjalnym praca calkowita jest rowna roznicy potencjałów w położeniu początkowym i końcowym.

Praca w potencjalnym polu sil nie zalezy od kształtu toru

Pole jednorodne to takie pole w którym pole sil sa wzajemnie równoległe

• Potencjalne pole sił

Funkcje pola sil nazywamy funkcje polozenia
, których rozniczka zuplena jest rowna pracy elementarnej sily pola

Pole sil można okreslic poprzez podanie wektora funkcja położenia

Pole w którym praca zelzy od kształtu toru nazywamy polami niepotencjalnymi lub wirowymi

39 Zasada zachowania energii mechanicznej

U=mgh nazywamy tak energie potencjalna jest to praca wykonana przez pole sil ciężkości przy przemieszczeniu masy m z wysokości h na powierzchnie ziemi.

Ponieważ
zatem mamy
stad wynika

+ rozniczkowa postac zasady zachowania energi mechanicznej
E+U=const
W polu potencjnym suma energi kinetycznej i potencjalnej w każdym położeniu jest wielkością stala dla poruszającego się punkty materialnego

40. Rownowaga układu

Wyroznia się 3 rodzaje równowagi
A- rownowaga stala
B- rownowaga chwiejna
C- rownowaga obojetna

• Dynamiczne równania ruchu postępowego ciała sztywnego
  

Aby ciało sztywne mogło się poruszać ruchem postępowym, suma geometryczna momentów względem środka masy sił zewnętrznych działających na to ciał musi być równa zeru.

Dynamiczne równania ruchu postępowego ciała sztywnego przyjmują postać:








gdzie :

M - masa ciala

• Twierdzenie o pochodnej krętu bryły materialnej
  

Kręt układu punktów materialnych względem dowolnego punktu 0 (bieguna), jest to wektor

równy sumie geometrycznej krętów wszystkich punktów materialnych układu względem

bieguna.

Wartości rzutów wektora krętu K₀ na osie xyz maja postać:


;
;

w związku z tym pochodna krętu ma postać:

Pochodna względem czasu krętu punktów materialnych względem dowolnego punktu 0 równa jest sumie geometrycznej momentów sił zewnętrznych, jeżeli punktem 0 jest punkt nieruchomy lub środek masy układu C.

• Charakterystyka ruchu płaskiego bryły materialnej

Ruchem płaskim nazywamy ruch, podczas którego wszystkie punkty ciała poruszają sie w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzna kierującą.

Punkty ciała leżące na prostej prostopadłej do płaszczyzny kierującej poruszają sie po takich samych torach, maja jednakowe prędkości i przyspieszenia. Zatem dla badania ruchu płaskiego wystarczy wziąć pod uwagę dowolny przekrój ciała płaszczyzna równoległa do kierującej.

Ruch płaski jest superpozycja (złożeniem) ruchów: postępowego dowolnie wybranego punktu ciała (bieguna) i obrotowego wokół tego wybranego punktu. Ruch płaski można też traktować jako ruch obrotowy, wokół pewnego punktu, tzw. środka obrotu. Środek obrotu zmienia swoje położenie podczas ruchu.

Prędkość bryły

Prędkość ciała w ruchu płaskim jest określona, jeżeli znamy prędkość bieguna oraz prędkość kątowa bryły w .

Prędkość bieguna obliczamy różniczkując współrzędne bieguna z równania względem czasu:

natomiast prędkość kątową obliczamy różniczkując kat obrotu ciała z równania
względem czasu i otrzymamy:

---