WMS	Imię i nazwisko: Bożena Skrzypek Tomasz Sumara			Zespół: 3	Grupa: Środa 14.45	Rok III
Nr ćwiczenia: 32	Temat: Mostek Wheatstone'a
Data wykonania: 02.11.09	Data oddania: 09.12.09	Zwrot do poprawy:	Data oddania:		Data zaliczenia:	Ocena:

1. CEL ĆWICZENIA:

Praktyczne zastosowanie praw Kirchhoffa i sprawdzenie zależności określających opór zastępczy dla połączeń szeregowych, równoległych oraz mieszanych.

2. WPROWADZENIE:

Pierwsze prawo Kirchoffa:

Algebraiczna suma naprężeń prądów przepływających przez punkt rozgałęzienia (węzeł) jest równa zeru.

Drugie prawo Kirchoffa:

Algebraiczna suma sił elektromotorycznych i przyrostów napięć w dowolnym obwodzie zamkniętym jest równa 0.

Mostek Wheatstone'a jest układem do pomiaru oporów. Tworzy go połączenie czterech oporów: R_x, R₂, R₃,R₄ oraz galwanometru o oporze R₅. Mostek jest zasilany z ogniwa galwanicznego lub zasilacza.

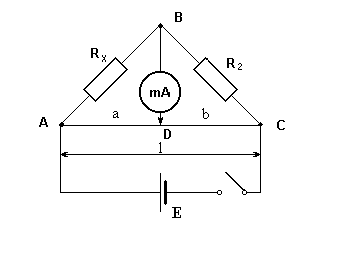
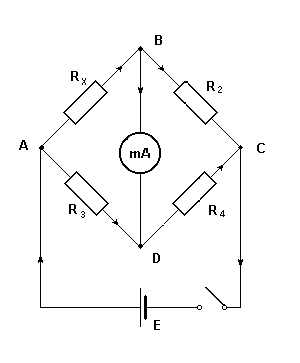
rys.1 Oporowy mostek Wheatstone`a rys.2 układ używany w ćwiczeniu

Oznaczmy natężenia prądu: I- płynącego z ogniwa, a w odcinkach obwodu AB, BC, AD, DC, i BGD odpowiednio: I₁, I₂, I₃, I₄, I₅. Dla 3 węzłów znajdujących się w układzie (spośród A, B, C, D) ułóżmy równania Kirchoffa. Jeśli kierunek prądu jest taki, jak wskazują strzałki, dla węzłów A, B i D otrzymujemy:

A: I - I₁ - I₃ = 0
B: I₁ - I₂ -I₅ = 0 (1)
D: I₅ +I₃ -I₄ = 0

Drugi układ równań Kirchoffa można ułożyć wydzielając w schemacie zamknięte obwody ABDA, BCDB i ACEA. Obchodząc każdy z tych obwodów według kierunku wskazówek zegara otrzymujemy dla obwodu:

ABDA: I₁R_x + I₅R₅ - I₃R₃ = 0
BCDB: I₂R₂ - I₄R₄ - I₅R₅ = 0 (2)
ACEA: I₃R₃ + I₄R₄ + IR_E =

Jeśli dana jest siła elektromotoryczna
oraz opory R₂, R₃,R₄ i R_E, można znaleźć natężenia wszystkich sześciu prądów I, I₁, I₂, I₃, I₄, I₅.

Metoda Wheatstone'a porównywania oporów polega na tzw. równoważeniu mostka, to znaczy na takim dopasowaniu oporów, by potencjały w punktach B i D były równe (V_B = V_D), czyli żeby prąd płynący przez galwanometr G był równy zeru. Przy I₅ = 0 drugie i trzecie równanie układu (1) dają:

I₂ = I₁ I₃ = I₄ (3)

a pierwsze i drugie równanie układu (2)

I₁R_x = I₃R₃ I₂R₂ ­= I₄R₄. (4)

Z równań (3) i (4) wynika, że

Ostatnie wyrażenie pozwala eksperymentalnie wyznaczyć R_x.

Mostek Wheatstone'a używany w ćwiczeniu przedstawiono na rysunku 2

Prąd płynący z ogniwa galwanicznego E rozgałęzia się w punkcie A. Jedna jego część płynie przez szeregowo połączone opory R_x i R₂, druga przez przewód AC. Przez zmiany położenia punktu D zmienia się stosunek oporów R₃ do R₄. Na odcinku BGD prąd nie będzie płynął, jeżeli

Ponieważ R_AD i R_DC są oporami odcinków tego samego jednorodnego drutu, ich wielkości są proporcjonalne do długości:

Ponadto b jest różnicą całkowitej długości drutu l i odległości a, b=l-a. Ostatecznie otrzymujemy:

Dokładność pomiaru mostkiem Wheatstone'a z drutem oporowym zależy przede wszystkim od błędu wyznaczenia odległości a. Zgodnie z prawem przenoszenia błędu:

(5)

Tak więc błąd pomiaru będzie najmniejszy gdy pochodna wyrażenia (5) będzie równa 0:

Rozwiązanie a=1/2 l odpowiada minimalnej wartości błędu, w związku z tym aby pomiar był najdokładniejszy, należy tak dobrać opór R₂, aby stan równowagi mostka można było uzyskać w przybliżeniu w połowie długości drutu oporowego.

3. UKŁAD POMIAROWY:

Mostek (jak na rys. 2 we wprowadzeniu) z drutem oporowym rozpiętym między punktami A i C o danej długości, opornikiem wzorcowym R₂ i Rx, którego opór będzie wyznaczany.

4. OPIS ĆWICZENIA:

1. Zapoznanie się ze schematem mostka Wheatstone'a używanym w ćwiczeniu i podłączenie według niego obwodu.

2. Pomiary oporów R_x1, R_x3, R_x5.

3. Pomiary oporu dla połączenia szeregowego R_x3 i R_x5.

4. Pomiary oporu dla połączenia równoległego R_x3 i R_x5.

5. Pomiary oporu dla połączenia szeregowego R_x1 z połączonymi równolegle R_x3 i R_x5.

5. WYNIKI POMIARÓW:

						Długość drutu l: 100 [cm]
Opór wzorcowy [Ω]	20	19	18	17	16	15	14	13	12	11
a [cm]	38,8	40	41,3	42,8	44,1	45,8	47,3	49,2	51,1	53,3
Rx1 [Ω]	12,68	12,67	12,66	12,72	12,62	12,68	12,57	12,59	12,54	12,55
12,630 [Ω]			0,020 [Ω]
Opór wzorcowy [Ω]	50	51	52	53	54	55	56	57	58	59
a [cm]	53	52,5	52,1	51,4	51	50,5	50,1	49,8	49,2	48,9
Rx3 [Ω]	56,38	56,37	56,56	56,05	56,20	56,11	56,22	56,55	56,17	56,46
56,308 [Ω]			0,057 [Ω]

Opór wzorcowy [Ω]	60	70	80	90	100	110	120	130	140	150
a [cm]	66	62,6	59,4	56,6	54	51,6	49,5	47,5	45,9	44,1
Rx5 [Ω]	116,47	117,17	117,04	117,37	117,39	117,27	117,62	117,62	118,78	118,34
117,51 [Ω]			0,21 [Ω]

Połączenie szeregowe: R₃, R₅

Opór wzorcowy [Ω]	230	220	210	200	190		180	170	160	150	140
a [cm]	43,7	44,8	45,9	47,1	48,2		49,7	51,1	52,5	54	55,9
R [Ω]	178,53	178,55	178,17	178,07	176,80		177,85	177,65	176,84	176,09	177,46
177,60 [Ω]		0,26 [Ω]				173,82 [Ω]			0,22 [Ω]

Połączenie równoległe: R₃, R₅

Opór wzorcowy [Ω]	30	32	34	36	38		40	42	44	46	48
a [cm]	55,7	54	52,6	51,1	49,9		48,6	47,3	46,3	45,1	44
R [Ω]	37,72	37,57	37,73	37,62	37,85		37,82	37,70	37,94	37,79	37,71
37,74[Ω]		0,035 [Ω]				38,067[Ω]			0,034 [Ω]

Połączenie mieszane: R₁ szeregowo z równolegle połączonymi R₃, R₅

Opór wzorcowy [Ω]	40	42	44	46	48		50	52	54	56	58
a [cm]	55,9	54,7	53,5	52,4	50,8		50,3	49,3	48,4	47,5	46,6
R [Ω]	50,70	50,72	50,62	50,64	49,56		50,60	50,56	50,65	50,67	50,61
50,94 [Ω]		0,11 [Ω]				50,697[Ω]			0,040 [Ω]

6. OPRACOWANIE WYNIKÓW POMIARÓW:

Wartości oporów R_x1, R_x2, R_x3 obliczyliśmy na podstawie wzoru:

, gdzie:

R_x - szukany opór

R - zadawany opór

a - odległość od początku drutu oporowego

l=100[cm] - długość drutu oporowego

Przykładowe obliczenie szukanego oporu R_x1 w pierwszej próbie:

=12,68[
]

Wartość średnią oporu
obliczyliśmy zgodnie ze wzorem:

, gdzie R_xi jest oporem uzyskanym w i-tej próbie

Wyniki obliczeń zamieściliśmy w tabelach.

Analogiczne obliczenia wykonaliśmy dla połączenia szeregowego, równoległego

i mieszanego.

Niepewności:

Dla wartości średniej wyznaczonego oporu:

u(

u(
)=0,01965
0,020[
]

u(
)=0,05692
0,057[
]

u(
)=
0,21[
]

Przy obliczaniu niepewności oporów zastępczych będziemy korzystać z prawa przenoszenia niepewności:

Połączenie szeregowe R_x3, R_x5

Wartość oporu zastępczego obliczyliśmy ze wzoru:

R= R_x3 + R_x5

R=56,308 +117,51=173,82(22)[
]

Niepewność dla oporu zastępczego w tym przypadku:

u(R)=

u(R)=

Połączenie równoległe R_x3, R_x5

Wartość oporu zastępczego:

<=> R=

R=

Niepewność (z prawa przenoszenia niepewności):

u(R)=

u(R)=
=0,034 [

Połączenie mieszane (szeregowo R_x1 z połączonymi równolegle R_x3, R_x5)

Niech R_x3x5=

Wtedy opór zastępczy dla tego obwodu obliczymy ze wzoru:

R=R_x1+R_x3x5

R=12,63+38,0667=50,697(040)

Niepewność (z prawa przenoszenia niepewności):

u(R)=

u(R)=

Porównanie wyników:

Połączenie szeregowe R_x3, R_x5

=0,34

Połączenie równoległe R_x3, R_x5

Połączenie mieszane (szeregowo R_x1 z połączonymi równolegle R_x3, R_x5)

6. WNIOSKI
   

Metoda pomiarowa sprawdza się w praktyce, o czym świadczą małe niepewności standardowe pomiarów oporów
,
i
.

Opór zastępczy połączenia mieszanego wyznaczony metodą pomiaru bezpośredniego jest niemal identyczny z oporem wyznaczonym za pomocą pomiaru pośredniego i mieści się w granicach rozszerzonej niepewności pomiarowej.

Niestety opory zastępcze połączeń szeregowego i równoległych wyznaczone metodami pomiaru bezpośredniego i pośredniego odbiegają od siebie i nie mieszczą się w granicach niepewności pomiarowych, na co wpływ ma niedokładność przy przeprowadzaniu doświadczenia.

Strona 3 z 7

---