Mechanika techniczna

Zagadnienia do ZALICZENIA dla sem. III - kurs inżynierski

1. Co to jest wektor, a co skalar? Podać przykłady wielkości wektorowych i skalarnych.

Skalar jest to wielkość dla określenia, której wystarczy podać jej wielkości liczbowe np. praca, czas, energia, ciśnienie.

Wektor jest to wielkość dla określenia, której oprócz wartości podać należy kierunek działania, zwrot i punkt zaczepienia np. siła, przyspieszenie, prędkość itp.

2. Podać cechy określające wektor.

Wartość wektora przedstawiona jest długością odcinka AB, którą można określić jedną nieujemną liczbą. Jest to wartość skalarowa.

Kierunek wektora określamy przez podanie kąta, który tworzy linia jego działania z pionem lub poziomem lub też z osiami układu współrzędnych.

Zwrot oznaczony strzałką mówi nam czy jest on zgodny z przyjętą dodatnią linią działania. Wtedy wielkość charakteryzowana przez wektor jest dodatnia, lub ujemna, jeśli zwrot jest z tą linią niezgodny.

Punkt zaczepienia stanowi początek wektora.

3. 
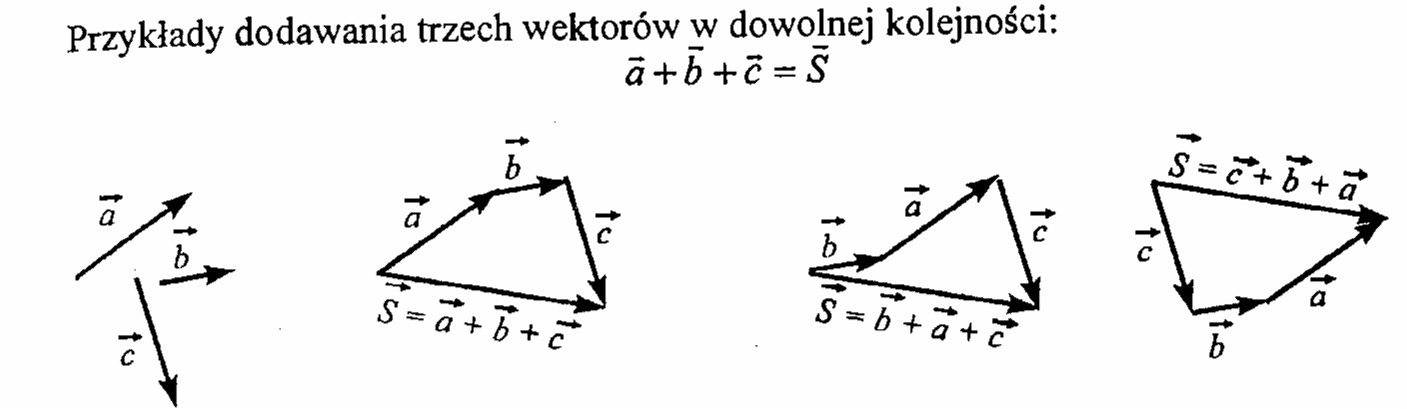
   Na czym polega zasada przemienności wektorów? Wykazać to na prostym przykładzie.

Kolejność dodawania wektorów jest dowolna.

4. Omówić zasadę równoległoboku i podać przykład.

Jeżeli mamy zaczepione w punkcie A dwie siły F₁ i F₂ o kącie między nimi α to prowadząc z końca siły F₂ (punkt D) równoległą do siły F₁, a także z końca siły F₁ (punkt B) równoległą do siły F₂ otrzymamy punkt przecięcia tychże równoległych będący czwartym wierzchołkiem równoległoboku (punkt C)

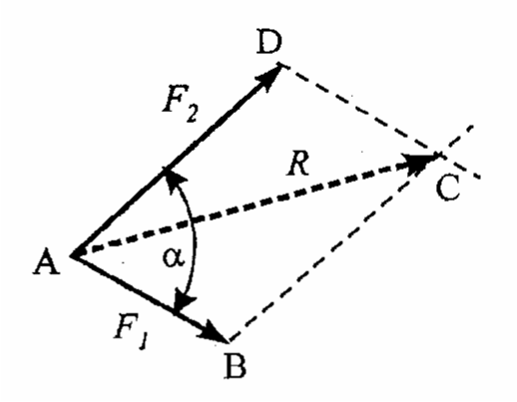
Zasada równoległoboku mówi, że łączne działanie sił F₁ i F₂ może być zastąpione przez siłę R będącą przekątną równoległoboku zbudowanego na wektorach tych sił.

Wartość tej przekątnej określa wzór:

R=√F₁² + F₂² + 2F₁F₂ cosα

5. Wymienić podstawowe typy więzów.

Przegub walcowy, podpora przegubowa stała, podpora przegubowa przesuwna, zawieszenie na cięgnach wiotkich, oparcie o gładką i chropowata powierzchnię, utwierdzenie całkowite.

6. Co to jest moment główny układu sił?

Moment główny układu sił na płaszczyźnie względem punktu O jest algebraiczną sumą momentów sił składowych układu względem tego samego bieguna (punkt O).

M_O = M_O1 + M_O2 +M_O3 + … +M_ON

7. Co to jest para sił? Narysować przykład i podać jej moment.

Para sił to dwie siły równoległe, równej wartości o przeciwnych zwrotach. Odległość r między siłami nazywany ramieniem pary sił.

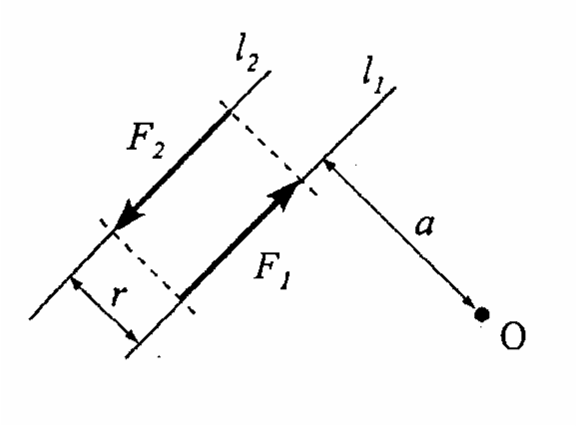
M_O = M₁ + M₂

M₁ = -F₁ ∙ a ; M₂ + F₂ (a + r)

F₁ = F₂

M_O = - F ∙ a + F ∙ a + F ∙ r = F ∙ r

8. Właściwości pary sił.

Parę sił można zastąpić jej momentem, którego wartość jest równa M = F ∙ r

Parę sił można przenieść w dowolne inne miejsce na tej samej płaszczyźnie.

Parę sił można przenieść z jednej płaszczyzny do drugiej płaszczyzny równoległej.

Działanie pary sił nie zmieni się, jeżeli dowolnie zmienimy jej składniki (siłę lub ramię), ale tak, aby wartość momentu pozostała stała.

Skutkiem działania pary sił jest wektor o określonej wartości i zwrocie. Jeżeli do układu przyłożymy inna parę sił o identycznej wartości momentu, ale przeciwnym zwrocie to układ zostanie zrównoważony.

9. Składanie i równowaga par sił.

Składanie polega na arytmetycznym dodawaniu momentów przy uwzględnieniu ich znaków, Wynikiem jest moment pary wypadkowej. Moment ten jest prostopadły do płaszczyzny, na której działają pary sił.

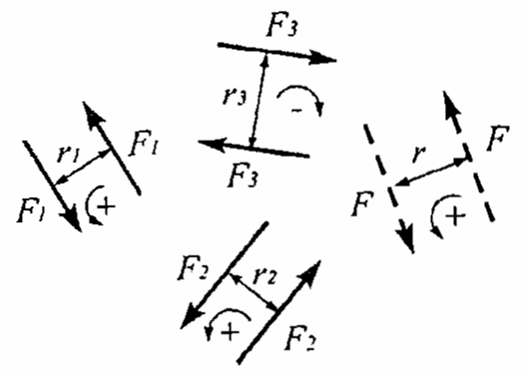
M_W = M₁ + M₂ - M₃ = F₁ ∙ r₁ + F₂ ∙ r₂ - F₃ ∙ r₃

M_W = F ∙ r

Moment pary wypadkowej równa się zero - warunek równowagi par sił.

M₁ + M₂ + M₃ + … + M_n = 0 lub ∑M_i = 0

10. 
    
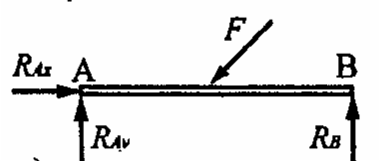
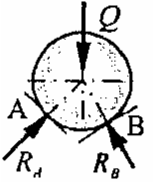
    Belka obciążona siłą ukośną P oparta jest w pkt. A na podporze przegubowej stałej i w pkt. B na podporze przegubowej przesuwnej. Narysować reakcje po usunięciu więzów.

11. 
    
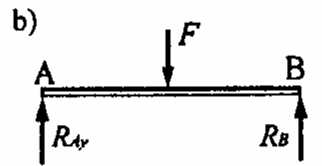
    Belka obciążona siła pionową P oparta jest w pkt. A na podporze przegubowej stałej i w pkt. B na podporze przegubowej przesuwnej. Narysować reakcje po usunięciu więzów.

12. Ciężar G zawieszony jest na dwóch linach jak na rysunku. Narysować reakcje po usunięciu więzów.

13. 
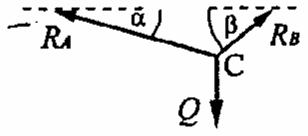
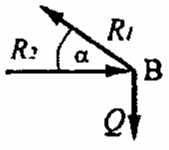
    Ciężar G zawieszony jest na wysięgniku w pkt. A. Narysować reakcje po usunięciu więzów.
    

14. 
    
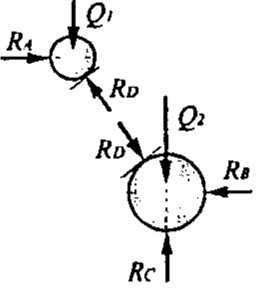
    Dwie kule o ciężarach Q₁ i Q₂ znajdują się w okrągłym pojemniku (rysunek). Narysować reakcje w punktach podparcia.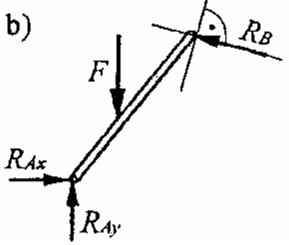

15. 
    Belka obciążona siłą F jest zamocowana przegubowo w punkcie A
    i oparta o gładką ścianę w punkcie B jak na rysunku. Narysować reakcje po uwolnieniu z więzów.

16. 
    
    Beczka o kształcie walca i ciężarze Q opiera się o krawędź w punkcie A oraz o płaską ścianę w punkcie B. Narysować reakcje po uwolnieniu z więzów.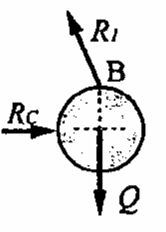

17. 
    
    Na linie AB zawieszono dużą kulę o ciężarze Q. Kula opiera się o ścianę w punkcie C (rysunek). Wyznaczyć reakcje po uwolnieniu z więzów.

18. 
    Znaleźć graficznie/analitycznie sumę wektorów sił F₁ = 200N, F₂ = 400N, F₃ = 300N (wartości sił podano przykładowo).

19. 
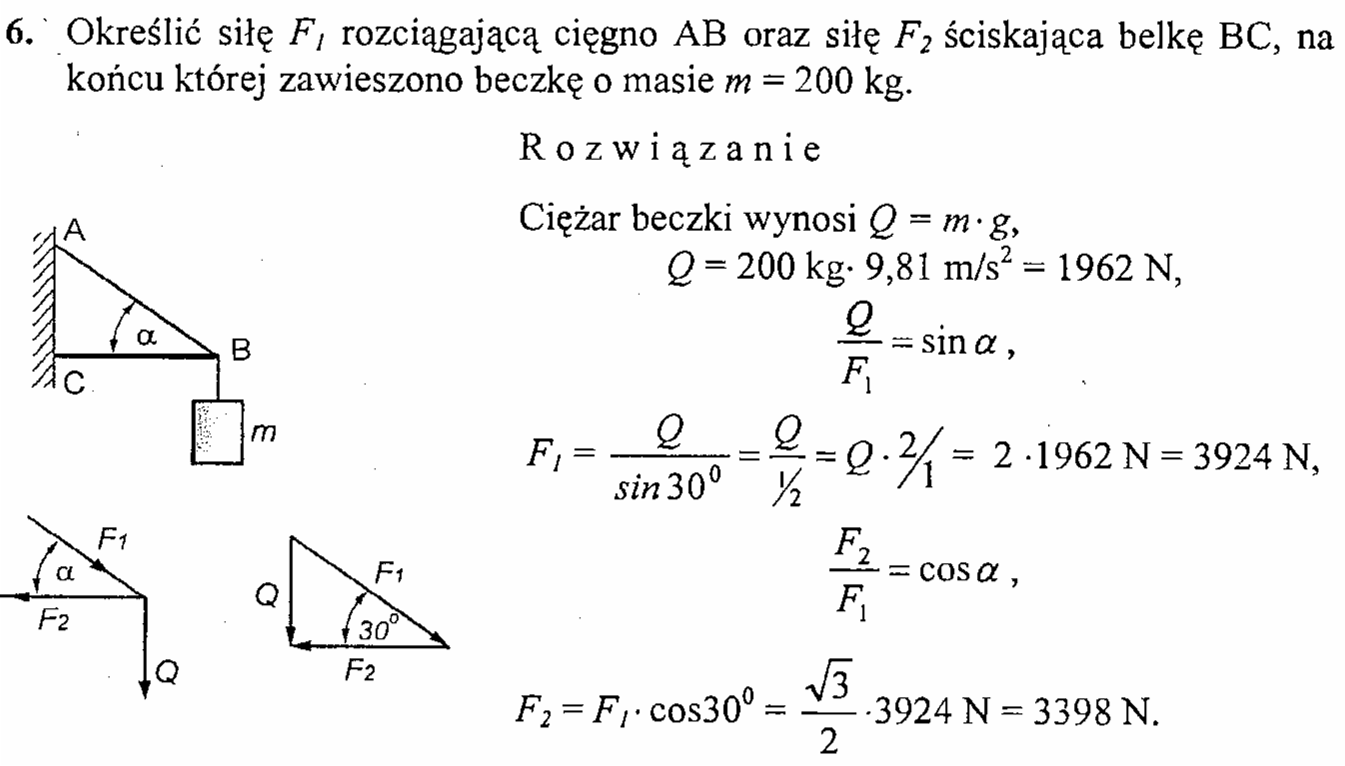
    Określić siłę F_S1 rozciągającą cięgno BC oraz siłę F_S2 ściskającą belkę AB, na końcu której zawieszono masę m = 200 kg (wartość przykładowa).

20. 
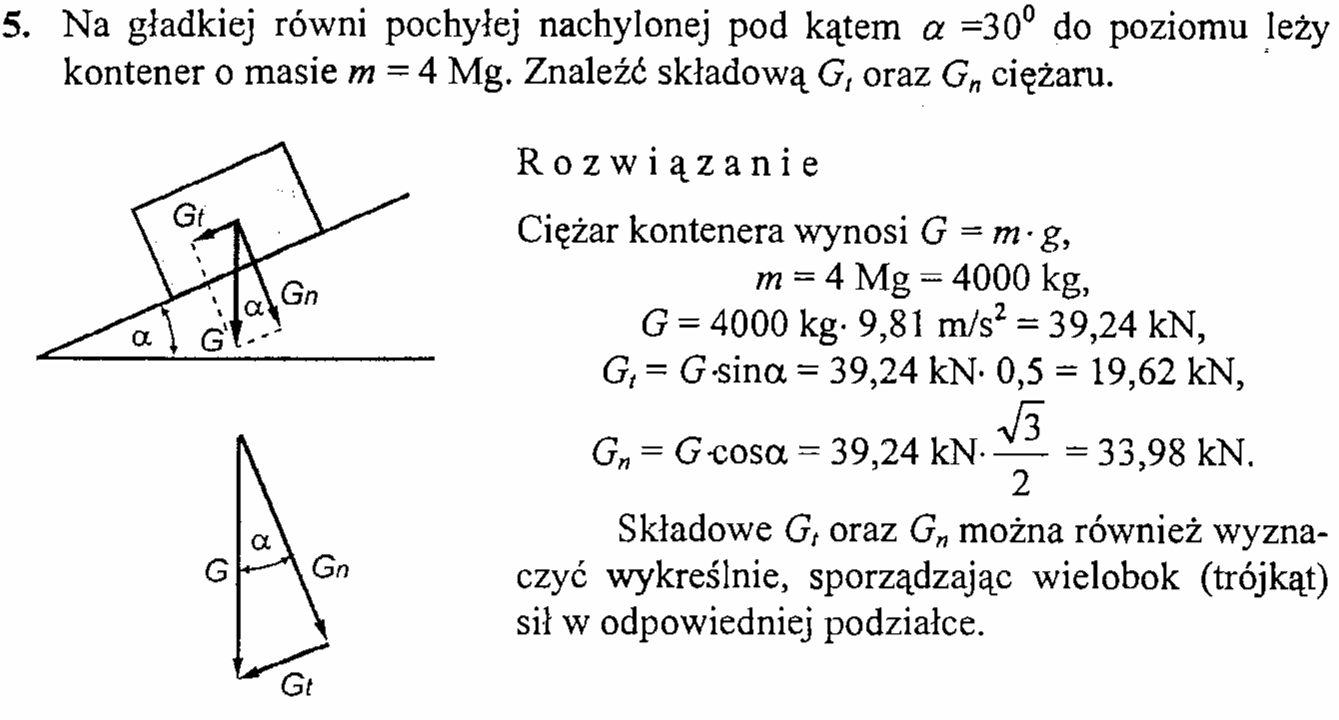
    Na gładkiej równi pochyłej, nachylonej do poziomu pod kątem α (np. 30^o) leży ciało o masie m (np. 4 Mg). Wyznaczyć wartość składowej G_n (prostopadłej do równi) oraz składowej G_t (równoległej do równi).

21. 
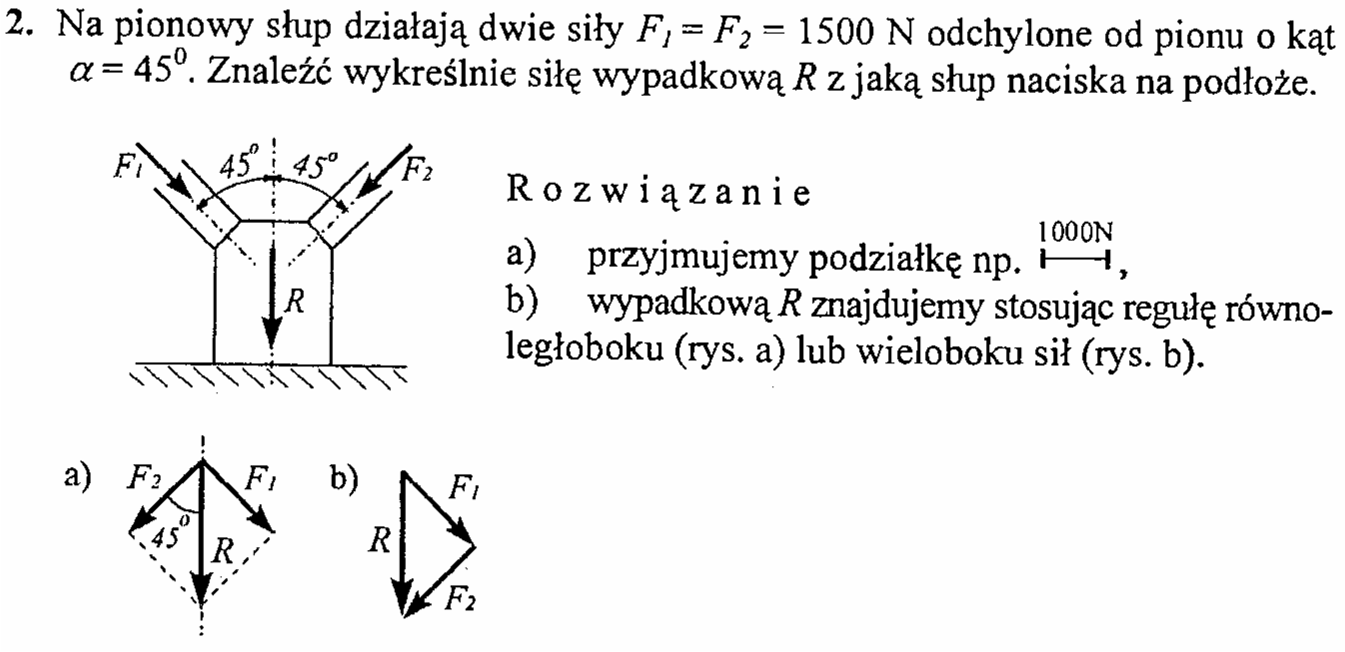
    Wyznaczyć graficznie/analitycznie reakcję R nacisku słupa na podłoże, jeżeli siły F₁ = F₂ = 100N są odchylone o 45^o od pionu (wartości sił podano przykładowo).

22. 
    Obliczyć całkowity nacisk koła pasowego na wał. Masa koła m = 450 kg. Pas tworzy z poziomem kąt 30^o, a jego naciąg Q = 26 kN (wartości przykładowe).

23. 
    
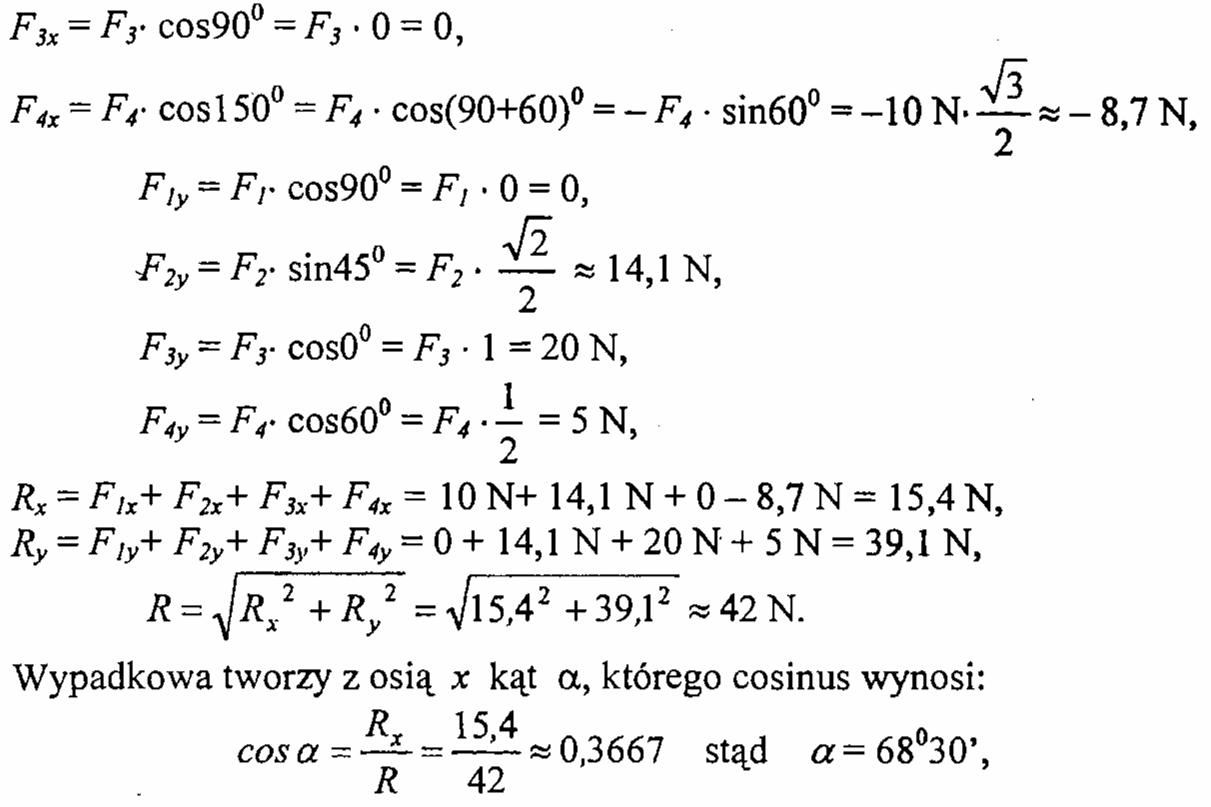
    Dla układu trzech sił zbieżnych F₁ = 10N, F₂ = 50N, F₃ = 20N (rysunek) wyznaczyć analitycznie wypadkową i jej kierunek na płaszczyźnie (wartości sił podano przykładowo).

24. 
    Na belkę o długości l (np. 8 m) działają równolegle siły F₁ = 2000N, F₂ = 2000N, F₃ = 3000N, F₄ = 4000N, F₅ = 1000N (wartości i zwroty sił są przykładowe). Wyznaczyć wartość momentu głównego względem punktu B i C.

a = 8 / 4 = 2

M_B = - F₁ ∙ a + F₃ ∙ a - F₄ ∙ (a + a) - F₅ ∙ (a + a + a)

M_C = - F₁ ∙ (a + a + a) + F₂ ∙ (a + a) + F₃ ∙ a - F₅ ∙ a

25. Belka jest obciążona parą sił F = 2000N, a ramię tej pary r = 1 m. Obliczyć reakcje R_A i R_B i wyznaczyć ich zwroty w punktach podparcia oddalonych od siebie o 2 m (podane wartości są przykładowe).

26. Dane są trzy pary sił na płaszczyźnie. Znaleźć parę wypadkową, jeżeli np.:

F1 = 200N; r1 = 0,6 m F2 = 300N; r2 = 0,6 m F3 = 150N; r1 = 0,9 m

M₁ = F₁ ∙ r₁

M₂ = F₂∙ r₂

M₃ = F₃ ∙ r₃

M_W = M₁ + M₂ + M₃

Przyjmujemy dowolne ramię pary wypadkowej np. r = 0,6 m i obliczamy F = M_W / r

Jeżeli moment pary wypadkowej jest dodatni, to zwrot sił F tworzących tę parę musi obracać w przeciwną stronę do ruchu wskazówek zegara. Jeżeli ujemny to zgodnie z ruchem.

27. 
    Obliczyć moment główny sił F₁ = 10N, F₂ = 30N, F₃ = 20
    N, F₄ = 5N zaczepionych w pkt. B względem pkt. A, w którym ciało jest podparte przegubowo (wartości przykładowe).

M_A = M₁ + M₂ + M₃ + M₄

M₁ = F₁ ∙ 2m

M₂ = F₂ ∙ 1m

M₃= -F₃ ∙ √2² + 1²

M₄ = F₄ ∙ 0

28. 
    Dla układu trzech sił równoległych F₁ = 20N, F₂ = 10N, F₃ = 20N (rysunek) wyznaczyć wypadkową i jej linię działania (wartości przykładowe)..

Wg mnie brakuje punktu odniesienia.

31. 
    Dla układu 4 sił zbieżnych F₁ = 10 N, F₂ = 20 N, F₃ = 20 N oraz F₄ = 10 N rozmieszczonych jak na rysunku wyznaczyć graficznie/analitycznie wartość wypadkowej R oraz jej kierunek na płaszczyźnie (wartości przykładowe).

Rozwiązanie analityczne patrz zadanie nr 23.

Rozwiązanie graficzne patrz zadanie nr 18.

Jeśli w treści zadania metoda rozwiązania określona jest graficznie/analitycznie tzn., że metoda rozwiązania zależy od zestawu zadań, który przypadnie Państwu na zaliczeniu.

Zadania wraz z rozwiązaniami znajdują się w skrypcie:

D. Ciesielska, J. Manuszak - Podstawy mechaniki technicznej i wytrzymałości materiałów

8































---